Площадь | это… Что такое Площадь?
У этого термина существуют и другие значения, см. Площадь (значения).
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры[1], неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.
Общий метод вычисления площади геометрических фигур предоставило интегральное исчисление. Обобщением понятия площади стала теория меры множества, пригодная для более широкого класса геометрических объектов.
Для приближенного вычисления площади на практике используют палетку или специальный измерительный прибор — планиметр.
Содержание
|
Свойства
- Площадь единичного квадрата равна 1.
- Площадь аддитивна.
- Площадь неотрицательна.
- Площади конгруэнтных фигур равны.
Для фигур на плоскости, не состоящих из целого количества единичных квадратов, а также для искривлённых трёхмерных поверхностей, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими [2].
Общий метод определения площади
Площадь плоской фигуры
Декартовы координаты
Определённый интеграл как площадь фигуры
Площадь между графиками двух функций равна разности интегралов от этих функций в одинаковых пределах интегрирования
Площадь, заключённая между графиком непрерывной функции на интервале и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:
Площадь, заключённая между графиками двух непрерывных функций на интервале находится как разность определённых интегралов от этих функций:
Полярные координаты
В полярных координатах: площадь, ограниченная графиком функции и лучами вычисляется по формуле:
- .
Площадь поверхности
Основная статья: Площадь поверхности
Площадь искривлённой поверхности A, заданной вектор-функцией , даётся двойным интегралом:
То же в координатах:
Здесь .
Единицы измерения площади
Метрические единицы
- Квадратный километр, 1 км² = 1 000 000 м²
- Гектар, 1 га = 10 000 м²
- Ар (сотка), 1 а = 100 м²
- Квадратный метр, производная единица системы СИ 1 м² = 1 са (сантиар)
- Квадратный дециметр, 100 дм² = 1 м²;
- Квадратный сантиметр, 10 000 см² = 1 м²;
- Квадратный миллиметр, 1 000 000 мм² = 1 м².
Русские устаревшие
- Квадратная верста = 1,13806 км²
- Десятина = 10925,4 м²
- Копна = 0,1 десятины — сенные покосы меряли копнами
- Квадратная сажень = 4,55224 м²
Мерами земли при налоговых расчетах были выть, соха, обжа
, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли:коробья, веревка, жеребья и др.Античные
- Арура
Формулы вычисления площадей простейших фигур
Планиметрические фигуры
| Фигура | Формула | Переменные |
|---|---|---|
| Квадрат | — длина стороны квадрата. | |
| Правильный треугольник | — длина стороны треугольника. | |
| Правильный шестиугольник | — длина стороны шестиугольника. | |
| Правильный восьмиугольник | — длина стороны восьмиугольника. | |
| Правильный многоугольник | — периметр, а — количество сторон. | |
| Прямоугольный треугольник | и — катеты треугольника. | |
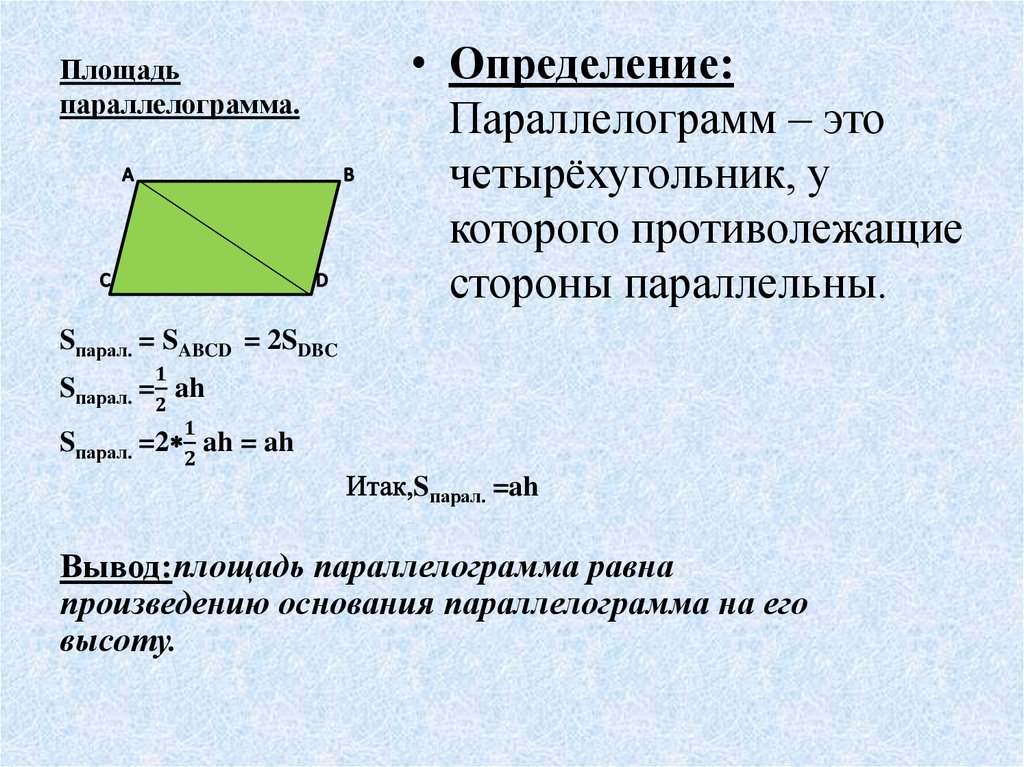
| Произвольный треугольник | — сторона треугольника, — высота, проведенная к этой стороне. | |
| , — любые две стороны, — угол между ними. | ||
| (формула Герона) | , , — стороны треугольника, — полупериметр . | |
| в случае обхода вершин треугольника по часовой стрелке получим положительный результат, иначе отрицательный. | ||
| Прямоугольник | и — длины сторон прямоугольника (его длина и ширина). | |
| Параллелограмм | и — длина стороны и опущенной на неё высоты соответственно. | |
| и — соседние стороны параллелограмма, — угол между ними. | ||
| Ромб | и — длины диагоналей ромба. | |
| Эллипс | и — длины малой и большой полуосей. | |
| Трапеция | та — параллельные стороны, и — расстояние между ними (высота трапеции). |
Формулы для вычисления площади круга, его частей, описанных и вписанных в круг фигур
| Фигура | Формула | Переменные |
|---|---|---|
| Круг | или | — радиус, а — диаметр круга. |
| Сектор круга | — радиус круга, — центральный угол сектора (в радианах). | |
| Сегмент | — радиус круга, — центральный угол сегмента (в радианах). | |
| Треугольник, вписанный в окружность | , , — стороны треугольника, — радиус описанной окружности. | |
| Произвольный многоугольник, описанный вокруг окружности | — радиус окружности, вписанной в многоугольник, и — периметр многоугольника. |
Формулы для вычисления площади поверхности тел в пространстве
| Тело | Формула | Переменные |
|---|---|---|
| Полная площадь поверхности цилиндра | и — радиус и высота соответственно. | |
| Площадь боковой поверхности цилиндра | и — радиус и высота соответственно. | |
| Полная площадь конуса | и — радиус и высота боковой поверхности соответственно. | |
| Площадь боковой поверхности конуса | и — радиус и образующая боковой поверхности соответственно. | |
| Площадь поверхности сферы (шара) | или | и радиус и диаметр, соответственно. |
См. также
- Площадь фигуры — математические аспекты понятия.
- Длина кривой
- Квадратура (математика)
- Объём
- Поверхность
Литература
- Рашевский П.
 К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.
К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967. - Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2
Ссылки
- Болтянский В. О понятиях площади и объёма. Квант, № 5, 1977.
- Рохлин В. А. Площадь и объём. Энциклопедия элементарной математики, Книга 5, Геометрия.
Примечания
- ↑ Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 4.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 6-е. — М.: ФИЗМАТЛИТ, 1966. — Т. 2. — С. 186-224. — 800 с.
Площадь | это… Что такое Площадь?
У этого термина существуют и другие значения, см. Площадь (значения).
Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры[1], неформально говоря, показывающая размер этой фигуры.
Общий метод вычисления площади геометрических фигур предоставило интегральное исчисление. Обобщением понятия площади стала теория меры множества, пригодная для более широкого класса геометрических объектов.
Для приближенного вычисления площади на практике используют палетку или специальный измерительный прибор — планиметр.
Содержание
|
Свойства
- Площадь единичного квадрата равна 1.
- Площадь аддитивна.
- Площадь неотрицательна.
- Площади конгруэнтных фигур равны.
Для фигур на плоскости, не состоящих из целого количества единичных квадратов, а также для искривлённых трёхмерных поверхностей, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими[2]
Общий метод определения площади
Площадь плоской фигуры
Декартовы координаты
Определённый интеграл как площадь фигуры
Площадь между графиками двух функций равна разности интегралов от этих функций в одинаковых пределах интегрирования
Площадь, заключённая между графиком непрерывной функции на интервале и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:
Площадь, заключённая между графиками двух непрерывных функций на интервале находится как разность определённых интегралов от этих функций:
Полярные координаты
В полярных координатах: площадь, ограниченная графиком функции и лучами вычисляется по формуле:
- .

Площадь поверхности
Основная статья: Площадь поверхности
Площадь искривлённой поверхности A, заданной вектор-функцией , даётся двойным интегралом:
То же в координатах:
Здесь .
Единицы измерения площади
Метрические единицы
- Квадратный километр, 1 км² = 1 000 000 м²
- Гектар, 1 га = 10 000 м²
- Ар (сотка), 1 а = 100 м²
- Квадратный метр, производная единица системы СИ 1 м² = 1 са (сантиар)
- Квадратный дециметр, 100 дм² = 1 м²;
- Квадратный сантиметр, 10 000 см² = 1 м²;
- Квадратный миллиметр, 1 000 000 мм² = 1 м².
Русские устаревшие
- Квадратная верста = 1,13806 км²
- Десятина = 10925,4 м²
- Копна = 0,1 десятины — сенные покосы меряли копнами
- Квадратная сажень = 4,55224 м²
Мерами земли при налоговых расчетах были выть, соха, обжа, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли:коробья, веревка, жеребья и др.
Существовали и различные местные меры земли:коробья, веревка, жеребья и др.
Античные
- Арура
Формулы вычисления площадей простейших фигур
Планиметрические фигуры
| Фигура | Формула | Переменные |
|---|---|---|
| Квадрат | — длина стороны квадрата. | |
| Правильный треугольник | — длина стороны треугольника. | |
| Правильный шестиугольник | — длина стороны шестиугольника. | |
| Правильный восьмиугольник | — длина стороны восьмиугольника. | |
| Правильный многоугольник | — периметр, а — количество сторон. | |
| Прямоугольный треугольник | и — катеты треугольника. | |
| Произвольный треугольник | — сторона треугольника, — высота, проведенная к этой стороне. | |
, — любые две стороны, — угол между ними. | ||
| (формула Герона) | , , — стороны треугольника, — полупериметр . | |
| в случае обхода вершин треугольника по часовой стрелке получим положительный результат, иначе отрицательный. | ||
| Прямоугольник | и — длины сторон прямоугольника (его длина и ширина). | |
| Параллелограмм | и — длина стороны и опущенной на неё высоты соответственно. | |
| и — соседние стороны параллелограмма, — угол между ними. | ||
| Ромб | и — длины диагоналей ромба. | |
| Эллипс | и — длины малой и большой полуосей. | |
| Трапеция | та — параллельные стороны, и — расстояние между ними (высота трапеции). |
Формулы для вычисления площади круга, его частей, описанных и вписанных в круг фигур
| Фигура | Формула | Переменные |
|---|---|---|
| Круг | или | — радиус, а — диаметр круга. |
| Сектор круга | — радиус круга, — центральный угол сектора (в радианах). | |
| Сегмент | — радиус круга, — центральный угол сегмента (в радианах). | |
| Треугольник, вписанный в окружность | , , — стороны треугольника, — радиус описанной окружности. | |
| Произвольный многоугольник, описанный вокруг окружности | — радиус окружности, вписанной в многоугольник, и — периметр многоугольника. |
Формулы для вычисления площади поверхности тел в пространстве
| Тело | Формула | Переменные |
|---|---|---|
| Полная площадь поверхности цилиндра | и — радиус и высота соответственно. | |
| Площадь боковой поверхности цилиндра | и — радиус и высота соответственно. | |
| Полная площадь конуса | и — радиус и высота боковой поверхности соответственно. | |
| Площадь боковой поверхности конуса | и — радиус и образующая боковой поверхности соответственно. | |
| Площадь поверхности сферы (шара) | или | и радиус и диаметр, соответственно. |
См. также
- Площадь фигуры — математические аспекты понятия.
- Длина кривой
- Квадратура (математика)
- Объём
- Поверхность
Литература
- Рашевский П. К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2
Ссылки
- Болтянский В. О понятиях площади и объёма. Квант, № 5, 1977.
- Рохлин В. А. Площадь и объём. Энциклопедия элементарной математики, Книга 5, Геометрия.
Примечания
- ↑ Математическая энциклопедия (в 5 томах). — М.
 : Советская Энциклопедия, 1982. — Т. 4.
: Советская Энциклопедия, 1982. — Т. 4. - ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 6-е. — М.: ФИЗМАТЛИТ, 1966. — Т. 2. — С. 186-224. — 800 с.
Определение и значение области — Merriam-Webster
площадь ˈer-ē-ə
ˈā-rē-ə
1
: поверхность, включенная в набор линий
конкретно : количество единичных квадратов, равных по размеру поверхности
см. Таблицу метрической системы, Таблицу мер и весов
Таблицу метрической системы, Таблицу мер и весов
2
: объем концепции, операции или деятельности : поле
вся область внешней политики
3
: область за пределами
4
: определенная протяженность пространства или поверхности или выполняющая особую функцию: например,
а
: часть поверхности тела
б
: A Географическая область
5
: A Уровень земли
6
: Часть мозговой коры, выполняющая определенную функцию
Синонимы
- Demesne 8
- Demesne 8
- Demesne
- Demesne
- Demesne
- поле
- регион
- зона
- Я пошел в магазин ______, чтобы купить поздравительную открытку.
- канцелярские товары стационарный
- {{randomImageQuizHook.

Просмотреть все синонимы и антонимы в тезаурусе
Примеры предложений
Поселенцы пришли в этот район с востока. Группа посетила зона во время охоты.
в районе , окружающем озеро
Шторм нанес ущерб многим районам вдоль побережья.
птица, обитающая только в отдаленных районах США.
во многих район мира
Он является самым популярным политиком столичного региона .
Он жил в немодном районе города.
Она отложила работу площадью на кухню.
Группа посетила зона во время охоты.
в районе , окружающем озеро
Шторм нанес ущерб многим районам вдоль побережья.
птица, обитающая только в отдаленных районах США.
во многих район мира
Он является самым популярным политиком столичного региона .
Он жил в немодном районе города.
Она отложила работу площадью на кухню. Столовая область имеет дополнительные окна.
Узнать больше
Столовая область имеет дополнительные окна.
Узнать больше
Недавние примеры в Интернете
С момента переезда в Хантсвилл Мерфи завязал отраслевые связи и завел дружеские отношения в Muscle Shoals, черпая вдохновение в тех зона — богатое музыкальное наследие.
— Мэтт Уэйк | [email protected], al , 26 декабря 2022 г.
Одной из областей , нуждающихся в росте, является их игра в краске, так как соперники имеют преимущество по блокам 67-32. — Тревор Хасс, BostonGlobe.com , 26 декабря 2022 г.
Район был эпицентром одной из первых вспышек в Китае после того, как государство ослабило COVID-19.контроля в ноябре и декабре.
— Дейк Канг, Anchorage Daily News , 25 декабря 2022 г.
В зону входят 15 штатов США и канадская провинция Манитоба, говорится на сайте оператора.
— Грант Ланкастер, Arkansas Online , 24 декабря 2022 г.
Мораторий не распространяется ни на один из существующих предприятий в этом районе 9.0082 .
— Кливленд , 24 декабря 2022 г.
«Нетс» набрали 21 очко за 17 бросков в пятницу вечером, опередив «Бакс» на 11 очков в этой зоне (когда стартовые игроки были в игре).
— Джим Овчарски, Journal Sentinel , 23 декабря 2022 г.
— Тревор Хасс, BostonGlobe.com , 26 декабря 2022 г.
Район был эпицентром одной из первых вспышек в Китае после того, как государство ослабило COVID-19.контроля в ноябре и декабре.
— Дейк Канг, Anchorage Daily News , 25 декабря 2022 г.
В зону входят 15 штатов США и канадская провинция Манитоба, говорится на сайте оператора.
— Грант Ланкастер, Arkansas Online , 24 декабря 2022 г.
Мораторий не распространяется ни на один из существующих предприятий в этом районе 9.0082 .
— Кливленд , 24 декабря 2022 г.
«Нетс» набрали 21 очко за 17 бросков в пятницу вечером, опередив «Бакс» на 11 очков в этой зоне (когда стартовые игроки были в игре).
— Джим Овчарски, Journal Sentinel , 23 декабря 2022 г. Ни одно судно не сообщало о столкновении с другим судном в районе этим утром.
—Майкл Уилсон, 9 лет.0081 New York Times , 22 декабря 2022 г.
Сетон Холл также возглавил защиту Ксавьера в краске, обогнав хозяев со счетом 24-16 в этой зоне .
— Cincinnati Enquirer, The Enquirer , 21 декабря 2022 г.
Узнать больше
Ни одно судно не сообщало о столкновении с другим судном в районе этим утром.
—Майкл Уилсон, 9 лет.0081 New York Times , 22 декабря 2022 г.
Сетон Холл также возглавил защиту Ксавьера в краске, обогнав хозяев со счетом 24-16 в этой зоне .
— Cincinnati Enquirer, The Enquirer , 21 декабря 2022 г.
Узнать больше
Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «район». Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
Отправьте нам отзыв.
История слов
Этимология
Латинское, открытое пространство, гумно; возможно, сродни латинскому arēre , чтобы быть сухим — больше в засушливом
Первое известное использование
около 1552 года, в значении, определенном в смысле 5
Путешественник во времени
Первое известное использование области было около 1552 г.
Другие слова того же года находятся
площадь
амниотическая область
Посмотреть другие записи поблизости
Процитировать эту запись «Площадь.
 » Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/area. По состоянию на 1 января 2023 г.
» Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/area. По состоянию на 1 января 2023 г.Ссылка на копию
Детское определение
область
существительное
площадь ˈar-ē-ə
ˈer-
1
: определенный участок земли или пространство, часто выделяемое для специального использования
пикник зона
ожидание зона
2
: поверхность внутри фигуры или формы
особенно : количество единичных квадратов, равное количеству пространства, которое покрывает поверхность
Круг с площадью из 500 квадратных метров
3
: область. : часть мозга, выполняющая определенную функцию (например, зрение или слух)
: часть мозга, выполняющая определенную функцию (например, зрение или слух)
Медицинское определение
область
существительное
площадь ˈar-ē-ə, ˈer-
: часть коры головного мозга, выполняющая определенную функцию
см. область ассоциаций, двигательная область, сенсорная область
Britannica English: Перевод области для говорящих на арабском языке
Britannica.com: Энциклопедическая статья о области
Последнее обновление: — Обновлены примеры предложений
Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!
Merriam-Webster без сокращений
год чудес
См. Определения и примеры »
Получайте ежедневно по электронной почте Слово дня!
Тест на часто путаемые слова
Проверьте свой словарный запас с помощью нашего теста из 10 вопросов!
ПРОЙДИТЕ ТЕСТ
Сможете ли вы составить 12 слов из 7 букв? Определение
PLAY
в кембриджском словаре английского языка
Примеры области
области
Я думаю, что у города был мандат на уборку территорий, где жили бездомные.
От Хаффингтон Пост
Без прозрачности в этой области , можем ли мы действительно считать себя автономными личностями, хозяевами своих судеб?
Из журнала Slate
Эти области поломки или проскальзывания называются разломами.
От Phys.Org
Но мы знаем, что судно несколько раз проходило через район .
Из США СЕГОДНЯ
Дождей и гроз в 9-м не было.0081 область .
Из США СЕГОДНЯ
Зона ожидания и билетная касса были снесены.
Из NBCNews.com
Другая ключевая область инноваций в политике заключается в поиске путей повышения нейтральной процентной ставки.
От Блумберга
Мало того, что в кино, телевидении и видеоиграх по-прежнему будет доминировать человеческая изобретательность, откроются новые области.
От TechCrunch
Ученые измеряют популяцию с точки зрения того, сколько площади леса занимают монархи, поскольку оценки отдельных бабочек могут сильно различаться.
Из NBCNews.com
Службы по уходу за животными играли в «убей крота» с проблемными областями вместо того, чтобы напрягать свой ограниченный персонал, чтобы быть везде одновременно.
Из Далласских утренних новостей
Эти примеры взяты из корпусов и источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Сочетания с областью
площадь
Эти слова часто используются в сочетании с районом.
Нажмите на словосочетание, чтобы увидеть больше его примеров.
область живота
Использование показателей безусловного и условного стандартного отклонения измерений области живота плода для прогнозирования задержки внутриутробного развития.
Из Кембриджского корпуса английского языка
смежная область
Однако иногда было трудно увидеть, где заканчивается одна область коры и начинается соседняя область.
Из Cambridge English Corpus
пораженная область
Мы предполагаем, что более локальное синаптическое торможение будет иметь аналогичные эффекты, но только над пораженной областью.
Из Cambridge English Corpus
Эти примеры взяты из корпусов и источников в Интернете. Любые мнения в примерах не отражают мнение редакторов Кембриджского словаря, издательства Кембриджского университета или его лицензиаров.
Посмотреть все словосочетания с областью
Переводы area
на китайский (традиционный)
地方, 地區, 區域…
Подробнее
на китайском (упрощенном)
地方, 地区, 区域…
Подробнее
на испанском языке
zona, campo, área…
Увидеть больше
на португальском языке
área, área [женский род], região [женский род]…
Увидеть больше
на других языкахна японском языке
на турецком языке
на французском языке
на каталанском языке
на голландском языке
на арабском языке
на чешском языке
на датском языке
в индонезийском
в Thai
в Вьетнамском языке
в польском
в Малайском
на немецком языке
на норвежском
на Кореи
на украинском
на итальянском
на украинском языке
на итальянский
地域, 地方, ~場…
Подробнее
саха, бельге, алан…
Увидеть больше
регион [женский род], zone [женский род], domaine [мужской род]…
Подробнее
зона, лагерь, район…
Подробнее
gebied, buurt, oppervlakte…
Узнать больше Увидеть больше
область, зона, уземи…
Узнать больше
område, area…
Узнать больше
bagian tempat, luas tanah, area…
Узнать больше
vùng, diện tích, lĩnh vực…
Подробнее
obszar, teren, miejsce…
Подробнее
kawasan, luas, bidang…
die Gegend, die Fläche, das Gebiet…
См. больше
больше
område [средний род], egn [мужской род], войлочный [средний род]…
Узнать больше
지역, 구역, 분야…
Подробнее
район, площа, сфера…
Подробнее
зона, зона, сетторе… Подробнее
район, площадка, место…
Увидеть больше
Нужен переводчик?
Получите быстрый бесплатный перевод!
Как произносится площадь ?
Обзор
с трудом
трудность
находятся
мои глаза меня обманывают? идиома
площадь
код города
зона франшизы
региональный франчайзи
краеведение
Проверьте свой словарный запас с помощью наших веселых викторин по картинкам

 1 Площадь плоской фигуры
1 Площадь плоской фигуры К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.
К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967. 3 Античные
3 Античные
 : Советская Энциклопедия, 1982. — Т. 4.
: Советская Энциклопедия, 1982. — Т. 4.