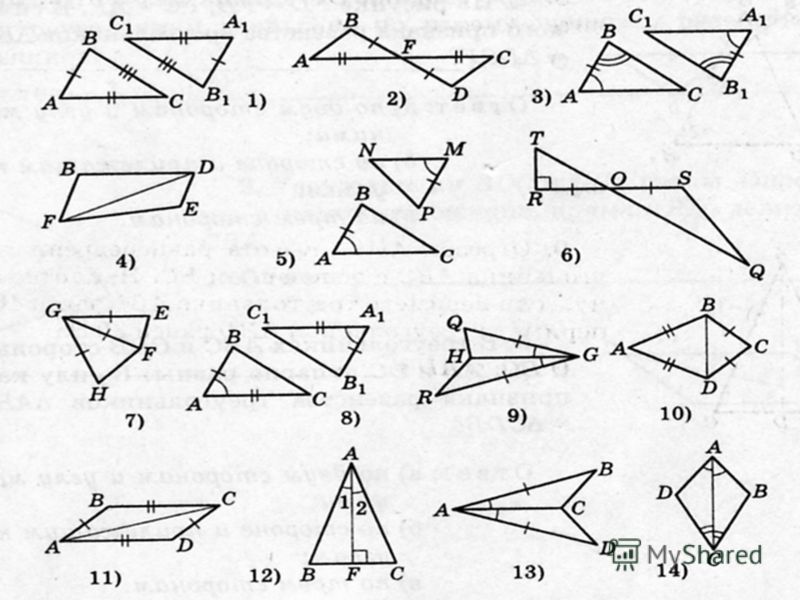
Два треугольника равны | Треугольники
Два треугольника равны, если об этом сказано в условии или это можно доказать по одному из признаков равенства треугольников (либо по одному из признаков равенства прямоугольных треугольников).
Один из наиболее важных моментов, с которых начинается доказательство — правильное название треугольников.
Какие треугольники называются равными?
Определение
Два треугольника равны, если у них соответствующие стороны равны и соответствующие углы равны.
(Треугольники равны, если их можно совместить наложением).
Это значит, что для равных треугольников выполняется шесть пар равенств, по три пары на углы и на стороны.
1)∠A =∠A1; 3) AB =A1B1;
2)∠B =∠B1; 4) BC =B1C1;
3)∠C =∠C1; 5) AC =A1C1.
Здесь треугольники ABC и A1B1C1 равны. Равные углы в названиях треугольников стоят на одинаковых местах:
∠A и∠A1 стоят на первом месте, ∠B и∠B1 — на втором, ∠C и∠C1 — на третьем.
Что получится, если второй треугольник назвать не A1B1C1 а, например, C1B1A1?
В этом случае ∆ ABC=∆ C1B1A1.
Из равенства этих треугольников следует равенство их соответствующих сторон и соответствующих углов.
Получается, что
1)∠A =∠С1; 3) AB =C1B1;
2)∠B =∠B1; 4) BC =B1A1;
3)∠C =∠A1; 5) AC =C1A1.
Но эти равенства не верны! (точнее, не все верны). Значит, треугольники ABC и C1B1A1 не равны.
В этом легко убедиться опытным путем. Вырежьте из бумаги два одинаковых разносторонних треугольника. Подпишите их углы A, B, C и A1, B1,C1 таким образом, чтобы ∠A=∠A1, ∠B=∠B1, ∠C=∠C1. Совместив треугольники, убедитесь, что при наложении они совпадают, а значит, равны. Теперь приложите к углу A угол B1 , к углу C — угол A1. Эти треугольники уже не совпадут.
В именах людей место каждой буквы важно. К примеру, имена «Аня» и «Яна» состоят из одинаковых букв, но никто не станет называть Аню Яной, и наоборот.
В «имени» треугольников позиция каждой буквы не менее значима.
Когда нужно доказать, что два треугольника равны, первый треугольник называем произвольно. А вот название второго треугольника уже нужно продумывать и подбирать правильно, чтобы равные углы и равные стороны стояли на одинаковых позициях.
Разработка урока по геометрии «Треугольники.
Равные треугольники»(7 класс))Тема урока: Треугольники. Равные треугольники
Цели урока:
Образовательные: на
базе уже полученных знаний о треугольнике сформировать геометрические понятия
«треугольник», «сторона треугольника», «вершина треугольника», «угол
треугольника», «периметр треугольника», «равные треугольники»; умения
изображать и распознавать на чертежах элементы треугольника, научить называть
элементы треугольника; записывать формулу периметра треугольника, решать
задачи, применяя формулу периметра треугольника; продолжить формировать
представления о геометрической фигуре – треугольнике, как о неотъемлемой
части окружающего нас мира, познакомить учащихся с математической символикой,
учить применять символику при решении задач.
Развивающие: расширение кругозора обучающихся; развивать умение видеть
математические понятия в окружающем нас мире; развивать устную и письменную
математическую речь; развивать логическое мышление, умение правильно излагать
свою мысль
Воспитательные:
воспитывать умение работать в группе, воспитывать устойчивый интерес к предмету
воспитывать культуру геометрического языка.
Оборудование: современный компьютер, мультимедийный проектор, демонстрационный экран, программное обеспечение Microsoft, Power Point и слайд-фильмы, раздаточный материал,
Задачи урока:
1. Вспомнить изученный материал по теме;
2. Совершенствовать способы решения задач;
3. Развивать самостоятельность и познавательную активность
Тип урока: комбинированный
Форма работы учащихся: фронтальная, в группах, индивидуальная
Оборудование: Учебник: Л.С. Атанасян и др. Геометрия, 7 класс – М.: Просвещение; рабочие тетради; наборы из треугольников; карточки с раздаточным материалом; мультимедийный проектор; слайдовая презентация.
Ход урока
I. Организационный момент
Здравствуйте, ребята. Выполнять задания по
геометрии бывает сложно, но я думаю, что вместе мы справимся.
Работать будем
вместе, индивидуально и в парах.
II. Актуализация опорных знаний и умений
· Словарь: «противолежащий» — лежит напротив
«прилежащий» — лежит рядом
· Фронтальная работа по основным вопросам ранее изученных тем.
А сейчас мы повторим те геометрические фигуры, которые мы изучали ранее и которые нам пригодятся при изучении данной темы урока.
1.Назовите фигуры, изображенные на рисунке.
2.Вспомните, как сравнивают отрезки?
3.Вспомните, как сравнивают углы?
4.Какие фигуры называют равными?
5. Как их сравнить?
· Практическое задание.
— Ребята, отметьте в тетради три точки, которые не лежат на одной прямой. Обозначьте их. Соедините эти точки отрезками.
— Узнали фигуру?
Сформулируем тему урока.
-Вам знакома данная фигура?
III. Изучение нового материала
Записываем тему урока «Треугольник. Равные треугольники»
Какие цели мы поставим перед собой, как вы думаете, чем мы будем заниматься на уроке?
— Как вы думаете, что мы сегодня будем изучать?
Определите тему
нашего урока.
Записывается тема урока в тетради
Учитель обращается с вопросом:
— Как вы думаете, ребята, зачем надо изучать треугольник?
А где, среди
окружающих предметов вы видели треугольник? Треугольники в жизни людей
Учащимся было предложено в качестве одного из домашних заданий
провести поисковую работу по применению треугольников в жизни людей.
Что же в этой фигуре такого особенного? Некоторые возможно считают, что знания о треугольниках им не пригодятся. Часто ли треугольники встречаются и применяются в жизни?
—
Треугольник – самая простая замкнутая прямолинейная фигура, одна из первых,
свойства которых человек узнал еще в глубокой древности, т.
к. эта фигура
всегда имела широкое применение в практической жизни.
Треугольник – письмо без марки и конверта, отправленное солдатом с фронта или солдату на фронт. (Солдатский)
Треугольник-самозвучащий музыкальный инструмент- стальной прут,
согнутый в виде треугольника, по которому ударяют палочкой
Кто-нибудь
понял по фотографиям, что это за загадочное место? (бермудский треугольник)
Бермудский треугольник — это необычный район в Атлантическом океане, в котором происходят таинственные исчезновения морских и воздушных судов. Сегодня бермудский треугольник часто называют самой опасной аномальной зоной на Земле – люди, корабли и самолеты исчезают совершенно бесследно.
Эпиграф
В старших классах каждый школьник
Изучает треугольник.
Три каких-то уголка,
А работы — на века
(Валентин Берестов,
Русский писатель и переводчик, поэт
— Что вы помните о треугольнике?
— Какие бывают треугольники?
— Что такое треугольник?
— А
знаете ли вы ребята, какая геометрическая фигура называется треугольником?
Попробуем сформулировать определение этой геометрической фигуры
· Работа с учебником
Стр.
28 (Атанасян)
Составить определение треугольника
Треугольник – это фигура, состоящая из трех точек, не лежащих на одной прямой, и трёх отрезков, которые их соединяют
Вместо слова “треугольник” употребляют знак, который ввел в математику древнегреческий ученый Герон (1в.). Запишем Δ АВС.
А сейчас я вам предлагаю разгадать анаграммы. Кто знает, что это такое?
ГОЛУ, ШЕРИНАВ, РЕНЬКО, ТОНАРОС
Какое слово лишнее? Почему? (угол, вершина, корень, сторона) Что объединяет остальные слова?
Ребята, эти три
точки, не лежащие на одной прямой, называются
Элементы треугольника
· вершины (точки, не лежащие на одной прямой): А, В, С;
· стороны (отрезки, попарно соединяющие вершины): АВ, ВС, СА;
· углы: АВС, ВСА, САВ
Задание:
В своих треугольниках, которые у вас нарисованы в тетрадях:
1.
Назовите его
вершины, стороны, углы.
2.Назовите углы треугольника, прилежащие стороне
3.Какой угол в ∆…. заключен между сторонами …
4.Какой угол противолежит стороне …?
5.Между какими сторонами заключен <…. ?
6. Найдите периметр треугольника, измерив линейкой его стороны
Между углами и сторонами в треугольнике существуют следующие соотношения:
— угол может быть противолежащим стороне и прилежащим стороне.
сторона может быть противолежащей углу и прилежащей.
— Например: <А- противолежит стороне ВС
Сторона АС противолежит < В и прилежит к <А
Определение: Сумму длин сторон треугольника называют периметром треугольника.
Обозначение периметра — Р
Р∆=АВ+ВС+АС — формула периметра треугольника
· Лабораторно-исследовательская работа «Найди равные треугольники»
среди представленных учащимся треугольников найти равные треугольники;
На
столе у каждого ученика лежит набор из шести разноцветных треугольников.
Такие,
что среди шести треугольников обязательно 2 треугольника равны.
Возьмите ребята наборы треугольников. Рассмотрите треугольники. Есть ли среди них равные? Как вы определили , что они равны?
— Все нашли равные треугольники?
— А как же вы это сделали?
— Какие элементы совпали?
— Таким образом, при наложении равные треугольники полностью совместились, т.е. попарно совместились их вершины и стороны. Ясно, что при этом совместились попарно и углы этих треугольников
Ребята поясняют. Дается определение равных треугольников. Равные треугольники обозначаются так: ∆АВС=∆MNK.
Изображает два равных треугольника на доске.
Задаёт вопросы ученикам и делает записи на доске.
— Назовите равные стороны
Назовите равные углы
РАВНЫЕ
ТРЕУГОЛЬНИКИ- это треугольники, которые можно совместить наложением. Записать
определение в тетрадь, выполнить чертеж равных треугольников, записать
равенство соответствующих элементов.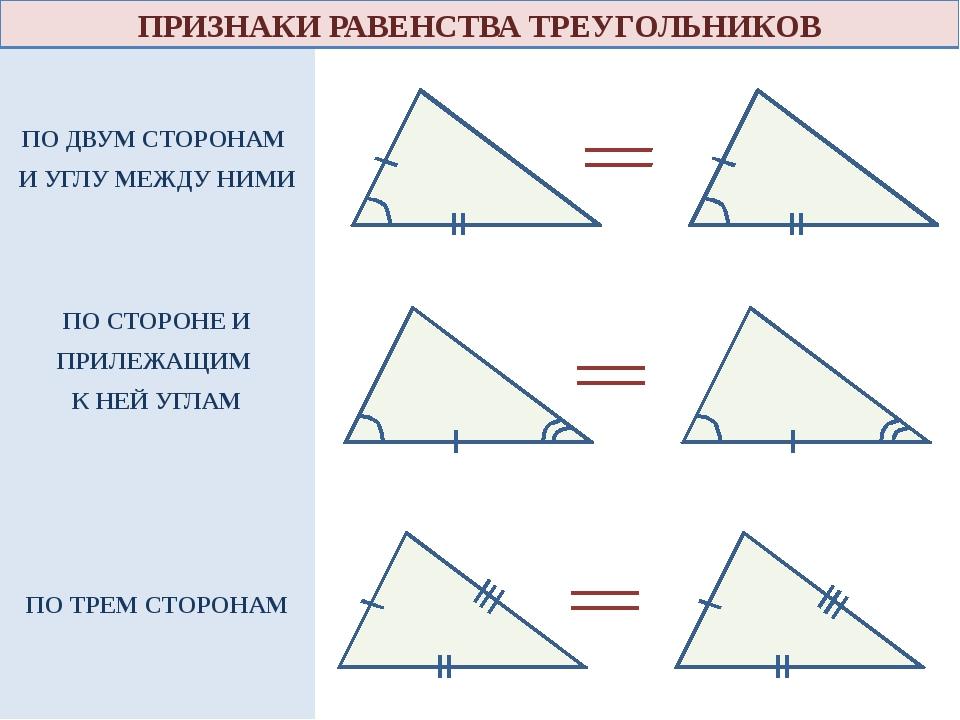
ЕСЛИ ДВА ТРЕУГОЛЬНИКА РАВНЫ, ТО ЭЛЕМЕНТЫ ОДНОГО ТРЕУГОЛЬНИКА СООТВЕТСТВЕННО РАВНЫ ЭЛЕМЕНТАМ ДРУГОГО. В РАВНЫХ ТРЕУГОЛЬНИКАХ ПРОТИВ СООТВЕТСТВЕННО РАВНЫХ УГЛОВ ЛЕЖАТ РАВНЫЕ СТОРОНЫ и наоборот
Задание: Назовите соответственные стороны и углы у треугольников АВС и MNK. Сделайте соответствующие записи.
Проверьте.
<А=<М;<В=<N;<С=<К.
АВ=MN;ВС=NK;АС=МК
— Всегда ли удобно таким образом проверять равенство треугольников? Почему?
— Оказывается, что равенство треугольников можно установить, не накладывая один треугольник на другой, а сравнивая только некоторые их элементы. С этим мы познакомимся с вами на следующем уроке.
IV. Физкультминутка
ЗАРЯДКА ДЛЯ РУК(Положите правую руку на левую. Показать с помощью рук угол прямой, тупой, острый, развёрнутый, угол в 30 , 90, 150, 180.
V. Первичная проверка понимания изученного:
а) Посмотрим, как вы умеете применять знания при решении задач по готовым чертежам
А теперь
узнаем, насколько вы внимательно слушали .
VI.
Практическая работа
На карточках обозначьте треугольники.
-Они равны?
— Поменяйтесь карточками с соседом и запишите равные элементы треугольников , измерить стороны треугольника и найти его периметр
— взаимопроверка
Обменяйтесь с соседом по парте тетрадями, проверяем ответы, выставляем карандашом оценки, комментируем результаты, исправляем ошибки.
VII. Подведение итогов урока. Рефлексия.
Подведение итогов урока.
— Тест
1. | Каждый треугольник состоит из трёх углов | ДА | НЕТ |
2. | Каждый треугольник состоит из трёх прямых | ДА | НЕТ |
3. | При наложении равные треугольники полностью совместятся | ДА | НЕТ |
4. | Периметр треугольника — это сумма градусных мер всех углов треугольника | ДА | НЕТ |
5. | Периметр треугольника — это сумма длин всех сторон треугольника | ДА | НЕТ |
6. | В треугольнике АВС против угла А лежит сторона ВС | ДА | НЕТ |
7. | В треугольнике АВС к стороне АС прилежат углы А и В | ДА | НЕТ |
8. | Если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого треугольника | ДА | НЕТ |
9. | Если два треугольника равны, то их периметры равны | ДА | НЕт |
10 | Если периметры двух треугольников равны, то эти треугольники равны | ДА | НЕТ |
Чтобы подвести итог нашей работы на уроке и установить достигли ли мы поставленной цели урока, мне, как и вам, хотелось бы знать: кто из вас работал на «3», кто на «4», а кто на «5»
Рефлексия.
У вас в руках треугольники трех цветов, если вы оцениваете усвоенные вами знания на « 5», то это красный треугольник, « 4»- желтый, «3»- фиолетовый
VIII.
Сообщение домашнего задания. Инструктаж.
выучить правила
№87, 88
— Выставление оценок учащимся за работу на уроке.
Известный
французский архитектор говорил, что образование-это то, что остается после
того, как все остальное забыто.
Надеюсь, этот материал вы не забудете. Думаю,
что знания, которые вы получили сегодня, помогут вам на уроках геометрии в
старших классах. Спасибо за урок!
IX. Логическая задача
Равностороннее определение и значение — Merriam-Webster
равно · широкий · и ˌē-kwə-la-tə-rəl
ˌe-,
-ˈla-trəl
1
: все стороны равны
равносторонний треугольник
равносторонний многоугольник
см.
рисунок треугольника
2
: все стороны равны
равносторонний многогранник
Знаете ли вы?
Поскольку equi- означает «равный», значение равносторонний легко угадать по корням. Слово в основном используется в геометрии. Стандартные многоугольники (многогранные геометрические фигуры) — пятиугольник, шестиугольник, восьмиугольник и т. д. — считаются равносторонними, если не оговорено иначе; равносторонний прямоугольник имеет специальное название квадрат . Но особенно важны треугольники, а многие треугольники не равносторонние. Стандартные многогранники (многогранники) также являются равносторонними. Наиболее распространенным является куб, все стороны которого квадратные. Тетраэдр имеет четыре треугольные стороны и, таким образом, представляет собой пирамиду с треугольным основанием, в отличие от пирамид Египта с их квадратными основаниями.
Примеры предложений
Недавние примеры в Интернете
У Уолдо висячие уши в форме идеальных равносторонних треугольников, а ступни слишком велики для его долговязого тела, которое продолжает расти.
— Джемма Тарлах, Discover Magazine , 25 ноября 2014 г.
В набор входят 48 обычных квадратов, восемь больших квадратов, восемь толстых квадратов, восемь квадратов в виде оконных стекол, 16 маленьких и 16 больших равносторонний треугольника плюс 16 равнобедренных треугольников.
— Джессика Хартсхорн, Good Housekeeping , 19 декабря 2022 г.
Равносторонний крест с ногами, согнутыми под прямым углом, является тысячелетним священным символом в индуизме, буддизме и джайнизме, олицетворяющим мир и удачу.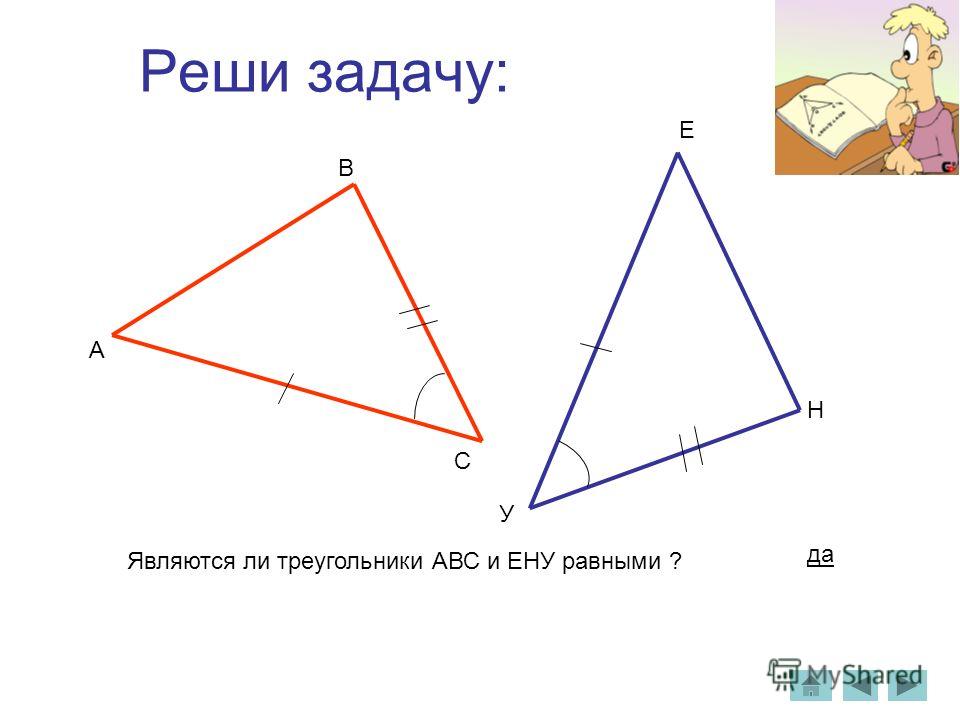
— Арканзас Онлайн , 28 ноября 2022 г. равносторонний крест с ногами, согнутыми под прямым углом, является тысячелетним священным символом в индуизме, буддизме и джайнизме, олицетворяющим мир и удачу.
— Дипа Бхарат, BostonGlobe.com , 27 ноября 2022 г.
Равносторонний крест с ногами, согнутыми под прямым углом, является тысячелетним священным символом в индуизме, буддизме и джайнизме, который представляет мир и удачу, а также широко использовался коренными народами во всем мире в аналогичном ключе.
— Дипа Бхарат, 9 лет.0031 Anchorage Daily News , 27 ноября 2022 г.
Этот болсон является единственным источником воды для трех крупных городов, расположенных на почти равностороннем треугольнике на расстоянии около двадцати пяти миль друг от друга.
— Анна Бадхен, Harper’s Magazine , 28 сентября 2022 г.
Три точки Лагранжа неустойчивы и лежат вдоль этой линии (L1, L2 и L3), а две устойчивы (L4 и L5) и симметричны выше и ниже этой линии как точки равносторонний треугольник.
— Манаси Ваг, Popular Mechanics , 29 апреля 2022 г.
Его идеализированная мужская фигура имеет широко расставленные ноги, образующие равносторонний треугольник.
— Los Angeles Times , 12 ноября 2021 г.
Узнать больше
Эти примеры предложений автоматически выбираются из различных онлайн-источников новостей, чтобы отразить текущее использование слова «равносторонний».
Мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв.
История слов
Этимология
Поздняя латынь aequilateralis , от латинской aequi- + позже-, latus сбоку — больше сбоку
Первое известное использование
1570, в значении, определенном в смысле 1
Путешественник во времени
Первое известное использование равностороннего было в 1570 г.
Посмотреть другие слова того же года
Словарные статьи Рядом с
равностороннийравносторонний
равносторонний
равносторонняя арка
Посмотреть другие записи поблизости
Процитировать эту запись «Равносторонний.
» Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/equilateral. По состоянию на 27 февраля 2023 г.Copy Citation
Детское определение
равносторонний
прилагательное
равно · широкий · и ˌē-kwə-ˈlat-ə-rəl
ˌek-wə-,
-la-trəl
: все стороны равны
равносторонний треугольник
Еще от Merriam-Webster о
равностороннийАнглийский: перевод равносторонний для говорящих на испанском языке
Последнее обновление: — Обновлены примеры предложений
Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!
Merriam-Webster без сокращений
эрзац
См. Определения и примеры »
Получайте ежедневно по электронной почте Слово дня!
Слова, названные в честь людей
- Тёзка купальника Жюль Леотар какую профессию имел?
- Пожарный Судить
- Акробат Врач хирург
Прослушайте слово и напечатайте его. Сколько вы можете получить правильно?
ПРОЙДИТЕ ТЕСТ
Сможете ли вы составить 12 слов из 7 букв?
ИГРАТЬ
Самый быстрый словарь в мире | Vocabulary.
comПЕРЕЙТИ К СОДЕРЖАНИЮ
равносторонний треугольник трехсторонний правильный многоугольник
равноугольный треугольник трехсторонний правильный многоугольник
остроугольный треугольник треугольник, все внутренние углы которого острые
остроугольный треугольник треугольник, все внутренние углы которого острые
внешний угол дополнение внутреннего угла многоугольника
равнобедренный треугольник треугольник с двумя равными сторонами
разносторонний треугольник треугольник, у которого нет двух сторон одинаковой длины
побочный ущерб (эвфемизм) непреднамеренные жертвы и разрушения, причиненные гражданскому населению в ходе военных действий
Южный треугольник небольшое яркое созвездие в полярной области южного полушария вблизи Циркуля и Апуса
эгалитаристская поддержка социального равенства
08″>боковой желудочек любой из двух подковообразных желудочков по одному в каждом полушарии головного мозга; они сообщаются с третьим желудочком через отверстие Монро
