Что такое обратные коэффициенты триггера и почему меня это волнует?
Purplemath
Вы узнали, как использовать коэффициенты триггера для решения прямоугольных треугольников, находя длины сторон треугольников. Но что, если у вас есть стороны, и нужно найти углы?
Вы знаете, что можете взять длины сторон и найти коэффициенты триггера, и вы знаете, что можете найти коэффициенты триггера (в своем калькуляторе) для углов.
Содержание продолжается ниже
MathHelp.com
Задачи синуса, косинуса и тангенса
Чего не хватает, так это способа вернуться от соотношений к исходным углам. И это то, что касается значений «обратного триггера».
Что такое обратные коэффициенты срабатывания?
Обратные тригонометрические соотношения — это обратные функции для синуса, косинуса и тангенса. Пока вы подставляете меры угла к синусу, косинусу и тангенсу, чтобы найти длины сторон; Вы подставляете длины сторон к арксинусу, арккосинусу и арктангенсу, чтобы найти меры угла.
Может ли мой калькулятор выполнять обратные коэффициенты запуска?
Любой калькулятор, который может работать с синусами, косинусами и тангенсами, также сможет работать с их обратными значениями, обычно в качестве «второй функции» обычных кнопок запуска.
Если вы посмотрите на свой калькулятор, вы должны увидеть прямо над кнопками sin, cos, tan обозначения вдоль линий sin −1 , cos −1 и tan −1 или, возможно, asin , акос и атан. Это то, что вы будете использовать, чтобы найти углы из соотношений.
Что означает буква а в словах асин, акос и атан?
Буква a в словах asin, acos и atan означает «дуга»; в этом контексте дуга является частью окружности круга.
Итак, арксинус, например, — это функция, в которую вы подставляете меру вытянутой дуги (то есть меру угла, стороны которого пересекают концы дуги окружности) и получаете числовой ответ. Дуговые функции отменяют триггерные функции (то есть дуговые функции являются обратными функциями), поэтому, например, atan указывает на функцию арктангенса, tan −1 ().
Первый набор обозначений с показателем степени «минус один» содержит арксинус, арккосинус и арктангенс. Второй набор обозначений, с a перед каждым именем, перечисляет арксинус, арккосинус и арктангенс. Другими словами, это два обозначения одного и того же.
Вы можете увидеть, как работают эти обратные триггерные функции: возьмите свой калькулятор и вычислите синус некоторого значения угла в диапазоне от нуля до девяноста градусов. Какой бы результат вы не получили, сделайте обратный синус (то есть используйте sin
Вот что делают обратные коэффициенты триггера: они дают вам угол, соответствующий этому коэффициенту триггера.
- Для приведенного ниже треугольника найдите угол m α с точностью до градуса.
Мне дали длину стороны, противоположной углу α , и длину гипотенузы.
Из «противоположный» и «гипотенуза» я могу составить отношение синусов:
9/10 = SIN ( α ) = 0,9
Подключение 0,9 в SIN −1 В моем калькуляторе I GET:
α = 64.15806724 …
Decking. Мне напомнили, что есть единица измерения градусов, которую мне нужно учитывать, наряду с округлением числового результата до ближайших целых чисел. Итак, мой ответ:
м ( α ) = 64°
Примечание. Существуют и другие единицы измерения углов. Здесь я буду использовать только градусы, но вам также может понадобиться использовать радианы. Если это так, вам необходимо правильно установить единицы измерения вашего калькулятора. Если вы находитесь в режиме градусов, вы получите значения в градусах, а не в радианах, и наоборот. Убедитесь, что вы правильно настроены.
- Найдите величину угла β в градусах с точностью до одного десятичного знака.
Мне дали длины стороны, противоположной β (равной 8), и стороны, прилегающей к β (равной 9).
Поскольку тангенс противоположен соседнему, я могу составить отношение тангенса с тем, что они мне дали:
8/9 = tan( β )
Я не буду использовать десятичную дробь для 8/ 9, потому что это может привести к ошибке округления. Вместо этого я буду работать с точной дробью и подставлю загар −1
(8/9) прямо в мой калькулятор. Результат: β = 41,63353934….
Округляя до одного десятичного знака и не забывая добавлять единицы к моему ответу, я получаю:
m( β ) = 41,6°
- Найдите длину стороны p и меру угла m, как показано на схеме. Дайте каждому ответу правильный ответ до ближайшего целого числа или степени.
Как же мне найти угол m и длину стороны p , когда у меня есть только одно число для этого треугольника? У меня есть только гипотенуза! О, подождите.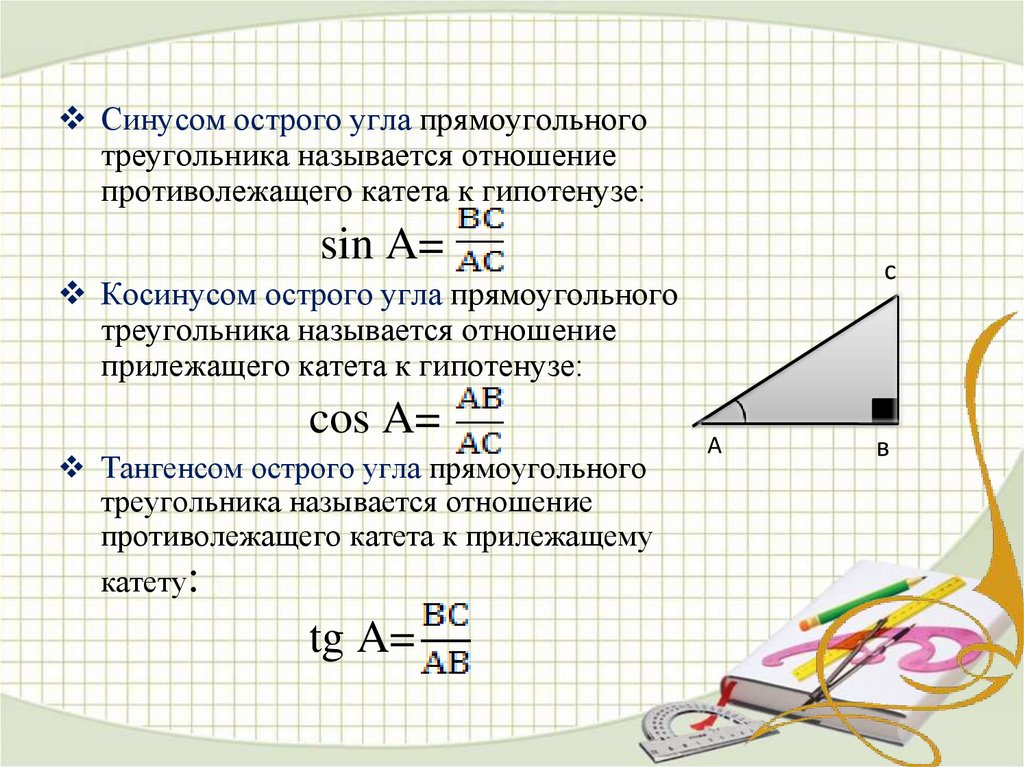
Я могу использовать угол и гипотенузу левого треугольника, чтобы найти высоту p для обоих треугольников, и это даст мне два числа для правого треугольника. С этим я могу найти меру m.
Левый треугольник имеет противоположную сторону, гипотенузу и угол, поэтому я буду работать с отношением синусов:0052 = 15×sin(47°) = 10,97030552…
Теперь, когда я знаю, что p = 11 (округлив до ближайшего целого числа), я могу найти меру угла m:
11/18 = sin(m°)
sin −1 (11/18) = m° = 37,66988696…
Я должен округлить этот угол до ближайшего целого градуса, поэтому мой ответ:
p = 11
м° = 38°
- 5-метровая лестница прислонена к зданию, основание которой находится в двух метрах от стены здания. Какой угол образует лестница с землей? Округлите ответ до одного десятичного знака.
Как обычно, начну с картинки. Это не должно быть «точно» или «в масштабе»; Мне просто нужно достаточное количество изображений, чтобы иметь возможность следить за тем, что я делаю.
Что касается угла, который они хотят, чтобы я нашел (который я указал на рисунке выше дугой, проведенной в нижней левой вершине), у меня есть смежный и гипотенуза, поэтому я буду использовать отношение косинуса .
2/5 = cos(θ)
cos −1 (2/5) = θ = 66,42182152…
Это моя мера в градусах угла, который образует основание лестницы с землей, на которой она стоит. Не забывая округлить свой ответ до одного десятичного знака и добавить соответствующие единицы измерения, мой ответ таков: лестница и земля образуют угол примерно: угол, определите коэффициент триггера, который использует эти две стороны, и используйте соответствующую кнопку инверсии, чтобы найти угол, соответствующий этому коэффициенту. И не забудьте поставить знак «градус» на свой ответ.
URL: https://www.purplemath.com/modules/invratio.htm
Использование закона синусов для нахождения неизвестного угла
Главная > Математика > Математика >Использование закона синусов для нахождения неизвестного угла
Закон синусов гласит:
a означает сторону, противоположную углу A, b — сторону, лежащую против угла B, а c — сторону, противоположную углу C.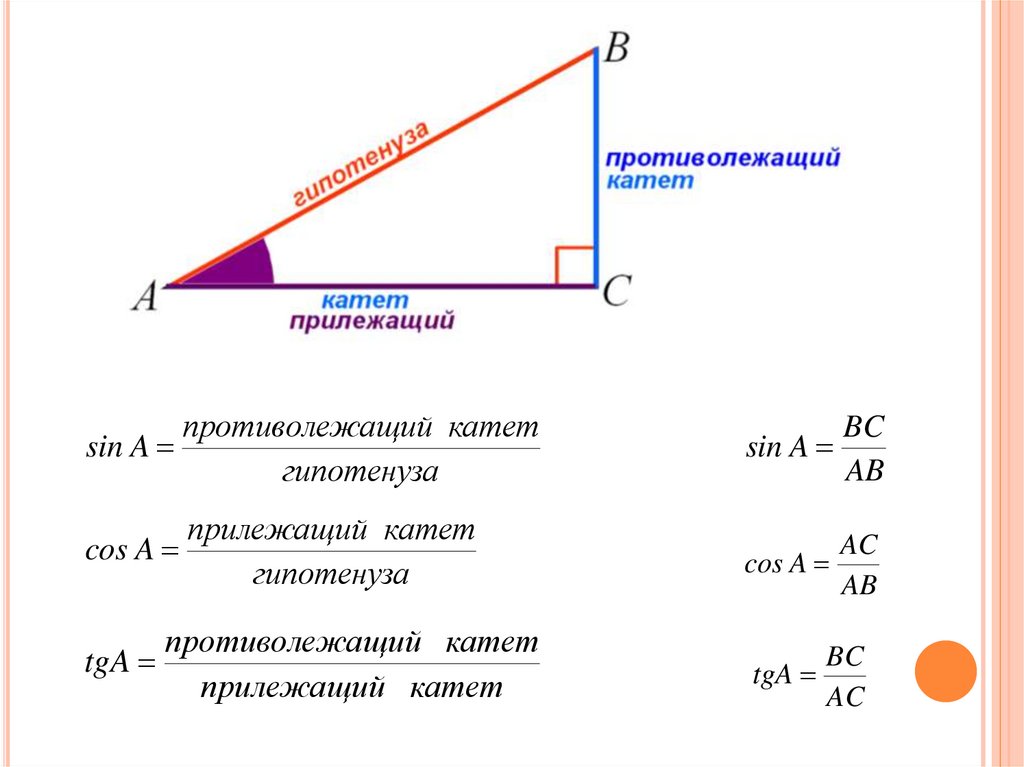
Этот закон чрезвычайно полезен, потому что он работает для любого треугольника,4 не просто прямоугольный треугольник. В частности, его часто можно использовать для нахождения неизвестного угла или неизвестной стороны треугольника.
Чтобы найти неизвестный угол по закону синусов:
1. Подставляем известные значения в формулу.
2. Удалите бесполезную фракцию.
3. Решите оставшееся уравнение.
Примеры:
1. Найдите градусную меру угла B.
Сначала мы подставим всю известную нам информацию в закон синусов:
Теперь мы удалим дробь, которая нам не нужна. Третья фракция содержит обе части информации, а вторая фракция содержит угол, который мы ищем. Но первая фракция не помогает. Перепишем закон без него:
Теперь перемножим и решим уравнение:
Внимательно введите это в свой калькулятор.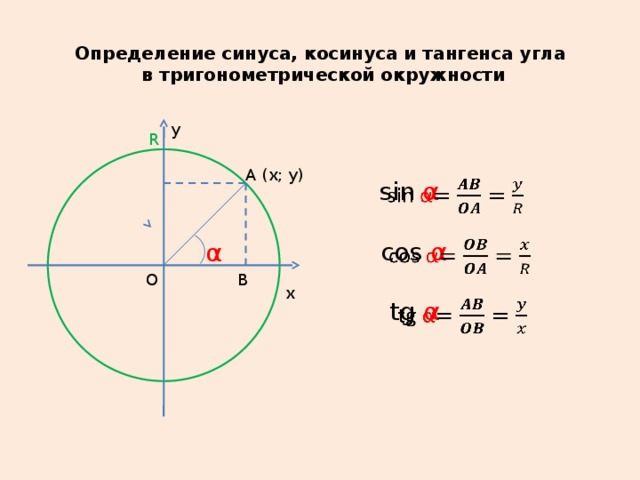
Помните, что на вашем калькуляторе кнопка арксинуса может выглядеть как
.
вот так:
2. Найдите величину угла A.
Теперь мы удалим дробь, которая нам не нужна. Фракция 1 st содержит угол, который мы ищем, а фракция 2 nd содержит обе части информации. Однако дробь 3/ совершенно бесполезна. Перепишем закон без него»
Теперь умножим крест и решим уравнение:
Внимательно введите это в свой калькулятор.
Примечание: Мы пока не рассматриваем неоднозначный случай. Мы изучим эту особую ситуацию на следующем уроке.
Практика: Используйте закон синусов, чтобы найти заданный угол для каждого треугольника. Округлите ответ до десятых, если необходимо.