python — Проверка на целое число—условие на проверку данных, введенных пользователем
Чтобы проверить является ли строка введённая пользователем целым числом, можно воспользоваться int в try/except, похожим образом как показано в ответе на вопрос «Python 3 Проверка на дробное число введённое пользователем», порекомендованный @Alex.B, заменив float на int как @gil9red предложил и @slippyk явно показал:
def isint(s):
try:
int(s)
return True
except ValueError:
return False
Пример:
>>> isint('10')
True
>>> isint('a') # не десятичная цифра
False
>>> isint('²') # верхний индекс
False
>>> isint('১') # Bengali (Unicode)
True
Это может сломаться, если ввод не строка, например:
>>> isint(0.5) # XXX не работает для float True >>> 0.5 .is_integer() False >>> from numbers import Integral >>> isinstance(0.5, Integral) False >>> isinstance(123, Integral) True >>> isinstance(1., Integral) # XXX float False >>> 1..is_integer() # но целое значение True >>> from fractions import Fraction >>> isint(Fraction(1, 2)) # XXX не работает для дробей True >>> isinstance(Fraction(1, 2), Integral) False >>> isinstance(Fraction(1), Integral) # XXX дробь False >>> Fraction(1) == 1 # даже если целое значение True
5, Integral)
False
>>> isinstance(123, Integral)
True
>>> isinstance(1., Integral) # XXX float
False
>>> 1..is_integer() # но целое значение
True
>>> from fractions import Fraction
>>> isint(Fraction(1, 2)) # XXX не работает для дробей
True
>>> isinstance(Fraction(1, 2), Integral)
False
>>> isinstance(Fraction(1), Integral) # XXX дробь
False
>>> Fraction(1) == 1 # даже если целое значение
True
См. How to check if a float value is a whole number.
Если вы хотите проверить, что переданная строка содержит только десятичные цифры и ничего более (к примеру, нет '+','-', ' ', '\n' символов в ней), то можно str.isdecimal использовать:
>>> '123'.isdecimal()
True
>>> '+123'.isdecimal()
False
>>> isint('+123')
True
>>> isint(' 123\n')
True
>>> ' 123\n'.isdecimal()
False
isdecimal() можно использовать, чтобы имена файлов, содержащие цифры, в «естественном» порядке отсортировать (как Windows-проводнике).
Если хотите несколько таких чисел из ввода извлечь, можно регулярное выражение использовать:
>>> import re >>> from datetime import datetime >>> date_string = '2016-11-01 23:04:05' >>> datetime(*map(int, re.findall(r'\d+', date_string))) datetime.datetime(2016, 11, 1, 23, 4, 5)
Последнее, это возможно более простой, менее строгий (и эффективный) вариант для:
>>> datetime.strptime(date_string, '%Y-%m-%d %H:%M:%S') datetime.datetime(2016, 11, 1, 23, 4, 5)
Если вы хотите разрешить задавать целые числа в произвольном основании как в исходном коде Питона, то передайте
>>> int('0b1110', 0) # binary ("01")
14
>>> int('0xcafe', 0) # hexadecimal
51966
Подробнее в документации int.
5 способов извлечения квадратных корней в Python
Существует несколько способов получения квадратных корней в Python.
Изучите 5 подходов к извлечению квадратных корней в Python + некоторые бонусные продвинутые приемы.
Узнав о 4 способах возведения числа в квадрат в Python, пришло время заняться противоположной операцией — квадратным корнем Python. Эта статья научит вас пяти различным способам извлечения квадратных корней в Python и завершится бонусным разделом о кубических корнях и квадратных корнях из списков Python.
Давайте начнем с введения в тему и рассмотрения потенциальных проблем, которые необходимо учитывать при вычислении квадратных корней в Python.
Знакомство с квадратными корнями в Python
Проще говоря, квадратный корень из числа — это значение, которое возвращает одно и то же число при умножении на себя. Это обратная операция возведения в квадрат.
Например, 3 в квадрате равно 9, а квадратный корень из 9 равен 3, потому что 3 x 3 равно 9. Это понятие довольно сложно объяснить в одном предложении, но вы улавливаете идею, как только видите ее в действии.
.
Прежде чем углубляться в различные способы извлечения квадратных корней в Python, давайте рассмотрим наборы чисел, для которых можно и нельзя извлекать квадратные корни.
Квадратный корень из положительного числа
Квадратный корень хорошо работает только с положительными числами. На данный момент игнорируйте код, отвечающий за вычисления, и просто сосредоточьтесь на результатах.
Следующий фрагмент кода выводит квадратный корень из чисел 1 и 25:
import math
а = 1
б = 25
# Квадратный корень из положительного числа
a_sqrt = math.sqrt(а)
b_sqrt = math.sqrt(b)
# Распечатать
print("Квадратный корень из положительного числа")
Распечатать("----------------------------------------------- ---")
print(f"Квадратный корень из {a} = {a_sqrt}")
print(f"Квадратный корень из {b} = {b_sqrt}") Вот результат:
Изображение 1 — Квадратный корень из положительного числа (изображение автора) Итак, 1×1 = 1, а 5×5 = 25 — по сути, так работают квадратные корни.
Квадратный корень из нуля
Нуль не является ни простым, ни составным числом, поэтому мы не можем найти его простую факторизацию. По этой причине квадратный корень из нуля равен нулю:
import math
а = 0
# Квадратный корень из нуля
a_sqrt = math.sqrt(а)
# Распечатать
print("Квадратный корень из нуля")
Распечатать("----------------------------------------------- ---")
print(f"Квадратный корень из {a} = {a_sqrt}") Вот результат:
Изображение 2 — Квадратный корень из нуля (изображение автора)Остался только один вариант использования, и это отрицательные числа.
Квадратный корень из отрицательного числа
Невозможно вычислить квадратный корень из отрицательного числа, используя действительные числа. Умножение двух отрицательных чисел всегда дает положительное число.
Тем не менее, давайте попробуем:
импортировать математику а = -10 # Квадратный корень из отрицательного числа a_sqrt = math.sqrt(а) # Распечатать print("Квадратный корень из отрицательного числа") Распечатать("----------------------------------------------- ---") print(f"Квадратный корень из {a} = {a_sqrt}")
Выдает ошибку:
Изображение 3 — Квадратный корень из отрицательного числа (изображение автора)Есть способы вычислить квадратный корень из отрицательного числа, записав его как кратное -1. Например, -9 можно записать как -1 x 9. Результат будет 3i . Шагнуть в царство мнимых чисел сегодня не входит в наши планы, поэтому я остановлюсь на этом.
Далее, давайте рассмотрим 5 способов решения квадратных корней в Python.
Вычисление квадратных корней с помощью функции sqrt()
Первый метод — это тот, который вы видели в предыдущем разделе. Он полагается на функцию math.pow() , чтобы добиться цели. Этот модуль поставляется с установкой Python по умолчанию, поэтому нет необходимости устанавливать какие-либо внешние библиотеки.
Ниже приведен фрагмент кода, демонстрирующий, как извлекать квадратные корни в Python с помощью этой функции:
import math а = 1 б = 25 с = 30,82 д = 100 е = 400,40 # Метод №1 - функция math.
sqrt()
a_sqrt = math.sqrt(а)
b_sqrt = math.sqrt(b)
c_sqrt = math.sqrt(с)
d_sqrt = math.sqrt(d)
e_sqrt = math.sqrt(e)
# Распечатать
print("Способ №1 - функция math.sqrt()")
Распечатать("----------------------------------------------- ---")
print(f"Квадратный корень из {a} = {a_sqrt}")
print(f"Квадратный корень из {b} = {b_sqrt}")
print(f"Квадратный корень из {c} = {c_sqrt}")
print(f"Квадратный корень из {d} = {d_sqrt}")
print(f"Квадратный корень из {e} = {e_sqrt}") И вот результаты:
Изображение 4. Математическая функция sqrt() (изображение автора)Вероятно, это единственный метод, который вам понадобится, но давайте также рассмотрим некоторые альтернативы.
Вычисление квадратных корней с помощью функции pow()
Если возведение числа в квадрат означает возведение его в степень 2, то извлечение квадратного корня, по сути, означает возведение его в степень 0,5. Это именно то поведение, которое вы можете реализовать с помощью функции math.pow(). Он принимает два аргумента — число и показатель степени.
Давайте рассмотрим пару примеров:
импортировать математику
а = 1
б = 25
с = 30,82
д = 100
е = 400,40
# Способ №2 - функция math.pow()
a_sqrt = math.pow(a, 0,5)
b_sqrt = math.pow(b, 0,5)
c_sqrt = math.pow(c, 0,5)
d_sqrt = math.pow(d, 0,5)
e_sqrt = math.pow(e, 0,5)
# Распечатать
print("Способ №2 - функция math.pow()")
Распечатать("----------------------------------------------- ---")
print(f"Квадратный корень из {a} = {a_sqrt}")
print(f"Квадратный корень из {b} = {b_sqrt}")
print(f"Квадратный корень из {c} = {c_sqrt}")
print(f"Квадратный корень из {d} = {d_sqrt}")
print(f"Квадратный корень из {e} = {e_sqrt}") Вывод идентичен тому, что у нас было раньше:
Изображение 5 — функция Math pow() (изображение автора)Отлично, но можем ли мы полностью исключить использование библиотеки? Конечно, вот как.
Оператор экспоненты Python (**) для извлечения квадратных корней
Здесь применяется та же логика, что и в предыдущей функции. Вы можете возвести число в степень 0,5 с помощью оператора экспоненты Python.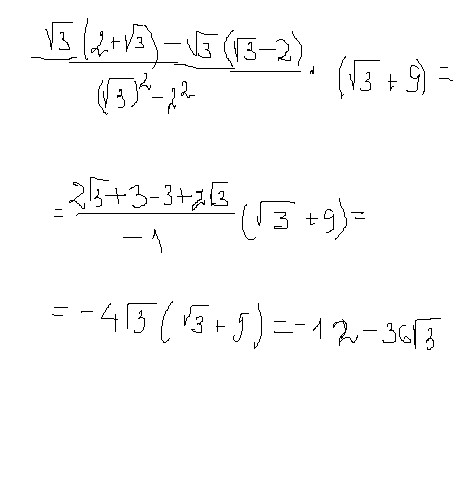
Он делает то же самое, что и math.pow(x, 0.5) , но синтаксис короче и не зависит от каких-либо библиотек.
Вот как это использовать в Python:
a = 1
б = 25
с = 30,82
д = 100
е = 400,40
# Способ №3 — Оператор экспоненты Python
а_кварт = а**0,5
b_sqrt = b**0,5
с_кварт = с**0,5
d_sqrt = d**0,5
e_sqrt = e**0,5
# Распечатать
print("Способ №3 — оператор экспоненты Python")
Распечатать("----------------------------------------------- ---")
print(f"Квадратный корень из {a} = {a_sqrt}")
print(f"Квадратный корень из {b} = {b_sqrt}")
print(f"Квадратный корень из {c} = {c_sqrt}")
print(f"Квадратный корень из {d} = {d_sqrt}")
print(f"Квадратный корень из {e} = {e_sqrt}") Результаты снова идентичны, никаких сюрпризов здесь нет:
Изображение 6. Оператор экспоненты Python (изображение автора)Теперь давайте посмотрим, как извлекать квадратные корни из чисел и массивов с помощью Numpy.
Numpy — вычисление корня числа или массива
Numpy — это библиотека для числовых вычислений в Python.
Он имеет встроенную функцию sqrt() , и вы можете использовать ее для извлечения квадратных корней как из чисел, так и из массивов.
Только учтите тип возврата — будет numpy.float64
numpy.ndarray для массива. Каждый элемент массива будет иметь тип numpy.float64 , конечно: import numpy as np
а = 1
б = 25
с = 30,82
д = 100
е = 400,40
обр = [а, б, с]
# Метод № 4 - Квадратные корни Numpy
a_sqrt = np.sqrt (а)
b_sqrt = np.sqrt (б)
c_sqrt = np.sqrt (с)
d_sqrt = np.sqrt(d)
e_sqrt = np.sqrt (е)
arr_sqrt = np.sqrt (арр)
# Распечатать
print("Способ №4 - Квадратные корни Numpy")
Распечатать("----------------------------------------------- ---")
print(f"Квадратный корень из {a} = {a_sqrt}")
print(f"Квадратный корень из {b} = {b_sqrt}")
print(f"Квадратный корень из {c} = {c_sqrt}")
print(f"Квадратный корень из {d} = {d_sqrt}")
print(f"Квадратный корень из {e} = {e_sqrt}")
print(f"Квадратный корень из {arr} = {arr_sqrt}") Вот вывод консоли:
Изображение 7 — Квадратные корни в Numpy (изображение автора) Это, безусловно, самый удобный метод, поскольку он основан на широко используемой библиотеке Python, а процедура вычисления одинакова независимо от тип данных.
Cmath — Take Python Квадратные корни комплексных чисел
Помните историю о квадратных корнях и отрицательных числах? Модуль Python math вызвал ошибку, но cmath здесь, чтобы спасти положение. Этот модуль используется для работы с комплексными числами.
В приведенном ниже фрагменте кода вы увидите квадратные корни, взятые из положительных целых, вещественных, комплексных и отрицательных чисел:
import cmath
а = 1
б = 25,44
с = cmath.pi
д = 10+10j
е = -100
# Способ №5 - Квадратные корни комплексных чисел
a_sqrt = cmath.sqrt(а)
b_sqrt = cmath.sqrt(b)
c_sqrt = cmath.sqrt (с)
d_sqrt = cmath.sqrt(d)
e_sqrt = cmath.sqrt(e)
# Распечатать
print("Способ №5 - Квадратные корни комплексных чисел")
Распечатать("----------------------------------------------- ---")
print(f"Квадратный корень из {a} = {a_sqrt}")
print(f"Квадратный корень из {b} = {b_sqrt}")
print(f"Квадратный корень из {c} = {c_sqrt}")
print(f"Квадратный корень из {d} = {d_sqrt}")
print(f"Квадратный корень из {e} = {e_sqrt}") На этот раз ошибок нет:
Изображение 8 — Квадратные корни комплексных чисел (изображение автора) У меня никогда не было необходимости использовать этот модуль, но приятно знать, что он существует.
Далее давайте рассмотрим несколько более сложных примеров использования квадратных корней в Python.
Бонус: расширенные темы Python Roots
Теперь мы переключим передачу и обсудим несколько более сложных тем. К ним относятся способы вычисления кубических корней в Python и извлечения квадратных корней из ванильных списков Python. Начнем с кубических корней.
Кубический корень в Python
Если извлечение квадратного корня означает возведение числа в степень 0,5, то кубический корень должен быть представлен степенью 0,333, или 1/3.
Вот как реализовать эту логику на Python без каких-либо внешних библиотек:
a = 1
б = 27
с = 30,82
д = 1000
е = 400,40
# Бонус №1 - Кубические корни
a_cbrt = а ** (1./3.)
b_cbrt = b ** (1./3.)
c_cbrt = c ** (1./3.)
d_cbrt = d ** (1./3.)
e_cbrt = e ** (1./3.)
# Распечатать
print("Бонус №1 - Кубические корни")
Распечатать("----------------------------------------------- ---")
print(f"Кубический корень из {a} = {a_cbrt}")
print(f"Кубический корень из {b} = {b_cbrt}")
print(f"Кубический корень из {c} = {c_cbrt}")
print(f"Кубический корень из {d} = {d_cbrt}")
print(f"Кубический корень из {e} = {e_cbrt}") Результаты напечатаны ниже:
Изображение 9 — Кубические корни (1) (изображение автора) Numpy предоставляет более простой способ извлечения кубических корней в Python.
Он имеет встроенную функцию cbrt() , что означает кубический корень . Вы можете использовать его как с числами, так и с массивами, как и с квадратными корнями:
import numpy as np
а = 1
б = 27
с = 30,82
д = 1000
е = 400,40
обр = [а, б, с]
# Бонус № 1.2 — Кубические корни с Numpy
a_cbrt = np.cbrt(а)
b_cbrt = np.cbrt(б)
c_cbrt = np.cbrt (с)
d_cbrt = np.cbrt(d)
e_cbrt = np.cbrt(e)
arr_cbrt = np.cbrt (обр)
# Распечатать
print("Бонус №1.2 — Кубические корни с Numpy")
Распечатать("----------------------------------------------- ---")
print(f"Кубический корень из {a} = {a_cbrt}")
print(f"Кубический корень из {b} = {b_cbrt}")
print(f"Кубический корень из {c} = {c_cbrt}")
print(f"Кубический корень из {d} = {d_cbrt}")
print(f"Кубический корень из {e} = {e_cbrt}")
print(f"Кубический корень {arr} = {arr_cbrt}") Давайте посмотрим на результаты:
Изображение 10 — Кубические корни (2) (изображение автора)Да, это так просто.
Квадратный корень списка в Python
Также есть простой способ вычислить квадратный корень из списков Python без Numpy.
Вы можете просто пройтись по списку и извлечь квадратный корень из отдельного элемента списка:
import math
обр = [1, 25, 30,82]
arr_sqrt = []
# Бонус №2 — Квадратный корень списка Python
для числа в обр:
arr_sqrt.append (math.sqrt (число))
# Распечатать
# Распечатать
print("Бонус №2 — Квадратный корень списка Python")
Распечатать("----------------------------------------------- ---")
print(f"Квадратный корень из {arr} = {arr_sqrt}") Вот результат:
Изображение 11 — Квадратный корень списка (1) (изображение автора)Или, если вы предпочитаете более питонический подход, нет причин не использовать понимание списка и просто вышеприведенное вычисление для одна строка кода:
импортировать математику
обр = [1, 25, 30,82]
# Бонус № 2.2 — Квадратный корень списка Python с использованием понимания списка
arr_sqrt = [math.sqrt(число) для числа в обр]
# Распечатать
# Распечатать
print("Бонус №2.2 — Квадратный корень списка Python с использованием понимания списка")
Распечатать("----------------------------------------------- ---")
print(f"Квадратный корень из {arr} = {arr_sqrt}") Результат идентичен:
Изображение 12 — Квадратный корень из списка (2) (изображение автора) Вот как легко извлекать квадратные корни в Python — для целых чисел, чисел с плавающей запятой, списков и даже комплексных чисел.
Далее сделаем краткий обзор.
Заключение
Теперь вы знаете 5 различных способов вычисления квадратных корней Python. На практике вам нужен только один, но знать пару альтернатив не помешает. Вы можете использовать встроенный модуль math , выберите numpy или используйте оператор экспоненты и вообще избегайте библиотек. Все подходы работают, а выбор за вами.
Следите за обновлениями блога, если хотите узнать больше об основных понятиях Python. Спасибо за прочтение!
Рекомендуемое чтение- 5 лучших книг для изучения основ обработки и анализа данных (математика, статистика и программирование)
- 5 лучших книг для изучения науки о данных в 2022 году
- 7 способов распечатать список на Python
- Наймите меня в качестве технического писателя
- Подпишитесь на YouTube
- Подключайтесь к LinkedIn
Мнимые и комплексные числа
Мнимые и комплексные числа
Математики выделили особое
число i, равное квадратному корню из минус 1. Отсюда следует, что i 2 =
-1. Чтобы определить квадратный корень из отрицательного числа (например, -16), возьмите
квадратный корень из абсолютного значения числа (квадратный корень из 16 = 4), а затем умножить его на
‘я’. Итак, квадратный корень из -16 равен 4i. Когда число имеет форму a + bi (действительное число плюс мнимое число), оно называется
«комплексное число». Как комплексные числа «возникают» в математике? Хорошим примером будет
корни квадратного уравнения x 2 -6x + 25 = 0, где 2 корня равны 3 + 4i и
3 — 4и. Сложение и вычитание комплексных чисел в значительной степени следуют правилам базовой арифметики и
так что мы не будем обсуждать это. Умножение начинает становиться немного сложнее. Учтите: Вы задавались вопросом — деление сложнее, чем умножение? Уверенный. ————— (7 + 5i) Знаменатель равен (7 + 5i), а его сопряженное число равно (7-5i) ————————— ((7 + 5i) * (7 — 5i)) (78 — 24 I) ————— 74 78 24i — — минус — 74 74 Теперь переходим к еще большей сложности. Далее мы определим эти две величины: Наконец, 2 квадратных корня комплексного числа: Пример должен сделать эту процедуру более понятной. Найдите квадратный корень из 12 + 16i Даже если у вас есть калькулятор, который может сделать эти расчеты для
Вы, теперь вы знаете процедуры для арифметики комплексных чисел. | ||||||
Как это может быть сделано ? В конце концов, положительное число в квадрате или
отрицательное число в квадрате всегда будет равняться положительному числу.
Можем ли мы быть уверены, что это корни уравнения? 
Сначала мы должны определить
новый терм — сопряженный , в силу чего сопряженный а + би = а-би. 
