Лекция по математике.Раздел 1. Линейная алгебра. Тема: Матрицы и опрделители. Занятие №2. | План-конспект урока по алгебре (11 класс) по теме:
Раздел 1. Линейная алгебра
Тема 1.1. Матрицы и определители
Урок №2.
Тема: Определители квадратных матриц. Свойства определителей.
Цель: приобретение базовых знаний в области фундаментального раздела математики – линейной алгебры. Изучить понятие определителя, методов его вычисления.
Задачи:
• развитие творческого профессионального мышления;
• познавательная мотивация;
• овладение языком науки, навыки оперирования понятиями;
• овладение умениями и навыками постановки и решения задач;
• углубление теоретической и практической подготовки;
• развитие инициативы и самостоятельности студентов.
Вид занятия: Семинар комбинированного типа
Ход занятия.
1.Формулирование темы занятия, пояснение связи темы с другими темами учебной дисциплины;
2.Проверка готовности студентов к занятию;
3.
Проведение непосредственно занятия согласно тематике и в соответствии с рабочей программой дисциплины:
› Изучить теоретический материал по теме «Определители .Вычисление определителей».
› Рассмотреть примеры решения типовых заданий.
› Ответить на контрольные вопросы.
1.Организационный момент.
2.Проверка домашнего задания.
3. Изучение нового материала.
Создание проблемной ситуации при постановке темы, цели и задач лекции.
В школьном курсе алгебры 7 – 9 классов рассматриваются различные способы решения систем линейных уравнений: метод подстановки, метод сложения, метод двойного сложения, графический метод, метод сравнения. Возникает вопрос, а существуют ли какие-либо другие способы решения данных систем. Действительно, кроме методов, изучаемых в школе, существуют и другие, доступные для учащихся старших классов методы решения систем линейных уравнений: метод Крамера, метод Гаусса, матричный метод. Эти методы способствуют развитию внимания, памяти.
При применении этих методов встречаются новые понятия: «матрица», «определитель», «минор», «дополнение». Возникает необходимость уметь вычислять определители, миноры, дополнения.
Что же такое определитель, как его можно вычислить?
Обозначение: (детерминант). Они существуют у квадратных матриц.
Определение 1. Определителем второго порядка называется выражение
Определение 2. Определителем третьего порядка называется выражение
Есть другие способы для нахождения определителя третьего порядка.
1. =
где — элементы определителя,
— миноры элементов а1, b1, c1
Минором Мij какого – либо элемента аij определителя порядка n называется определитель порядка n – 1, полученный из вычерчиванием i– й строки и j – го столбца.
2.
Определитель III порядка можно найти по схеме:
+ —
+ + +
3.
=
— — —
Для нахождения определителя III порядка можно использовать две теоремы.
Пусть задан определитель:
Теорема 1.Определитель равен сумме произведений элементов какой – либо строки на их алгебраические дополнения, т. е.
Теорема 2. Определитель равен сумме произведений элементов какого – либо столбца на их алгебраические дополнения, т.е.
Эти теоремы облегчают вычисления определителя, когда среди элементов есть нули.
Пример: Найти определитель
Решение: Воспользуемся формулой (2) теоремы 1.
Проверим, найдём этот же определитель способом 3.
Определителем четвёртого порядка называется
выражение где A1, B1, C1, D1 — алгебраические дополнения элементов a1, b1, c1, d1.
4.Закрепление изученного материала. Решение задач.
1. Вычислить данный определитель четвёртого порядка с помощью разложения по строке или столбцу:
Решение.
Удобнее всего делать разложение по строке или столбцу, в которых встречается наибольшее число нулевых элементов. В данном случае – это четвёртый столбец.
Полученные в итоге два определителя третьего порядка вычислим тем же методом. В определителе нулевых элементов нет, поэтому можно выбрать для разложения любой из столбцов, например, первый. В единственный нулевой элемент находится на пересечении первого столбца со второй строкой. Для разнообразия будем разлагать по второй строке:
2. Используя метод обращения в нуль всех, кроме одного, элементов строки или столбца вычислить определитель матрицы
Решение. Будем занулять все, кроме первого, элементы первой строки. С этой целью вычтем из второго, третьего и четвёртого столбцов первый столбец, умноженный соответственно на 2, 3 и 4. Получим
Представленный в таком виде определитель разложим по первой строке:
Определитель третьего порядка, к которому свёлся исходный определитель, будем вычислять тем же способом.
Вычтем из второго и третьего столбцов первый столбец, умноженный соответственно на 2 и 7. Получим (попутно вынося общие множители из столбцов)
3. Используя метод приведения к треугольному виду вычислить определитель из примера 2.
Решение. Воспользуемся видом определителя , который получился после процедуры зануления всех элементов (кроме первого) первой строки:
.
Далее с помощью второго столбца занулим элементы второй строки, кроме первых двух, для чего вычтем из третьего и четвёртого столбцов
второй столбец, умноженный соответственно на 2 и 7. Получим (попутно вынося общие множители из столбцов)
Наконец, вычтем третий столбец из четвёртого, в результате чего определитель сведётся к треугольному виду, величина которого равна произведению элементов главной диогонали: .
5.Итог занятия. Рефлексия.
6.Домашнее задание. Учить определения, составить опорную схему конспекта.
Выполнить упражнения:
Используя свойства определителей, вычислить следующие определители:
1. 2.
3.
4.
5.
Вычисление определителя матрицы 4 x 4 с примерами решения
Детерминанты — это скаляры, которые получаются суммой произведений элементов квадратной матрицы и их кофакторов по определенному правилу. Определители в математике помогают нам найти сопряженную матрицу, а также обратную матрицу. Мы можем использовать определители для решения линейных уравнений с помощью метода обращения матриц. Кроме того, определители помогают найти векторное произведение двух векторов.
Что такое определитель матрицы 4×4? Определитель матрицы 4×4 — это уникальное число, вычисляемое по специальной формуле. Если матрица имеет порядок n x n, то это квадратная матрица. Итак, здесь 4×4 — это квадратная матрица, состоящая из 4 строк и 4 столбцов. Также для квадратной матрицы A порядка \(4 \times 4 \) ее определитель записывается как |A|.
Могут быть разные способы нахождения определителей матрицы порядка \(4 \times 4 \).
Условия для того, чтобы определитель матрицы 4×4 был равен нулюПрежде чем пытаться вычислить значение определителя матрицы 4×4, нам сначала нужно проверить, является ли значение определителя ненулевым числом.
Это можно сделать, просто проанализировав предоставленный определитель.
Некоторые случаи, когда значение определителя матрицы 4×4 равно нулю: матрица}\справа|\)
В этом случае одна из строк матрицы равна нулю, поэтому значение определителя матрицы становится равным нулю.
Случай 2: \(\left|\begin{matrix}2&1&2&3\\6&7&6&9\\0&6&0&0\\1&2&1&4\end{matrix}\right|\)
В приведенной выше матрице, как мы видим, первый и третий столбцы имеют одинаковые значения, поэтому значение определителя матрицы \(4 \times 4 \) равно нулю.
Случай 3: \(\left|\begin{matrix}1&2&3&4\\2&5&7&3\\4&10&14&6\\3&4&2&7\end{matrix}\right|\)
В приведенном выше сценарии мы видим, что вторая и третья строки пропорциональны друг другу.
Итак, значение определителя матрицы \(4\times 4\) равно нулю.
Теперь, когда мы знаем случаи, когда значение определителя может быть равно нулю, давайте проверим, как найти значение определителя для матрицы \(4 \times 4 \) в случае, если он не равен нулю.
Узнать о свойствах определителей
Что такое исключение Гаусса?Метод исключения Гаусса также называется методом редукции строк и используется для решения линейных уравнений в линейной алгебре. Этот метод исключения на самом деле представляет собой серию операций, которые используются с матрицей, и очень полезен при нахождении ранга матрицы, обратной матрицы и даже определителя матрицы.
Чтобы выполнить это исключение, мы используем ряд алгебраических операций над матрицей, превращая все элементы ниже главной диагонали в нуль.
Мы можем использовать три вида операций над строками:
- Поменяв местами две строки: значение определителя меняет знак. Отрицательное становится положительным, а положительное становится отрицательным.
- Значение определителя остается неизменным при умножении строки на ненулевую константу.
- Значение определителя остается неизменным при добавлении или вычитании строки из любой другой строки.
Узнайте об инволютивной матрице
Свойство треугольности матрицыЧтобы найти определитель матрицы \(4 x 4 \), мы должны хорошо знать свойство треугольности матрицы. По свойству треугольности матрицы говорят, что если каждый элемент матрицы как выше, так и ниже главной диагонали равен нулю, то значение определителя равно произведению диагональных элементов.
Теперь существует три вида треугольных матриц, мы узнаем о каждом из них ниже:
1. Верхняя треугольная матрица: \(4 \times 4 \)Матрица называется верхней треугольной матрицей, когда все элементы ниже главной диагонали равны нулю. Или можно сказать, что все ненулевые элементы такой матрицы находятся выше главной диагонали.
Пример:
\(\left|\begin{matrix}1&2&3&4\\0&5&7&3\\0&0&4&6\\0&0&0&7\end{matrix}\right|\) — верхняя треугольная матрица.
2. Нижняя треугольная матрица: Матрица \(4 \times 4 \) называется нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю. Или можно сказать, что все ненулевые элементы такой матрицы находятся ниже главной диагонали.
Пример:
\(\left|\begin{matrix}2&0&0&0\\6&7&0&0\\0&6&4&0\\1&2&1&4\end{matrix}\right|\) — нижняя треугольная матрица.
3. Диагональная матрица: \(4 \times 4 \) Матрица называется диагональной матрицей, когда все элементы, кроме главной диагонали, равны нулю. Или можно сказать, что в такой матрице все, что выше или ниже главной диагонали, равно нулю.
Пример:
\(\left|\begin{matrix}2&0&0&0\\0&7&0&0\\0&0&4&0\\0&0&0&4\end{matrix}\right|\)
Значение определителя во всех трех вышеперечисленных случаях равно произведение диагональных элементов. Поясним это на примере:
Пример: Пусть задано
\(\left|\begin{matrix}2&3&3&1\\1&5&4&3\\4&6&8&5\\-2&-3&-3&4\end{matrix}\right| \)
Мы знаем, что добавление строк и столбцов к другим строкам и столбцам того же определителя не приводит к изменению значения определителя.
С помощью операций:
\(r_2-r_1\)
\(r_3-2r_1\)
\(r_4+r_1\)
Результирующая матрица будет иметь вид:
\(\left| \begin{matrix}2&3&3&1\\0&2&1&3\\0&0&2&5\\0&0&0&5\end{matrix}\right|\)
Как мы знаем, для треугольной матрицы определитель равен произведению диагональных элементов.
Итак, |В| = 2.2.2.5 = 40.
Узнайте о применении матриц и определителей
Что такое метод расширения кофактора?Чтобы найти определитель для матрицы \(4 \times 4 \), мы используем другой метод, который представляет собой разложение на кофакторы. Вот как выполнить этот метод.
В матрице \(4 x 4 \) выберите любую строку или столбец, и мы умножим каждый элемент строки или столбца на соответствующие им коэффициенты. И, наконец, находим сумму всех произведений.
Поэтому рекомендуется выбирать строку или столбец с максимальным количеством нулей. Это сократит время расчета, а также вероятность ошибки.
{3+1}\раз\влево|\начать{матрицу}0&-2\\ 95\times\left|\begin{matrix}-1&-2\\
1&-5\end{matrix}\right|+0\right)\)
\(\det\left(A\right)\ )=\(5\times -1\times \left|\begin{matrix}-1&-2\\
1&-5\end{matrix}\right|\)
\(\det\left(A\ right)\)= (5)(-7)= -35
Узнайте о матрице кофакторов
Решенные примеры определителя матрицы 4 × 4Вопрос 1: Найдите определитель матрицы \(B=\ влево|\начало{матрица}4&3&4&2\\8&7&5&3\\4&3&8&5\\4&3&4&3\конец{матрица}\вправо|\)
Ответ 1: Мы будем использовать эти операции на приведенной выше матрице;
\(r_3-r_1\)
\(r_2-2r_1\)
\(r_4-r_1\)
Матрица, полученная после операций, выглядит следующим образом;
\(B=\left|\begin{matrix}4&3&4&2\\0&1&3&-1\\0&0&4&3\\0&0&0&1\end{matrix}\right|\)
Матрица является верхней треугольной матрицей, поэтому определитель произведение всех диагональных элементов.
Итак, det(B)=4.1.4.1 = 16
Мы надеемся, что приведенная выше статья поможет вам понять и подготовиться к экзамену.
Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
В.1 Для чего используются определители?
Ответ 1 Детерминанты используются для нахождения решений линейных уравнений, для определения того, как линейные преобразования изменяют площадь и объем, а также для изменения переменных в интегралах.
Q.2 Каковы свойства определителей?
Ответ 2 Некоторыми из важных свойств определителей являются скалярное кратное свойство, свойство всех нулей, факторное свойство, свойство пропорциональности, свойство кофакторной матрицы, свойство отражения, свойство треугольника, свойство суммы и свойство инвариантности.
Q.
3 Что такое метод обратной матрицы?
Ответ 3 Обратная матрица находится только для квадратной матрицы. Это можно сделать, просто разделив сопряжение данной матрицы на определитель данной матрицы.
Q.4 Что такое формула определителя треугольной матрицы?
Ответ 4 Для треугольной матрицы определитель равен произведению всех диагональных элементов.
В.5 Являются ли определители коммутативными?
Ответ 5 Да, умножение определителей коммутативно. Мы можем понять это на примере. Пусть A и B — две квадратные матрицы порядка \(n\times n\). det(AB)=\(det(A)\times det(B)=det(B)\times det(A)\).
Скачать публикацию в формате PDF| Угол между двумя плоскостями: изучите понятие, формулу и примеры решения |
| Среднее значение сгруппированных данных: изучите понятие, формулу, методы и примеры решения Значения, формулы, таблицы, приложения с примерами |
| Формулировка теоремы Аполлония с доказательством теоремой Пифагора, правилом косинусов и векторами |
| Этин: узнайте его формулу, структуру, получение, свойства и применение |
ОДУ: определитель
Примечание: 1 лекция
Для квадратных матриц мы определяем полезную величину, называемую определителем .
Определите определитель матрицы \(1 \times 1\) как значение ее единственного элемента
\begin{уравнение*} \det \left( \begin{bматрица} а \end{bmatrix} \верно) \overset{\text{защита}}{=} а . \end{уравнение*}
Для матрицы \(2 \times 2\), определите 9п\) к себе. Таким образом, \(2 \times 2\) матрица \(A\) является отображением плоскости на себя. Определитель \(A\) — это коэффициент, на который изменяется площадь объектов. Если взять единичный квадрат (квадрат со стороной 1) на плоскости, то \(A\) переводит квадрат в параллелограмм площади \(\lvert\det(A)\rvert\text{.}\) Знак of \(\det(A)\) обозначает изменение ориентации (отрицательное, если оси перевернуты). Например, пусть
\begin{уравнение*} А = \begin{bматрица} 1 и 1 \\ -1 и 1 \end{bmatrix} . \end{уравнение*}
Тогда \(\det(A) = 1+1 = 2\text{.}\) Посмотрим, куда \(A\) отправляет единичный квадрат — квадрат с вершинами \((0,0)\text{ ,}\) \((1,0)\text{,}\) \((0,1)\text{,}\) и \((1,1)\text{.}\) Точка \ ((0,0)\) отправляется в \((0,0)\text{.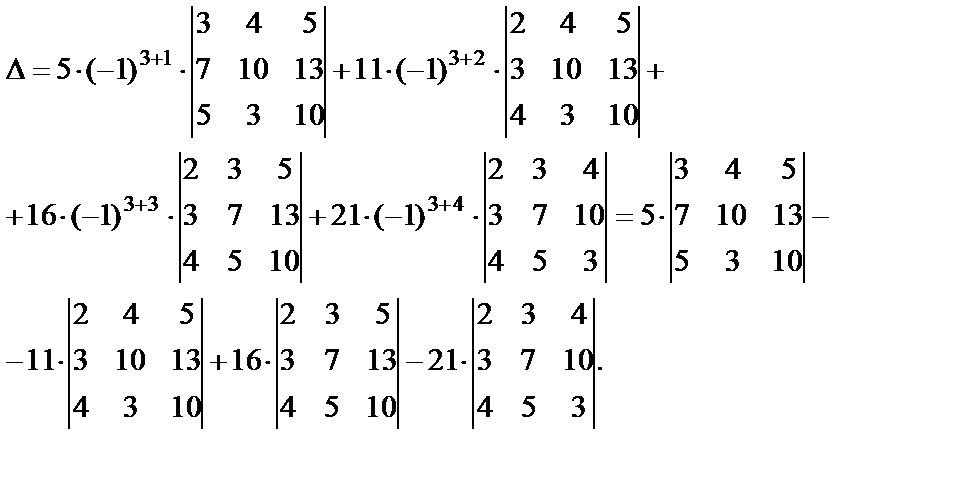
\begin{уравнение*} \begin{bматрица} 1 и 1 \\ -1 и 1 \end{bmatrix} \begin{bматрица} 1\0 \end{bmatrix} = \begin{bматрица} 1\\ -1 \end{bmatrix} , \qquad \begin{bматрица} 1 и 1 \\ -1 и 1 \end{bmatrix} \begin{bматрица} 0\1 \end{bmatrix} = \begin{bматрица} 1\\ 1 \end{bmatrix} , \qquad \begin{bматрица} 1 и 1 \\ -1 и 1 \end{bmatrix} \begin{bматрица} 1\1 \end{bmatrix} = \begin{bматрица} 2\\ 0 \end{bmatrix} . \end{уравнение*}
Образ квадрата — это другой квадрат с вершинами \((0,0)\text{,}\) \((1,-1)\text{,}\) \((1,1)\text{ ,}\) и \((2,0)\text{.}\) Квадрат изображения имеет длину стороны \(\sqrt{2}\text{,}\) и, следовательно, имеет площадь 2. См. Рисунок А.7.
Рисунок А.7. Изображение единичного квадрата через отображение \(A\text{.}\)В общем случае изображение квадрата будет параллелограммом. В средней школе геометрии вы, возможно, видели формулу для вычисления площади параллелограмма с вершинами \((0,0)\text{,}\) \((a,c)\text{,}\) \( (b,d)\) и \((a+b,c+d)\text{.}\) Площадь равна
\begin{уравнение*}
\left\lvert \, \det \left(
\begin{bmatrix} a & b \\ c & d \end{bmatrix}
\право) \, \право\перевернуть
«=»
\lvert
а г — б в
\вернуть
.
{1+j}
a_{1j} \det (A_{1j}) ,
\end{уравнение*}
или другими словами
\begin{уравнение*} \дет (А) = а_{11} \det (А_{11}) — а_{12} \det (А_{12}) + а_{13} \det (А_{13}) — \cdots \begin{случаи} + a_{1n} \det (A_{1n}) & \text{если } n \text{ нечетно,} \\ — a_{1n} \det (A_{1n}) & \text{if } n \text{ четное.} \end{случаи} \end{уравнение*}
Для матрицы \(3 \times 3\) мы получаем \(\det (A) = a_{11} \det (A_{11}) — a_{12} \det (A_{12}) + a_{13} \det (A_{13})\text{.}\) Например,
\begin{уравнение*} \начать{разделить} \det \left( \begin{bматрица} 1 и 2 и 3 \\ 4 и 5 и 6 \\ 7 и 8 и 9\end{bmatrix} \верно) «=» 1 \cdot \det \left( \begin{bматрица} 5 и 6 \\ 8 и 9 \end{bmatrix} \верно) — 2 \cdot \det \left( \begin{bматрица} 4 и 6 \\ 7 и 9 \end{bmatrix} \верно) + 3 \cdot \det \left( \begin{bматрица} 4 и 5 \\ 7 и 8 \end{bmatrix} \верно) \\ «=» 1 (5 \cdot 9 — 6 \cdot 8) — 2 (4 \cdot 9 — 6 \cdot 7) + 3 (4 \cdot 8 — 5 \cdot 7) = 0 . \конец{разделить} \end{уравнение*}
Получается, что не обязательно использовать первую строку.
То есть для любого \(i\text{,}\) 9{я+к}
a_{ij} \det (A_{ij}) .
\end{уравнение*}
Иногда полезно использовать строку, отличную от первой. В следующем примере удобнее расширяться по второй строке. Обратите внимание, что для второй строки мы начинаем с отрицательного знака.
\begin{уравнение*} \начать{разделить} \det \left( \begin{bматрица} 1 и 2 и 3 \\ 0 и 5 и 0 \\ 7 и 8 и 9 \end{bmatrix} \верно) «=» — 0 \cdot \det \left( \begin{bматрица} 2 и 3 \\ 8 и 9 \end{bmatrix} \верно) + 5 \cdot \det \left( \begin{bматрица} 1 и 3 \\ 7 и 9\end{bmatrix} \верно) — 0 \cdot \det \left( \begin{bматрица} 1 и 2 \\ 7 и 8 \end{bmatrix} \верно) \\ «=» 0 + 5 (1 \cdot 9 — 3 \cdot 7) + 0 = -60 . \конец{разделить} \end{уравнение*}
Проверим, действительно ли это то же самое, что расширение по первой строке,
\begin{уравнение*}
\начать{разделить}
\det \left(
\begin{bматрица}
1 и 2 и 3 \\
0 и 5 и 0 \\
7 и 8 и 9
\end{bmatrix}
\верно)
«=»
1 \cdot
\det \left(
\begin{bматрица}
5 и 0 \\
8 и 9
\end{bmatrix}
\верно)
—
2 \cdot
\det \left(
\begin{bматрица}
0 и 0 \\
7 и 9Т).
\end{уравнение*}
Матрица является верхнетреугольной , если все элементы ниже главной диагонали равны 0. Например,
\begin{уравнение*} \begin{bматрица} 1 и 2 и 3 \\ 0 и 5 и 6 \\ 0 и 0 и 9 \end{bmatrix} \end{уравнение*}
— верхний треугольник. Точно так же нижняя треугольная матрица
\begin{уравнение*} \begin{bматрица} 1 и 0 и 0 \\ 4 и 5 и 0 \\ 7 и 8 и 9\end{bmatrix} . \end{уравнение*}
Определитель треугольных матриц вычислить очень просто. Рассмотрим нижнюю треугольную матрицу. Если мы разложим по первой строке, мы обнаружим, что определитель в 1 раз больше определителя нижней треугольной матрицы \(\left[ \begin{smallmatrix} 5 & 0 \\ 8 & 9 \end{smallmatrix} \right]\text{.}\) Итак, определитель — это просто произведение диагональных элементов:
\begin{уравнение*}
\det \left(
\begin{bматрица}
1 и 0 и 0 \\
4 и 5 и 0 \\
7 и 8 и 9\end{bmatrix}
\верно)
«=»
1 \cdot 5 \cdot 9 = 45 .
\end{уравнение*}
Аналогично для верхних треугольных матриц
\begin{уравнение*} \det \left( \begin{bматрица} 1 и 2 и 3 \\ 0 и 5 и 6 \\ 0 и 0 и 9 \end{bmatrix} \верно) «=» 1 \cdot 5 \cdot 9 = 45 . \end{уравнение*}
Вообще, если \(A\) треугольна, то
\begin{уравнение*} \det (A) = a_{11} a_{22} \cdots a_{nn} . \end{уравнение*}
Если \(A\) диагональный, то он также треугольный (верхний и нижний), поэтому применяется та же формула. Например,
\begin{уравнение*} \det \left( \begin{bматрица} 2 & 0 & 0 \\ 0 и 3 и 0 \\ 0 и 0 и 5 \end{bmatrix} \верно) «=» 2 \cdot 3 \cdot 5 = 30 . \end{уравнение*}
В частности, единичная матрица \(I\) является диагональной, и все диагональные элементы равны 1. Таким образом,
\begin{уравнение*} \det(I) = 1 . \end{уравнение*}
Определитель говорит вам, как масштабируются геометрические объекты. Если \(B\) удваивает размеры геометрических объектов, а \(A\) утраивает их, то \(AB\) (которое применяет \(B\) к объекту, а затем применяет \(A\)) должно сделать размер увеличивается в \(6\text{.
Теорема А.6.1.
\begin{уравнение*} \det(AB) = \det(A)\det(B) . \end{equation*}
Это свойство является одним из самых полезных, и оно часто используется для фактического вычисления определителей. Особенно интересное следствие состоит в том, чтобы отметить, что это означает для существования инверсий. Возьмем \(A\) и \(B\) обратные, то есть \(AB=I\text{.}\) Тогда
\begin{уравнение*} \det(A)\det(B) = \det(AB) = \det(I) = 1 . \end{уравнение*}
Ни \(\det(A)\), ни \(\det(B)\) не могут быть равны нулю. Этот факт является чрезвычайно полезным свойством определителя и часто используется в этой книге: 9{-1} «=» \frac{1}{ad-bc} \begin{bматрица} д&-б\ -с и а \end{bmatrix} . \end{уравнение*}
Обратите внимание на определитель матрицы \([\begin{smallmatrix}a&b\\c&d\end{smallmatrix}]\) в знаменателе дроби. Формула работает только в том случае, если определитель отличен от нуля, иначе мы делим на ноль.
Обычным обозначением определителя является пара вертикальных линий:
\begin{уравнение*}
\begin{vmatrix}
а и б \\
CD
\end{vmatrix}
«=»
\det \left(
\begin{bматрица}
а и б \\
CD
\end{bmatrix}
\верно) .