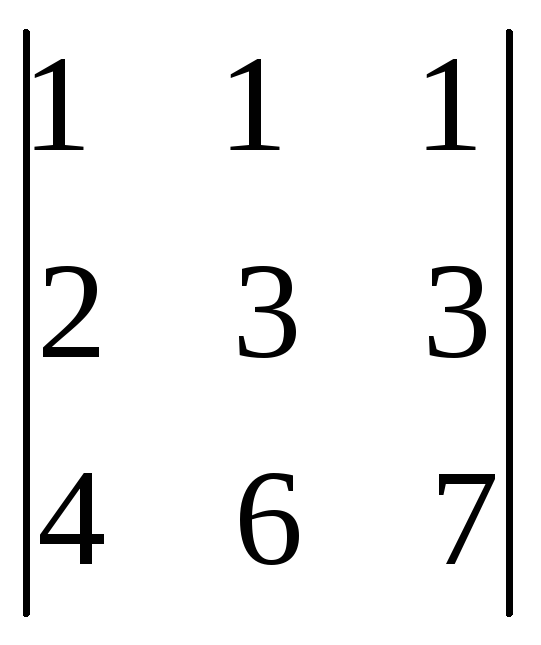
Основные свойства определителей матрицы
Автор Андрющенко Ольга Викторовна На чтение 3 мин. Просмотров 682 Опубликовано
Свойства определителей матриц помогают упрощать расчеты в курсе линейной алгебры. Какие это свойства и как они используются мы покажем на примерах.
Мы рассмотрели что такое определитель, как его вычислять и каков его геометрический смысл в статье «Определитель матрицы». А теперь подробно рассмотрим все свойства определителей матрицы.
Содержание
Свойство равноправности строк и столбцов
Определитель не изменится, если его строки поменять местами с соответствующими столбцами (то есть транспонировать):
\begin{vmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{vmatrix}= \begin{vmatrix} a_{11}& a_{21}\\ a_{12}& a_{22} \end{vmatrix}
Например,
\begin{vmatrix} 3& 4\\ 1& -2 \end{vmatrix}= \begin{vmatrix} 3& 1\\ 4& -2 \end{vmatrix}=3 \cdot (-2) -4 \cdot 1=-6-4=-10
Это свойство называют свойством равноправности строк и столбцов.
Свойство перестановок строк и столбцов
При перестановке двух строк (или двух столбцов) определитель изменит свой знак на противоположный:
\begin{vmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{vmatrix}= — \begin{vmatrix} a_{21}& a_{22}\\ a_{11}& a_{12} \end{vmatrix}
Например,
\begin{vmatrix} 3& 5\\ 1& 9 \end{vmatrix}= 3 \cdot 9-5 \cdot 1=27-5=22
Теперь поменяем местами строчки:
\begin{vmatrix} 1& 9\\ 3& 5 \end{vmatrix}= 1 \cdot 5-9 \cdot 3=5-27=-22
Свойство вынесения общего множителя в определителе
Общий множитель всех элементов строки (или столбца) можно вынести за знак определителя:
\begin{vmatrix} a_{11}& ka_{12}\\ a_{21}& ka_{22} \end{vmatrix}= k \begin{vmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{vmatrix}
Рассмотрим определитель:
\begin{vmatrix} 4& 3\\ 2& 7 \end{vmatrix}= 4 \cdot 7-3 \cdot 2=28-6=22
В первом столбце можно вынести множитель 2:
2\begin{vmatrix} 2& 3\\ 1& 7 \end{vmatrix}= 2 (2 \cdot 7-3 \cdot 1)=2 \cdot 11=22
Свойство определителя с равными строками или столбцами
Определитель с двумя одинаковыми строками или столбцами равен нулю.
Например,
\begin{vmatrix} 4& 3 & 2\\ 2& 7 & 1\\ 4& 3 & 2 \end{vmatrix}= 4 \cdot 7 \cdot 2+3\cdot 1 \cdot 4 + \\ + 2 \cdot 3 \cdot 2-2 \cdot 7 \cdot 4 — 2 \cdot 3 \cdot 2-1 \cdot 3 \cdot 4=\\ =56+12+12-56-12-12=0
Из данного свойства и свойства вынесения общего множителя вытекает следующее свойство.
Свойство определителя с пропорциональными элементами двух строк или двух столбцов
Если все элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю.
Проверим это свойство на примере:
\begin{vmatrix} 4& 3 & 2\\ 2& 7 & 1\\ 8& 6 & 4 \end{vmatrix}= 4 \cdot 7 \cdot 4+3\cdot 1 \cdot 8 + 2 \cdot 6 \cdot 2-\\ -2 \cdot 7 \cdot 8 — 2 \cdot 3 \cdot 4-1 \cdot 6 \cdot 4=\\=112+24+24-112-24-24=0
Свойство прибавления к строке или к столбцу
Если к какой-либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменится:
\begin{vmatrix} a_{11}+ka_{12}& a_{12}\\ a_{21}+ka_{22}& a_{22} \end{vmatrix}= — \begin{vmatrix} a_{11}& a_{12}\\ a_{21}& a_{22} \end{vmatrix}
Свойства определителя матрицы 3×3, у которого все элементы выше или ниже главной диагонали
Определитель 3×3, у которого все элементы, лежащие выше (или ниже) главной диагонали, — нули, равен произведению элементов главной диагонали:
\begin{vmatrix} a_{11}& 0 & 0\\ a_{21}& a_{22} & 0 \\ a_{31} & a_{32} & a_{33} \end{vmatrix}= \begin{vmatrix} a_{11}& a_{12} & a_{13}\\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{vmatrix}= a_{11}a_{22}a_{33}.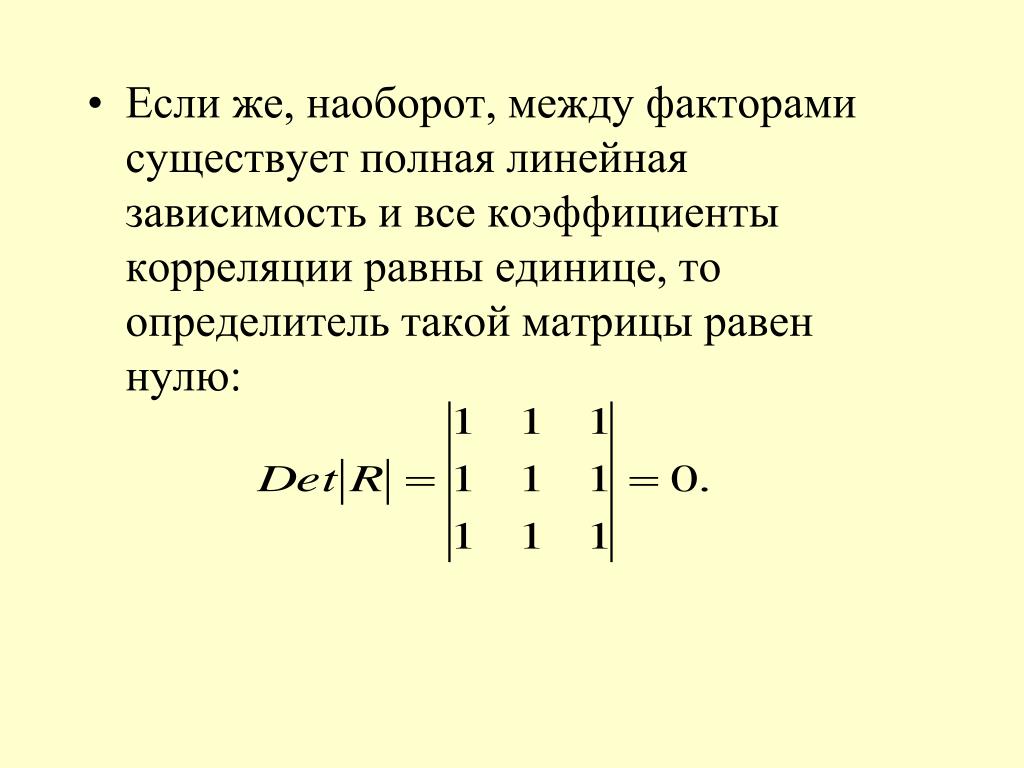
c++ — определитель собственной разреженной матрицы равен нулю
Задавать вопрос
спросил
Изменено 4 года, 1 месяц назад
Просмотрено 654 раза
Я пытаюсь вычислить, является ли разреженная матрица, с которой я работаю, положительно определенной. Для этого я пытаюсь использовать критерий Сильвестра, означающий, что ведущие миноры положительны.
Чтобы вычислить определитель матрицы, я создаю решатель sparseLU для каждого блока матрицы, который затем может дать мне определитель матрицы. Но, начиная с определенного размера (около 130 * 130), я получаю результат, что все определители равны 0. Это не какое-то особое измерение в моей проблеме (матрица имеет блоки 32 * 32), поэтому я считаю, что эта проблема связана к некоторому алгоритму усечения, примененному Эйгеном, с детерминантами, просто опускающимися ниже некоторых порогов.
Мои поиски такого механизма не дали достойных результатов. Моя матрица имеет размеры около 16k * 16k, и все ненулевые элементы находятся на 96 элементах рядом с диагональю.
Реализован ли в Eigen какой-либо механизм усечения и можно ли как-то управлять его порогами?
- c++
- разреженная матрица
- линейная алгебра
- собственный
4
Вероятно, это связано с недополнением, т. е. определитель вычисляется как произведение множества чисел, меньших 1,0 . Если вы вычислите произведение 130 значений около 0,5 , вы приблизитесь к границе того, что может быть представлено с плавающей запятой одинарной точности.
Вы можете использовать методы logAbsDeterminant и signDeterminant для получения значимых результатов.
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Почему мы всегда должны вычислять определитель | Анастасия Горина
Поскольку мы уже рассмотрели хардкор линейной алгебры, когда говорили о разложении по сингулярным числам, я решил, что было бы неплохо сделать шаг назад и обсудить то, что, как я предполагал, читатель уже знает — определитель .
Напоминаем, что мы заботимся о матрицах, потому что они, по сути, являются таблицами данных, а данные — это слон, на спине которого покоится современный мир. Но какое нам дело до det(A)? Что это означает?
Краткая заметка о вычислении
Вычислить определитель довольно просто, особенно если у нас есть матрица 2×2.
Учитывая приведенную выше матрицу, чтобы вычислить ее определитель, нам просто нужно взять разность произведений ее диагоналей: det(A) = ad-bc. Это немного сложнее, если у нас есть матрица 3×3, но также очень выполнимо.
Точная формула для вычисления определителя матрицы 3×3:
Но вот как об этом думать, не запоминая формулу. Вы записываете все элементы первой строки (a, b, c), а после этого закрываете пальцем первый столбец и первую строку, вычисляете определитель оставшейся матрицы 2×2 и ставите значение рядом с a. Затем вы закрываете пальцами второй столбец и первую строку, вычисляете определитель оставшейся матрицы 2×2 и ставите значение рядом с b.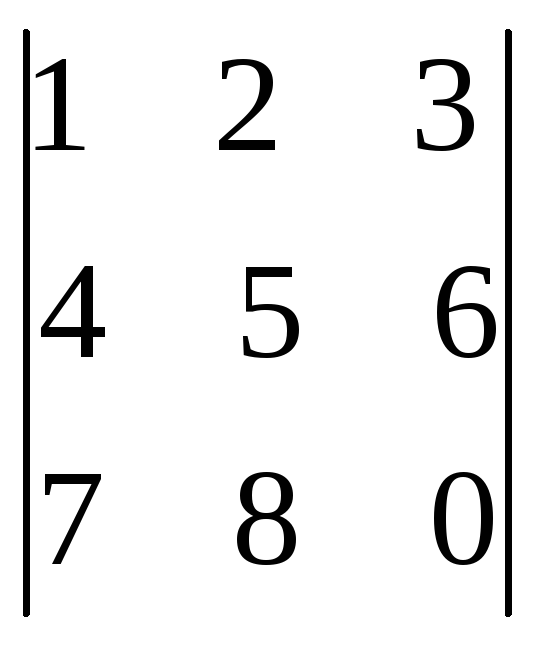
Повторите с третьим столбцом и первой строкой. Осталось только поставить чередующиеся знаки: начать с положительного перед a, отрицательного перед b и снова положительного перед c.
Это также работает со строками. Вы можете записать все элементы первого столбца, затем закрыть пальцем первый столбец и начать с просмотра оставшихся матриц после закрытия первой строки, второй строки и т. д. Это следствие первого свойства определителя : det(A)=det(A-транспонировать).
Итак, почему определитель?
Определитель работает почти таким же образом: это масштабный коэффициент , с помощью которого линейное преобразование изменяет любую площадь (для 2D) или объем (для 3D).
Если вы посмотрите на картинку вверху этого поста (опять же извините за мои плохие художественные навыки), слева мы видим квадрат 1×1, который представляет собой матрицу единичных векторов. Один указывает в направлении x и имеет величину 1 (1, 0), а другой указывает в направлении y и имеет величину 1 (0, 1). Это отправная точка. Линейное преобразование, связанное с матрицей ([2,0][0,3]), означает, что мы растягиваем первый вектор в 2 раза, а второй вектор в 3 раза. Если мы вычислим определитель этой матрицы, (2*3–0*0), получаем 6, то есть площадь получившегося прямоугольника.
Что произойдет, если определитель равен нулю? В 2D случае, когда у нас есть только матрица 2×2, это означает, что результирующая фигура после линейного преобразования имеет нулевую площадь. Вероятно, это просто плоская линия (я говорю «вероятно», потому что это может быть и точка). Если это матрица 3×3, то результирующая фигура после линейного преобразования имеет нулевой объем: это может быть плоская поверхность, линия или даже точка.