Ось тангенсов и котангенсов на окружности: Тригонометрические функции на единичной окружности. Тангенс и котангенс — урок. Алгебра, 10 класс.

Содержание

Определение тангенса и котангенса произвольного угла

Содержание:

Построим точку

По определению тангенса острого угла получим:

Определение тангенса угла

Определение:

Тангенсом угла называется отношение синуса угла к косинусу угла

Например,
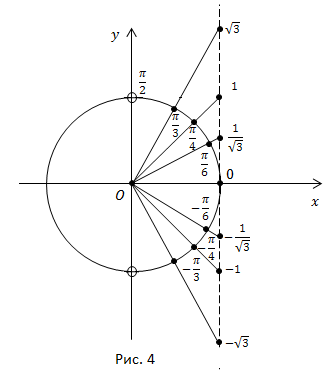
Используя определение тангенса угла и значения синуса и косинуса этого угла, найдем также значения тангенсов углов

Поскольку не существует.

Через точку проведем прямую, перпендикулярную оси абсцисс, и продолжим луч до пересечения с этой прямой в точке (рис. 52). Получим треугольник подобный треугольнику

Из подобия треугольников запишем равенство отношений их сторон:

Поскольку то ордината точки равна тангенсу угла

Прямая, перпендикулярная оси абсцисс, проходящая через точку называется осью тангенсов.

Нахождение тангенса произвольного угла

Для того чтобы найти тангенс произвольного угла а с помощью оси тангенсов, нужно:

Построить точку на единичной окружности.
Продолжить прямую до пересечения с осью тангенсов.
Найти ординату точки пересечения прямой с осью тангенсов.

Найдите тангенс угла

Значения тангенса произвольного угла с помощью оси тангенсов можно указать только приближенно. Для нахождения значения тангенса произвольного угла используют четырехзначные таблицы значений тангенса (синуса, косинуса)* или калькулятор. Методы высшей математики позволяют вычислять значения тангенса (синуса, косинуса) с любой заданной степенью точности.

Пример №1

Определите с помощью оси тангенсов:

Решение:

Пример №2

С помощью оси тангенсов сравните значения выражений

Решение:

Отметим на оси тангенсов точки, соответствующие углам (рис. 55), и сравним ординаты этих точек. Ордината точки больше ординаты точки значит,

Для углов тангенс не существует, так как косинусы этих углов равны нулю. Например, не существуют.
Построим точку единичной окружности поворотом точки вокруг начала координат на угол Рассмотрим прямоугольный треугольник , в котором гипотенуза равна 1 (радиусу единичной окружности), а его катеты равны: (рис. 56).

По определению котангенса острого угла получим:

Определение котангенса угла

Определение:

Котангенсом угла называется отношение косинуса угла к синусу угла

Например,
Поскольку

Воспользуемся полученным равенством и найдем значения котангенсов углов

Поскольку не существует.

Найденные значения синуса, косинуса, тангенса и котангенса углов занесем в таблицу.

Нахождение котангенса произвольного угла

Для того чтобы найти котангенс произвольного угла с помощью оси котангенсов, нужно:

Построить точку на единичной окружности.
Продолжить прямую до пересечения с осью котангенсов.
Найти абсциссу точки пересечения прямой с осью котангенсов.

Значения котангенса произвольного угла с помощью оси котангенсов можно указать только приближенно.

Заказать решение задач по высшей математике

Пример №3

Найдите значение выражения

Решение:

Через точку проведем прямую, перпендикулярную оси ординат, и продолжим луч до пересечения с этой прямой в точке (рис. 57).

Получим треугольник подобный треугольнику

Из подобия треугольников запишем равенство отношений их сторон: Поскольку то абсцисса точки равна котангенсу угла

Прямая, перпендикулярная оси ординат, проходящая через точку называется осью котангенсов.

Пример №4

Определите с помощью оси котангенсов:

Решение:

Пример №5

С помощью оси котангенсов сравните значения выражений

Решение:

Отметим на оси котангенсов точки, соответствующие углам (рис. 60), и сравним абсциссы этих точек. Абсцисса точки больше абсциссы точки значит,

Для углов и т. д. котангенс не существует, так как синусы этих углов равны нулю. Например, не существуют.

Пример №6

С помощью оси:

а) тангенсов найдите один из углов, тангенс которого равен

б) котангенсов найдите один из углов, котангенс которого равен

Решение:

а) 1 Отметим на оси тангенсов точку ордината которой равна (рис. 61).

2 Соединим эту точку с началом координат.

3 Найдем соответствующую точку на единичной окружности.

4 Отметим один из углов, соответствующий этой точке (см. рис. 61).

б) 1 Отметим на оси котангенсов точку абсцисса которой равна (рис. 62).

2 Соединим эту точку с началом координат.

3 Найдем соответствующую точку на единичной окружности.

4 Отметим один из углов, соответствующий этой точке (см. рис. 62).

Пример №7

Точка единичной окружности имеет координаты Используя определение тангенса и котангенса произвольного угла, найдите

Решение:

Так как точка единичной окружности имеет координаты
По определению тангенса:

По определению котангенса: значит,

Пример №8

Найдите значение выражения

Решение:

Пример №9

Найдите, если это возможно, значение выражения:

Решение:

не существует, так как

Пример №10

Если то может принимать значения:

Выберите правильные ответы.

Решение:

Так как тангенсом угла называется отношение синуса угла к косинусу угла , то нужно найти те углы синус которых равен нулю. Среди предложенных углов это углы

Можно также использовать ось тангенсов: найти точку на оси тангенсов, у которой ордината равна нулю (рис. 63), и определить соответствующие углы. Правильные ответы а) и г).

Пример №11

Расположите в порядке возрастания:

Решение:

Отметим на оси тангенсов точки, соответствующие углам (рис. 64), и сравним ординаты этих точек. Поскольку ордината точки меньше ординаты точки а ордината точки меньше ординаты точки

Пример №12

Верно ли, что

Решение:

Отметим на оси котангенсов точки, соответствующие углам (рис. 65), и сравним абсциссы этих точек. Поскольку абсцисса точки больше абсциссы точки то неравенство верное.

Пример №13

Определите знак выражения:

Решение:

а) Первый способ.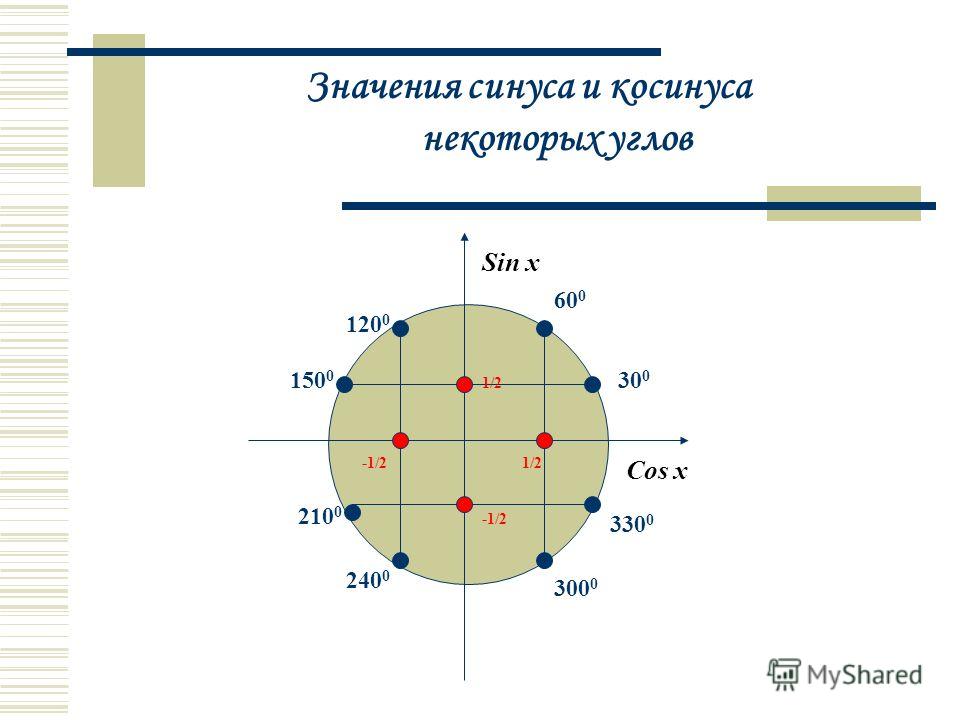 По определению тангенса: Так как угол находится во второй четверти, то значит, Второй способ. Отметим на оси тангенсов точку, соответствующую углу (рис. 66). Ордината точки равна Поскольку точка имеет отрицательную ординату, то

б) Первый способ. По определению котангенса Так как угол находится в третьей четверти, то значит,

Второй способ. Отметим на оси котангенсов точку, соответствующую углу (рис. 67). Абсцисса точки равна Поскольку точка имеет положительную абсциссу, то

Пример №14

Определите знак произведения

Решение:

Так как угол 3 радиана находится во второй четверти, а угол 4 радиана — в третьей, то значит,

Тригонометрические уравнения

Решение простейших тригонометрических уравнений

Градусы и радианы

Знакомство с тригонометрической окружностью

Повороты на тригонометрической окружности

Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает.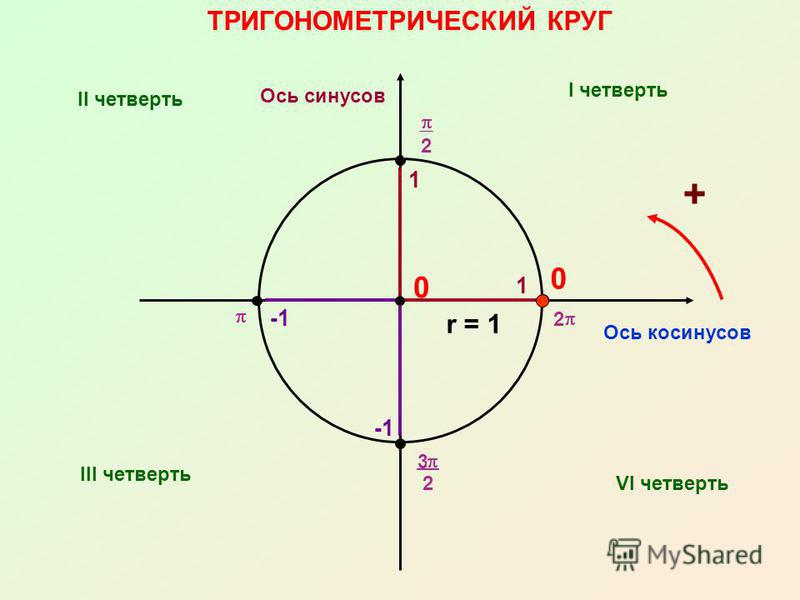 Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».

Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах.

1 радиан = 180/π ≈ 57,3 градусов

Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.

Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!

О графиках синуса, косинуса и тангеса поговорим в другой статье.

А сейчас начем с декартовой (прямоугольной) системы координат.

Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.

На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:

Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.

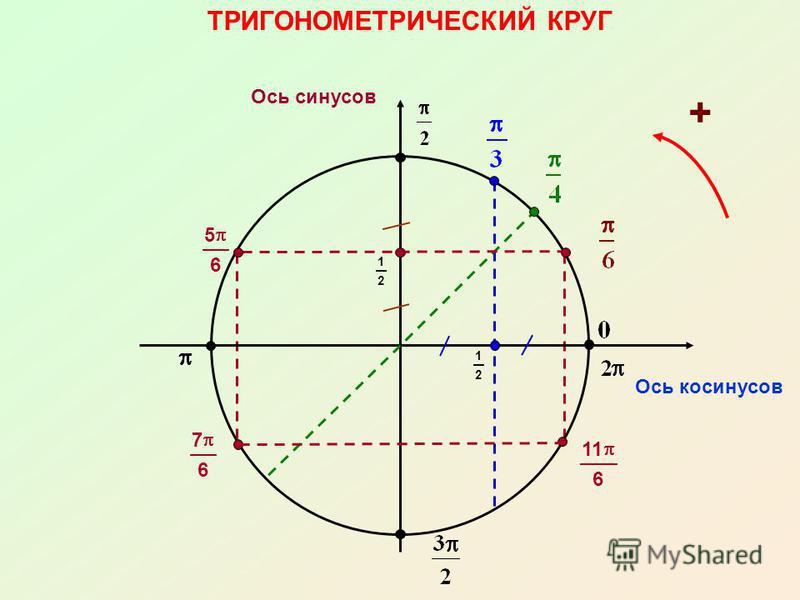
А теперь отметим основные значения градусов и радиан на окружности.

Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.

Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).

А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):

От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).

Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).

Главное — направление, куда мы будем смотреть, а не угол!

Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!

Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°. ..

А теперь у тебя есть два пути:

Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:

А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.

Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.

Сразу попробуем разобрать на примере:

Пример №1. cos(x) = ½

1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.

2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.

Дело за малым — найти эти углы.

Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.

Или запомнить такой прием:

Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).

Например, требуется найти sin(π/2): π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.

cos(π/4) — ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.

При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).

Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).

И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:

Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на …=-225°=135°=495°=…

То же самое и здесь! Разные углы могут отражать одно и то же направление.

Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.

Таким образом, попасть в первое направление 60° можно: …,60°-360°, 60°, 60°+360°,…

И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)

Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.

Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.

Ответ: x = π/3 + 2πn, x= −π/3 + 2πk, (n, k)∈Ζ.

Пример №2. 2sinx = √2

Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2

1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.

2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.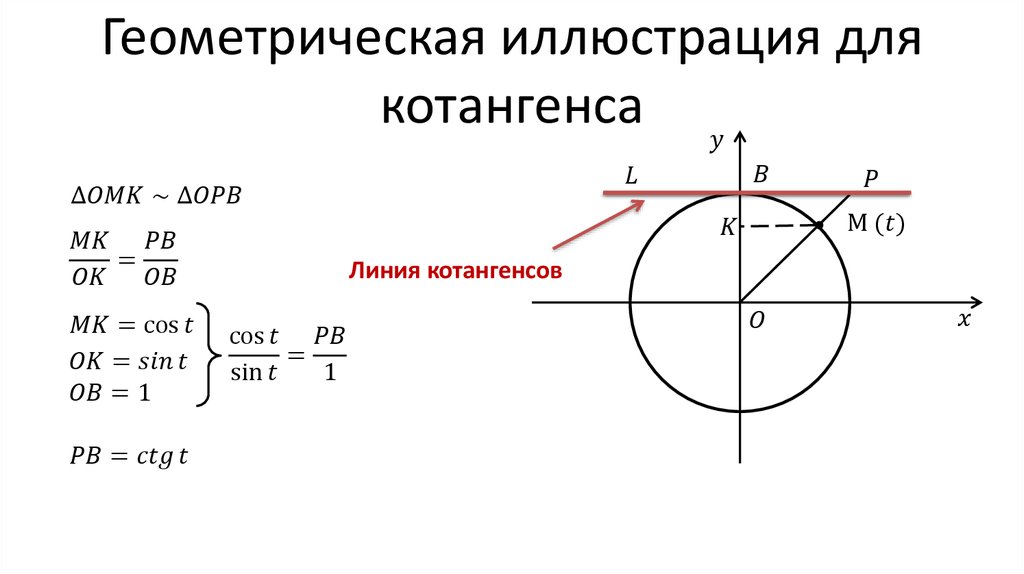

Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.

И еще не забудем добавить +2πn, n∈Ζ.

Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.

Пример №3. tg(x + π/4) = √3

Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.

tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.

1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.

2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.

По мнемоническому правилу при тангенсе √3 первое значение — это π/3.

3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.

4) Но мы нашли только y, вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.

Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.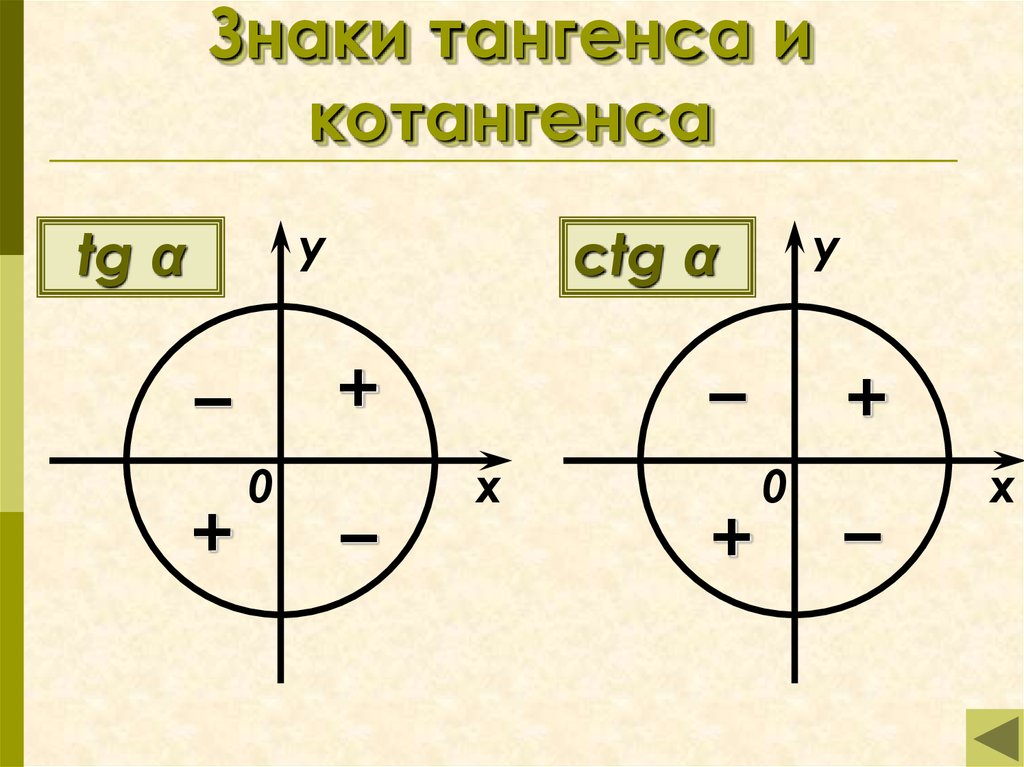

Теперь корни на окружности будут здесь:

Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.

Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).

Ответ можно записать и так: π/12 + πn, n∈Ζ.

Пример №4: −10ctg(x) = 10

Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.

1) Проведем прямую через эту точку и начало координат.

2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).

Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π…) так намного меньше шансов запутаться.

Не забываем добавить к каждой точке 2πk.

Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.

Алгоритм решения тригонометрических уравнений (на примере cos(x) = −√3/2):

Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
Точки пересечения с окружностью и будут являться корнями уравнения.
Значение одной точки (без разницы, как в нее попадете) +2πk.

Азов достаточно, прежде чем идти дальше закрепите полученные знания.

Будь в курсе новых статеек, видео и легкого математического юмора.

Где находится пи на окружности

Как вычислить значение Пи

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 10 человек(а).

Количество источников, использованных в этой статье: 7. Вы найдете их список внизу страницы.

Количество просмотров этой статьи: 215 446.

Пи (π) — одно из самых важных и интригующих чисел в математике. Эта константа, примерно равная 3,14, используется для вычисления длины окружности с учетом ее радиуса. [1] X Источник информации Это также иррациональное число, то есть оно может быть вычислено до бесконечного числа знаков после запятой. [2] X Источник информации Это не так-то просто сделать, но все-таки возможно.

Тригонометрический круг со всеми значениями, круг синусов и косинусов, линия, ось тангенса на окружности, как пользоваться и находить точки

В каждой профессии существуют свои инструменты, обеспечивающие решение и качественное выполнение определенных задач. Математики применяют тригонометрический круг, позволяющий легко и быстро вычислить значение какой-либо функции. Однако не все могут им правильно пользоваться, поскольку не понимают основных понятий.

Общие сведения

Для правильного решения тригонометрических задач следует изучить основные понятия, формулы, а также методы нахождения основных величин.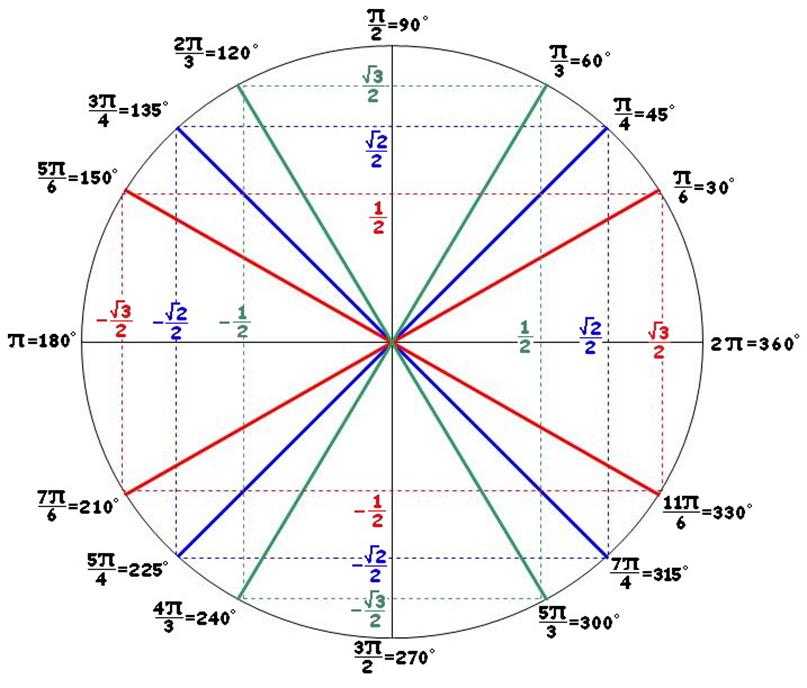 Раздел математики, изучающий функции косинуса, синуса, тангенса, котангенса, арксинуса, арккосинуса, арктангенса и арккотангенса, называется тригонометрией. Окружность, которая используется для решения геометрических задач на плоскости, имеет единичный радиус.

Значения функций, которые можно по ней находить, называются тригонометрическими. Однако существует множество способов нахождения их значений, но в некоторых ситуациях при использовании формул приведения решение затянется на продолжительное время, а вычисления будут громоздкими. Чтобы этого избежать, нужно использовать тригонометрический круг со всеми значениями. С его помощью также можно определить, является ли функция четной или нечетной.

Углы и их классификация

Перед тем как понять основное назначение тригонометрических функций, следует обратить внимание на классификацию углов. Она является важной для вычисления тригонометрических выражений. Углы в математических дисциплинах делятся на следующие типы:

Острые.
Прямые.
Тупые.
Развернутые.
Выпуклые.
Полные.

К первому типу относятся углы любой размерности градусной единицы измерения, которая не превышает 90 (а<90). Если значение соответствует 90, то он является прямым (а=90). Угол считается тупым, при выполнении следующего условия: 90<a<180. Если градусная размерность угла соответствует 180, то он является развернутым (а = 180). Выпуклым считается угол, когда выполняется такое условие: 180 < a < 360. Следует отметить, что он является смежным с острым углом. В случае, когда значение градусной размерности соответствует 360 градусам, то он является полным (а=360).

Однако углы измеряются не только в градусах, но и в радианах. Для решения тригонометрических задач оптимальным выбором градусной меры является радиан. Для соотношения между двумя единицами измерения применяется простая формула: 180 (град) = ПИ (рад). Из соотношения можно вывести формулу для перевода градусов в радианы: Pрад = (а * ПИ) / 180. Переменная «а» — значение величины градусной меры заданного угла. Обратное соотношение принимает следующий вид: а = (Ррад * 180) / ПИ.

Для быстрого перевода единиц измерения применяют такие инструменты: радианная табличка, программное обеспечение и тригонометрическая окружность. Однако для начала следует обратить внимание на тригонометрические функции, которые присутствуют в задачах физико-математического уклона.

Информация о функциях

Тригонометрических функций всего четыре вида: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg). Существует столько же типов обратных функций: арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg). Они получили широкое применение не только в математических задачах, но также используются в физике, электронике, электротехнике и других дисциплинах. Основной их особенностью считается возможность представления какого-либо закона.

Например, зависимость амплитуды напряжения переменного тока от времени описывается следующим законом: u = Um * cos (w*t) (графиком является косинусоида). Гармонические звуковые колебания также подчиняются определенному закону, в котором присутствует тригонометрическая функция. Кроме того, можно находить значения корня тригонометрического уравнения.

Синусом угла называется величина, равная отношению противолежащего катета прямоугольного треугольника к его гипотенузе. Следовательно, косинус — отношение прилежащего катета к гипотенузе. Тангенс — отношение величины противолежащего катета к прилежащему. Котангенс является обратной функцией тангенсу, т. е. отношение прилежащего к противолежащему.

Функции arcsin, arccos, arctg, arcctg применяются в том случае, когда нужно найти значение угла в градусах или радианах. Вычисления выполняются по специальным таблицам Брадиса или с помощью программ. Также можно использовать тригонометрическую окружность.

Тригонометрический круг

Чтобы воспользоваться тригонометрической окружностью для решения задач, нужны такие базовые знания: понятие о синусе, косинусе, тангенсе, котангенсе, системе координат и теореме Пифагора. Для построения единичной окружности используется декартовая система координат с двумя осями. Точка «О» — центр пересечения координатных осей, ОХ — ось абсцисс, ОУ — ординат.

Для решения задач различного типа применяется и теорема Пифагора. Она справедлива только для прямоугольного треугольника (один из углов — прямой). Ее формулировка следующая: квадрат гипотенузы в произвольном прямоугольном треугольнике равен сумме квадратов катетов. Следует также знать основные соотношения между функциями острых углов в заданном прямоугольном треугольнике:

a + b = 180.
cos(a) = sin(b).
cos(b) = sin(a).
tg(a) = ctg(b).
tg(b) = ctg(a).
tg(a) = 1 / ctg(a).
tg(b) = 1 / ctg(b).

Существуют и другие тригонометрические тождества, но для работы с кругом этого перечня будет достаточно.

Построение «инструмента»

Построить окружность, которая ускорит процесс решения задач, довольно просто. Для этого потребуются бумага, карандаш, резинка и циркуль. Далее необходимо нарисовать любую немаленькую окружность. После этого отметить ее центр карандашом, поставив точку. Пусть она будет называться «О». Через эту точку следует провести две перпендикулярные прямые (угол пересечения равен 90 градусам). Обозначить их следующим образом: «х» (горизонтальная) и «у» (вертикальная).

Окружность является единичной, но не стоит рисовать ее такой, поскольку работать будет неудобно. Этот прием называется масштабированием. Он широко применяется практически во всех сферах человеческой деятельности. Например, инженеры не чертят двигатель космического корабля в натуральную величину, поскольку с таким «рисунком» будет неудобно и невозможно работать. Они используют его макет.

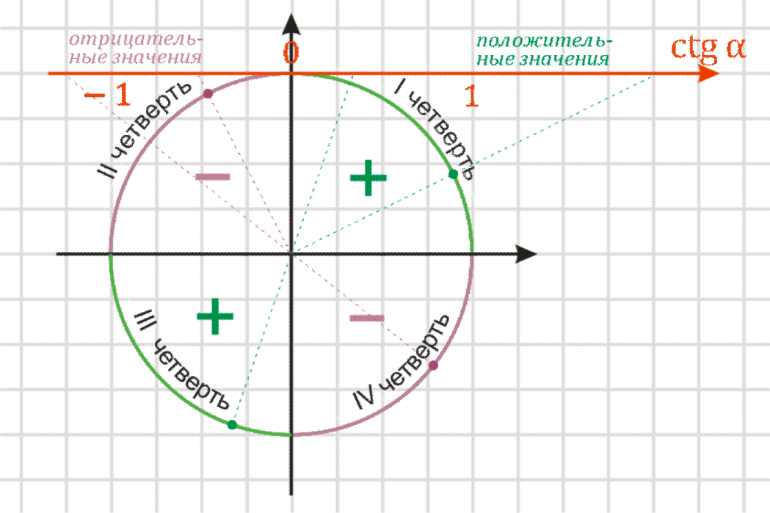
Окружность пересекается с осями декартовой системы координат в 4 точках со следующими координатами: (1;0), (0;1), (-1;0) и (0;-1). Области, которые делят декартовую систему координат на 4 части, называются четвертями. Их четыре:

Первая состоит из положительных координат по х и у.
Вторая имеет по х отрицательные и положительные по у.
Третья — только отрицательные значения.
Четвертая — положительные значения по х и отрицательные по у.

Исходя из этих особенностей, определяется числовой знак функции, позволяющий определить ее четность и нечетность. Кроме того, на ней следует отметить углы следующим образом: 0 и 2ПИ соответствует точке с координатами (1;0), ПИ/2 — (0;1), ПИ — (-1;0) и 3ПИ/2 — (0;-1).

Готовый макет

Для решения задач специалисты рекомендуют иметь рабочий и готовый макеты тригонометрических окружностей. Первый применяется для нахождения значений нестандартных углов (например, синуса 185 градусов). Тригонометрическим кругом (рис. 1) удобно пользоваться в том случае, когда значение угла является стандартным (90, 60 и т. д.).

Рисунок 1. Готовый макет тригонометрического круга синусов и косинусов.

Для нахождения необходимых значений объединяют две фигуры — единичную окружность и прямоугольный треугольник. 2] = sqrt(3) / 2.

Однако после всех вычислений следует выбрать знак функции. В данном случае угол находится в первой четверти. Следовательно, функция имеет положительный знак. Для нахождения тангенса и котангенса можно воспользоваться следующими формулами: tg(a) = sin(a) / cos(a) и ctg(a) = cos(a) / sin(a). Подставив значения синуса и косинуса, можно определить значение tg: tg(30) = 0,5 / (sqrt(3) / 2) = 1 / sqrt(3) = sqrt(3) / 3. Тогда котангенс можно найти двумя способами:

Через известный тангенс: ctg(30) = 1 / (1 / sqrt(3)) = sqrt(3).
Использовать основное отношение: ctg(30) = (sqrt(3) / 2) / (1/2) = sqrt(3).

Вычислить значения синуса и косинуса для угла 60 градусов очень просто. Для этого нужно воспользоваться основными тождествами: sin(60) = сos(30) = sqrt(3) / 2, cos(60) = sin(30) = 1/2, tg(30) = ctg(60) = sqrt(3) / 3, tg(60) = ctg(30) = sqrt(3). Значения для 45 градусов определяются следующим образом:

Прямоугольный треугольник с углом 45 градусов является равносторонним (катеты равны). 2 = 1.
sin(45) + cos(45) = sqrt(2) / 2.

Тангенс и котангенс равен 1. Если угол равен 90, то необходимо внимательно посмотреть на рисунок 1. Следовательно, sin(90) = 1, cos(90) = 0, tg(90) = 1 и ctg(90) не существует. Линия тангенса на окружности не отображается. В этом случае нужно пользоваться основными тригонометрическими тождествами.

Правила использования

Инструмент позволяет легко и быстро находить значения тригонометрических функций любых углов. Если при решении задачи требуется найти sin(270), то нужно выполнить простые действия:

Пройти против часовой стрелки (положительное направление) 180 градусов, а затем еще 90.
На оси синусов значение составляет -1 (точка лежит на оси).

Существуют задачи, в которых угол представлен отрицательным значением. Например, нужно определить синус, косинус, тангенс и котангенс угла (-7ПИ/6). В некоторых случаях заданное значение следует перевести в градусы: -7ПИ/6 = -210 (градусам). Если в условии отрицательный угол, то движение следует осуществлять по часовой стрелке от нулевого значения (пройти полкруга, а затем еще 30). Можно сделать вывод о том, что значение -210 соответствует 30. Следовательно, синус вычисляется следующим образом: sin(-210) = -(sin(ПИ + 30)) = — 1/2, cos(-210) = sqrt(3)/2, tg(-210) = sqrt(3)/3 и ctg(-210) = sqrt(3).

Пример случая, когда нет необходимости переводить радианы в градусы, является следующим: нужно вычислить значения тригонометрических функций угла 5ПИ/4. Необходимо расписать значение угла таким образом: 5ПИ/4 = ПИ + ПИ/4. Против часовой стрелки следует пройти половину круга (ПИ), а затем его четвертую часть (ПИ/4). Далее нужно спроецировать координаты точки на ось синусов и косинусов. Это соответствует значению sqrt(2)/2. Тангенс и котангенс заданного угла будут равны 1.

Встречаются задачи, в которых значение угла превышает 360 градусов. Например, требуется найти значения тригонометрических функций угла (-25ПИ/6). Для решения необходимо разложить угол следующим образом: (-25ПИ/6) = — (4ПИ + ПИ/6). Можно не делать обороты, поскольку 4ПИ соответствует двойному обороту и возврату в точку (-ПИ/6). Это объясняется периодом функций синуса и косинуса, который равен 2ПИ. Значения функций sin, сos, tg и ctg равны следующим значениям: — 1/2, sqrt(3)/2, sqrt(3)/3 и sqrt(3) соответственно.

Таким образом, тригонометрический круг позволяет оптимизировать вычисления в дисциплинах с физико-математическим уклоном, в которых используются тригонометрические функции. Не имеет смысла устанавливать дополнительное программное обеспечение, пользоваться таблицами, поскольку это занимает некоторое время. При помощи этого «универсального инструмента» можно найти значение любого угла.

Единичная числовая окружность на координатной плоскости

Тригонометрия берёт своё начало в Древней Греции. Само слово «тригонометрия» по-гречески означает «измерение треугольников». Эта наука в течение тысячелетий используется землемерами, архитекторами и астрономами.
Начиная с Нового времени, тригонометрия заняла прочное место в физике, в частности, при описании периодических процессов.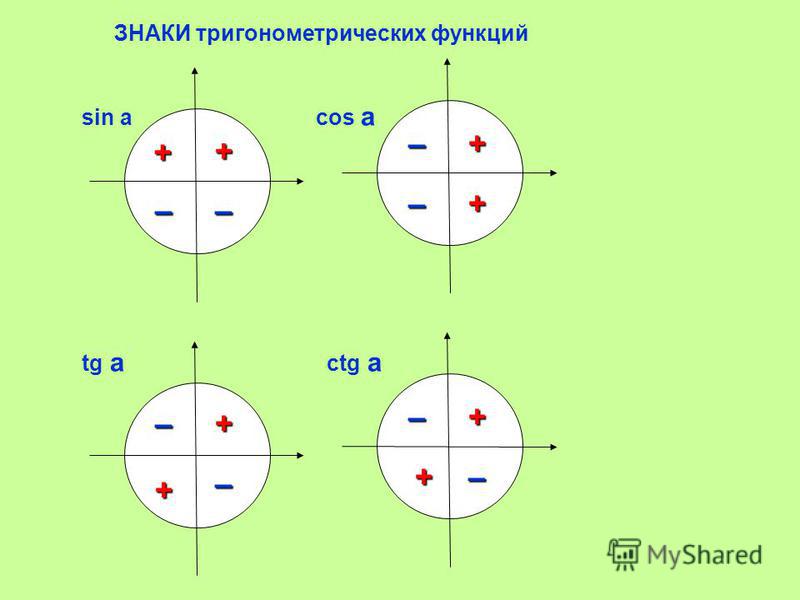 Например, переменный ток в розетке генерируется в периодическом процессе. Поэтому любой электрический или электронный прибор у вас в доме: компьютер, смартфон, микроволновка и т.п., — спроектирован с использованием тригонометрии.

Базовым объектом изучения в тригонометрии является угол.

Предметом изучения тригонометрии как раздела математики выступают:
1) взаимосвязи между углами и сторонами треугольника, которые называют тригонометрическими функциями;
2) использование тригонометрических функций в геометрии.

п.2. Числовая окружность

Мы уже знакомы с числовой прямой (см. §16 справочника для 8 класса) и координатной плоскостью (см. §35 справочника для 7 класса), с помощью которых создаются графические представления числовых промежутков и функций. Это удобный инструмент моделирования, с помощью которого можно провести анализ, начертить график, найти область допустимых значений и решить задачу.
Для работы с углами и их функциями существует аналогичный инструмент – числовая окружность.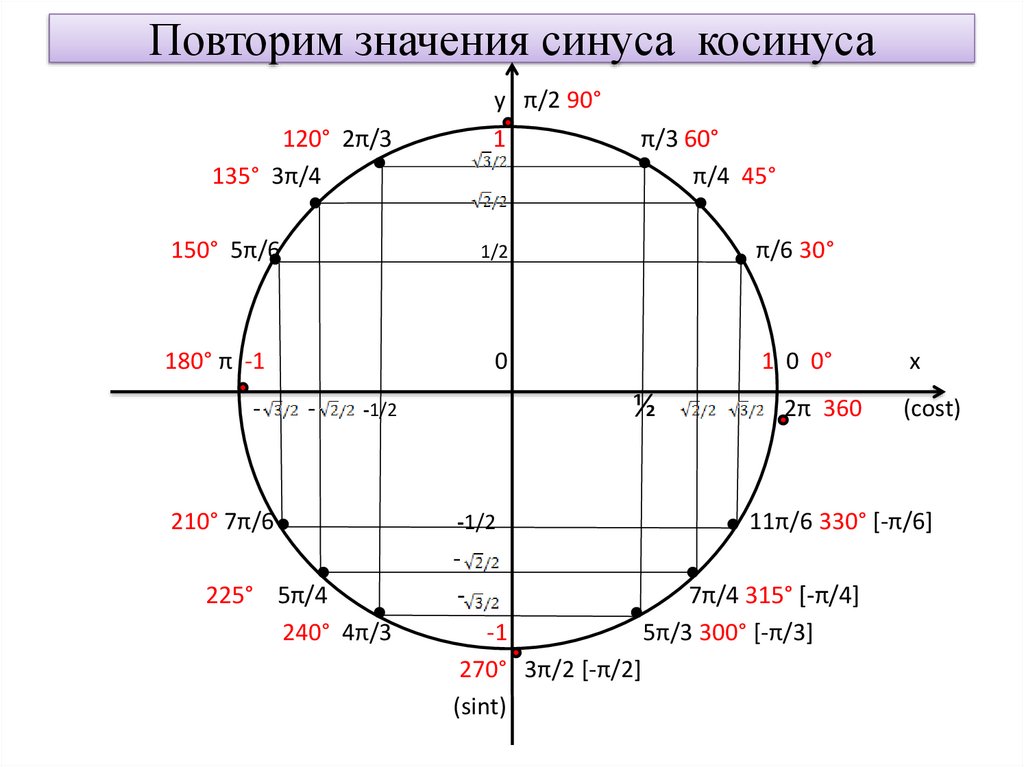

Числовая окружность (тригонометрический круг) – это окружность единичного радиуса R=1 с центром в начале координат (0;0).
Точка с координатами (1;0) является началом отсчета , ей соответствует угол, равный 0.
Углы на числовой окружности отсчитываются против часовой стрелки. Направление движения против часовой стрелки является положительным ; по часовой стрелке – отрицательным .

Отметим на числовой окружности углы 30°, 45°, 90°, 120°, 180°, а также –30°, –45°, –90&deg, –120°, –180°.

п.3. Градусная и радианная мера угла

Углы можно измерять в градусах или в радианах.
Известно, что развернутый угол, дуга которого равна половине окружности, равен 180°. Прямой угол, дуга которого равна четверти окружности, равен 90°. Тогда полная, замкнутая дуга окружности составляет 360°.
Приписывание развернутому углу меры в 180°, а прямому 90°, достаточно произвольно и уходит корнями в далёкое прошлое. С таким же успехом это могло быть 100° и 50°, или 200° и 100° (что, кстати, предлагалось одним из декретов во времена французской революции 1789 г.).

В целом, более обоснованной и естественной для измерения углов является радианная мера.

Найдем радианную меру прямого угла ∠AOB=90°.
Построим окружность произвольного радиуса r с центром в вершине угла – точке O. Длина этой окружности: L=2πr.
Длина дуги AB: $l_=\frac=\frac=\frac.$
Тогда радианная мера угла: $$ \angle AOB=\frac>=\frac=\frac $$

30°	45°	60°	90°	120°	135°	150°	180°	270°	360°
$\frac$	$\frac$	$\frac$	$\frac$	$\frac$	$\frac$	$\frac$	$\pi$	$\frac$	$2\pi$

п.4. Свойства точки на числовой окружности

Построим числовую окружность. Обозначим O(0;0), A(1;0)

Каждому действительному числу t на числовой окружности соответствует точка Μ(t).
При t=0, M(0)=A.
При t>0 двигаемся по окружности против часовой стрелки, описывая дугу
⌒ AM=t. Точка M — искомая.
При t<0 двигаемся по окружности по часовой стрелке, описывая дугу
⌒ AM=t. Точка M — искомая.

Отметим на числовой окружности точки, соответствующие $\frac,\ \frac,\ \frac,\ \frac,\ \pi$, а также $-\frac,\ -\frac,\ -\frac,\ -\frac,\ -\pi$
Для этого нужно отложить углы 30°, 45°, 90°, 120°, 180° и –30°, –45°, –90°, –120°, –180° с вершиной в начале координат и отметить соответствующие дуги на числовой окружности.

Отметим на числовой окружности точки, соответствующие $\frac,\ \frac,\ \frac$, и $-\frac$.
Все четыре точки совпадают, т.

к. \begin M\left(\frac\right)=M\left(\frac+2\pi k\right)\\ \frac-2\pi=-\frac\\ \frac+2\pi=\frac\\ \frac+4\pi=\frac \end

п.5. Интервалы и отрезки на числовой окружности

Каждому действительному числу соответствует точка на числовой окружности. Соответственно, числовые промежутки (см. §16 справочника для 8 класса) получают свои отображения в виде дуг.

Числовой промежуток	Соответствующая дуга числовой окружности
Отрезок
$$ -\frac \lt t \lt \frac $$ а также, с учетом периода $$ -\frac+2\pi k\lt t\lt\frac+2\pi k $$
Интервал
$$ -\frac \leq t \leq \frac $$ а также, с учетом периода $$ -\frac+2\pi k\leq t\leq\frac+2\pi k $$
Полуинтервал
$$ -\frac \leq t \lt\frac $$ а также, с учетом периода $$ -\frac+2\pi k\leq t\lt\frac+2\pi k $$

п.

\\ \frac=\frac\pi=3\pi-\frac\rightarrow \pi-\frac=\frac\\ \frac=\frac\pi=7\pi-\frac\rightarrow \pi-\frac=\frac \end

Пример 4. В какой четверти числовой окружности находится точка, соответствующая числу: 2; 4; 5; 7.

Сравниваем каждое число с границами четвертей: \begin 0,\ \ \frac\pi2\approx\frac=1,57,\ \ \pi\approx 3,14\\ 3\pi\ \ 3\cdot 3,14\\ \frac\approx \frac=4,71,\ \ 2\pi\approx 6,28 \end

$\frac\pi2\lt 2\lt \pi \Rightarrow $ угол 2 радиана находится во 2-й четверти
$\pi\lt 4\lt \frac \Rightarrow $ угол 4 радиана находится в 3-й четверти
$\frac\lt 5\lt 2\pi \Rightarrow $ угол 5 радиана находится в 4-й четверти
$7\gt 2\pi$, отнимаем полный оборот: $0\lt 7-2\pi\lt \frac\pi2\Rightarrow$ угол 7 радиан находится в 1-й четверти.

Пример 5. Изобразите на числовой окружности множество точек $(k\in\mathbb)$, запишите количество полученных базовых точек.

$$ \frac $$	$$ -\frac+2\pi k $$
Четыре базовых точки, через каждые 90°	Две базовых точки, через каждые 180°
$$ \frac+\frac $$	$$ -\frac $$
Три базовых точки, через каждые 120°	Пять базовых точек, через каждые 72°

Пример 6. Изобразите на числовой окружности дуги, соответствующие числовым промежуткам.

тригонометрических функций | Визуализируй это

Вы когда-нибудь задумывались, почему тригонометрические функции называются именно так? находятся?
Почему косинус называется «ко»синус, «косеканс» называется «ко»секанс и «котангенс» называется «ко»тангенсом?
Имеют ли эти функции какое-либо значение вне треугольников?
Разве такие термины, как «секанс» и «касательная», не связаны с окружностями?

Старые братья:

Синус и косинус

Этимология:

Слово «синус» происходит от латинского слова «синус».

что означает «бухта» или «складка». Это санскрит, арабский и персидский версии происходят от греческого слова «хорде», что означает тетива. В приведенной ниже визуализации, если мы представим, что ось X действует как зеркало, изображение станет симметричный. Отрезки OP и OP’ выглядят как тетивы лука, а перпендикуляры к оси X (их длина равна 2sin(θ)) выглядит как лук

Визуализация: Рассмотрим единичный круг (круг радиуса 1). Рассмотрим линию, проведенную из начала координат O, которая образует угол θ с осью X в направлении против часовой стрелки. Эта линия пересекает окружности в точке P. Длина проекции отрезка OP на Ось Y равна синусу θ

Отрегулируйте угол с помощью следующего ползунка:

Или введите угол здесь:

92 = 1 для всех углов θ

Значение синусов и косинусов, кратных 90 градусам:

Синус 0 градусов равен 0, так как прямая, совпадающая с осью X, не имеет проекции на ось Y
Косинус 0 градусов равен 1, поскольку линия, проведенная внутри единичного круга и совпадающая с осью X, имеет проекция длины 1 на ось X
Синус 90 градусов равен 1, так как линия, проведенная внутри единичного круга и совпадающая с осью Y, имеет проекция длины 1 на ось Y
Косинус 90 градусов равен 0, так как прямая, совпадающая с осью Y, не имеет проекции на ось X
Та же логика верна для 180 градусов и 270 градусов
Эта визуализация также позволяет нам расширить определение тригонометрических функций за пределы 90 градусов, поскольку мы больше не ограничены треугольником

Знаки функций синуса и косинуса:

Любой угол от 0 до 180 градусов имеет положительный синус, так как измеряется длина проекции на ось Y вдоль положительного направления Y
Синус отрицательный для остальных углов, потому что длина проекции на ось Y измеряется вдоль отрицательное направление Y
Любой угол от 0 до 90 градусов и от 270 до 360 градусов имеет положительный косинус, так как длина проекции на ось X измеряется вдоль положительного направления X
Косинус отрицателен для остальных углов, поскольку длина проекции на ось X измеряется вдоль отрицательное направление X

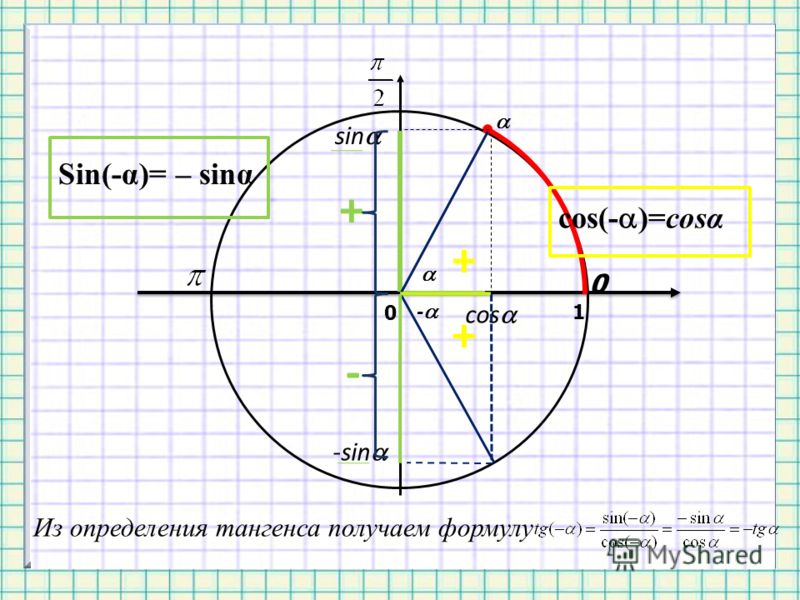
Синус — нечетная функция: \[ \sin (-\theta) = — \sin (\theta) \]

Рассмотрим угол θ, имеющий величину от 0 до 90 градусов
Синус +θ всегда положителен, так как проекция на ось Y всегда вдоль положительной Y-направление

Синус -θ всегда отрицательный, так как проекция на ось Y всегда вдоль отрицательной Y-направление
Следовательно, sin(-θ) = -sin(θ): Синус является нечетной функцией
То же верно и для угла θ, имеющего величину от 90 до 180 градусов: Sin(θ) равен всегда положительный, тогда как sin(-θ) всегда отрицательный

Косинус — четная функция: \[ \cos (-\тета) = \cos (\тета) \]

Рассмотрим угол θ, имеющий величину от 0 до 90 градусов
Косинус +θ всегда положителен, так как проекция на ось X всегда вдоль положительной Х-направление
Косинус -θ всегда положителен, так как проекция на ось X всегда вдоль положительной X-направление
Следовательно, cos(-θ) = cos(θ): косинус — четно-нечетная функция
То же верно и для угла θ, имеющего величину от 90 до 180 градусов: Cos(θ) и cos(-θ) оба отрицательны

The Circle Grazers:

Тангенс и Котангенс

Этимология: Слово «тангенс» происходит от латинского глагола «tangere», что означает «касаться».

Визуализация: Рассмотрим тот же единичный круг с тем же отрезком OP. Рассмотрим касательную, проведенную к окружность в точке P. Длина между точкой P и точкой пересечения этой касательной с осью X равна касательной угла θ

Отрегулируйте угол с помощью следующего ползунка:

Или введите угол здесь:

Отношение между тангенсом и котангенсом:

Длина той же касательной, но от точки Р до ее точка пересечения с осью Y равна котангенсу θ

Вычеты

Значения тангенсов и котангенсов кратных 90 градусов

Тангенс 0 градусов равен 0, так как точка P уже пересекает ось X
Котангенс 0 градусов бесконечен, так как тангенс никогда не пересекается с осью Y
Тангенс 90 градусов бесконечен, так как тангенс никогда не пересекается с осью X
Котангенс 90 градусов равен 0, так как точка P уже пересекается с осью Y
Та же логика верна для 180 градусов и 270 градусов

Внутренние преступники:

Секанс и Косеканс

Этимология: Слово «secant» происходит от французского глагола «secanter», что означает «резать».

Визуализация: Рассмотрим ту же единичную окружность с тем же отрезком OP и касательной, проведенной к окружность в точке P. Длина между началом координат и точкой пересечения касательной с осью X равна секанс θ

Отрегулируйте угол с помощью следующего ползунка:

Или введите угол здесь:

Связь между секансом и косекансом:

Расстояние между началом координат и точкой пересечения той же касательной с осью Y равно Косеканс θ 92 \тета\] Значения секанса и косеканса, кратных 90 градусам

Секанс 0 градусов равен 1, так как точка P совпадает с осью X
Косеканс 0 градусов бесконечен, так как касательная никогда не пересекается с осью Y
Секанс 90 градусов бесконечен, так как касательная никогда не пересекается с осью X
Косеканс 0 градусов равен 1, так как точка P совпадает с осью Y
Та же логика справедлива для 180 градусов и 270 градусов

Разработано ChanRT | Разветвите меня на Github

Тригонометрические функции и их знаки (2 способа запомнить) — JDM Educational

Тригонометрические функции часто используются в математике (включая исчисление), а также в реальных приложениях (например, в обработке сигналов).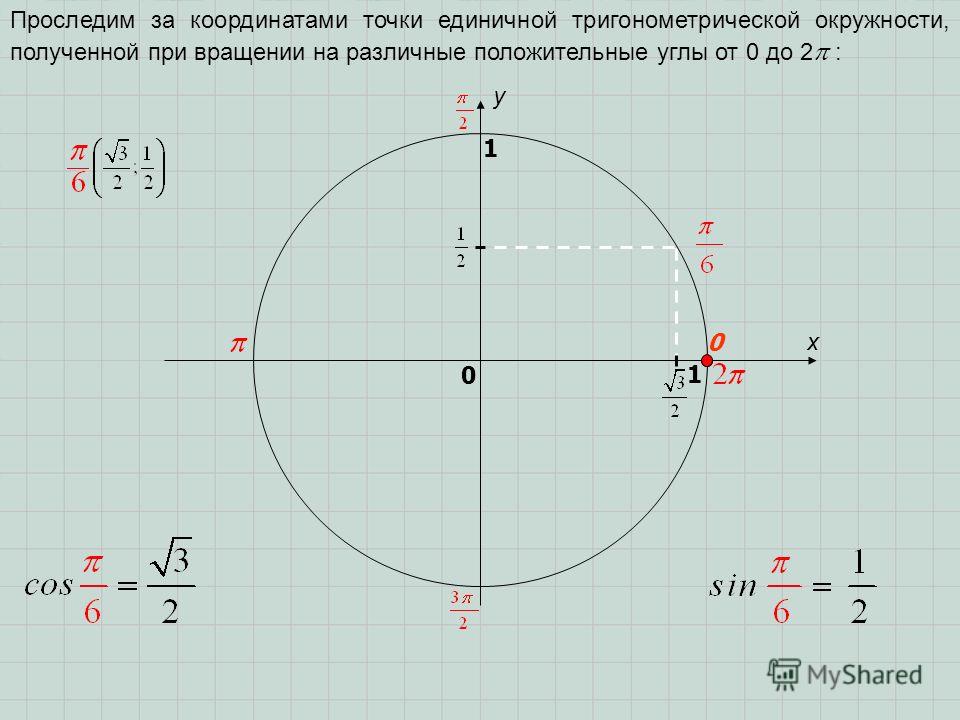 Однако может быть сложно запомнить знаки этих функций.

Итак, как вы запоминаете тригонометрические функции и их знаки? Используйте запоминающее устройство ASTC (все учащиеся выполняют вычисления) для обозначения квадрантов 1, 2, 3 и 4. A означает, что все триггерные функции положительны, а S, T, C обозначают синус, тангенс и косинус. Кроме того, косинус — это координата x точки на единичной окружности, а синус — это координата y точки на единичной окружности.

Конечно, если вы знаете знаки синуса, косинуса и тангенса в данном квадранте, вы также можете найти знаки их обратных триггерных функций (косеканс, секанс и котангенс).

В этой статье мы поговорим о способах запоминания знаков тригонометрических функций в зависимости от того, в каком квадранте они находятся (и связанных с ними углов). Мы также поговорим о некоторых частных случаях (когда триггерные функции равны нулю или не определены).

Начнем.

Есть два способа запомнить знаки тригонометрических функций:

По квадранту — используйте запоминающее устройство ASTC (все учащиеся выполняют исчисление), чтобы пометить 4 квадранта и выяснить, какие функции положительные или отрицательные (подробнее об этом ниже).
По координатам — помните, что косинус угла дает нам координату x соответствующего треугольника, а синус дает нам координату y соответствующего треугольника (подробнее об этом ниже).

Тригонометрические функции и их знаки по квадрантам

Мы можем использовать запоминающее устройство ASTC (все учащиеся проходят исчисление), чтобы отслеживать знаки тригонометрических функций по квадрантам. Мы назначаем каждому квадранту букву следующим образом:

A = 1 ^st Квадрант (вверху справа): Все триггерные функции положительны.
S = 2 ^nd Квадрант (вверху слева): Синус положителен (вместе с косекансом, обратным синусу).
T = 3 ^rd Квадрант (внизу слева): Тангенс положителен (наряду с котангенсом, обратным тангенсу).
C = 4 ^th Квадрант (внизу справа): косинус положителен (вместе с секансом, обратным косинусу).

Вы можете увидеть график с метками квадрантов ниже.

Квадранты (1, 2, 3, 4) соответствуют буквам (A, S, T, C) фразы «Все учащиеся сдают математический анализ». Это говорит нам, когда каждая триггерная функция положительна.

Обратите внимание, как работает запоминающее устройство: запомните фразу «все учащиеся изучают математику» и возьмите первую букву каждого слова: ASTC. Помните, что A означает все, S означает синус, t означает тангенс, а c означает косинус.

Расставляем их в том же порядке, что и числовые обозначения квадрантов: 1, 2, 3, 4.

Однако это не единственный способ запомнить и понять знаки триггерных функций.

Тригонометрические функции и их знаки по координатам

Другой способ отслеживать знаки тригонометрических функций состоит в том, чтобы использовать то, что мы знаем о координатах точки на единичной окружности и тригонометрических функциях.

На изображении ниже показана точка P на единичной окружности, отрезок прямой между точками P и O (где O — начало координат), угол между отрезком прямой PO и осью x и координаты точки P.

Координаты x и y точки на окружности являются косинусом и синусом соответствующего угла A (здесь угол равен t).

Если точка P имеет координаты (x _P , y _P ) и угол между OP и осью X равен A, то мы имеем:

x _P = cos(A)
y _P = sin(A)

Другими словами, косинус угла A дает нам координату x точки P, а синус угла A дает нам координату y точки P (обратите внимание, что это работает только для точек на единичной окружности с центром в начале координат).

Для окружности радиусом R с центром в начале координат точка P будет иметь координаты:

x _P = Rcos(A)
y _P 5 9031(A) Итак, как это поможет нам со знаками триггерных функций?
Ну, мы можем думать о точке P как о находящейся слева или справа от оси Y:
Если точка P находится справа от оси Y, то x _P это положительный , поэтому cos(A) должен быть положительным .
Если точка P находится на слева от оси Y, то x _P равно отрицательному , поэтому cos(A) должно быть отрицательным .
Точно так же мы можем думать о точке P как о находящейся выше или ниже оси x:
Если точка P на выше оси x, то y _P на положительна , поэтому sin(A) должен быть положительным .
Если точка P находится на ниже оси x, то y _P равно отрицательному , поэтому sin(A) должен быть отрицательным .
Зная знаки функций синуса и косинуса, мы можем легко найти знаки других триггерных функций: (A) = 1 / cos(A)
csc(A) = 1 / sin(A)
cot(A) = 1 /tan(A)

Так, например, если sin(A) и cos(A) имеют одинаковый знак, то tan(A) должен быть положительным. Если sin(A) и cos(A) имеют противоположные знаки, то tan(A) отрицателен.

Также:

sec(A) имеет тот же знак, что и cos(A)
csc(A) имеет тот же знак, что и sin(A)
cot(A) имеет тот же знак как tan(A)

Обратите внимание, что тангенс, секанс, косеканс и котангенс могут быть неопределенными, если они имеют нулевые знаменатели (это может произойти, когда либо синус, либо косинус равны нулю — подробнее об этом позже).

В таблице ниже приведены знаки тангенса, секанса, косеканса и котангенса на основе знаков sin(A) и cos(A).

Function	Q1	Q2	Q3	Q4
Sine	+	+	–	–
Cosine	+	–	–	+
Тангенс	+	–	+	–
Secant	+	–	–	+
Cosecant	+	+	–	–
Cotangent	+	–	+	–

В этой таблице показаны знаки каждой триггерной функции
по квадранту (Q1, Q2, Q3, Q4
соответствуют A, S, T, C).

Синус

Давайте рассмотрим, когда синус положительный, отрицательный, нулевой и неопределенный.

Когда синус положительный?

Синус положительный в квадрантах 1 ^st и 2 ^nd, когда координата y выше оси x. Это происходит, когда угол A находится в диапазоне от 0 до π радиан (от 0 до 180 градусов).

Когда синус отрицательный?

Синус отрицателен в 3-м ^-м-м и 4-м квадрантах, когда координата y находится ниже оси x. Это происходит, когда угол A находится между π и 2π радиан (180 и 360 градусов).

Когда синус 1?

Синус равен 1, когда угол A равен π/2 радианам (90 градусов). Это означает, что точка на единичной окружности лежит на оси Y (между квадрантами 1^, и 2^,).

Синус также будет равен 1, если A — любой угол, эквивалентный π/2, например:

-7π/2, -3π/2 , π/2, 5π/2, 9π /2, … (4k + 1)π / 2 для любого целого числа k

Обратите внимание, что синус равен -1, когда угол A равен –π/2 радиана (-90 градусов) или эквивалентно 3π/2 радиана (270 градусов ).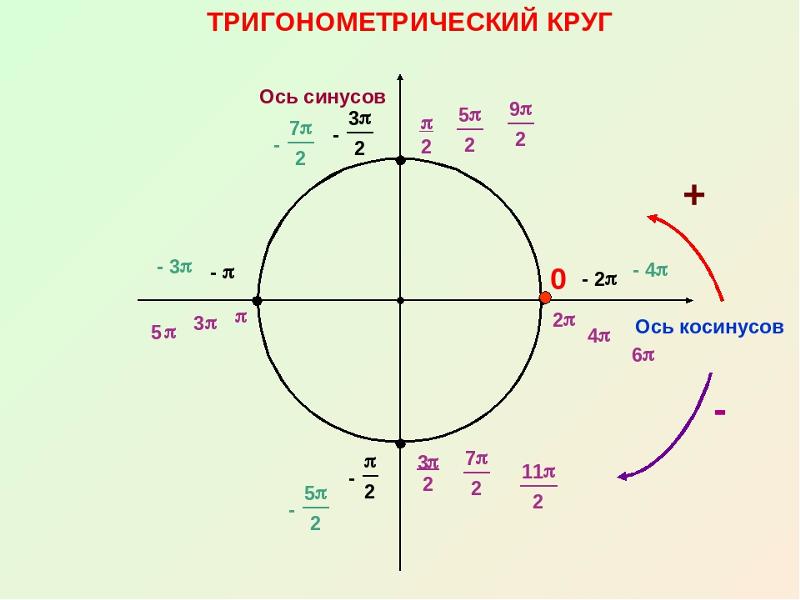 Это означает, что точка на единичной окружности лежит на оси y (между 3 ^-й-й и 4-й ^-й квадранты).

Синус также будет равен -1, если A — любой угол, эквивалентный -π/2 радианам, например: … (4k + 3)π / 2 для любого целого числа k

Когда синус равен 0?

Синус равен 0, когда угол A равен 0 радианам (0 градусов). Это означает, что точка на единичной окружности находится на оси x (между квадрантами 1 и 4 ).

Синус также равен 0, когда угол A равен π радианам (180 градусов). Это означает, что точка на единичной окружности лежит на оси x (между 2 ^-й-й и 3-й ^-й-й квадранты).

Синус также будет равен 0, если A представляет собой любой угол, эквивалентный 0 или π, например:

-3π, -2π, -π, 0, π, 2π, 3π … kπ для любого целого числа k

Когда синус не определен?

Синус никогда не бывает неопределенным. Он может принимать любое значение от -1 до 1, и мы можем использовать любой угол в качестве входных данных для функции синуса.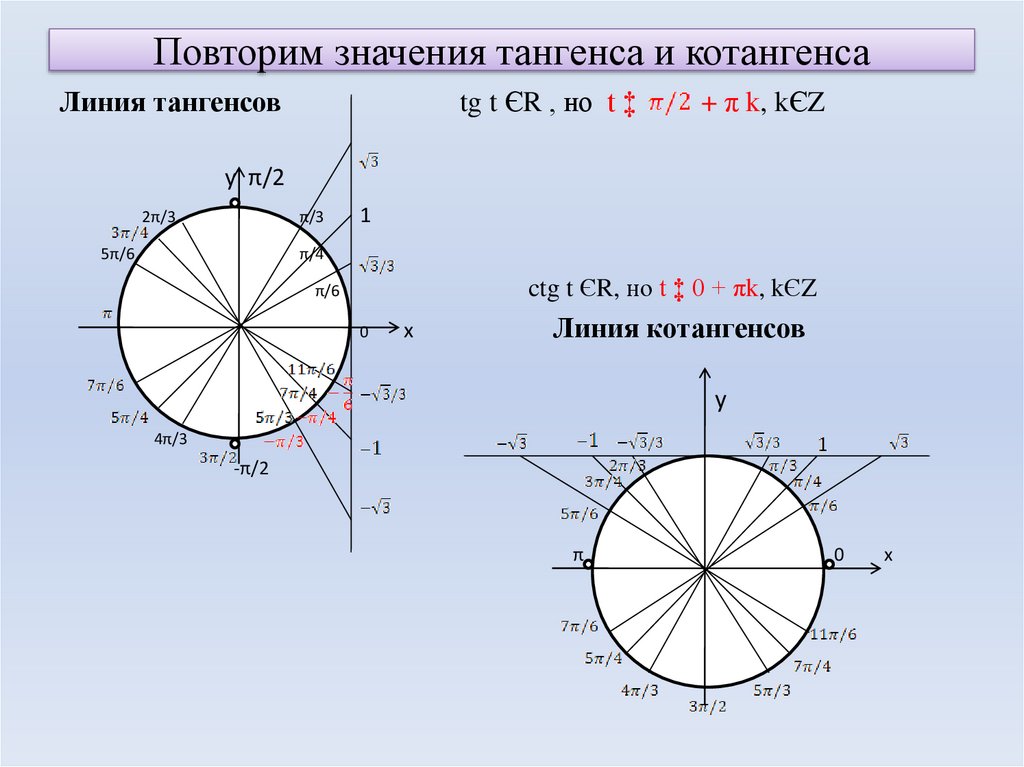

Когда синус равен косинусу?

Синус равен косинусу, если угол A равен π/4 радиана (45 градусов). Это означает, что точка на единичной окружности находится на середине окружности между (0, 0) и (0, 1) в первом квадранте.

Синус также равен косинусу, если угол A равен любому углу, эквивалентному π/4, например:

-15π/4, -7π/4, π/4, 9π/4, 17π/ 4, … (8k + 1)π / 4 для любого целого числа k

Косинус

Давайте рассмотрим, когда косинус положительный, отрицательный, нулевой и неопределенный.

Когда косинус положителен?

Косинус положителен в 1 ^st и 4 квадрантах, когда координата x находится справа от оси y. Это происходит, когда угол A находится между –π/2 и π/2 радиан (-90 и 90 градусов).

Когда косинус отрицателен?

Косинус отрицателен в квадрантах 2 ^nd и 3 ^rd, когда координата x находится слева от оси y. Это происходит, когда угол A находится между π/2 и 3π/2 радиан (90 и 270 градусов).

Когда косинус 1?

Косинус равен 1, если угол A равен 0 радианам (0 градусов). Это означает, что точка на единичной окружности лежит на оси x (между 1^, и 4-м квадрантами).

Косинус также будет равен 1, если A является любым углом, эквивалентным 0, например:

-4π, -2π, 0, 2π, 4π, … 2kπ для любого целого числа k

Обратите внимание, что косинус -1, когда угол A равен π радианам (180 градусов) или, что эквивалентно, -π радианам (-180 градусов). Это означает, что точка на единичной окружности лежит на оси x (между квадрантами 2 ^nd и 3 ^rd).

Косинус также будет равен -1, если A — любой угол, эквивалентный π радианам, например:

-3π, -π, π, 3π … (2k + 1)π для любого целого числа k

Когда косинус равен 0?

Косинус равен 0, если угол A равен π/2 радианам (90 градусов). Это означает, что точка на единичной окружности находится на оси Y (между квадрантами 1 ^st и 2 ^nd).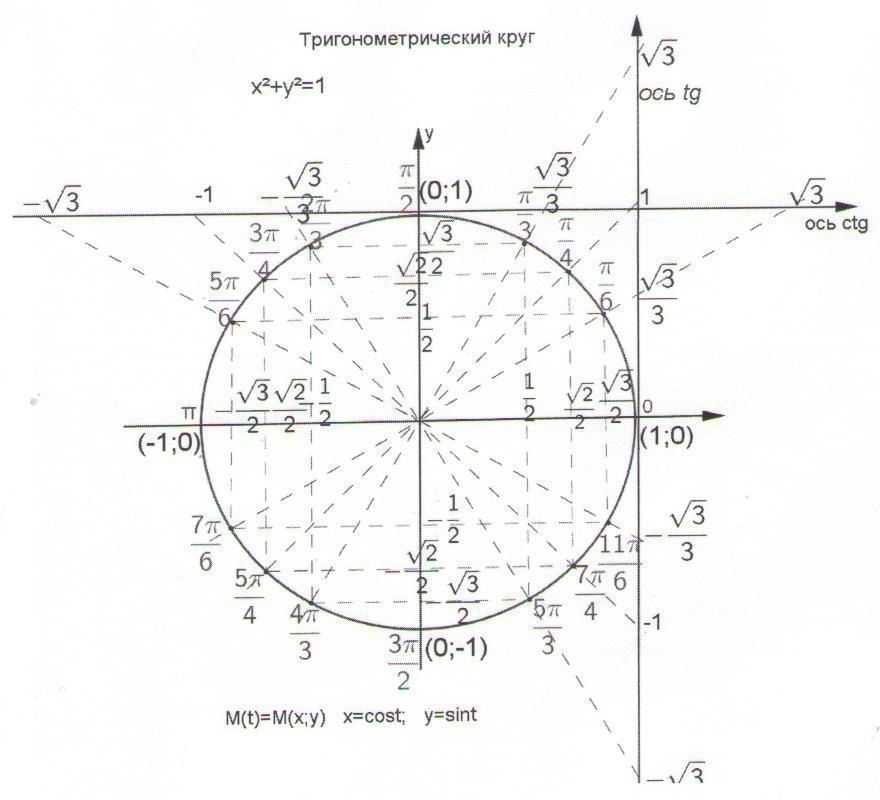

Косинус также равен 0, если угол A равен 3π/2 радиана (270 градусов). Это означает, что точка на единичной окружности лежит на оси Y (между 3 ^й и 4 ^й квадранты).

Косинус также будет равен 0, если A — любой угол, эквивалентный π/2 или 3π/2, например:

-3π/2, -π/2, π/2, 3π/2, … (2k + 1)π / 2 для любого целого числа k

Когда косинус не определен?

Косинус никогда не бывает неопределенным. Он может принимать любое значение от -1 до 1, и мы можем использовать любой угол в качестве входных данных для функции косинуса.

Тангенс

Давайте рассмотрим, когда тангенс положительный, отрицательный, нулевой и неопределенный.

Когда тангенс положительный?

Тангенс положителен в квадрантах 1 ^st и 3 ^rd, когда синус и косинус имеют одинаковый знак (оба положительные или оба отрицательные). Это происходит, когда угол A находится между 0 и π/2 радиан (0 и 90 градусов) или между π и 3π/2 радиан (180 и 270 градусов).

Когда тангенс отрицателен?

Тангенс отрицателен во 2-й и 4-й квадрантах, когда синус и косинус имеют противоположные знаки (один положительный, другой отрицательный). Это происходит, когда угол A находится между π/2 и π радиан (9от 0 до 180 градусов) или от 3π/2 до 2π радиан (от 270 до 360 градусов).

Когда тангенс 1?

Тангенс равен 1, когда синус и косинус имеют одинаковое значение (включая знак). Это происходит, когда угол A равен π/4 радиана (45 градусов) и sin(A) = cos(A) = √2 / 2.

Это означает, что точка на единичной окружности находится на середине окружность между (0, 0) и (0, 1) в первом квадранте.

Тангенс также будет равен 1, если угол A равен 5π/4 радианам (225 градусов) и sin(A) = cos(A) = -√2 / 2.

Это означает, что точка на единичной окружности находится на середине окружности между (-1, 0) и (0, -1) в третьем квадранте.

Тангенс также будет равен 1, если A — любой угол, эквивалентный π/4 или 5π/4, например:

-7π/4, -3π/4, π/4, 5π/4, 9π /4, … (4k + 1)π / 4 для любого целого числа k

Обратите внимание, что тангенс равен -1, когда синус и косинус имеют противоположные значения (одно положительное и одно отрицательное). Это происходит, когда угол A равен 3π/4 радиана (135 градусов).

Это означает, что точка на единичной окружности находится на середине окружности между (0, 1) и (-1, 0) во втором квадранте.

Тангенс также будет равен -1, если угол A равен 7π/4 радиана (315 градусов).

Это означает, что точка на единичной окружности находится на середине окружности между (0, -1) и (1, 0) в четвертом квадранте.

Тангенс также будет равен -1, если A — любой угол, эквивалентный 3π/4 или 7π/4 радианам, например:

-9π/4, -5π/4, -π/4, 3π/4, 7π/4, … (4k + 3)π / 4 для любого целого числа k

Когда тангенс равен 0?

Тангенс равен нулю, когда синус равен нулю. Это связано с тем, что tan(A) = sin(A)/cos(A), что означает, что sin(A) является числителем tan(A).

Мы знаем, когда синус равен нулю, из нашего предыдущего обсуждения (см. «Когда синус равен нулю» выше).

Тангенс равен 0, когда угол A равен 0 радианам (0 градусов). Это означает, что точка на единичной окружности находится на оси X (между 1 ^-й и 4-й ^-й квадранты).

Тангенс также равен 0, когда угол A равен π радианам (180 градусов). Это означает, что точка на единичной окружности лежит на оси x (между квадрантами 2 ^nd и 3 ^rd).

Тангенс также будет равен 0, если A — любой угол, эквивалентный 0 или π, например:

-3π, -2π, -π, 0, π, 2π, 3π … kπ для любого целого числа k

Когда тангенс не определен?

Тангенс не определен, когда косинус равен нулю. Это связано с тем, что tan(A) = sin(A)/cos(A), что означает, что cos(A) является знаменателем tan(A).

Мы знаем, когда косинус равен нулю, из нашего предыдущего обсуждения (см. «Когда косинус равен нулю» выше).

Тангенс равен 0, если угол A равен π/2 радиана (90 градусов). Это означает, что точка на единичной окружности находится на оси Y (между квадрантами 1 ^st и 2 ^nd).

Тангенс также равен 0, когда угол A равен 3π/2 радиана (270 градусов). Это означает, что точка на единичной окружности лежит на оси Y (между квадрантами 3 ^rd и 4 ^th).

Тангенс также будет равен 0, если A — любой угол, эквивалентный π/2 или 3π/2, например:

-3π/2, -π/2, π/2, 3π/2, … (2k + 1)π / 2 для любого целого числа k

Секанс

Давайте рассмотрим, когда секанс положителен, отрицателен, равен нулю и не определен.

Когда секанс положительный?

Секанс положителен, если косинус положителен. Это связано с тем, что sec(A) = 1/cos(A), что означает, что sec(A) является обратной величиной cos(A).

Мы знаем, когда косинус положителен, из нашего предыдущего обсуждения (см. «Когда косинус положителен» выше).

Секанс положителен в 1 ^st и 4 квадрантах, когда координата x находится справа от оси y. Это происходит, когда угол A находится между –π/2 и π/2 радиан (от –90 до 90 градусов).

Когда секанс отрицательный?

Секанс отрицательный, если косинус отрицательный. Это связано с тем, что sec(A) = 1/cos(A), что означает, что sec(A) является обратной величиной cos(A).

Мы знаем, когда косинус отрицательный, из нашего предыдущего обсуждения (см. «Когда косинус отрицательный» выше).

Секанс отрицателен в квадрантах 2 ^nd и 3 ^rd, когда координата x находится слева от оси y. Это происходит, когда угол A находится между π/2 и 3π/2 радиан (90 и 270 градусов).

Когда секанс 1?

Секанс равен 1, если косинус равен 1. Это связано с тем, что sec(A) = 1 / cos(A), что означает, что sec(A) является обратной величиной cos(A).

Мы знаем, когда косинус равен 1, из нашего предыдущего обсуждения (см. «Когда косинус равен 1» выше).

Секанс равен 1, когда угол A равен 0 радианам (0 градусов). Это означает, что точка на единичной окружности лежит на оси x (между 1^, и 4-м квадрантами).

Секанс также будет равен 1, если A — любой угол, эквивалентный 0, например:

-4π, -2π, 0, 2π, 4π, … 2kπ для любого целого числа k

Обратите внимание, что секанс равен -1, когда угол A равен π радианам (180 градусов) или, что эквивалентно, -π радианам (-180 градусов). Это означает, что точка на единичной окружности лежит на оси x (между 2 ^-й-й и 3-й ^-й-й квадранты).

Секанс также будет равен -1, если A — любой угол, эквивалентный π радианам, например:

-3π, -π, π, 3π … (2k + 1)π для любого целого числа k

Когда секанс равен 0?

Секанс никогда не равен нулю. Это связано с тем, что sec(A) = 1/cos(A), а cos(A) принимает только конечные значения (от -1 до 1).

Когда секанс не определен?

Секанс не определен, если косинус равен нулю. Это связано с тем, что sec(A) = 1/cos(A), а cos(A) = 0 дало бы нам нулевой знаменатель (неопределенный).

Мы знаем, когда косинус равен нулю, из нашего предыдущего обсуждения (см. «Когда косинус равен нулю» выше).

Секанс не определен, если угол A равен π/2 радианам (90 градусов). Это означает, что точка на единичной окружности находится на оси Y (между квадрантами 1 ^st и 2 ^nd).

Секанс также не определен, если угол A равен 3π/2 радиана (270 градусов). Это означает, что точка на единичной окружности лежит на оси Y (между 3 ^й и 4 ^й квадранты).

Секанс также будет неопределенным, если A — любой угол, эквивалентный π/2 или 3π/2, например:

-3π/2, -π/2, π/2, 3π/2, … (2k + 1)π / 2 для любого целого числа k

Когда секанс равен косекансу?

Секанс равен косекансу, если косинус равен синусу, поскольку: sin(x) = cos(x)

Мы знаем, когда синус и косинус равны из нашего предыдущего обсуждения (см. «Когда синус равен косинусу» выше).

Секанс равен косекансу, если угол A равен π/4 радиана (45 градусов). Это означает, что точка на единичной окружности находится на середине окружности между (0, 0) и (0, 1) в первом квадранте.

Секанс также равен косекансу, если угол А представляет собой любой угол, эквивалентный π/4, например:

-15π/4, -7π/4, π/4, 9π/4, 17π/4, … (8k + 1)π / 4 для любого целого числа k

Косеканс

Давайте рассмотрим, когда косеканс положительный, отрицательный, нулевой и неопределенный.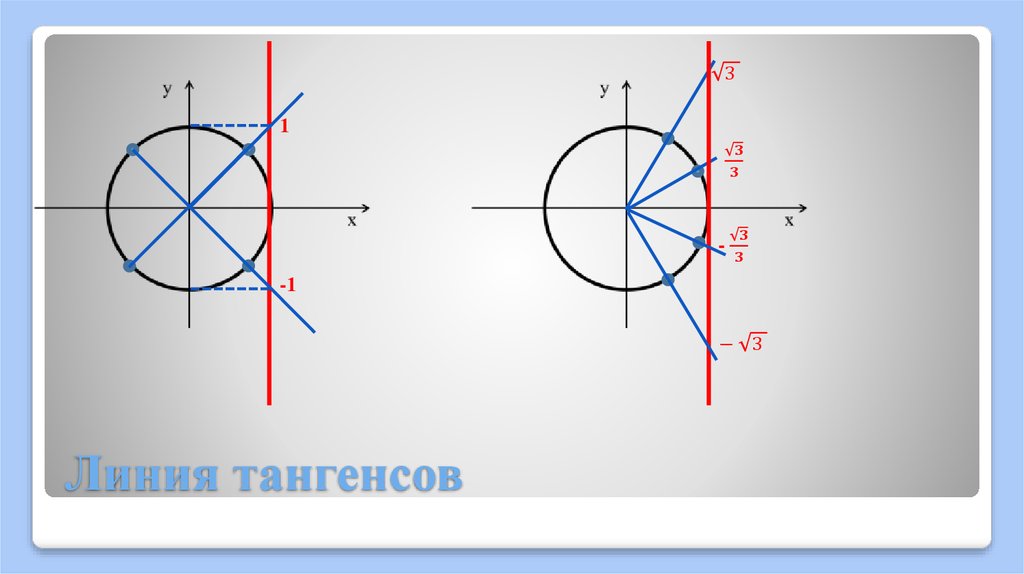

Когда косеканс положительный?

Косеканс положителен, если синус положителен. Это связано с тем, что csc(A) = 1/sin(A), что означает, что csc(A) является обратной величиной sin(A).

Из нашего предыдущего обсуждения мы знаем, когда синус положителен (см. «Когда синус положителен» выше).

Косеканс положителен в 1 ^st и 2 ^nd квадранты, когда координата y находится выше оси x. Это происходит, когда угол A находится в диапазоне от 0 до π радиан (от 0 до 180 градусов).

Когда косеканс отрицательный?

Косеканс отрицательный, если синус отрицательный. Это связано с тем, что csc(A) = 1/sin(A), что означает, что csc(A) является обратной величиной sin(A).

Из нашего предыдущего обсуждения мы знаем, когда синус отрицателен (см. «Когда синус отрицателен» выше).

Косеканс отрицательный в 3 ^rd и 4-й квадрант, когда координата y ниже оси x. Это происходит, когда угол A находится между π и 2π радиан (180 и 360 градусов).

Когда косеканс равен 1?

Косеканс равен 1, если синус равен 1. Это связано с тем, что csc(A) = 1 / sin(A), что означает, что csc(A) является обратной величиной sin(A).

Мы знаем, когда синус равен 1, из нашего предыдущего обсуждения (см. «Когда синус равен 1» выше).

Косеканс равен 1, когда угол A равен π/2 радиана (90 градусов). Это означает, что точка на единичной окружности лежит на оси y (между 1 ^ст и 2 ^й квадранты).

Косеканс также будет равен 1, если A — любой угол, эквивалентный π/2, например:

-7π/2, -3π/2 , π/2, 5π/2, 9π /2, … (4k + 1)π / 2 для любого целого числа k

Обратите внимание, что косеканс равен -1, когда угол A равен –π/2 радиана (-90 градусов) или, что эквивалентно, 3π/2 радиана (270 градусов ). Это означает, что точка на единичной окружности лежит на оси y (между 3 ^rd и 4 ^-й квадрант).

Косеканс также будет равен -1, если A — любой угол, эквивалентный -π/2 радианам, например: … (4k + 3)π / 2 для любого целого числа k

Когда косеканс равен 0?

Косеканс никогда не равен нулю. Это связано с тем, что csc(A) = 1/sin(A), а csc(A) принимает только конечные значения (от -1 до 1).

Когда косеканс не определен?

Косеканс не определен, если синус равен нулю. Это связано с тем, что csc(A) = 1 / sin(A), а sin(A) = 0 дало бы нам нулевой знаменатель (неопределенный).

Мы знаем, когда синус равен нулю, из нашего предыдущего обсуждения (см. «Когда синус равен нулю» выше).

Косеканс равен 0, если угол A равен 0 радианам (0 градусов). Это означает, что точка на единичной окружности находится на оси x (между квадрантами 1 и 4 ).

Косеканс также равен 0, когда угол A равен π радианам (180 градусов). Это означает, что точка на единичной окружности лежит на оси x (между квадрантами 2 ^nd и 3 ^rd).

Косеканс также будет равен 0, если A — любой угол, эквивалентный 0 или π, например:

-3π, -2π, -π, 0, π, 2π, 3π … kπ для любого целого числа k

Котангенс

Давайте рассмотрим, когда котангенс положительный, отрицательный, нулевой и неопределенный.

Когда котангенс положителен?

Котангенс положителен, если тангенс отрицателен. Это связано с тем, что cot(A) = 1/tan(A), что означает, что cot(A) является обратной величиной tan(A).

Из нашего предыдущего обсуждения мы знаем, когда тангенс положителен (см. «Когда тангенс положителен» выше).

Котангенс положителен в квадрантах 1 ^st и 3 ^rd, когда синус и косинус имеют одинаковый знак (оба положительные или оба отрицательные). Это происходит, когда угол A находится между 0 и π/2 радиан (0 и 90 градусов) или между π и 3π/2 радиан (180 и 270 градусов).

Когда котангенс отрицателен?

Котангенс отрицателен, если тангенс отрицателен. Это связано с тем, что cot(A) = 1/tan(A), что означает, что cot(A) является обратной величиной tan(A).

Мы знаем, когда тангенс отрицателен, из нашего предыдущего обсуждения (см. «Когда тангенс отрицателен» выше).

Котангенс отрицателен во 2-й и 4-й четвертях, когда синус и косинус имеют противоположные знаки (один положительный, другой отрицательный).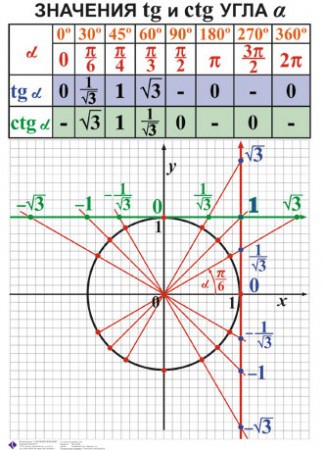 Это происходит, когда угол A находится между π/2 и π радиан (90 и 180 градусов) или между 3π/2 и 2π радиан (270 и 360 градусов).

Когда котангенс равен 1?

Котангенс равен 1, если тангенс равен 1. Это связано с тем, что cot(A) = 1 / tan(A), что означает, что cot(A) является обратной величиной tan(A).

Мы знаем, когда тангенс равен 1, из нашего предыдущего обсуждения (см. «Когда тангенс равен 1» выше).

Котангенс равен 1, когда синус и косинус имеют одинаковое значение (включая знак). Это происходит, когда угол A равен π/4 радиана (45 градусов) и sin(A) = cos(A) = √2 / 2.

Котангенс также будет равен 1, если угол A равен 5π/4 радианам (225 градусов) и sin(A) = cos(A) = -√2 / 2.

Котангенс также будет равен 1, если A — любой угол, эквивалентный π/4 или 5π/4, например:

-7π/4, -3π/4, π/4, 5π/4, 9π /4, … (4k + 1)π / 4 для любого целого числа k

Обратите внимание, что котангенс будет равен -1 всякий раз, когда тангенс равен -1.

Когда котангенс равен 0?

Котангенс равен нулю, если косинус равен нулю. Это связано с тем, что cot(A) = cos(A)/sin(A), что означает, что cos(A) является числителем tan(A).

Мы знаем, когда косинус равен нулю, из нашего предыдущего обсуждения (см. «Когда косинус равен нулю» выше).

Котангенс равен 0, когда угол A равен π/2 радианам (90 градусов). Это означает, что точка на единичной окружности находится на оси Y (между квадрантами 1 ^st и 2 ^nd).

Котангенс также равен 0, когда угол A равен 3π/2 радиана (270 градусов). Это означает, что точка на единичной окружности лежит на оси Y (между квадрантами 3 ^rd и 4 ^th).

Котангенс также будет равен 0, если A — любой угол, эквивалентный π/2 или 3π/2, например:

-3π/2, -π/2, π/2, 3π/2, … (2k + 1)π / 2 для любого целого числа k

Когда котангенс не определен?

Котангенс не определен, когда синус равен нулю. Это связано с тем, что cot(A) = cos(A)/sin(A), что означает, что sin(A) является знаменателем tan(A).

Мы знаем, когда синус равен нулю, из нашего предыдущего обсуждения (см. «Когда синус равен нулю» выше).

Котангенс равен 0, когда угол A равен 0 радианам (0 градусов). Это означает, что точка на единичной окружности находится на оси x (между квадрантами 1 и 4 ).

Котангенс также равен 0, когда угол A равен π радианам (180 градусов). Это означает, что точка на единичной окружности лежит на оси x (между квадрантами 2 ^nd и 3 ^rd).

Котангенс также будет равен 0, если A — любой угол, эквивалентный 0 или π, например:

-3π, -2π, -π, 0, π, 2π, 3π … kπ для любого целого числа k

Заключение

Теперь вы знаете все о знаках тригонометрических функций и о том, как их запомнить (рисунок координатные оси с цифрами и буквами ASTC помогает!)

Вы можете узнать о выходных значениях синуса здесь.

Вы можете узнать о выходных значениях косинуса здесь.

Вы можете узнать больше о реальных примерах использования триггерных функций в моей статье здесь.

В этой статье вы можете узнать о законе синусов (и о том, как он используется для решения треугольников).

Вы можете узнать больше о законе косинусов (и о том, как он помогает решить треугольник) здесь.

О других нелинейных функциях вы можете узнать из моей статьи здесь.

Надеюсь, эта статья оказалась вам полезной. Если это так, пожалуйста, поделитесь ею с теми, кто может использовать эту информацию.

Не забудьте подписаться на мой канал YouTube и получать обновления о новых математических видео!

Подпишитесь на наш канал на YouTube!

~Джонатон

Визуализация тригонометрических измерений с помощью окружности и касательной

Все тригонометрические измерения можно визуализировать с помощью окружности и касательной к окружности. Мы будем использовать следующую диаграмму единичного круга (т.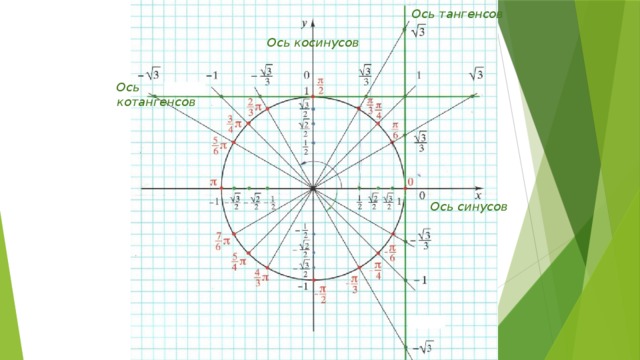 е. предполагается, что радиус равен 1) и касательной в точке P, чтобы найти все тригонометрические значения, представленные длинами различных сегментов.

Рисунок 1: Единичная окружность и касательная

Значения синуса и косинуса

Основными тригонометрическими величинами являются синус и косинус. Для единичного круга координата x представляет значение косинуса угла θ , а координата y представляет значение синуса угла θ . На рисунке 1 косинус равен отрезку OX, а синус равен OY для угла, образованного OP и осью x .

На рисунке показана величина угла приблизительно 53,13°, что соответствует углу, образованному точкой (0,6, 0,8). Мы будем использовать эту координату в качестве примера для остальных тригонометрических значений. 92 = \frac{9+16}{25} = 1 \).

Значения тангенса и котангенса

Значение тангенса, вероятно, является третьим наиболее известным тригонометрическим значением. Для значения касательной нам нужно провести касательную линию в точке P. Вероятно, поэтому она называется функцией касательной.

Тангенс определяется как $\tan\theta = \frac{\sin\theta}{\cos\theta}$. Сегмент EP представляет значение тангенса θ . На рисунке 1 много подобных прямоугольных треугольников. Я показал некоторые из равных углов, которые можно доказать, заметив, что углы являются дополнительными углами прямоугольного треугольника.

Чтобы доказать, что EP равен касательной θ , рассмотрим подобные треугольники PXE и PYO. Таким образом, мы имеем следующее соотношение: $\frac{\text{PY}}{\text{PO}} = \frac{\text{PX}}{\text{PE}}$.

Отрезок PO = 1, потому что это радиус единичной окружности. Следовательно, $\frac{\text{PY}}{1} = \frac{\text{PX}}{\text{PE}}$. Решая для PE, мы получаем следующее соотношение: $\text{PE} = \frac{\text{PX}}{\text{PY}}$. Однако мы уже знаем, что PX — это значение синуса, а PY — это значение косинуса. Следовательно, $\text{PE} = \frac{\sin\theta}{\cos\theta}$.

В нашем примере $\tan\theta = \frac{0,8}{0,6} = \frac{4}{3} \приблизительно 1,333$.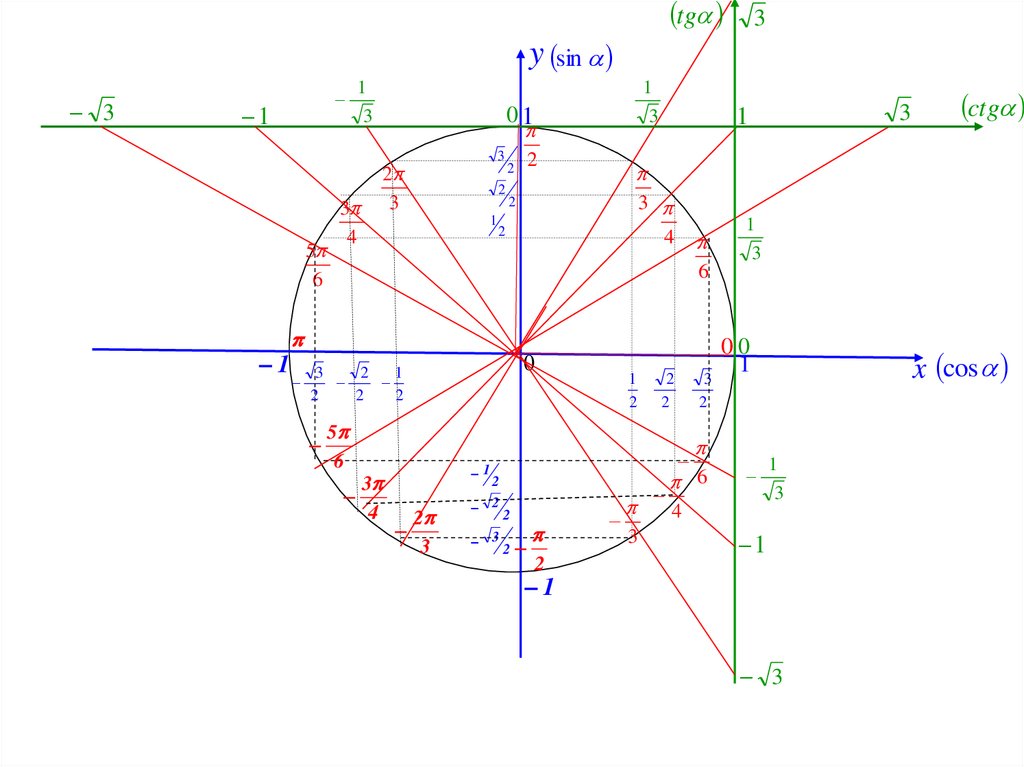

Значение котангенса равно $\frac{\cos\theta}{\sin\theta} $. Используя подобные треугольники PXO и PYF, мы получаем $\frac{\text{PY}}{\text{PF}} = \frac{\text{PX}}{\text{PO}}$. Решая для PF, мы получаем $\text{PF} = \frac{\text{PY}}{\text{PX}} = \frac{\cos\theta}{\sin\theta} = \cot\theta $.

В нашем примере $\cot\theta = \frac{0,6}{0,8} = \frac{3}{4} = 0,75$.

Как вы уже догадались, значения тангенса и котангенса обратны.

Значение секанса

Секанс определяется как величина, обратная косинусу или $ \frac{1}{\cos\theta} $. Отрезок OE представляет собой значение секущей угла θ .

Треугольники PXO и EOF являются подобными прямоугольными треугольниками. Это дает нам соотношение:

(i) $\frac{\text{PO}}{\text{PX}} = \frac{\text{EF}}{\text{EO}}$

(ii) $\frac{1}{\sin\theta} = \frac{\tan\theta + \cot\theta}{\text{EO}}$

(iii) $ \text{EO } = \sin\theta\left(\frac{\sin\theta}{\cos\theta} + \frac{\cos\theta}{\sin\theta}\right) $ 92\theta}{\cos\theta} = \sec\theta \)

В приведенном выше примере $\sec\theta = \frac{1}{0,6} = \frac{5}{3} \приблизительно 1,667$.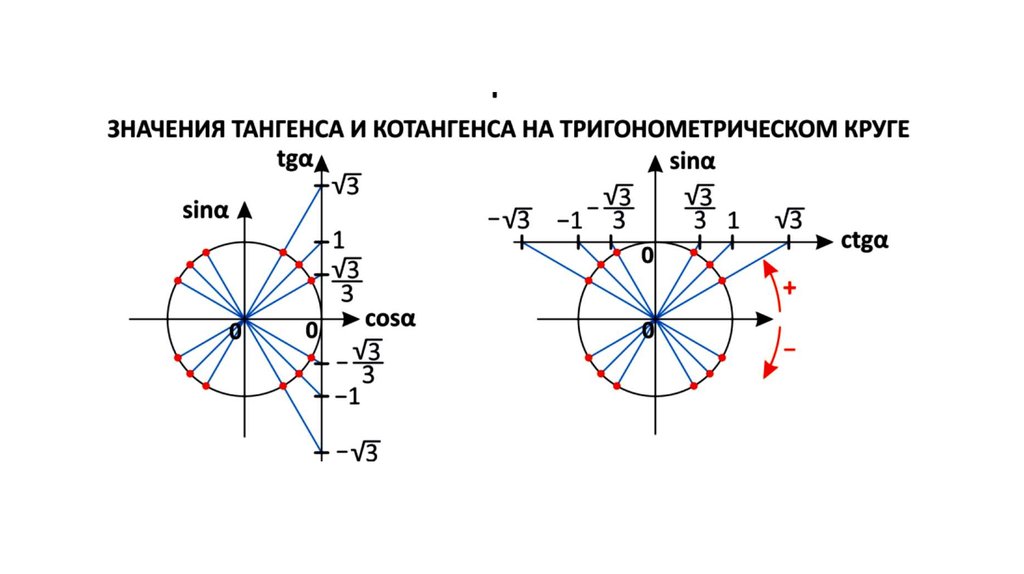

Значение косеканса

Косеканс определяется как величина, обратная синусу или $ \frac{1}{\sin\theta} $. Отрезок OF представляет собой значение косеканса угла θ .

Треугольники PYO и FOE — подобные прямоугольные треугольники. Это дает нам соотношение:

(i) $\frac{\text{PO}}{\text{PY}} = \frac{\text{EF}}{\text{OF}}$

92\theta}{\sin\theta} = \csc\theta \)

В приведенном выше примере $\csc\theta = \frac{1}{0,8} = \frac{5}{4} = 1,25 $.

Мы рассмотрели все 6 основных тригонометрических величин на одной диаграмме. Далее мы построим длины квадратов тригонометрических величин.

Квадраты тригонометрических значений

Предпосылки

Чтобы построить квадраты тригонометрических значений, нам сначала нужно иметь возможность построить значение x ², учитывая 9Значение 1117 x . Нам понадобится помощь следующего прямоугольного треугольника.

Рисунок 2: Прямоугольный треугольник и высота Рисунок 3

На рисунке 2 показан прямоугольный треугольник с высотой, проведенной к гипотенузе.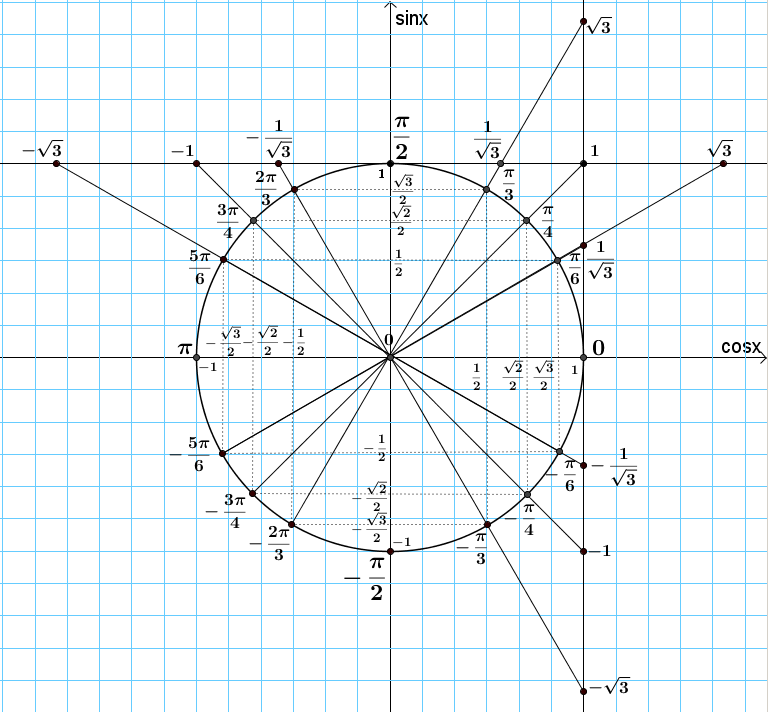 Высота делит гипотенузу на сегменты x и y и образует 3 подобных треугольника. По подобным треугольникам мы можем определить, что высота равна $\sqrt{xy}$. Если x = 1, то высота равна $\sqrt{y}$, как показано на рисунке 3. Это означает, что отрезок 92\) значение или значение $\sqrt{x}$ любого заданного сегмента длиной x . На самом деле, это невозможно!

Но разве мы не сделали это выше? Ответ — нет. На самом деле мы построили квадратный корень из произведения x и y . И x просто равно 1, потому что мы приравняли его к 1. Если нам дан отрезок длиной x , то возведение в квадрат или извлечение квадратного корня из x невозможно.

Имея 2 отрезка 2 длин, мы можем найти квадратный корень из их произведения, но мы не можем возвести в квадрат или извлечь квадратный корень из каждого из них по отдельности. Теперь должно быть ясно, что нам всегда понадобится один отрезок, равный 1, чтобы построить квадрат тригонометрических значений. Сказав это, мы продолжаем.

Чтобы построить измерения квадрата косинуса и квадрата синуса, нам просто нужно сделать значения синуса и косинуса высотой прямоугольного треугольника и одной частью гипотенузы, равной 1. Попробуйте это сами, прежде чем продолжить.

Значение в квадрате косинуса

Для значения в квадрате косинуса мы должны определить длину, равную 1, и высоту, которая является значением косинуса. Это на самом деле довольно легко. Рассмотрим рисунок 4 ниже.

Рисунок 4: Отрезок квадрата косинуса

На рисунке 4 OX, конечно же, равен $\cos\theta$. Например, мы использовали 9{\circ}) = 0,8\). Сначала мы перенесем эту длину на ось y . Следовательно, PX = AO = sin θ .

Затем мы рисуем отрезок AB, который пересекает окружность в точке B, так что OB = 1, радиус окружности. Теперь у нас есть отрезок гипотенузы, равный 1, и значение синуса в качестве высоты.

Затем проведите перпендикуляр к AB в точке A, чтобы завершить прямоугольный треугольник.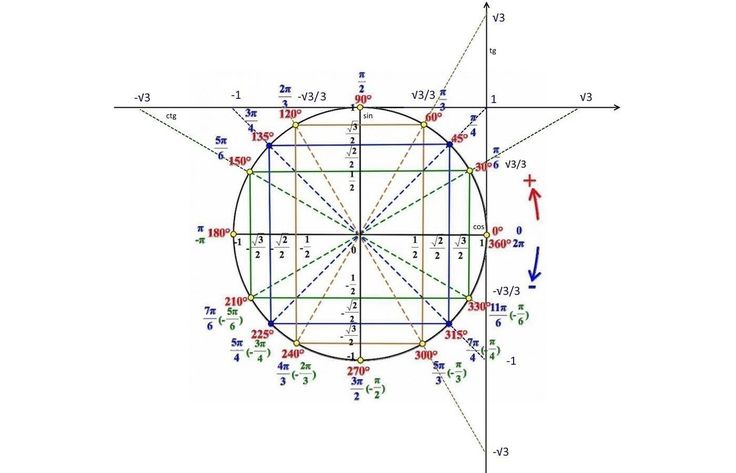 2 = 0,64\), что подтверждается расчетом Geogebra. 9{2}х\).

Квадрат тангенса

Если построение значений квадрата синуса и косинуса кажется сложным, вы можете подумать, что построение квадрата тангенса должно быть еще сложнее. Как оказалось, это проще, чем кажется.

Возможно, вы сами сможете понять это из рисунка 6 ниже.

Рис. 6: Касательный квадратный сегмент. (Вы видите секущую в квадрате?)

Мы уже установили, что PA равно значению тангенса. Удобно, поскольку она касается окружности, а линия, проведенная из точки P в центр окружности, образует прямой угол. Следовательно, АРО — прямой угол. 9{2}\тета\). Таким образом, $\text{AB} = \tan\theta\cdot\sec\theta$.

Секанс в квадрате

Наконец, мы создадим значение секанса в квадрате. Значение квадрата косеканса останется для читателя.

Рисунок 7: Секущая в квадрате

Сначала проведите касательную к окружности в точке P, которая пересекает ось x в точке A. Отрезок OA представляет значение секущей θ , как было установлено ранее.

Затем нарисуйте отрезок AC, где C — точка на окружности в точке (0, –1). У нас есть OA, высота нашего прямоугольного треугольника, как значение секанса и OC = 1,9{2}\тета\). Число «1», которое появляется в тождествах, явно является радиусом круга. На рис. 8 ниже показаны другой сегмент в квадрате с секущей и сегмент в квадрате с касательной. Квадрат секанса — это просто отрезок OD, потому что PD — это отрезок касательной в квадрате.

Рисунок 8: Квадрат секанса и тангенса

Два сегмента, которые представляют собой квадрат секанса, это OJ и OD. Мы можем провести окружность через точки J и D, потому что обе точки являются радиусами окружности с центром в точке O.

Отрезки EJ и PD, конечно, тоже равны квадрату тангенса. 9{\circ}) = 2\). Любопытно, что угол, при котором тангенс в четвертой степени равен 2, составляет приблизительно 49,939° (приблизительно 0,87161 радиан — это примерно $\frac{\pi}{3,604}$) и отрезок PB является диаметром окружности .

Для углов, отличных от 49,939°, точка B не будет лежать на окружности, но отрезок будет пересекать центр окружности.

30°	45°	60°	90°	120°	135°	150°	180°	270°	360°
\(\frac\)	\(\frac\)	\(\frac\)	\(\frac\)	\(\frac\)	\(\frac\)	\(\frac\)	\(\pi\)	\(\frac\)	\(2\pi\)