Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Тригонометрические функции, формулы и графики. Поделиться:
| |||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||
sin, cos, tg, ctg….Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества.
Введите свой запрос:10. Определение тригонометрических функций.
Синус, — отношение катета, лежащего против этого угла, к гипотенузе.
КО́СИНУС — катета, прилегающего к острому углу в прямоугольном треугольнике, к гипотенузе.
ТА́НГЕНС — отношение катета, лежащего против острого угла в прямоугольном треугольнике, к другому катету
КОТА́НГЕНС отношение катета, прилегающего к острому углу в прямоугольном треугольнике, к другому катет. Синус отвечает за ось у, а косинус за ось х
11. Свойства тригонометрических функций.
Числовые функции,заданные формулами y=sinx и у=cosx называются соответственно синусом и косинусом.
D(sin)=D(cos)=R
E(sin)=E(cos)=[-1;1]
Cosx – четная
Sinx –нечетная
T(sin)=T(cos)=2
Числовые функции, заданные формулами y=tgx и y=ctgx называют соответственно тангенсом и катангенсом.
D(tg)=( \2 -n; \2+n)
E(tg)=R
T(tg)=
Tgx – нечетн
D(ctg)= R, кроме х=n
D(ctg)=(0+n; +n)
E(ctg)=R
Ctgx –нечетн
T(ctgx)=
Функция
называется периодической с периодом Т
не равным 0, если для любого х из области
определения значения этой функции в
точках х, х-Т, х+Т равны, т.
е f(x+T)=f(x)=f(x-T)
12. Основные тождества тригонометрии .
Основные тригонометрические тождества
sin² α + cos² α = 1
tg α · ctg α = 1
tg α = sin α \ cos α
ctg α = cos α \ sin α
1 + tg² α = 1 \cos² α
1 + ctg² α = 1 \ sin² α
13.Формулы сложения.
Формулы сложения
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
cos (α — β) = cos α · cos β + sin α · sin β
tg (α + β) = (tg α + tg β) ÷ (1 — tg α · tg β)
tg (α — β) = (tg α — tg β) ÷ (1 + tg α · tg β)
ctg (α + β) = (ctg α · ctg β + 1) ÷ (ctg β — ctg α)
ctg (α — β) = (ctg α · ctg β — 1) ÷ (ctg β + ctg α)
14. Формулы сложения тригонометрических функций.
cos α + cos β = 2cos((α + β)/2) cos((α – β)/2)
cos α – cos β = 2sin((α + β)/2) sin((β – α)/2)
sin α + sin β = 2sin((α + β)/2) cos((α – β)/2)
sin α – sin β = 2sin((α – β)/2) cos((α + β)/2)
tg α + tg β = sin(α + β)/(cos α cos β)
tg α – tg β = sin(α – β)/(cos α cos β)
ctg α ± ctg β = sin(β ± α)/(sin α sin β)
15. Формулы приведения. Формулы двойных и половинных углов.
Формулы приведения
Формулы двойного угла
cos 2α = cos² α — sin² α
cos 2α = 2cos² α — 1
cos 2α = 1 — 2sin² α
sin 2α = 2sin α · cos α
tg 2α = (2tg α) ÷ (1 — tg² α)
ctg 2α = (ctg² α — 1) ÷ (2ctg α)
Формулы половинных углов
16. Свойства и график тригонометрической функции y=Sin x.
Графики и свойства тригонометрических функций
График
функции y = sin(x).
Синусом числа х (sin x) называется ордината точки тригонометрического круга, полученной поворотом точки (1;0) на х рад против часовой стрелки.
Основные свойства функции y = sin(x ).
1. Областью определения функции является множество всех действительных чисел: 2. Областью значений функции является множество значений всех чисел отрезка на интервале [−1;1], значит, синус — функция ограниченная.
3. Функция нечетная: . График нечетной функции симметричен относительно начала координат — точки О.
4. Функция периодическая с наименьшим положительным периодом T = 2π: .
5. | ||
6. | ||
7. |
8.
Функция возрастает от −1 до 1 на промежутках:
9. Функция убывает от 1 до −1 на промежутках:
10. Наибольшее значение sin x = 1 функция приобретает в точках:
11. Наименьшее значение sin x = −1 функция приобретает в точках:
17. Свойства и график тригонометрической функции y= ctg x.
Какие шесть функций тригонометрии?
Тригонометрию можно определить как раздел математики, определяющий и изучающий отношения между сторонами треугольника и углами, образуемыми ими. Тригонометрия в основном используется в случае прямоугольных треугольников. Тригонометрические функции определяют отношения между тремя сторонами и углами треугольника. В основном есть 6 тригонометрических функций. Прежде чем приступить к изучению тригонометрических функций, мы узнаем о трех сторонах прямоугольного треугольника.
Три стороны прямоугольного треугольника следующие:
- Основание Сторона, на которой лежит угол θ, называется основанием.
- Перпендикуляр Это сторона, противоположная рассматриваемому углу θ .
- Гипотенуза Самая длинная сторона прямоугольного треугольника, противоположная углу 90°.
Тригонометрические функции
Тригонометрия имеет 6 основных тригонометрических функций: синус, косинус, тангенс, косеканс, секанс и котангенс. Теперь давайте рассмотрим тригонометрические функции. Шесть тригонометрических функций следующие:
- синус Представляется как sin θ и определяется как отношение перпендикуляра к гипотенузе.
- косинус Представляется как cos θ и определяется как отношение основания к гипотенузе.
- тангенс Он представлен как тангенс θ и определяется как отношение синуса и косинуса угла. Таким образом, определение тангенса оказывается отношением перпендикуляра к основанию.
- косеканс Обратное значение sin θ и представляется как cosec θ.
- секанс Это величина, обратная cos θ, обозначается как sec θ.
- котангенс Обратная величина тангенса θ и представлена как cot θ.
Каковы шесть тригонометрических функций?
Шесть тригонометрических функций имеют формулы для прямоугольных треугольников, формулы помогают определить длины сторон прямоугольного треугольника, давайте посмотрим на все эти формулы,
| Trigonometric Functions | Formulae |
| sin θ | |
| cos θ | |
| tan θ | |
| cosec θ | |
| sec θ | |
| детская кроватка θ |
В таблице ниже показаны значения этих функций для некоторых стандартных углов,
| Function | 0° | 30° | 45° | 60° | 90° |
| ∞ | |||||
| ∞ | |||||
| ∞ | |||||
| ∞ |
Note : Рекомендуется запомнить первые 3 тригонометрические функции и их значения при этих стандартных углах для простоты вычислений.
Примеры задач
Вопрос 1: Оцените синус, косинус и тангенс на следующем рисунке .
Решение:
Учитывает
с использованием тригонометрических формул для синуса, косинуса и тангента,
Вопрос 2: В то же время. котангенс.
Решение:
Поскольку известны значения синуса, косинуса и тангенса, мы можем легко вычислить требуемые соотношения.
Вопрос 3: Учитывая , оцените sin θ.cos θ .
Решение:
Таким образом, P = 6, B = 8
с использованием теоремы Pythagoras,
H 2 = P 2 +B 2 = P . +64=100
Следовательно, H = 10
Теперь
Вопрос 4.
Если , оцените рыжевато-коричневый 2 θ.
Solution:
Given
Thus
Question 5: In the given triangle, verify sin 2 θ+cos 2 θ = 1
Solution:
Учитывая P=12, B=5, H=13
Таким образом,
Следовательно, проверено.
тригонометрия — Три тригонометрических функции или шесть?
Есть очень веский аргумент, что есть две важные функции, поведение которых вам нужно иметь четкое представление для тригонометрии, а затем несколько произвольный набор вспомогательных функций, которые находят различные применения, но чьи свойства полностью определяются этими двумя. Позвольте мне рассмотреть некоторые из этих аргументов, чтобы уточнить.
Почему не 1?
Во-первых, важно понять аргумент о том, что на самом деле может быть только одна важная функция: 9х$ и ты молодец.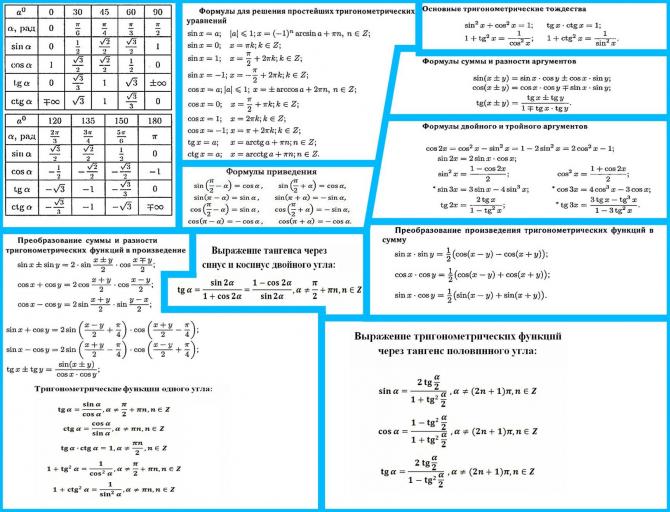
x$, когда многие из ключевых причин рассматривать пару функций вместо одной функции теряются в эти детали. 92 (x) = 1$$
, так что не являются ли они «на самом деле» все еще одной функцией, выраженной по-разному?
Проблема здесь в том, что мы ввели еще один важный «выбор 2» путем возведения в квадрат. Квадратный корень — многозначная функция, и при любом конкретном $x$ мы на самом деле имеем в виду только одну из этих ветвей. Как мы это описываем?
Чтобы сделать это, мы должны выразить
- конкретное значение, которое будет приниматься «другой» функцией в некоторой заданной точке
- требование непрерывности
- требование дифференцируемости
Таким образом, должна быть описана не одна функция, а функция + отношение с достаточным количеством внешних данных для описания другой функции. Так что это не очень естественный способ аргументировать одну функцию…
Но! Как насчет coup de grace, секретного оружия, которое раз и навсегда доказывает, что здесь действительно есть только одна функция и что существует простое отношение, позволяющее избежать всех двусмысленностей, которые привносят другие подходы:
$$\sin(x) = \cos(x-\frac{\pi}{2})$$
?? Это кажется недвусмысленным и четко определяет одну функцию через другую.
Правильно? Вам не нужны никакие дополнительные данные помимо отношений.
Ну… конечно. Все методы, описанные до сих пор, в основном недвусмысленны, потому что у нас есть четкое понимание данных, которые остаются невысказанными. Но всегда был аргумент, что невысказанные данные достаточно сложны, чтобы мы не должны игнорировать их при обсуждении «натурального числа тригонометрических функций». Так при чем здесь негласные данные?
Очевидным является использование $\frac{\pi}{2}$. Как мы это определяем? Ясно, что $\tau=2\pi$ — это естественный период одной функции, а функция имеет симметрии с пересечением нуля через каждые $\pi$ и каждое сечение между нулями, имеющее отражательную симметрию в средней точке и нечетную симметрию относительно нулей. Таким образом, чтобы получить эту константу как естественную часть функции, вы должны быть готовы принять четные и нечетные симметричные отношения одной функции как естественные на основе того, что вы используете для определения этой функции.
Большинство определений не обладают этим свойством (например, разложение Тейлора), но те, которые имеют его (например, проекции окружности), похоже, определяют функции $\sin$ и $\cos$ вместе. 9x$ применяется к операторам.
Так почему 2?
Предположим, что-то из вышеперечисленного относится к какому-то делу. Почему любой из этих аргументов в пользу того, что две функции естественны, а не «одна функция + одна точка», или 3 функции, или 10?
Посмотрите на определение с точки зрения проекций круга. Несмотря на то, что выбор основы произволен, и хотя одна основа может быть преобразована в другую, это все же двумерная система, и есть две основы для проектирования. Связь между двумя проекционными операторами очень похожа на связь между двумя тригонометрическими функциями. Отношение сдвига, упомянутое выше, на самом деле является представлением преобразования вращения, которое переводит один базис в другой. 92(x)=1$ на самом деле просто представление инвариантного расстояния точки на окружности от центра начала координат.
Мы не просто изучаем две точки и говорим, что изучили окружность, потому что это упускает из виду все другие отношения между другими точками на окружности. Точно так же мы не изучаем только одну тригонометрическую функцию, потому что именно отношения между функциями выражают отношения и симметрии между проекциями на два основания во всех точках окружности. 9{-ix}}{2i}$ приходится апеллировать ко второй функции, которая опять-таки внешне не определима посредством арифметических операций (и опять связь между ними, на этот раз оператор отражения, принципиально связана с изучаемыми симметриями ).
Собрав все это воедино, эту запутанную ситуацию можно изучить с помощью упомянутого выше оператора последовательного проектирования. Этот оператор обладает интересным свойством:
$$ D M_{m,n} = M_{m-1,n} D$$
, поэтому дифференцирование сдвигает проекции. Это именно то дифференциальное свойство, которое мы наблюдаем у двух основных тригонометрических функций: основания вращаются.