Основные геометрические формулы: Основные формулы по геометрии и их свойства.

Содержание

Основные геометрические формулы | Учебно-методический материал по геометрии (9 класс) по теме:

Опубликовано 20.09.2016 — 18:46 — Суромина Татьяна Николаевна

Материал для стенда по геометрии

Скачать:

Предварительный просмотр:

V – объём

а – длина

b – ширина

с – высота

V = a · b ·c

V = a · a ·a

S — площадь

а – длина

b – ширина

S = a · b

площадь = длину · ширину

S = a · a

Р – периметр

( сумма длин всех сторон)

b Р = a+b+a+b

P = (a + b) · 2

Предварительный просмотр:

Меры площади

1 см2 = 100 мм2

1 дм2 = 100 см2

1 м2 = 100 дм2

1 а = 100 м2

1 га = 100 а

1 км2 = 100 га

Меры длины

1см = 10 мм

1дм = 10 см

1м = 10 дм

1м = 100 см

1км = 1000 м

Меры объёма

1см3 = 1000 мм3

1дм3 = 1000 см3

1м3 = 1000 дм3

1км3 =1000 000 000 м3

1 литр = 1 дм3

Гектар –

площадь квадрата со стороной 100 м.

Ар (сотка) –

площадь квадрата со стороной 10 м.

Симметрия

Если при перегибании листа бумаги по прямой правая и левая половины фигуры совпадают, то такая фигура называется симметричной. Линия перегиба – ось симметрии.

По теме: методические разработки, презентации и конспекты

Интегрированный урок в 7 классе Основные геометрические фигуры. Графический редактор Paint

В связи с переходом на новые федеральные государственные образовательные стандарты перед школой и перед учителем стоит задача: не только дать знания по конкретным дисциплинам, но и научить учащихся пр…

«Основные геометрические фигуры» задания

Задания можно использовать как для самостоятельной работы всего класса , так и для индивидуальной работы на уроке и дома по теме «Основные геометрические фигуры»…

«Основные геометрические фигуры» задания

Задания можно использовать как для самостоятельной работы всего класса , так и для индивидуальной работы на уроке и дома по теме «Основные геометрические фигуры». ..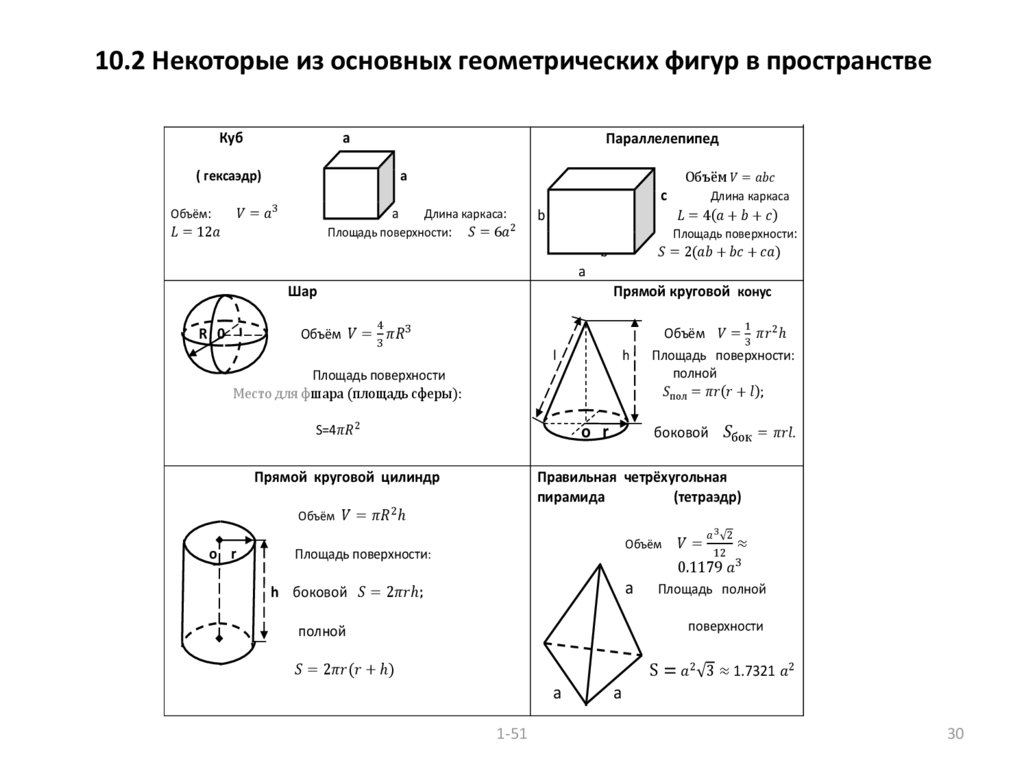

Тренажёры для отработки геометрических формул

В программу курса геометрии 8 класса входит большое количество формул: формулы площадей многоугольников, теорема Пифагора, определения синуса, косинуса и тангенса острого угла в прямоугольном тр…

Задачи на отработку геометрических формул 8 класс

Восемь задач, при решении каждой из которых необходимы знания теоремы Пифагора, формулы площади треугольника, свойств точки пересечения медиан треугольника.Отдельно в таблице предоставлены ответы к за…

Урок геометрии в 7 классе «Основные геометрические фигуры»

Урок разработан по модульной технологии….

Развитие творческого мышления учащихся на уроках математики через опытное обоснование геометрических формул

Для современной школы исключительно важной является проблема развития творческих способностей учащихся. Этой проблемой занимались и продолжают заниматься ряд отечественных и зарубежных ученых. В насто…

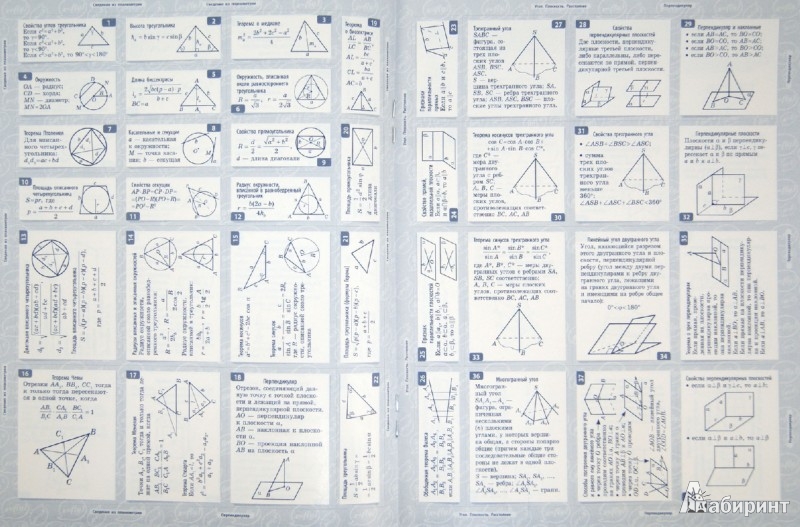
Справочник по геометрии 7-9 класс

Главная
Справочники
Справочник по геометрии 7-9 класс

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Угол

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Градусная мера угла

Измерение углов на местности

Смежные углы

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

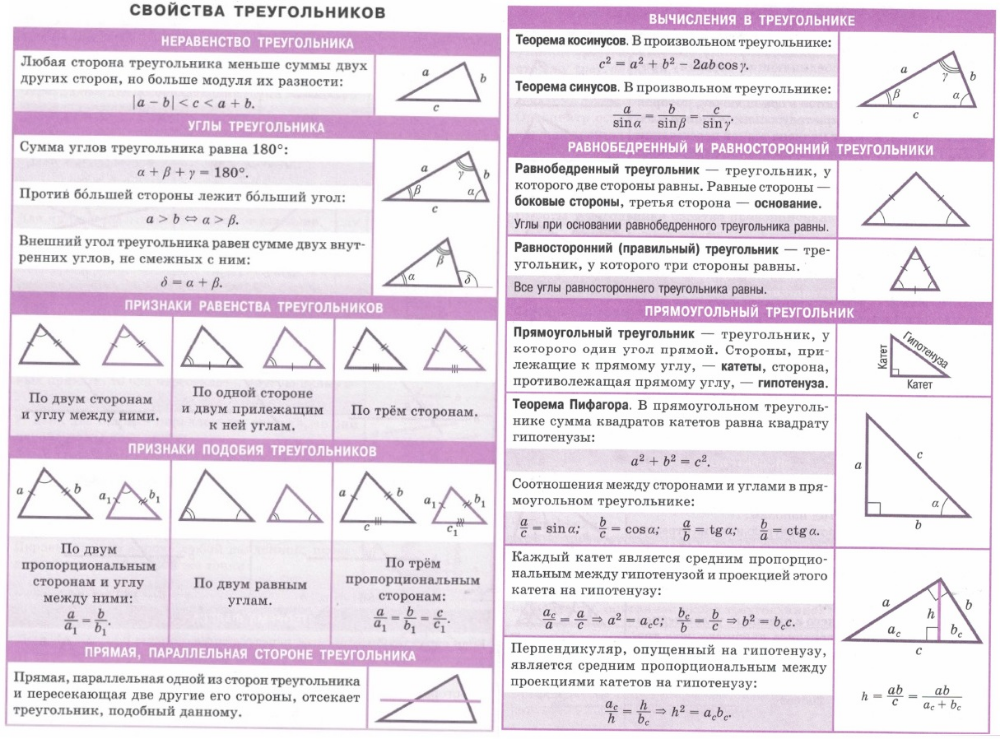
Треугольник

Равенство треугольников

Первый признак равенства треугольников

Перпендикуляр к прямой

Медианы треугольника

Биссектрисы треугольника

Высоты треугольника

Равнобедренный треугольник

Свойства равнобедренного треугольника

Второй признак равенства треугольников

Третий признак равенства треугольников

Окружность

Построения циркулем и линейкой

Построение угла, равного данному

Построение биссектрисы угла

Построение перпендикулярных прямых

Построение середины отрезка

Среднее пропорциональное

Параллельные прямые

Признаки параллельности двух прямых

Практические способы построения параллельных прямых

Аксиомы геометрии

Аксиома параллельных прямых

Теорема о накрест лежащих углах

Теорема о соответственных углах

Теорема об односторонних углах

Теорема об углах с соответственно параллельными сторонами

Теорема об углах с соответственно перпендикулярными сторонами

Теорема о сумме углов треугольника

Остроугольный, прямоугольный и тупоугольный треугольники

Теорема о соотношениях между сторонами и углами треугольника

Неравенство треугольника

Некоторые свойства прямоугольных треугольников

Признаки равенства прямоугольных треугольников

Уголковый отражатель

Расстояние от точки до прямой

Расстояние между параллельными прямыми

Построение треугольника по двум сторонам и углу между ними

Построение треугольника по стороне и двум прилежащим к ней углам

Построение треугольника по трем его сторонам

Многоугольник

Выпуклый многоугольник

Четырехугольник

Параллелограмм

Признаки параллелограмма

Трапеция

Прямоугольник

Ромб и квадрат

Осевая и центральная симметрии

Понятие площади многоугольника

Площадь квадрата

Площадь прямоугольника

Площадь параллелограмма

Площадь треугольника

Площадь трапеции

Теорема Пифагора

Теорема, обратная теореме Пифагора

Формула Герона

Пропорциональные отрезки

Определение подобных треугольников

Отношение площадей подобных треугольников

Первый признак подобия треугольников

Второй признак подобия треугольников

Третий признак подобия треугольников

Средняя линия треугольника

Пропорциональные отрезки в прямоугольном треугольнике

Практические приложения подобия треугольников

Задачи на построение

Измерительные работы на местности

О подобии произвольных фигур

Синус, косинус и тангенс острого угла прямоугольного треугольника

Значение синуса, косинуса и тангенса для углов 30, 45 и 60

Взаимное расположение прямой и окружности

Касательная к окружности

Градусная мера дуги окружности

Теорема о вписанном угле

Свойство биссектрисы угла

Свойства серединного перпендикуляра к отрезку

Теорема о пересечении высот треугольника

Вписанная окружность

Описанная окружность

Понятие вектора

Равенство векторов

Откладывание вектора от данной точки

Сумма двух векторов

Законы сложения векторов.

Правило параллелограмма

Сумма нескольких векторов

Вычитание векторов

Произведение вектора на число

Применение векторов к решению задач

Средняя линия трапеции

Разложение вектора по двум неколлинеарным векторам

Координаты вектора

Связь между координатами вектора его начала и конца

Простейшие задачи в координатах

Уравнение линии на плоскости

Уравнение окружности

Уравнение прямой

Взаимное расположение двух окружностей

Синус, косинус, тангенс, котангенс

Основное тригонометрическое тождество.

Формулы приведения.

Формулы для вычисления координат точки

Теорема о площади треугольника

Теорема синусов

Теорема косинусов

Решение треугольников

Измерительные работы

Угол между векторами

Скалярное произведение векторов

Скалярное произведение в координатах

Свойства скалярного произведения векторов

Правильный многоугольник

Окружность, описанная около правильного многоугольника

Окружность, вписанная в правильный многоугольник

Формулы для вычисления площади правильного многоугольника, его стороны и радиуса вписанной окружности

Построение правильных многоугольников

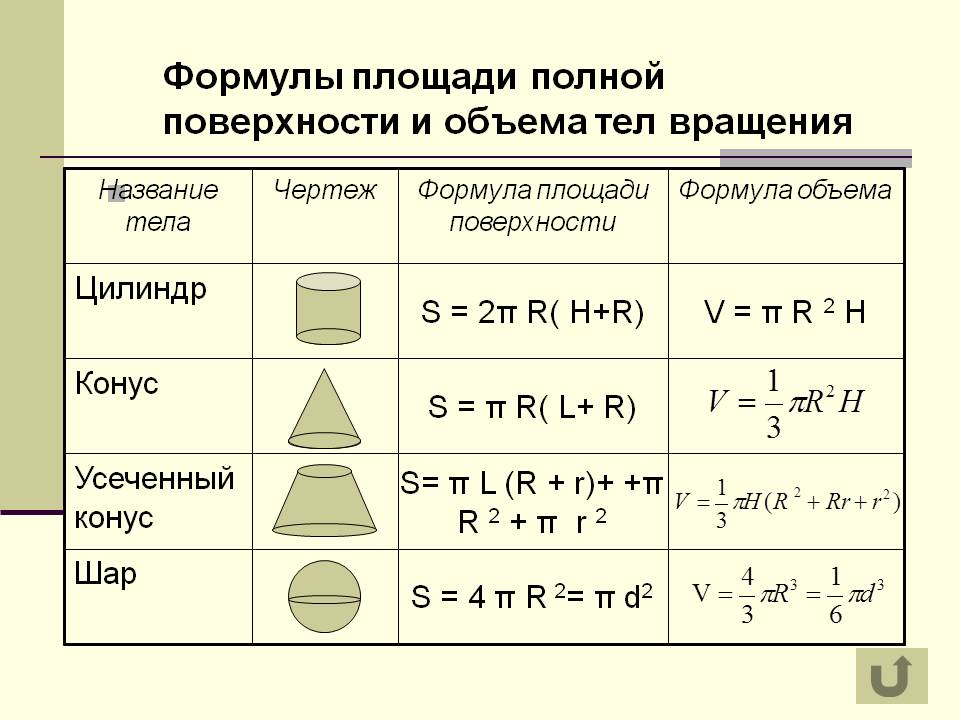
Длина окружности

Площадь круга

Площадь кругового сектора

Отображение плоскости на себя

Понятие движения

Наложения и движения

Параллельный перенос

Поворот

Предмет стереометрии

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Многогранник

Призма

Параллелепипед

Объём тела

Свойства прямоугольного параллелепипеда

Пирамида

Цилиндр

Конус

Сфера и шар

Поделись с друзьями в социальных сетях:

Формулы геометрии — празднование Дня числа Пи

13 марта 2018 г.

//Карьерные пути, STEM /Фонд студенческих исследований

Поскольку День числа Пи приближается 14 марта 2018 г., самое время рассмотреть наиболее важные формулы геометрии. что каждый ученик должен усвоить в средней школе.

О Дне Пи

Но сначала, что такое День Пи — если вы не знаете об этом. Мы не знаем, кто основал День Пи, но это всемирное образовательное событие, которое отмечается каждый год 14 марта.0009 th , который побуждает учителей участвовать в занятиях в классе, подтверждающих тот факт, что Пи можно использовать для вычисления площади и длины окружности кругов, объема сфер и других чисел, связанных с двух- и трехмерными формами, которые принципиально круговой.

Почему День Пи отмечается 14 марта ^-го-го года? (Не смущайтесь, если вы не знаете, кто-то должен был объяснить нам это в первый раз, когда мы услышали об этом.) Он называется День Пи, потому что 14 марта ^-й можно представить как 3/14. А как вы знаете, 3,14 — это первые три цифры числа Пи, которое представлено греческой буквой π .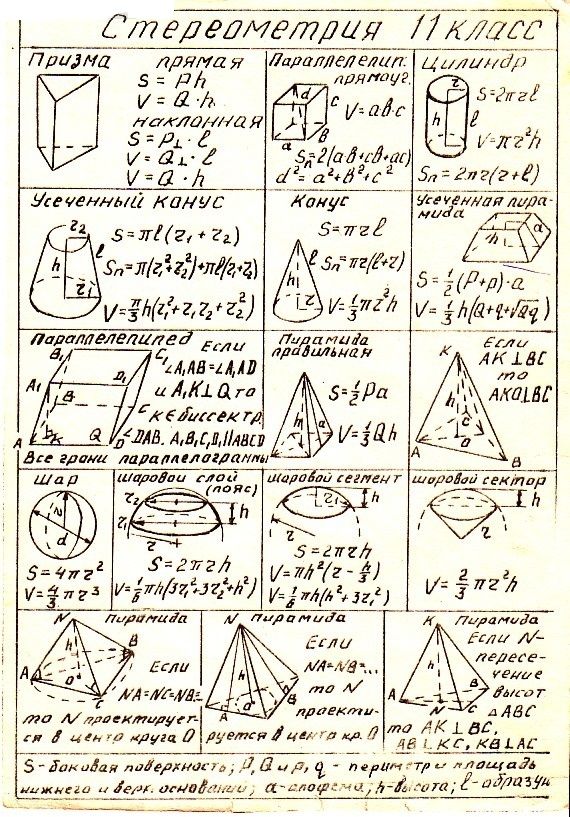 Это всего лишь первых трех цифр числа Пи, которое представляет собой отношение длины окружности к ее диаметру. Как известно, некоторым учащимся нравится уметь по памяти называть число Пи с точностью до десятков или сотен знаков справа от запятой. . . 3.14159 и далее. (Похоже, сообразительные студенты думают, что их примут в лучшие колледжи, если они смогут вспомнить эти цифры. Насколько нам известно, эта стратегия поступления в колледж не доказала свою эффективность.)

Базовые знания о том, как использовать число Пи

Помимо использования числа Пи для хвастовства, ваши ученики должны понимать эти формулы, в которых используется число.

πD (π x диаметр круга) или 2 πR (

π x удвоенный радиус круга) определят длину окружности.
πR ² (π x квадрат радиуса круга) определит площадь этого круга.
4/3 x π x R ³ (4/3 x π x куб радиуса сферы) будет определять площадь сферы.

Теорема Пифагора

Вот еще одна базовая формула, которую должен иметь под рукой каждый старшеклассник.

A ² + B ² = C ² (теорема Пифагора) используется для вычисления длины гипотенузы прямоугольного треугольника. Прямоугольный треугольник – это треугольник, в котором угол между двумя катетами образует 90ᴼ Чтобы получить длину гипотенузы (линии, противоположной прямому углу), нужно сложить квадраты длин двух сторон, образующих прямой угол. Затем вы находите квадратный корень из этой суммы, чтобы определить длину гипотенузы.

Нахождение площади геометрических фигур с прямыми сторонами

Это довольно простая вещь, но ее нужно знать.

Сторона ² используется для вычисления площади квадрата. Например, если сторона квадрата равна 4 дюймам, площадь этого квадрата равна 16 квадратных дюймов, или 4,² .
Основание x Высота используется для вычисления площади прямоугольника или параллелограмма. Странно, не правда ли, что одна и та же формула работает и для прямоугольника, и для параллелограмма? Когда мы учились в школе, мы любили спрашивать: «Что произойдет, если сжать параллелограмм так, чтобы он стал просто линией? Формула все еще работает?» Конечно, это не так. Но мы так и не нашли учителя геометрии, который мог бы объяснить нам, почему. Если вы знаете ответ, пожалуйста, сообщите нам.

Способны ли ученики, которых вы знаете, полностью использовать самые основные формулы, которые мы объясняем в сегодняшней статье? Мы рекомендуем вам поделиться своим мнением, приняв участие в исследовании карьеры Фонда студенческих исследований.

Related Posts
Каковы физические и умственные требования для карьеры STEM?
Подготавливают ли STEM-исследования студентов к успеху в гуманитарных науках?
STEM открывает двери для выбранной вами карьеры в сфере здравоохранения
Освещение готовности студентов к #STEM

Теги: 4IR, Pi Day, STEM, Технические колледжи

Поделитесь этой записью

0 ответов

Оставить комментарий

Хотите присоединиться к обсуждению?
Не стесняйтесь вносить свой вклад!

Тест по формулам геометрии

Вопросы Все вопросы5 вопросов6 вопросов7 вопросов8 вопросов9 вопросов10 вопросов

Настройки

Обратная связь

Во время викторины Конец викторины

Сложность

Последовательный Легкий сначала Жесткий первый

Играй за

Викторина Флэш карта

Если вы изучаете математику, вы должны были изучать геометрию.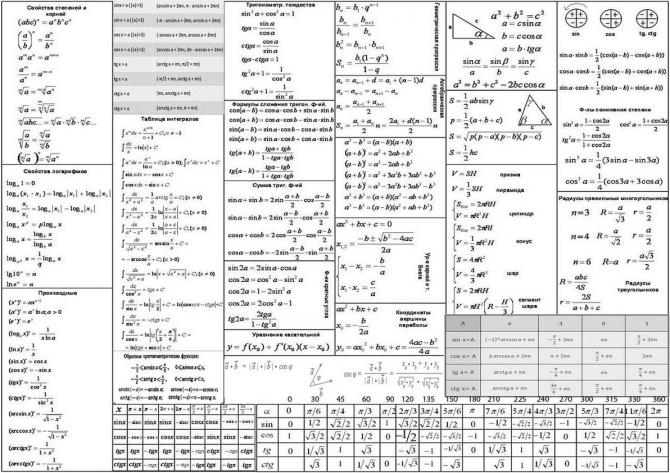

Вопросы и ответы

1.
Формула площади треугольника
- А.
  А = 1/2 × b × h
- Б.
  А = 2 × b × ч
- С.&nbsp
  А = 1/4 × b × h
- Д.&nbsp
  А = б × ч
2.
∏r² используется для
3.
Длина окружности равна
- А.
  №
- Б.
  2πr
- С.&nbsp
  1/2πr
- Д.&nbsp
  4πr
4.
Какова формула объема куба?
- А.
  V = а3
- Б.
  V = а4
- С.&nbsp
  В = а
- Д.&nbsp
  V = а х 1/2
5.
В = lwh/3 — это формула для
- А.
  Ширина пирамиды
- Б.
  Высота пирамиды
- С.&nbsp
  Объем сферы
- Д.&nbsp
  Объем пирамиды
6.
Площадь прямоугольника
7.
Формула для нахождения третьего угла:
- А.
  ∠А + ∠В = 180°
- Б.
  ∠А + ∠В + ∠С = 270°
- С.&nbsp
  ∠А + ∠В + ∠С = 180°
- Д.&nbsp
  ∠А + ∠В + ∠С = 360°
8.
Чему равен периметр квадрата?
- А.
  1/2 (сбоку)
- Б.
  No related posts.