Справочный материал по математике | Образовательная социальная сеть
Опубликовано 21.01.2020 — 18:27 — Голубева Эльвира Сериковна
| 5-11 классы | Латинский и греческий алфавиты | |
| 7-11 классы | Обозначения и сокращения в математике | |
| 10-11 классы | Справочный материал для подготовки к ЕГЭ | |
| Справочные материалы по математике, алгебре | ||
| 5 класс | Памятка по математике для 5 класса | |
| 6 класс | Памятка по математике для 6 класса | |
| 7 класс | Памятка по математике для 7 класса | |
| 8 класс | Решение квадратных неравенств с помощью параболы new | |
| 7-9 классы | Формулы основной школы | |
| 7-9 классы | Таблица степеней, таблица квадратов | |
| 8-9 классы | Построение графика квадратичной функции | |
| 8-9 классы | Алгоритм решения неравенств методом интервалов | |
| 8-9 классы | Решение квадратных неравенств графическим способом. Образцы решения | |
| 8-9 классы | Решение квадратных неравенств методом интервалов. Образцы решения | |
| 9 класс | Виды преобразований графиков функций | |
| 10 класс | Алгоритм исследования функции с помощью производной | |
| 10 класс | Свойства тригонометрических функций | |
| 10 класс | Таблица значений тригонометрических функций | |
| 10 класc | Тригонометрическая окружность + Формулы приведения | |
| 10 класc | Тригонометрическая окружность + Таблица значений тригонометрических функций | |
| 10 класс | Основные тригонометрические формулы | |
| 10 класс | 50 формул тригонометрии | |
| 10 класс | Решение тригонометрических уравнений | |
| 10 класс | Решение тригонометрических неравенств | |
| 10 класс | Формулы приведения | |
| 10-11 классы | Таблица производных и первообразных | |
| 11 класс | Показательная и логарифмическая функции | |
| 11 класс | Степени и корни. Свойства и графики степенных функций | |
| 11 класс | Важнейшие равносильные преобразования (при решении уравнений и неравенств) | |
| Справочные материалы по геометрии | ||
| 7-9 классы | Основные формулы планиметрии | |
| 8-11 класс | Пифагоровы тройки | |
| 7-9 классы | Треугольники | |
| 7-9 классы | Четырехугольники | |
| 9 класс | Таблица значений тригонометрических функций В.М. Брадиса | |
| 9 класс | Соотношения в правильных многоугольниках | |
| 10-11 классы | Стереометрия | |
Тесты по информатике математике русскому языку английскому языку и др
Список доступных заданий технологии ‘Тест знаний’ по предмету Математика:
Тест
Свойства и графики тригонометрических функций.
Сложность: 10 класс
[Проверить знания]
Тест
Тригонометрические уравнения и неравенства.Сложность: 10 класс
[Проверить знания]
Тест
Вычсление обратной функции.Сложность: 10 класс
[Проверить знания]
Тест
Формулы приведения.Сложность: 10 класс
[Проверить знания]
Тест
Простейшие тригонометрические уравнения.Сложность: 10 класс
[Проверить знания]
Тест
Тригонометрические функции.Сложность: 10 класс
[Проверить знания]
Тест
Тригонометрические функции.Сложность: 10 класс
[Проверить знания]
Тест
функция y=sinx.Сложность: 10 класс
[Проверить знания]
Тест
Свойства тригонометрических функций.Сложность: 10 класс
[Проверить знания]
Тест
Многочлены от одной переменной и действия над ними.
Сложность: 10 класс
[Проверить знания]
Тест
Теоретический опрос. 12 параграф. Тригонометрические функции угла и числового аргумента.Сложность: 10 класс
[Проверить знания]
Тест
Таблица тригонометрических функций. 12 параграф. Тригонометрические функции угла и числового аргумента.Сложность: 10 класс
[Проверить знания]
Тест
Основные тригонометрические формулы.Сложность: 10 класс
[Проверить знания]
Тест
Уравнения и неравенства, содержащие знак модуля(на время).Сложность: 10 класс
[Проверить знания]
Тест
Графики уравнений и неравенств с двумя переменными.Сложность: 10 класс
[Проверить знания]
Тест
10. Многочлены от одной переменной и действия над ними.Сложность: 10 класс
[Проверить знания]
Тест
10. Многочлены от одной переменной и действия над ними.
Сложность: 10 класс
[Проверить знания]
Тест
Тест: Решение простейших тригонометрических уравнений (2).Сложность: 10 класс
[Проверить знания]
Тест
§ 1. Множества и операции над ними.Сложность: 10 класс
[Проверить знания]
Тест
§ 1. Множества и операции над ними.Сложность: 10 класс
[Проверить знания]
Тест
§ 3. УРАВНЕНИЯ.Сложность: 10 класс
[Проверить знания]
Тест
Тригонометрические функции.Сложность: 10 класс
[Проверить знания]
Тест
Основные свойства функций.Сложность: 10 класс
[Проверить знания]
Тест
§ 3. УРАВНЕНИЯ.Сложность: 10 класс
[Проверить знания]
Тест
Преобразование степенных и иррациональных выражений.Сложность: 10 класс
[Проверить знания]
Тест
Радианная мера угла.
Сложность: 10 класс
[Проверить знания]
Тест
§ 1. Множества и операции над ними.Сложность: 10 класс
[Проверить знания]
Тест
Решение более сложных тригонометрических уравнений. Тест 1.Сложность: 10 класс
[Проверить знания]
Тест
Тест по теме: Понятие числовой функции. Простейшие свойства числовых функций. Косярский А.А..Сложность: 10 класс
[Проверить знания]
Тест
Свойства функций синуса, косинуса, тангенса и котангенса и их графики.Сложность: 10 класс
[Проверить знания]
Тест
Делимость целых чисел. Решение уравнений в целых числах.Сложность: 10 класс
[Проверить знания]
Тест
§ 3. УРАВНЕНИЯ.Сложность: 10 класс
[Проверить знания]
Тест
Радианная мера угла.Сложность: 10 класс
[Проверить знания]
Тест
Тест: Решение простейших тригонометрических уравнений.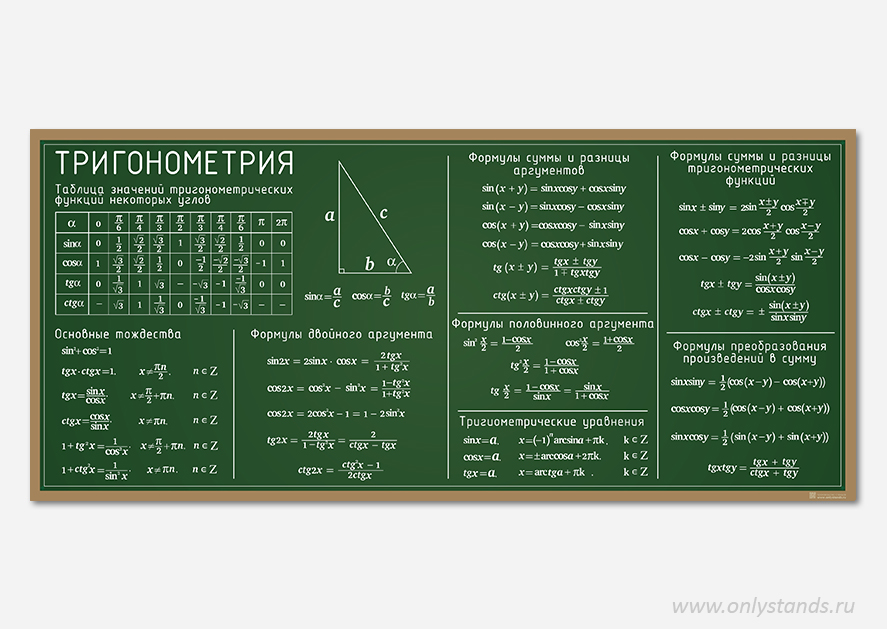
Сложность: 10 класс
[Проверить знания]
Тест
Тест по тригонометрии.Сложность: 10 класс
[Проверить знания]
Тест
Тест по тригонометрии уравнения и их системы.Сложность: 10 класс
[Проверить знания]
Тест
Решение более сложных тригонометрических уравнений. Тест 2.Сложность: 10 класс
[Проверить знания]
Тест
•Тест для проверки теоретических знаний по теме «Действительные числа».Сложность: 10 класс
[Проверить знания]
Тест
Многочлены от одной переменной и действия над ними.Сложность: 10 класс
[Проверить знания]
Тест
функция y=cosx.Сложность: 10 класс
[Проверить знания]
Тест
Построение графиков функций с помощью геометрических преобразований известных графиков.Сложность: 10 класс
[Проверить знания]
Тест
§ 3. УРАВНЕНИЯ.
Сложность: 10 класс
[Проверить знания]
Тест
Решение тригонометрических уравнений, отличающихся от простейших.Сложность: 10 класс
[Проверить знания]
Тест
Уравнения и неравенства, содержащие знак модуля.Сложность: 10 класс
[Проверить знания]
Тест
Неравенства: равносильные преобразования неравенств и общий метод интервалов.Сложность: 10 класс
[Проверить знания]
Тест
§ 6. Графики уравнений и неравенств с двумя переменными.Сложность: 10 класс
[Проверить знания]
Тест
Примеры решения более сложных тригонометрических уравнений и их систем.Сложность: 10 класс
[Проверить знания]
Тест
уравнения и неравенства.Сложность: 10 класс
[Проверить знания]
Тест
Тест № 3 по теме: "Тригонометрические функции угла и числового аргумента (Тангенс)".
Сложность: 10 класс
[Проверить знания]
Тест
Тест № 4 по теме: "Тригонометрические функции угла и числового аргумента (Котангенс)".Сложность: 10 класс
[Проверить знания]
Тест
Тест № 1 по теме: "Тригонометрические функции угла и числового аргумента (Синус)".Сложность: 10 класс
[Проверить знания]
Тест
Тест № 2 по теме: "Тригонометрические функции угла и числового аргумента (Косинус)".Сложность: 10 класс
[Проверить знания]
Тест
10. Многочлены от одной переменной и действия над ними.Сложность: 10 класс
[Проверить знания]
Тест
Повторение тем.Сложность: 10 класс
[Проверить знания]
Тест
Делимость целых чисел. Решение уравнений в целых числах.Сложность: 10 класс
[Проверить знания]
Тест
Соотношения между тригонометрическими функциями одного аргумента.
Сложность: 10 класс
[Проверить знания]
Тест
Формулы сложения, привидения.Сложность: 10 класс
[Проверить знания]
Тригонометрическая формула для класса 10 – все важные формулы
Здесь для учащихся приведены тригонометрические формулы для 10 класса. Тригонометрия изучает отношения между углами, длинами и высотами треугольников. Он включает отношения, функции, тождества и формулы для решения задач на их основе, особенно для прямоугольных треугольников. Приложения тригонометрии также можно найти в технике, астрономии, физике и архитектурном дизайне. Эта глава очень важна, потому что она охватывает многие темы, такие как линейная алгебра, исчисление и статистика.
| Содержание |
|
Все важные формулы тригонометрии, представленные учащимся 10-го класса, доступны на веб-сайте Physics Wallah.
Студенты могут в любое время выучить эти формулы из Physics Wallah и решить задачи, связанные с тригонометрией.
Тригонометрические формулы класса 10 для отношений в основном основаны на трех сторонах прямоугольного треугольника, таких как прилежащая сторона или перпендикуляр, основание и гипотенуза (см. Рисунок). Теперь, применяя теорему Пифагора для данного прямоугольного треугольника,
(Перпендикуляр)
(П) 2 + (Б) 2 = (Н) 2
Теперь проверим формулы на основе тригонометрических соотношений (синус, косинус, тангенс, секанс, косеканс и котангенс)
Основные тригонометрические формулы
| Серийный номер | Свойство | Математическое значение |
| 1 | грех А | Перпендикуляр/гипотенуза |
| 2 | Кос А | Основание/гипотенуза |
| 3 | желто-коричневый A | Перпендикуляр/Основание |
| 4 | детская кроватка А | Основание/перпендикуляр |
| 5 | косек А | Гипотенуза/перпендикуляр |
| 6 | сек А | Гипотенуза/основание |
Связь между тригонометрическими отношениями
| Серийный номер | Личность | Связь |
| 1 | желто-коричневый A | sin A/cos A |
| 2 | детская кроватка А | cos A/sin A |
| 3 | косек А | 1/sin А |
| 4 | сек А | 1/cos А |
Тригонометрические знаковые функции
- грех (-θ) = — грех θ
- cos (-θ) = cos θ
- тангенс (-θ) = — тангенс θ
- cosec (−θ) = − cosec θ
- сек (-θ) = сек θ
- детская кроватка (-θ) = — детская кроватка θ
Тригонометрические тождества
- sin 2 А + cos 2 А = 1
- загар 2 А + 1 = сек 2
- кроватка 2 A + 1 = cosec 2 A
Периодические тождества
- грех (2nπ + θ) = грех θ
- cos(2nπ + θ) = cos θ
- тангенс (2nπ + θ) = тангенс θ
- детская кроватка (2nπ + θ) = детская кроватка θ
- сек (2nπ + θ ) = сек θ
- cosec(2nπ + θ) = cosec θ
Дополнительные коэффициенты
Квадрант I
- грех (π / 2 — θ) = cos θ
- потому что (π / 2 — θ) = грех θ
- загар (π / 2 — θ) = детская кроватка θ
- раскладушка (π / 2 — θ) = тангенс θ
- сек (π / 2 — θ) = cosec θ
- cosec(π/2 − θ) = sec θ
Квадрант II
- грех (π — θ) = грех θ
- cos (π — θ) = -cos θ
- тангенс (π — θ) = -тангенс θ
- детская кроватка (π − θ) = – детская кроватка θ
- сек (π — θ) = -сек θ
- cosec(π − θ) = cosec θ
Квадрант III
- sin(π + θ) = – sin θ
- cos(π + θ) = – cos θ
- тангенс (π + θ) = тангенс θ
- детская кроватка (π + θ) = детская кроватка θ
- сек (π + θ) = -сек θ
- cosec(π + θ) = -cosec θ
Квадрант IV
- sin(2π − θ) = – sin θ
- cos (2π — θ) = cos θ
- тангенс (2π — θ) = – тангенс θ
- детская кроватка (2π − θ) = – детская кроватка θ
- сек (2π — θ) = сек θ
- cosec(2π − θ) = -cosec θ
Сумма и разность двух углов
- sin (A + B) = sin A cos B + cos A sin B
- sin (A − B) = sin A cos B – cos A sin B
- cos (A + B) = cos A cos B – sin A sin B
- cos (A – B) = cos A cos B + sin A sin B
- тангенс (А + В) = [(тангенс А + тангенс В) / (1 – тангенс А тангенс В)]
- загар (A – B) = [(загар A – загар B) / (1 + загар A загар B)]
Формулы двойного угла
- sin 2A = 2 sin A cos A = [2 тангенс A / (1 + тангенс 2 A)]
- cos 2A = cos 2 A – sin 2 A = 1 – 2 sin 2 A = 2 cos 2 A – 1 = [(1 – tan 2 A)/(1 + tan 2 А)]
- тангенс 2A = (2 тангенс A)/(1 – тангенс 2 A)
Формулы тройного угла
- sin 3A = 3 sinA – 4 sin 3 А
- cos 3A = 4 cos 3 A – 3 cos A
- tan 3A = [3 tan A – tan 3 A] / [1 − 3 tan 2 A]
Решенные примеры
Q1.
Если cot Q = tan P, то докажите, что P + Q = 90°.
Ответ. Дано,
загар P = детская кроватка Q
Как известно, раскладушка(90° – A) = Tan A.
Итак, кроватка Q = кроватка(90° – P)
Следовательно, Q = 90° – P
И
P + Q = 90°
Значит доказано.
Q2. Вычислить cos 55° sin 35° + cos 35° sin 55°.
Ответ. Заданное выражение:
cos 55° sin 35° + cos 35° sin 55°
Приведенное выше уравнение имеет вид sin A cos B + cos A sin B.
Теперь, используя sin(A + B) = sin A cos B + cos A sin B, мы получаем;
cos 55° sin 35° + cos 35° sin 55° = sin(35° + 55°) = sin 90° = 1
Q3. Если sin A = 3/5, то найти значение cos A и cot A
Ответ . Sin A = 3/5
Теперь sin 2 A + cos 2 A = 1
cos 2 А = 1- (3/5) 2
= (25 — 9) / 25
= 16 / 25
cos A = 4/5
Кроме того, кроватка A = cosA/sinA
= (4/5)(3/5)
= 4/3
Часто задаваемые вопросы (FAQ)
Q1.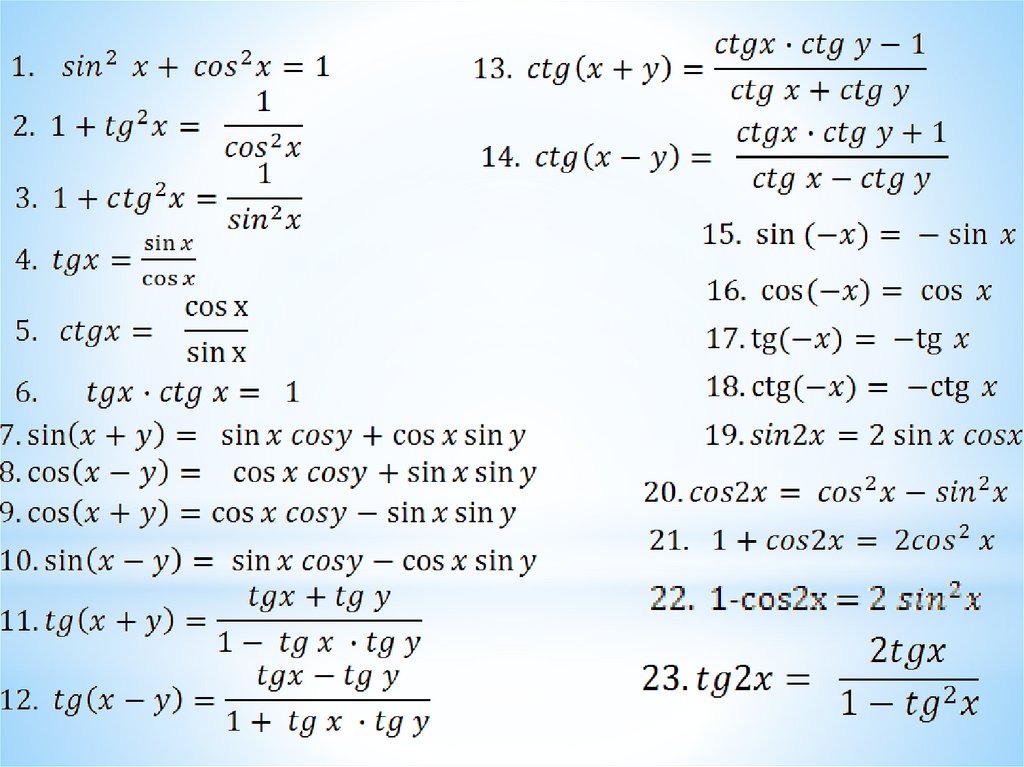
Ответ. Три тождества тригонометрии известны как пифагорейские тождества тригонометрии.
- sin 2 А + cos 2 А = 1
- загар 2 А + 1 = сек 2 А
- детская кроватка 2 А + 1 = cosec 2 А
Q2. Как ввести тригонометрию в 10 класс?
Ответ. Ниже приведены шаги для введения тригонометрии:
- Сначала измерьте длины сторон множества прямоугольных треугольников, а затем найдите отношение сторон.
- Найдите связь между отношениями и величиной угла.
- Всегда используйте калькуляторы или таблицы, чтобы найти синус, косинус и тангенс углов.
Q3. Кто является отцом тригонометрии в Индии?
Ответ. Первая тригонометрическая таблица была составлена Гиппархом, известным теперь как «отец тригонометрии».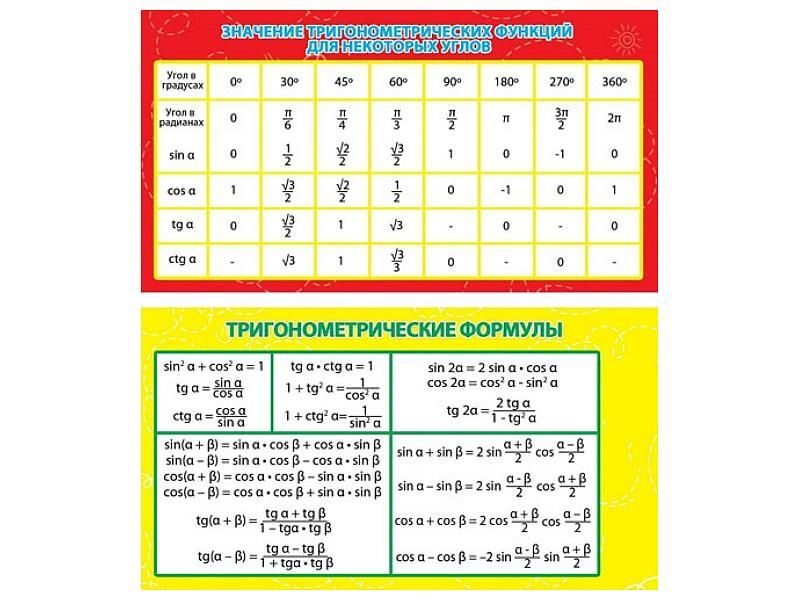
Q4. Каковы шесть отношений тригонометрии?
Ответ. Шесть тригонометрических соотношений: синус, косинус, тангенс, косеканс, секанс и котангенс.
Q5. Какие существуют два типа тригонометрии?
Ответ. Существует два типа тригонометрии: плоская тригонометрия и сферическая тригонометрия.
Тригонометрические формулы для класса 10
БЕСПЛАТНАЯ БЕСПЛАТНАЯ Консультирование
Тригонометрические формулы для класса 10 Тригонометрия — наиболее важная глава для студентов, как они изучают в CBSE/ . такие соревнования, как IIT или SSC. В CBSE/NCERT глава о тригонометрии представлена в 9 главе.0008 класс 10-й (глава 8), а в ICSE он вводится в 9-м классе. В большинстве случаев студенты находят главу «Тригонометрия» очень трудной для понимания и очень трудной для изучения всех тригонометрических формул .
В этой статье Вы найдете все тригонометрических формул для класса 10 .
Что вы поймете после прочтения этой статьи:-
- В этой статье мы постараемся помочь учащимся легко понять тригонометрию.
- Мы сделаем несколько коротких трюков , чтобы формулы тригонометрии для 10 класса становились легкими для изучения.
- Кроме того, вам не нужно заучивать их все наизусть. Вместо этого вы разработаете методику, позволяющую выводить некоторые формулы из , вместо того, чтобы запоминать их.
Тригонометрия-формулы-класс10-скачать-pdf
Чтобы узнать больше о том, как набрать 100/100 баллов по 10-му математику и другим предметам, подпишитесь на нас в Instagram:
Что такое тригонометрия?
Это слово «тригонометрия» в основном произошло от сочетания двух греческих слов «trigōnon», что означает «треугольник», и «metron», что означает «мера». Таким образом, оно используется для измерения треугольников .
Проще говоря, Тригонометрия — это раздел математики, в котором изучаются отношения между длинами сторон и углами треугольников.
Теперь позвольте мне сделать это проще!
- ВОПРОС (i):- Если нам даны две стороны прямоугольного треугольника и нас просят найти третью сторону, какое математическое понятие мы будем использовать, чтобы найти третью сторону?
ОТВЕТ:- Очевидно, это очень просто! Мы будем использовать теорему Пифагора . - ВОПРОС (ii):- Если нам даны одна сторона и один угол (кроме 90°) прямоугольного треугольника и вас попросили найти остальные стороны этого треугольника, как вы его найдете?
ОТВЕТ:- Для этого вам нужно будет понять новую концепцию, известную как «Тригонометрия».
Применение тригонометрии и формул в реальной жизни!
Большую часть времени нам интересно какая польза тригонометрии в нашей жизни?.
Возможно, вы не применяли тригонометрию напрямую для решения своих повседневных жизненных проблем, но косвенно она используется в различных вещах, которые мы видим вокруг себя.
- Как вы думаете, как мы узнали, что высота горы Эверест составляет 8848 метров. Очевидно, с помощью тригонометрии.
- Откуда мы узнали, что такое расстояние между «Землей» и «Солнцем»? когда мы ни разу не были на «Солнце». вы можете измерить расстояние до близлежащих объектов в пространстве с помощью тригонометрического метода, называемого Тригонометрический параллакс или Звездный параллакс.
- функции синуса и косинуса (которые вы изучите позже) являются фундаментальными для теории периодических функций, описывающих звуковые и световые волны.
- Тригонометрия также используется в строительстве, видеоиграх, бортовой технике, морской технике, археологии, криминологии, навигации, океанографии, картографии (создании карт), спутниковых системах.
- К вашему удивлению почти каждое научное открытие, связанное с расстоянием, подтверждается только благодаря тригонометрии.
ПРИМЕЧАНИЕ. Мы подробно обсудили эти реальных приложений тригонометрии в этой статье, пожалуйста, прочтите ее.
Получить обратный звонок
Наши специалисты помогут вам решить ваши вопросы и сдать экзамен
Тригонометрические отношения:-
Прежде всего, мы обсудим, что такое Тригонометрические отношения . Тригонометрические отношения — это, по сути, отношения между измерениями углов и длин сторон прямоугольного треугольника.
Теперь давайте обсудим, сколько типов тригонометрических соотношений может быть возможным.
В прямоугольном треугольнике у нас есть три стороны с именами (H) Гипотенуза (самая длинная сторона), (P) Перпендикуляр (сторона, противоположная углу) и (B) Основание . Если нас попросят взять любые две стороны из этих трех сторон и составить отношение, мы обнаружим, что возможны шесть отношений (P/H, B/H, P/B, H/P, H/B, B/P).
). Каждому соотношению мы присвоили определенное имя.
Тригонометрические отношения:-
- sinθ = (перпендикуляр(P))/(гипотенуза(H)).
- cosθ = (основание (B))/(гипотенуза (H)).
- tanθ = (Перпендикуляр(P))/(Основание(B)).
- cosecθ = (Гипотенуза(H))/(Перпендикуляр(P)).
- сек θ = (гипотенуза (H))/(основание (B)).
- cotθ = (Основание (B))/(Перпендикуляр (P)).
Обратные тригонометрические отношения:-
- sin θ = 1/(cosec θ)
- cosec θ = 1/(sin θ)
- cos θ = 1/(sec θ ) потому что θ)
- tan θ = 1/(cot θ)
- cot θ = 1/(tan θ)
Важные соотношения между тригонометрическими отношениями:-
tanθ = (sin θ θ ) / (cos 0 6 θ ) = (cos θ ) / (sin θ )
Тригонометрическая таблица:-
Эта таблица тригонометрических соотношений помогает нам найти значения тригонометрических стандартных углов , таких как 0°, 30°, 45°, 60°, и 90°.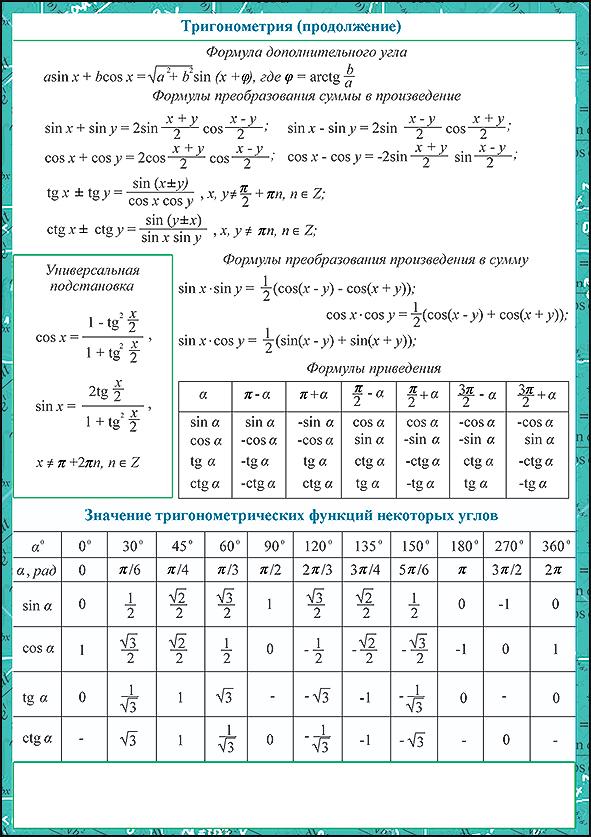
| Тригонометрические соотношения | 0° | 30° | 45° | 60° | 90° | ||||||||||
| sin A | 0 | 1/2 | 1/√2 | √3/2 | 1 | ||||||||||
| COS A | 1 | √3/2 | 1/√2 | 1/2 | 0 | ||||||||||
| TAN A | 0 | 1/√3 | 1 | √3 | Не определено | ||||||||||
| Cot A | Не определено | √3 | 1 | Не определено | √3 | 1 | 1111110 | 1110 | √3 | 0 | |||||
| cosec A | Not defined | 2 | √2 | (2√3)/3 | 1 | ||||||||||
| sec A | 1 | ( 2√3)/3 | √2 | 2 | Не определено |
youtube.com/embed/xgrUnjou2UA» frameborder=»0″ allowfullscreen=»allowfullscreen»> Тригонометрические формулы и тождества:-
Теперь есть определенные Тригонометрические формулы и тождества , которые вам нужно выучить. Эти соотношения и тождества очень полезны при решении тригонометрических задач.
Тригонометрические формулы для 10-го класса:-
Тригонометрические формулы для 10-го класса основаны на тригонометрических соотношениях. Существуют три основные тригонометрические формулы для 10-го класса, и с их помощью можно составить другие тождества.
1) cos 2 А + sin 2 А = 1.
- а) cos 2 А =1 – sin 2 А. – 7
- cos 2 9015 2 A.
2) 1 + TAN
- A) SEC 2 A — TAN 2 A = 1.
- B) TAN 2 2 2 A = 1.
- B) TAN 2 2 А = сек 2 А – 1.
