Все формулы тригонометрии для подготовки к ЕГЭ: тождества, функции, таблицы
Для того чтобы сдать ЕГЭ по математике, вам понадобится около 20 формул тригонометрии. Это не много. Но их надо знать наизусть!
Вот таблица, в которой собраны основные тригонометрические формулы. Здесь все самое необходимое. Их легко выучить и применять.
Эти формулы применяются и в заданиях 1 части ЕГЭ по математике, и в заданиях 2 части.
Эта полезная табличка – только одна из многих страниц Справочника Анны Малковой для подготовки к ЕГЭ. Скачай Справочник бесплатно здесь.
Кроме того, надо знать определения синуса, косинуса и тангенса, а также значения этих функций для основных углов.
Первые 3 блока формул из нашей таблицы часто встречаются в заданиях 1 части ЕГЭ и в задаче из второй части, где надо решить тригонометрическое уравнение.
В первую очередь это основное тригонометрическое тождество:
sincos
Это формулы, которые показывают, как выразить тангенс через косинус и котангенс через синус угла.
tg
1 + ctg
Формулы синуса и косинуса двойного угла, формулы синуса суммы, косинуса разности, – все это надо знать, чтобы без ошибок решать тригонометрические уравнения.
А вот формулы суммы синусов и косинусов, а также преобразование произведения в сумму могут пригодиться при решении задач с параметрами.
Где же могут встретиться формулы из двух последних блоков, внизу таблицы?
Формулы понижения степени могут присутствовать и в тригонометрических уравнениях, и в «параметрах». И даже в задачах с физическим содержанием из 1 части ЕГЭ, если там вдруг попадется тригонометрия.
А универсальная тригонометрическая замена, когда мы выражаем синус и косинус угла альфа через тангенс половинного угла? А формулы синуса и косинуса тройных углов? Где же они применяются? Оказывается, они помогают решать задачи по геометрии из 2 части ЕГЭ. Так что их тоже стоит знать, если хотите сдать на высокий балл.
Обратите внимание, что в этой таблице нет формул приведения. О них мы рассказываем в отдельной статье нашего сайта.
О них мы рассказываем в отдельной статье нашего сайта.
Как же выучить тригонометрические формулы?
1. Учите формулы сразу. Не рассказывайте себе сказки о том, что в последнюю ночь перед ЕГЭ все выучите. Каждый день – один блок, то есть три-четыре формулы из нашей таблицы.
2. Тренируйтесь. Выучить иностранный язык проще всего тому, кто вынужден постоянно на нем говорить. Так и здесь. Для тренировки можно из классического задачника Сканави выбрать 20-50 заданий на преобразование тригонометрических выражений и доказательство тождеств.
3. Универсальный способ: ежедневно, садясь за уроки, берите чистый листок и выписывайте наизусть все тригонометрические формулы, какие помните. Когда всё готово — сверяете. И к экзамену вы будете помнить всё.
4. Еще один отличный способ. Вырежьте из плотной бумаги карточки. На одной пишете левую часть формулы. На другой – правую. Перемешиваете. И собираете. Любые формулы запоминаются легко и быстро!
5. И конечно, решаем задания ЕГЭ на применение этих формул.
Задача 1.
Найдите tg, если cos и
Решение:
Воспользуемся формулой:
tg tg x
Какой знак будет у тангенса, «плюс» или «минус»?
В условии дано, что , то есть это угол из четвертой четверти, значит tgx
tgx
Ответ: -3.
Задача 2.
Найдите если sin
Решение:
Воспользуемся формулой синуса двойного угла: sin2 = 2sincos
Ответ: 4.
Задача 3.
Найдите 24cos если sin
Решение:
Воспользуемся формулой косинуса двойного угла: cos 2 = 1 — 2sin
24cos2 = 24(1 — 2sin
Ответ: 22,08.
Задача 4.
Найдите если tg
Решение:
Вынесем косинус альфа за скобки в числителе и знаменателе:
Ответ: -9.
Задача 5.
Найдите значение выражения:
Решение:
Воспользуемся формулой синуса двойного угла:
sin2 = 2sincos тогда sincos =
Ответ: 10.
Задача 6.
Найдите значение выражения: cossin
Решение:
Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:
cos = cos — sin
cos
Ответ: -1,5.
Задача 7.
Найдите значение выражения: tg
Решение:
Используя формулы приведения, получим: tg = tg = ctg
Пользуемся также тем, что тангенс и котангенс угла альфа — взаимно обратные величины,
Получим:
-50tg ctg
Ответ: -19.
Задача 8.
Найдите значение выражения: sin
Решение:
sinsin
cos cos cos
Мы вынесли за скобки множитель и применили формулу косинуса двойного угла, выразив его через квадрат синуса угла.
Ответ: 6.
Задача 9.
Найдите значение выражения: 5sin cos
Решение:
Воспользуемся формулой синуса двойного угла: sin = 2sincos Также применим одну из формул приведения: sin = -sin
5sin cos sin sin sin
Ответ: -1,25.
Задача 10.
Найдите значение выражения:
Решение:
Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:
cos2 = 1 — 2
cos cos cos
Ответ: -3.
Задача 11.
Найдите значение выражения:
Решение:
Вынесем общий множитель за скобки и воспользуемся формулой косинуса двойного угла:
cos2 =
coscos cos
Ответ: 4,5.
Задача 12.
Найдите значение выражения:
Мы воспользовались периодичностью функции синус: sinsin В нашей задаче 374 = 360 + 14.
Ответ: — 6.
Задача 13.
Найдите значение выражения:
Решение:
Воспользуемся формулой синуса двойного угла: sin2 = 2sincos
sin cos sin sin sin
Ответ: 3,5.
Заметим, что если в задаче нам встретилось произведение синуса альфа на косинус альфа, то, скорее всего, нужно будет применять формулу синуса двойного угла.
Задача 14.
Найдите tg если cos и
Решение:
Вспомним основное тригонометрическое тождество: Выразим из этой формулы синус альфа:
sin
Какой же знак выбрать, «плюс» или «минус»?
Угол альфа в третьей четверти, значит, его синус отрицателен.
sin
tg
Ответ: 1,25.
Задача 15.
Найдите sin если cos и
Решение:
Как и в предыдущей задаче, выразим синус альфа из основного тригонометрического тождества:
sin
Дан угол альфа, принадлежащий второй четверти, значит, его синус положителен.
sin
Ответ: 0,9.
Задача 16.
Найдите tg если sin и
Решение:
Аналогично предыдущим задачам, выразим косинус альфа из основного тригонометрического тождества:
cos
Угол альфа в третьей четверти, значит, его косинус отрицателен.
cos, тогда tg
Ответ: 0,8.
Задача 17.
Найдите значение выражения: — 42tg tg
Решение:
-42tg tg -42tg tg -42tg ctg
Мы применили формулу приведения, а также то, что тангенс и котангенс угла альфа — взаимно обратные величины, и их произведение равно единице.
Ответ: -42.
Задача 18.
Найдите значение выражения: sin
Решение:
Воспользуемся формулами приведения:
Также мы применили основное тригонометрическое тождество. Сумма квадратов синуса и косинуса угла альфа равна единице.
Ответ: 4,8.
Задача 19.
Найдите значение выражения:
Решение:
Так как то заменим на по формуле приведения и воспользуемся формулой синуса двойного угла:
sin2 = 2sincos
Ответ: 4.
Задача 20.
Найдите значение выражения:
Решение:
Воспользуемся формулой косинуса двойного угла:
Ответ: -21.
Задача 21.
Найдите значение выражения:
Решение:
Воспользуемся формулой синуса двойного угла:
Ответ: -0,25.
Задача 22.
Найдите значение выражения:
Решение:
И здесь тоже была формула косинуса двойного угла, но только в другой форме.
Ответ: 3.
Задача 23.
Найдите значение выражения:
Решение:
А здесь мы просто вычислили косинус и синус табличного угла
Ответ: -13.
Задача 24.
Найдите значение выражения:
Решение:
Это задача на вычисление тригонометрических функций для табличного угла Если этот угол выразить в градусах, то он равен 45 градусов.
Ответ: 18.
Задача 25.
Найдите значение выражения:
Решение:
Используя формулы приведения, получим:
Лайфхак: если вам сложно запомнить формулы приведения, вы можете вместо них использовать формулы косинуса разности и синуса суммы.
Ответ: -2,5.
Посмотрим, как формулы тригонометрии применяются при решении уравнений.
Задача 26.
Решите уравнение:
Решение:
Воспользуемся формулой понижения степени: sin
Ответ:
Задача 27.
Решите уравнение:
Решение:
Воспользуемся формулой понижения степени:
Умножим обе части на два:
Воспользуемся формулой суммы косинусов: cos + cos = 2cos cos
cos6x + cos10x = 2cos8x cos2x.
Уравнение примет вид:
2cos8x cos2x + cos8x =0.
Вынесем общий множитель за скобки. Теперь произведение двух множителей равно нулю, а с этим мы умеем работать.
Ответ:
Все о решении тригонометрических уравнений здесь.
Благодарим за то, что пользуйтесь нашими материалами. Информация на странице «Самые необходимые тригонометрические формулы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена: 08.04.2023
тригонометрические формулы синус косинус суммы углов разности углов синус косинус двойного тройного углов синус косинус тангенс через тангенс половинного угла
| Справочник по математике | Тригонометрия |
Содержание
| Связи между тригонометрическими функциями одного угла |
| Тригонометрические функции суммы и разности двух углов |
| Тригонометрические функции двойного угла |
| Формулы понижения степени для квадратов тригонометрических функций |
| Формулы понижения степени для кубов синуса и косинуса |
| Выражение тангенса угла через синус и косинус двойного угла |
| Преобразование суммы тригонометрических функций в произведение |
| Преобразование произведения тригонометрических функций в сумму |
| Выражение тригонометрических функций через тангенс половинного угла |
| Тригонометрические функции тройного угла |
Связи между тригонометрическими функциями одного угла
| sin2α + cos2α = 1 |
Тригонометрические функции суммы и разности двух углов
| Формула | Название формулы |
| sin (α + β) = sin α cos β + cos α sin β | Синус суммы |
| sin (α – β) = sin α cos β – cos α sin β | Синус разности |
| cos (α + β) = cos α cos β – sin α sin β | Косинус суммы |
| cos (α – β) = cos α cos β + sin α sin β | Косинус разности |
| Тангенс суммы | |
| Тангенс разности |
| Синус суммы |
| sin (α + β) = sin α cos β + + cos α sin β |
| Синус разности |
| sin (α – β) = sin α cos β – – cos α sin β |
| Косинус суммы |
| cos (α + β) = cos α cos β – – sin α sin β |
| Косинус разности |
| cos (α – β) = cos α cos β + + sin α sin β |
| Тангенс суммы |
| Тангенс разности |
Тригонометрические функции двойного угла
| Формула | Название формулы |
| sin 2α = 2 sin α cos α | Синус двойного угла |
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α | Косинус двойного угла |
| Тангенс двойного угла |
| Синус двойного угла |
| sin 2α = 2 sin α cos α |
| Косинус двойного угла |
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
| Тангенс двойного угла |
Формулы понижения степени для квадратов тригонометрических функций
| Формула | Название формулы |
Выражение квадрата синуса через косинус двойного угла | |
Выражение квадрата косинуса через косинус двойного угла | |
Выражение квадрата тангенса через косинус двойного угла |
| Выражение квадрата синуса через косинус двойного угла |
| Выражение квадрата косинуса через косинус двойного угла |
| Выражение квадрата тангенса через косинус двойного угла |
Формулы понижения степени для кубов синуса и косинуса
| Формула | Название формулы |
Выражение куба синуса через синус угла и синус тройного угла | |
Выражение куба косинуса через косинус угла и косинус тройного угла |
Выражение куба синуса через синус угла и синус тройного угла |
Выражение куба косинуса через косинус угла и косинус тройного угла |
Выражение тангенса через синус и косинус двойного угла
Преобразование суммы тригонометрических функций в произведение
| Формула | Название формулы |
| Сумма синусов | |
| Разность синусов | |
| Сумма косинусов | |
| Разность косинусов | |
| Сумма тангенсов | |
| Разность тангенсов |
| Сумма синусов |
| Разность синусов |
| Сумма косинусов |
| Разность косинусов |
| Сумма тангенсов |
| Разность тангенсов |
Преобразование произведения тригонометрических функций в сумму
| Формула | Название формулы |
| Произведение синусов | |
| Произведение косинусов | |
| Произведение синуса и косинуса |
| Произведение синусов |
| Произведение косинусов |
| Произведение синуса и косинуса |
Выражение тригонометрических функций через тангенс половинного угла
| Формула | Название формулы |
Выражение синуса угла через тангенс половинного угла | |
Выражение косинуса угла через тангенс половинного угла | |
Выражение тангенса угла через тангенс половинного угла |
| Выражение синуса угла через тангенс половинного угла |
| Выражение косинуса угла через тангенс половинного угла |
| Выражение тангенса угла через тангенс половинного угла |
Тригонометрические функции тройного угла
| Формула | Название формулы |
| sin 3α = 3sin α – 4sin3α | Синус тройного угла |
| cos 3α = 4cos3α –3cos α | Косинус тройного угла |
| Тангенс тройного угла |
| Синус тройного угла |
| sin 3α = 3sin α – 4sin3α |
| Косинус тройного угла |
| cos 3α = 4cos3α –3cos α |
| Тангенс тройного угла |
Наверх
Демонстрационные варианты ЕГЭ и ОГЭ
С демонстрационными вариантами ЕГЭ и ОГЭ по всем предметам, опубликованными на официальном информационном портале Единого Государственного Экзамена, можно ознакомиться на специальной страничке нашего сайта.
Наши учебные пособия для школьников
При подготовке к ЕГЭ и к ОГЭ по математике Вам могут также пригодиться наши учебные пособия.
Решение рациональных неравенств
Задачи на проценты
Решение показательных неравенств
Квадратный трехчлен
Метод координат на плоскости
Решение иррациональных неравенств
Фигуры на координатной плоскости
Решение алгебраических уравнений
Уравнения и неравенства с модулями
Решение показательных уравнений
Арифметическая и геометрическая прогрессии
Решение логарифмических уравнений
Решение логарифмических неравенств
Системы уравнений
Решение тригонометрических уравнений
Тригонометрия в ЕГЭ по математике
Степень с рациональным показателем
Основные тригонометрические функции | Brilliant Math & Science Wiki
Содержание
- Основные тригонометрические функции
- Конкретные значения — основные
- Конкретные значения — средний уровень
- Решение проблем 9\circ\) Прямоугольный треугольник
- Прямоугольная тригонометрия
Тригонометрические функции связывают углы прямоугольного треугольника с отношением сторон. Дан следующий треугольник:
Дан следующий треугольник:
\(\hspace{4cm}\)
основные тригонометрические функции определены для \( 0 < \theta < \frac{\pi}{2} \) как
\[\begin{array} &\sin \theta = \frac{b}{c}, &\cos \theta = \frac{a}{c}, &\tan \theta = \frac{b}{a}. \конец{массив} \]
Если рассмотреть угол \(\theta\) и обозначить стороны относительно \(\theta\), то \(a\) — это длина «прилегающей» стороны, \(b\) — это длина «противоположной» стороны, а \(с\) — длина гипотенузы. Тогда основные тригонометрические функции можно выразить следующим образом:
\[\begin{array} &\sin\theta = \frac{\text{напротив}}{\text{гипотенуза}}, &\cos \theta = \frac{\text{смежный}}{\text{гипотенуза}}, &\tan \ тета = \ frac {\ text {напротив}} {\ text {смежно}}. \конец{массив} \]
Обзор преобразования градусов в радианы см. в разделе Градусы и радианы. Однако более полезное определение исходит от единичного круга. Если мы рассмотрим окружность радиусом 1 единицу с центром в начале координат, то угол \(\theta\) внутри окружности описывает прямоугольный треугольник, когда мы опускаем перпендикуляр к оси \(x\) из точки пересечения с окружностью.
Единичный круг
Обратите внимание, что описанный таким образом прямоугольный треугольник имеет гипотенузу, равную радиусу окружности, прилежащую сторону, равную \(x\)-координате точки \((x, y),\), а противоположную сторону, равную к \(y\)-координате. Это естественным образом приводит к следующим уточненным определениям:
\[\begin{array} &\sin \theta = \frac{y}{\text{radius}}, &\cos \theta = \frac{x}{\text{radius}}, &\tan \theta = \frac{y}{ Икс}. \конец{массив} \]
Как показано на диаграмме выше, поскольку радиус равен \(1\) в единичной окружности, это упрощается до \(x= \cos \theta\) и \(y= \sin \theta \). 9\циркуляр\\ \hline \ sin \ theta & \ frac {\ sqrt {0}} {2} & \ frac {\ sqrt {1}} {2} & \ frac {\ sqrt {2}} {2} & \ frac {\ sqrt { 3}} {2} & \ frac {\ sqrt {4}} {2} \\ \hline \ cos \ theta & \ frac {\ sqrt {4}} {2} & \ frac {\ sqrt {3}} {2} & \ frac {\ sqrt {2}} {2} & \ frac {\ sqrt { 1}} {2} & \ frac {\ sqrt {0}} {2} \\ \hline \tan \theta & 0 & \frac { 1}{\sqrt{3} } & 1 & \sqrt{3} &\infty{} \\ \hline \end{array}\]
Причина, по которой они записываются таким образом, состоит в том, чтобы облегчить запоминание этих терминов. Например, числитель для \(\sin\theta\) — это просто квадратный корень из \(0, 1, 2, 3\) или \(4.\). Чтобы представить эти значения в единичном круге, см. конкретные значения тригонометрических функций.
Например, числитель для \(\sin\theta\) — это просто квадратный корень из \(0, 1, 2, 3\) или \(4.\). Чтобы представить эти значения в единичном круге, см. конкретные значения тригонометрических функций.
Какие значения \(\theta\) удовлетворяют
\[\begin{array} &0 \leq \theta < 2 \pi &\text{ и } &\cos \theta = 0? \конец{массив}\]
Хороший подход к решению такой задачи — представить себе единичную круговую диаграмму, показанную выше. На этой единичной круговой диаграмме \(\cos\theta\) — это \(x\)-координата. Таким образом, задача состоит в том, чтобы задать угол \(\theta\), координата \(x\) которого равна \(0\), который возникает в двух точках пересечения единичной окружности с осью \(y\) : \(\ theta = \ frac {\ pi} {2} \) и \ (\ theta = \ frac {3 \ pi} {2} \). Поскольку эти углы удовлетворяют заданным условиям, возможны два угла: \(\theta = \frac{\pi}{2}\) и \(\theta = \frac{3\pi}{2}\). \(_\квадрат\)
Если угол \(\theta \) такой, что \( \cos \theta = 0,\), то каковы возможные значения \(\sin \theta\)?
Решение 1 :
Как мы видели выше, \(\cos\theta=0\) соответствует точкам на единичной окружности, \(x\)-координата которых равна \(0\).Поскольку эти точки находятся в точках пересечения с осью \(y\), возможные значения \(\sin\theta\) являются возможными координатами \(y\), которые равны \(1\) и \(-1\). \(_\квадрат\)
Решение 2 :
Из первого примера, если \(\cos \theta=0\) и \(0 \leq \theta < 2 \pi\) , то \(\theta=\frac{\pi}{ 2}\) или \(\theta=\frac{3\pi}{2}\). Обратите внимание, что для всех других значений \(\theta\) за пределами этого диапазона мы имеем \(\sin \theta = \sin (\theta \pm 2\pi),\), поэтому мы можем складывать или вычитать кратные \ (2\pi\) до тех пор, пока \(\theta\) не окажется в этом диапазоне. Для \(\theta = \frac{\pi}{2}\) мы имеем \(\sin \theta = 1\), а для \(\theta = \frac{3\pi}{2}\) у нас есть \(\sin\theta=-1\). Следовательно, возможные значения \(\sin\theta\) равны \(1\) и \(-1\). \(_\квадрат\) 9{\circ}.\) Кроме того, поскольку \(y\)-координата точек на единичной окружности увеличивается по мере того, как \(\theta\) переходит от \(0\) к \(\frac{\pi} {2}\), значение \(\theta = \frac{\pi}{6}\) – это уникальное значение, такое что \(0 < \theta < \frac{\pi}{2}\) и \ (\sin\theta=\frac{1}{2}\).Тогда у нас есть \(\cos\theta=\cos\frac{\pi}{2} =\frac{\sqrt{3}}{2}\). \(_\квадрат\)
Почему в приведенной выше таблице конкретных значений тригонометрических функций нет значения для \(\tan \frac{\pi}{2}\)? Что происходит с \(\tan\theta\) по мере того, как \(\theta\) становится все ближе и ближе к \(\frac{\pi}{2}\)?
Из приведенного выше определения \(\tan\theta\) мы имеем \(\tan \theta=\frac{\sin \theta}{\cos \theta} = \frac{y}{x}\) , где \((x,y)\) — это \(x\)- и \(y\)-координаты точки угла \(\theta\) на единичной окружности. По мере того, как \(\theta\) движется к \(\frac{\pi}{2}\), \(\cos\theta\) (координата \(x\)) становится все меньше и меньше, тогда как \(\ sin\theta\) (координата \(y\)) становится все ближе и ближе к \(1\). Следовательно, числитель \(\tan \theta=\frac{y}{x}\) приближается к \(1\), а знаменатель приближается к \(0\), подразумевая, что \(\tan \theta\) приближается к бесконечности. \(_\квадрат\) 9\циркуляр\\ \hline \ sin \ theta & \ frac {\ sqrt {0}} {2} & \ frac {\ sqrt {1}} {2} & \ frac {\ sqrt {2}} {2} & \ frac {\ sqrt { 3}} {2} & \ frac {\ sqrt {4}} {2} \\ \hline \ cos \ theta & \ frac {\ sqrt {4}} {2} & \ frac {\ sqrt {3}} {2} & \ frac {\ sqrt {2}} {2} & \ frac {\ sqrt { 1}} {2} & \ frac {\ sqrt {0}} {2} \\ \hline \tan \theta & 0 & \frac { 1}{\sqrt{3} } & 1 & \sqrt{3} & \pm \infty \\ \hline \end{array}\]
Причина, по которой они записываются таким образом, состоит в том, чтобы облегчить запоминание этих терминов.
Например, числитель для \(\sin\theta\) — это просто квадратный корень из 0, 1, 2, 3, 4.
Визуализация в единичном круге
Мы также можем визуализировать значения косинуса и синуса для этих значений в единичном круге:
Поскольку функция косинуса соответствует значениям \(x\), функция косинуса будет положительной, если значения \(x\) положительны, и отрицательной, если значения \(x\) отрицательными. Точно так же, поскольку функция синуса соответствует значениям \(y\), функция синуса будет положительной, когда значения \(y\) положительны, и будет отрицательной, когда значения \(y\) отрицательны. Это дает нам следующее поведение в четырех квадрантах плоскости:
Затем, используя несколько конкретных значений из первого квадранта, мы можем вычислить конкретные значения функций косинуса и синуса во всех квадрантах. Вот визуализация для всех квадрантов:
Изображение предоставлено commons.
wikimedia.org
Каковы значения \(\theta\) в диапазоне \(0 \leq \theta < 2 \pi\) такие, что \(\sin \theta = \cos \theta\)?
Из приведенной выше визуализации единичного круга мы видим, что \(\theta = \frac{\pi}{4} \) и \(\theta = \frac{5\pi}{4} \) удовлетворяют
\[\begin{выравнивание} \ sin \ left ( \ frac {\ pi} {4} \ right) & = \ cos \ left ( \ frac {\ pi} {4} \ right) = \ frac {\ sqrt {2}} {2} \ \ \sin \left( \frac{5\pi}{4} \right) &= \cos \left( \frac{5\pi}{4} \right) = -\frac{\sqrt{2}}{ 2}. \конец{выравнивание}\]
Мы также замечаем, что линия \(y=x\) пересекает единичные окружности только для этих двух значений \(\theta\), поэтому значения \(\theta\), удовлетворяющие требуемым условиям, равны \(\theta = \ frac {\ pi} {4} \) и \ (\ theta = \ frac {5 \ pi} {4} . \ _ \ квадрат \)
Какие значения \(\theta\) в диапазоне \(0 \leq \theta < 2 \pi\) удовлетворяют \(\sin \theta \geq \frac{\sqrt{2}}{2}\)?
Проводя линию \(y = \frac{\sqrt{2}}{2},\), мы хотели бы найти значения \(\theta\) такие, что \(y\)-значение угла \(\theta\) на единичной окружности лежит выше этой прямой (поскольку \(\sin \theta \) соответствует \(y\)-координате единичной окружности).
Это справедливо для \(\theta\in \left[\frac{\pi}{4}, \frac{3\pi}{4} \right]\), так что это значения \(\theta\) удовлетворяющие \(\sin\theta\geq\frac{\sqrt{2}}{2}.\ _\square\)
Каковы значения \(\theta\) в диапазоне \(0 \leq \theta < 2 \pi\) такие, что \(\sin \theta = - \cos \theta\)?
Из приведенной выше визуализации единичного круга мы видим, что \(\theta = \frac{3\pi}{4} \) и \(\theta = \frac{7\pi}{4} \) удовлетворяют
\[\begin{выравнивание} \sin \left( \frac{3\pi}{4} \right) &= -\cos \left( \frac{3\pi}{4} \right) = \frac{\sqrt{2}}{ 2}\\ \sin \left( \frac{7\pi}{4} \right) &= — \cos \left( \frac{7\pi}{4} \right) = -\frac{\sqrt{2}} {2}. \конец{выравнивание}\] 9\circ < 9. \]
Это дает нам \( 84-64 + 1 = 21 \) целочисленных решений \(x\). \(_\квадрат\)
0 1 2 3 4 Бесконечно много решений
Сколько действительных чисел \(x\) в радианах удовлетворяют уравнению
9\circ &= \cos \left(\frac{\pi}{3} \right)= \frac{1}{2} = \frac{\text{смежный}}{\text{гипотенуза}}.\end{align}\]
Рассмотрим следующий прямоугольный треугольник:
Предположим, что нам даны две длины сторон треугольника: например, гипотенуза \(c\) и противоположная сторона \(b\). Затем мы находим
\[\sin \theta = \frac{\text{напротив}}{\text{гипотенуза}} = \frac{b}{c}.\]
Исходя из этого, можем ли мы определить \( \cos \theta?\) Поскольку треугольник прямоугольный, мы можем использовать теорему Пифагора, чтобы найти длину стороны \(a,\), и отсюда мы можем найти
\[\cos \theta = \frac{\text{adjacent}}{\text{гипотенуза}} = \frac{a}{c}.\]
Проиллюстрируем это на примере:
В прямоугольном треугольнике ниже даны две длины сторон \(a=3\) и \(b=4\). Найдите \(\sin\theta\) и \(\cos\theta.\)
Поскольку \(\tan \theta = \frac{\text{напротив}}{\text{adjacent}} = \frac{b}{a},\), мы имеем \(\tan \theta = \frac{ 4}{3}.\) Кроме того, из теоремы Пифагора следует, что гипотенуза \(c\) прямоугольного треугольника удовлетворяет условию \(c^2 = a^2 + b^2 = 3^2 + 4^2 = 25 \) или \(с = 5\).
Следовательно,
\[\begin{выравнивание} \sin \theta&= \frac{b}{c} = \frac{4}{5}\\ \cos \theta&= \frac{a}{c} = \frac{3}{5}. \ _\квадрат \конец{выравнивание}\]
Мы продолжим исследовать отношения между тригонометрическими функциями на прямоугольных треугольниках в вики Pyphagorean Identities.
Теперь предположим, что нам даны один из острых углов прямоугольного треугольника и одна из сторон треугольника. Можем ли мы использовать тригонометрические функции, чтобы найти значения других сторон треугольника?
Рассмотрим следующий прямоугольный треугольник:
Если угол \(\theta \) равен \(\frac{\pi}{3}\), а длина стороны \(a\) равна \(5\), найдите длину стороны \(b\).
У нас есть
\[\begin{выравнивание} \tan \theta = \tan \left(\frac{\pi}{3} \right) = \frac{b}{a} &= \frac{b}{5}\\ \sqrt{3} &= \frac{b}{5}\\ b&=5 \sqrt{3}. \ _\квадрат \конец{выравнивание}\]
Цитировать как: Основные тригонометрические функции.
Brilliant.org . Извлекаются из https://brilliant.org/wiki/basic-trigonometric-functions/
3.1: Основные тригонометрические тождества — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3285
- Майкл Коррал
- Schoolcraft College
Пока мы знаем несколько соотношений между тригонометрическими функциями. Например, мы знаем взаимные отношения:
- \(\csc\;\theta ~=~ \dfrac{1}{\sin\;\theta} \qquad \) когда \(\sin\;\theta \ne 0\)
- \(\sec\;\theta ~=~ \dfrac{1}{\cos\;\theta} \qquad \) когда \(\cos\;\theta \ne 0\)
- \(\cot\;\theta ~=~ \dfrac{1}{\tan\;\theta} \qquad \), когда определено \(\tan\;\theta \), а не \(0\)
- \(\sin\;\theta ~=~ \dfrac{1}{\csc\;\theta} \qquad \), когда определено \(\csc\;\theta \), а не \(0\)
- \(\cos\;\theta ~=~ \dfrac{1}{\sec\;\theta} \qquad \), когда определено \(\sec\;\theta \), а не \(0\)
- \(\tan\;\theta ~=~ \dfrac{1}{\cot\;\theta} \qquad \), когда определено \(\cot\;\theta \), а не \(0\)
Обратите внимание, что каждое из этих уравнений верно для всех углов \(\theta \), для которых определены обе части уравнения.
.Такие уравнения называются тождеств , и в этом разделе мы обсудим несколько тригонометрических тождеств , т. е. тождеств с участием тригонометрических функций. Эти тождества часто используются для упрощения сложных выражений или уравнений. Например, одним из наиболее полезных тригонометрических тождеств является следующее:
\[ \tan\;\theta ~=~ \frac{\sin\;\theta}{\cos\;\theta} \qquad \text{когда} \cos\;\theta \ne 0 \label{3.1 } \]
Чтобы доказать это тождество, выберите точку \((x,y) \) на конечной стороне \(\theta \) на расстоянии \(r >0 \) от начала координат и предположим, что \(\cos\ ;\тета\ne 0 \). Тогда \(x \ne 0 \) (поскольку \(\cos\;\theta = \frac{x}{r}\)), поэтому по определению
\[ \frac{\sin\;\theta}{\cos\;\theta} ~=~ \dfrac{~\dfrac{y}{r}~}{~\dfrac{x}{r}~} ~=~ \frac{y}{x} ~=~
\tan\;\theta ~.
\номер\]Обратите внимание, как мы доказали тождество, расширив одну из его сторон (\(\frac{\sin\;\theta}{\cos\;\theta}\)) до тех пор, пока не получили выражение, равное другой стороне ( \(\загар\;\тета\)).
2 \;\theta \) дает 92 \;\theta ~+~ 4
\end{align*} \nonumber \]Пример 3.3
Докажите, что \(\;\tan \;\theta ~+~ \cot \;\theta ~=~ \sec \;\theta ~ \csc \;\theta\; \).
Решение
Разложим левую часть и покажем, что она равна правой:
\[\nonumber \begin{alignat*}{3}
\tan \;\theta + \cot \;\theta ~ &= ~ \frac{\sin\;\theta}{\cos\;\theta} ~+~
\frac{\cos\;\theta}{\sin\;\theta} &{} \qquad &\ text{(по \ref{3.1} и
\ref{3.2})}\\ \nonumber 92 \;\theta}{\cos\;\theta ~ \sin\;\theta} &{} \qquad
&\text{(после получения общего знаменателя)}\\ \nonumber
&= ~ \frac{ 1}{\cos\;\theta ~ \sin\;\theta} &{} \qquad &\text{(by \ref{3.3})}\\ \nonumber
&= ~ \frac{1}{\ cos\;\theta} ~\cdot~ \frac{1}{\sin\;\theta}\\ \nonumber
&= ~ \sec \;\theta ~ \csc \;\theta
\end{alignat* } \nonumber \]Как в приведенном выше примере мы узнали, что нужно расширять левую сторону вместо правой? В целом, хотя этот метод не всегда работает, более сложную сторону идентичности, вероятно, будет легче расширить.
Причина в том, что из-за его сложности с этим выражением можно будет делать больше вещей. Например, если вас попросили доказать, что 92 \;\theta}{\sec\;\theta}
&{} \qquad &\text{(by \ref{3.11})}\\ \nonumber
&= ~ \dfrac{\csc\;\theta ~\cdot~ \dfrac{1}{\sin\;\theta}}{\dfrac{1}{\cos\;\theta}} &{}
&{}\\[2mm]\nonumber
&= ~ \csc\;\theta ~\cdot~ \frac{\cos\;\theta}{\sin\;\theta} &{} &{}\\ \nonumber
&= ~ \csc \;\theta ~ \cot \;\theta &{} \qquad &\text{(by \ref{3.2})}
\end{alignat*} \nonumber \]соотношение выражений, перекрестное умножение может быть эффективной техникой:
\[ \frac{a}{b} ~=~ \frac{c}{d} \quad\text{если и только если}\quad ad ~=~ bc
\nonumber \]Пример 3.6
Докажите, что \(\;\dfrac{1 ~+~ \sin\;\theta}{\cos\;\theta} ~=~ \dfrac{\cos\;\theta}{1 ~- ~ \sin\;\тета}\;\).
Решение
Перемножить и уменьшить обе стороны, пока не станет ясно, что они равны:
\[\nonumber \begin{align*}
( 1 ~+~ \sin\;\theta ) ( 1 ~- ~ \sin\;\theta ) ~ &= ~ \cos\;\theta ~\cdot~ \cos\;\theta\\ \nonumber 92 \;\тета = 1 \).

 Поскольку эти точки находятся в точках пересечения с осью \(y\), возможные значения \(\sin\theta\) являются возможными координатами \(y\), которые равны \(1\) и \(-1\). \(_\квадрат\)
Поскольку эти точки находятся в точках пересечения с осью \(y\), возможные значения \(\sin\theta\) являются возможными координатами \(y\), которые равны \(1\) и \(-1\). \(_\квадрат\) Тогда у нас есть \(\cos\theta=\cos\frac{\pi}{2} =\frac{\sqrt{3}}{2}\). \(_\квадрат\)
Тогда у нас есть \(\cos\theta=\cos\frac{\pi}{2} =\frac{\sqrt{3}}{2}\). \(_\квадрат\) Например, числитель для \(\sin\theta\) — это просто квадратный корень из 0, 1, 2, 3, 4.
Например, числитель для \(\sin\theta\) — это просто квадратный корень из 0, 1, 2, 3, 4.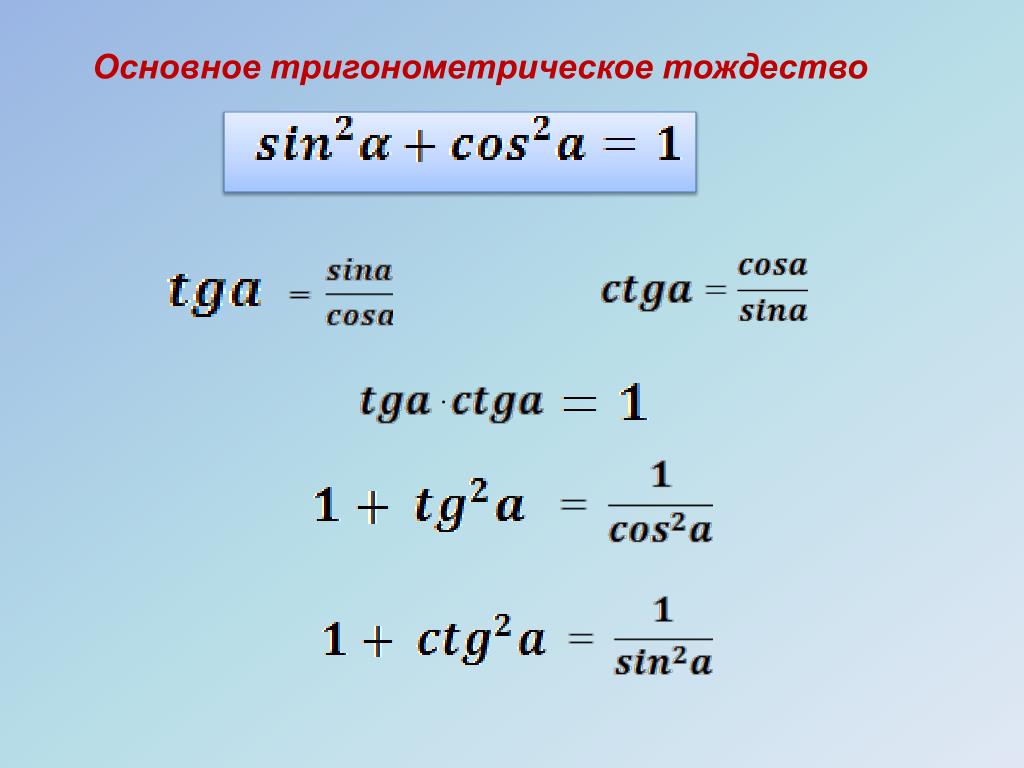 wikimedia.org
wikimedia.org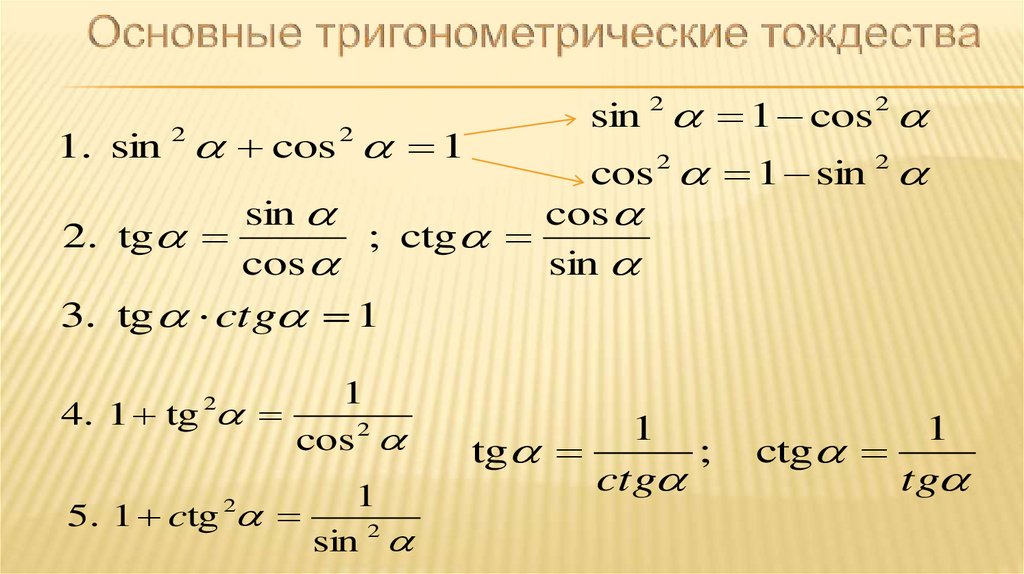 Это справедливо для \(\theta\in \left[\frac{\pi}{4}, \frac{3\pi}{4} \right]\), так что это значения \(\theta\) удовлетворяющие \(\sin\theta\geq\frac{\sqrt{2}}{2}.\ _\square\)
Это справедливо для \(\theta\in \left[\frac{\pi}{4}, \frac{3\pi}{4} \right]\), так что это значения \(\theta\) удовлетворяющие \(\sin\theta\geq\frac{\sqrt{2}}{2}.\ _\square\) \end{align}\]
\end{align}\] Следовательно,
Следовательно, Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/basic-trigonometric-functions/
Brilliant.org .
Извлекаются из
https://brilliant.org/wiki/basic-trigonometric-functions/ Такие уравнения называются тождеств , и в этом разделе мы обсудим несколько тригонометрических тождеств , т. е. тождеств с участием тригонометрических функций. Эти тождества часто используются для упрощения сложных выражений или уравнений. Например, одним из наиболее полезных тригонометрических тождеств является следующее:
Такие уравнения называются тождеств , и в этом разделе мы обсудим несколько тригонометрических тождеств , т. е. тождеств с участием тригонометрических функций. Эти тождества часто используются для упрощения сложных выражений или уравнений. Например, одним из наиболее полезных тригонометрических тождеств является следующее: 2 \;\theta \) дает 92 \;\theta ~+~ 4
2 \;\theta \) дает 92 \;\theta ~+~ 4  Причина в том, что из-за его сложности с этим выражением можно будет делать больше вещей. Например, если вас попросили доказать, что 92 \;\theta}{\sec\;\theta}
Причина в том, что из-за его сложности с этим выражением можно будет делать больше вещей. Например, если вас попросили доказать, что 92 \;\theta}{\sec\;\theta} 