Отношение чисел | СПАДИЛО
теория по математике 🎲 числа и вычисления
ОпределениеОтношением пары чисел называют результат их деления одно на другое. То есть понятия частного и отношения являются синонимами, обозначая одно и то же понятие. При этом число, которое делят, называют предыдущим членом, а число, на которое осуществляется деление, – последующим.
Для обозначения отношения чисел используется знак деления «:» либо черта дроби.
Общая форма записи отношения чисел: a : b или, соответственно
В таких записях a – предыдущий член отношения, b – последующий. Обязательное условие для всякого отношения: b≠0.
Свойства отношений
Свойство №1Членами всякого отношения могут быть как целые, так и дробные, рациональные или другие числа.
Свойство №2Если члены отношения умножить (либо разделить) на одно и то же число, то его значение не изменится. Это свойство называют основным для отношений чисел. Деление членов отношения на одно и то же число называют сокращением отношения.
Деление членов отношения на одно и то же число называют сокращением отношения.
Это свойство нередко используется для перехода от нецелых членов отношения к целым, что более удобно для расчетов.
Свойство №3В отношении могут участвовать и более 2-х членов. Так, в прикладных задачах нередко используются пропорциональные величины, значения которых выражаются как раз через их отношения. Количество членов при этом может быть произвольным и равняться трем, четырем и так далее. В общем виде такие отношения записываются как a:b:c:d:…n и читаются так: «величины относятся между собой как a, b, c…»
Пример №4. Имеется треугольник, длины сторон которого относятся как 3:4:5.
Пример №5. Даны 4 пропорциональных числа, которые относятся между собой как 1:2:4:5.
В задачах, в которых приведены такого рода отношения, обычно вводится коэффициент пропорциональности и, используя свойства объекта, для которого они приведены, и (или) данные из условия, по заданному отношению находят абсолютные значения величин для этого объекта.
Процентное отношение
ОпределениеПроцентное отношение – это характерное и одно из наиболее распространенных направлений прикладного использования отношения чисел. Обозначение процентного отношения – % (процент). 1 % – это сотая часть от целого.
Процентное отношение основывается на обычном отношении, которое множат на 100. Процентное отношение показывает часть объекта (величины) в сравнении с его 100 частями, которые принимаются за целое.
Математическая запись:
Где a – часть целого, выраженная в единицах измерения, b – значение целого, выраженное в тех же единицах, z – количество процентов, которое составляет данная часть от целого.
Пример. На книжной полке 80 книг. Сколько процентов от этого количества составляют 36 книг?
Обозначим искомую величину через х. Тогда получаем:
Пример.
Фермер посеял пшеницу на 2 га, что составляет 80 % от всех его посевных площадей. Какова общая посевная площадь, которой он располагает?
Обозначим искомую величину через х. Составим процентное отношение на основании данных задачи:
Нередко вместо понятия процентного отношения используют понятие долей. В этом случае целое абстрактно принимается за 1, а понятие процента не используется. Доля (часть) от данного целого в такой ситуации – это всегда будет величина, меньшая 1. Для определения доли (части) от целого используется обычное отношение:
Где b – часть от целого, c – величина целого, a – доля, которую b составляет от c.
Специальной единицы измерения доля не имеет и измеряется просто в единицах.
Пример. Какую долю тиража изданной книги удалось продать писателю, если тираж составляет 10 тысяч экземпляров, а приобретено было 6830 книг?
Обозначим искомую величину через х. Составим отношение и найдем х:
Переход от долей к процентам предельно прост: достаточно умножить долю на 100. Так, в предыдущем примере 0,683 по отношению к общему тиражу составит 0,683×100%=68,3% .
Так, в предыдущем примере 0,683 по отношению к общему тиражу составит 0,683×100%=68,3% .
Пример. С 1 га планировалось собрать 40 тонн картофеля. Реальная урожайность составила 0,7 от планируемой. Сколько тонн картофеля собрали?
Обозначим искомую величину через х. Составим выражение для расчета реальной урожайности и найдем х:
Пропорция
ОпределениеПропорцией называют равенство двух числовых отношений. В общем виде такое равенство записывают как:
где a и d называют крайними членами пропорции, b и c – средними. Прочтение пропорции: отношение a к b равно отношению c к d, или a относится к b как c к d, или a во столько раз больше b во сколько больше d.
Примеры конкретных пропорций:
При решении практических задач с использованием отношений в виде пропорции чаще всего от деления переходят к умножению ее членов. Для этого используют основное ее свойство.
Основное свойство пропорцииПроизведение ее крайних членов равно произведению средних. Математически это свойство записывается так:
Математически это свойство записывается так:
Пример:
Если провести дальнейшие вычисления, то в итоге мы должны прийти к равенству чисел слева и справа. А именно:
Отсюда следует важная особенность: основное свойство применяют для проверки истинности составленной пропорции. Если в результате числовых преобразований получено верное равенство, то это означает, что исходные 4 числа действительно могут составить пропорцию.
Как найти неизвестный член пропорции?Когда один из членов пропорции неизвестен и требуется найти его, то применяют правило: для вычисления неизвестного крайнего (среднего) члена перемножают средние (крайние) и делят полученное произведение на известный крайний (средний) член.
Математически это выражается так:
То есть для определения неизвестного члена перемножают пару соответствующих известных и делят их на тот известный член, который не имеет известной пары.
Пример. Дана пропорция:
Требуется найти х.
Пример. Дана пропорция:
Необходимо найти х.
Даниил Романович | Просмотров: 4k | Оценить:
Отношения / Отношения и пропорции / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Отношения и пропорции
- Отношения
Нам известно, что для ответа на вопрос во сколько раз одно число больше другого (или меньше), или какую часть одно из них составляет от другого надо найти частное данных чисел.
| Частное двух чисел и , отличных от нуля, называют отношением чисел и , или отношением числа к числу . |
Где и — члены отношения; число — предыдущий член отношения; — последующий член отношения.
Например:
14 : 7 — отношение числа 14 к числу 7;
6 : 25 — отношение числа 6 к числу 25;
— отношение числа к числу ;
1,15 : 0,36 — отношение числа 1,15 к числу 0,36.
Отношение двух чисел показывает, во сколько раз одно число больше другого, или какую часть одно число составляет от другого. То есть отношение чисел и показывает, во сколько раз число больше числа или какую часть число составляет от числа .
Мы помним, что деление можно заменить чертой дроби, значит, отношение чисел и можно записать двумя способами: : и .
Основное свойство отношения:
| Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю. |
Запишем отношение числа 3 к числу 10 и найдем его значение:
То есть отношение двух чисел можно выразить в процентах.
Процентное отношение двух чисел — это их отношение, выраженное в процентах. Процентное отношение показывает, сколько процентов одно число составляет от другого. Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента. |
Пример:
Сколько процентов составляет число 5 от числа 10?
51021·100%=12·100%=1002%=50%.
Ответ: 50% составляет число 5 от числа 10.
Если значение двух величин выражены одной и той же единицей измерения, то их отношение называют также отношением этих величин. При этом если значения величин выражены разными единицами измерения, то для нахождения отношения этих величин надо сначала перейти к одной единице измерения.
Например:
Дан прямоугольник, длина которого равна 12 см, а ширина 1 м. Найдем отношение длин сторон прямоугольника.
1 м = 100 см;
Отношение длины прямоугольника к его ширине равно 12 : 100 = .
Отношение ширины прямоугольника к его длине равно 100 : 12 = .
Дроби и взаимно обратны, поэтому и отношения 12 к 100 и 100 к 12 называют взаимно обратными.
На практике отношение величин используется, например, при составлении планов и географических карт. В этом случае участки земли на бумаге изображают в уменьшенном виде, при этом на карте или плане указывают отношение, которое показывает, во сколько раз длина отрезка на рисунке меньше длины длины соответствующего отрезка на местности.
| Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты (плана). |
Например:
Пусть на карте задан масштаб , то есть карта сделана в масштабе одна десятитысячная.
Найдем, какой длине на местности соответствует отрезок 5 см на карте.
Для решения обозначим через длину отрезка на местности (в сантиметрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : , данное отношение равно масштабу карты, поэтому получаем уравнение:
Тогда отношение длины отрезка на карте к длине отрезка на местности: 5 : , данное отношение равно масштабу карты, поэтому получаем уравнение:
5 : = 1 : 10 000;
Решаем данное уравнение:
= 510 000;
= 50 000;
50 000 см = 500 м = 0,5 км.
Ответ: отрезок 5 см на карте соответствует 0,5 км на местности.
Найдем, какой длине на карте соответствует отрезок 9,5 км на карте.
Для решения обозначим через длину отрезка на карте (в километрах). Тогда отношение длины отрезка на карте к длине отрезка на местности: : 9,5, данное отношение равно масштабу карты, поэтому получаем уравнение:
: 9,5 = 1 : 10 000;
Решаем данное уравнение:
= 9,5 : 10 000;
= 0,00095;
0,00095 км = 0,95 м = 95 см.
Ответ: отрезок 9,5 км на карте соответствует 95 см на карте.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Пропорции
Прямая и обратная пропорциональные зависимости
Длина окружности и площадь круга
Отношения и пропорции
Правило встречается в следующих упражнениях:
6 класс
Номер 582, Мерзляк, Полонский, Якир, Учебник
Номер 673, Мерзляк, Полонский, Якир, Учебник
Номер 1, Мерзляк, Полонский, Якир, Учебник
Номер 681, Мерзляк, Полонский, Якир, Учебник
Номер 686, Мерзляк, Полонский, Якир, Учебник
Задание 800, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 828, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 993, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1312, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1498, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 146, Мерзляк, Полонский, Якир, Учебник
Номер 149, Мерзляк, Полонский, Якир, Учебник
Номер 150, Мерзляк, Полонский, Якир, Учебник
Номер 198, Мерзляк, Полонский, Якир, Учебник
Номер 229, Мерзляк, Полонский, Якир, Учебник
Номер 405, Мерзляк, Полонский, Якир, Учебник
Номер 406, Мерзляк, Полонский, Якир, Учебник
Номер 846, Мерзляк, Полонский, Якир, Учебник
Номер 847, Мерзляк, Полонский, Якир, Учебник
Номер 943, Мерзляк, Полонский, Якир, Учебник
Основные правила математики 6 класс(кратко).

Основные правила математики 6 класс(кратко).
Содержание
- Делимость натуральных чисел
- Простые и составные числа
- Признаки делимости натуральных чисел
- Основное свойство дроби
- Сокращение дробей
- Приведение дробей к наименьшему общему знаменателю
- Целые числа. Рациональные числа
- Модуль числа
- Сложение и вычитание дробей
- Сложение и вычитание рациональных чисел
- Умножение. Свойства умножения
- Умножение обыкновенных дробей
- Умножение рациональных чисел
- Деление обыкновенных дробей
- Деление рациональных чисел
- Нахождение дроби от числа
- Нахождение числа по его дроби
- Степень числа
- Числовые и буквенные выражения
- Приведение подобных слагаемых
- Раскрытие скобок
- Свойства уравнений
- Отношения
- Пропорции
- Основное свойство пропорции
- Процентное отношение двух чисел
- Прямая и обратная пропорциональная зависимость
Делимость натуральных чисел
Если натуральное число делится нацело на натуральное число , то число называют кратным числа , число — делителем числа
. Для любого натурального числа каждое из чисел
Для любого натурального числа каждое из чисел
a · 1, a · 2, a · 3,…
является кратным числа .
Наименьшим делителем любого натурального числа является число , а наибольшим — само число .
Среди чисел, кратных , наибольшего нет, а наименьшее есть — это само число .
Если каждое из чисел и делится нацело на число ,то и сумма также делится нацело на число .
Если число делится нацело на число , а число не делится нацело на число , то сумма также не делится нацело на число .
Простые и составные числа
Натуральное число называют простым, если оно имеет только два разных делителя: единицу и само это число. Натуральное число, имеющее более двух делителей, называют составным.
Любое составное число можно представить в виде произведения простых чисел, то есть разложить на простые множители.
Если наибольший общий делитель двух натуральных чисел равен 1, то их называют взаимно простыми.
Признаки делимости натуральных чисел
Если запись натурального числа оканчивается цифрой 0, то это число делится нацело на 10.
Если запись натурального числа оканчивается любой цифрой, отличной от 0, то это число не делится нацело на 10.
Если натуральное число разделить на 10, то остаток равен числу, записанному последней цифрой этого числа.
Если запись натурального числа оканчивается четной цифрой, то это число делится нацело на 2.
Если запись натурального числа оканчивается нечетной цифрой, то это число не делится нацело на 2.
Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5.
Если запись натурального числа оканчивается любой цифрой, отличной от цифр 0 и 5, то это число не делится нацело на 5.
Если сумма цифр натурального числа делится нацело на 9, то и само число делится нацело на 9.
Если сумма цифр натурального числа не делится нацело на 9, то и само число не делится нацело на 9.
Если сумма цифр натурального числа делится нацело на 3, то и само число делится нацело на 3.
Если сумма цифр натурального числа не делится нацело на 3, то и само число не делится нацело на 3.
Основное свойство дроби
Если числитель и знаменатель данной дроби умножить на одно и то же натуральное число, то получим дробь, равную данной:
ab = a · nb · n
Если числитель и знаменатель данной дроби разделить на их общий делитель (или на одно и то же натуральное число), то получим дробь, равную данной:
a : nb : n = ab
Сокращение дробей
Деление числителя и знаменателя дроби на их общий делитель, отличный от 1, называют сокращением дроби.
Дробь, числитель и знаменатель которой — взаимно простые числа, называют несократимой.
Если сократить дробь на наибольший общий делитель числителя и знаменателя, то получим несократимую дробь.
Приведение дробей к наименьшему общему знаменателю
Чтобы привести дроби к наименьшему общему знаменателю, надо:
- найти наименьший общий знаменатель данных дробей;
- найти дополнительные множители для каждой из дробей, разделив общий знаменатель на знаменатели данных дробей;
- умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Целые числа. Рациональные числа
Все натуральные числа, противоположные им числа и число 0 называют целыми числами.
Натуральные числа называют целыми положительными числами. Числа -1, -2, -3, … называют целыми отрицательными числами.
Объединив натуральные числа с целыми отрицательными и нулем, получим целые числа.
Объединив целые числа с дробными, получим рациональные числа.
Модуль числа
Модулем числа называют расстояние от начала отсчета до точки, изображающей это число на координатной прямой.
Модуль числа обозначают так:
a
(читают: «модуль a»).
Модуль положительного числа равен этому числу; модуль отрицательного числа равен числу, противоположному данному;
a = a, a≥0—a, a<0
Модуль числа принимает только неотрицательные значения. Модули противоположных чисел равны:
a = —a
Сложение и вычитание дробей
Чтобы сложить две дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тот же.
Чтобы найти разность двух дробей с одинаковыми знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить тот же.
Чтобы сложить (вычесть) две дроби с разными знаменателями, надо привести их к общему знаменателю, а потом применить правило сложения (вычитания) дробей с одинаковыми знаменателями.
Сложение и вычитание рациональных чисел
Чтобы сложить два числа с разными знаками, надо:
- найти модули слагаемых;
- из большего модуля вычесть меньший модуль;
- перед полученным числом поставить знак слагаемого с большим модулем.
Чтобы сложить два отрицательных числа, надо:
- найти модули слагаемых;
- сложить модули слагаемых;
- перед полученным числом поставить знак «-».
Сумма двух противоположных чисел равна нулю:
—a+a=0 или a—a=0
Для любого рационального числа
a+0 = 0+a = a
Чтобы найти разность двух чисел можно
к уменьшаемому прибавить число, противоположное вычитаемому.
Умножение. Свойства умножения
Произведением числа на натуральное число не равное 1, называют сумму, состоящую из слагаемых, каждое из которых равно а:
a · b = a +a +a+…+a⏟b
Если один из двух множителей равен 1, то произведение равно второму множителю:
m · 1 = 1 · m = m
Если один из множителей равен нулю, то произведение равно нулю:
m · 0 = 0 · m = 0
Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Умножение обыкновенных дробей
Чтобы умножить дробь на натуральное число, надо ее числитель умножить на это число, а знаменатель оставить без изменения:
ab·n=a·nb
Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
ab · cd = a · cb · d
Чтобы умножить смешанные числа, надо сначала записать их в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
Умножение рациональных чисел
Чтобы умножить два числа с разными знаками, надо умножить их модули и перед полученным произведением поставить знак «-».
Чтобы умножить два отрицательных числа, надо умножить их модули.
Для любого рационального числа :
a · (—1) = —a
Если произведение • — положительное, то числа и имеют одинаковые знаки;
Если произведение • — отрицательное, то числа и имеют разные знаки.
Деление обыкновенных дробей
Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю:
ab : cd = ab · dc
Деление рациональных чисел
Чтобы найти частное двух чисел с разными знаками, надо модуль делимого разделить на модуль делителя и перед полученным числом поставить знак «-».
Чтобы найти частное двух отрицательных чисел, надо модуль делимого разделить на модуль делителя.
Нахождение дроби от числа
Чтобы найти проценты от числа, можно представить проценты в виде дроби и умножить число на эту дробь.
Нахождение числа по его дроби
Чтобы найти число по его процентам, можно представить проценты в виде дроби и разделить значение процентов на эту дробь.
[ads2]
Степень числа
Степенью числа с натуральным показателем , большим , называют произведение множителей, каждый из которых равен :
an=a · a · a ·…·a⏟n
Число при этом называют основанием степени.
Степенью числа с показателем называют само число
a1=a
Вторую степень числа называют также квадратом числа. Например, запись читают: « в квадрате». Третью степень называют кубом числа, а запись читают: « в кубе».
Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а затем производят другие действия.
Числовые и буквенные выражения
Запись, составленную из чисел, знаков арифметических действий и скобок, называют числовым выражением. Запись, составленную из чисел, букв, знаков арифметических действий и скобок, называют буквенным выражением.
Приведение подобных слагаемых
Чтобы привести подобные слагаемые, надо сложить их коэффициенты и полученный результат умножить на общую буквенную часть.
Раскрытие скобок
Если перед скобками стоит знак «-», то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, изменить на противоположные.
Если перед скобками стоит знак « + », то при раскрытии скобок надо опустить этот знак, а все знаки, стоящие перед слагаемыми в скобках, оставить без изменений.
Свойства уравнений
- Если к обеим частям данного уравнения прибавить (или из обеих частей вычесть) одно и то же число, то получим уравнение, имеющее те же корни, что и данное.
- Если данное уравнение не имеет корней, то, прибавив к обеим его частям одно и то же число, получим уравнение, тоже не имеющее корней.
- Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив при этом его знак на противоположный, то получим уравнение, имеющее те же корни, что и данное.

- Если обе части уравнения умножить (разделить) на одно и то же отличное от нуля число, то получим уравнение, имеющее те же корни, что и данное.
Отношения
- Частное двух чисел и , не равных нулю, еще называют отношением чисел и , или отношением числа к числу .
- Отношение положительных чисел и показывает, во сколько раз число больше числа , или какую часть число составляет число .
- Отношение не изменится, если его члены умножить или разделить на одно и то же число, не равное нулю.
Пропорции
Равенство двух отношений называют пропорцией. В буквенном виде пропорцию можно записать так:
a : b =c : d или ab = cd
Числа и называют крайними членами пропорции, а числа и — средними членами пропорции.
Основное свойство пропорции
Произведение крайних членов пропорции равно произведению ее средних членов:
ab = cd ⇒ ad = bc
Если , , и числа, не равные нулю, и • = • , то отношения
ab и cd
могут образовывать пропорцию
ab = cd
Процентное отношение двух чисел
Процентное отношение двух чисел — это их отношение, выраженное в процентах. Оно показывает, сколько процентов одно число составляет от другого.
Оно показывает, сколько процентов одно число составляет от другого.
Чтобы найти процентное отношение двух чисел, надо их отношение умножить на 100 и к результату дописать знак процента.
Прямая и обратная пропорциональная зависимость
Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз.
Если величины и обратно пропорциональны, то их соответствующие значения удовлетворяют равенству
y = kx
, где — число, постоянное для данных величин.
Данная информация составлена на базе УМК А.Г.Мерзляк, В.Б.Полонский, М.С. Якир
1. Отношение двух чисел — Стоматология в Химках
Соотношение математика
При делении одного числа на другое мы находим, во сколько раз одно число больше другого или, наоборот, какую часть одно число составляет от другого. В этом и есть смысл отношения двух чисел.
Поскольку 5 2 = 10 4 = 50 20 = 2,5 1 , то отношение \(5 : 2\) можно заменить и отношением \(10 : 4\), и отношением \(50 : 20\), и отношением \(2,5 : 1\).
Отношение не изменится, если члены его умножить или разделить на одно и то же отличное от нуля число.
Например, найдём отношение \(30\) см к \(2\) м. Сначала выразим обе эти величины в сантиметрах, а потом разделим одну на другую:
При делении одного числа на другое мы находим, во сколько раз одно число больше другого или, наоборот, какую часть одно число составляет от другого. В этом и есть смысл отношения двух чисел.
Поскольку 5 2 = 10 4 = 50 20 = 2,5 1 , то отношение \(5 : 2\) можно заменить и отношением \(10 : 4\), и отношением \(50 : 20\), и отношением \(2,5 : 1\).
Отношение не изменится, если члены его умножить или разделить на одно и то же отличное от нуля число.
Например, найдём отношение \(30\) см к \(2\) м. Сначала выразим обе эти величины в сантиметрах, а потом разделим одну на другую:
В этом и есть смысл отношения двух чисел.
Www. yaklass. ru
18.07.2018 0:27:02
2018-07-18 00:27:02
Источники:
Https://www. yaklass. ru/p/matematika/6-klass/otnosheniia-proportcii-protcenty-13922/otnoshenie-dvukh-chisel-13923/re-865b0783-d38a-488d-bcbd-2d02677303c9
Соотношение и Пропорция » /> » /> .keyword { color: red; }
Соотношение математика
Основой математических исследований является возможность получить знание об определённых величинах, сравнивая их с другими величинами, которые либо Равны, либо Больше или Меньше, чем те которые являются предметом исследования. Это обычно производится с помощью ряда Уравнений и Пропорций. Когда мы используем уравнения, то мы определяем искомую величину, находя её Равенство с какой-то другой уже знакомой величиной или величинами.
Однако, часто бывает, что мы сравниваем неизвестную величину с другими, которые Не равны ей, а больше или меньше её. Здесь нужен другой подход к обработке данных. Нам может понадобиться узнать, например, На сколько одна величина больше чем другая, или Сколько раз одна содержит другую. Для нахождения ответа на эти вопросы мы узнаем что такое Соотношение двух величин. Одно соотношение называется Арифметическим, а другое Геометрическим. Хоть и стоит заметить, что оба эти термина не были приняты случайно или только в целях отличия. Как арифметическое, так и геометрическое соотношения применимы как к арифметике, так и к геометрии.
Здесь нужен другой подход к обработке данных. Нам может понадобиться узнать, например, На сколько одна величина больше чем другая, или Сколько раз одна содержит другую. Для нахождения ответа на эти вопросы мы узнаем что такое Соотношение двух величин. Одно соотношение называется Арифметическим, а другое Геометрическим. Хоть и стоит заметить, что оба эти термина не были приняты случайно или только в целях отличия. Как арифметическое, так и геометрическое соотношения применимы как к арифметике, так и к геометрии.
Являясь компонентом обширного и важного предмета, пропорция зависит от соотношений, поэтому необходимо чёткое и полное понимание этих понятий.
338. Арифметическое соотношение Это Разница Между двумя величинами или рядом величин. Сами по себе величины называются Членами соотношения, то есть члены, между которыми есть соотношение. Таким образом 2 это арифметическое соотношение 5 и 3. Это выражается помещая знак минус между двумя величинами, то есть 5 — 3. Конечно термин арифметического соотношения и его расписывание по пунктам практически бесполезно, так как происходит лишь замещение слова Разница на знак минус в выражении.
Конечно термин арифметического соотношения и его расписывание по пунктам практически бесполезно, так как происходит лишь замещение слова Разница на знак минус в выражении.
339. Если оба члена арифметического соотношения Умножить или Разделить на одну и ту же величину, то Соотношение, в конечном итоге, будет умножено или разделено на эту величину.
Таким образом, если имеем a — b = r
Тогда перемножим обе стороны на h, (Акс. 3.) ha — hb = hr
И разделив на h, (Акс. 4.) $\frac-\frac=\frac$
340. Если члены арифметического соотношения добавляют или отнимают от соответствующих членов другого, то соотношение суммы или разности будет равно сумме или разности двух соотношений.
Если a — b
И d — h,
Являются двумя соотношениями,
Тогда (a + d) — (b + h) = (a — b) + (d — h). Что в каждом случае = a + d — b — h.
И (a — d) — (b — h) = (a — b) — (d — h). Что в каждом случае = a — d — b + h.
Таким образом арифметическое отношение 11 — 4 равно 7
И арифметическое отношение 5 — 2 равно 3
Отношение суммы членов 16 — 6 это 10, — сумма соотношений.
Отношение разности членов 6 — 2 это 4, — разность соотношений.
341. Геометрическое соотношение — это отношение между величинами, которое выражается ЧАСТНЫМ, если одну величину делят на другую.
Таким образом соотношение 8 к 4, можно записать как 8/4 или 2. То есть частное деления 8 на 4. Другими словами, оно показывает сколько раз 4 содержится в 8.
Тем же самым способом, соотношение любой величины к другой может быть определено, разделив первую на вторую или, что, в принципе, одно и то же, сделав первую числителем дроби, а вторую — знаменателем.
Так соотношение a к b это $\frac$
Соотношение d + h к b + c это $\frac$.
342. Геометрическое соотношение также записывается, размещая две точки одну над другой между сравниваемыми величинами.
Таким образом a:b это запись соотношения a к b, а 12:4 — соотношения 12 к 4. Две величины вместе формируют Пару, в которой первый член называется Антецедентом, а последний — Консеквентом.
343. Эта запись с помощью точек и другая, в форме дроби, являются взаимозаменяемыми по мере необходимости, при этом антецедент становится числителем дроби, а консеквент — знаменателем.
Таким образом 10:5 это то же, что и $\frac$ а b:d, то же, что и $\frac$.
344. Если из этих трёх значений: антецедента, консеквента и соотношения даны любые Два, то третье можно найти.
Соотв. 1. Если у двух пар антецеденты и консеквенты равны, то их соотношения тоже равны.
Соотв. 2. Если у двух пар соотношения и антеценденты равны, то и консеквенты равны и если соотношения и консеквенты равны, то и антецеденты равны.
345. Если две сравниваемые величины Равны, то их соотношение равно единице или соотношению равенства. Соотношение 3*6:18 равно единице, так как частное любой величины разделённой на саму себя равно 1.
Если антецедент пары Больше, чем консеквент, то соотношение больше единицы. Так как делимое больше, чем делитель, то частное больше единицы. Так соотношение 18:6 равно 3. Это называется соотношение Большего неравенства.
Так соотношение 18:6 равно 3. Это называется соотношение Большего неравенства.
С другой стороны, если антецедент Меньше, чем консеквент, то соотношение меньше единциы и это называется соотношением Меньшего неравенства. Так соотношение 2:3 меньше единицы, потому что делимое меньше делителя.
Отсюда обратное соотношение выражается Путём инвертирования дроби, которая отображает прямое соотношение, либо, когда запись ведётся с помощью точек, Инвертируя порядок записи членов.
Таким образом a относится к b обратно тому, как b к a.
347. Сложное соотношение это соотношение Произведений соответствующих членов с двумя и более простыми соотношениями.
Так соотношение 6:3, равно 2
И соотношение 12:4, равно 3
Составленное из них соотношение 72:12 = 6.
Здесь сложное соотношение получается, умножая между собой два антецедента и также два консеквента простых соотношений.
Так соотношение составленное
Из соотношения a:b
И соотношения c:d
И соотношения h:y
Это соотношение $ach:bdy=\frac$.
Сложное соотношение не отличается по своей Природе от любого другого соотношения. Этот термин используется, чтобы в определённых случаях показать происхождение соотношения.
Соотв. Сложное соотношение равно произведению простых соотношений.
Соотношение a:b, равно $\frac$
Соотношение c:d, равно $\frac$
Соотношение h:y, равно $\frac$
И соотношение сложенное из этих трёх будет ach/bdy, что является произведением дробей, которые выражают простые соотношения.
348. Если в последовательности соотношений в каждой предыдущей паре консеквент является антецедентом в последующей, то Соотношение первого антецедента и последнего консеквента равны тому, которое получено из промежуточных соотношений.
Так в ряде соотношений
A:b
B:c
C:d
D:h
Соотношение a:h равно соотношению, сложенному из соотношений a:b, и b:c, и c:d, и d:h. Так сложное соотношение в последней статье равно $\frac=\frac$, или a:h.
Таким же образом все величины, которые являются и антецедентами и консеквентами Исчезнут, когда произведение дробей будет упрощено до своих младших членов и в остатке сложное соотношение будет выражаться первым антецедентом и последним консеквентом.
349. Особый класс сложных соотношений получается при умножении простого соотношения на Самого себя или на другое Равное соотношение. Эти соотношения называются Двойными, Тройными, Четверными, и так далее, в соответствии с количеством операций умножения.
Соотношение, составленное из Двух равных соотношений, то есть, Квадрата простого соотношения, называют Двойным соотношением.
Составленное из Трёх, то есть, Куб простого соотношения, называют Тройным, и так далее.
Аналогично соотношение Квадратных корней двух величин, называется соотношением Квадратного корня, а соотношение Кубических корней — соотношением Кубического корня, и так далее.
Таким образом простое соотношение a к b, равно a:b
Двойное соотношение a к b, равно a 2 :b 2
Тройное соотношение a к b, равно a 3 :b 3
Соотношение квадратного корня a к b, равно √ a :√ b
Соотношение кубического корня a к b, равно 3 √ a : 3 √ b, и так далее.
Термины Двойной, Тройной, и так далее не нужно смешивать с Удвоенным, Утроенным, и так далее.
Соотношение 6 к 2 равно 6:2 = 3
Удвоим это соотношение, то есть, соотношение дважды, то получим 12:2 = 6
Утроим это соотношение, то есть это соотношение трижды, то получим 18:2 = 9
А Двойное соотношение, то есть Квадрат соотношения, равен 6 2 :2 2 = 9
И Тройное соотношение, то есть куб соотношения, равен 6 3 :2 3 = 27
350. Для того, чтобы величины можно соотнести друг с другом, они должны быть одинакового рода, так, чтобы можно было с уверенностью утверждать равны ли они между собой, или одна из них больше или меньше. Фут относится к дюйму, как 12 к 1: он в 12 раз больше, чем дюйм. Но нельзя, например, сказать, что час длиннее или короче, чем палка, или акр больше или меньше, чем градус. Однако, если эти величины выражены в Числах, то может существовать соотношение между этими числами. То есть может существовать соотношение между количеством минут в часе и количеством шагов в миле.
351. Обратившись к Природе соотношений, следующим шагом нам нужно учесть способ, каким образом скажется на самом соотношении изменение одного или двух членов, которые сравнивают между собой. Вспомним, что прямое соотношение выражается в виде дроби, где Антецедет пары всегда это Числитель, а Консеквент — Знаменатель. Тогда будет легко из свойства дробей получить, что изменения в соотношении происходят путём варьирования сравниваемых величин. Соотношение двух величин такое же как и Значение дробей, каждая из которых представляет Частное: числитель делённый на знаменатель. (Статья. 341.) Теперь было показано, что умножать числитель дроби на любую величину, это то же, что и умножать Значение на эту же величину и что деленить числитель, это то же, что и деленить значения дроби. Поэтому,
352. Умножать антецедент пары на любую величину, значит умножать соотношения на эту величину, а делить антецедент — деленить это соотношение.
Таким образом соотношение 6:2 равное 3
И соотношение 24:2 равное 12.
Здесь антецедент и соотношение в последней паре в 4 раза больше, чем в первой.
Отношение a:b равно $\frac$
И отношение na:b равно $\frac$.
Соотв. При известном консеквенте, чем больше Антецедент, тем больше Соотношение, и, наоборот, чем больше соотношение, тем больше антецедент.
353. Умножая консеквент пары на любую величину, в результате получаем деление соотношения на эту величину, а деля консеквент — умножаем соотношение. Умножая знаменатель дроби, делим значение, а деля знаменатель — значение умножается..
Так соотношение 12:2 равно 6
И соотношение 12:4 равно 3.
Здесь консеквент второй пары в Два раза больше, а соотношение В два раза меньше, чем первое.
Соотношение a:b равно $\frac$
И соотношение a:nb равно $\frac$.
Соотв. При данном антецеденте, чем больше консеквент, тем меньше соотношение. И наоборот, чем больше соотношение, тем меньше консеквент.
354. Из двух последних статей следует, что Умножение антецедента пары на любую величину окажет такой же эффект на соотношение, как Деление консеквента на эту величину, а Деление антецедента, окажет такой же эффект, как Умножение консеквента.
Поэтому соотношение 8:4, равно 2
Умножая антецедент на 2, соотношение 16:4 равно 4
Разделив антецедент на 2, соотношение 8:2 равно 4.
Соотв. Любой Множитель или Делитель может быть перенесён от антецедента пары к консеквенту или от консеквента к антецеденту без изменения соотношения.
Стоит заметить, что когда множитель таким образом переносится от одного члена к другому, то он становится делителем, а переносимый делитель становится множителем.
Так соотношение 3.6:9 = 2
Перенеся множитель 3, $6:\frac=2$
То же самое соотношение.
355. Как очевидно из Статей. 352 и 353, Если антецедент и консеквент оба умножить или разделить на одну и ту же величину, то соотношение не меняется.
Соотв. 1. Соотношение двух Дробей, у которых есть общий знаменатель, такое же как отношение их Числителей.
Таким образом соотношение a/n:b/n, то же самое, что и a:b.
Соотв. 2. Прямое соотношение двух дробей, у которых есть общий числитель, равно обратному соотношению их Знаменателей.
356. Из статьи легко определить соотношение любых двух дробей. Если каждый член умножить на два знаменателя, то соотношение будет задано интегральными выражениями. Таким образом умножая члены пары a/b:c/d на bd, получаем $\frac$:$\frac$, что становится ad:bc, путём сокращения общих величин из числителей и знаменателей.
356. b. Соотношение Большего неравенства, сложенное с другим соотношением, Увеличивает его
Пусть соотношение большего неравенства будет задано как 1+n:1
И любое соотношение как A:b
Сложное соотношение будет (Статья. 347,) a + na:b
Что больше, чем соотношение a:b (Статья. 351. соотв.)
Но соотношение Меньшего неравенства, сложенное с другим соотношением, Уменьшает его.
Пусть соотношение меньшей разности 1-n:1
Любой заданное соотношение A:b
Сложное соотношение a — na:b
Что меньше, чем a:b.
357. Если к или от членов любой пары Прибавить Или отнять две другие величины, которые находятся в таком же соотношении, то суммы или остатки будут иметь такое же соотношение.
Пусть соотношение a:b
Будет такое же, как и c:d
Тогда соотношение Суммы антецедентов к сумме консеквентов, а именно, a + c to b + d, тоже одинаковое.
То есть $\frac$ = $\frac$ = $\frac$.
Соотношение Разницы антецедентов к разнице консеквентов также одинаковое.
358. Если в нескольких парах соотношения равны, то Сумма всех антецедентоа относится к сумме всех консеквентов, как любой антецедент к своему консеквенту.
Таким образом соотношение
|12:6 = 2
|10:5 = 2
|8:4 = 2
|6:3 = 2
Таким образом соотношение (12 + 10 + 8 + 6):(6 + 5 + 4 + 3) = 2.
Так как последний числитель больше, чем другой, то Соотношение больше.
Если вместо добавления ту же самую величину Отнять от двух членов, то очевидно, что эффект на соотношение будет обратным.
1. Что больше: соотношение 11:9, или соотношение 44:35?
3. Если антецедент пары равен 65, а соотношение равно 13, то какой консеквент?
4. Если консеквент пары равен 7, и соотношение равно 18, то какой антецедент?
5. Как выглядит сложное соотношение составленное из 8:7, и 2a:5b, а также (7x+1):(3y-2)?
6. Как выглядит сложное соотношение составленное из (x+y):b, и (x-y):(a + b), а также (a+b):h? Отв. (x 2 — y 2 ):bh.
7. Если соотношения (5x+7):(2x-3), и $(x+2):\left(\frac+3\right)$ образуют сложное соотношение, то какое соотношение получится: большее или меньшее неравенство? Отв. Соотношение большего неравенства.
8. Каково соотношение составленное из (x + y):a и (x — y):b, и $b:\frac$? Отв. Соотношение равенства.
9. Каково соотношение сложенное из 7:5, и удвоенного соотношения 4:9, и утроенного соотношения 3:2?
Отв. 14:15.
10. Каково соотношение составленное из 3:7, и утроенного соотношения x:y, и извлечения корня из соотношения 49:9?
Отв. x 3 :y 3 .
© 2005 — 2022
Копирование запрещено! В случае копирования администрация сайта обратится в компетентные органы.
Каково соотношение составленное из x y a и x — y b, и b frac.
Www. math20.com
21.07.2017 7:52:55
2017-07-21 07:52:55
Источники:
Https://www. math20.com/ru/algebra/proporcia/sootnoshenie-proporcia. html
Пропорции математика. Пропорция – это равенство двух отношений. Соотношение. » /> » /> .keyword { color: red; }
Соотношение математика
Пропорция – это равенство, утверждающее, что два отношения равны. Пропорциональный — значит находящийся в определенном отношении к какой-либо величине. Четыре величины \(4, 2, 8 \) и \(4\) находятся в отношении, если \(\frac=\frac\) . Произведение крайних членов пропорции равно произведению средних.
Произведение крайних членов пропорции равно произведению средних.
Пропорция всегда включает равные коэффициенты. Когда соотношение остается постоянным, это соотношение называется пропорциональным.
- \(AB=CD\) \(AD=BC\)
Три величины считаются пропорциональными, если отношение первого ко второму равно соотношению второго и третьего.
\(12\) человек → \(5\) дней \(6\) человек → \(x\) дней \(\frac= \frac\) умножаем крест на крест члены пропорции и сокращаем на \(6\) : \(2*15=5x\) \(30 =5x\) Делим на 5 обе части равенства: \(\frac=x\) , откуда находим
Задача 3. Что должно быть добавлено к каждому из четырех чисел 10, 18, 22, 38, чтобы сделать их пропорцией?
\((10+x)(18+x)=(22+x)(38+x)\) \(380+48x+2x=396+40x+2x\) \(8x=16\) \(x=2\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Репетитор по русскому языку 5-11 классы. Подготовка к ОГЭ, ЕГЭ, ВПР по русскому языку. Повышение общего уровня знаний. Всё обсудим и поможем. Если ученик будет выполнять то, что от него потребуется, хороший результат ему обеспечен.
Повышение общего уровня знаний. Всё обсудим и поможем. Если ученик будет выполнять то, что от него потребуется, хороший результат ему обеспечен.
Репетитор 1-11 классов. Считаю математику своим призванием. Имею большой опыт работы в школе, а также индивидуально с учениками разных возрастов, лично и онлайн, в России и за рубежом. Работаю по классической методике преподавания, с применением новых форм обучения.
Репетитор по математике 8-11 классы. Веду подготовку к ОГЭ/ЕГЭ/ВПР Математика-царица точных наук, следовательно, она помогает в жизни выстраивать точные последовательности действий, организует, а также всегда может пригодится в быту. Работаю по принципу «пирамиды»: от простого к сложному. Всегда ищу индивидуальный подход к каждому ученику, разрабатываю индивидуальные планы осваивания материала. Люблю работать как с сильными, так и слабыми учениками. Нравится разбираться в задачах вместе с учеником, наводящими вопросами выстраивать логическую цепочку решений.
Когда соотношение остается постоянным, это соотношение называется пропорциональным.
Myalfaschool. ru
02.05.2017 2:16:00
2017-05-02 02:16:00
Источники:
Https://myalfaschool. ru/articles/proporciya-v-matematike
Презентация по математике на тему Отношение чисел доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация по математике на тему Отношение чисел, предмет презентации: Математика. Этот материал в формате pptx (PowerPoint) содержит 32 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 32 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Тема урока:
Отношение двух чисел
Урок математики в 6 классе
Ипатова Ирина Викторовна – учитель математики
высшей квалификационной категории
МАОУ СОШ № 6 с УИОП г. Калининград
УРОК 1
1) Латунь – это сплав меди и цинка, взятых в отношении 3 : 2.
2) Готовя варенье, смешивают сливы и сахар в отношении два к трем.
3) От куска материи длиной 5м отрезали 2м. Какую часть куска материи отрезали?
Какую часть куска материи отрезали?
4) Масса станка 9,6 ц, а масса электромотора 36 кг. Найдите отношение массы электромотора к массе станка.
5) В автопарке стоят 36 легковых машин и 12 грузовых. Во сколько раз легковых машин больше, чем грузовых?
Тема урока:
Отношение двух чисел
Задачи урока:
познакомиться с понятием «отношение», узнать, что оно показывает;
научиться составлять и читать
отношения;
решать задачи на определение отношений.
«Отношение — взаимная связь разных величин, предметов, действий.»
Дружеские отношения
Семейные отношения
Ожегов С.И.
Учитель строг в отношении к ученикам.
В математике
Отношение двух чисел — это частное от деления одного из них на другое.
a : b
Что показывает отношение
двух чисел?
a : b
Отношение показывает, во сколько раз
первое число больше второго
Или
какую часть первое число
составляет от второго числа.
ЗАДАЧА 1. В классе 36 учащихся
15
?
Какую часть учащихся составляют мальчики, а какую девочки?
ЗАДАЧА 2.
Масса станка 9,6 ц, а масса электромотора
36 кг. Найдите отношение массы
электромотора к массе станка.
Запомни!
Единицы измерения величин в отношении должны быть одинаковыми.
Найдите отношение:
1) 56 к 7
2) 8 к 10
3) 9,6 к 0,32
4) 0,25 к 0,55
Домашнее задание:
У: стр. 104-105 Читать пункт
104-105 Читать пункт
«Что называют отношением
двух чисел»,
№322, 327, 328.
УРОК 2
Устные упражнения:
Что называют отношением
двух чисел?
Отношение двух чисел — это частное от деления одного из них на другое.
Записать возможные отношения:
а) зеленые к желтым
б) зеленые к розовым
в) розовые к желтым
Ответ
На столе стоят кружки.
Что означают отношения:
а) 6 к 10
б) 4 к 10
в) 4 к 6
г) 6 к 4
Заполни пропуски
«Отношение 64:16 (или _____) показывает,__________________________
«Отношение 9:__ (или 9/11) показывает, _________________________________________
Молоко разлили в три бидона.
В первый налили 0,1 всего молока.
0,1
Во второй налили 0,3 всего молока.
0,3
А в третий – 0,6 всего молока.
0,6
Что показывает отношение?
Подсказка
Ответ
Ответ
Отношение a к b равно 1,25
Найдите обратное отношение.
Общее количество спортсменов на Зимней Олимпиаде в Сочи — 2800 человек из 88 стран мира, Россию представят 223 спортсмена. Какую часть спортсмены из России составляет от общего количества участников олимпиады?
1
2
3
9
6
12
11
10
8
7
4
5
Какую часть урока заняла самостоятельная работа,
которая длилась 10 минут, если продолжительность
урока 45 мин?
Ответ
1) Латунь – это сплав меди и цинка, взятых в отношении 3 : 2.
2) Готовя варенье, смешивают малину и сахар в отношении два к трем.
3) Сплав содержит золото и серебро в отношении 57: 41
4) Число 120 разделить в отношении 4 : 11
МЕДЬ
ЦИНК
3 ЧАСТИ
ЛАТУНЬ
5 ЧАСТЕЙ
2 ЧАСТИ
ЛАТУНЬ – ЭТО СПЛАВ МЕДИ И ЦИНКА, ВЗЯТЫХ В ОТНОШЕНИИ 3 : 2
Готовя варенье, смешивают малину и сахар в отношении два к трем.
Для приготовления ягодного варенья берутся объемы ягод и сахара в отношении 1 : 1. Сколько литров сахара нужно досыпать к 5 литрам ягод, чтобы получить качественное варение?
2 части
3 части
57 частей
41 часть
Сплав содержит золото и серебро
в отношении 57: 41
ЗОЛОТО
СЕРЕБРО
Задача 1. Число 120 разделить в отношении 4 : 11
Число 120 разделить в отношении 4 : 11
Задача 2.
Мама купила сливы и груши в отношении 3 : 4. Сколько фруктов каждого вида купила мама, если всего она купила 2 кг 800г фруктов.
Решение
1) 2800 : (3 + 4) = 400 (г) – 1 часть фруктов.
2) 400 * 3 = 1200 (г) – слив.
3) 400 * 4 = 1600(г) – груш.
Ответ: 1 кг 200 г и 1 кг 600 г
Описать ситуацию:
Отношение числа учащихся, не выполнивших домашнее задание к общему числу учащихся равно 1 : 25
а) ___ часть учащихся выполнили домашнее задание
б) каждый _______ учащийся не выполнил домашнее задание
в) ____ ученика из ____ выполнили домашнее задание
Домашнее задание:
№324, 329, 330 (а, б).
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Кол-во подписок | % | Название журнала | Кол-во подписок | % | |
«Победа» | 107 | 77 | «1000 советов» | 24 | 16 |
«Республика молодая» | 9 | 6 | «Чилисема» | 1 | |
«Известия Мордовии» | 22 | «Моя семья» | 2 | ||
«Столица «С» | 21 | «Сядко» | 1 | ||
«Жизнь» | 7 | «Айболит» | 1 | ||
«Сельская газета» | 2 | «Непоседа « | 2 | ||
«Вечерний Саранск» | 7 | «Диагональ» | 2 | ||
«Эрзянь правда» | 1 | «Пенсионер» | 7 |
Соотношение — значение, упрощение, таблица, примеры
Соотношение в математике — это термин, который используется для сравнения двух или более чисел. Он используется, чтобы указать, насколько велика или мала величина по сравнению с другой. В отношении две величины сравниваются с помощью деления. Здесь делимое называется «антецедентом», а делитель — «консеквентом». Например, в группе из 30 человек 17 из них предпочитают ходить по утрам, а 13 — ездить на велосипеде. Чтобы представить эту информацию в виде соотношения, запишем его как 17:13. Здесь символ ‘:’ читается как «есть к». Таким образом, отношение людей, предпочитающих ходить пешком, к людям, предпочитающим езду на велосипеде, читается как «17 к 13».
Он используется, чтобы указать, насколько велика или мала величина по сравнению с другой. В отношении две величины сравниваются с помощью деления. Здесь делимое называется «антецедентом», а делитель — «консеквентом». Например, в группе из 30 человек 17 из них предпочитают ходить по утрам, а 13 — ездить на велосипеде. Чтобы представить эту информацию в виде соотношения, запишем его как 17:13. Здесь символ ‘:’ читается как «есть к». Таким образом, отношение людей, предпочитающих ходить пешком, к людям, предпочитающим езду на велосипеде, читается как «17 к 13».
| 1. | Что такое отношение? |
| 2. | Расчет коэффициентов |
| 3. | Как упростить пропорции? |
| 4. | Эквивалентные соотношения |
| 5. | Часто задаваемые вопросы о Ratio |
Что такое соотношение?
Отношение определяется как сравнение двух количеств одних и тех же единиц , который указывает, сколько одного количества присутствует в другом количестве. Соотношения можно разделить на два типа. Одно отношение части к части, а другое отношение части к целому. Соотношение частей к частям показывает, как связаны два отдельных объекта или группы. Например, соотношение мальчиков и девочек в классе составляет 12:15, тогда как отношение части к целому обозначает отношение конкретной группы к целому. Например, из каждых 10 человек 5 любят читать книги. Следовательно, соотношение части к целому составляет 5:10, а значит каждые 5 человек из 10 любят читать книги.
Соотношения можно разделить на два типа. Одно отношение части к части, а другое отношение части к целому. Соотношение частей к частям показывает, как связаны два отдельных объекта или группы. Например, соотношение мальчиков и девочек в классе составляет 12:15, тогда как отношение части к целому обозначает отношение конкретной группы к целому. Например, из каждых 10 человек 5 любят читать книги. Следовательно, соотношение части к целому составляет 5:10, а значит каждые 5 человек из 10 любят читать книги.
Формула отношения
Мы используем формулу отношения при сравнении отношений между двумя числами или количествами. Общая форма представления отношения между двумя величинами, скажем, «а» и «b», представляет собой а: b, , что читается как «а к b».
Форма дроби, которая представляет это соотношение, — a/b. Чтобы еще больше упростить отношение, мы следуем той же процедуре, которую используем для упрощения дроби. а:б = а/б. Давайте разберемся в этом на примере.
а:б = а/б. Давайте разберемся в этом на примере.
Пример: В классе из 50 учеников 23 девочки, остальные мальчики. Найдите отношение количества мальчиков к количеству девочек.
Общее количество студентов = 50; Количество девочек = 23.
Общее количество мальчиков = Общее количество учащихся — Общее количество девочек
= 50 — 23
= 27
Таким образом, искомое соотношение равно (Количество мальчиков: Количество девочек), то есть 27:23.
Расчет коэффициентов
Чтобы рассчитать отношение двух величин, мы можем использовать следующие шаги. Давайте разберемся в этом на примере. Например, если для приготовления пышных оладий необходимо 15 стаканов муки и 20 стаканов сахара, рассчитаем соотношение муки и сахара в рецепте.
- Шаг 1: Найдите количества для обоих сценариев, для которых мы определяем соотношение. В данном случае это 15 и 20.
- Шаг 2: Запишите в виде дроби a/b.
 Итак, мы пишем это как 15/20.
Итак, мы пишем это как 15/20. - Шаг 3: Если возможно, еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 15/20 можно упростить до 3/4.
- Шаг 4: Следовательно, отношение муки к сахару можно выразить как 3:4.
Используйте бесплатный онлайн-калькулятор коэффициентов Cuemath, чтобы проверить свои ответы при расчете коэффициентов.
Как упростить пропорции?
Отношение показывает, сколько одного количества требуется по сравнению с другим количеством. Два члена отношения можно упростить и выразить в самой низкой форме. Соотношения, выраженные в самых низких терминах, легко понять, и их можно упростить так же, как мы упрощаем дроби. Чтобы упростить отношение, мы используем следующие шаги. Давайте разберемся в этом на примере. Например, упростим соотношение 18:10.
- Шаг 1: Запишите данное отношение a:b в виде дроби a/b. Записав отношение в виде дроби, мы получим 18/10.

- Шаг 2: Найдите наибольший общий делитель чисел ‘a’ и ‘b’. В этом случае GCF 10 и 18 равен 2, .
- Шаг 3: Разделите числитель и знаменатель дроби на GCF, чтобы получить упрощенную дробь. Здесь, разделив числитель и знаменатель на 2, получим (18÷2)/(10÷2) = 9/5.
- Шаг 4: Представьте эту дробь в форме отношения, чтобы получить результат. Следовательно, упрощенное соотношение равно 9:5.
Используйте бесплатный онлайн-калькулятор коэффициентов упрощения Cuemath, чтобы проверить свои ответы.
Советы и рекомендации по соотношению:
- В случае, если оба числа ‘a’ и ‘b’ равны в соотношении a:b, то a:b = 1.
- Если a > b в отношении a : b, то a : b > 1.
- Если a < b в отношении a : b, то a : b < 1,
- Перед их сравнением необходимо убедиться, что единицы измерения двух величин одинаковы.
Эквивалентные отношения
Эквивалентные соотношения аналогичны эквивалентным дробям. Если антецедент (первый член) и консеквент (второй член) данного отношения умножить или разделить на одно и то же число, отличное от нуля, то получится эквивалентное отношение. Например, если антецедент и консеквент отношения 1:3 умножить на 3, мы получим (1 × 3) : (3 × 3) или 3: 9.. Здесь 1:3 и 3:9 являются эквивалентными соотношениями. Точно так же, когда оба члена соотношения 20:10 делятся на 10, получается 2:1. Здесь 20:10 и 2:1 — эквивалентные соотношения. Бесконечное число эквивалентных отношений любого заданного отношения можно найти, умножив антецедент и консеквент на положительное целое число.
Если антецедент (первый член) и консеквент (второй член) данного отношения умножить или разделить на одно и то же число, отличное от нуля, то получится эквивалентное отношение. Например, если антецедент и консеквент отношения 1:3 умножить на 3, мы получим (1 × 3) : (3 × 3) или 3: 9.. Здесь 1:3 и 3:9 являются эквивалентными соотношениями. Точно так же, когда оба члена соотношения 20:10 делятся на 10, получается 2:1. Здесь 20:10 и 2:1 — эквивалентные соотношения. Бесконечное число эквивалентных отношений любого заданного отношения можно найти, умножив антецедент и консеквент на положительное целое число.
Таблица соотношений
Таблица соотношений представляет собой список, содержащий эквивалентные соотношения любого заданного соотношения в структурированном виде. В следующей таблице соотношений показано соотношение между соотношением 1:4 и четырьмя его эквивалентными соотношениями. Эквивалентные отношения связаны друг с другом путем умножения числа. Эквивалентные соотношения получаются путем умножения или деления двух членов отношения на одно и то же число. В примере, показанном на рисунке, возьмем соотношение 1:4 и найдем четыре эквивалентных отношения, умножив оба члена отношения на 2, 3, 6 и 9.. В итоге получаем 2:8, 3:12, 6:24 и 9:36.
В примере, показанном на рисунке, возьмем соотношение 1:4 и найдем четыре эквивалентных отношения, умножив оба члена отношения на 2, 3, 6 и 9.. В итоге получаем 2:8, 3:12, 6:24 и 9:36.
Воспользуйтесь бесплатным онлайн-калькулятором эквивалентных соотношений Cuemath, чтобы проверить свои ответы.
☛ Похожие темы
- Процентная доля
- Определение скорости
- Калькулятор нормы прибыли
Примеры соотношений
Пример 1: В школьной аудитории 49 мальчиков и 28 девочек. Выразите отношение количества мальчиков к количеству девочек.
Решение:
Дано, количество мальчиков = 49; а количество девочек = 28. НОД 49 и 28 равен 7. Теперь, чтобы упростить, разделите два слагаемых на их НОД, который равен 7. Это означает, что (49 ÷ 7)/(28 ÷ 7) = 7/ 4. Следовательно, соотношение числа мальчиков и девочек = 7:4.
Пример 2: В музыкальном классе 30 учеников.
 Из них 10 взрослых, остальные дети. Каково отношение количества детей к общему количеству учащихся в музыкальном классе?
Из них 10 взрослых, остальные дети. Каково отношение количества детей к общему количеству учащихся в музыкальном классе? Решение:
Учитывая, что общее количество учащихся в музыкальном классе = 30, а общее количество взрослых = 10. Следовательно, количество детей, посещавших музыкальный класс = 30 -10, что равно к 20. Отношение общего количества детей к общему количеству учащихся в музыкальном классе = 20:30, что при упрощении дает 2:3.
Пример 3: Упростите данное соотношение, 87:75.
Решение:
Чтобы упростить данное отношение, мы сначала найдем НОД 87 и 75, что равно 3. Затем мы разделим каждый член на 3. Это означает, что (87 ÷ 3)/(75 ÷ 3) = 29/25. Таким образом, соотношение 87:75 в простейшем виде равно 29:25.
перейти к слайдуперейти к слайдуперейти к слайду
Как ваш ребенок может освоить математические понятия?
Мастерство математики приходит с практикой и пониманием «почему» за «что». Почувствуйте разницу Cuemath.
Почувствуйте разницу Cuemath.
Записаться на бесплатный пробный урок
Практические вопросы по соотношению
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о Ratio
Что такое соотношение в математике?
Соотношение можно определить как соотношение или сравнение между двумя числами одной и той же единицы для проверки того, насколько одно число больше другого. Например, если количество баллов, набранных за тест, равно 7 из 10, то отношение полученных баллов к общему количеству баллов записывается как 7:10.
Какие существуют способы записи отношения?
Соотношение можно записать, разделив две величины двоеточием (:), или его можно записать в дробной форме. Например, если есть 4 яблока и 8 дынь, то отношение яблок к дыням можно записать как 4:8 или 4/8, что можно еще упростить как 1:2.
Как рассчитать соотношение между двумя числами?
Чтобы рассчитать отношение двух величин, мы можем использовать следующие шаги. Давайте разберемся в этом на примере. Например, если для приготовления глазури необходимо 14 чашек масла и 28 чашек сахара, каково соотношение масла и сахара?
Давайте разберемся в этом на примере. Например, если для приготовления глазури необходимо 14 чашек масла и 28 чашек сахара, каково соотношение масла и сахара?
- Шаг 1: Обратите внимание на количество обоих ингредиентов, для которых мы определяем соотношение. В данном случае это 14 и 28.
- Шаг 2: Запишите в виде дроби a/b. Итак, мы пишем это как 14/28.
- Шаг 3: Если возможно, еще больше упростите дробь. Упрощенная дробь даст окончательное соотношение. Здесь 14/28 можно упростить до 1/2.
- Этап 4: Следовательно, отношение масла к сахару можно выразить как 1:2.
Как найти эквивалентные соотношения?
Два отношения называются эквивалентными, если они представляют одно и то же значение в упрощенном виде. Это понятие похоже на эквивалентные дроби. Например, когда отношение 1: 4 умножается на 2, это означает умножение обоих членов отношения на 2. Таким образом, мы получаем, (1 × 2) / (4 × 2) = 2/8 или 2: 8 , Здесь 1:4 и 2:8 являются эквивалентными соотношениями. Точно так же отношение 30:10 при делении на 10 дает соотношение 3:1. Здесь 30:10 и 3:1 — эквивалентные соотношения. Итак, эквивалентные отношения можно найти, используя операцию умножения или деления в зависимости от чисел.
Точно так же отношение 30:10 при делении на 10 дает соотношение 3:1. Здесь 30:10 и 3:1 — эквивалентные соотношения. Итак, эквивалентные отношения можно найти, используя операцию умножения или деления в зависимости от чисел.
Что такое таблица соотношений?
Таблица соотношений показывает список эквивалентных соотношений, которые получаются путем умножения или деления обеих величин на одно и то же значение. Например, если таблица соотношений начинается с соотношения 1 : 3, то в последующих строках будет соотношение 2 : 6, 3 : 9, 4 : 12 и т. д. Когда эти соотношения упрощены, они представляют одно и то же значение, то есть 1:3.
Что такое золотое сечение?
Золотое сечение — это число, значение которого примерно равно 1,618. Символом для этого является греческая буква «фи», представленная как ϕ. Это особый атрибут, который используется в искусстве, геометрии и архитектуре, потому что считается, что золотое сечение создает наиболее приятную и красивую форму. Это также известно как божественная пропорция, которая существует между двумя величинами, и соотношение для расчета золотого сечения представлено как ϕ = a/b = (a + b)/a = 1,6180339.8875… где а и b — размеры двух величин, а а — большее из них.
Это также известно как божественная пропорция, которая существует между двумя величинами, и соотношение для расчета золотого сечения представлено как ϕ = a/b = (a + b)/a = 1,6180339.8875… где а и b — размеры двух величин, а а — большее из них.
Почему коэффициенты важны?
Соотношения важны, потому что они позволяют нам выражать количества таким образом, чтобы их было легче интерпретировать. Это инструмент, который используется для сравнения размера двух или более величин по отношению друг к другу. Например, если в классе 30 девочек и 20 мальчиков. Мы можем представить количество девочек к количеству мальчиков с помощью соотношения, которое в данном случае равно 3:2.
Что такое формула соотношения?
Формула отношения используется для сравнения отношений между двумя числами или количествами. Общая форма представления отношения между двумя величинами, скажем, «а» и «b», представляет собой а: b, , что читается как «а к b».
Что такое соотношение и пропорция?
Соотношение — это отношение или сравнение между двумя величинами одной и той же единицы измерения для проверки того, насколько одно число больше другого. Записывается как a/b или a:b, где b не равно нулю. Пропорция – это равенство двух отношений. Пропорции используются для записи эквивалентных отношений, которые помогают решать неизвестные величины. Например, пропорция выражается как: a: b = c: d
Записывается как a/b или a:b, где b не равно нулю. Пропорция – это равенство двух отношений. Пропорции используются для записи эквивалентных отношений, которые помогают решать неизвестные величины. Например, пропорция выражается как: a: b = c: d
Как сравнить коэффициенты?
Существуют различные методы сравнения коэффициентов. Например, сравним 1:2 и 2:3 методом НОК.
- Шаг 1: Запишите коэффициенты в виде дроби. Здесь это означает 1/2 и 2/3.
- Шаг 2: Сократите дроби по отдельности. Здесь обе дроби 1/2 и 2/3 уже находятся в сокращенной форме.
- Шаг 3: Теперь сравните 1/2 и 2/3, найдя НОК (наименьшее общее кратное) знаменателей. LCM 2 и 3 равен 6,9.0084
- Шаг 4: Приравняйте знаменатели, умножив числитель и знаменатель первой дроби на 3, то есть (1 × 3)/(2 × 3) = 3/6. Затем умножьте числитель и знаменатель второй дроби на 2, то есть (2 × 2)/(3 × 2) = 4/6.
- Шаг 5: Теперь можно легко сравнить 3/6 и 4/6. Это показывает, что 4/6 больше, чем 3/6.
 Следовательно, 2:3 > 1:2.
Следовательно, 2:3 > 1:2.
Как преобразовать пропорции в дроби?
Соотношения можно записать в виде дробей очень простым способом. Предшественник записывается как числитель, а консеквент — как знаменатель. Например, если мы возьмем соотношение 3: 5. Здесь 3 — это антецедент, а 5 — консеквент. Таким образом, мы можем записать это как 3/5.
Как преобразовать дроби в отношения?
Дроби могут быть записаны в виде отношений после упрощения. Это означает, что мы сначала приводим данную дробь к ее наименьшему члену, а затем записываем числитель как антецедент, а знаменатель как следствие. Например, дробь 16/48 сначала уменьшится до 1/3, а затем ее можно будет выразить в виде отношения 1:3.
Как преобразовать отношения в десятичные дроби?
Соотношения можно легко преобразовать в десятичные, записав отношение в виде дроби, а затем дробь преобразуется в десятичную путем деления числителя на знаменатель. Например, 3:7 можно записать как 3/7. Теперь 3/7 = 0,428.
Теперь 3/7 = 0,428.
Как преобразовать соотношения в проценты?
Соотношения можно преобразовать в проценты, выполнив следующие действия. Например, переведем 5:6 в виде процентов.
- Шаг 1: Запишите коэффициент в виде дроби. Здесь 5:6 можно записать как 5/6.
- Шаг 2: Умножьте эту дробь на 100 и добавьте символ процента. В этом случае 5/6 × 100 = 83,33%.
Прочтите эту статью о «отношении к процентам», чтобы узнать больше.
Скачать БЕСПЛАТНЫЕ учебные материалы
Скачать бесплатно рабочие листы для 6 класса
Рабочие листы по отношениям
Отношения в математике
Отношение — это отношение между сущностями в нашем мире. Это могут быть числа, физические величины, предметы, продукты или даже люди.
В математике отношение чаще используется как «сколько раз одно число содержит другое».
Например, если есть четыре яблока и две груши, то отношение «четыре к двум» (то есть 4∶2, что эквивалентно отношению 2∶1), или если мы поменяем местами яблоки и груши , «от двух до четырех».
Отношение выражается как a к b (где вместо a и b любые числа), но чаще можно увидеть так a : b . Существуют различные способы прочтения этого обозначения:
- от a до b
- отношение a к b
Запишем соотношение четырех яблок и двух груш, используя символ отношения ( двоеточие ):
4 : 2
Это соотношение можно прочитать как «четыре к двум» или « отношение четырех». яблоки к двум грушам » или « четыре яблока к двум грушам ».
Если мы поменяем местами яблоки и груши, то получим соотношение 2 : 4. Это соотношение можно прочитать как «два к четырем» или «две груши к четырем яблокам». «.
Что такое соотношение?
Соотношение, как упоминалось ранее, записывается в виде a:b. Его также можно записать в виде дроби. А мы знаем, что такое обозначение в математике означает деление. Тогда результатом отношения является частное чисел a и b. Частное означает «сколько раз» и происходит от латыни.
Частное означает «сколько раз» и происходит от латыни.
Отношение в математике — это частное двух чисел. Равные частные соответствуют равным отношениям.
Отношение позволяет узнать, сколько раз одно число содержит другое
Вернемся к соотношению четырех яблок к двум грушам (4 : 2). Это соотношение позволяет нам узнать, сколько яблок приходится на единицу груши. Под одной мы подразумеваем одну грушу. Сначала запишем отношение 4 : 2 в виде дроби:
Это отношение есть деление числа 4 на число 2. Если мы произведем это деление, то получим ответ на вопрос « Каково соотношение яблок и груш?»
Получили 2. Итак, четыре яблока на две груши (4 : 2)
На диаграмме показано, как четыре яблока и две груши связаны друг с другом Вы видите, что на каждую грушу приходится два яблока.
Отношение можно изменить, написав его как . Тогда мы получим отношение двух груш к четырем яблокам, или » отношение двух груш к четырем яблокам «. Это соотношение покажет, сколько груш приходится на единицу яблока. Под единицей яблока мы подразумеваем одно яблоко.
Это соотношение покажет, сколько груш приходится на единицу яблока. Под единицей яблока мы подразумеваем одно яблоко.
Чтобы найти значение дроби нужно вспомнить как делить меньшее число на большее
Получили 0,5. Преобразуем эту десятичную дробь в обыкновенную:
Уменьшим полученную дробь на 5
Ответ: (половина груши). Таким образом, две груши и четыре яблока (2 : 4) относятся друг к другу так, что одно яблоко составляет половину груши
На рисунке показано, каково отношение между двумя грушами и четырьмя яблоками. Вы видите, что на каждое яблоко приходится половинка груши.
Числа, составляющие отношение, называются членами отношения .
. другие примеры соотношений. Рецепт предназначен для приготовления чего-либо. Рецепт основан на соотношении продуктов. Например, для овсянки обычно требуется чашка хлопьев на две чашки молока или воды. Соотношение 1:2 (« один к двум » или « одна чашка хлопьев к двум чашкам молока «).
Преобразуем соотношение 1 : 2 в дробь, получим . Подсчитав эту дробь, получим 0,5. Итак, один стакан хлопьев а два стакана молока связаны друг с другом таким образом, что один стакан молока равен половине стакана хлопьев
Если мы инвертируем соотношение 1 : 2, то получим соотношение 2 : 1 («два к одному»). » или «два стакана молока на один стакан каши»). Преобразуем соотношение 2 : 1 в дробь, получим . Подсчитав эту дробь, получим 2. Значит, два стакана молока и один стакан каши связаны друг к другу таким образом, что на один стакан хлопьев приходится два стакана молока.
Пример 2. В классе 15 учеников. Из них 5 мальчиков и 10 девочек. Мы можем записать соотношение девочек и мальчиков 10:5 и преобразовать это соотношение в дробь. Если мы посчитаем эту дробь, то получим 2. Вот и все, девочки и мальчики связаны друг с другом таким образом, что на каждого мальчика приходится две девочки
На рисунке показано, как связаны между собой десять девочек и пять мальчиков Другой. Вы видите, что на каждого мальчика приходится две девочки.
Вы видите, что на каждого мальчика приходится две девочки.
Не всегда возможно перевести отношение в дробь и найти частное. В некоторых случаях это будет нелогично.
Итак, если вы перевернете соотношение, вы получите , то есть соотношение мальчиков и девочек. Если вы вычислите эту дробь, вы получите 0,5. Получается, что пять мальчиков относятся к десяти девочкам так, что каждая девочка наполовину мальчик. Математически, конечно, это правильно, но с точки зрения реальности не совсем разумно, потому что мальчик — живой человек и его нельзя просто так взять и разделить, как грушу или яблоко.
Умение построить правильное соотношение является важным навыком при решении задач. Итак, в физике отношение пройденного расстояния ко времени есть скорость движения.
Расстояние обозначается переменной S , время переменной t , а скорость символом v . Тогда фраза «отношение пройденного пути ко времени есть скорость движения» будет описываться следующим выражением:
Предположим, автомобиль проехал 100 километров за два часа. Тогда отношение пройденных ста километров к двум часам будет скоростью автомобиля:
Тогда отношение пройденных ста километров к двум часам будет скоростью автомобиля:
Скоростью принято называть расстояние, пройденное телом за единицу времени. Единицей времени является 1 час, 1 минута или 1 секунда. А соотношение, как упоминалось ранее, позволяет узнать, сколько одного объекта приходится на единицу другого объекта. В нашем примере отношение ста километров к двум часам показывает, сколько километров приходится на один час движения. Мы видим, что на каждый час движения приходится 50 километров
Следовательно, скорость измеряется в км/ч, м/мин, м/с . Символ дроби (/) указывает на отношение расстояния ко времени: километров в час, метров в минуту и метров в секунду соответственно.
Пример 2. Отношение стоимости товаров к их количеству равно цене одной единицы товара
Если мы взяли в магазине пять шоколадных пирожных и их общая стоимость составила 100 долларов, то мы можем определить цена одного торта. Для этого нам нужно найти отношение ста долларов к количеству пирожных. Тогда мы получаем, что один торт стоит 20 долларов.
Для этого нам нужно найти отношение ста долларов к количеству пирожных. Тогда мы получаем, что один торт стоит 20 долларов.
Сравнение величин
Ранее мы узнали, что соотношение между величинами различных форм природы является новой величиной. Например, отношение пройденного пути ко времени есть скорость движения. Отношение стоимости товара к его количеству есть цена одной единицы товара.
Но соотношение также можно использовать для сравнения значений. Результатом соотношения является число, показывающее, во сколько раз первое значение больше второго.
Чтобы узнать, во сколько раз первое значение больше второго, запишите большее значение в числитель, а меньшее — в знаменатель.
Чтобы узнать, какая часть первого значения является второй, запишите в числитель меньшее значение, а в знаменатель большее значение.
Рассмотрим числа 20 и 2. Выясним, во сколько раз число 20 больше числа 2. Для этого найдем отношение числа 20 к числу 2. Запишем число 20 в числитель и цифра 2 в знаменателе
Для этого найдем отношение числа 20 к числу 2. Запишем число 20 в числитель и цифра 2 в знаменателе
Значение этого отношения равно десяти
Отношение числа 20 к числу 2 составляет число 10. Это число показывает, во сколько раз число 20 больше числа 2. Таким образом, число 20 в десять раз число 2.
Пример 2. В классе 15 учеников. Из них 5 мальчиков и 10 девочек. Определите, во сколько раз девочек больше, чем мальчиков.
Запишите соотношение девочек и мальчиков. Запишите количество девочек в числителе и количество мальчиков в знаменателе:
Значение этого отношения равно 2. Таким образом, в классе из 15 учащихся вдвое больше девочек, чем мальчиков.
Вопрос о том, сколько девочек приходится на одного мальчика, больше не стоит. В этом случае соотношение используется для сравнения числа девочек и числа мальчиков.
Пример 3. Какая часть числа 20 равна числу 2.
Найдите отношение 2 к 20. Запишите число 2 в числителе и число 20 в знаменателе
Запишите число 2 в числителе и число 20 в знаменателе
Чтобы найти значение этого отношения, нужно вспомнить, как делить меньшее число на большее
Значение отношения числа 2 к числу 20 равно числу 0,1
В этом случае десятичную 0,1 можно преобразовать в правильную дробь. Этот ответ будет легче понять:
Таким образом, число 2 из 20 составляет одну десятую.
Вы можете сделать тест. Для этого нужно найти число 20. Если мы все сделали правильно, то должно получиться число 2
20 : 10 = 2
2 × 1 = 2
Мы получили число 2. Значит одна десятая от 20 это число 2. Отсюда делаем вывод, что задача решена правильно.
Пример 4. В классе 15 человек. Из них 5 мальчиков и 10 девочек. Определить, какую часть от общего числа учащихся составляют мальчики.
Запишите долю мальчиков к общему количеству учащихся. Запишите пять мальчиков в числителе и общее количество учеников в знаменателе. Всего учеников 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения 9 запишем 15.0003
Всего учеников 5 мальчиков плюс 10 девочек, поэтому в знаменателе отношения 9 запишем 15.0003
Чтобы найти значение этого отношения, нужно вспомнить, как делить меньшее число на большее. В этом случае число 5 делится на число 15.
Разделив 5 на 15, мы получим периодическую дробь. Преобразуем эту дробь в обыкновенную
Уменьшим полученную дробь на 3
Окончательный ответ . Итак, мальчики составляют треть класса.
Из рисунка видно, что в классе из 15 учеников треть класса составляют 5 мальчиков.
Если мы найдем из 15 учеников, которых нужно проверить, мы получим 5 мальчиков
15 : 3 = 5
5 × 1 = 5
Пример 5. Во сколько раз 35 больше числа
?Напишите отношение числа 35 к числу 5. Запишите число 35 в числителе и число 5 в знаменателе, но не наоборот.
Значение этого отношения равно 7. Таким образом, число 35 в семь раз больше , чем число 5.
Пример 6. В классе 15 человек. Из них 5 мальчиков и 10 девочек. Определите, какую часть от общего числа составляют девочки.
Запишите соотношение девушек к общему количеству учащихся. Запишите в числителе коэффициента десять девочек, а в знаменателе — общее количество студентов. Общее количество учеников 5 мальчиков плюс 10 девочек, поэтому запишем 15 в знаменателе отношения
Чтобы найти значение этого отношения, нужно вспомнить, как делить меньшее число на большее. В этом случае число 10 нужно разделить на число 15
Деление 10 на 15 дает периодическую дробь. Преобразуем эту дробь в обыкновенную
Уменьшим полученную дробь на 3
Окончательный ответ . Итак, девочки составляют две трети класса.
Из рисунка видно, что в классе из 15 учеников две трети класса составляют 10 девочек.
Если мы найдем 15 школьников для проверки, мы получим 10 девочек
15 : 3 = 5
5 × 2 = 10
Пример 7. Какая часть 25 сантиметров равна 10 сантиметрам?
Какая часть 25 сантиметров равна 10 сантиметрам?
Запишите отношение десяти сантиметров к двадцати пяти сантиметрам. Запишите в числителе 10 см, а в знаменателе 25 см
Чтобы найти значение этого отношения, нужно вспомнить, как делить меньшее число на большее. В этом случае нам нужно число 10 разделить на число 25
Преобразовать полученную десятичную дробь в обыкновенную дробь
Уменьшим полученную дробь на 2
Получили окончательный ответ . Значит 10 см это 25 см.
Пример 8. Во сколько раз 25 см больше 10 см
Запишите отношение двадцати пяти сантиметров к десяти сантиметрам. Запишем 25 см в числителе и 10 см в знаменателе
Найдем значение этого отношения
Ответ 2,5. Итак, 25 см в 2,5 раза больше 10 см (в два с половиной раза).
Важное примечание. При нахождении соотношения одноименных физических величин эти величины должны быть выражены в одной и той же единице измерения , иначе ответ будет неверным.
Например, если мы имеем дело с двумя длинами и хотим узнать, во сколько раз первая длина больше второй, то сначала обе длины должны быть выражены в одной единице (км, м, мили).
Пример 9. Во сколько раз 150 см больше 1 метра?
Во-первых, давайте выразим обе длины в одной единице. Для этого переведем 1 метр в сантиметры. Один метр — это сто сантиметров.
1 м = 100 см
Теперь найдем отношение ста пятидесяти сантиметров к ста сантиметрам. Запишем в числителе 150 сантиметров, а в знаменателе 100 сантиметров
Найдем значение этого отношения
Ответ: 1,5. Значит 150 см в 1,5 раза больше 100 см (в полтора раза).
А если бы мы не переводили метры в сантиметры, а сразу попытались найти отношение 150 см к одному метру, то мы бы имели следующее:
Получилось бы, что 150 см в сто пятьдесят раз больше более одного метра, и это неправильно. Поэтому необходимо обратить внимание на единицы физических величин, которые участвуют в соотношении. Если эти величины выражены в разных единицах, то для того, чтобы найти отношение этих величин, необходимо перейти к одной единице измерения.
Если эти величины выражены в разных единицах, то для того, чтобы найти отношение этих величин, необходимо перейти к одной единице измерения.
Пример 10. В прошлом месяце зарплата директора банка составляла 25 000 долларов, а в этом месяце зарплата увеличилась до 27 000 долларов. Определите, во сколько раз новая заработная плата больше старой.
Запишите соотношение двадцать семь тысяч к двадцати пяти тысячам. Запишем 27000 в числителе и 25000 в знаменателе
Найдем значение этого отношения
Ответ был 1,08. Это означает, что заработная плата увеличилась на 1,08. В дальнейшем, когда мы познакомимся с процентами, такие показатели, как заработная плата, будем выражать в процентах.
Пример 11. Жилой дом имеет ширину 80 метров и высоту 16 метров. Каково соотношение между шириной дома и его высотой?
Запишите отношение ширины дома к его высоте:
Значение этого отношения равно 5. Значит, ширина дома в пять раз больше его высоты.
Значит, ширина дома в пять раз больше его высоты.
Свойства из Отношение
- Отношение остается неизменным, если его члены умножаются или делятся на одно и то же ненулевое число ,
- a/b = pa/pb = qa/qb , p, q ≠0
- a/b = (a/p) / (b/p) = (a/q) / (b/q) , p, q ≠0
- Два отношения в представлении дробей можно сравнивать так же, как мы сравниваем действительные числа .
- a/b = p/q ⟺ aq = bp
- a/b > p/q ⟺ aq > bp
- a/b < p/q ⟺ aq < bp
- Если два отношения a/b и c/d равны
- a/b = c/d ⟹ b/a = d/c (Invertendo)
- a/b = c/d ⟹ a/c = b/d (Альтернэндо)
- a/b = c/d ⟹ (a+b)/b = (c+d)/d (Componendo)
- a/b = c/d ⟹ (a-b)/b = (c-d)/d (дивидендо)
- Отношение остается неизменным, если его члены умножаются или делятся на одно и то же ненулевое число ,
Отношение не изменится, если его члены умножить или разделить на одно и то же число.
Это одно из наиболее важных свойств следующего соотношения. Мы знаем, что если частное и делитель умножить или разделить на одно и то же число, то частное не изменится. А так как отношение есть не что иное, как деление, то свойство частного работает и на него.
Вернемся к соотношению девочек и мальчиков (10 : 5). Это соотношение показывает, что на каждого мальчика приходится две девочки. Проверим, как работает свойство отношения, а именно попробуем умножить или разделить его члены на одно и то же число.
В нашем примере удобнее делить члены отношения на их наибольший общий делитель (НОД).
НОД членов 10 и 5 равен числу 5. Следовательно, можно разделить члены отношения на число 5
У нас есть новый коэффициент . Это соотношение два к одному (2:1). Это соотношение, как и предыдущее соотношение 10:5, показывает, что на каждого мальчика приходится две девочки.
На рисунке показано соотношение 2 : 1 (два к одному). Как и в прошлом соотношении 10:5, на одного мальчика приходится две девочки. Другими словами, соотношение не изменилось.
Как и в прошлом соотношении 10:5, на одного мальчика приходится две девочки. Другими словами, соотношение не изменилось.
Пример 2. В одном классе 10 девочек и 5 мальчиков. В другом классе 20 девочек и 10 мальчиков. Во сколько раз девочек в первом классе больше, чем мальчиков? Во сколько раз девочек во втором классе больше, чем мальчиков?
В обоих классах девочек в два раза больше, чем мальчиков, потому что отношения и равны .
Свойство ratio позволяет создавать разные модели, имеющие параметры, схожие с реальным объектом. Предположим, что многоквартирный дом имеет ширину 30 м и высоту 10 м.
Чтобы нарисовать подобный дом на бумаге, нужно нарисовать его в том же соотношении 30 : 10.
Разделим оба члена этого соотношения на число 10. Тогда получим соотношение 3 : 1. Это отношение равно 3, как и предыдущее отношение равно 3
Переведем метры в сантиметры. 3 метра это 300 сантиметров, а 1 метр это 100 сантиметров.
3 м = 300 см
1 м = 100 см
Соотношение 300 см : 100 см. Разделим слагаемое этого соотношения на 100. Получится соотношение 3 см : 1 см. Теперь мы можем нарисовать дом шириной 3 см и высотой 1 см.
Конечно, нарисованный дом намного меньше реального дома, но соотношение ширины и высоты остается прежним. Это позволило нам нарисовать дом максимально похожим на настоящий дом
Отношение можно понимать и по-другому. Изначально было сказано, что настоящий дом имеет ширину 30 метров и высоту 10 метров. Итого 30+10, то есть 40 метров.
Эти 40 метров можно представить как 40 частей. Соотношение 30 : 10 означает, что 30 частей относятся к ширине и 10 частей к высоте.
Затем члены соотношения 30 : 10 поделили на 10. Получилось соотношение 3 : 1. Это соотношение можно понимать как 4 части, три из которых — ширина, а одна — высота. В этом случае обычно требуется знать, сколько конкретных метров приходится на ширину и высоту.
Другими словами, нужно узнать, сколько метров в 3 частях и сколько метров в 1 части. Для начала нужно узнать, сколько метров приходится на одну деталь. Для этого разделите сумму 40 метров на 4, так как в соотношении 3 : 1 всего четыре части
40 м : 4 = 10 м
Затем с помощью умножения определите, сколько метров приходится на ширину и высоту . В качестве коэффициента используются условия, которые приведены в соотношении.
Определить, сколько метров приходится на ширину:
10 м × 3 = 30 м
Определим, сколько метров приходится на высоту:
10 м × 1 = 10 м
Несколько членов в соотношении
Если в соотношении дано более одного члена , их можно понимать как части чего-то.
Пример 1. Купили 18 яблок. Яблоки раздали маме, папе и дочке в соотношении 2 : 1 : 3. Сколько яблок получил каждый?
Соотношение 2 : 1 : 3 означает, что мама получила 2 части, папа – 1 часть, а дочь – 3 части. Другими словами, каждый член соотношения 2 : 1 : 3 представляет собой определенную долю 18 яблок:
Другими словами, каждый член соотношения 2 : 1 : 3 представляет собой определенную долю 18 яблок:
Если сложить члены отношения 2 : 1 : 3, то можно узнать, сколько всего частей:
2 + 1 + 3 = 6 (частей)
Давайте узнаем, сколько яблок на одну часть. Для этого 18 яблок разделим на 6
18 : 6 = 3 (яблоки на одну часть)
Теперь определим, сколько яблок получил каждый человек. Умножив три яблока на каждого члена соотношения 2 : 1 : 3, можно определить, сколько яблок досталось маме, сколько яблок досталось папе и сколько яблок досталось дочери.
Посмотрим, сколько яблок получила мама:
3 × 2 = 6 (яблок)
Посмотрим, сколько яблок получил папа:
3 × 1 = 3 (яблок)
Посмотрим, сколько яблок Дочь получила:
3 × 3 = 9 (яблоки)
Пример 2. Новое серебро (альпака) — сплав никеля, цинка и меди в соотношении 3 : 4 : 13. Сколько килограммов каждый металл должен быть взят, чтобы сделать 4 кг нового серебра?
4 килограмма нового серебра будут содержать 3 части никеля, 4 части цинка и 13 частей меди. Сначала узнаем общее количество частей в четырех килограммах серебра:
Сначала узнаем общее количество частей в четырех килограммах серебра:
3 + 4 + 13 = 20 (деталей)
Определим, сколько килограммов будет в одной части:
4 кг : 20 = 0,2 кг
Определим, сколько килограммов никеля будет содержаться в 4 кг новой Серебряный. Соотношение 3 : 4 : 13 указывает на то, что три части сплава содержат никель. Поэтому умножаем 0,2 на 3:
0,2 кг × 3 = 0,6 кг никеля
Теперь определим, сколько килограммов цинка будет содержаться в 4 кг нового серебра. Соотношение 3 : 4 : 13 указывает на то, что четыре части сплава содержат цинк. Поэтому умножаем 0,2 на 4:
0,2 кг × 4 = 0,8 кг цинка
Теперь определим, сколько килограммов меди будет содержаться в 4 килограммах нового серебра. Соотношение 3 : 4 : 13 говорит о том, что тринадцать частей сплава содержат медь. Поэтому умножаем 0,2 на 13:
0,2 кг × 13 = 2,6 кг меди
Итак, чтобы получить 4 кг нового серебра, нужно взять 0,6 кг никеля, 0,8 кг цинка и 2,6 кг меди.
Пример 3. Латунь представляет собой сплав меди и цинка, масса которого составляет 3 : 2. Для изготовления куска латуни требуется 120 г меди. Сколько цинка требуется для изготовления этого куска латуни?
Определить, сколько граммов сплава содержится в изделии. В условии сказано, что для изготовления куска латуни требуется 120 граммов меди. Там же сказано, что три части сплава содержат медь. Если 120 разделить на 3, то узнаем, сколько граммов сплава в одной детали:
120 : 3 = 40 грамм на деталь
Теперь определим, сколько цинка нужно для изготовления куска латуни. Для этого умножьте 40 граммов на 2, так как соотношение 3 : 2 указывает на то, что две части содержат цинк:
40 г × 2 = 80 г цинка
Пример 4. Берут два сплава золота и серебра. В одном из них соотношение этих металлов 1:9, а в другом 2:3. Сколько нужно взять каждого сплава, чтобы получить 15 кг нового сплава, содержащего золото и серебро в соотношении 1:4?
Раствор
15 кг нового сплава должны состоять из соотношения 1 : 4. Это соотношение указывает на то, что одна часть сплава будет состоять из золота, а четыре части из серебра. Всего пять частей. Схематически это можно представить следующим образом
Это соотношение указывает на то, что одна часть сплава будет состоять из золота, а четыре части из серебра. Всего пять частей. Схематически это можно представить следующим образом
Определим массу одной детали. Для этого сначала сложите все части (1 и 4), затем разделите массу сплава на количество этих частей
1 + 4 = 5
15 кг : 5 = 3 кг
Одна часть сплав будет иметь массу 3 кг. Тогда 15 кг нового сплава будут содержать 3 × 1 = 3 кг золота и 3 × 4 = 12 кг серебра.
Следовательно, нам потребуется 3 кг золота и 12 кг серебра для получения сплава массой 15 кг.
Теперь ответим на вопрос задачи — « Сколько нужно взять каждого сплава? »
Возьмем 10 кг первого сплава, так как золото и серебро в нем находятся в соотношении 1 : 9. То есть этот первый сплав даст нам 1 кг золота и 9 кг серебра.
Для второго сплава возьмем 5 кг, так как золото и серебро находятся в соотношении 2 : 3. Таким образом, этот второй сплав даст нам 2 кг золота и 3 кг серебра
Видео урок
youtube.com/embed/LLNaxctU8JE» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Соотношение и пропорция
План математических исследований состоит в том, чтобы прийти к познанию конкретных величин путем сравнения их с другими величинами, либо равными , либо большими , либо меньшими , чем те, которые являются объектами исследования. Конец чаще всего достигается с помощью ряда уравнений и пропорций . Пользуясь уравнениями, мы определяем искомую величину, находя ее равенство с некоторым другим количеством или количествами, которые уже известны.
Однако нам часто приходится сравнивать неизвестную величину с другими, которые не равны ей, а больше или меньше. Здесь необходим другой способ действий. Мы можем исследовать, либо насколько одна из величин больше другой; или сколько раз одно содержит другое. Находя ответ на любой из этих вопросов, мы обнаруживаем то, что называется соотношение двух величин. Один называется арифметическим , а другой геометрическим отношением. Следует, однако, заметить, что оба эти термина были приняты произвольно, просто для различия. И арифметическое соотношение, и геометрическое соотношение применимы к арифметике и оба к геометрии.
Находя ответ на любой из этих вопросов, мы обнаруживаем то, что называется соотношение двух величин. Один называется арифметическим , а другой геометрическим отношением. Следует, однако, заметить, что оба эти термина были приняты произвольно, просто для различия. И арифметическое соотношение, и геометрическое соотношение применимы к арифметике и оба к геометрии.
Поскольку весь обширный и важный вопрос о пропорциях зависит от соотношений, необходимо, чтобы они были ясно и полностью поняты.
338. Арифметическое отношение есть разность между двумя величинами или наборами величин . Сами количества называются членами отношения, то есть членами, между которыми существует отношение. Таким образом, 2 есть арифметическое отношение 5 к 3. Это выражается посредством помещения минуса между величинами, таким образом, 5 — 3. Действительно, термин арифметическое отношение и его обозначение точками почти не нужны. Ибо единица является лишь заменой слова разница и другой для знака -.
Ибо единица является лишь заменой слова разница и другой для знака -.
339. Если оба члена арифметического отношения равны , умноженному на , или , разделенному на на одну и ту же величину, то отношение на будет фактически умножено или разделено на эту величину.
Таким образом, если a — b = r
Затем умножьте обе стороны на A, (Ax. 3.) ha — hb = hr
И деля на A, (Ax. 4.) $\frac{a}{h}-\frac{b}{h}=\frac{r}{h}$
340. Если члены одного арифметического отношения прибавить или вычесть из них соответствующие члены другого отношения, то отношение их суммы или разности будет равно сумме или разности двух отношений.
Если а — б
И д — ч,
— это два соотношения,
Тогда (а + d) — (b + h) = (a — b) + (d — h). Foreach = a + d — b — h.
А (а — г) — (б — з) = (а — б) — (г — з). Для каждого = a — d — b + h.
Таким образом, ариф. соотношение 11 — 4 равно 7
И арифм. соотношение 5 — 2 равно 3
Отношение суммы членов 16 — 6 равно 10, сумма отношений.
Отношение разности слагаемых 6 — 2 равно 4, разности соотношений.
341. Геометрический коэффициент есть такое отношение между величинами, которое выражается ЧАСТНЫМ , если одно разделить на другое.
Таким образом, отношение 8 к 4 равно 8/4 или 2. Ибо это есть частное 8, деленное на 4. Другими словами, оно показывает, как часто 4 содержится в 8.
Таким же образом можно выразить отношение любой величины к другой, разделив первую на вторую или, что то же самое, сделав первую числителем дроби, а вторую знаменателем.
Таким образом, отношение a к b равно $\frac{a}{b}$
Отношение d + h к b + c равно $\frac{d+h}{b+c}$.
342. Геометрическое отношение также выражается размещением двух точек, одной над другой, между сравниваемыми величинами,
Таким образом, a:b выражает отношение a к b; и 12:4 отношение 12 к 4. Две величины вместе называются парой , первый член которой антецедент , а последний член консеквент .
343. Это обозначение точками, а другое в виде дроби может быть заменено одно на другое, как того требует удобство; наблюдая, чтобы сделать антецедент куплета, числитель дроби, а следствие знаменатель.
Таким образом, 10:5 совпадает с $\frac{10}{5}$, а b:d совпадает с $\frac{b}{d}$.
344. Из этих трех, антецедента, следствия и отношения, если даны любые два , можно найти другое.
Пусть a = антецедент, c = следствие, r = отношение.
По определению $r=\frac{a}{c}$; то есть отношение равно антецеденту, деленному на консеквент.
Умножение на c, a = cr, то есть антецедент равен консеквенту, умноженному на отношение.
Деление на $r$, $c=\frac{a}{r}$, то есть консеквент равен антецеденту, деленному на отношение.
Кор. 1. Если два куплета имеют одинаковые антецеденты и равные консеквенты, их отношения должны быть равны.
Кор. 2. Если в двух куплетах отношения равны и предшествующие равны, то и последующие равны; и если отношения равны и следствия равны, то равны и антецеденты.
345. Если две сравниваемые величины равны , то отношение есть единица, или отношение равенства. Отношение 3,6:18 есть единица, ибо частное любого количества, деленного само на себя, равно 1.
Если антецедент куплета на 90 435 больше, чем консеквент, на 90 438, отношение больше единицы. Ведь если делимое больше своего делителя, то частное больше единицы. Таким образом, соотношение 18:6 равно 3. Это называется соотношением 9.0435 большее неравенство .
С другой стороны, если антецедент на 90 435 меньше 90 438, чем последующий, то отношение меньше единицы и называется отношением 90 435 за вычетом неравенства 90 438 . Таким образом, отношение 2:3 меньше единицы, потому что делимое меньше делителя.
346. Обратное или обратное отношение есть отношение обратных величин двух величин.
Таким образом, обратное отношение 6 к 3 составляет ⅙ на ⅓, то есть ⅙:⅓.
Прямое отношение $a$ к $b$ равно $\frac{a}{b}$, то есть антецедент делится на консеквент.
Обратное отношение равно $\frac{1}{a}:\frac{1}{b}$ или $\frac{1}{a}.\frac{b}{1}=\frac{b}{ а}$.
что т.е. консеквент b делится на антецедент a.
Следовательно, обратное отношение выражается как 90 435, инвертируя дробь 90 438, которая выражает прямое отношение; или, когда обозначение точками, инвертирует порядок терминов .
Таким образом, а относится к b в обратном порядке, как b к а.
347. Составное отношение — это отношение произведений соответствующих членов двух или более простых отношений.
Таким образом, соотношение 6:3 равно 2
И соотношение 12:4 равно 3
Соотношение, составленное из них, равно 72:12 = 6.
Здесь сложное отношение получается путем умножения двух предшествующих, а также двух последующих простых отношений.
Итак, отношение усугубилось,
Из отношения a:b
И отношение c:d
И отношение h:y
Является отношением $ach:bdy=\frac{ach}{bdy}$.
Составное соотношение по своей природе не отличается от любого другого отношения. Этот термин используется для обозначения происхождения соотношения в конкретных случаях.
Кор. Сложное отношение равно произведению простых отношений.
Отношение $a:b$ равно $\frac{a}{b}$
Отношение $c:d$ равно $\frac{c}{d}$
Отношение $h:y$ равно $\frac{h}{y}$
И отношение, составленное из них, равно ach/bdy, которое является произведением дробей, выражающих простые отношения.
348. Если в ряду соотношений следствие каждого предшествующего двустиший является антецедентом следующего, отношение первого антецедента к последнему последующему равно тому, что составлено из всех промежуточных соотношений.
Таким образом, в ряду соотношений
а:б
б:с
c:d
д:ч
отношение a:h равно тому, что составлено из отношений a:b, b:c, c:d, d:h. Для сложного соотношения по последней статье $\frac{abcd}{bcdh}=\frac{a}{h}$, или a:h.
Для сложного соотношения по последней статье $\frac{abcd}{bcdh}=\frac{a}{h}$, или a:h.
Таким же образом все количества, которые являются как антецедентами, так и консеквентами, исчезнут , когда дробное произведение будет сведено к самому низкому члену, и останется сложное отношение, выражаемое первым антецедентом и последним консеквентом.
349. Особый класс составных отношений получается путем умножения простого отношения на само или на другое отношение , равное . Они называются дубликатов , тройных , четверных повторов и т. д. в зависимости от количества умножений.
Отношение, составленное из 90 435 двух равных 90 438, то есть 90 435 в квадрате 90 438 простого отношения, называется отношением 90 435 дубликатов 90 438.
Один составленный из три , то есть куб простого отношения, называется тройным и т. д.
Аналогичным образом, отношение квадратных корней двух величин называется отношением субдупликатов ; отношение кубических корней субтройных и т. д.
д.
Таким образом, простое отношение a к b равно a:b
Двойное отношение a к b равно a:b 2
Тройное отношение a к b равно a 3 :b 3
Соотношение субдубликатов a к b равно √a:√b
Подтройное число от a до b равно 3 √a: 3 √b и т. д.
Термины двойное , тройное и т. д. не следует смешивать с двойным , тройным и т. д.
Отношение 6 к 2 равно 6:2 = 3
Удвоить это соотношение, то есть удвоить соотношение, 12:2 = 6
Утроить соотношение, т. е. утроить соотношение, 18:2 = 9.
Но отношение дубликатов , то есть в квадрате отношения, равно 6 2 :2 2 = 9
И тройное отношение , т.е. куб отношения равен 6 3 :2 3 = 27
350. Чтобы количества могли иметь отношение друг к другу, необходимо, чтобы они были настолько одной и той же природы, чтобы можно было в собственном смысле сказать, что одно из них либо равно, либо больше, либо меньше другого. Фут имеет отношение к дюйму, ибо один в двенадцать раз больше другого. Но нельзя сказать, что час короче или длиннее жезла; или что акр больше или меньше градуса. Тем не менее, если эти количества выражены через числа , между числами может быть соотношение. Существует соотношение между количеством минут в часе и количеством стержней в миле.
Фут имеет отношение к дюйму, ибо один в двенадцать раз больше другого. Но нельзя сказать, что час короче или длиннее жезла; или что акр больше или меньше градуса. Тем не менее, если эти количества выражены через числа , между числами может быть соотношение. Существует соотношение между количеством минут в часе и количеством стержней в миле.
351. Обратив внимание на природу отношений, мы должны затем рассмотреть, каким образом на них будет воздействовать изменение одного или обоих членов, между которыми производится сравнение. Следует иметь в виду, что, когда прямое отношение выражается дробью, антецедент пары всегда является числитель , а следствие знаменатель . Тогда будет легко вывести из свойств дробей изменения в отношениях, вызванные вариациями сравниваемых величин. Ибо отношение двух величин такое же, как значение дробей, каждая из которых представляет собой частное числителя, деленное на знаменатель. (Статья 341.) Теперь было показано, что умножение числителя дроби на любую величину есть умножение значение по этому количеству; и что деление числителя равно делению значения. Следовательно,
(Статья 341.) Теперь было показано, что умножение числителя дроби на любую величину есть умножение значение по этому количеству; и что деление числителя равно делению значения. Следовательно,
352. Умножение антецедента куплета на любую величину есть умножение отношения на эту величину; а деление антецедента равно делению отношения .
Таким образом, отношение 6:2 равно 3
И отношение 24:2 равно 12.
Здесь антецедент и отношение в последнем двустишии каждое в четыре раза больше, чем в первом.
Отношение $a:b$ равно $\frac{a}{b}$
И отношение $na:b$ равно $\frac{na}{b}$.
Кор. С данным следствием, чем больше антецедент , тем больше отношение ; а с другой стороны, чем больше отношение, тем больше антецедент.
353. Умножение следствия двустишия на любую величину в действительности равносильно делению отношения на эту величину; а деление консеквента равно умножению отношения . Для умножения знаменателя дроби деление значения ; и деление знаменателя умножает значение.
Для умножения знаменателя дроби деление значения ; и деление знаменателя умножает значение.
Таким образом, соотношение 12:2 равно 6
А соотношение 12:4 равно 3.
Здесь консеквент во втором двустишии вдвое больше , а отношение только вдвое меньше , чем в первом.
Отношение $a:b$ равно $\frac{a}{b}$
И отношение $a:nb$ равно $\frac{a}{nb}$.
Кор. При данном антецеденте, чем больше следствие, тем меньше отношение; и чем больше отношение, тем меньше следствие.
354. Из двух последних статей видно, что умножение предшественника двустишия на любую величину будет иметь тот же эффект на отношение, что и деление последующего на эту величину; и , разделяющее предшествующее , будет иметь тот же эффект, что и , умноженное на последующее .
Таким образом, отношение 8:4 равно 2
Множ. антецедент на 2, соотношение 16:4, равно 4
Дел. следствие на 2, отношение 8:2, равно 4.
следствие на 2, отношение 8:2, равно 4.
Кор. Любой фактор или делитель может быть перенесен из антецедента двустиший в консеквент или из консеквента в антецедент без изменения соотношения.
Следует заметить, что когда множитель таким образом переносится с одного члена на другой, он становится делителем; и когда делитель переносится, он становится множителем.
Таким образом, отношение $3\cdot 6:9 = 2$
Перенос коэффициента 3, $6:\frac{9}{3}=2$
такое же соотношение.
Отношение $\frac{ma}{y}:b=\frac{ma}{by}$
Перенос $y$ $ma:by=\frac{ma}{by}$
Передача $m$, $a$ равно $a:\frac{m}{by}=\frac{ma}{by}$.
355. Более того, из ст. 352 и 353, что если антецедент и консеквент оба умножаются или оба делятся на одно и то же количество, отношение не изменится .
Кор. 1. Отношение двух дробей , имеющих общий знаменатель, равно отношению их числителей .
Таким образом, соотношение a/n:b/n такое же, как и соотношение a:b.
Кор. 2. Прямое отношение двух дробей, имеющих общий числитель, равно обратному отношению их знаменателей .
356. Из последней статьи несложно будет определить соотношение любых двух дробей. Если каждый член умножить на два знаменателя, отношение будет присвоено в интегральных выражениях. Таким образом, умножая члены пары a/b:c/d на bd, мы получаем $\frac{abd}{b}:\frac{bcd}{d}$, который превращается в ad:bc путем сокращения равных величин из числители и знаменатели.
356. б. Соотношение большее неравенство , соединенное с другим соотношением увеличивает оно
Пусть отношение большего неравенства будет отношением 1+n:1
И любое заданное отношение a:b
Составное из них соотношение (Статья 347) равно a + na:b
Что больше, чем у a:b (ст. 351. кор.)
Но отношение меньшего неравенства , соединенного с другим отношением, уменьшает его.
Пусть отношение меньшего неравенства равно 1-n:1
И любое заданное отношение, отношение a:b
Соотношение, составленное из них, равно a — na:b
Что меньше, чем у a:b.
357. Если к или из членов какого-либо двустишия прибавить или вычесть две другие величины, имеющие такое же отношение, суммы или остатки также будут иметь такое же отношение .
Пусть отношение a:b
Такой же, как у c:d
Тогда соотношение сумма антецедентов к сумме следствий, а именно. от a + c до b + d тоже самое.
Это $\frac{a+c}{b+d} = \frac{c}{d} = \frac{a}{b}$.
Демонстрация.
1. По условию $\frac{a}{b} = \frac{c}{d}$
2. Умножение на b и d, $ad = bc$
3. Добавление cd к обеим сторонам, $ad + cd = bc + cd$
4. Деление на d, $a+c=\frac{bc+cd}{d}$
5. Деление на b + d, $\frac{a+c}{b+d} = \frac{c}{d} = \frac{a}{b}$.
Отношение 90 435 различия 90 438 антецедентов к различию следствий также одинаково.
358. Если в нескольких двустишиях отношения равны, сумма всех антецедентов имеет такое же отношение к сумме всех последующих, какое имеет любой из антецедентов к своему консеквенту.
Таким образом, соотношение
|12:6 = 2
|10:5 = 2
|8:4 = 2
|6:3 = 2
Следовательно, соотношение (12 + 10 + 8 + 6): (6 + 5 + 4 + 3) = 2.
92+ab+ax}{a(a+x)}$.
Поскольку последний числитель явно меньше другого, отношение должно быть меньше. (Статья 351. кор.)
Но отношение 90 435 меньшего неравенства 90 438 равно 90 435, увеличенному 90 438, путем прибавления одного и того же количества к обоим условиям.
Пусть данное отношение равно отношению (a-b):a или $\frac{a-b}{a}$.
Если добавить x к обоим терминам, получится (a-b+x):(a+x) или $\frac{a-b+x}{a+x}$
Приведение их к общему знаменателю,
Первый становится $\frac{a^2-ab+ax-bx}{a(a+x)}$
92-ab+ax)}{a(a+x)}$.
Поскольку последний числитель больше другого, отношение 90 435 больше, чем 90 438.
Если одно и то же количество вместо того, чтобы прибавлять, вычесть из обоих членов, очевидно, что влияние на отношение должно быть обратным.
Примеры.
1. Что больше, соотношение 11:9 или 44:35?
2. Что больше: отношение $(a+3):\frac{a}{6}$ или отношение $(2a+7):\frac{a}{3}$?
3. Если антецедент двустишия равен 65, а отношение 13, то какой консеквент?
4. Если следствие двустишие равно 7, а отношение 18, что такое антецедент.
5. Какое отношение составляет соотношение 8:7, 2а:5б и (7х+1):(3у-2)?
6. Каково отношение, составленное из (x+y):b и (x-y):(a + b) и (a+b):h? Ответ (x 2 — y 2 ):bh.
7. Если сложить отношения (5x+7):(2x-3) и $(x+2):\left(\frac{x}{2}+3\right)$, получится ли отношение большего неравенства или меньшего неравенства? Ответ Коэффициент большего неравенства. 92}{а}$? Ответ Соотношение равенства.
92}{а}$? Ответ Соотношение равенства.
9. Что такое соотношение, составляющее 7:5, и двойное соотношение 4:9, и тройное соотношение 3:2?
Ответ. 14:15.
10. Что представляет собой соотношение, составленное из 3:7, тройного соотношения x:y и соотношения субдубликатов 49:9?
Ответ. х 3 :у 3 .
Определение, обозначения, шкала и формула |
Много раз, когда нам дают свою долю шоколада или печенья, мы хотим знать, как они были разделены между нами, нашими братьями, сестрами или друзьями.
Концепция соотношения , которая будет обсуждаться здесь, поможет вам определить это в дальнейшем.
Определение рациона
Отношение — это сравнение двух или более величин, показывающее взаимосвязь в их различных размерах. Он говорит нам, какую часть количества можно найти в другом количестве.
Соотношения показывают нам взаимосвязь между количествами, и это важно, когда вещи должны быть разделены или разделены среди группы.
Соотношения могут быть выражены в их простейшей форме или упрощены, когда они делятся на самые высокие общие множители.
Следует отметить, что сравнение отношений может быть между количествами в отдельности в целом или, возможно, между частью целого и его целым. Это будет объяснено в дальнейшем.
Обозначение отношения
Обозначение отношения говорит нам о различных способах представления или выражения отношений. Существует три обозначения соотношения: числовое обозначение, словесное обозначение и дробное обозначение.
Числовая запись
Числовая запись возникает, когда отношения выражаются с помощью записи чисел и двоеточия ( : ) между цифрами или косой чертой ( / ).
Например,
Обозначение слова
Обозначение слова возникает, когда слово «is to» используется для обозначения пайков.
Например,
3 равно 4
5 равно 6 равно 1
2 равно 7
7 равно 2 равно 11 равно 15.
Обозначение дробей
Например,
Формула отношения
Формула отношения — это выражение, используемое при расчете отношений. Общий принцип действия ведущего отношения и его формула деление . Ранее мы упоминали, что отношения могут быть либо в качестве отношения между целыми количествами, либо между частью целого и его целым . Это фактически определяет вид формулы, которая будет применяться.
Отношение двух целых величин
Чтобы найти отношение между двумя целыми величинами , мы применяем частное между первой и второй величинами. Это означает, что первая величина делится на вторую величину.
Первая величина известна как антецедент , а вторая называется консеквент . Итак, если первое количество равно m, а второе количество равно n, то
Хендерсону и Робинсону дали по 5 и 7 апельсинов соответственно, найдите соотношение апельсинов между Хендерсоном и Робисоном.
Решение
У Хендерсона 5 апельсинов, а у Робинсона 7 апельсинов.
Следовательно, отношение апельсинов между Хендерсоном и Робинсоном равно
Отношение между частью и целым
Чтобы найти отношение между частью и целым , мы применяем частное между частью и целым целый . Обратите внимание, что иногда могут быть указаны общие количества, в других случаях нам нужно будет вычислить их, найдя сумму частей.
Например, если m является частью t, где t является целым или суммой количеств, отношение m к t равно,
Между тем, отношение m к сумме количеств m, n и o,
, где m + n + o — общее количество величин.
Из 6 пачек конфет в коробке Дойлу досталось 5. Каково отношение доли Дойла к конфетам в коробке?
Решение
Всего пачек конфет в коробке 6, а доля конфет Дойла 5.
Следовательно, отношение доли Дойла к конфетам в коробке равно
В мешочке 3 черных шара, 2 красные шары и 7 белых шаров. Каково соотношение белых шаров ко всем шарам в мешке?
Каково соотношение белых шаров ко всем шарам в мешке?
Решение
Сначала мы определяем, какой коэффициент мы вычисляем. В данном случае это соотношение белых шаров ко всем шарам.
Далее нам говорят, что в мешке 7 белых шаров.
Далее находим общее количество шаров в мешке,
Теперь, найдя их значения, выражаем их в соотношении,
.
Шкала отношений
Шкала отношений позволяет получить эквивалентные отношения при умножении или делении констант.
Сохраняя то же соотношение, мы можем увеличивать или уменьшать размеры геометрических фигур.
На приведенном ниже рисунке длина прямоугольника равна 4 единицам, а ширина — 2 единицам, таким образом,
Теперь обратите внимание, что размеры того же прямоугольника увеличивались и уменьшались по отношению к двум другим прямоугольникам рядом с ним: здесь мы применили соответствующее масштабирование к исходному прямоугольнику.
Иллюстрация масштабирования отношений — StudySmarter Originals
Существует два типа масштабирования: масштабирование u p и уменьшение масштаба .
Увеличение масштаба
Мы увеличиваем отношение, умножая антецедент и следствие на одно и то же число с, где с больше 1.
Когда это происходит, мы говорим, что отношение увеличилось на . Число c также известно как масштабный коэффициент или множитель .
Иллюстрация масштабирования отношения — StudySmarter Originals
На приведенной выше диаграмме размеры полученного прямоугольника умножаются на 2, отношения исходного прямоугольника и увеличенного прямоугольника эквивалентны.
Уменьшение масштаба
Мы уменьшаем отношение, разделив антецедент и следствие на одно и то же число d, где d больше 1.
Когда это происходит, мы говорим, что отношение уменьшено на . Число d также известно как масштабный коэффициент или множитель .
Иллюстрация уменьшения отношения — StudySmarter Originals
На приведенной выше диаграмме размеры полученного прямоугольника делятся на 2, отношения исходного прямоугольника и уменьшенного прямоугольника эквивалентны.
Длина и ширина прямоугольного блока равны 9 см и 7 см соответственно. Каковы будут его новые размеры при увеличении в 5 раз?
Решение
Сначала найдем отношение длины к ширине. Таким образом,
Отношение увеличивается в 5 раз. Итак, умножаем отношение на 5;
Таким образом, новые размеры прямоугольного блока составляют 45 см (длина) и 35 см (ширина).
Соотношение и пропорция
Пропорция сравнивает и устанавливает отношения между двумя отношениями. Выражается знаком равенства ( = ) или двойное двоеточие (::).
Таким образом, для двух отношений a:b и c:d их пропорция определяется как
или
Типы пропорций
Мы различаем два типа пропорций: прямую пропорцию и косвенную пропорцию.
Прямая пропорция имеет место, когда увеличение количества приводит к увеличению другого связанного количества.
Обратная пропорция имеет место, когда увеличение количества приводит к уменьшению другого связанного количества.
Различия между соотношением и пропорцией
Соотношения отличаются от пропорций следующим образом.
1. Соотношения — это сравнения между количествами, а пропорции — это сравнения между отношениями.
2. Соотношения представляют собой выражения в форме
Однако пропорции представляют собой уравнения в форме
3. Соотношения представляются одним двоеточием (:) или косой чертой (/), а пропорции представляются с помощью двойное двоеточие (::) или знак равенства (=).
4. Соотношения упоминаются с помощью фразы «соответствует», тогда как пропорции определяются с помощью фразы «из».
Некоторые примеры, приведенные ниже, будут более подробно раскрывать взаимосвязь, а также различия в применении соотношения и пропорции.
Если 5 пар фирменной обуви стоят 120 фунтов стерлингов, сколько пар обуви той же марки купил бы Томас на 48 фунтов стерлингов?
Решение
Сначала мы определяем, какой тип пропорции у нас есть. Для этого ответим на вопрос: если количество обуви увеличится, придется ли нам платить больше или меньше?
Для этого ответим на вопрос: если количество обуви увеличится, придется ли нам платить больше или меньше?
Ваш ответ скажет вам, является ли это прямой или обратной пропорцией.
Ответ ДА. Конечно, больше обуви потребует больше денег, так что это прямая пропорция.
Следующее, что нужно сделать, это записать свои значения,
5 пар по 120 фунтов стерлингов
Затем присвоить букву неизвестному значению. Таким образом, пусть y представляет собой количество туфель, которые купил бы Томас. Таким образом, у нас есть y пар по £48.
Напомним, что соотношение выражается только количествами одной и той же единицы.
Следовательно, мы должны соединить количества, используя отношение и порядок, в котором количества упоминаются в вопросе,
5 пар к y парам
120 фунтов стерлингов к 48 фунтам стерлингов
Далее, помните, что пропорция — это уравнение отношений, таким образом, у нас есть
Затем мы преобразуем отношения в дроби и решим, чтобы получить
Теперь перемножим, чтобы получить
Таким образом, Томас может позволить себе только 2 пары обуви за 48 фунтов стерлингов.
12 рабочих расчищают определенный участок земли за 3 дня, сколько дней потребуется 4 рабочим, чтобы расчистить тот же участок?
Решение
Сначала мы определяем, какой тип пропорции у нас есть. Для этого ответим на вопрос:
Если количество рабочих уменьшится, потребуется ли меньше времени для расчистки того же участка?
Ваш ответ скажет вам, является ли это прямой или обратной пропорцией.
Ответ НЕТ. Конечно, чем меньше рабочих, тем больше времени уходит на расчистку участка, таким образом, это обратная пропорция.
Затем мы записываем наши значения:
12 рабочих за 3 дня
Теперь мы присваиваем неизвестному значению букву, поэтому пусть q представляет собой время, которое требуется 4 рабочим для выполнения работы. Таким образом, мы имеем
4 рабочих за q дней
Далее напомним, что отношение выражается только количествами одной и той же единицы. Таким образом, мы должны соединять величины, используя отношения, и в том порядке, в котором они были упомянуты в вопросе.
Однако, поскольку это обратная пропорция, нам пришлось бы поменять местами позиции в одной из величин. Это означает, что отношения находятся в другом направлении. Следовательно, мы имеем
12 рабочих на 4 рабочих
от q дней до 3 дней
Теперь запомните, что пропорция — это уравнение отношений. Следовательно,
Далее, мы преобразуем отношение в дробь, чтобы получить
Перекрестим умножим;
Следовательно, чтобы очистить этот участок земли, потребуется 4 рабочих за 9 дней.
Обратите внимание, что если бы это была прямая пропорция, то было бы 12 рабочих на 4 рабочих и 3 дня на q дней, оба сохраняют свой порядок или положение; но поскольку оно обратное, мы решили поменять местами второе соотношение (дни)
Примеры соотношений
Использование соотношений очень важно, поскольку они используются в нашей повседневной деятельности. Особенно, когда речь идет о дележе, а также об определении части или доли от целого количества. Ниже приведены некоторые примеры для дополнительной иллюстрации.
Ниже приведены некоторые примеры для дополнительной иллюстрации.
Мужчина делит свое состояние между тремя своими сыновьями Иаковом, Иоанном и Петром в соотношении 4:3:2. Если он стоит 90 000 фунтов стерлингов, сколько достается Джону?
Решение
Сначала найдем сумму отношения
Затем мы находим, какая часть богатства этого человека достается Джону. Это то же самое, что найти соотношение между стоимостью акций Джона и общей стоимостью акций;
Затем мы умножаем долю богатства человека, которая идет на присоединение, на стоимость этого человека,
Доля Джона составляет 27000 фунтов стерлингов.
В выпускном классе из 125 учеников 50 мальчиков. Каково соотношение мальчиков и девочек?
Решение
Поскольку известно количество мальчиков и общее количество учеников, мы должны найти количество девочек, равное 9.0003
Поскольку число девочек было подсчитано, теперь мы можем найти соотношение мальчиков и девочек как
. get
get
Соотношение — основные выводы
- Соотношение — это сравнение двух или более величин, показывающее отношения в их различных размерах. Он говорит нам, какую часть количества можно найти в другом количестве.
- Существует три обозначения соотношения: числовое, словесное и дробное.
- Формула соотношения — это выражение или уравнение, используемое при расчете соотношений.
- Масштабирование отношений — это увеличение или уменьшение отношений при их умножении или делении.
- Пропорция — это уравнение, которое сравнивает и определяет соотношение между двумя отношениями.
1.3: Тема C — Пропорции — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 101236
Пропорция — это утверждение о том, что два отношения равны или эквивалентны .
Вот некоторые пропорции:
| Пропорция | Форма дроби | Читать так… |
|---|---|---|
| \(1:2 = 2:4\) | \(\dfrac{1}{2} = \dfrac{2}{4}\) | 1 соответствует 2, как 2 соответствует 4 |
| \(1:4 = 25:100\) | \(\dfrac{1}{4} = \dfrac{25}{100}\) | 1 соответствует 4, как 25 соответствует 100 |
| \(18:9 = 10:5\) | \(\dfrac{18}{9} = \dfrac{10}{5}\) | 18 соответствует 9, как 10 соответствует 5 |
| \(15:20 = 3:4\) | \(\dfrac{15}{20} = \dfrac{3}{4}\) | 15 соответствует 20, как 3 соответствует 4 |
Пропорции можно использовать для решения многих математических задач. Вскоре вы научитесь использовать пропорции для решения задач, связанных с процентами. Техники, которые вы практикуете на следующих нескольких страницах, важны для работы по решению проблем.
Техники, которые вы практикуете на следующих нескольких страницах, важны для работы по решению проблем.
Проблемы часто дают неполную информацию; то есть один из терминов отсутствует. Чтобы решить такие задачи, вы сначала находите сравнение или соотношение, которое дано. Это может быть:
- Количество одного предмета, смешанного с большим количеством чего-то другого
- Шкала измерения, указанная на карте, например, 1 см на карте соответствует 100 км расстояния на суше
- Стоимость определенного количества предметов
- Время прохождения определенного расстояния
Тогда задача даст один член второго отношения пропорции. Например, если вам сказали, что 3 кочана салата стоят 1,49 доллара, вас могут попросить найти стоимость 7 кочанов салата.
Отсутствующий термин — вторая стоимость. Пропорция будет такой:
\(\dfrac{\text{количество кочанов салата}}{\text{стоимость}} = \dfrac{\text{количество кочанов салата}}{\text{стоимость}} \)
\(\dfrac{3}{$1. 49} = \dfrac{7}{?}\)
49} = \dfrac{7}{?}\)
\(3: $1.49 = 7: ?\)
Самое главное помнить, что порядок сравнения одинаков в первом и втором соотношениях в пропорции. Если первое отношение сравнивает время с расстоянием, то второе соотношение в пропорции должно сравнивать время с расстоянием.
\(\dfrac{время}{расстояние} = \dfrac{время}{расстояние}\)
Или это может быть:
\(\dfrac{расстояние}{время} = \dfrac{расстояние}{время }\)
После того, как вы определились с порядком сравнения, несложно написать пропорцию, используя числа, данные в задаче. Используйте букву для обозначения пропущенного термина.
Как бы вы нашли пропущенный термин?
- Вы можете использовать свои навыки с эквивалентными отношениями (нахождение более высоких и более низких членов)
- Вы можете использовать свои навыки дробного умножения, а затем деления, чтобы найти пропущенный член
Решение задачи на пропорции с использованием эквивалентных отношений
- Шаг 1
Определите порядок сравнения и запишите отношение, которое описывает информацию, приведенную в задаче. Напишите пропорцию, используя слова предметов, которые сравниваются в форме дроби.
Напишите пропорцию, используя слова предметов, которые сравниваются в форме дроби. - Шаг 2
Напишите еще два соотношения с числами, соответствующими словам в первом соотношении. Отсутствующий термин (число) можно обозначить буквой (пример N ). - Шаг 3
Мысленно отложите соотношение со словами (первое соотношение) в сторону. - Шаг 4
Умножьте или разделите полное отношение, чтобы найти пропущенный член. Пример A
Используйте 1 чайную ложку разрыхлителя на каждые 2 стакана муки. Если в рецепте используется 6 чашек муки, сколько потребуется разрыхлителя? Отсутствующий термин — чайные ложки разрыхлителя на 6 чашек муки. Назовите этот термин N . Соотношение: {\text{мука}} = \dfrac{1}{2} = \dfrac{N}{6}\)
Шаг 3
\(\dfrac{1}{2} = \dfrac{N }{6}\)
Шаг 4
\(\dfrac{1}{2} \times \left( \dfrac{3}{3} \right) = \dfrac{1 \times 3}{ 2 \times 3} = \dfrac{3}{6}\), поэтому \(\dfrac{1}{2} = \dfrac{3}{6}\), поэтому \(N = 3\)
Используйте 3 чайные ложки разрыхлителя на 6 чашек муки.

Упражнение 2
Используйте эквивалентные отношения, чтобы найти ответы.
A. Одна чашка сахара и четыре чашки воды – отличная еда для колибри. Сколько сахара нужно на 8 стаканов воды?
\(\dfrac{\text{сахар}}{\text{вода}} \rightarrow \dfrac{1}{4} = \dfrac{N}{8} \rightarrow \dfrac{1}{4} \ раз \влево( \dfrac{2}{2} \right) = \dfrac{1 \times 2}{4 \times 2} = \dfrac{2}{8} \rightarrow N=2\)
B. Отчеты показывают, что на каждые 100 автомобилей, проверенных полицией, 20 автомобилей не соответствуют стандартам безопасности. Если будет проверено всего 50 автомобилей, сколько из них не будут соответствовать стандарту безопасности?
C. Четыре литра краски покрывают 24 квадратных метра стены. Сколько краски нужно, чтобы покрыть 72 квадратных метра?
D. Для приготовления сухого молока используется 1 часть сухого молока на 3 части воды. Сколько порошка нужно добавить на 9 частей воды?
- Ответы на упражнение 2
B.
 10 автомобилей не будут соответствовать стандартам безопасности
10 автомобилей не будут соответствовать стандартам безопасностиC. 12 литров краски
D. 3 части сухого молока
Просмотр перекрестных произведений:
Умножьте числитель каждой дроби на знаменатель другой дроби.
\(\dfrac{2}{5} \nearrow \dfrac{4}{10}\)
\(\dfrac{2}{5} \searrow \dfrac{4}{10}\)
\(2 \х 10 = 5 \х 4\)
\(20 = 20\)
\(2 \х 10 = 20\) и \(5 \х 4 = 20\)
Следовательно: \(\dfrac{2}{5} = \dfrac{4}{10}\)
Помните, что когда перекрестные произведения одинаковы, дроби эквивалентны.
При нахождении недостающих членов в пропорции можно использовать перекрестное умножение. Внимательно следуйте примерам.
Пример A
\(\dfrac{2}{3} = \dfrac{N}{45}\)
Перекрестное умножение:
\(2 \times 45 = 3 \times N\)
\ (90 = 3N\)
Идея состоит в том, чтобы иметь неизвестный член N отдельно по одну сторону от знака равенства. Для этого вспомните то, что вы уже знаете:
Для этого вспомните то, что вы уже знаете:
- Деление и умножение — противоположные операции
- Все, что делается с одной частью уравнения или пропорции, должно быть сделано с другой частью, чтобы уравнение оставалось равным
3 N означает, что N умножается на 3. Чтобы избавиться от 3, разделите на 3 .
Вы также должны разделить другую часть уравнения на 3.
\(\dfrac{90}{3} = \dfrac{3N}{3}\)
Решите, уменьшив \(\dfrac{3}{3}\) и разделив 90 на 3.
\( \dfrac{90}{3} = \dfrac{3N}{3}\)
\(\dfrac{90}{3} = \dfrac{1N}{1}\)
\(\dfrac{90 }{3} = N\)
\(90 \div 3 = N\)
\(30 = N\)
Сокращение дроби \(\dfrac{3N}{3}\) к \(dfrac {1N}{1}\) на \(N\) также называется , отменяя . В математике дробь можно сократить, если числитель и знаменатель совпадают.
напр. \(\dfrac{6P}{6} = \dfrac{1P}{1} = P\)
Пример B
\(\dfrac{6}{7} = \dfrac{24}{N}\)
Крест умножить:
\(6 \× N = 7 \× 24\)
\(6N = 168\)
Разделить обе стороны на 6. Шестерки с N отменят (уменьшат) и N будет один.
Шестерки с N отменят (уменьшат) и N будет один.
\(\dfrac{6N}{6} = \dfrac{168}{6}\)
\(\dfrac{\cancel{6}N}{\cancel{6}} = \dfrac{168} {6}\)
\(N = 168 \дел 6\)
\(N = 28\)
\(\dfrac{6}{7} = \dfrac{24}{28}\)
Проверить перекрестным умножением:
Является ли \(6 \times 28 = 7 \times 24\)?
\(6 \times 28 = 168\)
\(7 \times 24 = 168\)
перекрестное произведение \(168 = \text{перекрестное произведение} 168\)
\(\ text{Yes}-6:7 = 24:28\)
Решение задачи на пропорции с помощью перекрестного умножения
- Шаг 1
Напишите первое отношение, используя предоставленную информацию. - Шаг 2
Напишите пропорцию, используя букву вместо пропущенного члена. Убедитесь, что порядок сравнения один и тот же как в первом, так и во втором соотношении в вашей пропорции. - Шаг 3
Запишите пропорцию в виде дроби. (Попробуйте упростить отношение до вы сделаете все расчеты).
(Попробуйте упростить отношение до вы сделаете все расчеты). - Шаг 4
Перемножьте и установите перекрестные произведения равными друг другу. - Шаг 5
Разделите обе части уравнения на число с неизвестным членом. - Шаг 6
Проверьте, вернув ответ в исходную пропорцию и перемножив. Упражнение 4
Попрактикуйтесь в перекрестном умножении, чтобы найти пропущенный член в этих пропорциях.
A. \(\dfrac{5}{8} = \dfrac{N}{32}\)
\(5 \times 32 = 8 \times N\)
\(160 = 8N\) )
\(\dfrac{160}{8} = \dfrac{8N}{8}\)
\(160 \div 8 = N\)
\(20 = N\)
B. \ (\dfrac{4}{N} = \dfrac{24}{30}\)
C. \(\dfrac{12}{4} = \dfrac{18}{x}\)
D. \(\dfrac{y}{6} = \dfrac{20}{12}\)
E.
 \(4:15 = 8:N\)
\(4:15 = 8:N\)F. \(W :100 = 6:50\)
- Ответы на упражнение 4
Б. \(N=5\)
С. \(х = 6\)
Д. \(у = 10\)
Э. \(N = 30\)
Ф. \(W = 12\)
Числа в отношении часто представляют собой обыкновенные дроби, десятичные дроби или смешанные числа. Выполните точно такие же шаги, которые вы использовали для решения пропорций целых чисел. Расчеты будут использовать ваши навыки работы с дробями.
Пример A
\(2\dfrac{1}{4}:3 = N:7\)
Перепишите пропорцию:
\(\dfrac{2 \frac{1}{4}}{3} = \dfrac{N}{7}\)
Перекрестное умножение:
\(2\dfrac{1}{4} \times 7 = 3 \times N\)
\(\dfrac{9}{4} \times \dfrac{7}{1} = 3 \times N\)
\(\dfrac{63}{4 } = 3N\)
\(\dfrac{63}{4} \div \dfrac{3}{1} = \dfrac{3 \times N}{3} \rightarrow \dfrac{63}{4} \ раз \dfrac{1}{3} = N\)
\(\dfrac{63}{12} = N \rightarrow 5\dfrac{3}{12} \rightarrow 5\dfrac{1}{4} = N\)
Оценка /20 17/20
- Решите эти пропорции.

(6 баллов)- \(N:14 = 28:56\)
- \(3:11 = Н:22\)
- \(50:45 = 10:N\)
- \(4\dfrac{1}{5}:Y = 3:2\)
- (14 баллов)
- Получите карту Британской Колумбии, карту Канады и карту вашего города.
- Найдите масштаб на каждой карте (обычно внизу) и запишите отношение расстояния карты к фактическому расстоянию.
- Вместе с другим учеником или инструктором рассчитайте фактическое расстояние между местами, измерив расстояние на карте и вычислив пропорцию в соответствии с заданным масштабом. Выполните не менее трех расчетов расстояния на каждой карте.
Попросите инструктора оценить вашу работу.
Ответы на тему C Самопроверка
- \(N=7\)
- \(N=6\)
- \(N=9\)
- \(Y = 2\dfrac{4}{5}\) или \(2,8\)
- Обратитесь к инструктору.

Эта страница под названием 1.3: Тема C-Proportion распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Венди Тагами и Лиз Жирар
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Теги
- источник@https://opentextbc.
 ca/alfm6
ca/alfm6
- источник@https://opentextbc.
Числа, операции, скорости и отношения
В каждой области математики и почти во всех приложениях математики числа и операции используются для рассуждений и решения задач. Приложения Connected Mathematics (CMP) включают целые числа, целые числа, дроби, десятичные дроби, проценты, отношения и иррациональные числа. Главной целью раздела CMP3 «Числа и операции» является расширение понимания и навыков учащихся в использовании чисел и операций для представления и анализа количественной информации.
В цепи CMP3 Число, Операции и Пропорциональное Рассуждение есть десять Единиц. Целью этих модулей является:
- Расширить знания о целых числах, дробях и десятичных дробях, развить способность знать, какое представление и какую операцию выбрать, и развить беглость в операциях с этими числами;
- Разработать концепции отношения, скорости и пропорции, особенно эквивалентности отношений, и применить их к реальным проблемам;
- Развить понимание значения процентов и средств с приложениями;
- Познакомить с отрицательными, иррациональными и комплексными числами и структурными свойствами каждой системы счисления.

Процессы обучения, направленные на достижение каждой из этих широких целей, описаны в следующих разделах.
Расширение целых чисел, дробей и десятичных дробей
Умение пользоваться обыкновенными дробями зависит от понимания мультипликативной структуры целых чисел. Это включает в себя понимание понятий множителя, кратного, простого числа, наибольшего общего делителя и наименьшего общего кратного. Prime Time начинает учебную программу CMP3, развивая идеи элементарной теории чисел, одновременно вовлекая учащихся в игры и задачи по решению задач, которые задают тон классу, работающему как сообщество учащихся, в котором все участники являются активными участниками. Prime Time также начинает раздел «Алгебра и функции» в учебной программе, развивая у учащихся понимание арифметических выражений, распределительного свойства и порядка операций. Обзор и расширение понимания дробей и десятичных чисел и навыков сосредоточены в трех модулях 6 класса: «Сравнение битов и кусочков», «Давайте будем рациональны» и «Десятичные операции». В этих модулях учащиеся развивают чувство числа и привычку решать проблемы, отвечая на четыре ключевых вопроса:
В этих модулях учащиеся развивают чувство числа и привычку решать проблемы, отвечая на четыре ключевых вопроса:
- Какие числа будут точно представлять вовлеченные количества?
- Какие операции над этими числами дадут ответы на основные поставленные вопросы?
- Какова хорошая оценка результата этих операций?
- Какой точный результат дает применение стандартного вычислительного алгоритма для операций?
Изменение названия с Bits and Pieces II (CMP2) на Let’s be Rational, Bits и Pieces I – Сравнение битов и фрагментов и Биты и фрагменты III – Десятичные операции сигнализирует о расширении понимания учащимися дробей и десятичных знаков. Вводятся отрицательные числа, и учащиеся упорядочивают эти числа на числовой прямой, замечая, что, например, — ¾ и ¾ находятся на одинаковом расстоянии от нуля, но по разные стороны от нуля. Следствием добавления ручных вычислений с многозначными числами в Десятичные операции является то, что учащиеся могут видеть, что любая дробь a / b можно записать в виде десятичной дроби, которая либо повторяется, либо заканчивается, путем вычисления a ÷ b .
Let’s Be Rational и Decimal Ops Подразделения, ориентированные на дроби и десятичные операции, также начинают работу над основными идеями алгебры, исследуя семейств фактов , которые соединяют пары связанных операций, эквивалентных уравнений и эквивалентных выражений.
Семейство фактов умножения/деления, относящихся к числам 4, 6 и 24, включает:
4 x 6 = 24
6 x 4 = 24
4 = 24 ÷ 6
6 = 24 ÷ 4
Учащиеся работают над вычислительными навыками и одновременно развивают навыки решения простых уравнений. Использование рассуждений семейства фактов позволяет решать одношаговые уравнения. Например, чтобы решить 4 x = 24, учащиеся считают, что x = 24 ÷ 4, или чтобы решить 6% от x = 4,80 доллара, учащиеся считают, что x = 4,80 доллара : 0,06.
Распределительное свойство умножения над сложением и вычитанием, введенное в Prime Time позволяет записывать арифметические вычисления в различных эквивалентных формах.
4(5 + 1) = 4(5) + 4(1).
Распределяющее свойство используется в разделе «Алгебра и функции» для поддержки общей цели написания и интерпретации эквивалентных выражений. По мере того как целочисленная, рациональная, вещественная и комплексная системы счисления развиваются в последующих модулях, студентов постоянно спрашивают, применимы ли и должны ли такие очень полезные структурные свойства операций применяться в новых контекстах.
Соотношение, коэффициенты, масштабные коэффициенты и пропорции
Задача 1.1 в Сравнение деталей представляет некоторые цели по сбору средств, а затем спрашивает учащихся, верны ли некоторые утверждения о каждой цели по сбору средств. Цель задачи 1.1 — привлечь внимание учащихся к общей математической задаче точного и справедливого сравнения величин. Он также подчеркивает разницу между сравнением путем вычитания (или сложения) и сравнением путем деления (или умножения).
В задаче 1.1 вводятся пропорциональные понятия отношения, скорости и процента, которые затем развиваются в последующих задачах на единицу измерения. Задача выполняет вторую важную функцию, помогая учителям определить широту и глубину предварительных знаний учащихся об отношении, норме и проценте. Проблема 1.1 также иллюстрирует наш руководящий принцип, заключающийся в том, что учащиеся с большей готовностью усваивают новые понятия, если они сталкиваются с ними в знакомых контекстах, к которым они могут сначала применить свое неформальное осмысление, а затем абстрагироваться, лежащие в основе общих математических структур.
Задача выполняет вторую важную функцию, помогая учителям определить широту и глубину предварительных знаний учащихся об отношении, норме и проценте. Проблема 1.1 также иллюстрирует наш руководящий принцип, заключающийся в том, что учащиеся с большей готовностью усваивают новые понятия, если они сталкиваются с ними в знакомых контекстах, к которым они могут сначала применить свое неформальное осмысление, а затем абстрагироваться, лежащие в основе общих математических структур.
Последующие задачи в Сравнение битов и кусочков развивают концепцию отношения и скорости более явно, основываясь на идее, что отношение a к b означает, что каждое a одной величины связано с b второй величины. Эквивалентность отношений развивается путем рассуждений о том, что имеет смысл в осмысленных контекстах, а затем эквивалентность отношений связывается с эквивалентностью дробей. Также выделены отличия работы с пропорциями от работы с дробями.
Предположим, в одном классе 10 мальчиков и 15 девочек, а в другом 12 мальчиков и 9 девочек. Соотношение мальчиков и девочек в этих двух классах вместе взятых составляет 22 к 24.
Соотношение мальчиков и девочек в этих двух классах вместе взятых составляет 22 к 24.
С этого неформального, осмысленного, интуитивного начала концепции отношения и скорости развиваются вширь и вглубь на курсах CMP3 для 6 и 7 классов. Тарифы за единицу и таблицы тарифов представлены во втором исследовании «Сравнение битов и фрагментов» и повторно рассмотрены в алгебраическом контексте в Переменные и шаблоны ближе к концу 6-го класса.
В 7-м классе Растяжение и сжатие развивает мышление о соотношениях с точки зрения геометрического подобия и масштабных коэффициентов, а Сравнение и масштабирование знакомит с соотношениями, коэффициентами, масштабными коэффициентами и оцените таблицы вместе, чтобы разработать стратегии решения пропорций. Эти фундаментальные идеи пропорциональных рассуждений затем расширяются и применяются для работы с линейными функциями, скоростями изменения и наклоном графиков в 9 единицах алгебры.0367 Движение прямо вперед в 7 классе и Мышление с помощью математических моделей в начале 8 класса.
Направление «Число» и направление «Алгебра и функции» используют понятия скорости и пропорциональности.
В процессе развития концепций и навыков пропорционального мышления учащимся постоянно задаются два ключевых вопроса.
Когда имеет смысл сравнивать количества по соотношению или скорости?
Как можно выразить отношения или доли в эквивалентных формах, чтобы ответить на вопросы, связанные с пропорциями?
Основываясь на понятиях эквивалентности и масштабирования, Сравнение и масштабирование позволяет учащимся разработать разумные алгоритмы для решения пропорций, подкрепленные глубоким концептуальным пониманием.
Проценты
Почти в каждой практической задаче на количественные рассуждения проценты являются наиболее распространенным инструментом для постановки и решения вопросов, требующих сравнения величин. Они предлагают стандартизированный язык и процедуры для описания отношений между двумя величинами как с аддитивной, так и с мультипликативной точки зрения.
Если товар, первоначальная цена которого составляла 15 долларов, продается за 9 долларов, снижение цены составит 6 долларов. Кроме того, 6 долларов – это 40 % от первоначальной цены, или цена продажи – 60 % от первоначальной цены.
Если население города увеличивается с 25 000 до 30 000 человек, это увеличение составляет 5 000 человек, что составляет 20% первоначального населения. Новое население составляет 120% от исходного населения.
Хотя каждый из этих примеров представляет собой аддитивное рассуждение, увеличение или уменьшение можно выразить в процентах.
Что такое 30% от 90?
0,30 x 90 = n
36 сколько процентов от 90?
р x 90 = 36
45 составляет 25% от какого числа?
45 = 0,25 x n
Предыдущая работа с семействами фактов, связанными с умножением и делением, приносит богатые дивиденды в обучении тому, как справляться с процентными задачами. Конечно, проценты появляются в единицах геометрии, данных, вероятности и алгебры каждого класса.
Отрицательные числа
Традиционное знакомство с отрицательными числами сосредоточено на целых положительных и отрицательных целых числах и 0. Развитие CMP3 идет по несколько иному пути. В соответствии с требованиями CCSSM мы начинаем в шестом классе Unit Сравнение битов и кусочков путем расширения строки рациональных чисел для включения отрицательных чисел. Развитие там ограничивается расположением положительных чисел и их противоположностей и понятием абсолютного значения. Позже, в 6-м классе, проблема в Переменные и шаблоны расширяет плоскость координат до всех четырех квадрантов графика, используя неформально отрицательные числа с предположением, что ученики шестого класса почти наверняка сталкивались с ними.
В основе развития отрицательных чисел лежит 7-й класс, 9-й раздел.0367 Подчеркните отрицательное . Мы способствуем осмыслению через игры с выигрышами и проигрышами и другими сюжетными контекстами, моделями числовых линий и моделями фишек, чтобы опираться на интуицию учащихся и выводить стандартные правила для работы с отрицательными числами. В духе связной математики мы смешиваем задачи об отрицательных рациональных числах с задачами, ограниченными целыми значениями.
В духе связной математики мы смешиваем задачи об отрицательных рациональных числах с задачами, ограниченными целыми значениями.
Помимо использования неформальных рассуждений и моделей для чисел и операций, мы снова связываемся с идеей семейства фактов при выводе алгоритмов.
После установления правил умножения (тонкий случай — произведение двух отрицательных чисел) следуют правила деления:
(-30) ÷ 5 = -6, потому что -30 = 5(-6)
(-30) ÷ (-5) = 6, потому что -30 = (-5)(6)
Окончательное исследование . Подчеркните отрицательное. общие для всех основные структурные свойства, особенно распределительное свойство. С Подчеркните отрицательное значение встречается относительно рано в 7 классе, отрицательные числа доступны для применения в других модулях, особенно в Движение прямо вперед о линейных функциях.
Иррациональные и комплексные числа
Разработка стандартных систем счисления и операций в CMP3 завершена в двух разделах программы 8 класса — В поисках Pythagoras и Функциональное соединение. Поиск по Пифагору делает стандартную связь между квадратными корнями и диагоналями квадратов или гипотенузами прямоугольных треугольников. Он имеет дело с десятичным представлением рациональных (повторяющихся) и иррациональных (неповторяющихся) чисел и, согласно спецификациям CCSSM, также вводит кубические корни. Число π появляется раньше, в 7 классе, когда окружность и площадь кругов решаются в 9 классе.0367 Наполнение и упаковка.
Поиск по Пифагору делает стандартную связь между квадратными корнями и диагоналями квадратов или гипотенузами прямоугольных треугольников. Он имеет дело с десятичным представлением рациональных (повторяющихся) и иррациональных (неповторяющихся) чисел и, согласно спецификациям CCSSM, также вводит кубические корни. Число π появляется раньше, в 7 классе, когда окружность и площадь кругов решаются в 9 классе.0367 Наполнение и упаковка.
Комплексные числа традиционно были предметом изучения алгебры II в старших классах, но учебная программа CCSSM по алгебре I требует введения комплексных чисел. Таким образом, пытаясь предложить материалы CMP3, которые поддерживают полный вводный курс алгебры, мы включили комплексные числа в Function Junction . Развитие там математически довольно стандартно, продолжая шаблон расширения системы счисления, чтобы включить значащие числа, которые обеспечивают решения уравнений, не разрешимых в предыдущих более простых системах счисления.

 Фермер посеял пшеницу на 2 га, что составляет 80 % от всех его посевных площадей. Какова общая посевная площадь, которой он располагает?
Фермер посеял пшеницу на 2 га, что составляет 80 % от всех его посевных площадей. Какова общая посевная площадь, которой он располагает?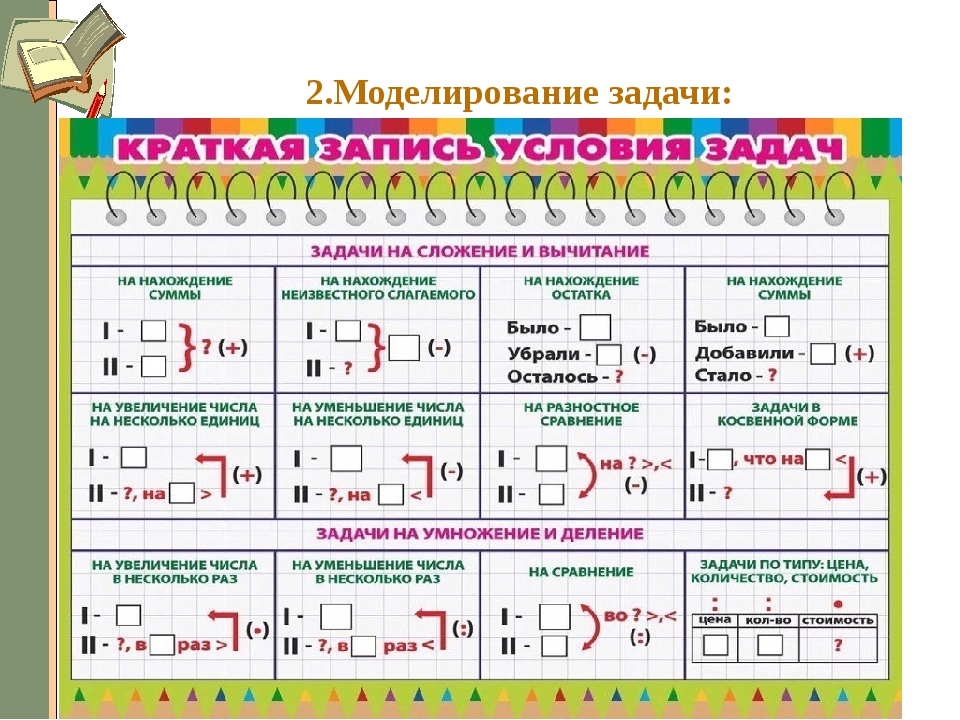








 Определите, во сколько раз 26 больше 13
Определите, во сколько раз 26 больше 13 Итак, мы пишем это как 15/20.
Итак, мы пишем это как 15/20.
 Из них 10 взрослых, остальные дети. Каково отношение количества детей к общему количеству учащихся в музыкальном классе?
Из них 10 взрослых, остальные дети. Каково отношение количества детей к общему количеству учащихся в музыкальном классе?  Следовательно, 2:3 > 1:2.
Следовательно, 2:3 > 1:2.