Изображение отношений между множествами с помощью кругов Эйлера. — Мегаобучалка
Понятие множества. Способы задания множеств.
Множество – совокупность объектов, рассматривая как одно целое. Понятие множества принимается за основное, т.к. не сводится к другим понятиям. Объекты, составляющие данное множество, называются его элементами. Множества бывают конечные и бесконечные (натуральные, целые, рациональные, действительные числа). Множества принято обозначать: А,В,С; Элементы множества принято обозначать а,б,с…Есть и пустое множество( ноль перечеркнутый) Способы задания множества:
Перечисление объектов, и характеристическое свойство множества-свойством, которым обладает каждый элемент этого множества, и не имеет ни один элемент не принадлежащий элементу не входящего в это множество.
Отношения между множествами: пересечение, подмножество, равенство.
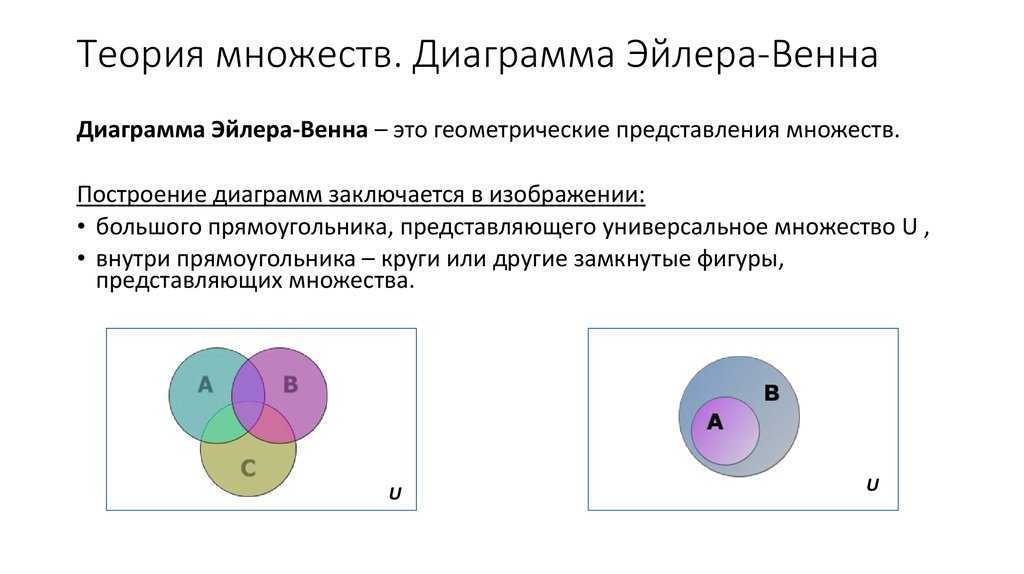
Если множества А и В имеют общие элементы, т.е. элементы принадлежащие одновременно А и В, то говорят, что эти множества пересекаются.
Множество В называют подмножеством А, если каждый элемент множества В является также элементом множества А. (Пустое множество является подмножеством любого множества, любое множество является подмножеством самого себя, количество подмножеств равно числу 2 в степени равной количеству элементов во множестве).
Множества А и В называются равными(А=В), если А принадлежит В, а В принадлежит А.
Операции над множествами: объединение, пересечение, дополнение,вычитание.
Пересечением множеств А и В называют множество, содержащее те и только те элементы, которые принадлежат множеству А и В (два способа нахождения элементов пересечения, (перечисление элементов, характерический способ) ( более сильная операция и выполняется первой перед объединением, если нет скобок.)
Объединением множества А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А или множеству В.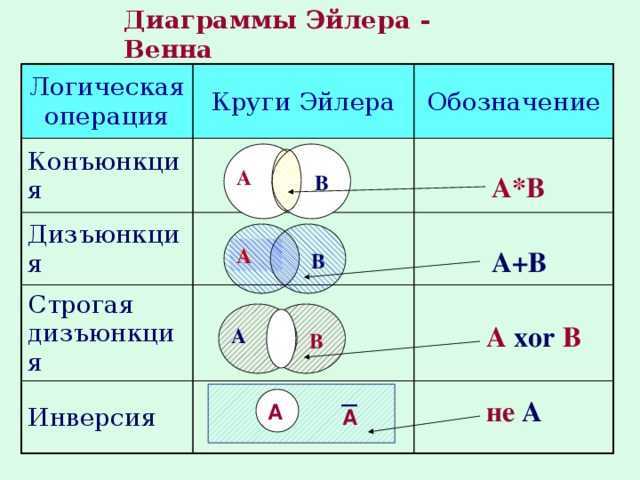
Свойства объединения и пересечения.
1) Переместительно или коммуникативное.
2) Сочетательное или ассоциативное.
3) Распределительное или дистрибутивное
Разностью множества А и В называют множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В. (два способа нахождения элементов пересечения, (перечисление элементов, характерический способ) А/В.
Пусть В ( А .Дополнением подмножества в ДО множества А называют множество, содержащие те и только те элементы множества А, которые не принадлежат множеству В.
| Разность |
| Пересечение |
| Объединение |
Изображение отношений между множествами с помощью кругов Эйлера.
Круги эйлера используются для того, чтобы показать отношения между множествами. Существуют следующие отношения: Пересечением множеств А и называют множество, содержащее те и только те элементы, которые принадлежат множеству А и В (два способа нахождения элементов пересечения, (перечисление элементов, характерический способ) ( более сильная операция)
Существуют следующие отношения: Пересечением множеств А и называют множество, содержащее те и только те элементы, которые принадлежат множеству А и В (два способа нахождения элементов пересечения, (перечисление элементов, характерический способ) ( более сильная операция)
Пусть В ( А .Дополнением подмножества в ДО множества А называют мнржество, содержащие те и только те элементы множества А, которые не принадлежат множеству В.
Разностью множества А и В называют множество, содержащее те и только те элементы, которые принадлежат множеству А и не принадлежат множеству В. (два способа нахождения элементов пересечения, (перечисление элементов, характерический способ) А/В.
Объединением множества А и В называется множество, содержащее те и только те элементы, которые принадлежат множеству А или множеству В.
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Информатика
| Похожие вопросы |
Решено
Рассказ, набранный на компьютере, содержит 8 страниц, на каждой странице 40 строк, в каждой строке 48 символов. Определите информационный объем
Определите информационный объем
1)Некоторый алгоритм из одной цепочки символов получает новую цепочку следующим образом. Сначала вычисляется длина исходной цепочки символов; если
Решено
Нарисуйте алгоритм (блок-схему) поиска фальшивой…
«A»: Напишите программу, которая получает три числа и выводит количество одинаковых чисел в этой цепочке. Пример: Введите три числа: 5 5 5 Все числа одинаковые
Файл размером 4 Кбайт передаётся через некоторое соединение со скоростью 4096 бит в секунду. Определите размер файла (в байтах), который можно…
Пользуйтесь нашим приложением
диаграмм Венна | Что нового
Популярный способ визуализации взаимосвязей между некоторым конечным числом множеств — это диаграммы Венна или, в более общем случае, диаграммы Эйлера. На этих диаграммах множество изображается в виде двумерной формы, такой как диск или прямоугольник, и различные логические отношения между этими множествами (например, то, что одно множество содержится в другом, или что пересечение двух множеств равен трети) представлен булевой алгеброй этих форм; Диаграммы Венна соответствуют случаю, когда множества находятся в «общем положении» в том смысле, что все нетривиальные булевы комбинации множеств непусты.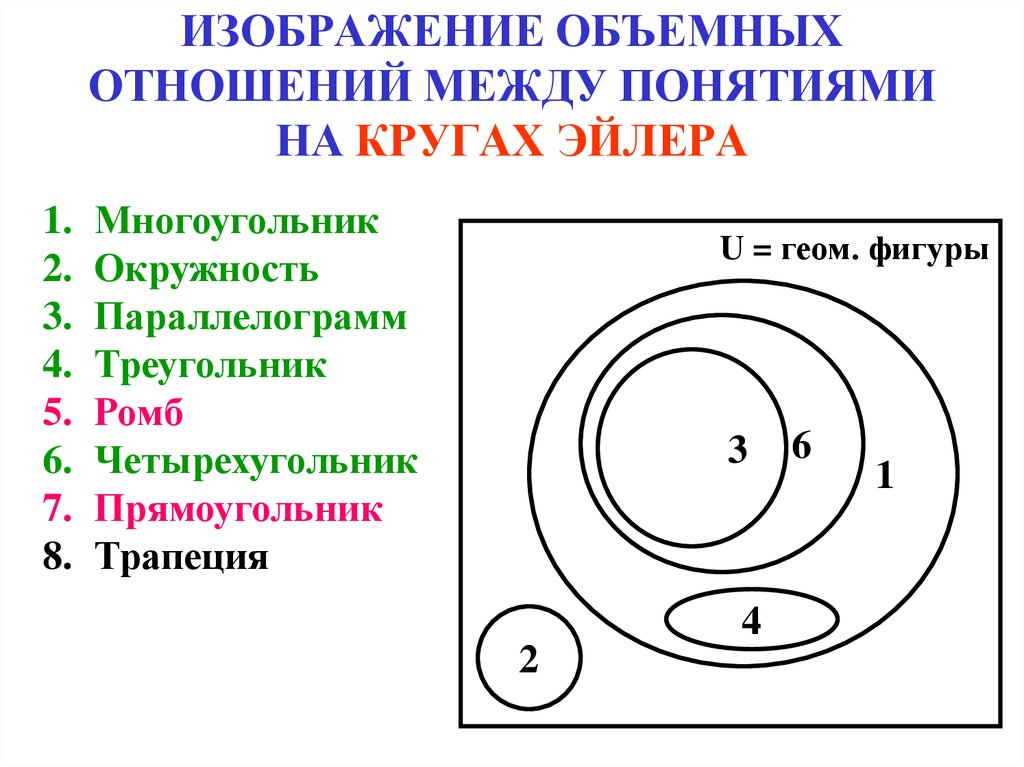
(где мы обозначили каждую область разным цветом и немного отодвинули края каждой области друг от друга, чтобы сделать их видимыми по отдельности), но если бы кто-то хотел вместо этого изобразить ситуацию, в которой пересечение было пустым , можно было бы использовать диаграмму Эйлера, такую как
Можно использовать площадь различных областей на диаграмме Венна или Эйлера в качестве эвристического заместителя мощности (или меры) множества, соответствующего такой области. Например, приведенную выше диаграмму Венна можно использовать для интуитивного обоснования формулы включения-исключения 9.0003
для конечных множеств, в то время как приведенная выше диаграмма Эйлера аналогичным образом оправдывает частный случай
для конечных непересекающихся множеств.
Хотя диаграммы Венна и Эйлера традиционно двумерны по своей природе, ничто не мешает использовать одномерные диаграммы, такие как
или даже трехмерные диаграммы, такие как эта из Википедии:
Конечно, в таких случаях можно было бы использовать длину или объем в качестве эвристического показателя мощности или меры, а не площади.
С добавлением стрелок диаграммы Венна и Эйлера также могут вмещать (в некоторой степени) функции между наборами. Вот, например, изображение функции, изображение этой функции и изображение некоторого подмножества:
Здесь можно проиллюстрировать сюръективность, заполнив все ; аналогичным образом можно проиллюстрировать инъективность, задав точно такую же форму (или, по крайней мере, ту же площадь), что и . Вот, например, как можно проиллюстрировать инъективную функцию:
Декартовы операции произведения могут быть включены в эти диаграммы с помощью соответствующих комбинаций одномерных и двумерных диаграмм. Вот, например, диаграмма, иллюстрирующая тождество:
Вот, например, диаграмма, иллюстрирующая тождество:
В этом сообщении блога я хотел бы предложить аналогичное семейство диаграмм для иллюстрации взаимосвязей между векторными пространствами (над фиксированным базовым полем, таким как вещественные числа) или абелевыми группами , а не множествами. Категории (-)векторных пространств и абелевых групп во многом очень похожи; первая состоит из модулей над базовым полем, а вторая состоит из модулей над целыми числами; кроме того, обе категории являются основными примерами абелевых категорий. Понятие размерности векторного пространства во многом аналогично понятию мощности множества; см. этот предыдущий пост для примера этой аналогии (в контексте энтропии Шеннона). (ОБНОВЛЕНИЕ: я узнал, что по существу идентичная запись была также предложена в неопубликованной рукописи Рави Вакиля.)
Прочитать остальную часть записи »
Наборы и пересечения | Природные методы
Множества и пересечения
Скачать PDF
Скачать PDF
- Опубликовано:
Точки зрения
- Александр Лекс 1 и
- Нильс Геленборг 2
Природные методы том 11 , страница 779 (2014)Процитировать эту статью
18 тыс. обращений
59 цитирований
85 Альтметрический
Сведения о показателях
Предметы
- Публикации
- Данные исследований
- Статистические методы
Сложные отношения требуют компромиссов.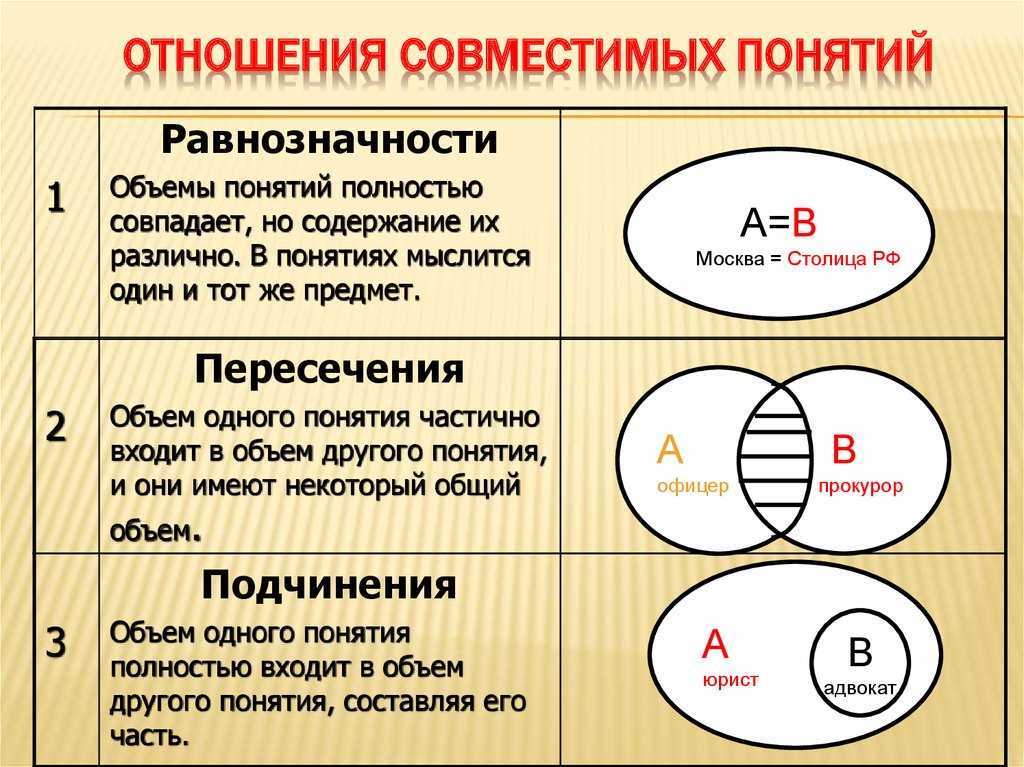
— универсальное понятие в научном анализе данных. Виды бактерий, обнаруженные в образце почвы, ферменты, обнаруженные в биохимическом пути, варианты, обнаруженные в геноме, белки, обнаруженные в образце сыворотки с помощью масс-спектрометрии, или гены, мутировавшие в когорте больных раком, — все это можно рассматривать как наборы. Хотя цель некоторых исследований ограничивается идентификацией таких множеств, общей задачей является анализ общих черт и различий множественных множеств путем их пересечения. Мы изучили данные, опубликованные в Nature в период с декабря 2011 г. по октябрь 2012 г. и обнаружил 20 рисунков с 51 диаграммой, изображающей пересечения до 6 наборов.
Наборы и их пересечения легко визуализировать до трех или четырех наборов. Однако, если количество наборов превышает этот тривиальный порог, визуализация пересечений становится серьезной проблемой. В то время как 3 набора имеют только 8 возможных пересечений, 10 наборов имеют 1024 возможных пересечения, так как имеется 2 n возможные пересечения для комплектов n .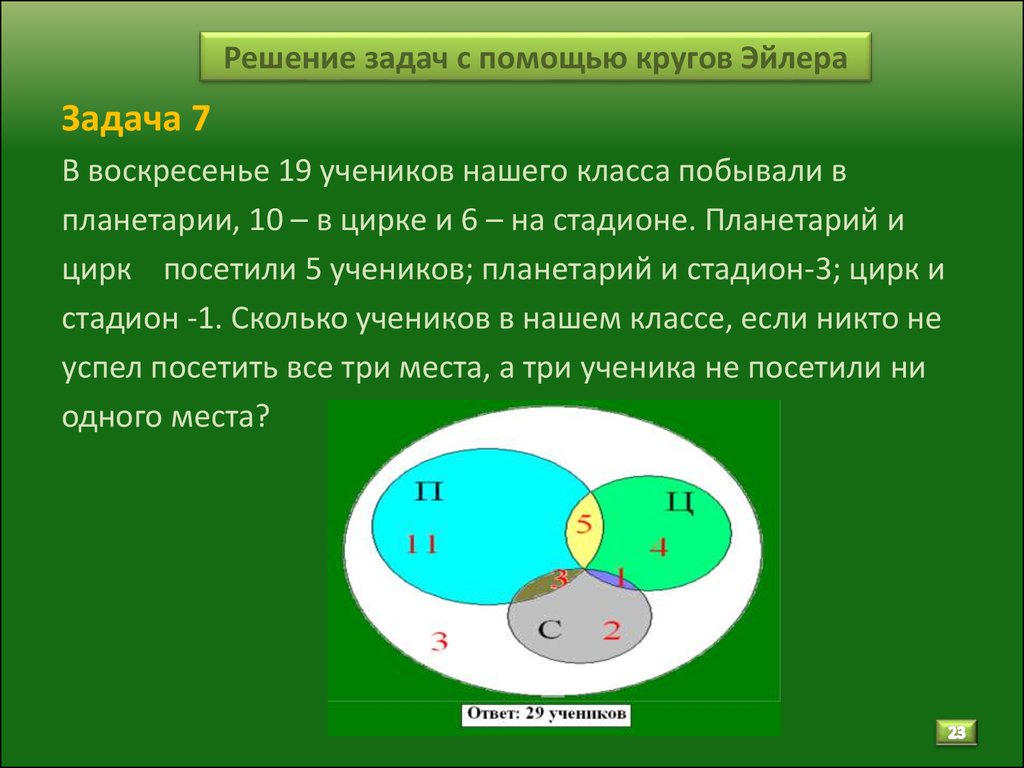
Пересечения множеств обычно иллюстрируются с помощью диаграмм Эйлера или Венна. Диаграммы Эйлера представляют пересекающиеся множества в виде перекрывающихся фигур, обычно кругов или эллипсов, которые часто рисуются так, что их площадь пропорциональна количеству элементов, которые они представляют. Диаграммы Венна идентичны диаграммам Эйлера за исключением того, что на диаграммах Венна показаны все возможные пересечения, в том числе и пустые, которые не показаны на диаграммах Эйлера.
Диаграммы Эйлера (рис. 1а) подходят для представления размеров пересечений двух или трех множеств. Диаграмма должна отображаться пропорционально площади, чтобы размер перекрывающихся областей передал информацию о размерах пересечения, что сделало бы визуализацию более эффективной. Это представление размеров пересечения не так точно, как использование положения или длины 1 , но небольшое количество пересечений и тот факт, что диаграммы Эйлера и Венна хорошо известны из-за их использования в качестве помощи в обучении теории множеств, делают это приемлемый компромисс.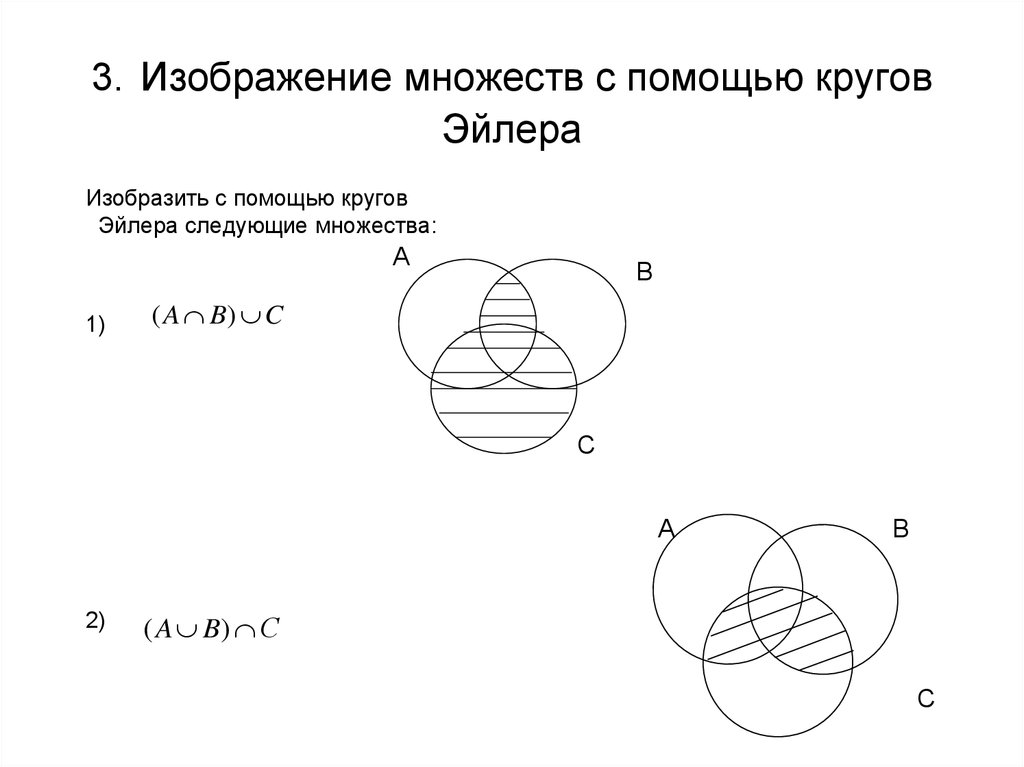 Приблизительно пропорциональные площади диаграммы Эйлера с использованием кругов можно построить с помощью пакета venneuler R 9.0070 2 . Поскольку многие диаграммы Эйлера, пропорциональные площади, нельзя точно нарисовать с помощью кругов, альтернативный подход состоит в использовании эллипсов, которые в большинстве случаев дают решения, пропорциональные площади. Инструментом для создания таких диаграмм является EulerAPE (http://www.eulerdiagrams.org/eulerAPE/).
Приблизительно пропорциональные площади диаграммы Эйлера с использованием кругов можно построить с помощью пакета venneuler R 9.0070 2 . Поскольку многие диаграммы Эйлера, пропорциональные площади, нельзя точно нарисовать с помощью кругов, альтернативный подход состоит в использовании эллипсов, которые в большинстве случаев дают решения, пропорциональные площади. Инструментом для создания таких диаграмм является EulerAPE (http://www.eulerdiagrams.org/eulerAPE/).
( a ) Диаграмма Эйлера, отображающая пересечение трех генов. Наборы представляют собой гены, мутировавшие в опухолях пациентов с мультиформной глиобластомой 3 , а набор пересечений указывает на комутантные гены. Количество пациентов, показанных в a , b и c , различается, поскольку включены только пациенты, у которых есть мутация по крайней мере в одном из выбранных генов. ( b ) Макет матрицы для всех пересечений пяти генов, отсортированных по размеру.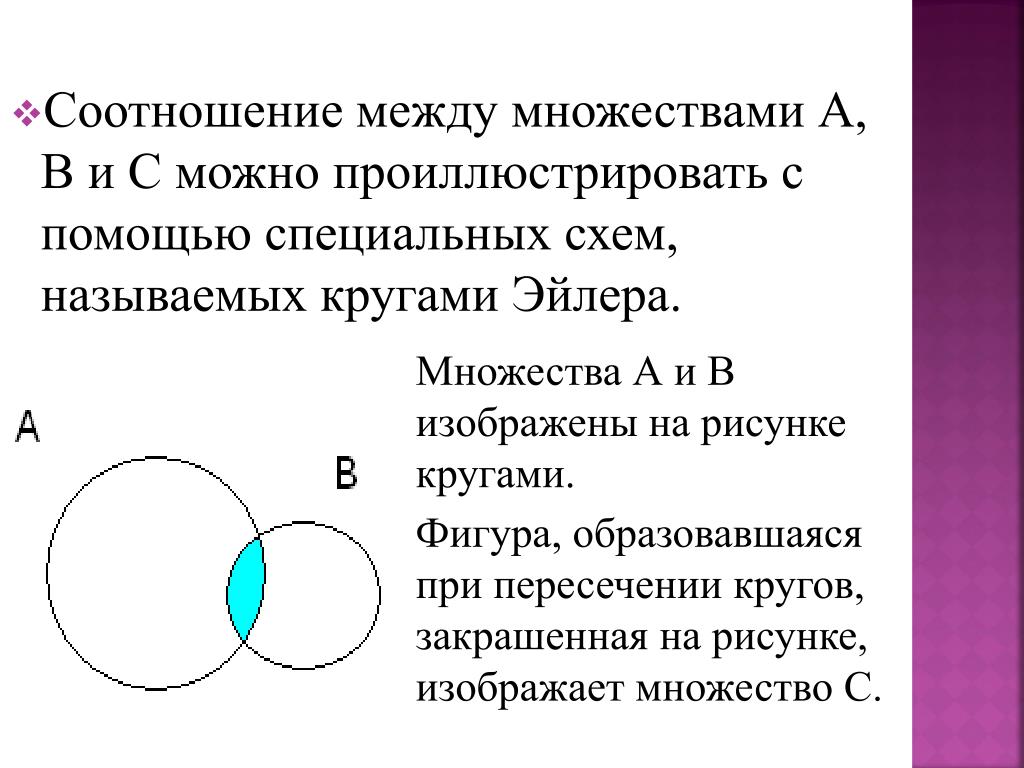 Темные кружки в матрице обозначают наборы, являющиеся частью пересечения. Дополнительные наборы RB1 и PIK3R1 вызывают размеры пересечений, также показанные на a , чтобы стать меньше, так как некоторые пациенты из этих пересечений находятся в пересечениях с дополнительными наборами. ( c ) Кластерная тепловая карта, показывающая попарные пересечения 15 генов. В отличие от a и b пересечение двух наборов вычисляется независимо от других наборов.
Темные кружки в матрице обозначают наборы, являющиеся частью пересечения. Дополнительные наборы RB1 и PIK3R1 вызывают размеры пересечений, также показанные на a , чтобы стать меньше, так как некоторые пациенты из этих пересечений находятся в пересечениях с дополнительными наборами. ( c ) Кластерная тепловая карта, показывающая попарные пересечения 15 генов. В отличие от a и b пересечение двух наборов вычисляется независимо от других наборов.
Полноразмерное изображение
Эффективная визуализация пересечений более чем трех наборов требует более масштабируемого подхода, чем диаграммы Эйлера. Одним из решений является кодирование всех установленных пересечений в столбцах матрицы с использованием двоичного шаблона и отображение столбцов над столбцами матрицы для представления количества элементов в каждом пересечении (рис. 1b). Столбцы могут быть логарифмически преобразованы, чтобы учесть большие различия в размерах пересечений, и могут быть отсортированы, чтобы показать распределение размеров пересечений. В зависимости от задачи столбцы также можно сортировать по комбинациям наборов, чтобы сгруппировать пересечения по количеству перекрывающихся наборов или расположить все пересечения определенного набора рядом друг с другом. При построении большого количества наборов пустые пересечения можно удалить для экономии места. Чтобы иметь возможность судить о размерах пересечения в контексте заданных размеров, столбцы, представляющие последние, могут быть нанесены вдоль строк матрицы. Интерактивный инструмент для создания таких визуализаций в веб-браузере доступен по адресу http://vcg.github.io/upset/.
В зависимости от задачи столбцы также можно сортировать по комбинациям наборов, чтобы сгруппировать пересечения по количеству перекрывающихся наборов или расположить все пересечения определенного набора рядом друг с другом. При построении большого количества наборов пустые пересечения можно удалить для экономии места. Чтобы иметь возможность судить о размерах пересечения в контексте заданных размеров, столбцы, представляющие последние, могут быть нанесены вдоль строк матрицы. Интерактивный инструмент для создания таких визуализаций в веб-браузере доступен по адресу http://vcg.github.io/upset/.
Нанесение сразу всех пересечений 10 или более наборов обычно невозможно. Однако в зависимости от данных и вопросов может быть полезно нанести размеры всех парных пересечений с помощью кластерной тепловой карты (рис. 1c). Для контекста размеры набора должны быть нанесены в виде гистограммы вдоль строк или столбцов тепловой карты. Этот тип кодирования поддерживает качественные суждения о распределении размеров парных пересечений и наличии кластеров сильно перекрывающихся множеств, но скрывает информацию о пересечениях более высокого порядка.
Из-за комбинаторного взрывного роста количества наборов пересечений почти всегда приходится идти на компромиссы при визуализации этих данных. Чтобы найти подходящее представление, необходимо понимать задачи, для решения которых предназначены диаграммы, и знать структуру данных.
Ссылки
Wong, B. Nat. Методы 7 , 665 (2010).
Артикул КАС Google Scholar
Wilkinson, L. IEEE Trans. Вис. вычисл. График 18 , 321–331 (2012).
Артикул Google Scholar
Центр анализа геномных данных Broad Institute TCGA. Мутационный анализ (MutSig v2.0). Мультиформная глиобластома, 23 мая 2013 г.; doi: 10.7908/C1HD7SP0 (2013).
Ссылки на скачивание
Информация об авторе
Авторы и филиалы
Александр Лекс — докторант в области компьютерных наук Гарвардского университета.
 ,
,Александр Лекс
Нильс Геленборг — научный сотрудник Гарвардской медицинской школы и Института Броуда Массачусетского технологического института и Гарварда.,
Нильс Геленборг
Авторы
- Александр Лекс
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Академия
- Нильс Геленборг
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Декларации этики
Конкурирующие интересы
Авторы не заявляют об отсутствии конкурирующих финансовых интересов.
Права и разрешения
Перепечатка и разрешения
Об этой статье
Эта статья цитируется
Специфические для пола модели и пожизненный риск полиморбидности в общей популяции: 23-летнее проспективное когортное исследование
- Пржемысл Велек
- Аннемари И.
 Луйк
Луйк - Сильван Лихер
БМС Медицина (2022)
Стеатоз печени и стеатогепатит: функциональный метаанализ половых различий в транскриптомных исследованиях
- Хосе Ф. Катала-Сенент
- Марта Р. Идальго
- Франсиско Гарсия-Гарсия
Биология половых различий (2021)
Распространение открытого доступа в Германии, 2010–2018 гг.


 .. — Учеба и наука
.. — Учеба и наука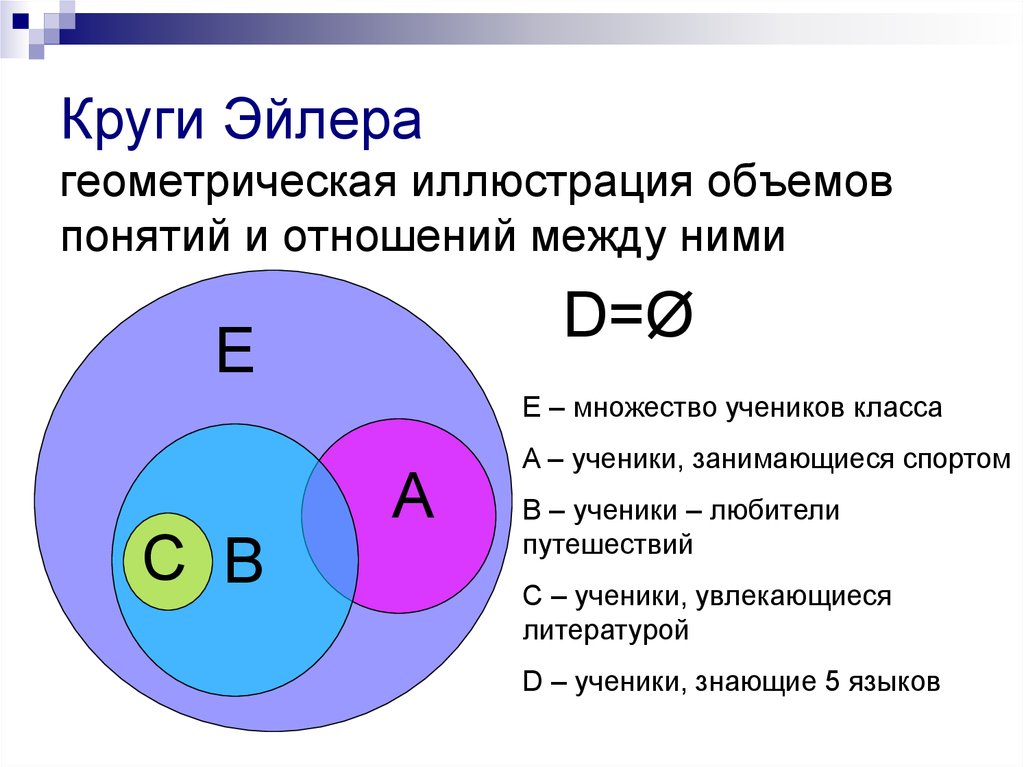 02.17
02.17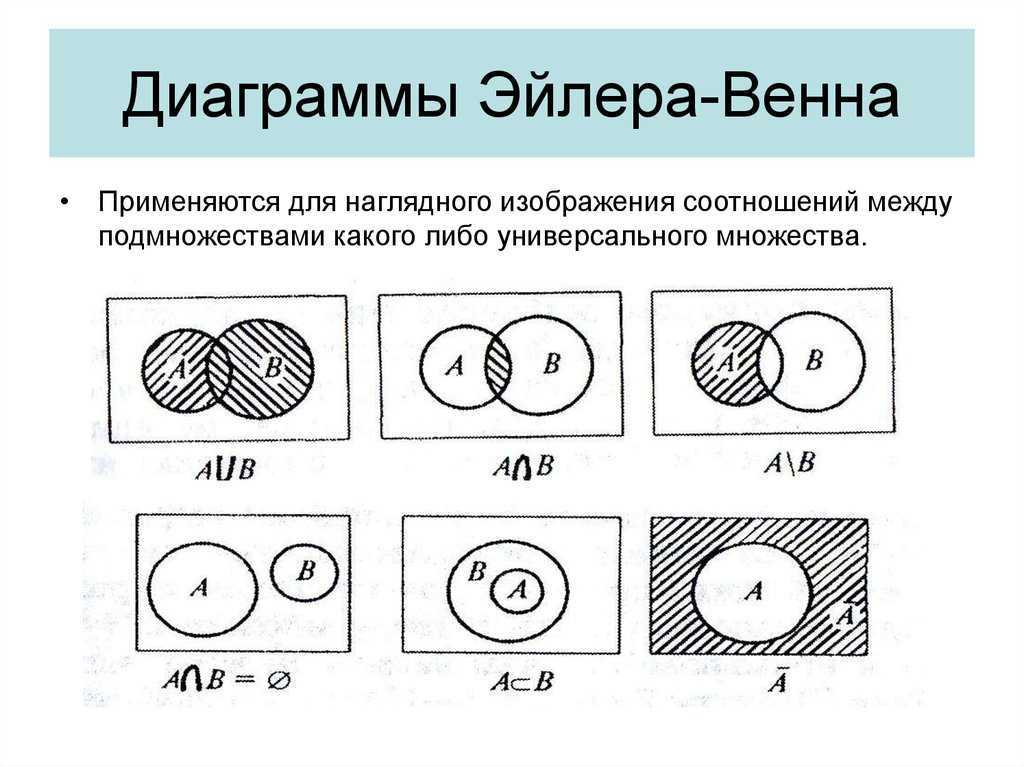 ,
, Луйк
Луйк