Отрицательное число плюс положительное: Сложение Чисел с Разными Знаками

Как складывать и вычитать отрицательные и положительные числа?

Как складывать и вычитать отрицательные и положительные числа?

То есть вычитание положительных и отрицательных чисел можно заменить сложением. Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому. Или по другому можно сказать, что вычитание числа «b» — это тоже самое сложение, но с числом противоположным числу «b».

Что будет если сложить два отрицательных числа?

Также понятно, что результатом сложения двух отрицательных чисел является отрицательное число, о чем свидетельствует знак минус, который ставится перед суммой модулей.

Как найти сумму чисел с разными знаками?

Чтобы сложить числа с разными знаками, нужно из большего модуля вычесть меньший модуль, и перед полученным ответом поставить знак того числа, модуль которого больше. Чтобы из меньшего числа вычесть большее, нужно из большего числа вычесть меньшее и перед полученным ответом поставить минус.

Что нужно сделать чтобы вычесть числа с разными знаками?

Правило вычитания чисел с разными знаками дословно совпадает с правилом вычитания отрицательных чисел. Его формулировка такова: вычесть из числа a число b – это все равно, что к числу a прибавить число −b, где b и −b – противоположные числа.

Каким будет результат если отрицательное рациональное число разделить на отрицательное целое число?

Очевидно, что данное правило сводит деление отрицательных чисел к делению положительных чисел (модулей делимого и делителя), следовательно, результатом деления отрицательного числа на отрицательное число будет положительное число.

Как поделить отрицательное число на положительное?

Итак, правило деления чисел с разными знаками имеет следующую формулировку: чтобы разделить положительное число на отрицательное или отрицательное число на положительное, надо модуль делимого разделить на модуль делителя, и перед полученным числом поставить знак минус.

Как умножать и делить положительные и отрицательные числа?

Умножение положительных и отрицательных чисел (то есть чисел с разными знаками) выполняется по следующему правилу: Чтобы перемножить два числа с разными знаками (положительное и отрицательное число), надо перемножить их модули и перед полученным произведением поставить знак «минус».

Что будет если умножить плюс на минус?

Существуют определенные правила умножения отрицательных чисел. «−−»− при умножении минус на минус результат становится положительным; «−+»− при умножении минуса на плюс результат становится отрицательным; … «++»− при умножении плюса на плюс результат становится положительным.

Сколько будет минус умножить на минус?

Минус умноженный на минус дает плюс, минус деленный на минус будет плюс. Произведение двух отрицательного чисел — положительное число, частное двух отрицательного чисел — число положительное. При делении или умножении двух отрицательных чисел получается положительное число.

Что получится если у отрицательного числа убрать минус?

При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.

Как из отрицательного числа вычесть отрицательное?

Имеет место следующее правило вычитания отрицательных чисел: чтобы из числа a вычесть отрицательное число b, нужно к уменьшаемому a прибавить число −b, противоположное вычитаемому b. В буквенном виде правило вычитания отрицательного числа b из произвольного числа a выглядит так: a−b=a+(−b).

Как объяснить действия с отрицательными числами?

Отрицательные числа — это числа со знаком минус (−), например −1, −2, −3. Читается как: минус один, минус два, минус три. Примером применения отрицательных чисел является термометр, показывающий температуру тела, воздуха, почвы или воды.

Как складывать рациональные числа?

Правило. Чтобы вычислить сумму рациональных чисел , нужно отдельно сложить все положительные числа (заключив в скобки и поставив перед скобкой знак «+») и отдельно сложить все отрицательные числа (заключив в скобки и поставив перед скобкой знак «-»).

Как сложить рациональные дроби с разными знаменателями?

Чтобы сложить две дроби с разными знаменателями, надо привести их к общему положительному знаменателю и сложить полученные дроби. Чтобы вычесть две дроби с одинаковым положительными знаменателями, надо из числителя уменьшаемого вычесть числитель вычитаемого, а знаменатель оставить прежним.

Что значит выражение является рациональным?

Целые выражения – это такие выражения, которые состоят из чисел и переменных с помощью действий сложения, вычитания, умножения и деления на число, отличное от нуля. … Рациональное выражение – это любое выражение, составленное из чисел, буквенных переменных, арифметических операций и возведения в степень.

Что такое рациональные дроби?

Дробно-рациональное выражение — это дробь, числителем и знаменателем которой являются многочлены с рациональными(целыми) коэффициентами. … Рациональная дробь называется правильной, если порядок знаменателя больше порядка числителя, и неправильной, если наоборот.

Как сократить дробь на дробь?

Сократить дробь — значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы. В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби. К примеру, возьмем обыкновенную дробь 624 и сократим ее.

Что является произведением двух рациональных дробей?

Произведение двух дробей есть дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей этих дробей. Чтобы умножить натуральное число на дробь, можно числитель дроби умножить на это число, а знаменатель оставить тот же.

Какие числа называют рациональными 6 класс?

Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби. Множество рациональных чисел принято обозначать латинской буквой Q. Подружиться с математикой и повысить оценки в школе — проще, чем кажется.

Что такое целое число 6 класс?

Целые числа – это множество чисел, состоящие из натуральных чисел, целых отрицательных чисел и нуля. Ряд целых чисел в положительную и в отрицательную сторону является бесконечным множеством. Если мы возьмём два любых целых числа, то числа, стоящие между этими целыми числами, будут называться конечным множеством.

Как найти рациональное и иррациональное число?

Любое рациональное число представимо в виде периодической бесконечной десятичной дроби. Множество рациональных чисел обозначается Q. Если действительное число не является рациональным, то оно иррациональное число. Десятичные дроби, выражающие иррациональные числа бесконечны и не периодичны.

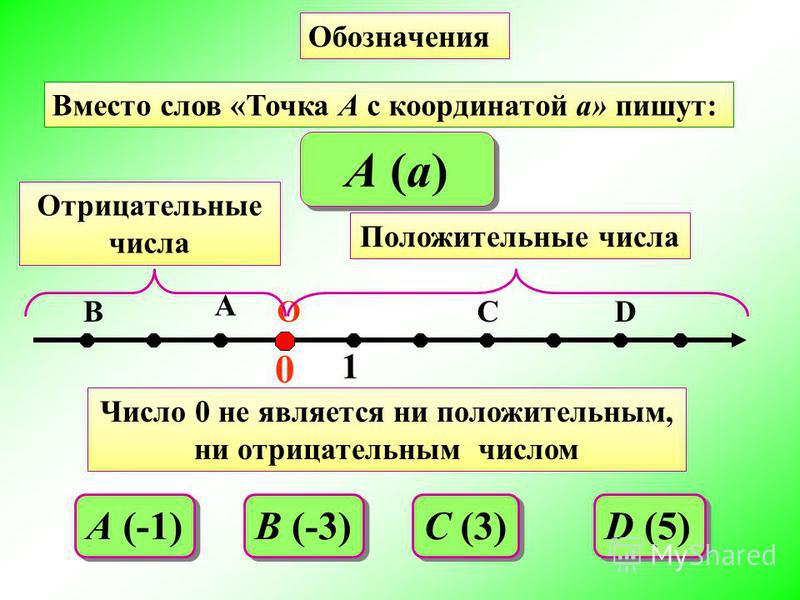
Целые числа: положительные и отрицательные. Сравнение целых чисел

• Положительные и отрицательные числа
• Сравнение целых чисел

Целые числа — это положительные и отрицательные числа, не имеющие дробной части и число нуль.

Число  0  целое, но не является ни положительным, ни отрицательным числом.

Ставить перед числом нуль какой-либо знак (+ или -) не имеет смысла, так как записи

+0,  -0  и  0

представляют собой одно и тоже число:

+0 = -0 = 0.

Положительные и отрицательные числа

Существуют величины, отсчёт которых производиться в двух противоположных направлениях.

Пример. Температура отсчитывается в двух противоположных направлениях от температуры тающего льда, принимаемой за нулевую:

1) Уровень ртути при нулевой температуре (температуре тающего льда).

2) Уровень ртути при температуре, более низкой, чем нулевая.

3) Уровень ртути при температуре, более высокой, чем нулевая.

Если мы имеем какую-либо величину, отсчёт которой производится в двух противоположных направлениях, то одно из направлений, безразлично какое, принято называть положительным, а другое отрицательным.

Положительное число — это число, полученное в результате измерения величины, отсчитанной в положительном направлении. Положительное число изображается в виде числа со знаком + (плюс) впереди. Например,  +16  — положительное число.

Пример.

16 °C тепла  или  +16 °C.

Примечание: все градусы пишутся с буквой  C (Цельсия),  знак градуса отделяется от числа пробелом. Например,  +7 °C.

Наименьшее целое положительное число – это  1  (единица).

Отрицательное число — это число, полученное в результате измерения величины, отсчитанной в отрицательном направлении. Отрицательное число изображается в виде числа со знаком

— (минус) впереди. Например,  -16  — отрицательное число.

Пример.

16 °C мороза  или  -16 °C.

Наибольшее целое отрицательное число – это  -1  (минус один).

Все числа, кроме нуля, записанные со знаком + (плюс) впереди, являются положительными, а записанные со знаком — (минус) — отрицательными.

Пример.

+1,  +15,  +57  и т. д. — положительные числа;

-1,  -15,  -57  и т. д. — отрицательные числа.

Положительные числа можно обозначать предшествующим знаком + (плюс) или опускать его. Числа, перед которыми не стоит знака (+ или -), считаются положительными числами. Например, вместо

+8,  +14,  +100  и т. д.

можно написать просто

8,  14,  100  и т. д.

Сравнение целых чисел

Сравнить два целых числа — значит, узнать, какое из них больше, какое меньше, или определить, что числа равны.

Сравнивать целые числа можно с помощью ряда целых чисел, так как числа в нём расположены от меньшего к большему, если двигаться по ряду слева направо. Поэтому в ряду целых чисел можно заменить запятые на знак меньше:

… -5 < -4 < -3 < -2 < -1 < 0 < 1 < 2 < 3 < 4 < 5 < …

Следовательно, из двух целых чисел больше то число, которое в ряду стоит правее, и меньше то, которое стоит левее, значит:

1) Любое положительное число больше нуля и больше любого отрицательного числа:

1 > 0;    15 > -16.

2) Любое отрицательное число меньше нуля:

-7 < 0;    -357 < 0.

3) Из двух отрицательных чисел больше то, которое в ряду целых чисел стоит правее:

-31 < -28.

Что такое минус плюс минус?

Алгебра — одна из старейших областей математики, занимающаяся теорией чисел и геометрическим анализом. Алгебра — это изучение математических символов и правил , в том числе управление этими математическими символами. Алгебра охватывает практически все, от решения простых уравнений до изучения абстракций.

Алгебра также охватывает широкий круг предметов, от решения фундаментальных задач до изучения абстракций. В основном сосредоточены на переменных с неопределенными значениями. Раздел математики имеет дело с переменными и арифметическими операциями, выполняемыми над этими символами. Эти переменные не имеют установленных значений. В повседневной жизни мы сталкиваемся с проблемами. Некоторые значения постоянно меняются.

Эти значения или переменные часто представляются в алгебре такими символами, как a, b, c, d, x, y, z, p или q. Эти переменные обрабатываются с помощью различных математических операций, таких как сложение, вычитание, умножение и деление, для определения их значений.

Выражение представляет собой комбинацию терминов, объединенных вместе с помощью математических операций, таких как вычитание, сложение, умножение и деление.

• Константа — это число или цифра, имеющая фиксированное значение.
• Переменная — это символ с нефиксированным значением.
• Термин определяется как константа, отдельная переменная или комбинация переменной и константы в сочетании с умножением или делением.

Примеры выражений в алгебре: 5x+9, 7x + 12 и т. д.

Переменные: Переменная — это буквенно-цифровой символ, представляющий числовое значение или число. Переменная в алгебре используется для представления неизвестного количества неизвестных значений.

Чаще всего в качестве переменных в уравнениях используются буквы «a», «b», «c», p, q, «x», «y», «z». Термин «переменная» относится к значению другой переменной или уравнения.

Что такое минус плюс минус?

Решение:

Существуют разные правила сложения отрицательных чисел.

Обычно добавление означает увеличение значения. Однако в случае целых чисел операция сложения может привести к увеличению или уменьшению значения данного числа.

Когда мы добавляем отрицательное целое число, значение данного числа уменьшается.

Type of numbers	Operation sign	Outcome	Example
Positive + Positive	+	Positive (+)	3 + 2 = 4
Отрицательный + Отрицательный	+	Отрицательный (-)	(-3)+(-2) = -5
Положительный + Отрицательный	+	+ или – (в зависимости от знака большего числа)	3 +(-2) = 1 или (-3 106 1007) +2 = -1 9000 поэтому, когда мы добавляем отрицательный плюс отрицательный термин, результат будет отрицательным. Всякий раз, когда мы складываем два отрицательных целых числа, получается сумма абсолютного значения целых чисел с отрицательным знаком. Решенные примеры на основе целых чисел Пример 1: Сложите два положительных числа 5 и 2. Какой будет конечный знак? Решение: Указанные номера: 5 и 2 Теперь добавьте: 5 + 2 = 7 Если мы добавим два положительных числа, то результат будет положительным числом. Пример 2: Сложите два отрицательных числа 5 и 2. Что получится в результате? Решение: Указанные номера: 5 и 2 Теперь добавить: -5 + (-2) = -5 -2 = -7 Если мы добавим два отрицательных числа, то результат будет отрицательным номером. Пример 3: Если мы сложим отрицательные и положительные числа -5 и 2? Каков будет результат? Решение: Даны числа: -5 и 2          0005 Если большее число отрицательное, то результат будет отрицательным. Пример 4. Если мы сложим отрицательные и положительные числа 5 и -2? Каков будет результат? Решение: Указанные номера: 5 и -2 Теперь добавьте: 5 + (-2) = 5 -2 = 3 , если большее число положительное, тогда результат будет будь позитивным. Часто задаваемые вопросы о целых числах Вопрос 1. Что такое целые числа? Ответ: Целые числа представляют собой комбинацию нуля, натуральных чисел и их аддитивной инверсии. Его можно представить в виде числовой строки без дробной части. Обозначается Z. Вопрос 2: Что такое целочисленная формула? Ответ: Целое число представляет собой набор положительных и отрицательных чисел вместе с нулем и не имеет никакой формулы. Вопрос 3: Каковы примеры целых чисел? Ответ: Примеры целых чисел: 3, -5, 0, 99, -45 и т. д. Вопросы 4. Могут ли целые числа быть отрицательными? Ответ: Да, целые числа могут быть отрицательными. Аддитивными обратными натуральными числами являются отрицательные целые числа, такие как -1, -2, -3, -4, -5 и т. д. Вопрос 5: Какие бывают типы целых чисел? Ответ: Целые числа бывают трех типов: Ноль, положительные целые и отрицательные числа Вычитание отрицательных чисел из положительных чисел вовлеченный. Вот почему, прежде чем мы углубимся в вычитание отрицательных чисел из положительных чисел, мы сначала вернемся к основам чисел, сложению и вычитанию, чтобы концепции строились друг на друге. Числа могут быть положительными или отрицательными Числа могут быть положительными или отрицательными. Подумайте обо всех числах, которые существуют; все они находятся в спектре от отрицательного через ноль к положительному. Представьте все эти числа в строке; это облегчит вам представление каждого числа как положительного или отрицательного. Например: -9, -8, -7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Все числа справа от нуля положительные. Обозначение положительных целых чисел При обозначении положительных чисел или целых чисел нам не нужно добавлять знак плюс «+» перед числом; предполагается, что число положительное, если нет отрицательного знака «-». Это означает, что число «3» на самом деле равно «+3». Если мы хотим, чтобы число 3 было отмечено как отрицательное, мы должны указать его как «-3». Добавление положительного числа к другому положительному числу Когда мы складываем два или более положительных числа вместе, мы обычно используем знак плюс ‘+’. Например: 5 + 7 = 12 5 и 7 — положительные числа. 7 добавляется к значению 5 и, таким образом, увеличивает общее значение суммы. Вычитание положительного числа из другого положительного числа Когда мы вычитаем положительное число из другого положительного числа, мы обычно используем знак минус ‘-‘. Например: 8 — 4 = 4 8 и 4 и оба положительных числа (обратите внимание на отсутствие знака минус перед каждым из них) и, таким образом, 4 отнимает значение от восьми. Добавление отрицательного числа к положительному или наоборот При сложении отрицательного знака «-» и положительного знака знак с большим значением будет знаком суммы. Например: 3 + (-2) = 1, т.е. (+1), потому что положительный знак имеет большее значение, чем отрицательный. Другой пример: 2 + (-4) = (-2), потому что отрицательный знак имеет более высокое значение, чем положительный знак. или даже (-5) + 7 = 2, то есть (+2), потому что положительный знак имеет большее значение. Помните, что положительное число плюс отрицательное число всегда является вычитанием, и знак суммы определяется тем, какой из знаков имел большую величину. т.е. 4 +(-2) = 4 — 2 = 2 и 4 + (-6) = 4 — 6 = (-2) Вычитание положительного числа из отрицательного числа При вычитании положительного числа из отрицательного числа разница всегда будет иметь отрицательный знак. Это потому, что вы фактически добавляете числа на отрицательной стороне числовой строки. Подумайте о числовой строке: -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5 Теперь представьте, что из 5 нужно убрать 2, что бы вы сделали? Вы бы сделали два шага влево от пяти, и это сделало бы ваш ответ 3. Та же концепция применяется при вычитании положительного числа из отрицательного числа. Например, (-3) — 2 = (-5), то есть вы делаете два шага влево от отрицательной тройки на числовой прямой, чтобы получить свою разницу. Это дает тот же эффект, что и сложение двух положительных чисел, только с добавлением отрицательного знака перед ответом. Итак, в следующий раз, когда вы застрянете при вычитании положительного числа из отрицательного числа, просто сложите два числа вместе и поставьте знак минус «-» перед общей суммой. Например: -5 — 7 = -5 — (+7) = (-12), но если вы застряли, просто измените вопрос на 5 + 7 = 12, а затем добавьте к ответу знак минус «-«. Вычитание отрицательного числа из другого отрицательного числа При вычитании отрицательного числа из другого отрицательного числа знак минус становится положительным. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт