Функции Excel для перевода из РАДИАНЫ в ГРАДУСЫ и обратно
Функция РАДИАНЫ (на английском RADIANS) – это одна из математических и тригонометрических функций, которая часто применяется для инженерных расчетов. Данная функция в Excel легко преобразует градусы в радианы – угол, соответствующий дуге, а длина этой дуги равна ее радиусу.
Как работает функция индекс в Excel?
ПРИМЕР 1. Для инженерных расчетов связанных с движением по окружности зачастую необходимо вычислять угловые скорости и переводить градусы в радианы и радианы в градусы. В Excel для этого предусмотрены специальные функции. Для упрощения математических расчетов может потребоваться выразить в одной и второй величине.
Нам необходимо найти сколько будет в Радианах 180°. Нажимаем кнопку fx возле строки формул для вызова окна выбора функций «Вставка функции» (SHIFT+F3) и в окне поиска вводим функцию «РАДИАНЫ». Выбираем высветившуюся нужную функцию, как показано на ниже рисунке.
Появляется окно, в которое нужно ввести аргументы функции.
Вводим значение 180, так как нам нужно найти сколько будет радиан в 180 градусах. Жмем ОК.
В 180 градусах будет 3,1415 радиан.
Найдем радианы для угла в 90°. Откроем окно функций и введем функцию, что необходимо вычислить. Находим ее в окне мастера функций и выбираем аргумент 90.
ОК. В 90 градусах будет 1,5707 радиан.
В следующих примерах рассмотрим, как конвертировать эти единицы измерения углов в обоих направлениях.
Как перевести Радианы в Градусы средствами Excel
ПРИМЕР 2. Иногда нужно единицу измерения углов rad перевести в значение gradus°. Для этого предусмотрена функция ГРАДУСЫ. Она позволяет перевести значения выраженные в радианах в градусы в десятичном исчислении.
Нам нужно найти сколько будет в градусах 4,1 радианы. Нажимаем кнопку fx для вызова окна выбора функции и в окне поиска вводим соответствующее название функции.
Появляется окно в которое нужно ввести аргументы функции. Вводим значение 4,1, так как нам следует найти сколько будет gradus° в 4,1 rad.
Нажимаем ОК.
Для исходного значения 4,1 получаем ровно 235 градусов.
Таким образом выполняется перевод из радиан в градусы в Excel.
Сколько радиан в нескольких значениях градуса?
ПРИМЕР 3. Иногда нужно определить сколько радиан в сразу нескольких значениях градуса и вводить тогда каждый раз аргумент очень долго. В таком случае можно воспользоваться немного иным способом конвертирования величин для измерения углов.
Требуется найти сколько будет в Радианах 45, 67, 23, 12, 57 градусов. Нажимаем кнопку fx (SHIFT+F3) для вызова окна выбора функции и в окне поиска вводим необходимо функцию как показано ниже на рисунке. Указываем на высветившуюся функцию.
Выбираем диапазон градусов (А3 по А7) и нажимаем на кнопку ОК.
Протягиваем строку вниз для того, чтобы мы могли узнать сколько радиан во всех приведенных градусах, не вызывая функцию по несколько раз.
Получаем сразу значения всех радиан:
Для 45 градусов – это 0,7853, для 67 градусов – это 1,1693, для 23 градусов – это 0,4014, для 12 градусов – это 0,2094, для 57 градусов – это 0,9948 в радианах.
Градусная мера углов
Наверное, при изучении курса геометрии вы не раз задавались вопросом, что же такое эти градусы, радианы и с чем их едят? Попробуем разобраться.
Само понятие «градус» появилось еще в Древнем Вавилоне около 40 веков назад. Придумали его очень просто – взяли и разбили окружность на 360 частей, поэтому так и вышло, что 1/360 окружности и есть 1 градус. В это же время в Древнем Египте пытались измерить, во сколько же раз окружность больше, чем диаметр этой самой окружности. Установить это смогли лишь через 35 веков, и то, получили неровное число, а 3,141592, в общем, бесконечное иррациональное. Для удобства его округлили до 3,14 и получили не что иное, как всем известное число Пи.
Однако вернемся к градусам. Градусная мера угла, конечно же, хорошо, но для высшей математики не подходит. Поэтому и придумали радиан.
Что же это за зверь такой? На самом деле ничего сложного, просто чуть-чуть запутанно на первый взгляд. В основе определения радиана лежит все та же старая и добрая окружность, с которой так долго мучились египтяне.
Угол величиной в 1 радиан – это угол, который вырезает в окружности такую дугу, длина которой равна радиусу окружности. Не вдаваясь в подробности, скажем лишь одно – радиан в несколько раз больше градуса. Но давайте определим все-таки приблизительное соотношение градуса и радиана. На самом-то деле доказано, что в 180 градусов вмещается 3 радиана с хвостиком. А что же за хвостик? Его величина составляет 0,141592, то есть в 180 градусов вмещается 3,141592 радиан (число Пи). Не зря в начале статьи мы заговорили о древних египтянах, которые так долго с ним мучились.
Но все же самым главным в теме градусов и радиан остается умение переводить их друг в друга, то есть радианы в градусы и наоборот, градусы в радианы.
π ≈ 3,1415926535897932384626433832795
| 1 радиан = | 180° π | ≈ 57°17’45» |
| 1° = | π 180° | радиана ≈ |
≈ 0,017453292519943295769236907684886
| 1′ = | π 180 * 60 | радиана ≈ |
≈ 0,00029088820866572159615394846141477
| 1» = | π 180 * 60 * 60 | радиана ≈ |
≈ 0,0000048481368110953599358991410235795
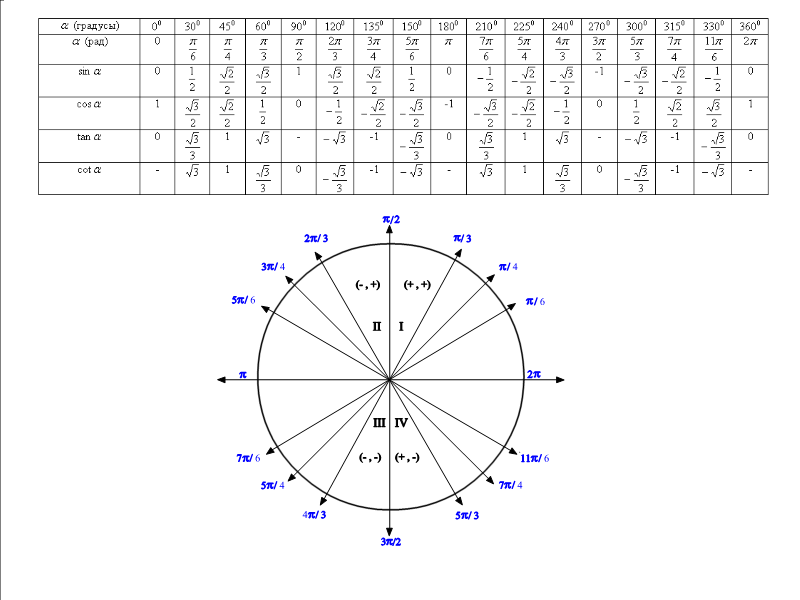
| 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° |
|---|---|---|---|---|---|---|---|---|
| 0 | π 6 | π 4 | π 3 | π 2 | 2π 3 | 3π 4 | 5π 6 | π |
| 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|
| 7π 6 | 5π 4 | 4π 3 | 3π 2 | 5π 3 | 7π 4 | 11π 6 | 2π |
градусов/минут/секунд (DMS) в сравнении с десятичными градусами (DD)
Для позиционирования мы можем найти любое место на Земле, используя координаты широты и долготы.
И мы измеряем эти координаты, используя десятичные градусы или градусы/минуты/секунды .
В то время как линии широты находятся в диапазоне от -90 до +90 градусов, координаты долготы находятся в диапазоне от -180 до +180 градусов.
Вы заметили, как мы используем градуса для координат широты и долготы? Давайте начнем с некоторых ключевых примеров того, как мы используем угловые единицы.
Обзор географических систем координат
В географической системе координат (ГСК) мы можем ссылаться на любую точку на Земле по ее координатам долготы и широты. Поскольку GCS использует сферу для определения местоположения на Земле, мы используем углы, измеряемые в градусах от центра Земли до любой точки на поверхности.
Координаты (0°N, 0°E) — это пересечение экватора и нулевого меридиана. Самое смешное, что если вы посмотрите на это место на карте, то увидите, что это весь океан.
Но из-за того, что специалисты по ГИС иногда ошибочно определяют свой проект при добавлении координат XY, (0°N, 0°E) превратилось в вымышленное местоположение, называемое «нулевым островом».
Когда мы движемся на север вдоль нулевого меридиана, значение долготы остается фиксированным на 0°. Но угол широты и координата увеличиваются, потому что мы движемся на север.
Если двигаться на север под углом 51,5°, вы окажетесь в Королевской обсерватории в Гринвиче, Англия, как показано на рисунке ниже. Собственно, поэтому линия долготы 0° является исходной точкой отсчета. От Гринвичского меридиана мы можем найти позиции на восток и запад.
Так как начальный меридиан является начальной точкой 0° для координат долготы, отсюда все ссылки.
Например, мы можем изменить угол на 80,4° на запад.
Это смещает нас на 80,4° западной долготы от нулевого меридиана. И совершенно случайно Питтсбург расположен на этой линии долготы примерно на (40,4° с.ш., 80,4° з.д.)
Напомним:
Экватор — это 0° широты, где мы измеряем север и юг. Это означает, что все к северу от экватора имеет положительные значения широты. Принимая во внимание, что все к югу от экватора имеет отрицательные значения широты.
Альтернативно, Гринвичский меридиан (или нулевой меридиан) — это нулевая линия долготы, от которой мы измеряем восток и запад.
Десятичные градусы и градусы/минуты/секунды
Одним из способов записи сферических координат (широт и долгот) является использование градусов-минут-секунд (ГМС). Минуты и секунды находятся в диапазоне от 0 до 60. Например, географическая координата Нью-Йорка, выраженная в градусах-минутах-секундах:
ШИРОТА: 40 градусов, 42 минуты, 51 секунда N
ДОЛГОТА: 74 градуса, 0 минут, 21 секунда W
Но вы также можете выразить географические координаты в десятичных градусах.