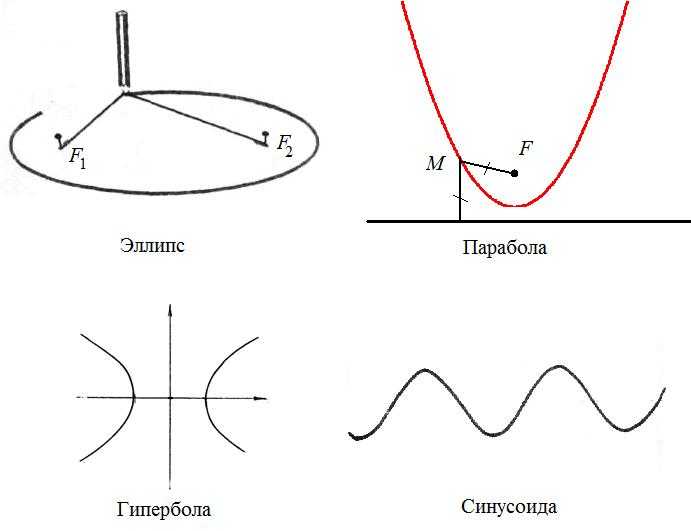
Парабола гипербола эллипс: Эллипс, гипербола, парабола. Директориальное свойство эллипса и гиперболы. Полярный параметр.

Содержание

Оптическое свойство

эллипса, параболы, гиперболы

Переход между слайдами — стрелочками.

Поместим в одном из фокусов зеркального эллипса лампочку

Поместим в одном из фокусов зеркального эллипса лампочку
и проследим за выпущенными из неё лучами света.

Отразившись от эллипса, они соберутся в другом фокусе!

Причём окажутся там одновременно (почему, кстати?).

Оптическое свойство эллипса:
углы касательной с отрезками,
соединяющими точку касания с фокусами, равны.

Как это доказать?

Напомним геометрическое определение эллипса:

эллипс есть множество точек

M плоскости, сумма расстояний от которых до данных точек A и B постоянна.

Чтобы доказать оптическое свойство, решим сначала вспомогательную задачу.

Даны две точки по одну сторону от прямой.

Решим вспомогательную задачу.

Даны две точки по одну сторону от прямой.

Мы хотим пройти из A в B, набрав по пути воды из реки l.

В какой точке M надо набирать воду, чтобы общий путь имел минимальную длину?

Рассмотрим точку B’, симметричную точке B.

XB = XB’

Длина AX+XB = AX+XB’ минимальна, когда ломаная AXB’ превращается в прямую.

Мы хотим пройти из A в B, набрав по пути воды из реки l. В какой точке набирать воду?

Ответ: в точке пересечения l с AB’
(где B’ симметрична B относительно l).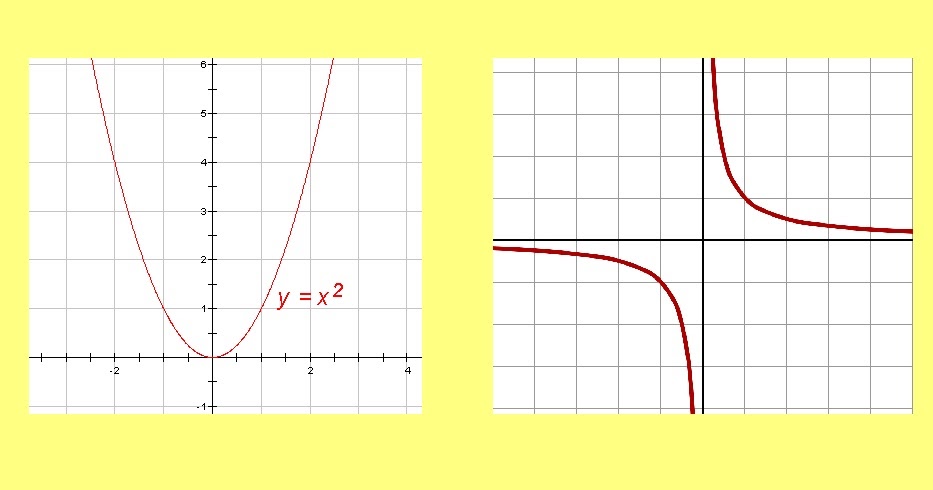

Мы хотим пройти из A в B, набрав по пути воды из реки l. В какой точке набирать воду?

Ответ: в точке пересечения l с AB’.

Заодно мы доказали равенство углов.

Мы хотим пройти из A в B, набрав по пути воды из реки l.
Где набирать воду?

Ответ 1: в точке пересечения l с AB’.

Ответ 2: там, где «угол падения равен углу отражения».

Принцип Ферма: свет выбирает кратчайший путь между двумя точками.

Вернемся к доказательству оптического свойства эллипса.

На эллипсе сумма AM+MB постоянна.
А для точек вне эллипса эта сумма больше, AX+XB > AM+MB.

В частности, если провести в точке M касательную к эллипсу, то для любой другой точки X на этой касательной
AX+XB > AM+MB.

Значит, по предыдущей задаче «угол падения равен углу отражения».

…по предыдущей задаче «угол падения равен углу отражения».

Оптическое свойство эллипса доказано.

…по предыдущей задаче «угол падения равен углу отражения».

Оптическое свойство эллипса доказано.

Поместим теперь лампочку в фокус параболы

Поместим теперь лампочку в фокус параболы
и проследим за выпущенными из нее лучами света.

После отражения от параболы получится параллельный пучок.

Другими словами, касательная к параболе является биссектрисой угла между отрезком из точки касания в фокус и перпендикуляром из неё на директрису.

Напомним геометрическое определение параболы:

парабола есть множество точек плоскости, равноудаленных от данной точки и данной прямой.

Докажем оптическое свойство параболы.

Предположим, что биcсектриса не является касательной, а пересекает параболу ещё в одной точке.

Предположим, что биссектриса не является касательной, а пересекает параболу ещё в одной точке.

Соединим точку N с фокусом и с точкой G.

Предположим, что биссектриса не является касательной, а пересекает параболу ещё в одной точке.

Отрезки NG и NF равны (так как треугольники MNG и MNF равны по двум сторонам и углу между ними).

Предположим, что биссектриса не является касательной, а пересекает параболу ещё в одной точке.

Итак, NG = NF.

Но опустим из точки N перпендикуляр NH на директрису.

Предположим, что биссектриса не является касательной, а пересекает параболу ещё в одной точке.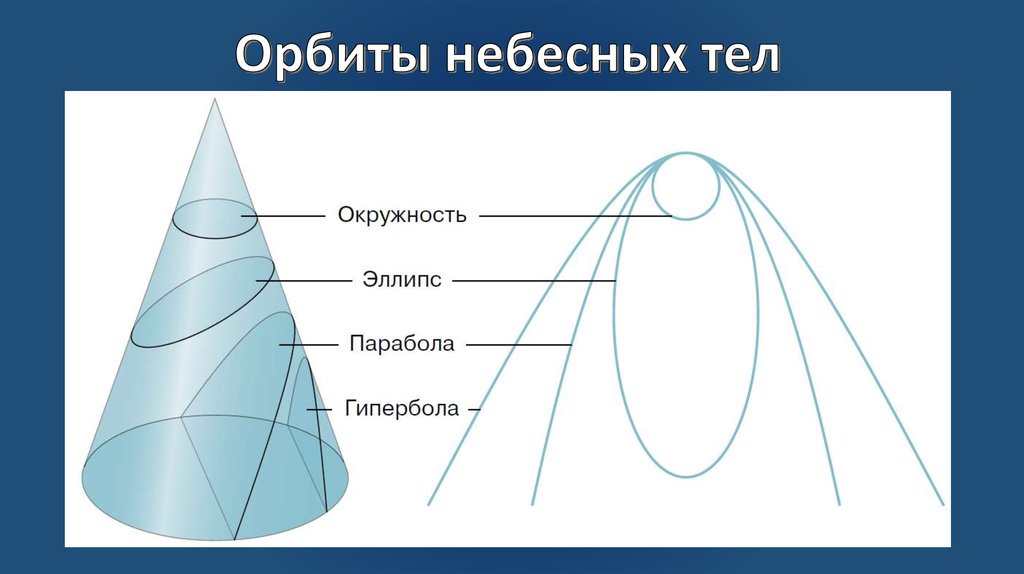

NG = NF. Но и NH = NF (по определению параболы).

Противоречие.

Оптическое свойство параболы доказано.

На оптическом свойстве параболы основана работа спутниковых антенн и не только.

Из доказательства видно и кое-что ещё.

Например, что основания перпендикуляров, опущенных из фокуса на касательные, лежат на одной прямой.

То есть если через каждую точку M данной прямой провести перпендикуляр к отрезку, соединяющему M с данной точкой, то возникнет семейство прямых…

…возникнет семейство прямых,
огибающей которого является парабола.

(А как подобным образом получить эллипс и гиперболу?
К этому мы ещё вернёмся.)

Напомним геометрическое определение гиперболы:

гипербола есть множество точек M плоскости, модуль разности расстояний от которых до данных точек A и B постоянен.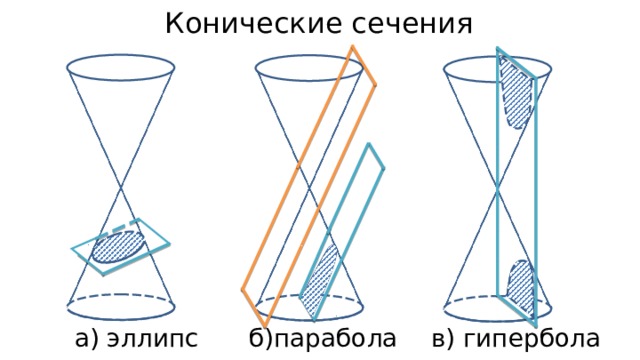

Есть оптическое свойство и у гиперболы.

Попробуйте его доказать.

Для доказательства оптического свойства полезно, как и в случае эллипса, начать с задачи на максимум:
для какой из точек M прямой разность AM − MB максимальна?

Зная оптические свойства и эллипса, и гиперболы, несложно доказать (сделайте это!), что эллипс и гипербола с общими фокусами перпендикулярны (т. е. перпендикулярны касательные в точках пересечения).

Вернемся к оптическому свойсту эллипса.

При решении вспомогательной задачи возникала точка, симметричная фокусу относительно «реки» (касательной).
Как выглядит ее траектория?

Точка, симметричная фокусу относительно касательной движется по окружности с центром во втором фокусе.

Точка, симметричная фокусу относительно касательной движется по окружности.

Значит, основание перпендикуляра, опущенного из фокуса на касательную, тоже движется по окружности (вдвое меньшей).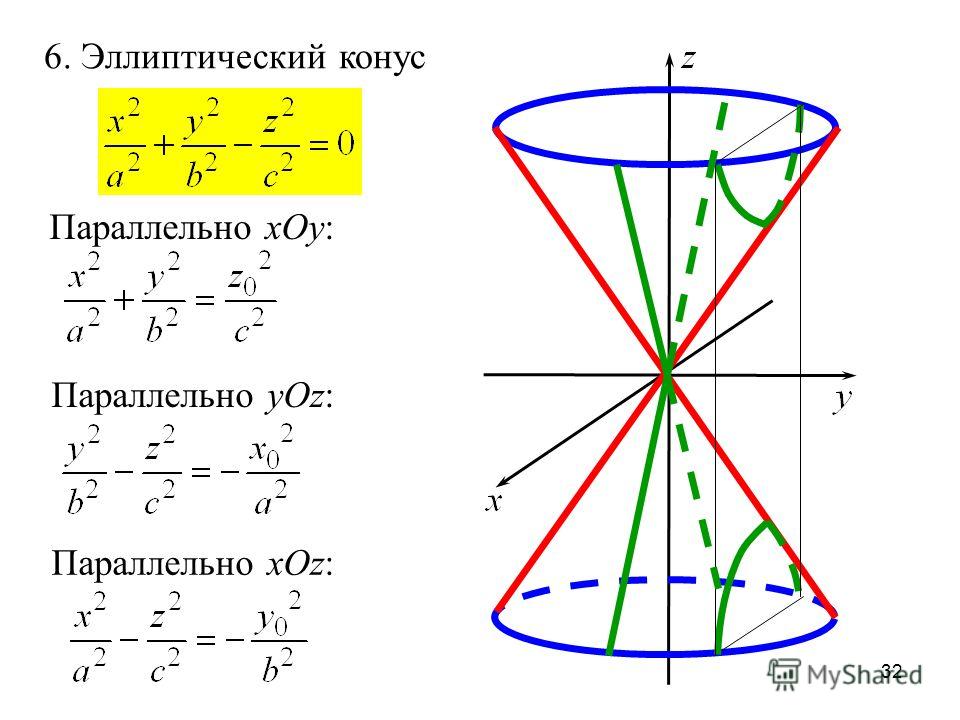

Основание перпендикуляра, опущенного из фокуса эллипса на касательную, движется по окружности.

То есть эллипс получается как огибающая соответствующего семейства прямых.

Похожим образом возникает
как огибающая семейства прямых
и гипербола.

версия 1.0.3 (июль 2018)

поделиться: vk / fb

больше можно узнать из книги «Прямые и кривые»
Н. Б. Васильева и В. Л. Гутенмахера

другие истории: про котёнка на лестнице

4. Порядок алгебраических линий. Окружность. Эллипс. Гипербола. Парабола . Высшая математика. Шпаргалка

Линия L, представленная в декартовой системе уравнением

n–степени называется алгебраической линией n–порядка.

Окружность с радиусом R и центром в начале координат описывается уравнением: х² + у² = R², если центром окружности является некоторая точка С (а, b), то уравнением:

(х – а)² + (у – b)² = R².

Чтобы уравнение Ах² + Вх + Ау² + Су + D = 0 описывало окружность, необходимо, чтобы оно не содержало члена с произведением ху, чтобы коэффициенты при х² и у² были равны, чтобы В² + С² – 4АD > 0 (при невыполнении данного неравенства уравнение не представляет никакой линии).

Координаты центра окружности, описанной уравнением Ах² + Вх + Ау² + Су + D = 0 и ее радиус: a = –B / 2A, b = –C / 2A, R²= (В² + С² – 4АD) / 4A².

Эллипс – сжатая окружность (рис. 3).

Рис. 3

Прямая АА₁ называется осью сжатия, отрезок АА₁ = 2а – большой осью эллипса, отрезок ВВ₁ = 2b – малой осью эллипса (a > b) точка О – центром эллипса, точки А, А₁, В, В₁ –

вершинами эллипса. Отношение k = b / a коэффициент сжатия величина ? = 1 – k = (a – b) / a – сжатие эллипса. Эллипс обладает симметрией относительно большой и малой осей и относительно своего центра.

Каноническое уравнение эллипса: x² / a² + y² / b² = 1.

Другое определение эллипса: эллипс есть геометрическое место точек (М), сумма расстояний которых до двух данных точек F, F₁ имеет одно и то же значение 2а (F₁M + FM = 2a) (рис. 4).

Рис. 4

Точки F и F₁ называются фокусами эллипса, а отрезок FF₁ – фокусным расстоянием, обозначается FF₁ = 2с, причем с < а. Эксцентриситет эллипса ? – это отношение фокусного расстояния к большой оси ? = с / а. Эксцентриситет эллипса меньше единицы, имеем: k² = 1 – ?².

Гипербола – это геометрическое место точек, разность расстояний которых до двух данных точек F, F₁ имеет одно и то же абсолютное значение (рис. 5). |F₁M – FM| = 2a. Точки F, F₁ называются фокусами гиперболы, расстояние FF₁ = 2c – фокусным расстоянием. Справедливо: c > a.

Каноническое уравнение гиперболы: х² / а² + у² / (а²– с²) = 1. Асимптоты гиперболы заданы уравнениями у = bx / a и y = – bx / a (b² = c² – a²).

Парабола – это геометрическое место точек равноудаленных от данной точки F (фокуса параболы) и данной прямой PQ (директрисы параболы). Расстояние от фокуса до директрисы FC называется параметром параболы и обозначается р. Вершина параболы – точка О. Каноническое уравнение параболы: у² = 2рх.

Рис. 5

Данный текст является ознакомительным фрагментом.

Красота эллипсов, парабол и гипербол

Коники стали темой главы, которую я больше всего ненавидел в старшекурсниках. Но это потому, что упражнения включают множество ужасных алгебраических вычислений. В этой статье я предлагаю просто взглянуть на их красоту, их удивительные математические свойства и их бесчисленные приложения!

Их красота? Действительно?

Конечно! Во-первых, проверьте, как можно определить коники. Они представляют собой пересечения конуса с плоскостью. В зависимости от того, как плоскость расположена относительно конуса, вы получаете либо эллипс, либо параболу, либо гиперболу! Насколько это сладко?

Но простота их геометрии — не единственная причина красоты этих форм. Что необычно, так это то, как они появляются и играют ключевую роль во многих областях!

Эллипсы, Орбиты и Галерея Витторио Эмануэле

Начнем с эллипсов. Потребовались тысячелетия, чтобы понять это, но движение космоса не состоит из идеальных кругов, как считалось долгое время. Скорее, как утверждают законы Иоганна Кеплера, траектории объектов во Вселенной управляются геометрией эллипсов!

Но почему?

Это было тревожной загадкой на целое столетие! Пока не появился гениальный Исаак Ньютон.

Что сделал Ньютон?

Ньютон доказал, что несколько основных законов механики могут объяснить эллиптическое движение планет! А поскольку эти законы также соответствовали законам движения Галилея (включая параболическую кривую свободного падения объектов, к которой мы вернемся позже), Ньютон постулировал, что это универсальные законы Природы! 18 месяцев спустя он опубликовал самую важную книгу Истории физики, Принципы математики . Эта книга должна была полностью изменить наше представление о Вселенной, поскольку впервые в Истории было заявлено об универсальном законе! Что-то, что было правдой на всех уровнях, везде и всегда. Это показано в этом отрывке из другого замечательного научного документального фильма NOVA.

Итак, как говорится в видео, закон обратных квадратов всемирного тяготения подразумевает эллиптические орбиты для планет?

Да! Однако, к сожалению, единственное известное мне доказательство — это доказательство с использованием дифференциального исчисления, которое является длинным и неглубоким… Давайте лучше поговорим о красоте формы эллипса!

Но если вы знаете другое, более проницательное или более геометрическое доказательство эллиптических орбит планет, мне будет более чем интересно его услышать! Вы можете отправить мне свое доказательство по электронной почте или через Facebook или Twitter. Кроме того, я хотел бы подчеркнуть, что закон обратных квадратов — это очень естественный закон. Действительно, если вы посылаете сигнал из точки, то мощность сигнала будет уменьшаться соответственно этому закону обратных квадратов, как объясняется в этом замечательном видео на Veritasium, которое также объясняет дискретную природу света!

Несмотря на то, что я получил определение во введении, я не уверен, что знаю, что такое эллипс!

Хе-хе… Хорошая идея! Более естественный взгляд на эллипсы состоит в том, чтобы определить их как сплющенные круги. Точнее, эллипс получается путем применения гомотетии относительно оси, как это делается ниже:

Такая гомотетия описана в моей статье о симметриях и играет ключевую роль в специальной теории относительности Эйнштейна. Мне нравится это определение, так как оно объясняет, почему круг в перспективе воспринимается как эллипс.

Да?

Да! Когда мы видим в перспективе, некоторые оси круга наклонены больше, чем другие.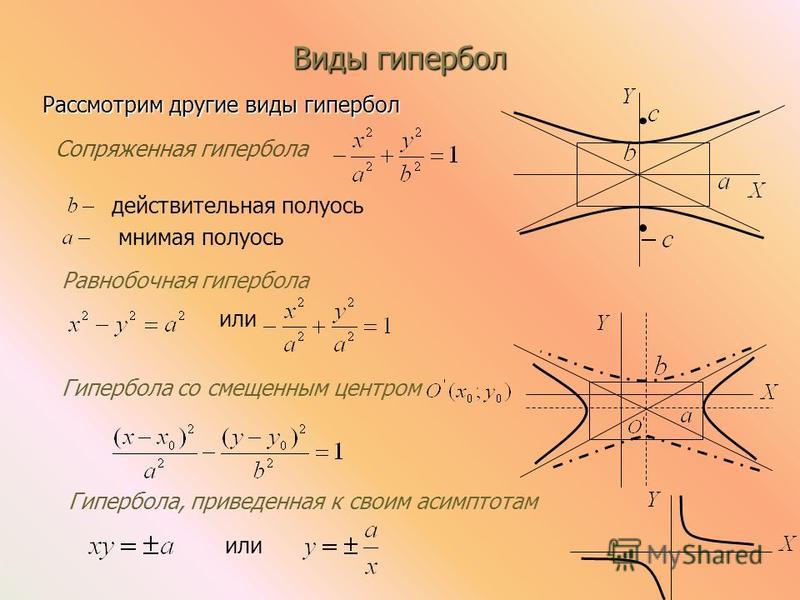 С нашей точки зрения, расстояния по этим осям сокращаются еще больше. Таким образом, мы видим сплющенный круг, причем сплющивание неодинаково по разным осям. Вот почему мы воспринимаем круги как эллипсы! Так обстоит дело, например, с кругами на стеклянном потолке галереи Витторио Эмануэле в Милане, которые вы видите справа. Довольно круто, правда?

Думаю, теперь я буду видеть эти эллипсы повсюду!

Еще одно преимущество определения эллипсов как сплющенных окружностей заключается в том, что их легко обобщить на эллипсоиды более высокой размерности! Затем они определяются как уплощения $n$-сфер! Прочтите мою статью о гипотезе Пуанкаре, чтобы узнать, как выглядит трехмерная сфера!

Хммм… Можешь вернуться к вещам, которые я понимаю?

Извините, я просто увлекся! Давайте посмотрим на свойства симметрии эллипсов.

Кажется, есть осевая симметрия вдоль двух перпендикулярных осей, верно?

Точно! Эти оси известны как младшая и большая оси. Давайте перерисуем эллипс галереи, чтобы появились эти оси.

Большая и малая полуоси затем определяются как наибольшее и наименьшее расстояния между центром и точками эллипсов. Центр обычно обозначается как $O$, а большая и малая полуоси обычно обозначаются как $a$ и $b$.

Значит, если мы сократим расстояния вдоль большой оси, то получим круг?

Точно! Или вы также можете растянуть расстояние вдоль малой оси! Кстати, вы забыли последнюю симметрию…

Я знаю! Центральная симметрия относительно центра эллипса!

Точно! Теперь у нас есть все! На самом деле группа симметрий эллипса такая же, как группа симметрий японского моста Хойан во Вьетнаме, которую я обсуждал в своей статье о симметриях.

Значит, Солнце находится в этом центре?

Нет! Нет нет нет! Это повторяющееся заблуждение! Солнце не является центром эллипса, описываемого Землей! Но у него есть определенное положение, так как он расположен в фокусе эллипса.

Что такое фокус?

Эллипс имеет 2 фокуса. Это точки большой оси, находящиеся на расстоянии $a$ от пересечения малой оси с эллипсом. Это соответствует следующей цифре: 92$. Но не будем слишком останавливаться на алгебраических свойствах эллипса!

Да! Скорее расскажите нам, что такого особенного в фокусах эллипса!

Установите две булавки, расположенные в фокусах. Затем, используя петлю длиной $2a+2f$, вы можете нарисовать идеальный эллипс, как показано ниже в видео от Mezon Videos!

Вы уверены, что мы получаем эллипс? И что штифты будут в его очагах?

Да! Это потому, что для любой точки эллипса два расстояния от этой точки до фокусов в сумме составляют $2a$ !

Это наводит меня на мысль, что должно быть какое-то элегантное доказательство эллиптических орбит планет путем введения виртуальной звезды в другом фокусе… Но я не могу это доказать! Еще раз, если вы знаете элегантное доказательство этого, я был бы рад услышать его!

Магия исчисления позволяет сразу сделать вывод, что углы, выделенные оранжевым цветом на рисунке выше, равны. У этого свойства есть довольно удивительное последствие: если вы играете в снукер на эллиптическом бильярдном столе и помещаете белый шар в фокус, а черный — в другой фокус, то независимо от того, как вы ударяете по белому шару (пока вы бьете достаточно сильно и не даете ему странного вращения), вы будете бить черный мяч белым мячом! Потрясающе, правда?

Вау! Это круто!

Еще лучше, совмещая два свойства, можно доказать, что сигнал, отправленный из одного фокуса, сразу принимается в другом фокусе! Это то, что показано в следующем видео с волнами:

Затем важная особенность эллипса описывается отношением $e=f/a$, называемым эксцентриситетом . Как вы понимаете, если $e$ близко к нулю, то $f$ очень мало по сравнению с $a$, а это значит, что фокусы расположены почти в центре эллипса. Тогда эллипс выглядит почти как круг. Наоборот, если $e$ близко к 1, то $f$ почти равно $a$, что означает, что фокусы находятся почти на краю большой оси. Это делает эллипс очень плоским. Короче говоря, чем эксцентричнее эллипс, тем меньше он похож на идеальный круг!

Давайте завершим этот раздел еще одним интересным фактом об эллипсах! Другой, еще более точный способ рисования эллипсов известен как трамвай Архимеда (хотя мы не знаем, знал ли об этом Архимед!). Он состоит в том, чтобы прикрепить стержень к двум челнокам, движущимся по перпендикулярным рельсам, и добавить ручку на конце стержня. Сдвигая челноки, ручка волшебным образом рисует красивый эллипс! Делается это в следующем видео от pocket83:

Вау! Все эти свойства эллипсов звучат так волшебно!

Я знаю! И я сожалею, что не привожу никаких доказательств в этой статье. Большинство этих свойств трудно доказать без мощи алгебры и исчисления. Думаю, именно поэтому греческие математики не хотели включать эллипсы в свои модели Вселенной.

Позвольте мне закончить этот раздел классическим замечанием ленивого математика! А именно: я оставляю вам задачу доказать все эти свойства в качестве упражнения. Наслаждаться!

Параболы, Гравитация и Архимедово Зеркало Луча Смерти

Перейдем к параболам. Исторически параболы играли ключевую роль в понимании физики еще до появления эллипсов. Действительно, за столетие до шедевра Ньютона Галилей обнаружил, что все свободно падающие объекты описывают параболические траектории. Точно так же Маркус дю Сотуа применяет этот принцип в следующем отрывке из документального фильма BBC «Код »:

траектории канонических шаров!

Так какова траектория?

Лучший способ визуализировать траектории свободно падающих объектов — смотреть на фонтаны. Давайте рассмотрим, например, фонтан справа с могучей Эйфелевой башней сзади!

Вау! Хорошее фото!

Спасибо. А теперь попробуйте отвести взгляд от Эйфелевой башни и посмотреть на брызги воды. Капли воды описывают параболические траектории!

Ну траектории не совсем совпадают с параболами, особенно ближе к концу…

Это из-за этих надоедливых воздушных трений! Тем не менее, вы можете видеть, что, по крайней мере, до тех пор, пока трение о воздух не станет слишком важным, траектории совпадают с траекториями парабол. И если вы не верите, что траектории свободно падающих объектов совпадают с траекториями парабол, посмотрите на википедийную картинку красивого фонтана, похожего на параболу!

Не волнуйся, я тебе верю! Но почему траектории свободно падающих тел параболичны?

Хм… Еще раз, единственное объяснение, которое у меня есть, связано с силой исчисления. Но я не собираюсь на этом останавливаться. Одна вещь, которую вы должны знать, это то, что в правильной системе координат координаты точек параболы задаются уравнением $y=x^2$.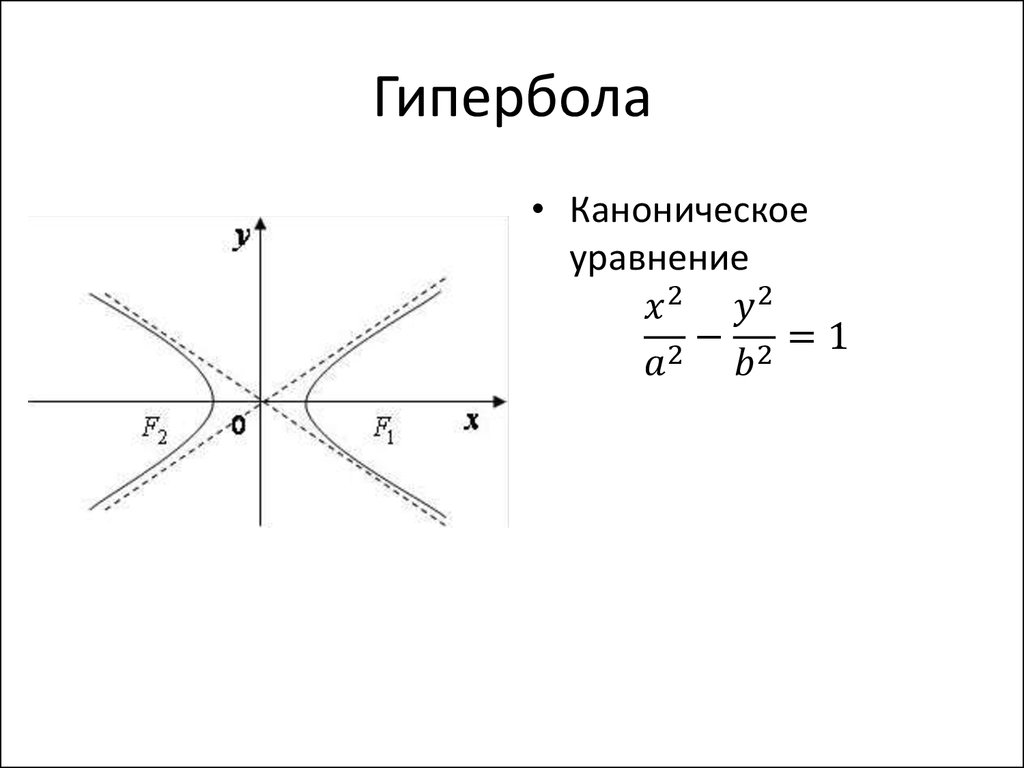 Все остальные параболы получаются гомотетией и классической симметрией этой параболы, подобно тому как эллипсы получаются деформацией окружности. Это значит, что растягивая и вращая параболу вдоль осей, можно сделать любую параболу! На самом деле, если вы играете Angry Birds , вы, наверное, хорошо понимаете все возможные нисходящие параболы!

Изображение справа взято из этой классной статьи Math Movement.

У этого есть замечательное следствие. Если вы находитесь в плоскости, которая повторяет кривую параболы, вы почувствуете, как будто сила тяжести изменилась! В частности, если самолет движется по параболической траектории свободно падающего объекта, вы будете чувствовать себя невесомым в самолете! Разве это не удивительно!

Разве это не обман? Они не совсем невесомые, не так ли?

Это то же самое явление, которое делает космонавтов невесомыми! Посмотрите потрясающее объяснение Дерека Мюллера на Veritasium:

И по какой траектории следуют астронавты? (Подсказка: они в свободном падении!)

Эллипсы, как мы обсуждали ранее! Вау! Есть ли связь между параболами и эллипсами?

Да есть! Парабола — это на самом деле эллипс, один из фокусов которого ушел в бесконечность!

Центр эллипсов тоже уходит в бесконечность, верно?

Точно! Фактически, вы могли заметить, что $f$ становится почти равным $a$. На пределе у нас фактически есть $e=f/a=1$! Это означает, что парабола — это своего рода эллипс с эксцентриситетом 1. Другими словами, парабола — это бесконечно сплющенный эллипс. Вот почему траектории свободно падающих объектов на Земле кажутся нам параболами: это настолько сплющенные эллипсы, что их невозможно отличить от парабол!

Подождите… Этот предел также можно увидеть на описании конуса введения, верно?

Вы очень прозорливы! В самом деле, по мере того как мы увеличиваем наклон эллипса, мы получаем все более и более уплощенные эллипсы, пока вдруг не получим параболу! Это описано ниже.

Мы говорили о пределах… Но имеет ли это вообще математический смысл?

Хе-хе… Отличный вопрос, но он выходит далеко за рамки этой статьи. Чтобы ответить на этот вопрос, вам нужно покопаться в удивительности топологии!

Значит ли это, что свойства эллипсов по-прежнему сохраняются для парабол?

Те, которые еще имеют смысл делать! В частности, это случай равенства углов!

Хммм… Я не знаю, как это работает для парабол…

По мере того, как другой фокус уходит в бесконечность, линии, исходящие из него и попадающие в часть эллипса рядом с первым фокусом, наклоняются все меньше и меньше. На самом деле уместно и общепринято считать, что линии, исходящие из точки на бесконечности все параллельны.

Значит, параллельные линии, идущие из бесконечности, отражаются от параболы и оказываются в ее фокусе?

Да! Точнее, линии, параллельные оси симметрии, отражаются параболой по направлению к фокусу. Это соответствует рисунку ниже:

Теперь возьмите эту параболу и сделайте ее телом вращения, вращая ее вдоль оси симметрии. Затем вы получаете то, что известно как круговой параболоид . Отличный способ получить его — заставить жидкость вращаться в чашке, как в этом видео потрясающей инициативы Арвинда Гупты «Игрушки из мусора».

Из мусора Арвинд Гупта и его коллеги создают игрушки, раскрывающие удивительные физические явления! Это так здорово! В частности, мне удалось увидеть выступление Видулы Мхайскар на коллоквиуме BtSM 2013, и это одно из самых удивительных выступлений, которые я когда-либо видел! Проверьте их веб-сайт!

Круговые параболоиды обладают тем свойством, что все пересечения с плоскостью, содержащей ось симметрии, являются параболами с одним и тем же фокусом. Следствием этого является то, что, когда сообщение отправляется издалека, поскольку принимаемые сигналы параллельны, мы можем очень хорошо зафиксировать его, используя круглое параболическое зеркало и помещая рецептор в фокус! Вот почему антенны в телекоммуникациях имеют параболическую форму!

Вау! Это так здорово!

Но эта идея не нова. На самом деле он был изобретен и использован Исааком Ньютоном (да, снова им!), который сконструировал телескоп, чтобы лучше наблюдать за движением звезд и придумал свои законы механики!

Этот мужчина потрясающий! Что он не открыл?

Ну, вообще-то, он был не первым, кто додумался использовать параболические зеркала! За 2000 лет до него гениальный Архимед из Сиракуз использовал ту же идею, чтобы защитить свою землю от римских захватчиков: он использовал эти зеркала, чтобы сфокусировать параллельные горящие солнечные лучи на одной точке вражеского корабля, чтобы сжечь его! Следующий отрывок представляет собой видео, которое я взял из Musei Capitolini в Риме во временной экспозиции, посвященной греческому ученому:

Архимед Зеркало Луча Смерти! Это так здорово!

Я знаю! К сожалению, этого было недостаточно для Сиракуз, чтобы противостоять формирующейся Римской империи. Это позволило Риму обнаружить бесчисленные изобретения Архимеда, что, я считаю, является ключевым шагом к его господству в Средиземном море! На самом деле, мне кажется, что Архимед был на вершине человеческих знаний в течение следующих 2000 лет, пока Галилей, наконец, заново не открыл некоторые из его блестящих достижений!

А мусульмане? Индейцы? Китайский?

Ну, на самом деле мусульмане первыми заново открыли труды Архимеда, которые, вероятно, помогли им стать самой развитой цивилизацией в период их апогея… Но хватит истории, вернемся к математике!

Гиперболы, воронки и неевклидова геометрия

Когда я сдавал устный вступительный экзамен в престижную Высшую нормальную школу в Париже (где побывали 10 из 52 медалистов!), я было дано следующее упражнение:

Две звезды вращаются вокруг друг друга. Один взрывается. Что случается?

Решил?

Я сделал! У меня ушел целый час, но я сделал! По крайней мере, я справился намного лучше, чем на устном экзамене TIPE. Увы, не попал…

Так какой ответ?

Я нашел, почему ты не можешь?

Хммм… Не уверен, что хочу потратить на это целый час!

Хорошо! В определенной системе координат две звезды будут либо иметь эллиптические траектории, либо, если количество вещества, потерянного при взрыве, велико, они будут следовать гиперболическим кривым! Это не удивительно, учитывая, что траектории планет и комет, вращающихся вокруг звезды, на самом деле либо эллиптические, либо гиперболические!

Порог можно вычислить исходя из энергетических соображений.

Так что я предполагаю, что гиперболы в некотором смысле также являются естественным продолжением эллипсов…

Так и есть! Это как если бы, раз фокус ушел в бесконечность, то вернулся из нее, но в другом смысле, и как антифокус!

Что вы подразумеваете под антифокусом?

Когда фокус возвращается в другую сторону, как если бы ему придали отрицательный знак. Действительно, точки гиперболы теперь таковы, что разница расстояний до фокусов является постоянной, как показано ниже. Обратите внимание, что эта разница противоположна в зависимости от того, какие плечо рассматриваемой гиперболы.

Последняя важная особенность гипербол известна как ее асимптоты . Если вы читали мою статью о дифференциальном исчислении, то знаете, что производные — это увеличение масштаба. Что ж, асимптоты в значительной степени противоположны. А именно, они показывают, что происходит, когда мы уменьшаем масштаб:

Когда мы уменьшаем масштаб, в конечном итоге гипербола выглядит как две линии. Эти две линии являются асимптотами гиперболы. Теперь особенно интересен вид гипербол, у которых асимптоты горизонтальны и вертикальны, как у синей и зеленой справа.

Почему интересно?

Хе-хе… Поверните его по вертикальной оси. Тогда вы получите два тела вращения, одно вверху, другое внизу. Удалите тот, что сверху. То, что у вас осталось, называется гиперболической воронкой . Эта воронка точно описывает гравитационную потенциальную энергию вокруг Солнца в соответствии с законами гравитации Ньютона!

Что это значит?

Это означает, что если вы запустите шарики, катящиеся по этой воронке, вы получите точно такие же траектории, какие предсказывал Ньютон для планет (если, опять же, не было этих надоедливых трений!).

Но причина, по которой гиперболы являются самыми крутыми из всех коник, заключается в их приложениях к неевклидовой геометрии! Эта геометрия необходима для описания пространства-времени в специальной теории относительности, а также и в основном в общей теории относительности. Забавно, что в то время как Ньютон использовал эллипсы для создания своих законов, Эйнштейн использовал гиперболы, чтобы превзойти Ньютона! Но приложения не ограничиваются физикой гравитации, поскольку неевклидова геометрия также значительно расширила наше понимание поверхностей и пространств в целом!

Правда? Почему?

В основном из-за чипсов!

Картофельные чипсы?

Да! Особенно чипсы Pringles, как тот, что справа! Математически они известны как гиперболических параболоидов . Его название происходит от того факта, что пересечения с вертикальными плоскостями дают параболы, а пересечения с горизонтальными плоскостями дают гиперболы! В дифференциальном исчислении картофельная стружка — это локальное описание седловой точки 9.0060 , что соответствует горному перевалу в топографии.

Что такого особенного в картофельных чипсах?

Долгое-долгое время единственной известной геометрией была евклидова геометрия, застрявшая в листе бумаги, математически известном как плоскость. Но затем, когда были начерчены карты, люди осознали важность неевклидовой геометрии. Тем не менее, эта геометрия часто ограничивалась геометрией на сферах. Пока чипсы не были найдены!

Что это меняет?

Один из странных аспектов картофельных чипсов заключается в том, что сумма углов треугольника в сумме составляет менее 180°… И это имеет множество причудливых последствий, таких как существование бесконечного числа параллельных прямых, проходящих через точку. ! И это имеет чрезвычайно полезные применения в геометрии и физике! Например, из-за этой особенности плоский лист бумаги нельзя согнуть в картофельную стружку. В противном случае треугольник на листе бумаги по-прежнему будет иметь углы, которые в сумме составляют 180° на согнутом листе. Забавно, что этот простой факт объясняет, почему мы едим кусочки пиццы именно так!

Правда?

Да! Посмотрите это потрясающее видео TedEd от Колма Келлехера!

Эти замечания породили необыкновенную область гиперболической геометрии ! Если можно, напишите о гиперболической геометрии!
Подведем итоги
Надеюсь, я убедил вас в красоте эллипсов, парабол и гипербол. Мало того, что их довольно легко определить, используя конические пересечения или что-то еще, но также и, что более важно, они везде! И чтобы по-настоящему оценить их, мне почему-то кажется, что лучше избегать классического аналитического подхода… В завершение этой статьи вот последняя ссылка с отличной анимацией, которая усиливает важность этих коников!
Введение в конические сечения | безграничная алгебра |
Что такое конические сечения?
Конические сечения получаются пересечением поверхности конуса плоскостью и имеют определенные особенности.
Цели обучения
Описать части конического сечения и то, как конические сечения можно рассматривать как поперечные сечения двойного конуса
Основные выводы
Ключевые моменты
Ключевые термины
вершина : Крайняя точка на коническом сечении.
асимптота : Прямая линия, к которой кривая приближается произвольно близко, уходя в бесконечность.
locus : Набор всех точек, координаты которых удовлетворяют заданному уравнению или условию.
фокус : точка, используемая для построения и определения конического сечения, в котором сходятся лучи, отраженные от кривой (множественное число: фокусы).
подкладка : половина двойного конуса.
коническое сечение : Любая кривая, образованная пересечением плоскости с конусом из двух покровов.
направляющая : линия, используемая для построения и определения конического сечения; парабола имеет одну направляющую; эллипсы и гиперболы имеют два (множественное число: направляющие).
Определение конических сечений
Коническое сечение (или просто коническое) — это кривая, полученная в результате пересечения поверхности конуса с плоскостью. Три типа конических сечений — это гипербола, парабола и эллипс. Круг является типом эллипса и иногда считается четвертым типом конического сечения.
Конические сечения могут быть созданы путем пересечения плоскости с конусом. Конус состоит из двух частей одинаковой формы, называемых покровами. Один подгузник — это то, что большинство людей подразумевают под «конусом», и он имеет форму праздничной шляпы.
Конические сечения генерируются пересечением плоскости с конусом. Если плоскость параллельна оси вращения (ось
yyy
), то коническое сечение представляет собой гиперболу. Если плоскость параллельна образующей, то коническое сечение представляет собой параболу. Если плоскость перпендикулярна оси вращения, то коническое сечение представляет собой окружность.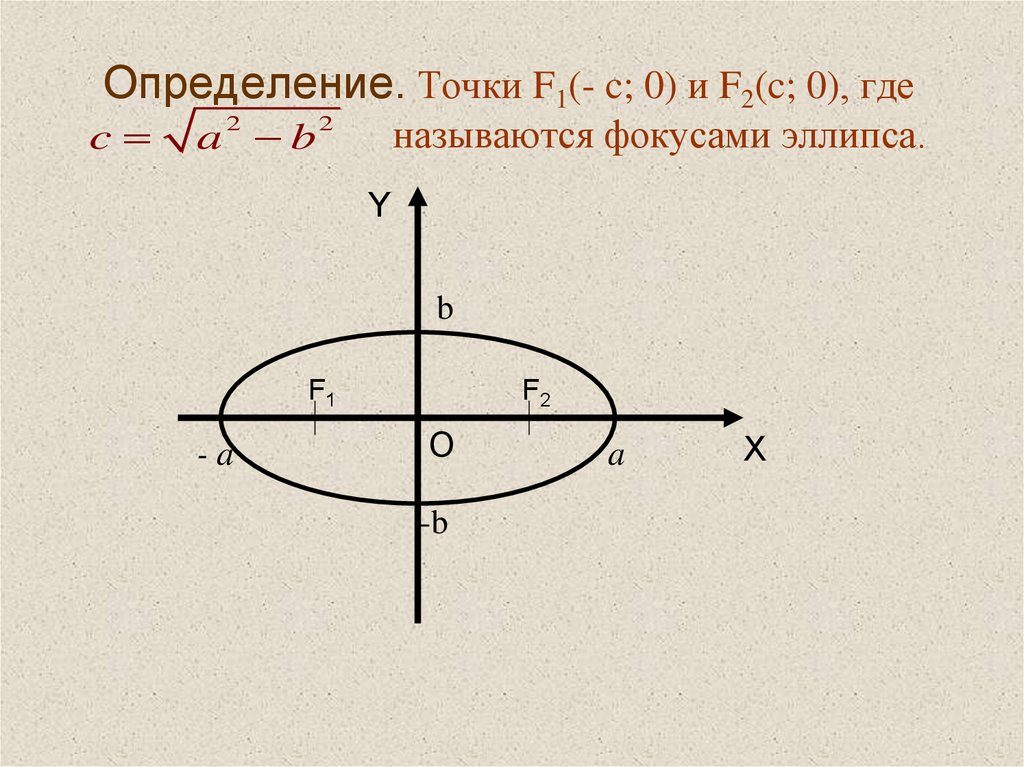 Если плоскость пересекает один покров под углом к оси (отличным от 9{\circ}90∘
), то коническое сечение представляет собой эллипс.
Конус и конические секции: Покровы и четыре конические секции. Каждая коника определяется углом, который плоскость образует с осью конуса.
Общие части конических сечений
Хотя каждый тип конического сечения выглядит очень по-разному, у них есть некоторые общие черты. Например, у каждого типа есть как минимум один фокус и директриса.
Фокус – это точка, относительно которой строится коническое сечение. Другими словами, это точка, вокруг которой сходятся лучи, отраженные от кривой. Парабола имеет один фокус, вокруг которого построена форма; эллипс и гипербола имеют два.
Направляющая — это линия, используемая для построения и определения конического сечения. Расстояние директрисы от точки на коническом сечении имеет постоянное отношение к расстоянию от этой точки до фокуса.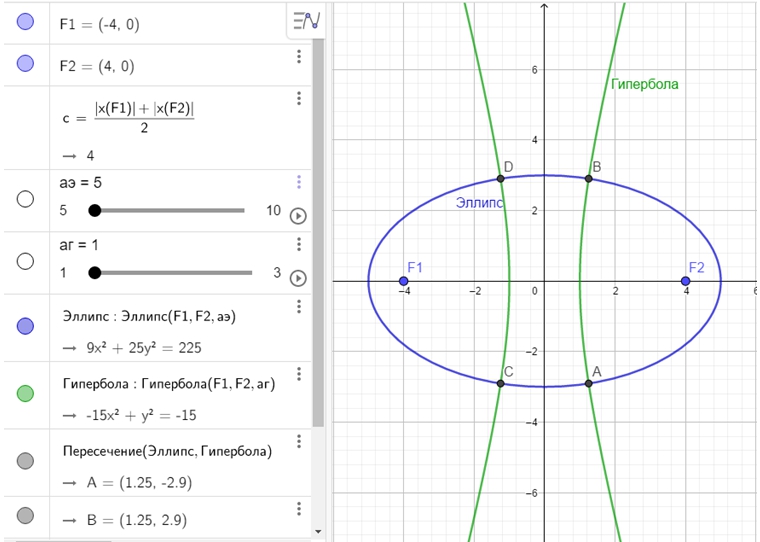 Как и в случае с фокусом, парабола имеет одну направляющую, а эллипсы и гиперболы — две.
Эти общие свойства конических сечений часто представляются в виде следующего определения, которое будет разработано в следующем разделе. Коническое сечение — это геометрическое место точек
PPP
, расстояние которого до фокуса постоянно кратно расстоянию от
PPP
до направляющей коники. Эти расстояния отображаются оранжевыми линиями для каждой конической секции на следующей диаграмме.
Детали конических сечений : Три конических сечения с обозначенными фокусами и направляющими.
Каждый тип конического сечения более подробно описан ниже.
Парабола
Парабола — это множество всех точек, расстояние которых от фиксированной точки, называемой фокусом, равно , равному расстоянию от фиксированной линии, называемой директрисой.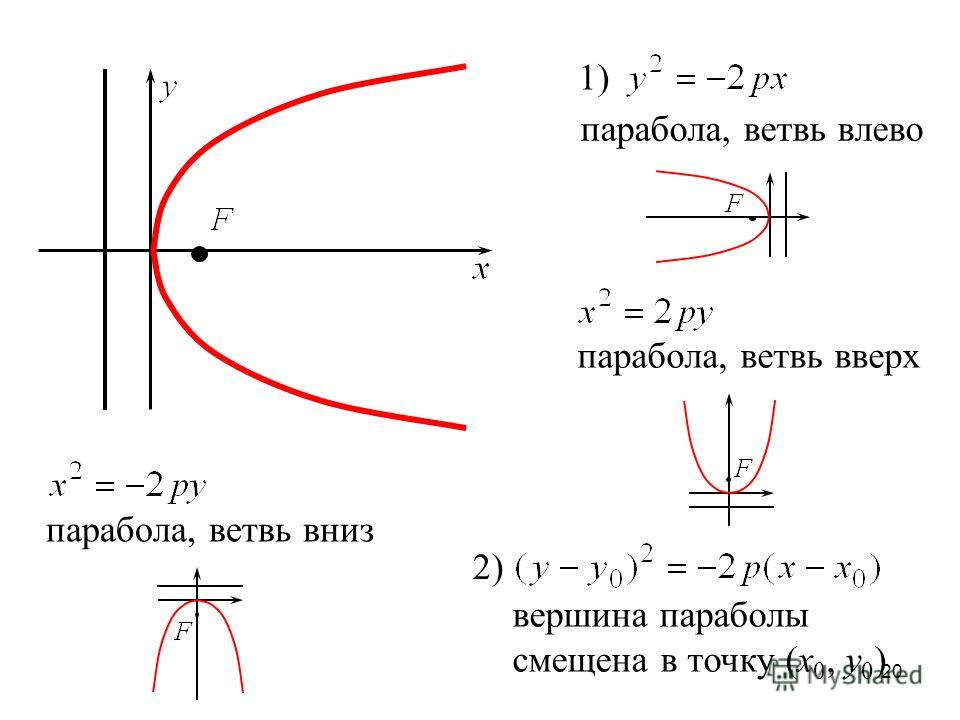 Точка на полпути между фокусом и директрисой называется вершиной параболы.
На следующем рисунке четыре параболы изображены в виде графика на координатной плоскости. Они могут открываться вверх, вниз, влево или вправо.
Четыре параболы, раскрывающиеся в разные стороны: Вершина лежит посередине между директрисой и фокусом.
Многоточие
Эллипс — это множество всех точек, для которых сумма расстояний от двух фиксированных точек (фокусов) постоянна. В случае эллипса есть два фокуса и две директрисы.
На следующем рисунке изображен типичный эллипс в координатной плоскости.
Эллипс: Сумма расстояний от любой точки эллипса до фокусов постоянна.
Гипербола
Гипербола — это множество всех точек, разность расстояний которых от двух фиксированных точек (фокусов) постоянна. В случае гиперболы есть два фокуса и две директрисы. Гиперболы также имеют две асимптоты.
График типичной гиперболы показан на следующем рисунке.
Гипербола: Разность расстояний от любой точки эллипса до фокусов постоянна. Поперечная ось также называется большой осью, а сопряженная ось также называется малой осью.
Применение конических сечений
Конические сечения используются во многих областях науки, особенно для описания форм. Например, они используются в астрономии для описания формы орбит объектов в космосе. Два массивных объекта в космосе, которые взаимодействуют в соответствии с законом всемирного тяготения Ньютона, могут двигаться по орбитам, имеющим форму конических сечений. Они могли следовать эллипсам, параболам или гиперболам, в зависимости от их свойств.
Эксцентриситет
Каждое коническое сечение имеет постоянный эксцентриситет, который дает информацию о его форме.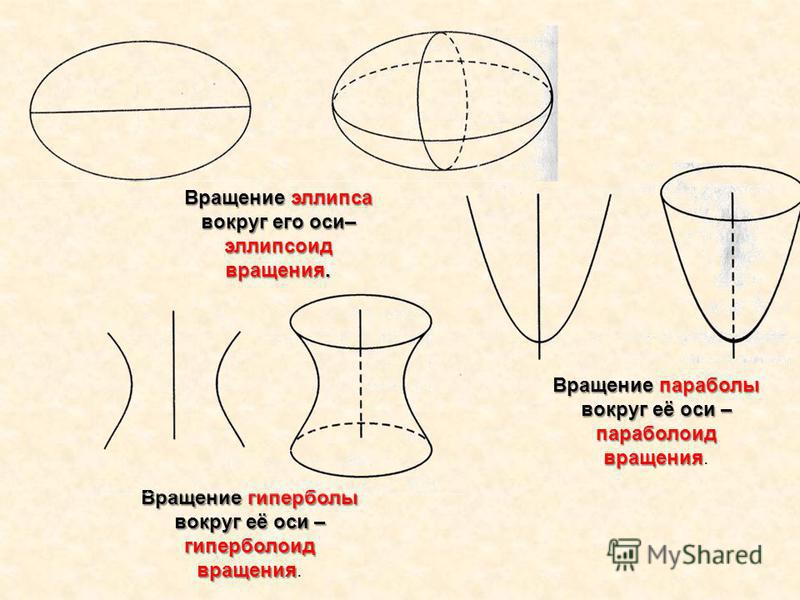
Цели обучения
Обсудите, как эксцентриситет конического сечения описывает его поведение.
Определение эксцентриситета
Эксцентриситет, обозначаемый
eee
, является параметром, связанным с каждым коническим сечением. Его можно рассматривать как меру отклонения конического сечения от круглого.
Эксцентриситет конического сечения определяется как расстояние от любой точки конического сечения до его фокуса, деленное на расстояние по перпендикуляру от этой точки до ближайшей направляющей. Значение
eee
является постоянным для любого конического сечения. Это свойство можно использовать как общее определение для конических сечений. Значение
eee
можно также использовать для определения типа конического сечения:
Если
e=1e = 1e=1
, коника является параболой
Если
e<1e < 1e<1
, это эллипс
Если
e>1e > 1e>1
, это гипербола
Эксцентриситет окружности равен нулю. Обратите внимание, что два конических сечения подобны (одинаковой формы) тогда и только тогда, когда они имеют одинаковый эксцентриситет.
Напомним, что гиперболы и некруглые эллипсы имеют два фокуса и две связанные с ними директрисы, а параболы имеют один фокус и одну директрису. На следующем рисунке каждый тип конического сечения изображен с фокусом и направляющей. Оранжевые линии обозначают расстояние между фокусом и точками на коническом сечении, а также расстояние между теми же точками и директрисой. Это расстояния, используемые для нахождения эксцентриситета.
Конические сечения и их части: Эксцентриситет представляет собой отношение расстояния от любой точки конического сечения до его фокуса и расстояния по перпендикуляру от этой точки до ближайшей директрисы.
Концептуализация эксцентриситета
По определению параболы расстояние от любой точки параболы до фокуса равно расстоянию от этой же точки до директрисы. Следовательно, по определению эксцентриситет параболы должен быть равен
111
.
Для эллипса эксцентриситет меньше
111
. Это означает, что в отношении, определяющем эксцентриситет, числитель меньше знаменателя. Другими словами, расстояние между точкой конического сечения и его фокусом меньше, чем расстояние между этой точкой и ближайшей директрисой.
И наоборот, эксцентриситет гиперболы больше, чем
111
. Это указывает на то, что расстояние между точкой на коническом сечении и ближайшей направляющей меньше, чем расстояние между этой точкой и фокусом.
Типы конических сечений
Конические сечения образуются пересечением плоскости с конусом, и их свойства зависят от того, как происходит это пересечение.
Цели обучения
Обсудите свойства различных типов конических сечений
Основные выводы
Ключевые моменты
Конические сечения представляют собой особый тип формы, образованной пересечением плоскости и прямого кругового конуса. В зависимости от угла между плоскостью и конусом могут быть образованы четыре различные формы пересечения.
Типы конических сечений: окружности, эллипсы, гиперболы и параболы.
Каждое коническое сечение также имеет вырожденную форму; они принимают форму точек и линий.
Ключевые термины
вырожденный : Коническое сечение, которое не соответствует стандартной форме уравнения.
асимптота : Линия, к которой криволинейная функция или форма приближается, но никогда не касается.
гипербола : Коническое сечение, образованное плоскостью, перпендикулярной основанию конуса.
focus : Точка вдали от изогнутой линии, вокруг которой изгибается кривая.
круг : Коническое сечение, образованное плоскостью, параллельной основанию конуса.
эллипс : Коническое сечение, образованное плоскостью, расположенной под углом к основанию конуса.
эксцентриситет : Безразмерный параметр, характеризующий форму конического сечения.
Парабола : Коническое сечение, образованное плоскостью, параллельной конусу.
вершина : точка поворота изогнутой формы.
Конические сечения представляют собой особый тип формы, образованной пересечением плоскости и прямого кругового конуса. В зависимости от угла между плоскостью и конусом могут быть образованы четыре различные формы пересечения. Каждая форма также имеет вырожденную форму. Существует свойство всех конических сечений, называемое эксцентриситетом, которое принимает форму числового параметра
eee
. Каждая из четырех форм конического сечения имеет разные значения
эээ
.
Типы конических сечений: На этом рисунке показано, как конические сечения, выделенные голубым цветом, являются результатом пересечения плоскости с конусом.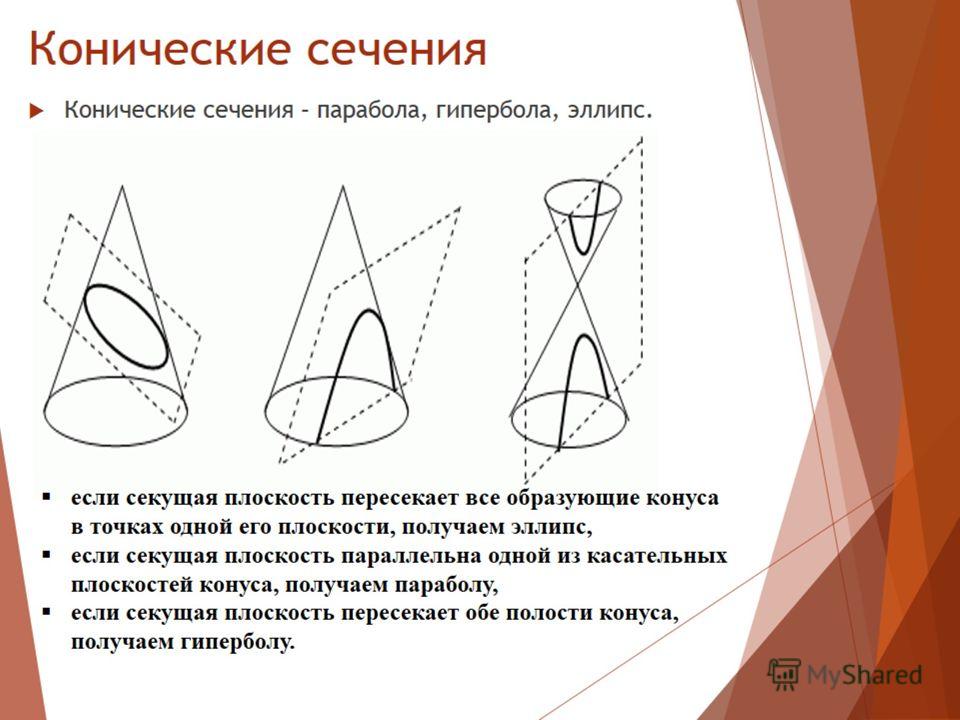 На изображении 1 показана парабола, на изображении 2 — круг (внизу) и эллипс (вверху), а на изображении 3 — гипербола.
Парабола
Парабола образуется, когда плоскость параллельна поверхности конуса, в результате чего получается U-образная кривая, лежащая на плоскости. Каждая парабола имеет определенные особенности:
Вершина, в которой кривая поворачивается вокруг
Фокус, являющийся точкой вне кривой, вокруг которой изгибается кривая
Ось симметрии, представляющая собой линию, соединяющую вершину и фокус, которая делит параболу на две равные половины
Все параболы имеют значение эксцентриситета
e=1e=1e=1
. В результате одинакового эксцентриситета все параболы подобны, а это означает, что любую параболу можно преобразовать в любую другую, изменив положение и масштабирование. Вырожденный случай параболы — это когда плоскость едва касается внешней поверхности конуса, что означает, что она касается конуса.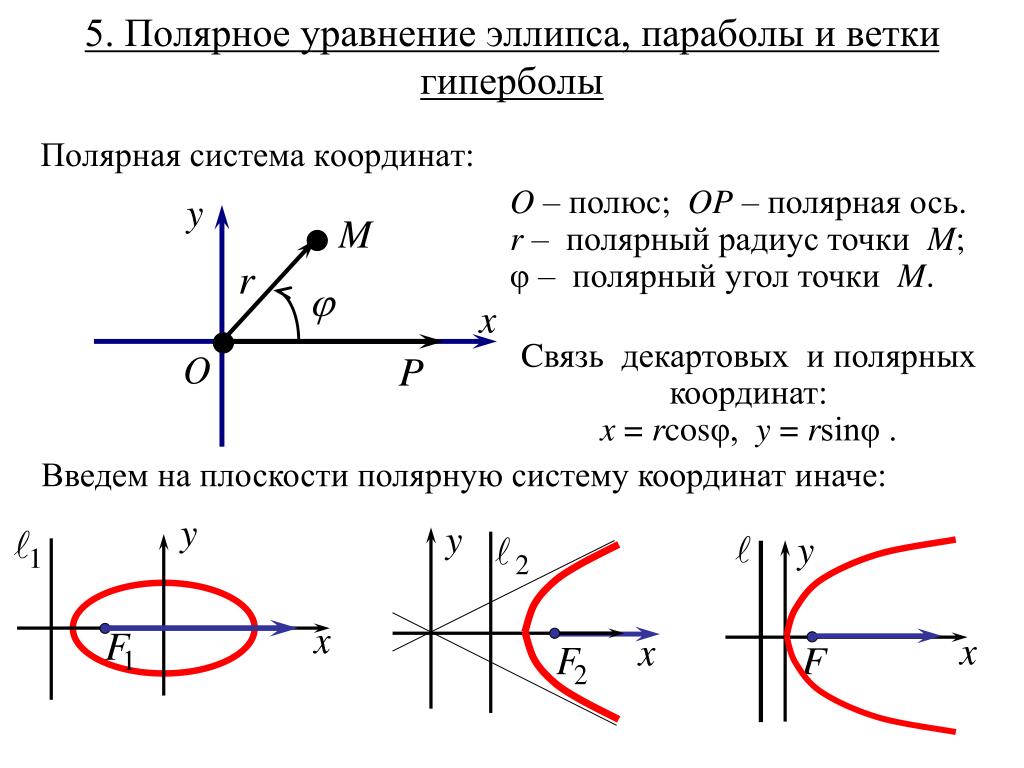 Это создает пересечение прямых линий диагонали конуса. 92f(x)=x2
Окружность
Окружность образуется, когда плоскость параллельна основанию конуса. Таким образом, его пересечение с конусом представляет собой множество точек, равноудаленных от общей точки (центральной оси конуса), что соответствует определению окружности. Все круги имеют определенные особенности:
Центральная точка
Радиус, который представляет собой расстояние от любой точки окружности до центральной точки
Все окружности имеют эксцентриситет
92(x−h)2+(y−k)2=r2
, где
(h,k)(h,k)(h,k)
— координаты центра окружности, а
ррр
это радиус.
Вырожденная форма окружности возникает, когда плоскость пересекает только самую вершину конуса. Это пересечение в одной точке или, что то же самое, круг нулевого радиуса.
Конические сечения, построенные по эксцентриситету: На этом графике показан эллипс красного цвета с примерным значением эксцентриситета
0.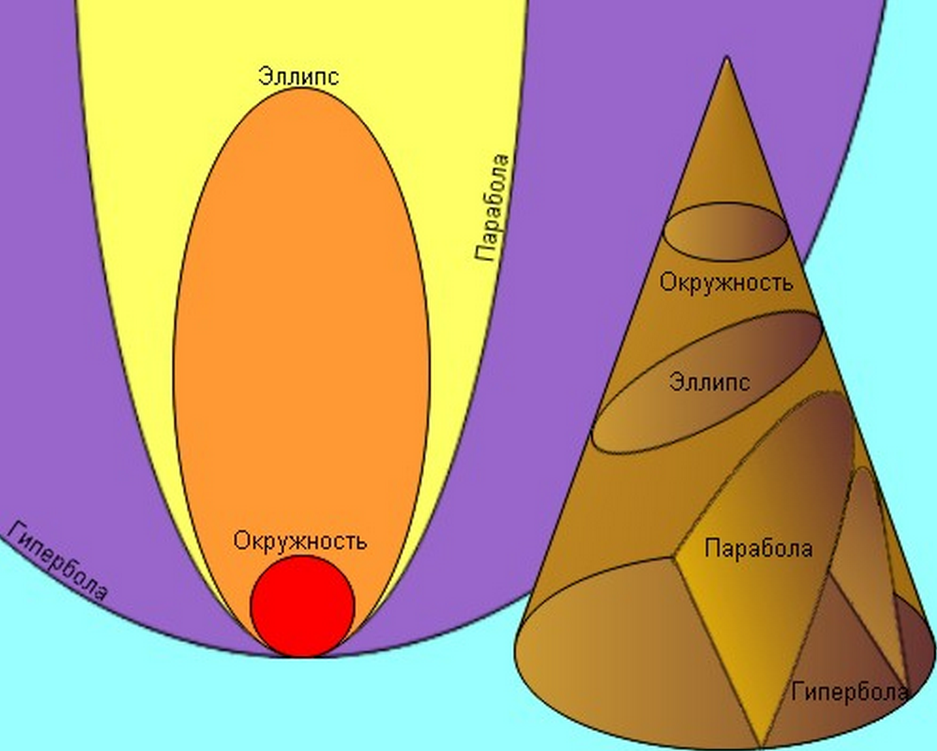 50.50.5
, парабола зеленого цвета с требуемым эксцентриситетом
111
и гипербола синего цвета с примерным эксцентриситетом
222
. На нем также показан один из случаев вырожденной гиперболы, прямая черная линия, соответствующая бесконечному эксцентриситету. Окружность находится внутри параболы, которая находится внутри одной стороны гиперболы, под которой проходит горизонтальная линия. Таким образом, увеличение эксцентриситета можно отождествить с своего рода развертыванием или открытием конического сечения.
Эллипс
Когда угол плоскости относительно конуса находится между внешней поверхностью конуса и основанием конуса, результирующее пересечение представляет собой эллипс. Определение эллипса также включает параллельность основанию конуса, поэтому все окружности являются частным случаем эллипса. Эллипсы имеют следующие особенности:
Большая ось, которая представляет собой наибольшую ширину эллипса
Малая ось, которая представляет собой наименьшую ширину эллипса
Центр, являющийся пересечением двух осей
Два фокуса — для любой точки эллипса сумма расстояний до обоих фокусов является константой
Эллипсы могут иметь диапазон значений эксцентриситета:
0≤e<10 \leq e < 10≤e<1
. Обратите внимание, что значение
000
включено (круг), но значение
111
не включено (это будет парабола). Поскольку существует диапазон значений эксцентриситета, не все эллипсы одинаковы. Общая форма уравнения эллипса с большой осью, параллельной оси x: 92} = 1 }a2(x−h)2+b2(y−k)2=1
где
(h,k)(h,k)(h,k)
– координаты центра,
2a2a2a
– это длина большой оси, а
2b2b2b
– длина малой оси. Если эллипс имеет вертикальную большую ось, метки
aaa
и
bbb
поменяются местами.
Вырожденная форма эллипса — это точка или окружность нулевого радиуса, как это было для окружности.
Гипербола
Гипербола образуется, когда плоскость параллельна центральной оси конуса, то есть пересекает обе части двойного конуса. Гиперболы имеют две ветви, а также следующие особенности:
Линии асимптоты — это два линейных графика, к которым кривая гиперболы приближается, но никогда не касается
Центр, являющийся пересечением асимптот
Два фокуса, вокруг которых изгибается каждая из двух ветвей
92} = 1 }a2(x−h)2−b2(y−k)2=1
, где
(h,k)(h,k)(h,k)
— координаты центра. В отличие от эллипса,
aaa
не обязательно является большим номером оси. Это длина оси, соединяющей две вершины.
Эксцентриситет гиперболы ограничен
e>1e > 1e>1
и не имеет верхней границы. Если допустить эксцентриситет до предела
+∞+\infty+∞
(положительная бесконечность), гипербола становится одним из своих вырожденных случаев — прямой линией. Другой вырожденный случай гиперболы состоит в том, чтобы стать ее двумя прямолинейными асимптотами.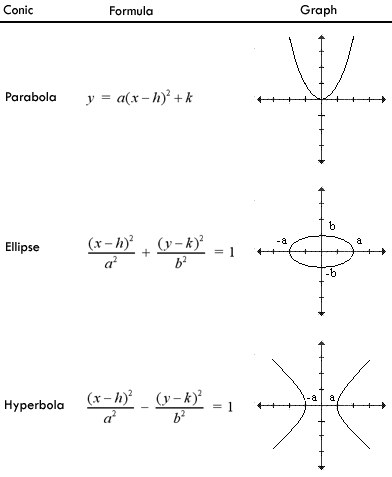 Это происходит, когда плоскость пересекает вершину двойного конуса.
Лицензии и атрибуции
Контент под лицензией CC, совместно используемый ранее
Курирование и пересмотр. Автор : Boundless.com. Лицензия : Общественное достояние: Неизвестно Авторские права
Лицензионный контент CC, конкретное указание авторства
Locus. Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary.org/wiki/locus. Лицензия : CC BY-SA: Attribution-ShareAlike
Коническое сечение. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Conic_section. Лицензия : CC BY-SA: Attribution-ShareAlike
Фокус. Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary. org/wiki/focus. Лицензия : CC BY-SA: Attribution-ShareAlike
Конические сечения. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
Асимптота. Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary.org/wiki/asymptote. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_008.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_004.jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_002.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_016.jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_012.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
Эксцентриситет (математика). Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Eccentricity_(mathematics). Лицензия : CC BY-SA: Attribution-ShareAlike
Конические сечения. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
Конические сечения. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_008.jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_004.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_002.jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_016.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_012.jpg. Предоставлено : ОпенСтакс. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_016.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
Коническое сечение. Предоставлено : Википедия. Расположен по адресу : https://en.wikipedia.org/wiki/Conic_section. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_008.jpg. Предоставлено : OpenStax. Расположен по адресу : https://cnx.org/contents/[email protected]. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_004.jpg. Предоставлено : OpenStax. Лицензия : CC BY-SA: Attribution-ShareAlike
CNX_Calc_Figure_11_05_002.jpg. Предоставлено : OpenStax.
No related posts.