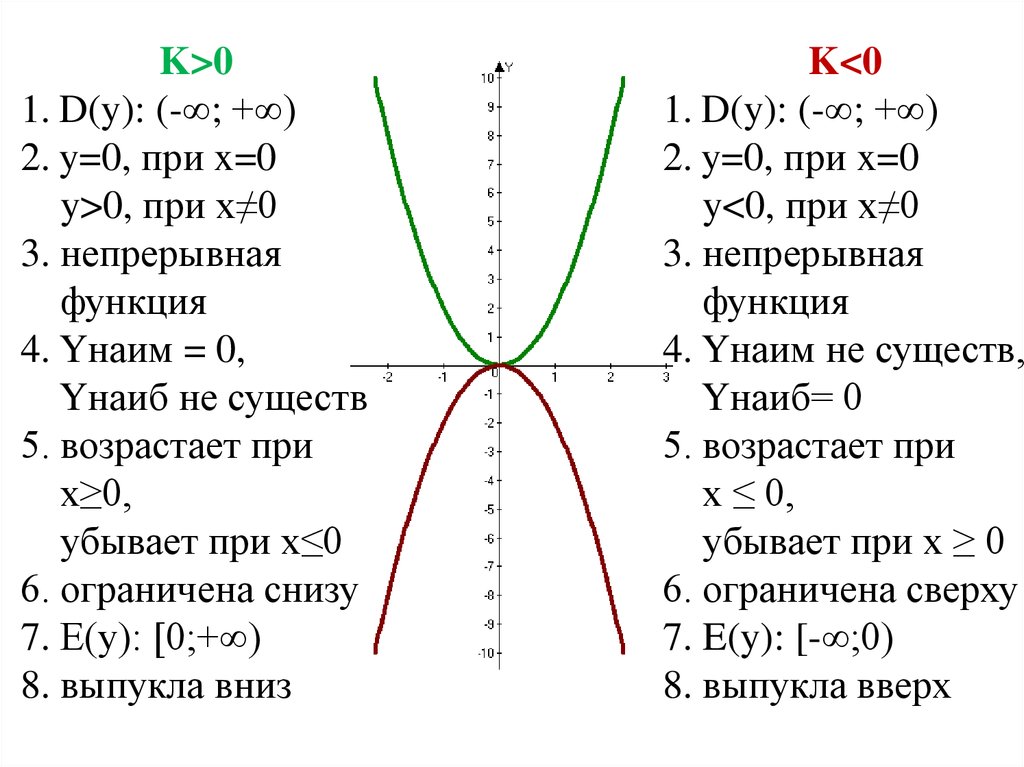
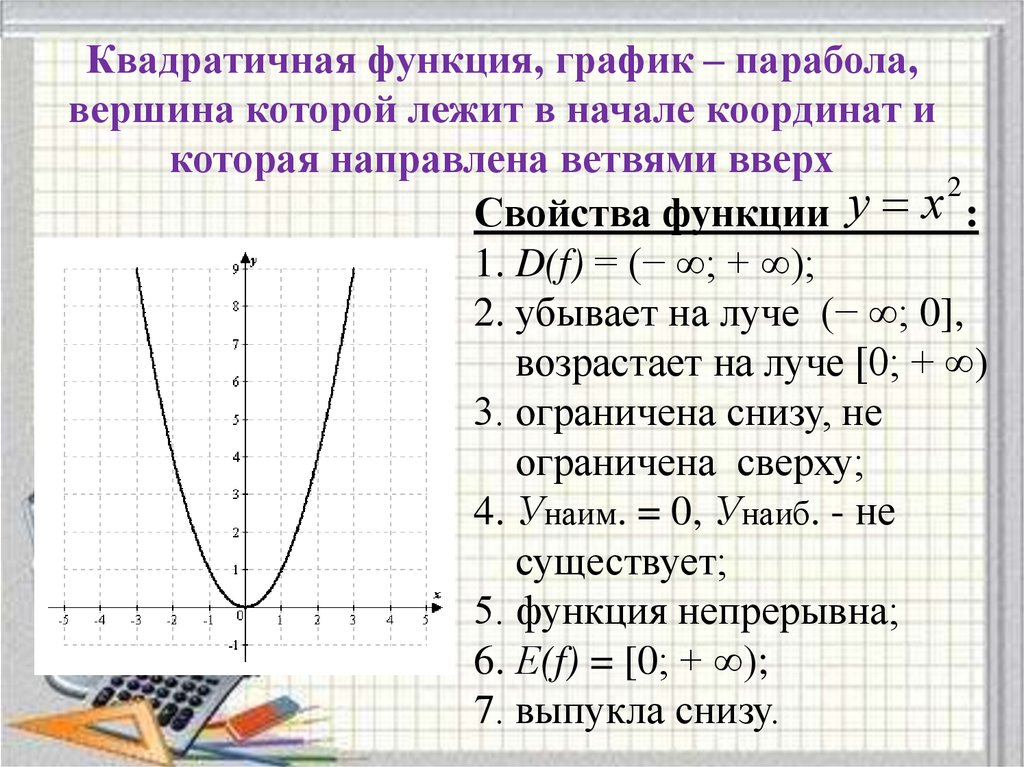
1. Область определения. Мы можем вычислить значение функции в любой точке х. Тогда функция определена при $хϵ(-∞;+∞)$.
2. $y=0$ при $x=0$, $y>0$ при $x≠0$. Данное свойство очевидно и хорошо видно на графике.
3. Непрерывная функция. График проходит сплошной линией, точек где функция разрывается нет.
4. Наибольшего значения нет. По графику видно, что функция бесконечно уходит вверх.
Наименьшее значение $y=0$ при $х=0$. Чтобы найти наименьшее значение, надо на графике найти самую нижнюю точку. Такой является точка с координатами $(0;0)$.
5. Функция возрастает при $x>0$. Функция убывает при $x
Давайте посмотрим внимательно на наш график. По нему видно, что функция всегда проходит выше прямой $y=0$. Такое свойство называется «ограниченность снизу».
6. Функция ограничена снизу прямой $y=0$.
Так же бывает и «ограниченность сверху». Если функция всегда проходит ниже некоторой прямой, то она является ограниченной сверху.
7. Область значений функции: $[0;+∞)$.
1. Область определения $хϵ(-∞;+∞)$.
2. $y=0$ при $x=0$, $y
3. Непрерывная функция.
4. Наименьшего значения нет. Наибольшее значение – $y=0$ при $х=0$.
5. Функция возрастает при $x0$.
6. Функция ограничена сверху прямой $y=0$.
7. Область значений функции: $(-∞;0]$.
8. Функция выпукла вверх.
Функция у=ах², её график и свойства
Класс: 9.
Цели урока: закрепить умения раскладывать на множители квадратный трехчлен, применяя это разложение для сокращения дробей и упрощения выражений, повторить основные свойства функции.
Планируемые результаты: Знать и понимать функции y=ax², особенности графика. Уметь строить y=ax² в зависимости от параметра а.
Метапредметные:
- Коммуникативные: вступать в учебный диалог с учителем, участвовать в общей беседе.
- Познавательные: осознавать познавательную задачу, читать и слушать, извлекая необходимую информацию.

- Регулятивные: планировать необходимые действия, операции. Оценивать возникающие трудности, вносить коррективы в работу.
Личностные: осваивать новые виды деятельности.
Тип урока: комбинированный.
Оборудование: учебные принадлежности для урока математики, учебник
Основные понятия: трехчлен, многочлен, квадратное уравнение, корень, дискриминант, функция, область определения функции, область значения функции.
Ход урока
1. Организационный моментВключение учащихся в учебную деятельность. Приветствие, проверка подготовленности к учебному занятию, организации рабочего места.
Устная работа.
Дана функция: у = х².
1) Найдите значения функции в точках -1; 0; 1/9.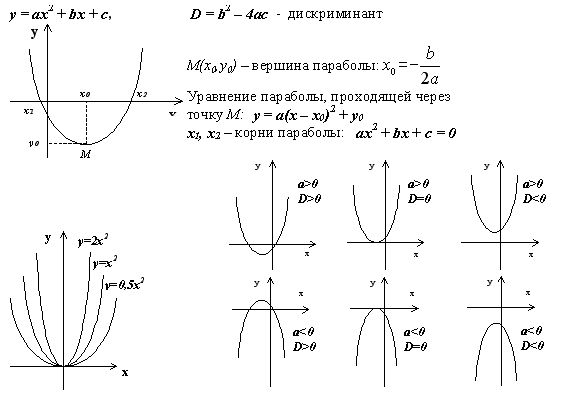
2) В каких точках значение функции равно 4; 1/25?
III. Объяснение нового материалаКвадратичной называют функцию вида:
Графиком квадратичной функции является парабола. Она состоит из двух ветвей и имеет вершину.
Ветви могут быть направлены вверх:
Ветви могут быть направлены вниз:
Квадратичная функция имеет свои свойства. Поговорим о них. В своей вершине квадратичная функция сменяет своё поведение с убывания на возрастание и с возрастания на убывание.
Понятно, что областью определения в обоих случаях будет множество всех действительных чисел. Если говорим о нулях функции, то мы имеем ввиду те значения, при которых функция у=0. Когда находят нули функции по графику, то ищут точки пересечения графика с осью х. Если же находят нули функции по уравнению, то значение функции принимают равное 0.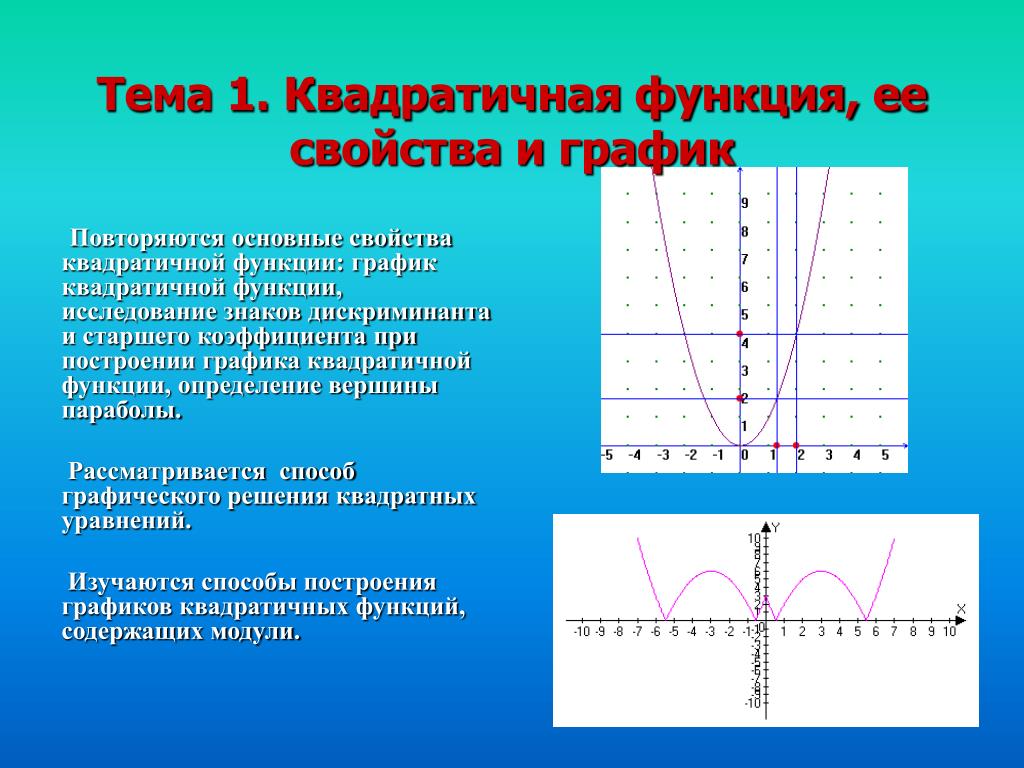 Тем самым получаем квадратное уравнение. Оно может иметь 2, 1 корень или не иметь корней. Соответственно, график может иметь 2 точки пересечения с осью х, 1 точку пересечения с осью х или не пересекать её. Понятно, что нулями квадратичной функции являются корни соответствующего квадратного уравнения. По графику удобно находить промежутки знакопостоянства и промежутки монотонности функции.
Тем самым получаем квадратное уравнение. Оно может иметь 2, 1 корень или не иметь корней. Соответственно, график может иметь 2 точки пересечения с осью х, 1 точку пересечения с осью х или не пересекать её. Понятно, что нулями квадратичной функции являются корни соответствующего квадратного уравнения. По графику удобно находить промежутки знакопостоянства и промежутки монотонности функции.Рассмотреть свойства из учебника.
Пример: по графику квадратичной функции опишите её свойства.
На рисунке изображена парабола, ветви которой направлены вверх, значит a>0. Опишем её свойства.
Областью определения и областью значений являются:
Нулями функции являются:
y = 0 при x = -3 и x = 3
Промежутки знакопостоянства:
Промежутки монотонности:
Заметим, что описать свойства функции по её графику проще, чем по формуле.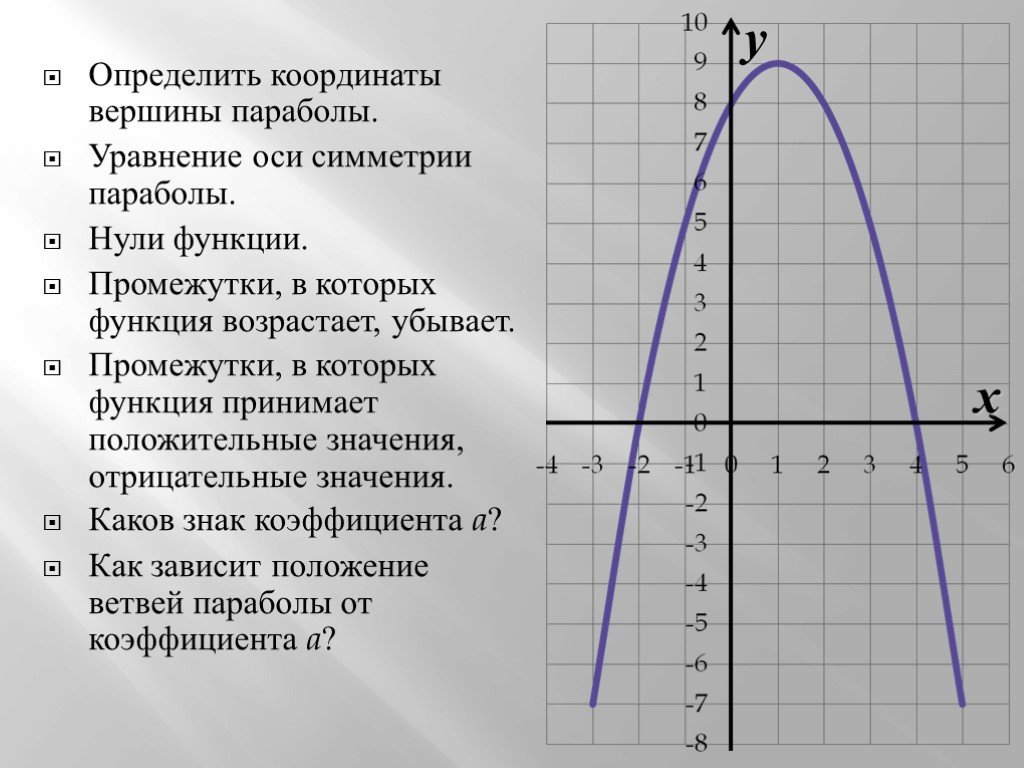 Поэтому очень важно уметь изображать график функции.
Поэтому очень важно уметь изображать график функции.
Рассмотрим частный случай квадратичной функции: y=ax²
Изобразим график этой функции схематично и обратим внимание на некоторые её свойства. Возможны два случая изображения графика.
Областью определения в обоих случаях является:
Область значений:
Функция такого вида обращается в ноль только при х=0, график будет пересекать ось х в одной точке. Первым свойством мы запишем, что если: х = 0, то y= 0.
Другими словами график такой функции всегда проходит через точку начала координат. Причём эта точка является вершиной параболы.
Если же , то график расположен выше или ниже оси Х.
Если взять противоположные значения аргумента, то видно, что им соответствуют одинаковые значения функции. Противоположным значениям аргумента соответствуют равные значения функции. Другими словами график функции симметричен относительно оси у.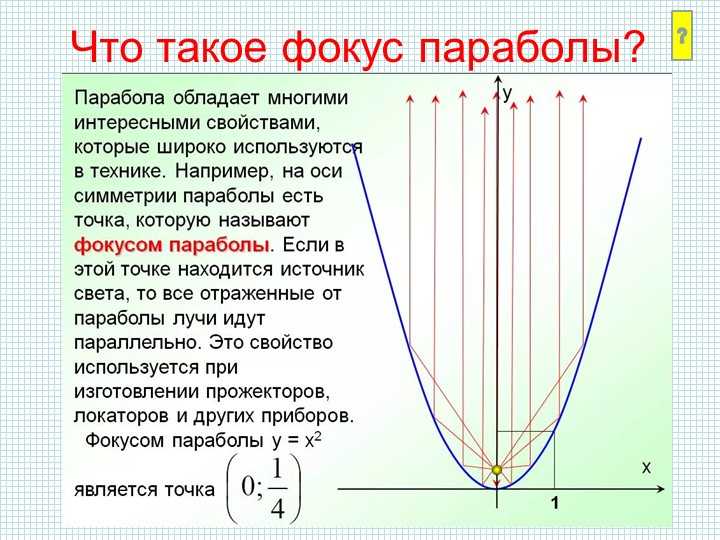
Пример.
В одной координатной плоскости изобразим графики функций:
Получим два графика, они симметричны относительно оси х.
Рассмотрим пример: изобразим в одной координатной плоскости графики функции:
Изобразим графики этих функций:
График функции у=ах² можно получить из параболы у=х² растяжением от оси х в а раз, если а>0, и сжатием к оси х в 1/а раз к оси х, если 0<а<1.
IV. Формирование умений и навыковУпражнения:
1. № 90, № 92, № 94.
V. Итоги урокаВопросы учащимся:
— Как называется график функции у = ах²?
— Куда направлены ветви параболы, если а > 0 (а < 0)?
— Как может быть получен график функции у = 5х² из графика функции у = х²?
— Как может быть получен график функции у =1/7 · х² из графика функции у = х²?
— Как может быть получен график функции у = -4х² из графика функции у = 4х²?
— Перечислите свойства функции у = ах² при а < 0.
Домашнее задание: № 91, № 93, № 95.
Парабола — определение, уравнение, свойства, примеры
- Автор Ритеш Кумар Гупта
- Последнее изменение 20-10-2022
Что приходит на ум, когда вы слышите слово ПАРАБОЛА? Не правда ли, первое, что приходит на ум, это МАТЕМАТИКА? Но одно мы не знаем, это значение параболы. Все мы понимаем, что парабола — это базовая кривая. Параболическая форма играет важную роль в реальном мире. Электрический камин, фонарик, солнечная плита, спутниковая антенна и параболический микрофон используют параболическую форму, чтобы действовать как передатчик или приемник. Так что есть причина использовать параболическую форму. Давайте углубимся, чтобы узнать об этом подробнее.
Парабола — это сечение прямого круглого конуса, полученное путем разрезания его плоскостью, параллельной наклону или образующей конуса. Это геометрическое место движущейся точки на плоскости, расстояние которой от фиксированной точки равно ее расстоянию от фиксированной линии, не содержащей фиксированной точки.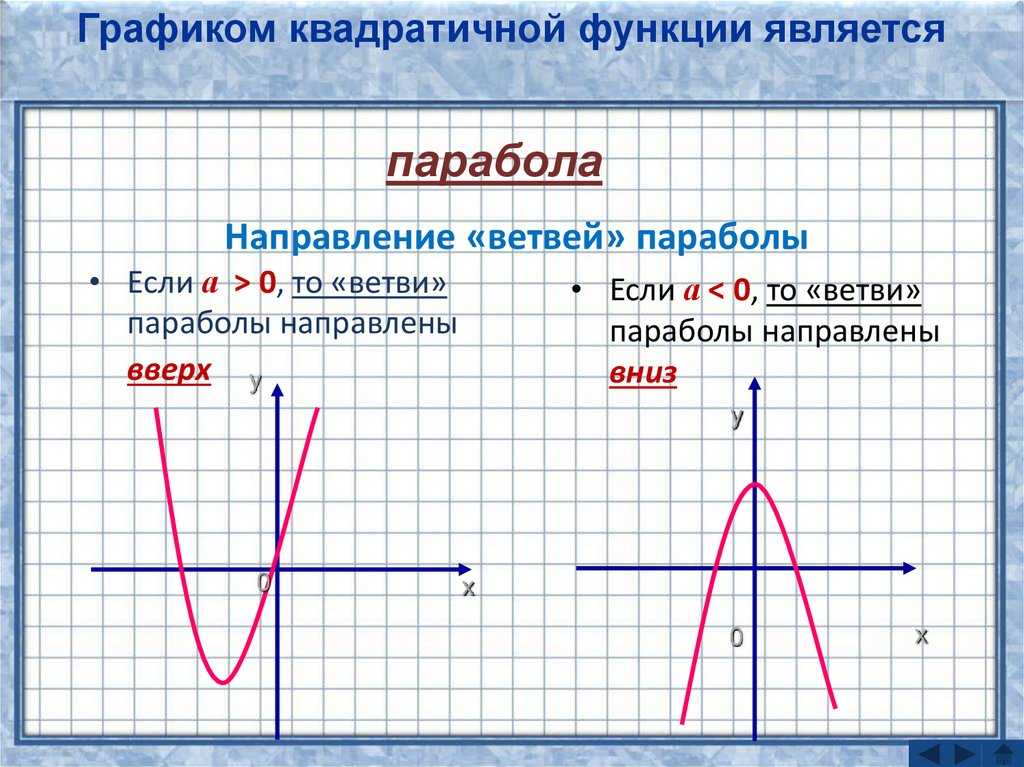 Фиксированная точка называется фокусом , , а фиксированная линия называется директрисой .
Фиксированная точка называется фокусом , , а фиксированная линия называется директрисой .
Ось симметрии — это линия, перпендикулярная директрисе и проходящая через фокус (то есть линия, которая делит параболу пополам).
Фокусное расстояние — это расстояние между вершиной и фокусом, измеренное вдоль оси симметрии.
Хорда параболы, параллельная директрисе и проходящая через фокус, известна как широкая прямая кишка .
Параболы могут открываться в любом направлении: вверх, вниз, влево, вправо или в любую другую сторону. 92} = 4ax\), вершина которого \(\left({0,0} \right)\), фокус \(\left({a,0} \right)\) и направляющая \(x= -a\) (где \(a\) — расстояние между вершиной и фокусом) приведены ниже:
Здесь \(a > 0\) парабола раскрыта справа. 2} + bx + c\) задаются как \(\left({\frac{{ – b}}{{2a}},0} \right )\)
92} + 2x + 3\) показаны ниже:
2} + bx + c\) задаются как \(\left({\frac{{ – b}}{{2a}},0} \right )\)
92} + 2x + 3\) показаны ниже:
Свойства параболы
1. Эксцентриситет — это коэффициент конического сечения, который указывает, насколько круглым является коническое сечение. Больший эксцентриситет указывает на менее сферическое поведение, а меньший эксцентриситет указывает на более сферическое поведение. Он обозначается буквой \({\rm{e}}{\rm{.}}\) Отношение расстояния между фокусом и точкой на плоскости к вершине и только этой точке является эксцентриситетом парабола. Таким образом, любая парабола имеет эксцентриситет \(1\).
2. Парабола симметрична относительно своей оси.
3. Ось проходит перпендикулярно направляющей.
4. Фокус и вершина связаны через ось.
5. В вершинах касательная параллельна директрисе.
6. Вершина – это середина фокуса и место пересечения директрисы и оси.
7. Если \(a\) — расстояние между фокусом и вершиной, то расстояние между фокусом и точкой на плоскости равно \(2a\), что равно расстоянию между фокусом и директрисой.
 Ось симметрии проходит посередине широкой прямой кишки, что указывает на то, что половина широкой прямой кишки равна \(2а\), а длина широкой прямой кишки равна \(4а\).
Ось симметрии проходит посередине широкой прямой кишки, что указывает на то, что половина широкой прямой кишки равна \(2а\), а длина широкой прямой кишки равна \(4а\).Примеры параболы в реальной жизни
Есть много примеров из жизни, где парабола играет важную роль; вот некоторые из них:
1. Когда жидкость вращается, гравитационные силы заставляют жидкость принимать форму, подобную параболе. Самый распространенный пример — это когда вы вращаете стакан с апельсиновым соком вокруг своей оси, чтобы взболтать его. Уровень сока поднимается по бокам стакана и несколько снижается в середине (по оси). Водоворот — еще один пример вращающихся жидкостей.
2. Спутниковые антенны также используют параболы для отражения сигналов, которые впоследствии отправляются на приемник. Например, в Национальной радиоастрономической обсерватории, расположенной в Грин-Бэнке, Западная Вирджиния, находится самый совершенный в мире астрономический телескоп, работающий в диапазоне длин волн от сантиметров до миллиметров.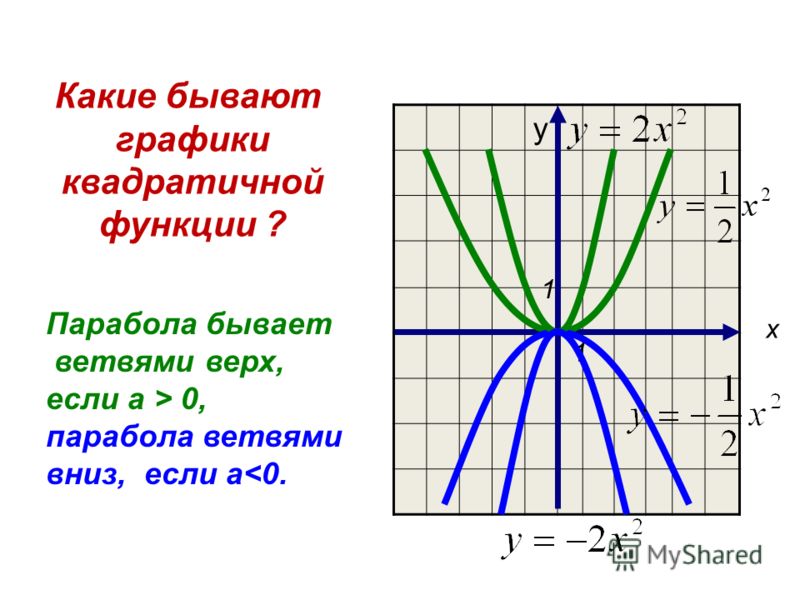 Из-за отражающих свойств парабол сигналы, отправленные непосредственно на спутник, будут отражаться и возвращаться к приемнику после отражения от фокуса.
Из-за отражающих свойств парабол сигналы, отправленные непосредственно на спутник, будут отражаться и возвращаться к приемнику после отражения от фокуса.
3. В области архитектуры и техники используются параболы. Парабола, сооружение в Лондоне, созданное в \(1962\), состоящее из медной крыши с параболическими и гиперболическими линиями, является примером параболической формы. В Сан-Франциско, штат Калифорния, мост Золотые Ворота имеет параболы с каждой стороны боковых пролетов.
4. Отражающие свойства парабол используются в ряде обогревателей. Источник тепла находится в центре, с параллельными лучами, концентрирующими тепло. 92} = 8x\)
Q.3. Если расстояние между фокусом и вершиной параболы равно \(10\,{\text{см}}\). Какова будет длина широкой прямой кишки этой параболы?
Ответ: Поскольку мы знаем, что если \(a\) — это расстояние между фокусом и вершиной, то расстояние между фокусом и точкой на плоскости равно \(2a\), что равно к расстоянию между фокусом и директрисой. Ось симметрии проходит посередине широкой прямой кишки, что указывает на то, что половина широкой прямой кишки равна \(2а\), а длина широкой прямой кишки равна \(4а\). Итак, Здесь \(a = 10\,{\text{см}} \Rightarrow \) Длина широкой прямой кишки равна \(4 \times 10\,{\text{см=40}}\,{\text{см }}\) 92} + b \times 0 + c\)
Ось симметрии проходит посередине широкой прямой кишки, что указывает на то, что половина широкой прямой кишки равна \(2а\), а длина широкой прямой кишки равна \(4а\). Итак, Здесь \(a = 10\,{\text{см}} \Rightarrow \) Длина широкой прямой кишки равна \(4 \times 10\,{\text{см=40}}\,{\text{см }}\) 92} + b \times 0 + c\)
\( \Стрелка вправо 5 = b + c\) и \(c = 3\)
\( \Стрелка вправо 5 = b + 3\)
\( \Стрелка вправо b = 2\)
Резюме
Парабола не просто о математике или о том, как мы строим параболу. Парабола имеет свое значение, которое понимают лишь немногие, значение, которое может произвести нечто экстраординарное, и значение, которое может восхищать других своей красотой и уникальностью в зданиях. Мы видели его огромное применение в реальном мире, что привело к значительной роли в математическом мире.
Часто задаваемые вопросы (FAQ) – Parabola
Q.1. Каково определение параболы? Приведите пример.
Ответ: Парабола — это симметричная плоская кривая, образованная при пересечении конусом плоскости, параллельной одной из его сторон. U-образный график квадратного выражения является примером параболы.
U-образный график квадратного выражения является примером параболы.
Q.2. Является ли радуга параболой?
Ответ: Радуга не имеет форму параболы. Это часть круга. Радугу можно увидеть везде, где угол между прямым светом от солнца и преломленным светом, достигающим ваших глаз, фиксирован.
Q.3. Что такое форма параболы?
Ответ: Парабола — это зеркально-симметричная плоская кривая, которая в математике имеет примерно U-образную форму. Он подходит для различных разнообразных математических описаний, все из которых, как можно показать, определяют одни и те же кривые. У параболы есть точка (фокус) и линия (директриса). 92} + bx + c\) будет минимумом (низшей точкой) графика, если \(a > 0\), и максимумом графика (высшей точкой), если \(a < 0\).
Ниже приведены некоторые другие полезные статьи Embibe:
Мы надеемся, что эта статья о параболе принесла вам значительную пользу. Если у вас есть какие-либо вопросы или предложения, не стесняйтесь записывать их в разделе комментариев ниже. Мы будем рады услышать от вас. Embibe желает вам удачи!
Если у вас есть какие-либо вопросы или предложения, не стесняйтесь записывать их в разделе комментариев ниже. Мы будем рады услышать от вас. Embibe желает вам удачи!
Математические формулы для 7 класса: все важные математические формулы
- Автор Вайбхав_Радж_Астхана
- Последнее изменение 08.05.2022
Математические формулы для 7-го класса : Учащиеся должны подготовиться к экзамену по математике для 7-го класса, выучив наизусть математические формулы для 7-го класса. Почти каждая глава требует, чтобы учащиеся были знакомы с формулами, чтобы избежать каких-либо сложностей. Формула играет важную роль в улучшении критического мышления детей. Желательно, чтобы учащиеся тщательно следовали формулам.
Учащиеся также могут записать формулу по математике для 7-го класса на копии, чтобы попрактиковаться. Кроме того, учащиеся также могут выбрать загрузку PDF-формулы по математике для 7-го класса. Студенты должны следовать формуле по главам, чтобы улучшить свою подготовку по математике. В приведенной ниже статье мы предоставили PDF-файлы для математических формул для класса 7 в разных главах. Учащиеся могут обращаться к ним при отработке вопросов.
В приведенной ниже статье мы предоставили PDF-файлы для математических формул для класса 7 в разных главах. Учащиеся могут обращаться к ним при отработке вопросов.
Прежде чем доказывать формулы, давайте взглянем на список глав, изучаемых в математике для 7 класса.
- Целые числа
- Фракции и десятичные десятички
- Обработка данных
- Простые уравнения
- Линии и углы
- Треугольник и его свойства
- Конгресс 9000 9000 9000.
- 9000. и 9000
- 9000. и 9000
- 9000. и
- . Площадь
- Алгебраические выражения
- Экспоненты и степени
- Симметрия
- Визуализация объемных фигур
Теперь перейдем к математическим формулам для 7-го класса.
Важные математические формулы для 7-го класса
Важные математические формулы для 7-го класса приведены ниже:
| Целочисленные формулы = a + аддитивная обратная величина b = a + (– b) 2) a – (– b) = a + аддитивная обратная величина (– b) = a + b 3) a + (b + c) = (a + б) + в 4) а × (– б) = (– а) × б = – (а × б) 5) (– а) × (– б) = а × б 6) (а × б) × с = а × (б × с) 7) a × (b + c) = a × b + a × c 8) a × (b – c) = a × b – a × c 9) a ÷ (–b) = (– a) ÷ b, где b ≠ 0 10) (– a) ÷ (– b) = a ÷ b, где b ≠ 0 11) a ÷ 0 не определено & a ÷ 1 = a | |
| Дроби и десятичные дроби | 1) \(\frac{произведение \,из \,числителей}{Произведение \,из \,знаменателей}\) . Например, \(\frac{4}{5}\times \frac{3}{7}= \frac{4\times3}{5\times7}=\frac{12}{35}\) Например, \(\frac{4}{5}\times \frac{3}{7}= \frac{4\times3}{5\times7}=\frac{12}{35}\) 2) Чтобы умножить десятичное число на 10, 100 или 1000, мы передвигаем десятичную точку в числе вправо на столько знаков, сколько нулей стоит над 1. 3) Деление десятичного числа – Чтобы разделить десятичное число на целое число, мы сначала разделим их как целые числа. |
| Обработка данных | 0263 |
| Простые уравнения | Уравнение — это условие для переменной, при котором два выражения в переменной должны иметь одинаковое значение. Пример: 5x + 6 = 26, левая и правая стороны должны быть сбалансированы, поэтому для балансировки уравнения значение x должно быть равно 4. Приведенное выше уравнение можно решить как > 5x = 26 – 6 > 5x = 20 > x = \(\frac{20}{5}\) > x = 4 |
| Линии и углы | Два дополнительных угла: Сумма мер составляет 90° Два дополнительных угла: Сумма мер составляет 180° Два смежных угла: Имеют общую вершину и общее плечо, но не имеют общей внутренней части.  Линейная пара: Прилегающая и дополнительная. Вершин: 9{2}\) «В прямоугольном треугольнике квадрат гипотенузы = сумма квадратов катетов». P\times R\times T}{100}\) Где P=Основная сумма, T= Время в годах, R=Процентная ставка в год Ставка \(R=\frac{SI\times 100}{P \times T}\) Основной \(P=\frac{SI\times 100}{R\times T}\) Time \(T=\frac{SI\times 100}{P\times Р}\) 92+x(a+b)+(ab)\) |
| Показатели и степени | p m x p n = p m+n {p} N } = P M -N 4 -M = 1/P M |
Теперь у вас есть полный список математических формул для 7 класса. Изучайте формулы по мере продвижения по учебной программе и регулярно применяйте их, чтобы лучше усвоить предмет.
Применение математических формул 7-го класса
Поскольку математические формулы 7-го класса охватывают основные и практические формулы, они могут применяться в различных сферах жизни.
- Математические формулы 7 класса помогают понять, как работает повседневная деятельность. Эти формулы используются во всем мире, будь то для расчета прибыли и убытков или для расчета процентов на деньги.
- Формулы измерения и геометрии помогают нам определять размеры форм, с которыми мы сталкиваемся в повседневной жизни. Например, если человеку нужно узнать, сколько кирпичей нужно, чтобы построить комнату, то требуется знание формул практической геометрии.
- Алгебраические формулы позволяют нам находить неизвестные значения. Любую задачу с неизвестной переменной можно выразить в виде алгебраического уравнения, которое затем можно легко решить с помощью алгебраических сущностей.

Советы по изучению математических формул для 7 класса
Ниже приведены советы по изучению математических формул для 7 класса:
- Постарайтесь сосредоточиться на одной теме или одной формуле за раз. Как только конкретная концепция или формула станут ясными, переходите к следующей теме. Чтобы понять логику, стоящую за ней, убедитесь, что вы попрактиковались в достаточном количестве задач, связанных с этой формулой.
- При отработке задач потренируйтесь писать пошаговое описание проблемы, которое называется формулировкой задачи. Это помогает установить взаимосвязь между постановкой задачи и используемой формулой, тем самым обеспечивая хорошую привычку заучивать формулы в письменном виде.
Часто задаваемые вопросы о математических формулах для 7-го класса
Q.1: Что такое математические формулы?
Ответ : Формулы в математике представляют собой набор правил или отношений, которые используют числа, буквы или числа и буквы для решения запроса.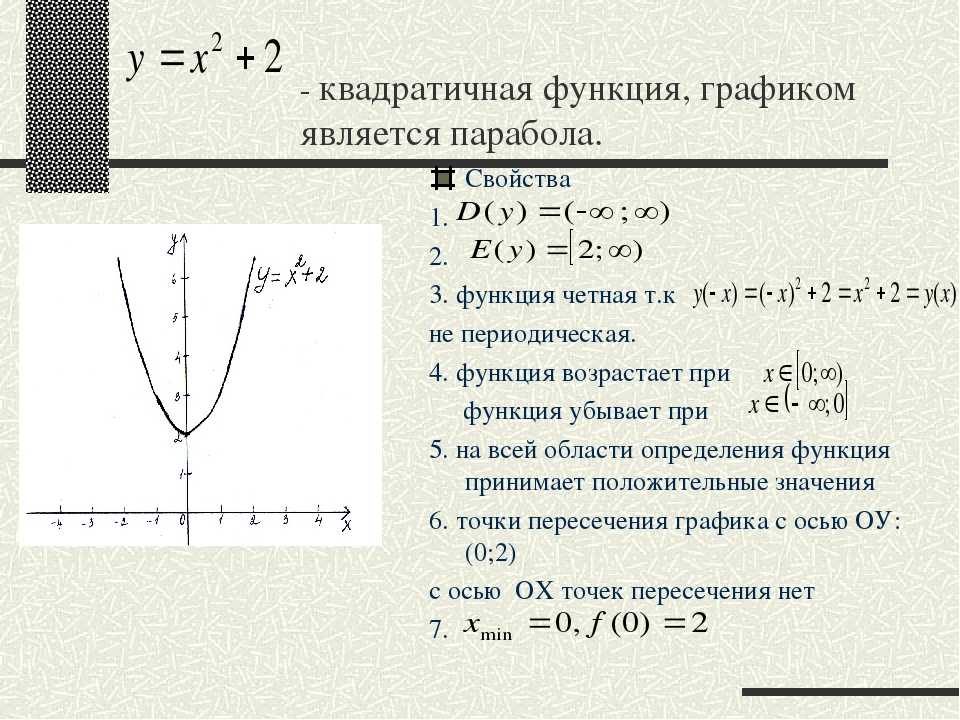 Пример: (a+b)2=a2+2ab+b2(a+b)2=a2+2ab+b2
Пример: (a+b)2=a2+2ab+b2(a+b)2=a2+2ab+b2
Q.2: Как я могу изучать математику в 7 классе?
Ответ : Математика для 7 класса состоит из 15 глав, которые представляют собой расширенные версии тем из 6 класса. Чтобы выучить математику для 7 класса easilt=yu, вы должны практиковаться в вопросах и понимать концепции. Вы можете использовать математические формулы, предоставленные нами для вашей подготовки.
Q.3: Где я могу найти формулу целых чисел для класса 7?
Ответ : В этой статье доступны целочисленные формулы, такие как a × (– b) = (– a) × b = – (a × b). Вы можете просмотреть их здесь.
Q.4: Каковы формулы Главы 11 Математики Класса 7?
Ответ : Класс 7 Математика Глава 11 — это периметр и площадь, и его формулы приведены в этой статье.
Q.5: Каковы основные формулы в математике 7 класса?
Ответ: Основные формулы в математике 7 класса могут включать в себя объекты алгебраических выражений, отношение пропорции, расчет законов прибыли и убытков, связанных с показателями и степенями, а также проценты по теме сравнения величин и исследования площади и периметра фигур в практической геометрии.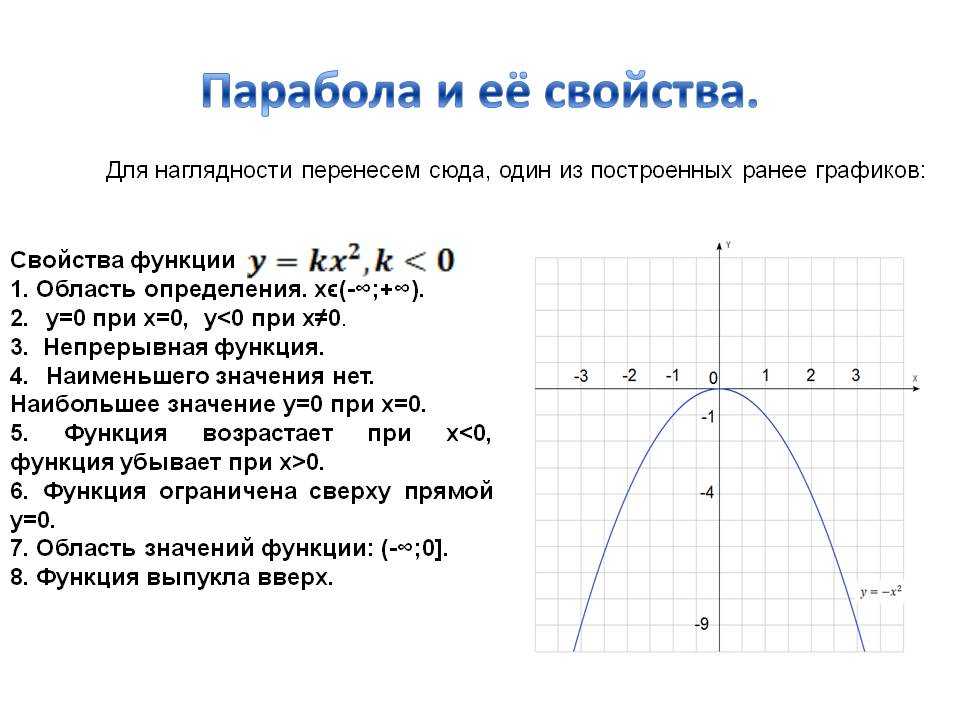


 1
1