5. Биссектриса угла в параллелограмме отсекает от него равнобедренный треугольник.
$∆АВК$ — равнобедренный
6. В параллелограмме биссектрисы углов, прилежащих к одной стороне (соседних углов), пересекаются под углом в $90°$.
Площадь параллелограмма:
1. Площадь параллелограмма равна произведению двух соседних сторон на синус угла между ними.
$S=a·b·sinα$, где $а$ и $b$ — длины сторон параллелограмма, а $α$ — угол между этими сторонами.
2. Площадь параллелограмма равна произведению основания на высоту.
$S=h_a·a$, где $a$ — сторона параллелограмма, $h_a$ — высота, проведенная к стороне $a$.
Периметр параллелограмма: $P=2(a+b)$, где $а$ и $b$ — длины сторон параллелограмма.
Пример:
Периметр параллелограмма равен $14$. Одна сторона параллелограмма на $1$ больше другой. Найдите меньшую сторону параллелограмма.
Решение:
Пусть меньшая сторона $ВС-х$, тогда $АВ-(х+1)$, так как она на $1$ больше.
Запишем формулу периметра параллелограмма: $P=2(a+b)$, где $а$ и $b$ — длины сторон параллелограмма.
Подставим в формулу известные данные и значения сторон, записанные через «х».
$2(х+х+1)=14$
Получили линейное уравнение, разделим обе части на $2$.
$х+х+1=7$
$2х=6$
$х=3$.
За «х» брали меньшую сторону параллелограмма, следовательно, это и есть ответ.
Ответ: $3$
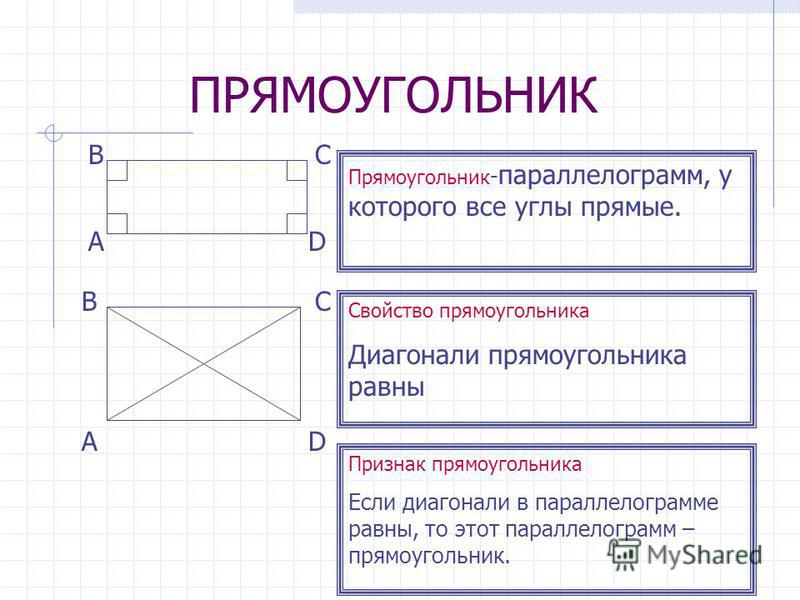
Прямоугольник — это параллелограмм, у которого все углы прямые.
Свойства прямоугольника:
1. Все свойства параллелограмма (Так как прямоугольник – это тот же параллелограмм, только особенный, поэтому у него присутствуют все свойства параллелограмма).
2. Диагонали прямоугольника равны.
$BD= AC$.
Площадь прямоугольника равна половине произведения смежных (соседних) сторон.
$S=a·b$, где $а$ и $b$ — смежные стороны.
Периметр прямоугольника: $P=2(a+b)$, где $а$ и $b$ — длины сторон прямоугольника.
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Все свойства прямоугольника.
 2}/{2}$, где $d$ — диагональ квадрата.
2}/{2}$, где $d$ — диагональ квадрата.
Периметр квадрата: $P=4a$
Прямоугольный треугольник — это треугольник, у которого один угол прямой (равен $90$ градусов).
Катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
- Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
- В прямоугольном треугольнике $АВС$, с прямым углом $С$
- Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.
- Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.
 2=9$
2=9$$ВН=3$
Подставляем найденную длину в формулу косинуса
$cos В = {3}/{15}=1/5=0.2$
$sin A= cos B=0.2$
Ответ: $0.2$
Значения тригонометрических функций некоторых углов:
$α$ $30$ $45$ $60$ $sinα$ ${1}/{2}$ ${√2}/{2}$ ${√3}/{2}$ $cosα$ ${√3}/{2}$ ${√2}/{2}$ ${1}/{2}$ $tgα$ ${√3}/{3}$ $1$ $√3$ $ctgα$ $√3$ $1$ ${√3}/{3}$ Практика: решай 3 задание и тренировочные варианты ЕГЭ по математике (профильной)
математика (база): Прямоугольник и Параллелограмм
Четырёхугольник
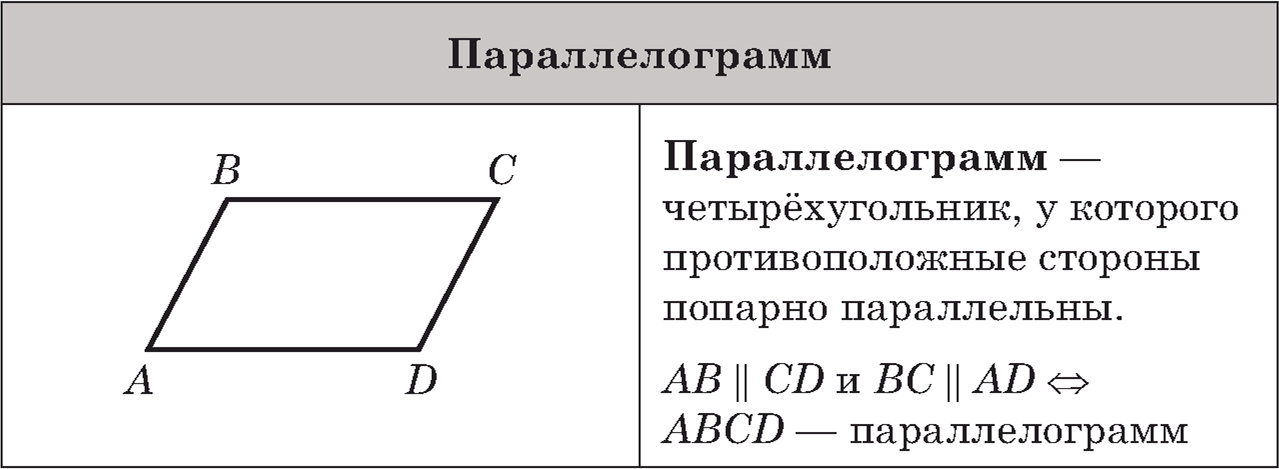
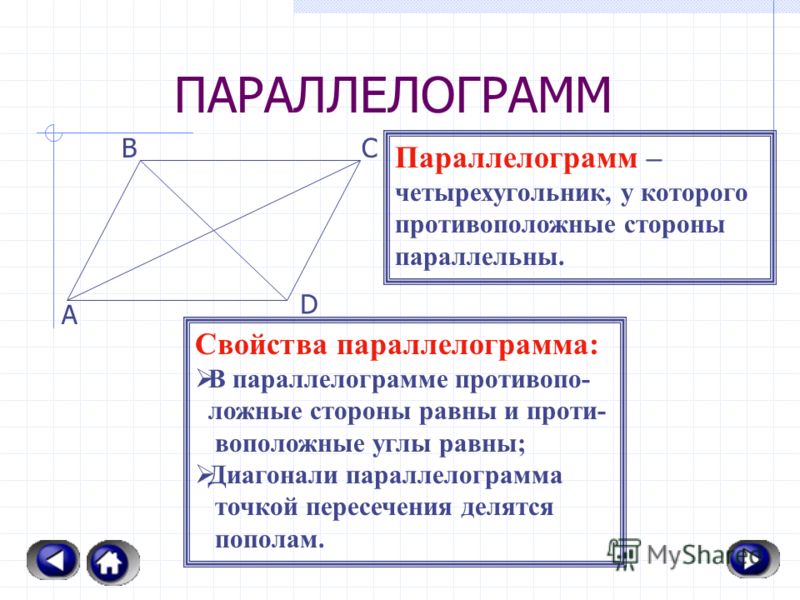
Параллелограмм. Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма
1. Диагональ разбивает параллелограмм на два равных треугольника.
Диагональ разбивает параллелограмм на два равных треугольника.
2. Противоположные стороны параллелограмма попарно равны.
3. Противоположные углы параллелограмма попарно равны.
4. Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
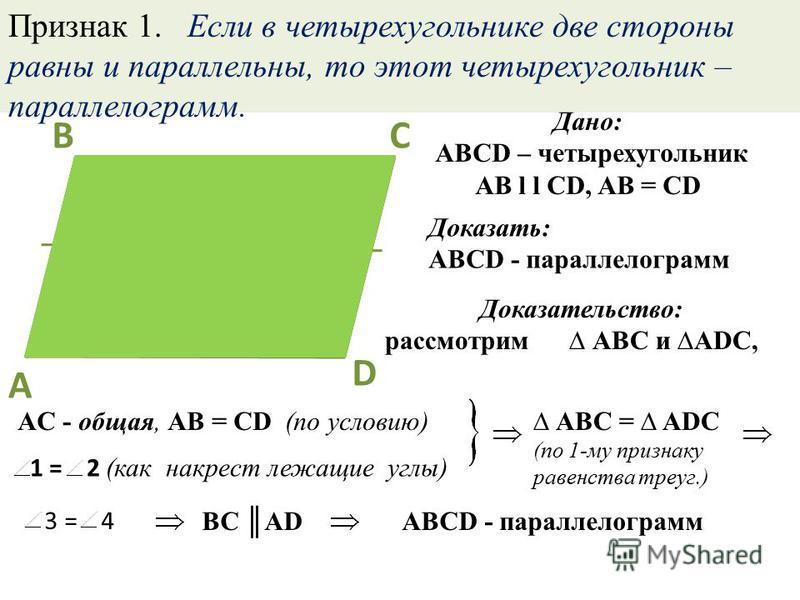
6. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
7. Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник — параллелограмм.Свойство середин сторон четырёхугольника. Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырёхугольника.
Прямоугольник. Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника
1. Диагонали прямоугольника равны.
2. Если диагонали параллелограмма равны, то этот параллелограмм — прямоугольникКвадрат.
 Квадратом называется прямоугольник, все стороны которого равны.
Квадратом называется прямоугольник, все стороны которого равны.Формулы площади четырёхугольника
1. Площадь параллелограмма равна произведению основания на высоту
2. Площадь параллелограмма равна произведению его соседних сторон на синус угла между ними.
3. Площадь прямоугольника равна произведению двух его соседних сторон.Основные формулы
Далее S — площадь фигуры, P — периметр, p — полупериметр.Чертежи Обозначения Формулы a, b, c, d — стороны;
D1, D2 — диагонали;
γ — угол между диагоналями;
h2, h3 — длины перпендикуляров, опущенных на диагональ D1;
α, β — два противолежащих угла четырёхугольника.a, b — стороны;
h — расстояние между сторонами b;
α — угол параллелограмма;
D1, D2 — диагонали;
γ — угол между диагоналямиПлощадь четырёхугольника
Площадь прямоугольника равна произведению его смежных сторон:
S = ab.

На рисунке 156 приведены чертежи некоторых прямоугольников, у которых показаны смежные стороны a и b
Задачи с решениями
На клетчатой бумаге с клетками размером 1 см×1 см изображён прямоугольник (см. рис. 157). Найдите его площадь в квадратных сантиметрах.Решение.
1-й способ.
Площадь прямоугольника равна произведению его смежных сторон a и b. Для того чтобы найти стороны прямоугольника, рассмотрим прямоугольный треугольник ABC с катетами AB = 2 и BC = 1 и гипотенузой AC = b (см. рис. 158).
Ответ: 10.2-й способ.
Площадь прямоугольника BKMD равна 4 · 5 = 20. Следовательно, площадь искомого прямоугольника будет равна 20 − 1 − 1 − 4 − 4 = 10.
Достроим прямоугольник ACEH до прямоугольника BKMD (см. рис. 159). Чтобы найти площадь ACEH, нужно из площади прямоугольника BKMD вычесть площади прямоугольных треугольников AKH, HME, EDC и ABC.
Так как площадь прямоугольного треугольника равна половине произведения катетов, то площадь каждого из двух больших треугольников (AKH и EDC) равна 4, а площадь каждого из двух маленьких треугольников (HME и ABC) равна 1.
Ответ: 10.
Заметим, что подобным «достраиванием» можно найти площадь любого многоугольника на клетчатой бумаге.Могут ли параллелограммы иметь прямые углы?
Комментариев к записи Может ли параллелограмм иметь прямые углы? и площадь. Мир полон различных форм. Эти формы имеют свои размеры. Есть двумерные фигуры и трехмерные фигуры. Куб, прямоугольный параллелепипед, конус, сфера и цилиндр — это трехмерные фигуры, поскольку они имеют длину, ширину и высоту. Квадрат, прямоугольник, треугольник, многоугольники, ромб и параллелограмм являются двумерными фигурами, они имеют длину и ширину. Продолжайте читать, чтобы узнать, есть ли у параллелограмма прямые углы?
Параллелограмм – это четырехугольник с двумя парами параллельных сторон. Противоположные углы конгруэнтны, несколько примеров параллелограмма — это крыша, черепица и солнечная батарея.
 Это замкнутая плоская фигура с диагоналями, делящими друг друга пополам. Прямоугольник, ромб и квадрат являются типами параллелограммов. Итак, могут ли параллелограмм иметь прямые углы? Да, параллелограмм может иметь прямые углы. Квадрат является параллелограммом, у которого все углы и диагонали пересекаются пополам под прямым углом. Прямоугольник, этот четырехугольник имеет 9углы 0°. Любой четырехугольник, у которого стороны параллельны, как и прямоугольник, считается параллелограммом. Таким образом, прямоугольник, являющийся параллелограммом, имеет прямые углы. У ромба нет прямых углов, но биссектрисы образуют в центре углы 90°. Читайте дальше, чтобы понять различные типы четырехугольников.
Это замкнутая плоская фигура с диагоналями, делящими друг друга пополам. Прямоугольник, ромб и квадрат являются типами параллелограммов. Итак, могут ли параллелограмм иметь прямые углы? Да, параллелограмм может иметь прямые углы. Квадрат является параллелограммом, у которого все углы и диагонали пересекаются пополам под прямым углом. Прямоугольник, этот четырехугольник имеет 9углы 0°. Любой четырехугольник, у которого стороны параллельны, как и прямоугольник, считается параллелограммом. Таким образом, прямоугольник, являющийся параллелограммом, имеет прямые углы. У ромба нет прямых углов, но биссектрисы образуют в центре углы 90°. Читайте дальше, чтобы понять различные типы четырехугольников.Взломы Starbucks Rewards – Знайте больше…
Включите JavaScript
Взломы Starbucks Rewards – Знайте больше
Четырехугольный префикс «Quad» означает четыре, а «lateral» означает стороны. Четырехугольник – это четырехсторонняя замкнутая фигура, в результате чего общая сумма внутренних углов равна 360°.
 Существуют различные типы четырехугольников. Те немногие, о которых говорилось выше, это квадрат, прямоугольник, ромб и параллелограмм. Четырехугольник – это четырехугольник. Кроме того, трапеция также является четырехугольником.
Существуют различные типы четырехугольников. Те немногие, о которых говорилось выше, это квадрат, прямоугольник, ромб и параллелограмм. Четырехугольник – это четырехугольник. Кроме того, трапеция также является четырехугольником.Какие бывают виды углов?
Угол — это фигура, образованная пересечением двух сторон. Две стороны имеют одну общую конечную точку, называемую вершиной. Типы углов следующие:-
- Острый угол:
Угол меньше прямого угла и имеет значение меньше 90°, считается острым углом.
- Тупой угол:
Тупой угол — это угол, значение которого больше 90°.
- Прямоугольный или 9Угол 0°:
Угол создается перпендикулярной линией, которая образует прямую линию, образующую угол 90° на плоскости 180°. В четырехугольниках, таких как квадраты и ромбы, этот угол образован делением диагоналей пополам.
Что такое трапеция?
У трапеции одна сторона параллельна другой. Но другая сторона не параллельна, а значит, линии не имеют равного расстояния друг от друга.
 Следовательно, трапеция не является параллелограммом, потому что не все соответствующие стороны параллельны. Трапеция, называемая трапецией, может иметь 9Угол 0° дает прямоугольную трапецию. У равнобедренной трапеции две непараллельные стороны одинаковой длины. Определение прямоугольника включает квадрат, а определение параллелограмма включает ромб, квадрат и прямоугольник. Точно так же определение трапеции включает параллелограмм.
Следовательно, трапеция не является параллелограммом, потому что не все соответствующие стороны параллельны. Трапеция, называемая трапецией, может иметь 9Угол 0° дает прямоугольную трапецию. У равнобедренной трапеции две непараллельные стороны одинаковой длины. Определение прямоугольника включает квадрат, а определение параллелограмма включает ромб, квадрат и прямоугольник. Точно так же определение трапеции включает параллелограмм.Чем прямоугольник отличается от параллелограмма?
Благодаря свойствам параллелограмма они считаются параллельными, поскольку обе пары противоположных сторон являются соответствующими. Точно так же в определении прямоугольника все пары считаются соответствующими. Но они перпендикулярны друг другу. Следовательно, 9Углы, равные 0°, делают прямоугольник отличным от параллелограмма. Но кроме углов все противоположные стороны прямоугольника равноудалены. Таким образом, параллелограмм является разновидностью прямоугольника. Но прямоугольник не может быть разновидностью параллелограмма.
 Точно так же прямоугольник и параллелограмм могут быть квадратом, но не наоборот.
Точно так же прямоугольник и параллелограмм могут быть квадратом, но не наоборот.Вывод:
Четырехугольник, у которого противоположные стороны параллельны, является параллелограммом. Параллельные прямые — это прямые, которые не пересекаются и находятся на одинаковом расстоянии друг от друга. Квадрат, прямоугольник и ромб являются типами параллелограммов. Каждая форма имеет свои индивидуальные свойства. Параллелограмм не может иметь прямого угла, а квадрат, прямоугольник и ромб имеют прямые углы в силу различных особенностей. Квадрат и прямоугольник имеют прямые углы. В то время как ромб и квадрат имеют прямые углы при бисекции диагоналей. Трапеция также известна как трапеция. У этой формы одна сторона параллельна другой. Три типа трапеций: равнобедренная трапеция, разносторонняя трапеция и правильная трапеция.
Часто задаваемые вопросы:
- Что такое законы параллелограмма?
Есть два типа законов. Первый закон — закон сложения параллелограмма, который доказывает, что противоположные стороны параллелограмма равны.
 И второй закон, закон параллелограмма вектора, обозначает вектор по величине и направлению.
И второй закон, закон параллелограмма вектора, обозначает вектор по величине и направлению.- Каковы свойства параллелограмма?
Стороны, обращенные друг к другу, параллельны и соответствуют друг другу. Один угол является дополнительным к другому с той же внутренней стороной. А сумма двух смежных углов всегда равна 180°.
- Какие существуют типы параллелограммов?
Существуют различные типы параллелограммов. Ромб, прямоугольник и квадрат считаются параллелограммами, потому что противоположные стороны равноудалены, а сумма смежных углов равна 180°. Диагонали параллелограмма пересекаются пополам. Квадрат и ромб образуют в точке пересечения прямые углы.
Геометрия: самые популярные параллелограммы
Прямоугольники, ромбы и квадраты — это три особых вида параллелограммов. Все они обладают свойствами параллелограмма: их противоположные стороны параллельны, их диагонали делят друг друга пополам и делят параллелограмм на два конгруэнтных треугольника, а противоположные стороны и углы конгруэнтны.
 Но у прямоугольников, ромбов и квадратов есть дополнительные характеристики, которых нет у других параллелограммов.
Но у прямоугольников, ромбов и квадратов есть дополнительные характеристики, которых нет у других параллелограммов.Прямоугольники
Прямоугольник — это параллелограмм с прямым углом. На самом деле, из этого небольшого количества информации вы знаете обо всех четырех углах прямоугольника. Прямоугольник является параллелограммом, поэтому его противоположные углы конгруэнтны, а смежные углы смежны. Напомним, что дополнением к прямому углу является еще один прямой угол. Таким образом, у прямоугольника на самом деле четыре прямых угла.
Solid Facts
Прямоугольник — это параллелограмм с прямым углом.
Прямоугольники обладают некоторыми свойствами, которых нет у общих параллелограммов. Одним из таких свойств является то, что диагонали прямоугольника равны. Я сформулирую это как теорему и обсужу план ее доказательства. Я оставлю детали на ваше усмотрение.

- Теорема 15.9 : Диагонали прямоугольника равны.
Чтобы доказать эту теорему, взгляните на прямоугольник на рис. 15.9.. Прямоугольник ABCD имеет диагонали ¯AC и ¯BD. Чтобы доказать, что они конгруэнтны, вы захотите использовать CPOCTAC. Но какие два треугольника, как вы показываете, равны? Я бы порекомендовал вам показать ADC ~= DAB. Разделите эти два треугольника и соедините их. Они оба прямоугольные, так что это одна пара конгруэнтных углов. Поскольку противоположные стороны конгруэнтны, вы сможете использовать наш постулат SAS, чтобы показать ADC ~ = DAB.
Рисунок 15.9 Прямоугольник ABCD имеет диагонали ¯AC и ¯BD .
Ромбы
Ромб представляет собой параллелограмм с двумя конгруэнтными смежными сторонами. Как и в случае с прямоугольником, ромб наследует все желаемые свойства параллелограмма. А ромбы обладают особыми свойствами, которых нет у общих параллелограммов и прямоугольников.

Первое свойство ромба состоит в том, что все стороны ромба равны. Это не удивительно, потому что вы уже знаете, что противоположные стороны ромба равны (потому что это параллелограмм). Если противоположные стороны и смежные стороны равны, то все они конгруэнтный. Не все параллелограммы и прямоугольники gles обладают этим особым свойством.
Solid Facts
Ромб представляет собой параллелограмм с двумя конгруэнтными смежными сторонами.
- Теорема 15.10 : Все стороны ромба равны.
Следующее свойство ромба, о котором стоит упомянуть, это то, что его диагонали перпендикулярны. Это может быть не так очевидно, и стоит написать формальное доказательство.
- Теорема 15.11 : Диагонали ромба перпендикулярны.
- Пример 4 : Напишите формальное доказательство теоремы 15.
 11.
11. - Решение : Как обычно, я напишу формальное доказательство шаг за шагом. На рис. 15.10 показан ромб ABCD с диагоналями ¯AC и ¯BD, пересекающимися в точке M.
Рис. 15.10 Ромб ABCD с диагоналями ¯AC и ¯BD, пересекающимися в точке M.
- Дано: Ромб ABCD с диагоналями ¯AC и ¯BD.
- Докажите: ¯AC ¯BD.
- Доказательство: вам нужен план игры. Держитесь за свою шляпу, потому что это довольно сложно. Чтобы показать, что ¯AC ¯BD, нужно показать, что ¯AC и ¯BD пересекаются и образуют прямой угол. Итак, вам нужно показать, что угол AMB прямой. Поскольку AMB и BMC образуют прямой угол, они дополняют друг друга. Если бы вы могли показать, что они конгруэнтны, то они должны были бы быть прямыми углами. Самый простой способ показать AMB ~= BMC — это показать AMB ~= CMB и использовать CPOCTAC. Теперь, поскольку вы имеете дело с ромбом, ¯AB ~= ¯BC. По рефлексивному свойству ~= вы знаете, что ¯BM ~= ¯BM. Поскольку ромб является параллелограммом, и показано, что диагонали параллелограмма делят друг друга пополам, ¯AM ~= ¯MC.

Утверждения Причины 1. Параллелограмм ABCD имеет диагонали ¯AC и ¯BD При условии, что диагонали ¯AC и ¯BD пересекаются в точке 9 M 2. ¯AM ~= ¯MC Теорема 15.6 3. ¯AB ~= ¯BC Определение ромба 4. ¯BM ~= ¯BM Рефлексивное свойство ~= 5. АМБ ~= СМБ Постулат ССС 6. АМБ ~= БМК КПОКТАК 7. AMB и BMC образуют прямой угол Определение прямого угла 8. mAMB + mBMC = 180º Постулат сложения углов 9. 
мАМВ + мАМВ = 180º Замена (этапы 6 и 8) 10. АМБ прав Алгебра 11. AMB правый Определение прямого угла 12. ¯AC ¯BD Определение Квадраты
Квадрат является и прямоугольником, и ромбом. Квадрат можно определить как прямоугольник с конгруэнтными смежными сторонами или как ромб с прямым углом. Я выберу прежнее описание в качестве официального определения. Квадрат наследует все свойства параллелограмма, прямоугольника и ромба. Квадрат имеет лучшее из всех миров. Он обладает свойствами параллелограмма (противоположные стороны конгруэнтны, противоположные углы конгруэнтны, противоположные стороны параллельны, а диагонали делят пополам), прямоугольника (диагонали конгруэнтны и все четыре угла конгруэнтны) и ромба (диагонали перпендикулярны и все четыре угла равны).


 2}/{2}$, где $d$ — диагональ квадрата.
2}/{2}$, где $d$ — диагональ квадрата. 2=9$
2=9$ Диагональ разбивает параллелограмм на два равных треугольника.
Диагональ разбивает параллелограмм на два равных треугольника.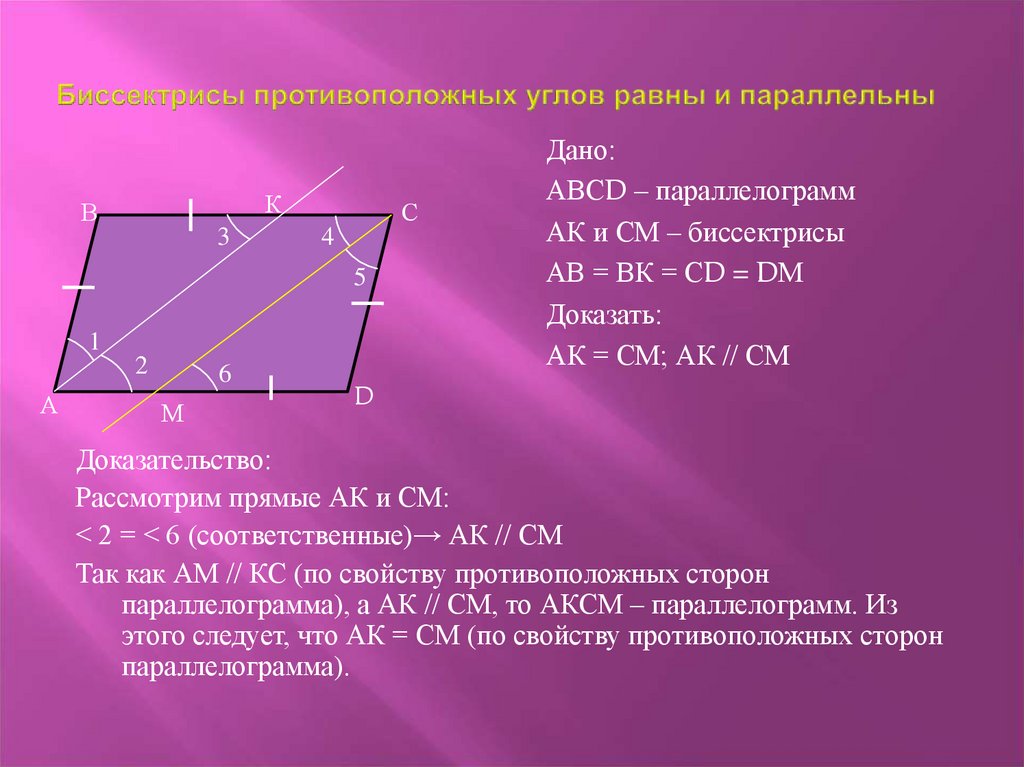 Квадратом называется прямоугольник, все стороны которого равны.
Квадратом называется прямоугольник, все стороны которого равны.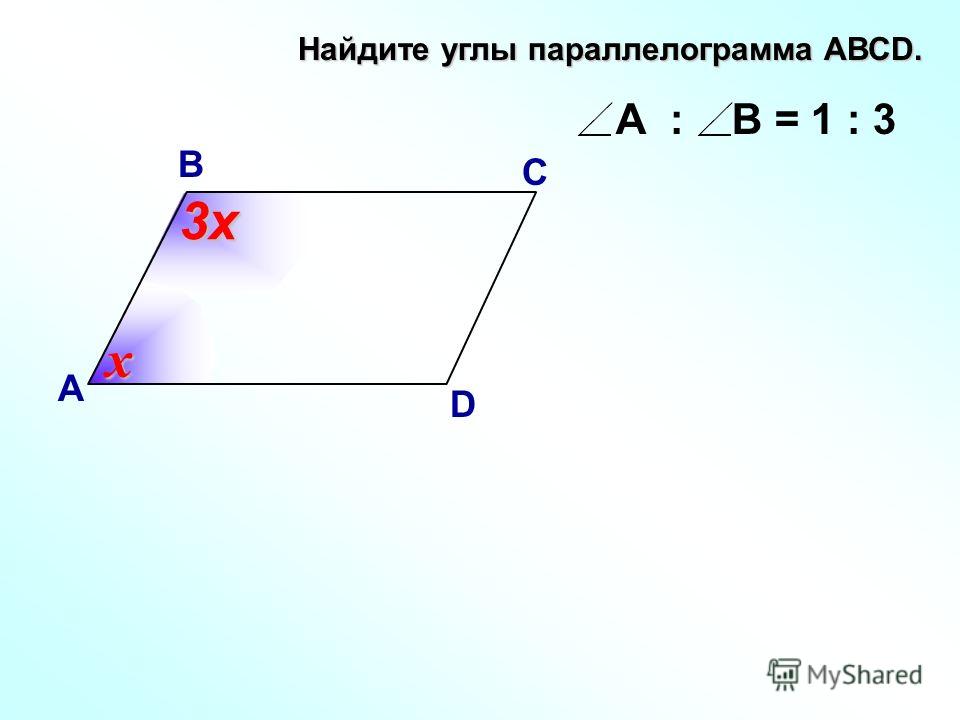
 Это замкнутая плоская фигура с диагоналями, делящими друг друга пополам. Прямоугольник, ромб и квадрат являются типами параллелограммов. Итак, могут ли параллелограмм иметь прямые углы? Да, параллелограмм может иметь прямые углы. Квадрат является параллелограммом, у которого все углы и диагонали пересекаются пополам под прямым углом. Прямоугольник, этот четырехугольник имеет 9углы 0°. Любой четырехугольник, у которого стороны параллельны, как и прямоугольник, считается параллелограммом. Таким образом, прямоугольник, являющийся параллелограммом, имеет прямые углы. У ромба нет прямых углов, но биссектрисы образуют в центре углы 90°. Читайте дальше, чтобы понять различные типы четырехугольников.
Это замкнутая плоская фигура с диагоналями, делящими друг друга пополам. Прямоугольник, ромб и квадрат являются типами параллелограммов. Итак, могут ли параллелограмм иметь прямые углы? Да, параллелограмм может иметь прямые углы. Квадрат является параллелограммом, у которого все углы и диагонали пересекаются пополам под прямым углом. Прямоугольник, этот четырехугольник имеет 9углы 0°. Любой четырехугольник, у которого стороны параллельны, как и прямоугольник, считается параллелограммом. Таким образом, прямоугольник, являющийся параллелограммом, имеет прямые углы. У ромба нет прямых углов, но биссектрисы образуют в центре углы 90°. Читайте дальше, чтобы понять различные типы четырехугольников.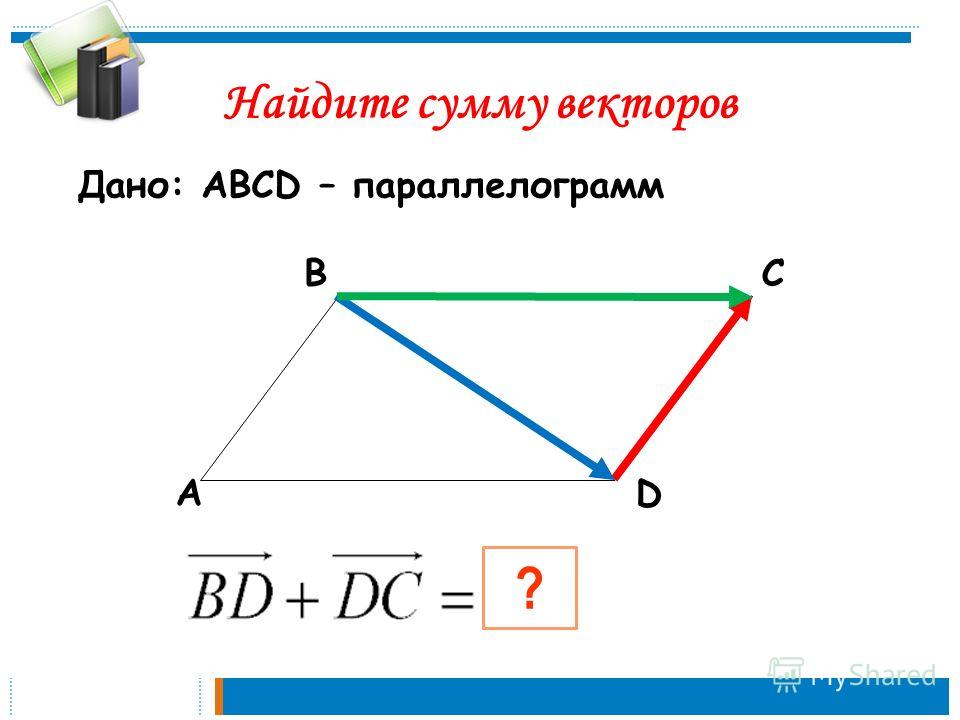 Существуют различные типы четырехугольников. Те немногие, о которых говорилось выше, это квадрат, прямоугольник, ромб и параллелограмм. Четырехугольник – это четырехугольник. Кроме того, трапеция также является четырехугольником.
Существуют различные типы четырехугольников. Те немногие, о которых говорилось выше, это квадрат, прямоугольник, ромб и параллелограмм. Четырехугольник – это четырехугольник. Кроме того, трапеция также является четырехугольником. Следовательно, трапеция не является параллелограммом, потому что не все соответствующие стороны параллельны. Трапеция, называемая трапецией, может иметь 9Угол 0° дает прямоугольную трапецию. У равнобедренной трапеции две непараллельные стороны одинаковой длины. Определение прямоугольника включает квадрат, а определение параллелограмма включает ромб, квадрат и прямоугольник. Точно так же определение трапеции включает параллелограмм.
Следовательно, трапеция не является параллелограммом, потому что не все соответствующие стороны параллельны. Трапеция, называемая трапецией, может иметь 9Угол 0° дает прямоугольную трапецию. У равнобедренной трапеции две непараллельные стороны одинаковой длины. Определение прямоугольника включает квадрат, а определение параллелограмма включает ромб, квадрат и прямоугольник. Точно так же определение трапеции включает параллелограмм.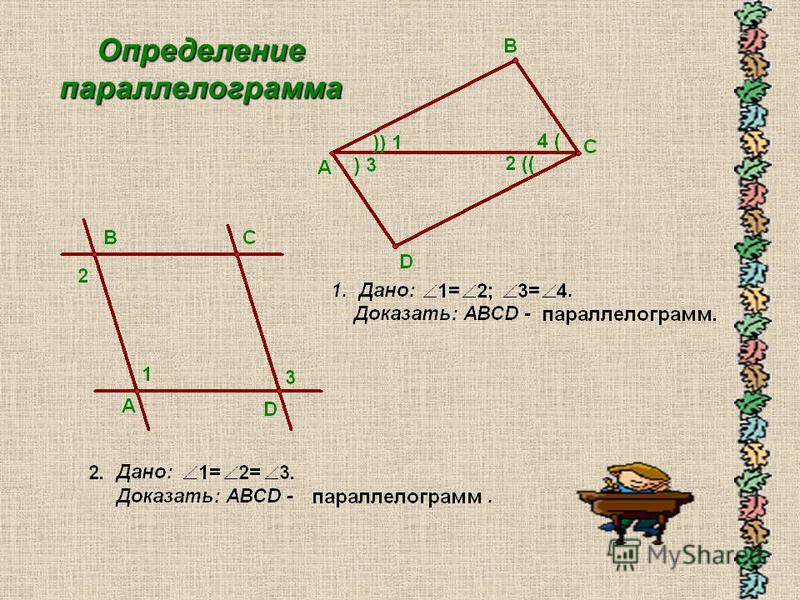 Точно так же прямоугольник и параллелограмм могут быть квадратом, но не наоборот.
Точно так же прямоугольник и параллелограмм могут быть квадратом, но не наоборот.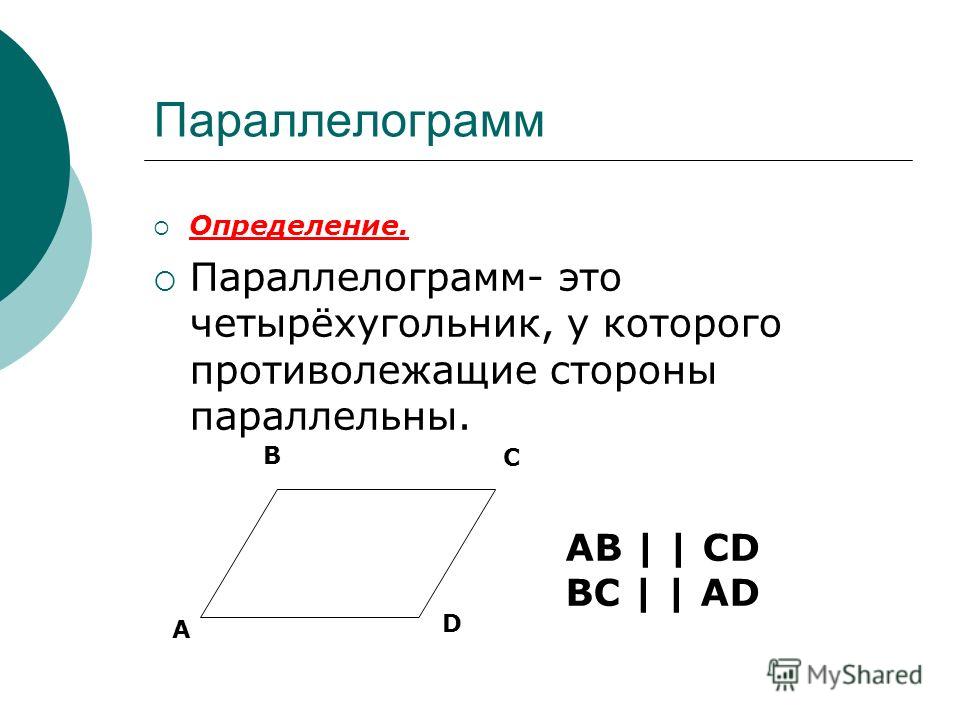 И второй закон, закон параллелограмма вектора, обозначает вектор по величине и направлению.
И второй закон, закон параллелограмма вектора, обозначает вектор по величине и направлению.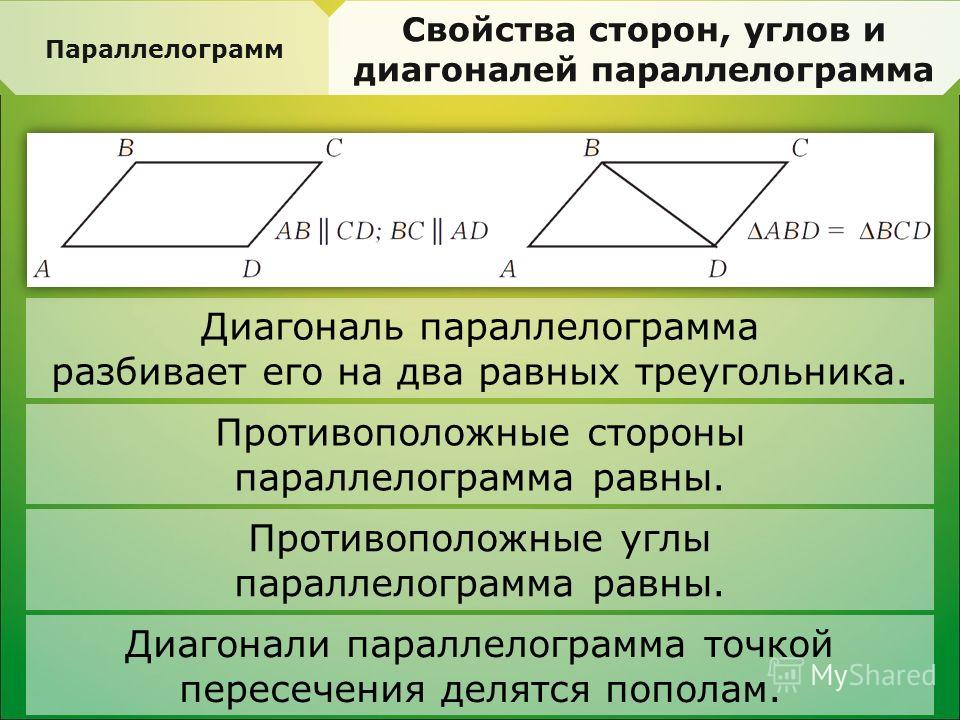 Но у прямоугольников, ромбов и квадратов есть дополнительные характеристики, которых нет у других параллелограммов.
Но у прямоугольников, ромбов и квадратов есть дополнительные характеристики, которых нет у других параллелограммов.
 11.
11.