Преобразование графиков элементарных функций
Основные элементарные функции в чистом виде без преобразования встречаются редко, поэтому чаще всего приходится работать с элементарными функциями, которые получили из основных с помощью добавления констант и коэффициентов. Такие графики строятся при помощи геометрических преобразований заданных элементарных функций.
Рассмотрим на примере квадратичной функции вида y=-13x+232+2, графиком которой является парабола y=x2, которая сжата втрое относительно Оу и симметрична относительно Ох, причем сдвинутую на 23 по Ох вправо, на 2 единицы по Оу вверх. На координатной прямой это выглядит так:
Геометрические преобразования графика функции
Применяя геометрические преобразования заданного графика получаем, что график изображается функцией вида ±k1·f(±k2·(x+a))+b, когда k1>0, k2>0 являются коэффициентами сжатия при 0<k1<1, 0<k2<1 или растяжения при k1>1, k2>1 вдоль Оу и Ох. Знак перед коэффициентами k1 и k2 говорит о симметричном отображении графика относительно осей, a и b сдвигают ее по Ох и по Оу.
Существует 3 вида геометрических преобразований графика:
- Масштабирование вдоль Ох и Оу. На это влияют коэффициенты k1 и k2 при условии не равности 1, когда 0<k1<1, 0<k2<1, то график сжимается по Оу, а растягивается по Ох, когда k1>1, k2>1, то график растягивается по Оу и сжимается по Ох.
- Симметричное отображение относительно координатных осей. При наличии знака «-» перед k1 симметрия идет относительно Ох, перед k2 идет относительно Оу. Если «-» отсутствует, тогда пункт при решении пропускается;
- Параллельный перенос (сдвиг) вдоль Ох и Оу. Преобразование производится при наличии коэффициентов a и b неравных 0. Если значение a положительное, до график сдвигается влево на |а|единиц, если отрицательное a, тогда в право на такое же расстояние. Значение b определяет движение по оси Оу, что значит при положительном b функция движется вверх, при отрицательном – вниз.
Степенная функция
Рассмотрим решения на примерах, начиная со степенной функции.
Преобразовать y=x23 и построить график функции y=-12·8x-423+3.
Решение
Представим функции таким образом:
y=-12·8x-423+3=-12·8x-1223+3=-2x-1223+3
Где k1=2, стоит обратить внимание на наличие «-», а=-12 , b=3. Отсюда получаем, что геометрические преобразования производятся с растяжения вдоль Оу вдвое, отображается симметрично относительно Ох, сдвигается вправо на 12 и вверх на 3 единицы.
Если изобразить исходную степенную функцию, получим, что
при растягивании вдвое вдоль Оу имеем, что
Отображение, симметричное относительно Ох, имеет вид
а движение вправо на 12
движение на 3 единицы вверх имеет вид
Показательная функция
Преобразования показательной функции рассмотрим на примерах.
Пример 2Произвести построение графика показательной функции y=-1212(2-x)+8.
Решение.
Преобразуем функцию, исходя из свойств степенной функции. Тогда получим, что
y=-1212(2-x)+8=-12-12x+1+8=-12·12-12x+8
Отсюда видно, что получим цепочку преобразований y=12x:
y=12x→y=12·12x→y=12·1212x→→y=-12·1212x→y=-12·12-12x→→y=-12·12-12x+8
Получаем, что исходная показательная функция имеет вид
Сжимание вдвое вдоль Оу дает
Растягивание вдоль Ох
Симметричное отображение относительно Ох
Отображение симметрично относительно Оу
Сдвигание на 8 единиц вверх
Логарифмическая функция
Рассмотрим решение на примере логарифмической функции y=ln(x).
Построить функцию y=lne2·-12×3 при помощи преобразования y=ln(x).
Решение
Для решения необходимо использовать свойства логарифма, тогда получаем:
y=lne2·-12×3=ln(e2)+ln-12×13=13ln-12x+2
Преобразования логарифмической функции выглядят так:
y=ln(x)→y=13ln(x)→y=13ln12x→→y=13ln-12x→y=13ln-12x+2
Изобразим график исходной логарифмической функции
Производим сжимание строе по Оу
Производим растягивание вдоль Ох
Производим отображение относительно Оу
Производим сдвигание вверх на 2 единицы, получаем
Для преобразования графиков тригонометрической функции
необходимо подгонять под схему решения вида ±k1·f(±k2·(x+a))+b. Необходимо , чтобы k2 приравнивался к Tk2. Отсюда получаем, что 0<k2<1 дает понять, что график функции увеличивает период по Ох, при k1 уменьшает его. От коэффициента k1 зависит амплитуда колебаний синусоиды и косинусоиды.Преобразования y = sin x
Рассмотрим примеры решения заданий с преобразованиями y=sinx.
Построить график y=-3sin12x-32-2 с помощью преобразований функции y=sinx.
Решение
Необходимо привести функцию к виду ±k1·f±k2·x+a+b. Для этого:
y=-3sin12x-32-2=-3sin12(x-3)-2
Видно, что k1=3, k2=12, a=-3, b=-2. Так как перед k1 имеется «-», а перед k2 — нет, тогда получим цепочку преобразований вида:
y=sin(x)→y=3sin(x)→y=3sin12x→y=-3sin12x→→y=-3sin12x-3→y=-3sin12(x-3)-2
Подробное преобразование синусоиды. При построении графика исходной синусоиды y=sin(x) получаем, что наименьшим положительным периодом считается T=2π. Нахождение максимума в точках π2+2π·k; 1, а минимума — -π2+2π·k; -1, k∈Z.
Производится растягивание по Оу втрое, значит возрастание амплитуды колебаний возрастет в 3 раза. T=2π — это наименьший положительный период. Максимумы переходят в π2+2π·k; 3, k∈Z , минимумы — -π2+2π·k; -3, k∈Z.
При растягивании по Ох вдвое получаем, что наименьший положительный период увеличивается в 2 раза и равняется T=2πk2=4π. Максимумы переходят в π+4π·k; 3, k∈Z, минимумы – в -π+4π·k; -3, k∈Z.
Максимумы переходят в π+4π·k; 3, k∈Z, минимумы – в -π+4π·k; -3, k∈Z.
Изображение производится симметрично относительно Ох. Наименьший положительный период в данном случае не меняется и равняется T=2πk2=4π. Переход максимума выглядит как -π+4π·k; 3, k∈Z, а минимума – π+4π·k; -3, k∈Z.
Производится сдвижение графика вниз на 2 единицы. Изменение наименьшего общего периода не происходит. Нахождение максимумов с перехождением в точки -π+3+4π·k; 1, k∈Z, минимумов — π+3+4π·k; -5, k∈Z.
На данном этапе график тригонометрической функции считается преобразованным.
Преобразование функции y = cos x
Рассмотрим подробное преобразование функции y=cosx.
Пример 5Построить график функции y=32cos2-2x+1 при помощи преобразования функции вида y=cosx.
Решение
По алгоритму необходимо заданную функцию привести к виду ±k1·f±k2·x+a+b. Тогда получаем, что
y=32cos2-2x+1=32cos(-2(x-1))+1
Из условия видно, что k1=32, k2=2, a=-1, b=1, где k2 имеет «-», а перед k1 он отсутствует.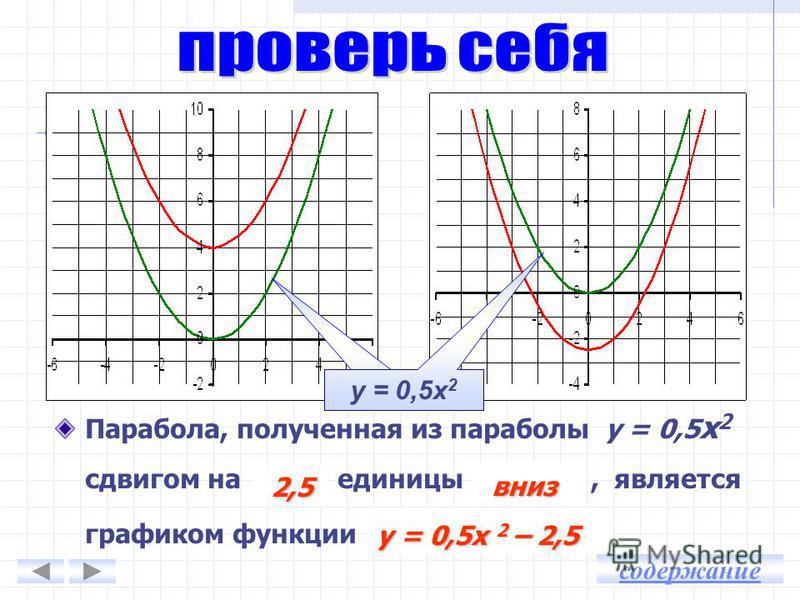
Отсюда получаем, что получится график тригонометрической функции вида:
y=cos(x)→y=32cos(x)→y=32cos(2x)→y=32cos(-2x)→→y=32cos(-2(x-1))→y=32cos-2(x-1)+1
Пошаговое преобразование косинусоиды с графической иллюстрацией.
При заданной графике y=cos(x) видно, что наименьший общий период равняется T=2π. Нахождение максимумов в 2π·k; 1, k∈Z, а минимумов π+2π·k; -1, k∈Z.
При растягивании вдоль Оу в 32 раза происходит возрастание амплитуды колебаний в 32 раза.T=2π является наименьшим положительным периодом. Нахождение максимумов в 2π·k; 32, k∈Z, минимумов в π+2π·k; -32, k∈Z.
При сжатии вдоль Ох вдвое получаем, что наименьшим положительным периодом является число T=2πk2=π. Производится переход максимумов в π·k; 32, k∈Z,минимумов — π2+π·k; -32, k∈Z.
Симметричное отображение относительно Оу. Так как график нечетный, то он не будет изменяться.
При сдвигании графика на 1. Отсутствуют изменения наименьшего положительного периода T=π. Нахождение максимумов в π·k+1; 32, k∈Z, минимумов — π2+1+π·k; -32, k∈Z.
Нахождение максимумов в π·k+1; 32, k∈Z, минимумов — π2+1+π·k; -32, k∈Z.
При сдвигании на 1 наименьший положительный период равняется T=π и не изменен. Нахождение максимумов в π·k+1; 52, k∈Z, минимумов в π2+1+π·k; -12, k∈Z.
Преобразования функции косинуса завершено.
Преобразования y = tgx
Рассмотрим преобразования на примере y=tgx.
Пример 6Построить график функции y=-12tgπ3-23x+π3 при помощи преобразований функции y=tg(x).
Решение
Для начала необходимо привести заданную функцию к виду ±k1·f±k2·x+a+b, после чего получаем, что
y=-12tgπ3-23x+π3=-12tg-23x-π2+π3
Отчетливо видно, что k1=12, k2=23, a=-π2, b=π3, а перед коэффициентами k1 и k2 имеется «-». Значит, после преобразования тангенсоиды получаем
y=tg(x)→y=12tg(x)→y=12tg23x→y=-12tg23x→→y=-12tg-23x→y=-12tg-23x-π2→→y=-12tg-23x-π2+π3
Поэтапное преобразование тангенсоиды с графическим изображением.
Имеем, что исходный график – это y=tg(x).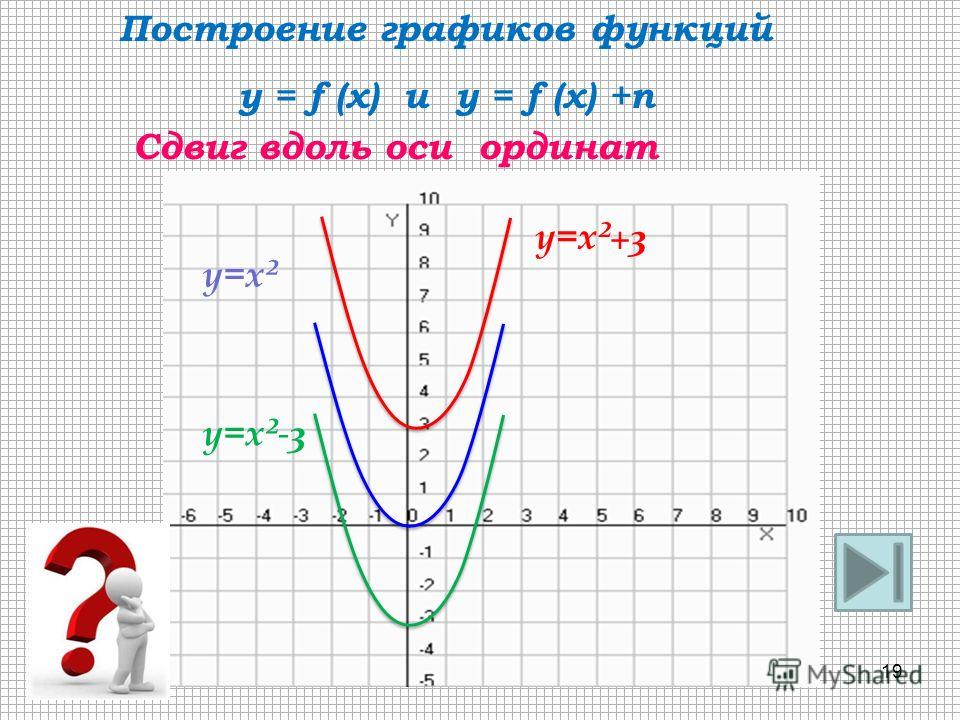 Изменение положительного периода равняется T=π. Областью определения считается -π2+π·k; π2+π·k, k∈Z.
Изменение положительного периода равняется T=π. Областью определения считается -π2+π·k; π2+π·k, k∈Z.
Сжимаем в 2 раза вдоль Оу. T=π считается наименьшим положительным периодом, где область определения имеет вид -π2+π·k; π2+π·k, k∈Z.
Растягиваем вдоль Ох в 32 раза. Вычислим наименьший положительный период, причем равнялся T=πk2=32π. А область определения функции с координатами -3π4+32π·k; 3π4+32π·k, k∈Z , меняется только область определения.
Симметрия идет по сторону Ох. Период не изменится в этот момент.
Необходимо симметрично отображать оси координат. Область определения в данном случае неизменна. График совпадает с предыдущим. Это говорит о том, что функция тангенса нечетная. Если к нечетной функции задать симметричное отображение Ох и Оу, тогда преобразуем до исходной функции.
При движении вправо на π2 видим, что наименьшим положительным периодом является T=32π. А изменения происходят внутри области определения -π4+32π·k; 5π4+32π·k, k∈Z.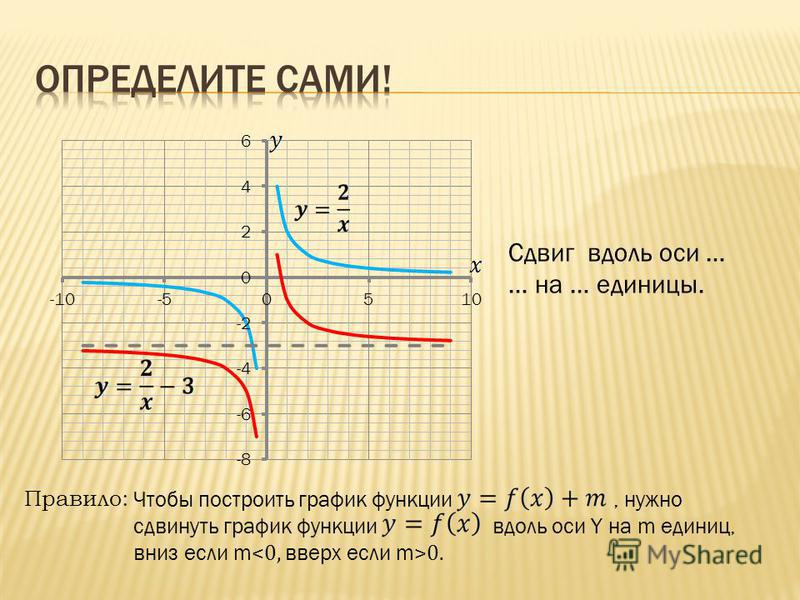
При сдвигании графика на π3 получаем, что изменение области определения отсутствует.
Преобразование тангенса завершено.
Тригонометрическая функция вида y=arccosx
Рассмотрим на примере тригонометрической функции вида y=arccosx.
Пример 7Построить график функции y=2arcsin13(x-1) при помощи преобразования y=arccosx.
Решение
Для начала необходимо перейти от арккосинуса к арксинусу при помощи обратных тригонометрических функций arcsin x+arcocos x=π2. Значит, получим, что arcsinx=π2-arccosx.
Видно, что y=arccosx→y=-arccosx→y=-arccosx+π2.
Поэтапное преобразование арккосинуса и графическое изображение.
График, данный по условию
Производим отображение относительно Ох
Производим движение вверх на π2.
Таким образом, осуществляется переход от арккосинуса к косинусу. Необходимо произвести геометрические преобразования арксинуса и его графика.
Видно, что k1=2, k2=13, a=-1, b=0, где отсутствует знак «-» у k1 и k2.
Отсюда получаем, что преобразования y=arcsinx примет вид:
y=arcsin(x)→y=2arcsin(x)→→y=2arcsin13x→y=2arcsin13(x-1)
Поэтапное преобразование графика арксинуса и графическое изображение.
График y=arcsinx имеет область определения вида x∈-1; 1, тогда интервал y∈-π2; π2 относится к области значений.
Необходимо растянуть вдвое по Оу, причем область определения останется неизменной x∈-1; 1, а область значений y∈-π; π.
Растягивание по Ох строе. Происходит расширение области определения x∈-3; 3, но область значений остается неизменной y∈-π; π.
Производим сдвигание вправо на 1, причем область определения становится равной x∈-2; 4. Без изменений остается область значений y∈-π; π.
Задача преобразования графика обратной тригонометрической функции завершена. Если по условию имеются сложные функции, тогда необходимо прибегнуть к полному исследованию функция.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Кафедра бизнес-информатики Российского университета транспорта
Движение графиков функций
ГБОУ «Гимназия «Диалог»
- учитель математики Джигкаева Т.З.
Движения графиков функций
y
y=f(x)
Данная презентация может быть использована при проведении уроков в 8-ом классе по теме «Построение графика квадратичной функции с использованием движения графиков», а также для самостоятельного изучения данного материала.
Презентация может быть использована как полностью, так и частично в зависимости от желания преподавателя.
В предлагаемой работе показано пошаговое построение графика функции с использованием некоторых видов движения графиков, что дает возможность учащемуся самостоятельно разобраться с данным материалом.
Также присутствуют задания для самостоятельной работы трех уровней.
Предполагается дальнейшая разработка данной презентации для учащихся старших классов с использованием показательной, логарифмической и тригонометрических функций.
х
o
Рассмотрим некоторые виды движения графиков функций.
Пусть y=f(x) – исходная функция.
f(x) f(x + а )
f(x) f(x) + b
f(x) — f(x)
f(x) f( x )
f(x) f(x)
Задания для самостоятельной работы
f(x) f(x+a)
Сдвиг графика исходной функции вдоль оси ОХ на | а | единиц:
- вправо, если а 0,
- влево, если а 0.
Рассмотрим пример:
Построить график функции у = ( x- 3 ) 2
y
1) y = x 2 – исходная функция;
y=x 2
у=( x -3) 2
2 ) Сдвигаем каждую точку графика функции у = x 2 на 3 единицы вправо вдоль оси ОХ;
•
•
•
•
3 ) Через полученные точки проводим параболу;
4 ) График функции у = ( x -3) 2 построен.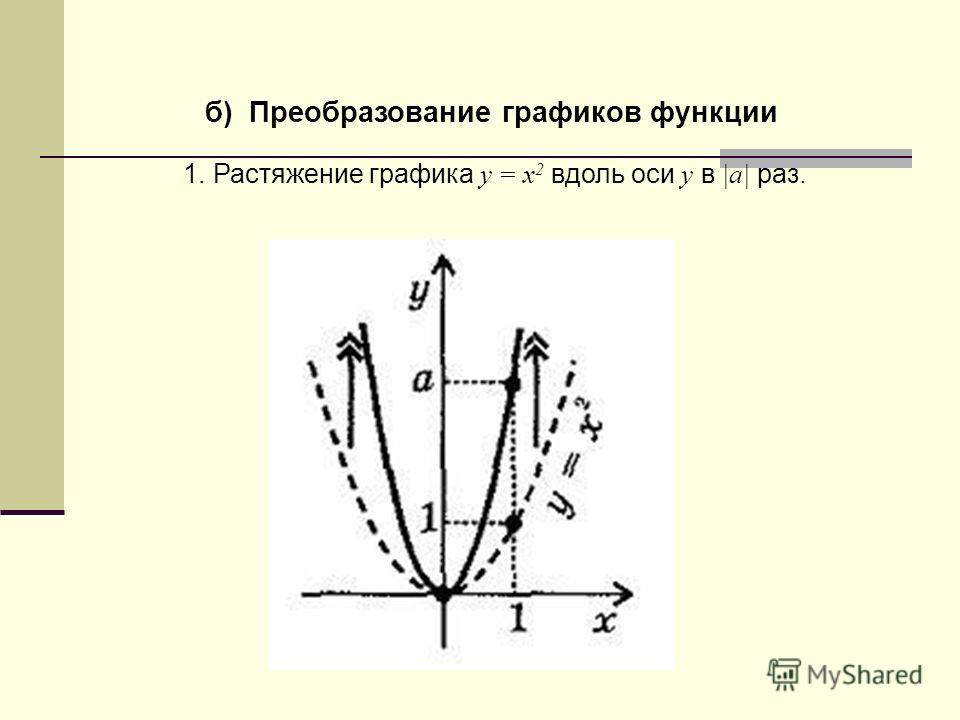
•
•
•
•
•
•
о
х
3
1
f(x) f(x) + b
Сдвиг графика исходной функции вдоль оси О Y на | b | единиц:
- вверх, если b 0,
- вниз, если b 0.
Построить график функции у = x 2 — 3
Рассмотрим пример:
y
1) y = x 2 – исходная функция;
y=x 2
у= x 2 — 3
2 ) Сдвигаем каждую точку графика функции у = x 2 на 3 единицы вниз вдоль оси О Y ;
•
•
3 ) Через полученные точки проводим параболу;
•
•
•
•
•
о
х
4 ) График функции у = x 2 — 3 построен.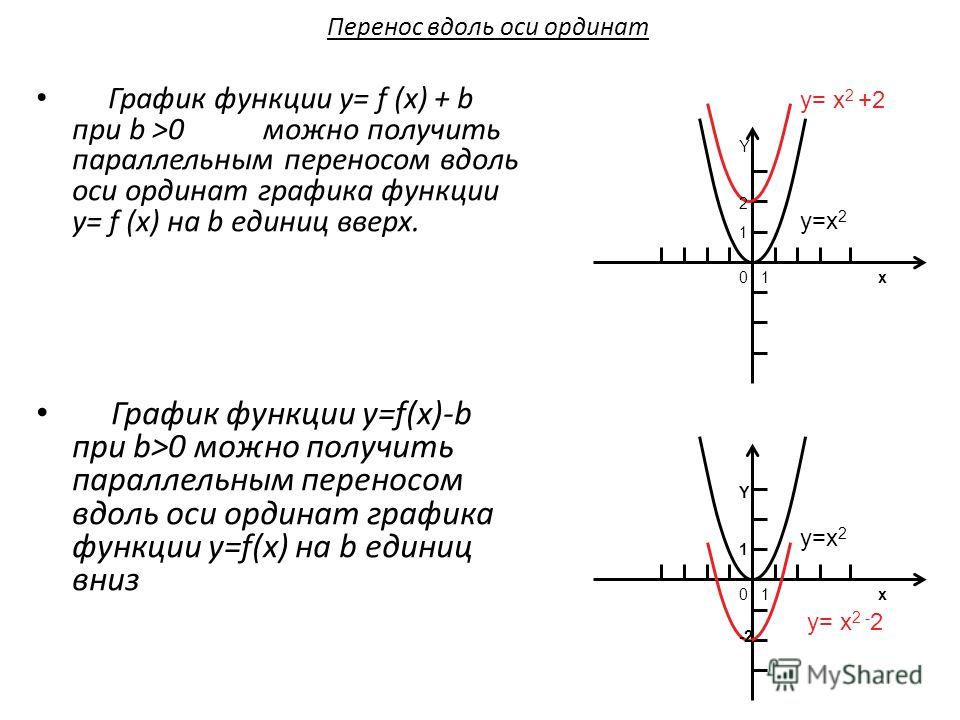
1
•
•
•
-3
f(x) — f(x)
Симметричное отображение графика исходной функции относительно оси ОХ.
Рассмотрим пример:
Построить график функции у = — x 2 + 4
y
1) y = x 2 — 4 – исходная функция;
y=x 2 — 4
•
2 ) Симметрично отображаем каждую точку графика функции у = x 2 — 4 относительно оси ОХ, при этом точки пересечения графика с осью ОХ остаются на месте;
•
4
•
•
•
•
•
•
о
х
1
3 ) Через полученные точки проводим параболу;
4 ) График функции у = x 2 — 3 построен.
-4
•
•
у = — x 2 + 4
f(x) f( | x | )
Симметричное отображение части графика исходной функции, построенной при х х 0 , относительно прямой х=х 0 , где х 0 – точка смены знака модуля.
Построить график функции у = x 2 — 4 | х |
Рассмотрим пример:
y
1) y = x 2 – 4х – исходная функция, построим ее график при х 0;
у = x 2 – 4х
————————————— •
•
2 ) Симметрично отображаем каждую точку части графика функции у = x 2 – 4х, построенной при х 0, относительно прямой х=0;
о
х
2
4
-2
-4
3 ) Через полученные точки проводим кривую;
4 ) График функции у = x 2 – 4х построен.
——————— •
•
— •
•
•
————— •
-4
f(x) | f(x) |
Симметричное отображение части графика исходной функции, лежащей под осью ОХ, относительно этой оси.
Рассмотрим пример:
Построить график функции у = | x 2 – 2х – 3 |
1) y = x 2 – 2х – 3 – исходная функция;
y
у = x 2 – 2х – 3
2 ) Симметрично отображаем каждую точку части графика функции у = x 2 – 2х – 3, лежащей под осью ОХ,относительно этой оси;
•
4
•
•
•
•
•
•
•
о
х
3 ) Через полученные точки проводим кривую;
3
-1
4 ) График функции у = x 2 – 2х – 3 построен.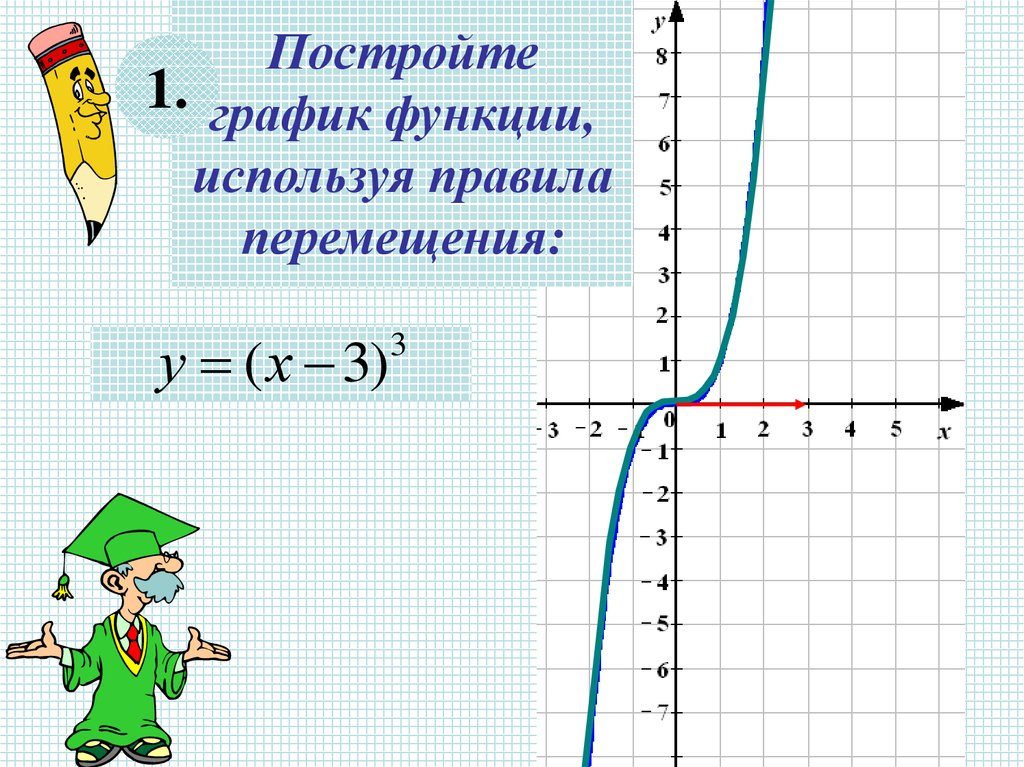
-4
Вам предлагается выполнить построение графиков функций с использованием движения графиков
1 уровень
2 уровень
3 уровень
1 уровень
Постройте график функции с использованием движения графиков:
- y =(x+2) 2 ( f(x) f(x+a) )
- y = x 2 +1 ( f(x) f(x) + b )
- y = -x 2 ( f(x) — f(x) )
- y = | x 2 — 4 | ( f(x) f(x) + b , f(x) | f(x) | )
2 уровень
Постройте график функции с использованием движения графиков:
- y = — (x — 1 ) 2 ( f(x) f(x+a) , f(x) — f(x) )
- y = | x 2 — 3 | — 1 ( f(x) f(x) + b , f(x) — f(x) , f(x) f(x) + b)
- y = x 2 – 4х + 5
3 уровень
Постройте график функции с использованием движения графиков:
- y = | — ( 3 — x) 2 + 1 |
- y = | x 2 + 4 | х | + 3 |
операций над функциями: переводы | SparkNotes
Переводы
График функции можно перемещать вверх, вниз, влево или вправо, добавляя или
вычитание из вывода или ввода.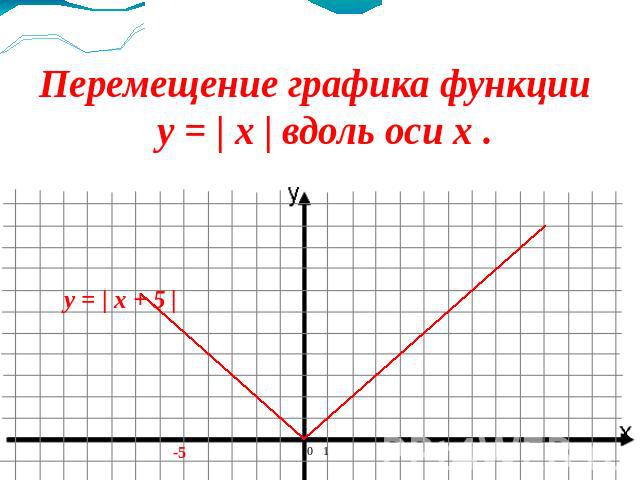
Добавление к выходу функции перемещает график вверх. Вычитание из вывода функции сдвигает график вниз. Вот графики y = f ( x ), y = f ( x ) + 2 и y = f ( x ) — 2. Примечание что если ( x , y 1 ) точка на графике f ( x ), ( x , y 2 ) 9003 точка на 0 график f ( x ) + 2, а ( x , y 3 ) является точкой на графике f ( x ) — 2, затем у 2 = у 1 + 2 и у 3 = y 1 — 2. Например, (1, 2) на графике f ( x ), (1, 4) находится на графике f ( x ) + 2, и (1, 0) находится на графике f ( x ) — 2. Графики f ( x ), f ( x ) + 2 и f ( x ) — 2
При добавлении ко входу функция увеличивается в направлении y , добавляя к
вход уменьшает функцию в x направление.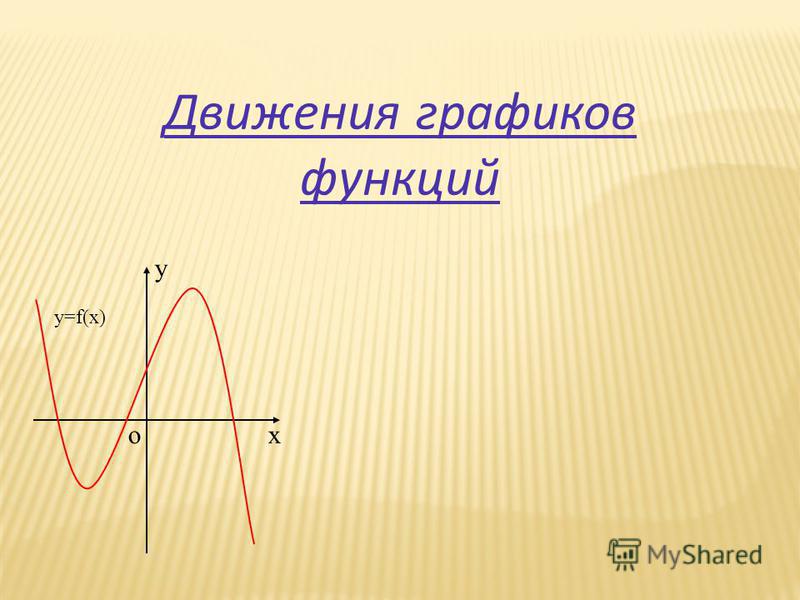 Это потому что
функция должна компенсировать добавленный ввод. Если функция выводит «7»
когда вводится «3», и мы вводим x + 2, функция выводит «7», когда х = 1.
Это потому что
функция должна компенсировать добавленный ввод. Если функция выводит «7»
когда вводится «3», и мы вводим x + 2, функция выводит «7», когда х = 1.
Таким образом, добавление к входу функции перемещает график влево, и
вычитание из ввода функции сдвигает график вправо.
Вот графики y = f ( x ), y = f ( x + 2), и х = f ( х — 2). Примечание
что если ( x 1 , y ) является точкой на графике f ( x ), ( x 2 , y 9000) является точкой на
график f ( x + 2), а ( x 3 , y ) является точкой на графике f ( x — 2),
тогда х 2 = х 1 — 2 и x 3 = x 1 + 2. Например, (1, — 2) находится на
график f ( x ), (- 1, — 2) находится на графике f ( x + 2), а (3, — 2) находится на
график f ( x — 2).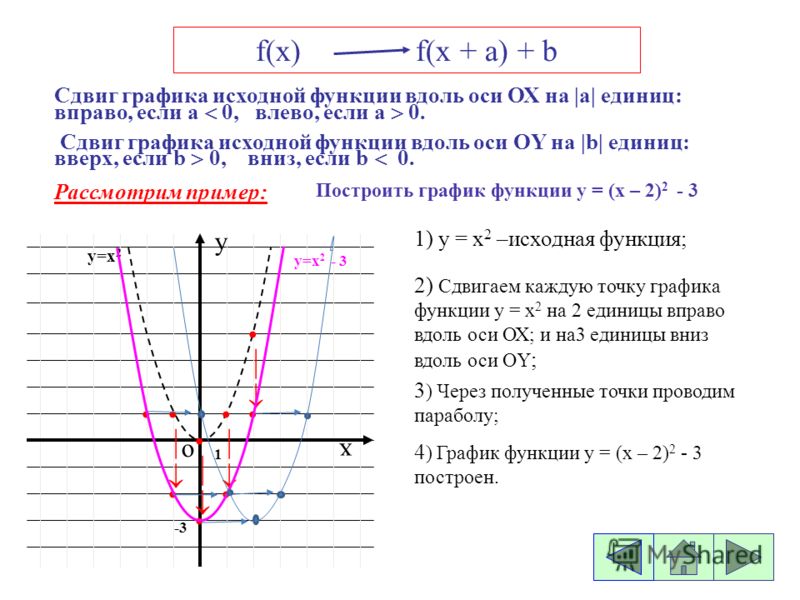 Графики f ( x ), f ( x + 2) и f ( x — 2)
Графики f ( x ), f ( x + 2) и f ( x — 2)
Сдвиг графика вверх, вниз, влево или вправо без изменения формы, размера, или размеры графа, называется переводом.
Примеры : Если f ( x ) = x 2 + 2 x , то каким уравнением будет уравнение, если график
перешел:
a) 4 единицы вверх
b) 4 единицы вниз
c) 4 единицы влево
d) 4 единицы вправо
Решения:
а) f 1 ( x ) = f ( x ) + 4 = x 2 + 2 x + 4
б) ф 2 ( x ) = f ( x ) — 4 = x 2 + 2 x — 4
в) f 3 ( х ) = f ( х + 4) = ( х + 4) 2 + 2(7 х 0 4 0 4 + 4 )
2 +8 х + 16 + 2 х + 8 = х 2 + 10 х + 24
г) ф 4 ( х ) = ф ( х — 4) = ( х — 4) 2 +2( х — 4) = х 2 -8 х + 16 + 7 0 — 8 х 0 2 — 6 х + 8
Преобразование функций
| Как и в преобразованиях в геометрии, мы можем перемещать и изменять размеры графиков функций |
Начнем с функции, в данном случае это f(x) = x 2 , но это может быть что угодно:
f(x) = x 2
Вот несколько простых вещей, которые мы можем сделать, чтобы переместить или масштабировать его на графике:
Мы можем переместить его вверх или вниз, добавив константа для значения y:
gif»> g(x) = x 2 + CПримечание: чтобы переместить линию вниз , мы используем отрицательное значение для C.
- C > 0 перемещает вверх
- C < 0 перемещает его вниз
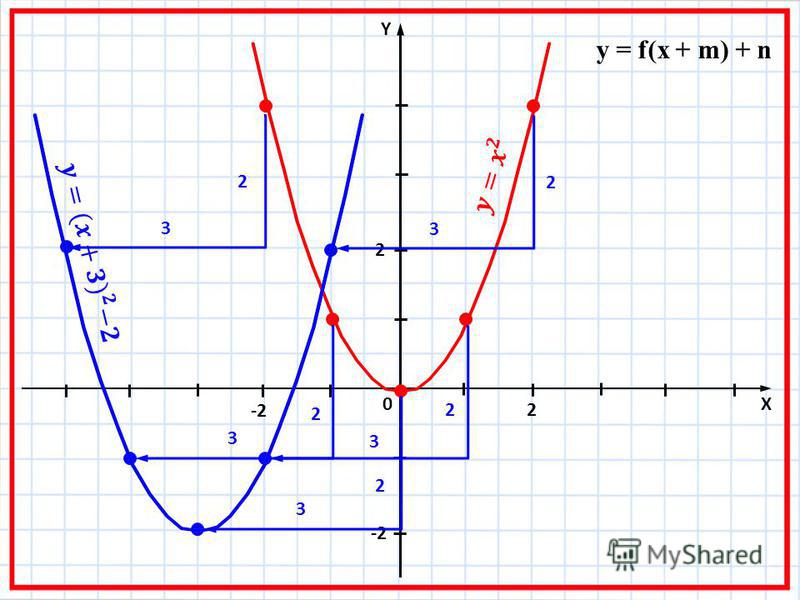
Мы можем перемещать ее влево или вправо, добавляя константу к значению x:
g(x) = (x+C) 2
Добавление C перемещает функцию на влево (отрицательное направление).
Почему? Представьте, что вы унаследуете состояние, когда ваш возраст=25 . Если вы измените это на (возраст + 4) = 25 , то вы получите его, когда вам будет 21 год. Добавление 4 сделало это раньше.
- C > 0 перемещает влево
- C < 0 перемещает вправо
НО мы должны добавить C везде, где x встречается с в функции (мы заменяем x+C на x).
Пример: функция v(x) = x
3 — x 2 + 4xЧтобы переместить C пробелов влево, прибавьте C к x везде, где x появляется :
w(x) = (x + C) 3 − (x + C) 2 + 4(x + C)
Простой способ запомнить, что происходит с графиком, когда мы добавляем константу:
добавить к y чтобы перейти высокий
добавить к x , чтобы перейти влево
Мы можем растянуть или сжать его в направлении Y, умножив всю функцию на константу.
g(x) = 0,35(x 2 )
- C > 1 растягивает
- 0 < C < 1 сжимает его
Мы можем растянуть или сжать его в направлении x, умножив x на константу.
g(x) = (2x) 2
- C > 1 сжимает
- 0 < C < 1 растягивает
Обратите внимание, что (в отличие от направления Y) большие значения вызывают большее сжатие .
Мы можем перевернуть ее, умножив всю функцию на −1:
g(x) = −(x 2 )
Это также называется отражением относительно оси x ( ось, где y=0)
Мы можем комбинировать отрицательное значение с масштабированием:
Пример: умножение на -2 перевернет его вверх дном И растянет в направлении y.
Мы можем перевернуть его влево-вправо, умножив значение x на −1:
gif»>g(x) = (−x) 2
Это действительно переворачивает его влево и вправо! Но вы этого не видите, потому что x 2 симметрично относительно оси Y. Итак, вот еще один пример использования √(x):
g(x) = √(−x)
Это также называется отражением относительно оси Y (ось, где x=0)
Итог
| y = f(x) + C |
|
| y = f(x + C) |
|
| у = Cf(x) |
|
| у = f(Сх) |
|
| у = -f(х) |
|
| у = f(-x) |
|
Примеры
Пример: функция g(x) = 1/x
Вот что мы можем сделать:
Сдвинуться на 3 клетки вниз: h(x) = 1/x − 3
Сдвинуться на 4 позиции вправо: h(x) = 1/(x−4) graph
Переместить на 5 делений влево: h(x) = 1/(x+5)
Растянуть на 2 в направлении y: h (x) = 2/x
Сжать на 3 в направлении x: h(x) = 1/(3x)
Перевернуть вверх дном: h(x) = −1/x
Пример: функция v(x) = x
3 − 4xВот что мы можем сделать:
Переместиться на 2 пробела вверх: w(x) = x 3 − 4x + 2
Сдвинуться на 3 позиции вниз: w(x) = x 3 − 4x − 3
Сдвинуться на 4 позиции вправо: w(x) = (x−4) 3 − 4(x−4)
Переместить на 5 мест влево: w(x) = (x+5) 3 − 4(x+5) graph
Растянуть на 2 в направлении y: w(x) = 2 (x 3 − 4x)
= 2x 3 − 8x
Сжать на 3 в направлении x: 27x 3 − 12x
Перевернуть вверх дном: w(x) = −x 3 + 4x
Все в одном .