Перестановки размещения сочетания формулы: Перестановки, размещения и сочетания. Формулы.

2 часа лекции, 2 часа семинарское занятие

Существуют две схемы выбора m элементов из множества, состоящего из n элементов:

— без возвращения, когда выбранные элементы после извлечения не возвращаются в исходное множество;

— с возвращением, когда выбор осуществляется поэлементно с обязательным возвращением отобранного элемента в исходное множество на каждом шаге выбора.

Схема выбора без возвращений.

Соединения. Виды соединений

Пусть А – совокупность некоторых n объектов (предметов, элементов и пр.) а₁, а₂, … а_n, объединенных некоторым признаком или свойством. Из различных элементов множества А можно образовать группы. Если в каждую группу входит одно и то же количество элементов, например, m (m ≤

n), взятых из множества А, то говорят, что они образуют соединения из n элементов по m в каждом.

В зависимости от того, входят ли в соединение все элементы множества А,- или только часть элементов этого множества, имеет ли значение порядок следования элементов, или порядок следования элементов значения не имеет, под общим именем соединений принято понимать следующие три типа комбинаций: перестановки; размещения; сочетания.

Перестановки

Перестановками называются такие изменения, в результате которых количество выбираемых предметов сохраняется, а порядок их извлечения может изменяться случайным способом.

Определение 1. Соединения, в которые входят все n

элементов множества А и которые отличаются только порядком следования элементов, называются перестановками из n элементов. Количество перестановок обозначается и читается «Пэ из эн».

Число перестановок Р из n элементов равно:

Произведение n·(n — 1)·(n — 2)·… ·1 называется факториалом числа n, обозначается символом n!, который читается «эн-факториал».

Принято, что 0! = 1 и 1! = 1.

Размещения

Определение 2. Соединения, каждое из которых содержит m различных элементов (m ≤ n), взятых из n элементов множества А

, отличающихся друг от друга или составом элементов или порядком расположения элементов, называются размещениями из n элементов по m в каждом.

Число таких размещений обозначается символом , читается «А из эн по эм».

Число возможных размещений из n элементов по m в каждом равно произведению m последовательно убывающих на единицу чисел, из которых большее есть n, т. е.

Это еще одна, на мой взгляд, более удобная расчетная формула для Размещений. По определению, перестановки являются частным случаем размещений, когда m = n: Р_n

= А.

Сочетания

Сколькими способами можно выбрать из n различных объектов (предметов) m штук?

Определение 3. Соединения, каждое из которых содержит m различных элементов (m ≤ n), взятых из n элементов множества А, отличающихся друг от друга по крайней мере одним элементом, называются сочетаниями из n элементов по m.

Число таких сочетаний обозначается символом илии читается «цэ из эн по эм».

Из определения следует, что сочетания отличаются друг от друга хотя бы одним элементом, т.е. составом входящих элементов. Изменение порядка следования элементов внутри одного сочетания не приводит к образованию нового сочетания.

Число всех возможных сочетаний из n элементов по m в каждом выражается формулой

Факториальная запись этой формулы.

Основные формулы комбинаторики. Комбинаторика: формула перестановки, размещения

В данной статье речь пойдет об особом разделе математики под названием комбинаторика. Формулы, правила, примеры решения задач – все это вы сможете найти здесь, прочитав статью до самого конца.

Итак, что же это за раздел? Комбинаторика занимается вопросом подсчета каких-либо объектов. Но в данном случае объектами выступают не сливы, груши или яблоки, а нечто иное. Комбинаторика помогает нам находить вероятность какого-либо события. Например, при игре в карты – какова вероятность того, что у противника есть козырная карта? Или такой пример – какова вероятность того, что из мешка с двадцатью шариками вы достанете именно белый? Именно для подобного рода задач нам и нужно знать хотя бы основы данного раздела математики.

Комбинаторные конфигурации

Рассматривая вопрос основных понятий и формул комбинаторики, мы не можем не уделить внимание комбинаторным конфигурациям. Они используются не только для формулировки, но и для решения различных комбинаторных задач. Примерами таких моделей служат:

• размещение;
• перестановка;
• сочетание;
• композиция числа;
• разбиение числа.

О первых трех мы поговорим более подробно далее, а вот композиции и разбиению мы уделим внимание в данном разделе. Когда говорят о композиции некого числа (допустим, а), то подразумевают представление числа а в виде упорядоченной суммы неких положительных чисел. А разбиение – это неупорядоченная сумма.

Разделы

Прежде чем мы перейдем непосредственно к формулам комбинаторики и рассмотрению задач, стоит обратить внимание на то, что комбинаторика, как и другие разделы математики, имеет свои подразделы. К ним относятся:

• перечислительная;
• структурная;
• экстремальная;
• теория Рамсея;
• вероятностная;
• топологическая;
• инфинитарная.

В первом случае речь идет об исчисляющей комбинаторике, задачи рассматривают перечисление или подсчет разных конфигураций, которые образованы элементами множеств. На данные множества, как правило, накладываются какие-либо ограничения (различимость, неразличимость, возможность повтора и так далее). А количество этих конфигураций подсчитывается при помощи правила сложения или умножения, о которых мы поговорим немного позже. К структурной комбинаторике относятся теории графов и матроидов. Пример задачи экстремальной комбинаторики – какова наибольшая размерность графа, который удовлетворяет следующим свойствам… В четвертом пункте мы упомянули теорию Рамсея, которая изучает в случайных конфигурациях наличие регулярных структур. Вероятностная комбинаторика способна нам ответить на вопрос – какова вероятность того, что у заданного множества присутствует определенное свойство. Как нетрудно догадаться, топологическая комбинаторика применяет методы в топологии. И, наконец, седьмой пункт – инфинитарная комбинаторика изучает применение методов комбинаторики к бесконечным множествам.

Правило сложения

Среди формул комбинаторики можно найти и довольно простые, с которыми мы достаточно давно знакомы. Примером является правило суммы. Предположим, что нам даны два действия (С и Е), если они взаимоисключаемы, действие С выполнимо несколькими способами (например а), а действие Е выполнимо b-способами, то выполнить любое из них (С или Е) можно а+b способами.

В теории это понять достаточно трудно, постараемся донести всю суть на простом примере. Возьмем среднюю численность учеников одного класса — допустим, это двадцать пять. Среди них пятнадцать девочек и десять мальчиков. Ежедневно в классе назначается один дежурный. Сколько есть способов назначить дежурного по классу сегодня? Решение задачи достаточно простое, мы прибегнем к правилу сложения. В тексте задачи не сказано, что дежурными могут быть только мальчики или только девочки. Следовательно, им может оказаться любая из пятнадцати девочек или любой из десяти мальчиков. Применяя правило суммы, мы получаем достаточно простой пример, с которым без труда справится школьник начальных классов: 15 + 10. Подсчитав, получаем ответ: двадцать пять. То есть существует всего двадцать пять способов назначить на сегодня дежурного класса.

Правило умножения

К основным формулам комбинаторики относится и правило умножения. Начнем с теории. Допустим, нам необходимо выполнить несколько действий (а): первое действие выполняется с1 способами, второе – с2 способами, третье – с3 способами и так далее до последнего а-действия, выполняемого са способами. Тогда все эти действия (которых всего у нас а) могут быть выполнены N способами. Как высчитать неизвестную N? В этом нам поможет формула: N = с1 * с2 * с3 *…* са.

Опять же, в теории ничего не понятно, переходим к рассмотрению простого примера на применение правила умножения. Возьмем все тот же класс из двадцати пяти человек, в котором учится пятнадцать девочек и десять мальчиков. Только на этот раз нам необходимо выбрать двух дежурных. Ими могут быть как только мальчики или девочки, так и мальчик с девочкой. Переходим к элементарному решению задачи. Выбираем первого дежурного, как мы решили в прошлом пункте, у нас получается двадцать пять возможных вариантов. Вторым дежурным может быть любой из оставшихся человек. У нас было двадцать пять учеников, одного мы выбрали, значит вторым дежурным может быть любой из оставшихся двадцати четырех человек. Наконец, применяем правило умножения и получаем, что двоих дежурных можно избрать шестью сотнями способов. Мы данное число получили умножением двадцати пяти и двадцати четырех.

Перестановка

Сейчас мы рассмотрим еще одну формулу комбинаторики. В данном разделе статьи мы поговорим о перестановках. Рассмотреть проблему предлагаем сразу же на примере. Возьмем бильярдные шары у нас их n-ое количество. Нам нужно подсчитать: сколько есть вариантов расставить их в ряд, то есть составить упорядоченный набор.

Начнем, если у нас нет шаров, то и вариантов расстановки у нас так же ноль. А если у нас шар один, то и расстановка тоже одна (математически это можно записать следующим образом: Р1 = 1). Два шара можно расставить двумя разными способами: 1,2 и 2,1. Следовательно, Р2 = 2. Три шара можно расставить уже шестью способами (Р3=6): 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,2,1; 3,1,2. А если таких шаров не три, а десять или пятнадцать? Перечислять все возможные варианты очень долго, тогда нам на помощь приходит комбинаторика. Формула перестановки поможет нам найти ответ на интересующий нас вопрос. Pn = n *P (n-1). Если попытаться упростить формулу, то получаем: Pn = n* (n — 1) *…* 2 * 1. А это и есть произведение первых натуральных чисел. Такое число называется факториалом, а обозначается как n!

Рассмотрим задачу. Вожатый каждое утро выстраивает свой отряд в шеренгу (двадцать человек). В отряде есть три лучших друга – Костя, Саша и Леша. Какова вероятность того, что они будут стоять рядом? Чтобы найти ответ на вопрос, нужно вероятность «хорошего» исхода поделить на общее количество исходов. Общее число перестановок составляет 20! = 2,5 квинтиллиона. Как посчитать количество «хороших» исходов? Предположим, что Костя, Саши и Леша – это один сверхчеловек. Тогда мы имеем всего восемнадцать субъектов. Число перестановок в данном случае равняется 18 = 6,5 квадриллионов. При всем этом, Костя, Саша и Леша могут произвольно перемещаться между собой в своей неделимой тройке, а это еще 3! = 6 вариантов. Значит всего «хороших» расстановок у нас 18! * 3! Нам остается только найти искомую вероятность: (18! * 3!) / 20! Что равняется примерно 0,016. Если перевести в проценты, то это получается всего 1,6%.

Размещение

Сейчас мы рассмотрим еще одну очень важную и необходимую формулу комбинаторики. Размещение – это наш следующий вопрос, который предлагаем вам рассмотреть в данном разделе статьи. Мы идем на усложнение. Предположим, что мы хотим рассмотреть возможные перестановки, только не из всего множества (n), а из меньшего (m). То есть мы рассматриваем перестановки из n предметов по m.

Основные формулы комбинаторики стоит не просто заучивать, а понимать их. Даже несмотря на то, что они усложняются, так как у нас не один параметр, а два. Предположим, что m = 1, то и А = 1, m = 2, то А = n * (n — 1). Если далее упрощать формулу и перейти на запись при помощи факториалов, то получится вполне лаконичная формула: А = n! / (n — m)!

Сочетание

Мы рассмотрели практически все основные формулы комбинаторики с примерами. Теперь перейдем к заключительному этапу рассмотрения базового курса комбинаторики – знакомство с сочетанием. Сейчас мы будем выбирать m предметов из имеющихся у нас n, при этом всем мы будем выбирать всеми возможными способами. Чем же тогда это отличается от размещения? Мы не будем учитывать порядок. Этот неупорядоченный набор и будет являться сочетанием.

Сразу введем обозначение: С. Берем размещения m шариков из n. Мы перестаем обращать внимание на порядок и получаем повторяющиеся сочетания. Чтобы получить число сочетаний нам надо поделить число размещений на m! (m факториал). То есть С = А / m! Таким образом, способов выбрать из n шаров немножко, равняется примерно столько, сколько выбрать почти все. Этому есть логическое выражение: выбрать немножко все равно, что выкинуть почти все. Еще в данном пункте важно упомянуть и то, что максимальное число сочетаний можно достигнуть при попытке выбрать половину предметов.

Как выбрать формулу для решения задачи?

Мы подробно рассмотрели основные формулы комбинаторики: размещение, перестановка и сочетание. Теперь наша задача – облегчить выбор необходимой формулы для решения задачи по комбинаторике. Можно воспользоваться следующей довольно простой схемой:

1. Задайте себе вопрос: порядок размещения элементов учитывается в тексте задачи?
2. Если ответ нет, то воспользуйтесь формулой сочетания (С = n! / (m! * (n — m)!)).
3. Если ответ нет, то необходимо ответить на еще один вопрос: все ли элементы входят в комбинацию?
4. Если ответ да, то воспользуйтесь формулой перестановки (Р = n!).
5. Если ответ нет, то воспользуйтесь формулой размещения (А = n! / (n — m)!).

Пример

Мы рассмотрели элементы комбинаторики, формулы и некоторые другие вопросы. Теперь перейдем к рассмотрению реальной задачи. Представьте, что перед вами лежат киви, апельсин и банан.

Вопрос первый: сколькими способами их можно переставить? Для этого воспользуемся формулой перестановок: Р = 3! = 6 способов.

Вопрос второй: сколькими способами можно выбрать один фрукт? Это очевидно, у нас всего три варианта – выбрать киви, апельсин или банан, но применим формулу сочетаний: С = 3! / (2! * 1!) = 3.

Вопрос третий: сколькими способами можно выбрать два фрукта? Какие есть у нас вообще варианты? Киви и апельсин; киви и банан; апельсин и банан. То есть три варианта, но это легко проверить при помощи формулы сочетания: С = 3! / (1! * 2!) = 3

Вопрос четвертый: сколькими способами можно выбрать три фрукта? Как видно, выбрать три фрукта можно одним-единственным способом: взять киви, апельсин и банан. С = 3! / (0! * 3!) = 1.

Вопрос пятый: сколькими способами можно выбрать хотя бы один фрукт? Это условие подразумевает, что мы можем взять один, два или все три фрукта. Следовательно, мы складываем С1 + С2 + С3 =3 + 3 + 1 = 7. То есть у нас есть семь способов взять со стола хотя бы один фрукт.

задач на перестановки и комбинации | GMAT GRE Maths Tutorial

В этой статье вы узнаете о задачах на перестановку и комбинацию: определение, формулы, решенные примеры и тест с практическими вопросами.

Перестановки

Определение

Перестановки — это различные способы организации набора элементов.

Например:

Различные способы группировки алфавитов A, B и C, взятые все одновременно, это ABC, ACB, BCA, CBA, CAB, BAC.

Обратите внимание, что ABC и CBA не совпадают, поскольку отличается порядок расположения. То же правило применяется при решении любой задачи в Permutations.

Количество способов, которыми можно упорядочить n вещей, взятых одновременно, ⁿ P _n = n!, называемое «n факториалом».

Формула факториала

определяется как произведение всех чисел от n до 1.

Например, факториал 5, 5! = 5*4*3*2*1 = 120.

Таким образом, количество способов, которыми можно расположить 3 буквы за все время, равно 3! = 3*2*1 = 6 способов.

Количество перестановок n вещей, взятых по r за раз, обозначается:

ⁿ P _r = n! / (н-р)!

Например:

Три буквы, взятые по две за раз, можно расставить по-разному: 3!/(3-2)! = 3!/1! = 6 способов.

Важные формулы перестановок

1! = 1

0! = 1

Давайте рассмотрим несколько примеров:

Задача 1: Найдите количество слов со значением или без значения, которые можно составить из букв слова «СТУЛ».

Решение :

«КРЕСЛО» состоит из 5 букв.

Следовательно, количество слов, которые можно составить из этих 5 букв = 5! = 5*4*3*2*1 = 120.

 
Задача 2: Найдите количество слов со значением или без значения, которые можно составить из букв слова «ИНДИЯ».

Решение :

Слово «ИНДИЯ» состоит из 5 букв, а «И» встречается дважды.

Если буква встречается в слове более одного раза, мы делим факториал числа всех букв в слове на количество вхождений каждой буквы.

Следовательно, количество слов, образованных словом «ИНДИЯ» = 5!/2! = 60.

 
Задача 3: Найдите количество слов со значением или без значения, которые можно составить из букв слова «ПЛАВАНИЕ?»

Решение :

Слово «ПЛАВАНИЕ» состоит из 8 букв. Из которых I встречается дважды, а M встречается дважды.

Следовательно, количество слов, образованных этим словом = 8! / (2!*2!) = 10080.

 
Задача 4: Сколько различных слов можно составить из букв слова «СУПЕР» так, чтобы гласные всегда совпадали?

Решение :

Слово «СУПЕР» состоит из 5 букв.

Чтобы найти количество перестановок, которые могут быть образованы, когда две гласные U и E встречаются вместе.

В этих случаях мы группируем буквы, которые должны собраться вместе, и рассматриваем эту группу как одну букву.

Итак, буквы S,P,R, (UE). Теперь количество слов равно 4.

Следовательно, количество способов, которыми можно расположить 4 буквы, равно 4!

В U и E количество способов, которыми можно расположить U и E, равно 2!

Следовательно, общее количество способов, которыми буквы «SUPER» могут быть расположены так, чтобы гласные всегда были вместе, равно 4! * 2! = 48 способов.

 
Задача 5: Найдите количество различных слов, которые можно составить из букв слова «МАСЛО» так, чтобы гласные всегда были вместе.

Решение :

Слово «МАСЛО» состоит из 6 букв.

Буквы U и E всегда должны совпадать. Итак, буквы Б, Т, Т, Р, (УЭ).

Количество способов, которыми можно расположить буквы выше = 5!/2! = 60 (поскольку буква «Т» повторяется дважды).

Количество способов расположения U и E = 2! = 2 способа

Следовательно, общее количество возможных перестановок = 60*2 = 120 способов.

Задача 6: Найдите количество перестановок букв в слове «ОСТАТКИ» так, чтобы гласные всегда стояли в нечетных местах.

Решение :

Слово «ОСТАТКИ» состоит из 7 букв.

В нем 4 согласных и 3 гласных.

Написание следующим образом облегчает решение подобных вопросов.

(1) (2) (3) (4) (5) (6) (7)

Количество способов, которыми 3 гласных могут встречаться в 4 разных местах = ⁴ P ₃ = 24 способа.

После 3 гласных занимают 3 места, нет. 4 согласных могут занимать 4 места = ⁴ P ₄ = 4! = 24 способа.

Следовательно, общее количество возможных перестановок = 24*24 = 576 способов.

Комбинации

Определение

Различные варианты выбора из набора элементов называются комбинациями.

Например:

Возможны различные варианты выбора из алфавитов A, B, C, взятые по 2 за раз: AB, BC и CA.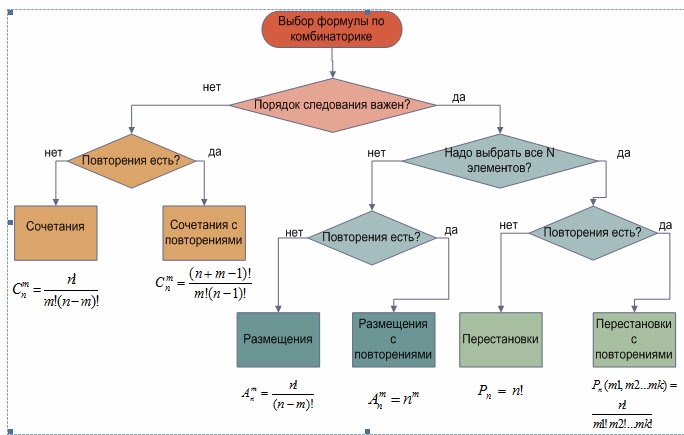

Не имеет значения, выбираем ли мы A после B или B после A. Порядок выбора не важен в комбинациях.

Чтобы найти количество возможных комбинаций из данной группы элементов n, взятых по r за раз, формула, обозначенная как ⁿ C _r , равна

ⁿ C _r = n! / [р! * (н-р)!]

Например, проверяя приведенный выше пример, различные возможные варианты выбора из алфавитов A, B, C, взятые по два за раз, составляют

³ C ₂ = 3! / (2! * (3-2)!) = 3 возможных варианта выбора (т. е. AB, BC, CA)

Важно Формулы комбинаций

ⁿ C _n = 1

ⁿ C _{3 0 = 1}

ⁿ C ₁ = n

ⁿ C _r = ⁿ C _(n-r)

Количество возможных вариантов выбора с A, B, C, взятых одновременно, равно ³ C ₃ = 1 (т. е. ABC)

Решенные примеры комбинации

взгляните на несколько примеров, чтобы понять, как работают комбинации:

 
Задача 1: Сколькими способами можно составить комитет из 1 мужчины и 3 женщин из группы из 3 мужчин и 4 женщин?

Решение :

Количество способов 1 человек может быть выбран из группы из 3 человек = ³ С ₁ = 3! / 1!*(3-1)! = 3 способа.

Количество способов 3 женщины могут быть выбраны из группы из 4 женщин = ⁴ C ₃ = 4! / (3!*1!) = 4 способа.

 

Задача 2: Сколько среди набора из 5 черных и 3 красных шаров можно выбрать 5 шаров так, чтобы хотя бы 3 из них были черными.

Решение :

Выбор не менее 3 черных шаров из набора из 5 черных шаров при общем выборе из 5 шаров может быть

3 B и 2 R

4 B и 1 R и

5 B и 0 R мячи.

Таким образом, наше выражение решения выглядит так.
⁵ C ₃ * ³ C ₂ + ⁵ C ₄ * ³ C ₁ + ⁵ C ₅ * ³ . способы .

 
Задача 3: Сколько четырехзначных чисел, которые делятся на 10, можно составить из чисел 3, 5, 7, 8, 9, 0 такое, что ни одно число не повторяется?

Решение :

Если число делится на 10, его разряд единиц должен содержать 0.
_ _ _ 0

остальные 5 цифр.

Выбор одной цифры из 5 может быть выполнен ⁵ C ₁ = 5 способами.

После заполнения разряда десятков у нас осталось 4 цифры. Выбор 1 цифры из 4 цифр можно сделать за ⁴ C ₁ = 4 направления.

После заполнения разряда сотен можно заполнить разряд тысяч ³ C ₁ = 3 способами.

Следовательно, общее количество возможных комбинаций = 5*4*3 = 60.

 

Викторина по перестановкам и комбинациям

Попробуйте решить эти практические задачи.
 

---

Задача 1: Нажмите здесь

Ответ 1: Нажмите здесь

---

Задача 2: Нажмите здесь

Ответ 2: Нажмите здесь

---

Задача 3: Нажмите здесь

Ответ 3: Нажмите здесь

---

Песня MBA | Начните здесь | Истории успеха | проверка реальности | База знаний | Стипендии | Услуги

Перестановка и комбинация — Распределение объектов | Handa Ka Funda

Четверг, 21 мая 2020 г.

---

Как однажды сказал один проницательный человек мистер Гамп: «Жизнь похожа на коробку конфет. Никогда не знаешь, что получишь». Перестановки и комбинации, которые жизнь представляет нам ежедневно, сбивают с толку, и, вероятно, это из-за врожденного страха перед выбором и случаями, которые нас пугают такими вопросами на экзамене. Я понимаю, что перестановка и комбинирование — одна из страшных тем, но я надеюсь, что как только вы поймете принципы, приведенные ниже, ваш страх уменьшится.

Перестановка и комбинирование Принцип 1: Перестановка

Если ‘n’ различных предметов расположены в ряд, то число способов, которыми их можно переставить так, чтобы ни один из них не занял исходное положение, равно:

Примечание: Размещение 1 объекта невозможно.

Дирр(2) = 1; Дирр(3) = 2; Дирр(4) = 12 – 4 + 1 = 9; Dearr(5) = 60 – 20 + 5 – 1 = 44

Пример 1.1: У человека есть восемь писем и восемь адресованных конвертов, соответствующих этим письмам. Сколькими способами он может положить письма в конверты так, чтобы ровно 5 из них были доставлены правильно?

Решение: Сначала выберите пять писем, которые доставляются правильно. Это можно сделать ⁸ C ₅ способами.

Теперь остальные три должны быть доставлены не по тому адресу. Это можно сделать в Dearr(3) = 2 способами.

Итак, всего путей 2 x ⁸ C ₅ = 2 x 56 = 112 путей.

Перестановка и комбинация Принцип 2: Разделение

‘n’ идентичных элементов в ‘r’ отдельные группы	Без ограничений:           n+r-1 C r-1
	Нет пустой группы:          n-1 C r-1
«n» отдельных объектов в «r» отдельных групп	Без ограничений:            r n
	Расположение в группе важно:

Примечание. Помимо стандартных проблем с распределением/разбиением, эти идеи можно использовать для решения вопросов, требующих определенного количества решений.

Пример 2.1: Сколько решений есть у уравнения a + b + c = 100; учитывая, что

а)      a, b и c — целые числа.

b)      a, b и c — натуральные числа.

Решение:

Случай а) идентичен случаю, в котором 100 одинаковых шоколадных конфет раздаются трем детям а, b и с. Возможно, что один ребенок получит все конфеты. В этом случае мы будем использовать формулу распределения «n» одинаковых предметов по «r» различных групп, где n = 100 и r = 3,

Итак, это можно сделать ¹⁰² C ₂ способами.

Случай b) идентичен случаю, в котором 100 одинаковых шоколадных конфет раздаются трем детям а, b и с. Каждый ребенок должен получить хотя бы одну шоколадку. В этом случае мы будем использовать формулу для распределения «n» одинаковых предметов в «r» различных группах, где ни одна группа не пуста, n = 100 и r = 3.

Итак, это можно сделать в ⁹⁹ C ₂ пути.

Пример 2.2: Сколькими способами можно распределить 5 колец в

а)      4 коробки.

б)      4 пальца.

Решение: В первую очередь необходимо определить разницу между раздачей в ящики и раздачей в 4 пальца. Отличие состоит в том, что в случае с пальцами, в отличие от коробок, порядок расположения колец имеет значение.

В случае ; Кольцо 1 может быть помещено в любую из четырех коробок, поэтому у него есть четыре варианта. Кольцо 2 также можно положить в любую из четырех коробок, поэтому у него есть четыре варианта. Аналогично для кольца 3, кольца 4 и кольца 5; у каждого по 4 варианта. Итак, общее количество способов распределения = 4 х 4 х 4 х 4 х 4 = 4 ⁵ . По сути, так получается формула r ⁿ .

В случае b; Кольцо 1 можно надеть на любой из четырех пальцев, поэтому у него есть 4 варианта.

Кольцо 2 можно надеть на любой из четырех пальцев, но есть пять вариантов. Есть палец, скажем, F3, который содержит кольцо R1. Теперь, на F3, у R2 есть два варианта: он может подняться выше R1 или ниже R1. Таким образом, общее количество вариантов для R2 равно 5.

Кольцо 3 можно надеть на любой из четырех пальцев, но теперь у него есть 6 вариантов.

Кольцо 4 можно надеть на любой из четырех пальцев, но теперь у него будет 7 вариантов.

Кольцо 5 можно надеть на любой из четырех пальцев, но теперь у него будет 8 вариантов.

Таким образом, общее количество способов распределения колец равно

По сути, так получается формула

.

Перестановка и комбинация Funda 3:

Количество способов расположения n предметов, из которых p одинаковы, q одинаковы и r одинаковы при условии, что p + q + r = n

Количество способов распределения «n» отдельных предметов в группах размером «p», «q» и «r» при условии, что p + q + r = n

Я надеюсь, что это поможет вам решить проблемы на экзамене. Может быть, шоколад, который вы в конечном итоге получите, — это Борнвиль. Может быть, вы бы это заслужили.

Другие сообщения, связанные с количественными способностями — современная математика

Теория множеств — максимальные и минимальные значения
Как решать вопросы, основанные на не менее n в теории множеств для экзамена CAT?
Перестановки и комбинации – фундаментальный принцип подсчета
Как найти ранг слова в словаре (с повторениями или без них)
Основные концепции вероятностей для подготовки к экзамену CAT
Последовательности и серии Задачи и концепции для подготовки к экзамену CAT

Вопросы CAT, относящиеся к количественному анализу Способности — современная математика

Все вопросы из экзамена CAT Количественные способности — современная математика
Количественные способности — современная математика — прогрессия — Q1: если a1 = 1/(2*5), a2 = 1/(5*8), a3 = 1/(8*11),……, тогда a1 + a2 +……..+ a100 равно
Количественные способности – Современная математика – Прогрессии – Q2: Бесконечная геометрическая прогрессия a1, a2, a3,… обладает тем свойством, что an = 3(a(n+l) + a(n+2) +…. ) для каждого n ≥ 1. Если сумма a1 + a2 + a3 +……. = 32, тогда a5 равно
Количественные способности — Современная математика — Прогрессии — Q3: Пусть a1, a2, a3, a4, a5 — последовательность из пяти последовательных нечетных чисел. Рассмотрим новую последовательность из пяти последовательных четных чисел, оканчивающуюся на 2a3.
Количественные способности – Современная математика – Прогрессии – Q4: Пусть a1, a2,……..a3n будет арифметической прогрессией с a1 = 3 и a2 = 7. Если a1 + a2 + ….+a3n = 1830, то какова наименьшее натуральное число m такое, что m (a1 + a2 + …. + an ) > 1830?
Количественные способности – Современная математика – Прогрессии – Q5: Если квадрат 7-го члена арифметической прогрессии с положительной общей разностью равен произведению 3-го и 17-го членов, то отношение первого члена к общей разности равно
Количественный Способности – Современная математика – P&C – Q1: Сколько четырехзначных чисел, которые делятся на 6, можно составить из цифр 0, 2, 3, 4, 6 так, чтобы ни одна цифра не использовалась более одного раза, а 0 не происходят в крайнем левом положении?
Количественные способности — Современная математика — P&C — Q2: Сколькими способами можно распределить 8 одинаковых ручек между Амалем, Бималом и Камалем так, чтобы Амал получил не менее 1 ручки, Бимал — не менее 2 ручек, а Камаль — не менее 3 ручки?
Quantitative Aptitude – Modern Maths – P&C – Q3: Сколькими способами можно распределить 7 одинаковых ластиков между 4 детьми так, чтобы каждый ребенок получил хотя бы один ластик, но никто не получил более 3 ластиков?
Количественные способности — Современная математика — P&C — Q4: Пусть AB, CD, EF, GH и JK — пять диаметров окружности с центром в O.