5 в виде обыкновенной дроби
Калькулятор «Конвертер десятичных дробей в обыкновенные»
Десятичная дробь
Как записать 5 в виде дроби?
Ответ: Десятичная дробь 5 в обыкновенном виде это 5/1
5=
Число 5 в виде обыкновенной дроби это 5/1
Объяснение конвертации дроби 5 в десятичную
Для того, чтобы найти простейшую дробную форму числа 5 необходимо сперва записать нашу десятичную дробь 5 как обыкновенную. Любое число можно легко записать в виде дроби, для этого нужно всего лишь разделить его на 1 (единицу):
Далее, нам необходимо избавиться от дробной части в числителе (5), т.е. сделать числитель целым числом. Для этого мы умножим числитель и знаменатель на 1 (т.к. в дробном числе 5 после запятой находится 0 знака)
5 × 1
/
1 × 1
=
Теперь необходимо сократить получившуюся дробь до самой простой формы. Для этого нужно найти Наибольший Общий Делитель (НОД) для чисел 5 и 1. Для того чтобы найти НОД для двух чисел, вы можете воспользоваться нашим Калькулятором НОД . НОД для чисел 1 и 5 равен 1. Следовательно, для того, чтобы упростить нашу дробь, необходимо разделить числитель и знаменатель на 1:
Для этого нужно найти Наибольший Общий Делитель (НОД) для чисел 5 и 1. Для того чтобы найти НОД для двух чисел, вы можете воспользоваться нашим Калькулятором НОД . НОД для чисел 1 и 5 равен 1. Следовательно, для того, чтобы упростить нашу дробь, необходимо разделить числитель и знаменатель на 1:
5 ÷ 1
/
1 ÷ 1
=
Вот и все! 5 как обыкновенная правильная дробь в самой простой форме это 5/1.
Поделитесь текущим расчетом
Печать
https://calculat.io/ru/number/decimal-as-a-fraction/5
<a href=»https://calculat.io/ru/number/decimal-as-a-fraction/5″>5 в виде обыкновенной дроби — Calculatio</a>
О калькуляторе «Конвертер десятичных дробей в обыкновенные»
Данный онлайн-конвертер десятичных дробей в обыкновенные дроби — это инструмент, который поможет вам быстро и легко конвертировать любое десятичное число в обыкновенную дробь. Например, он может помочь узнать как записать 5 в виде дроби? Конвертер будет особенно полезен тем, кто ежедневно работает с дробями или использует их в учебных или профессиональных целях.
Например, он может помочь узнать как записать 5 в виде дроби? Конвертер будет особенно полезен тем, кто ежедневно работает с дробями или использует их в учебных или профессиональных целях.
Чтобы использовать данный конвертер, все, что вам нужно сделать, это ввести десятичное число, которое вы хотите конвертировать, в соответствующее поле, например, ‘5’. После того как вы ввели десятичное число, нажмите кнопку ‘Конвертировать’, чтобы начать процесс конвертации.
Конвертер выведет результат и покажет обыкновенную дробь, которая эквивалентна введенному вами десятичному числу, а также предоставит пошаговое объяснение процесса конвертации. Кроме того, конечная дробь будет упрощена до простейшей формы, используя наибольший общий делитель (НОД).
Например, если вы введете ‘5’ в конвертер, он покажет вам, что данное десятичное число эквивалентно дроби ‘5/1’. Он также объяснит, как был получен данный ответ, показав шаги, выполненные в процессе конвертации.
В целом, онлайн-конвертер десятичных дробей в обыкновенные дроби — это необходимый инструмент для всех, кто работает с дробями в повседневной жизни, в учебной или профессиональной сфере. Он быстрый, простой в использовании и предоставляет точные результаты, что делает его ценным инструментом для всех, кто нуждается в конвертации десятичных дробей в обыкновенные.
Он быстрый, простой в использовании и предоставляет точные результаты, что делает его ценным инструментом для всех, кто нуждается в конвертации десятичных дробей в обыкновенные.
Калькулятор «Конвертер десятичных дробей в обыкновенные»
Десятичная дробь
Таблица конвертации десятичных дробей в обыкновенные
Как перевести обыкновенную дробь в десятичную?
Поможем понять и полюбить математику
Начать учиться
Перевести слово с английского на русский поможет словарь или онлайн-переводчик. С переводом дробей дела обстоят иначе: тут нужно усвоить теорию и практиковаться. В этой статье узнаем способы перевода обыкновенной дроби в десятичную и наоборот.
Что такое дробь: понятие
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
По сути, это всего лишь одна из форм, в которой можно представить число. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 5/9 или (1,5 — 0,2)/15.
- Алгебраические — состоят из переменных. Например, (x + y)/(x — y). В этом случае значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 3/7 и 31/45.
Неправильной — ту, у которой числитель больше знаменателя или равен ему. Например, 21/4. Такое число является смешанным и читается, как «пять целых одна четвертая», а записывается — 5 1\4.
Например, 21/4. Такое число является смешанным и читается, как «пять целых одна четвертая», а записывается — 5 1\4.
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Что такое десятичная дробь
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,8
- 7,42
- 9,932
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.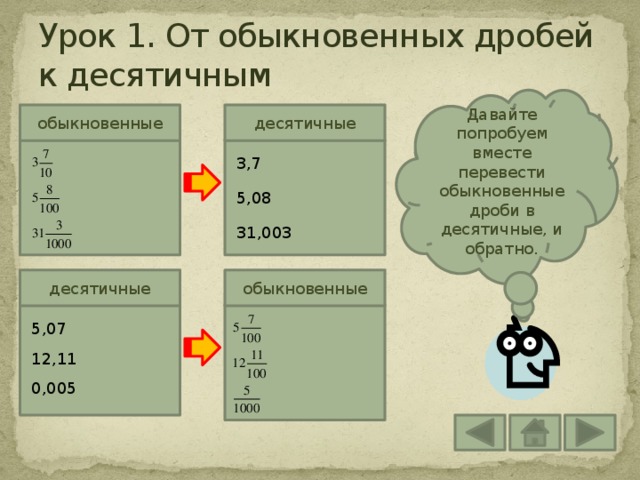
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».
Обучение на курсах математики в Skysmart поможет улучшить оценки в школе и подготовиться к выпускным экзаменам!
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
- 0,600 = 0,6
- 21,10200000 = 21,102
Обыкновенная и десятичная дробь — давние друзья. Вот как они связаны:
Вот как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если знаменатель обыкновенной дроби равен 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Как перевести обычную дробь в десятичную
Прежде чем узнать, как от обычной записи перейти к десятичной, вспомним различия двух видов дробей и сформулируем важное правило.
Десятичные дроби — это конструкции вида 0,5; 2,16 и -7,42. А так выглядят эти же числа в форме обыкновенных дробей:
Обыкновенную дробь можно перевести в конечную десятичную дробь только при условии, что её знаменатель можно разложить на простые множители 2 и 5 любое количество раз.
Дробь 11/40 можно преобразовать в конечную десятичную, потому что знаменатель раскладывается на множители 2 и 5.
Дробь 17/60 нельзя преобразовать в конечную десятичную дробь, потому что в её знаменателе кроме множителей 2 и 5, есть 3.
А теперь перейдем к самому главному вопросу: рассмотрим несколько алгоритмов перевода обыкновенной дроби в десятичную.
Способ 1. Превращаем знаменатель в 10, 100 или 1000
Чтобы превратить дробь в десятичную, нужно числитель и знаменатель умножить на одно и то же число так, чтобы в знаменателе получилось 10, 100, 1000 и т.д. Но прежде, чем приступать к вычислениям, нужно проверить, можно ли вообще превратить данную дробь в десятичную.
Для примера возьмем дробь 3/20. Ее можно привести в конечную десятичную, потому что её знаменатель раскладывается на множители 2 и 5.
Мы можем получить в нижней части 100: достаточно умножить 20 на 5. Про верхнюю часть тоже не забываем: получаем 15.
Про верхнюю часть тоже не забываем: получаем 15.
Теперь запишем числитель отдельно. Отсчитываем справа столько же знаков, сколько нулей стоит в знаменателе, и ставим запятую. В нашем примере в знаменателе 100 (у него два нуля), значит ставим запятую после отсчета двух знаков и получаем 0,15. Преобразование готово.
Еще пример:
Способ 2. Делим числитель на знаменатель
Чтобы перевести обыкновенную дробь в десятичную, достаточно разделить ее верхнюю часть на нижнюю. Проще всего это сделать, конечно же, на калькуляторе — но на контрольных им пользоваться не разрешают, поэтому учимся по-другому.
Для примера возьмем дробь 78/200. Убедимся, что дробь можно привести в конечную десятичную.
Делим столбиком числитель на знаменатель — преобразование готово:
Если при делении уголком стало ясно, что процесс не заканчивается и после запятой выстраиваются повторяющиеся цифры — эту дробь нельзя перевести в конечную десятичную. Ответ можно записать в виде периодической дроби — для этого нужно записать повторяющееся число в скобки, вот так: 1/3 = 0,3333.. = 0,(3).
Ответ можно записать в виде периодической дроби — для этого нужно записать повторяющееся число в скобки, вот так: 1/3 = 0,3333.. = 0,(3).
Для удобства мы собрали табличку дробей со знаменателями, которые чаще всего встречаются в заданиях по математике. Скачайте ее на гаджет или распечатайте и храните в учебнике как закладку:
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед. По сути, алгоритм превращения десятичной дроби в обыкновенную противоположен тем, что мы разобрали в предыдущей части. Вот, как это выглядит в обратную сторону:
- Перепишем исходную дробь в новый вид: в числитель поставим исходную десятичную дробь, а в знаменатель — единицу:
- 0,35 = 0,35/1
- 2,34 = 2,34/1
- Умножим числитель и знаменатель на 10 столько раз, чтобы в числителе исчезла запятая.
 При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:- 0,35 = 0,35/1 = 3,5/10 = 35/100
- 2,34 = 2,34/1 = 23,4/10 = 234/100
- А теперь сокращаем — то есть делим числитель и знаменатель на кратные им числа:
- 0,35 = 35/100, делим числитель и знаменатель на пять, получаем 7/20.
- 2,34 = 234/100 = 117/50 = 2 17/50.
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
| Еще алгоритм: как преобразовать десятичную дробь в обыкновенную
|
Вот и всё! Эта схема значительно проще и быстрее. Проверим:
Как видим, в дроби 0,55 после запятой стоит две цифры — 5 и 5. Поэтому n = 2. Если убрать запятую и нули слева, то получим число 55. Переходим ко второму шагу: 10n = 102 = 100, поэтому в знаменателе стоит 100. Остается сократить числитель и знаменатель. Вот и ответ: 11/20.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
200.
Простая формула, чтобы подсчитать среднее арифметическое
К следующей статье
232.4K
Основные геометрические фигуры
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Калькулятор процентов к дробям
Базовый калькулятор
Калькулятор процентных долей
Введите процент:
%
Ответ:
\[ = \frac{5}{8} \]Показ работы:
\[ 62,5\% = \frac{62,5}{100} \]\[ = 0,625\]\[ = \frac{0,625}{ 1} \times \frac{1000}{1000} \]\[ = \frac{625}{1000} \]\[ = \frac{5}{8} \]
Поделитесь этой ссылкой для ответа: help
Вставьте эту ссылку в электронное письмо, текст или социальные сети.
Получить виджет для этого калькулятора
© Calculator Soup
Поделитесь этим калькулятором и страницей
Калькулятор Использование
Этот онлайн-калькулятор переводит проценты в дроби. Если процентное значение больше 100%, оно преобразуется в дробь смешанного числа. Введите проценты, чтобы преобразовать их в дроби. Вводимое число также может содержать десятичные разряды, например 3,5% или 0,625%.
Чтобы преобразовать проценты в дроби, вы сначала преобразуете проценты в десятичные числа, а затем используете ту же процедуру, что и преобразование десятичная дробь.
Как преобразовать проценты в дроби
- Разделите процент на 100, чтобы получить десятичное число.
- Используйте это число как числитель (верхнюю часть) дроби. Поставьте 1 в знаменателе (внизу) дроби.
- Преобразование десятичной дроби в целое число: подсчитайте, сколько знаков справа от десятичной дроби.
 Если у вас есть x знаков после запятой, умножьте числитель и знаменатель на 10 x .
Если у вас есть x знаков после запятой, умножьте числитель и знаменатель на 10 x . - Сократите дробь: Найдите наибольший общий делитель (НОД) числителя и знаменателя и сократите дробь, разделив числитель и знаменатель на НОД.
- Упростите оставшуюся дробь до дроби смешанного числа, если это возможно.
Пример: преобразовать 35,5% в дробь
1. Разделить на 100
\( \dfrac{35.5}{100} = 0,355\)
2. Переписать десятичное число в виде дроби (больше 1)
\( \dfrac{0.355}{1} \)
3. Умножить числитель и знаменатель на 10 3 = 1000, чтобы удалить 3 знака после запятой
\( \dfrac{0.355}{1}\times \dfrac {1000}{1000}= \dfrac{355}{1000} \)
4. Найдите наибольший общий делитель (НОД) чисел 355 и 1000 и сократите дробь, разделив числитель и знаменатель на НОД = 5.
\( \dfrac{355 \div 5}{1000 \div 5}= \dfrac{71}{200} \)
Следовательно,
\( 35,5\% = \dfrac{71}{200} \ )
Связанные калькуляторы
Чтобы преобразовать дробь в проценты, см. Калькулятор доли в процентах.
Калькулятор доли в процентах.
Подписаться на калькуляторSoup:
Преобразование десятичных дробей в дроби
Чтобы преобразовать десятичную дробь в дробь, выполните следующие действия:
- Шаг 1: Запишите десятичную дробь, деленную на 1, например: десятичный 1
- Шаг 2: Умножьте верхнее и нижнее число на 10 для каждого числа после запятой. (Например, если после запятой два числа, используйте 100, если их три, используйте 1000 и т. д.)
- Шаг 3: Упростите (или уменьшите) дробь
Пример: преобразование 0,75 в дробь
Шаг 1: Запишите 0,75, деленное на 1:
0,75 1
Шаг 2: Умножьте верхнее и нижнее число на 100 (поскольку после запятой 2 цифры, то есть 10×10=100):
| × 100 | ||
| 0,75 1 | = | 75 100 |
| × 100 | ||
(Видите, как это превращает верхнее число
в целое число?)
Шаг 3: Упростите дробь (это заняло у меня два шага):
| ÷5 | ÷ 5 | |||
| 75 100 | = | 15 20 | = | 3 4 |
| ÷5 | ÷ 5 | |||
Ответ =
3 4
Примечание: 75/100 называется десятичной дробью , а 3/4 называется обыкновенной дробью !
Пример: преобразование 0,625 в дробь
Шаг 1: запишите:
0,625 1
Шаг 2: умножить верх и низ на 1000 (3 цифры после запятой, поэтому 10×10×10=1000)
625 1000
Шаг 3: Упростите дробь (здесь мне потребовалось два шага):
| ÷ 25 | ÷ 5 | |||
| 625 1000 | = | 25 40 | = | 5 8 |
| ÷ 25 | ÷ 5 | |||
Ответ =
5 8Когда есть целая часть числа, отложите целое число и верните его в конец:
Пример: преобразование 2,35 в дробь
Отложите 2 и просто поработайте над 0,35
Шаг 1: запишите:
0,35 1
Шаг 2: умножить верх и низ на 100 (2 цифры после запятой, так что 10×10=100):
35 100
Шаг 3: Упростить дробь:
| ÷ 5 | ||
| 35 100 | = | 7 20 |
| ÷ 5 | ||
Верните 2 (для получения смешанной дроби):
Ответ = 2
7 20Пример: преобразование 0,333 в дробь
Шаг 1: Запишите:
0,333 1
Шаг 2: Умножьте верхнее и нижнее число на 1000 (3 знака после запятой, так что 10×10×10=1000)
333 1000
Шаг 3: Упростить дробь:
Проще не бывает!
Ответ =
333 1000 Если вы действительно имели в виду 0,333.

 При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче:
При этом после каждого умножения запятая в числителе сдвигается вправо на один знак, а у знаменателя соответственно добавляются нули. На примере легче: Обозначим это количество буквой n.
Обозначим это количество буквой n. Если у вас есть x знаков после запятой, умножьте числитель и знаменатель на 10 x .
Если у вас есть x знаков после запятой, умножьте числитель и знаменатель на 10 x .