|
Random converter |
Длина окружности и площадь кругаЭтот калькулятор определяет длину окружности и площадь круга по известным радиусу или диаметру окружности. Пример: Рассчитайте точную и примерную длину окружности и площадь круга радиусом 5 дюймов. Радиус Rметр (м)дециметр (дм)сантиметр (см)миллиметр (мм)километр (км)футдюймярдмиля Диаметр Dметр (м)дециметр (дм)сантиметр (см)миллиметр (мм)километр (км)футдюймярдмиля Длина окружности Cметр (м)дециметр (дм)сантиметр (см)миллиметр (мм)километр (км)футдюймярдмиля Площадь Aквадратный метр (м²)квадратный дециметр (дм²)квадратный сантиметр (см²)квадратный миллиметр (мм²)квадратный километр (км²)квадратный фут² (фут²)квадратный дюйм (дюйм²)квадратный ярд (ярд²)квадратная миля (миля²) Для расчета введите одну из величин: радиус, диметр, площадь или длину окружности и нажмите на кнопку Рассчитать для расчета остальных величин. Конвертер длины и расстояния • Конвертер площади Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Определения и формулы Длина окружности Площадь круга Окружности в архитектуре Окружность в технике Окружности в сельском хозяйстве Определения и формулыВ геометрии окружностью называется совокупность точек на плоскости, которые находятся на одном расстоянии от точки, называемой центром окружности. Иными словами, окружность — это геометрическое место точек, находящихся в одной плоскости и равноудаленных от точки, называемой центром. Расстояние между любой точкой окружности до центра этой окружности называется радиусом. Мы привыкли видеть окружность в форме круглой линии или круга. Однако так окружность выглядит только в евклидовой геометрии. В некоторых метрических пространствах, например, в чебышевском или манхэттенском пространстве окружности выглядят скорее квадратными. Диаметр круга — это наибольший отрезок, соединяющий две точки на окружности. Или, точнее, это отрезок, соединяющий две точки окружности и проходящий через ее центр. Диаметр окружности равен ее удвоенному радиусу. Любой диаметр разделяет окружность, а точнее, круг, на две равные половины. Говоря точным языком, окружность — это линия или замкнутая кривая, которая окружает часть плоскости, называемую кругом. Длина окружностиДлина C окружности — это длина замкнутой плоской кривой, ограничивающей круг, то есть это расстояние, равное длине границы круга. Она измеряется в единицах длины. Если разделить длину любой окружности на ее диаметр D, получится число 3.14159265359… Это число — одна из самых важных констант в математике, которое обозначается греческой буквой пи (π): где R — радиус окружности. Если решить это уравнение для длины окружности, мы получим формулу, которая всем нам знакома с детства: Математическая константа π широко используется в многих формулах в математике, технике, архитектуре и строительстве. Площадь кругаПоскольку TranslatorsCafe.com — сайт для переводчиков, в том числе с английского языка, вначале отметим, что в английском языке площадь круга не совсем корректно называется area of a circle, что буквально означает «площадь окружности», то есть площадь кривой линии (окружность — это кривая!), а, как известно, у линии не может быть площади. Итак, площадь A круга, то есть части плоскости, лежащей внутри окружности радиуса R, равна произведению числа π на квадрат радиуса: Во многих других языках, в том числе и в русском, такой путаницы в терминах «круг» и «окружность» нет. Впрочем, она есть в других терминах. Площадь круга можно также описать как число единичных квадратов, которые покрывают круг, лежащий внутри окружности. Окружности в архитектуреОкружность — весьма совершенная форма, потому что каждая точка окружности находится на одном и том же расстоянии от ее центра. Как и другие совершенные формы, окружность часто используют архитекторы. Круг и окружность широко применяются в архитектуре, и это при том, что круглые здания строить труднее, чем здания прямоугольной формы. Поэтому для постройки круглых зданий всегда была нужна особая мотивация. Возможно, что самая серьезная мотивация была религиозной. Тысячи лет люди наблюдали Солнце и Луну, и первые строители использовали их форму в конструкциях жилищ и поселений, потому что ведь на земле легко было разметить окружность — все, что для этого требовалось — это веревка из кожи или другого материала, да пара колышков. Среди наиболее известных деталей собора Парижской Богоматери — три огромных окна-розетки с витражами. На фотографии показана западная роза над главным порталом собора Северное окно-розетка с витражом в парижском Нотр-Даме Архитекторы считают окружность и сферу самыми совершенными из всех геометрических форм. Покрытия зданий в форме верхней части сферы, то есть купола, широко применяются в архитектуре и бывают различных форм и размеров. Они могут быть полусферическими или заостренной на вершине формы, или с конусным верхом, который можно увидеть в исламской архитектуре. Позолоченный купол Исаакиевского собора в Сант-Петербурге имеет почти полусферическую форму Тадж-Махал в индийском городе Агре — знаменитый пример архитектуры стиля моголов с пятью луковичными куполами Сферические купола часто используются в архитектуре индуистских храмов, как например, в этом беломраморном индуистском храме Шри Сварминараян Мандир в канадском городе Торонто Полукруглые арки известны со второго тысячелетия до нашей эры. Древнеримские архитекторы систематически использовали их в своих сооружениях. На снимке показан арочный мост Турнель над р. Сеной в Париже Окружность в техникеНевозможно представить себе технику без колес и других деталей в форме окружности. Некоторые из них (например, шасси самолетов и колеса автомобилей) хорошо видны. Сферические радиопрозрачные купола антенн часто используются для защиты механизмов поворота антенн и электронного оборудования радиолокационных станций Люки в космических кораблях, такие как этот люк в спускаемом аппарате корабля Союз ТМА-А, часто делаются круглой формы, так как такая конструкция без углов позволяет сильно уменьшить механические напряжения, а также облегчает их герметизацию В машинном отделении в музее Тауэрского моста в Лондоне можно увидеть старые работающие механизмы подъема моста Сколько колес можно насчитать на этой фотографии, сделанной на первом этаже Музея науки и техники в Лондоне? Окружности в сельском хозяйствеПролетая над пустынями, в которых ничего не растет, мы часто видим зеленые круги. Это поля, которые имеют такую форму из-за того, что фермеры используют системы кругового орошения с центральной осью, вокруг которой вращается оросительное устройство. Круглые поля с системами кругового орошения в пустыне Мохаве в штате Невада можно наблюдать, пролетая из Торонто в Сан-Франциско; радиус окружности обычно равен ¼ мили или 400 м, длина окружности 2,5 км, а площадь такого поля составляет 125 акров или чуть более 50 гектаров Автор статьи: Анатолий Золотков Вас могут заинтересовать и другие калькуляторы из группы «Математика»:Калькулятор расстояния между двумя точками Калькулятор комплексных чисел Калькулятор для расчета процентилей Калькулятор процентов Калькуляторы Математика |
Калькулятор Перевода Диаметра В Окружность
Инструкции: Используйте этот калькулятор для вычисления окружности круга с заданным диаметром, показывая все шаги. Пожалуйста, введите диаметр d в поле ниже.
Подробнее об этом калькуляторе перевода диаметра в окружность
Данный калькулятор позволит вам рассчитать Окружность круга
 Все, что вам нужно предоставить, — это правильное числовое выражение для диаметра. Это может быть число или дробь, или даже составное числовое выражение, при условии, что оно больше 0.
Все, что вам нужно предоставить, — это правильное числовое выражение для диаметра. Это может быть число или дробь, или даже составное числовое выражение, при условии, что оно больше 0.
Как только вы укажете действительный диаметр d, вам просто нужно нажать кнопку «Рассчитать», и все этапы процесса будут показаны и представлены вам.
Кроме того, вас может заинтересовать обратный процесс, который заключается в том, как вычислите диаметр из окружности из круга.
Формула расчета отношения диаметра к окружности
Наиболее типичная ситуация — получить окружность круга, начиная с радиуса, но в формуле есть сокращение, которое позволяет перейти непосредственно от диаметра к окружности, как показано в формуле ниже:
\[ C = \pi d \]
Может ли это стать еще проще? Вы просто умножаете диаметр d на \(\pi\).
Как перейти от диаметра к окружности?
- Шаг 1: Определите диаметр d и его потенциальную единицу длины. Это значение должно быть положительным, иначе вы не сможете продолжить
- Шаг 2: После того, как вы получили действительный диаметр d, окружность получается путем умножения d на π
- Шаг 3: После вычисления C = π d, вы оставляете ответ в терминах π, или оцениваете численно.
В наиболее типичном случае результат измерения окружности будет зависеть от π, поэтому вам может понадобиться
оценить выражение
чтобы получить числовое значение.
Калькулятор соотношения диаметра и радиуса
Возможно, вы из тех, кто не любит диаметры и предпочитает работать с радиусом, в таком случае вы помните, что d = 2r, и тогда вы можете вычислить радиус из диаметра, как показано ниже:
\[\displaystyle r = \frac{d}{2} \]
Если говорить простым языком, то радиус равен половине диаметра
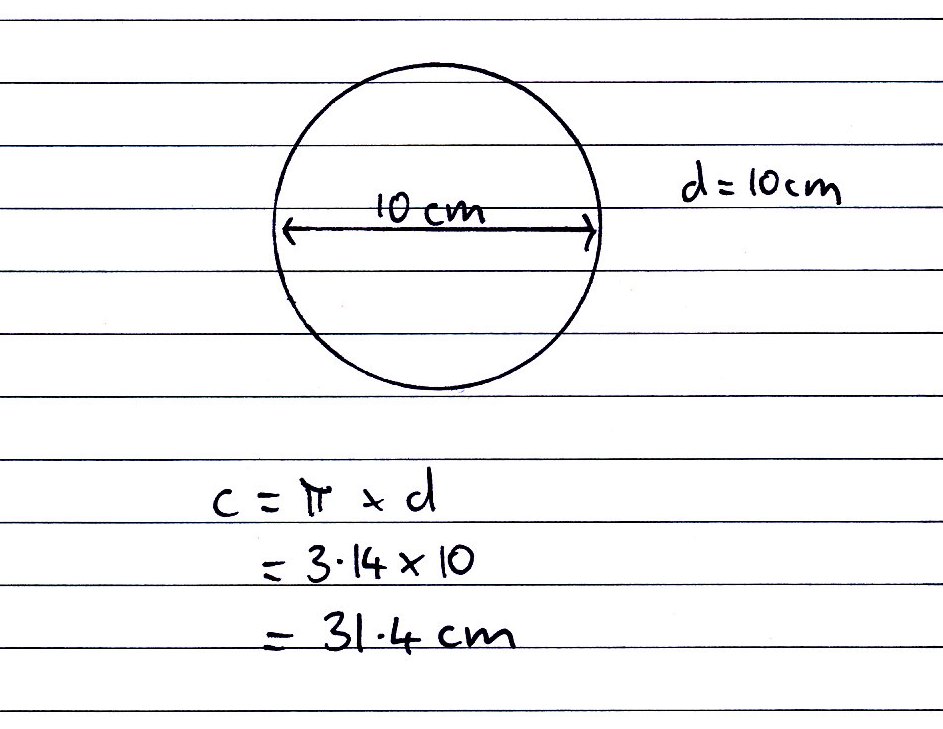
Какова окружность диаметра 12 дюймов?
Это пример, который можно использовать для понимания формулы. Итак, диаметр непосредственно представлен как d = 12 дюймов, и он поставляется с единицей длины.
Из приведенной выше формулы следует, что окружность равна C = π d = 12 π дюймов. Теперь, если мы захотим перевести это в числовое значение, то получим, что C = 37,699112 дюйма.
Почему я должен использовать диаметр для вычисления окружности?
Хорошее замечание. Использование диаметра — это одна из известных нам форм нахождения окружности круга, поэтому мы включили ее сюда для полноты картины.
Большинство людей просто вычисляют радиус по диаметру, а для окружности используют общую формулу.
Пример: вычисление окружности из диаметра
Вычислите окружность круга, если его диаметр равен \(\frac{3}{4}\)
Отвечать:
Нам нужно найти окружность \(C\) круга, а из предоставленной информации мы знаем, что диаметр круга равен \(d = \frac{3}{4}\).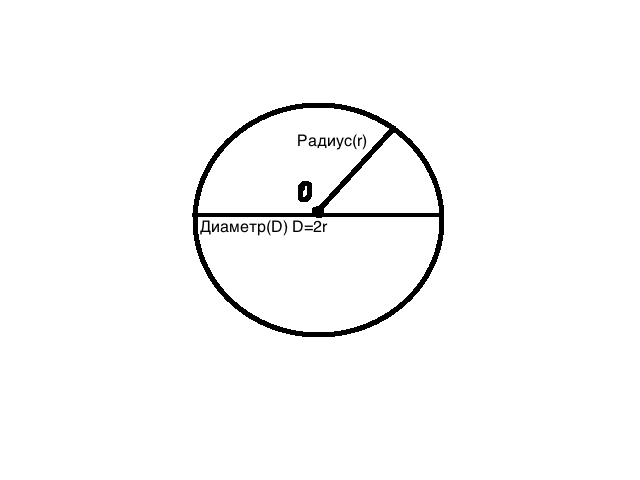
Теперь формула для окружности \(C = 2\pi r\), но так как диаметр равен удвоенному периметру, то получается \(d = 2r\), и, следовательно, формула окружности становится:
\[C = d \pi \]
Поэтому все, что нам нужно сделать, это подставить в приведенную выше формулу известное значение известного диаметра \(d = \frac{3}{4}\). Получается следующее:
\[ \begin{array}{ccl}\displaystyle C & = & \displaystyle d \pi \\\\ \\\\ & = & \pi \cdot \frac{3}{4} \\\\ \\\\ & = & \displaystyle \frac{3}{4}\pi{} \end{array} \]
На этом расчеты завершены.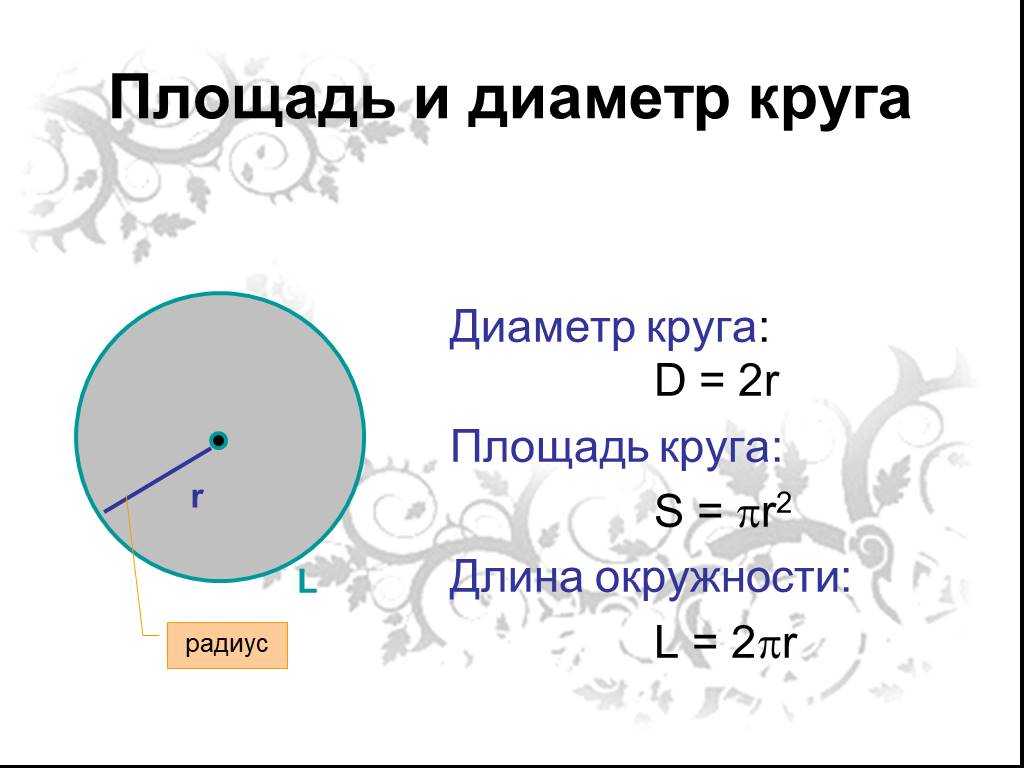 Мы выяснили, что окружность круга равна \(\displaystyle C = \frac{3}{4}\pi{}\).
Мы выяснили, что окружность круга равна \(\displaystyle C = \frac{3}{4}\pi{}\).
Пример: диаметр к окружности
Теперь, если предположить, что диаметр равен 3, то какова окружность?
Отвечать: Нам нужно найти окружность \(C\) круга, и теперь мы знаем, что \(d = 3 \).
\[C = d \pi \]
Поэтому мы просто подставляем значение \(d = 3\) в следующую формулу:
\[ \begin{array}{ccl}\displaystyle C & = & \displaystyle d \pi \\\\ \\\\ & = & \pi \cdot \frac{3}{4} \\\\ \\\\ & = & \displaystyle 3\pi{} \end{array} \]
Следовательно, в данном случае окружность круга равна \(\displaystyle C = 3 \pi{}\).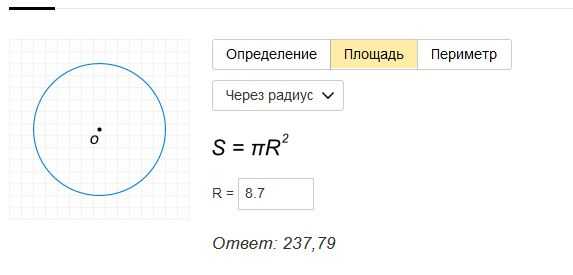
Пример: отношение диаметра к окружности
Какова будет окружность круга, если его диаметр d = -3?
Отвечать: В этом случае окружность не будет четко определенной, потому что диаметр ДОЛЖЕН быть положительным числом. Другими словами, вы не можете построить круг с отрицательным диаметром.
Другие калькуляторы окружностей
Круги встречаются в математике ВЕЗДЕ. Нет такой области математики, в которой окружности не были бы важны. Они дают понятия, знакомые каждому из нас, такие как
площадь круга
и
Окружность круга
.
Идеи площади и окружности кажутся сейчас очень знакомыми, но потребовалось немало времени, чтобы они были поняты так, что стали привычными для нас.
Одним из интересных элементов является то, что площади и окружности не зависят от уравнение окружности только на радиусе. Другими словами, центр не имеет значения для вычисления площади и периметра.
Калькулятор круга| Pi Day
Радиус(r)
Диаметр(d)
Окружность(c)
Площадь(a)
Вернуться на страницу калькуляторов
окружность круга обозначена как a, r, d и c соответственно.
Для тех, кто испытывает трудности с использованием формул вручную, чтобы найти площадь, длину окружности, радиус и диаметр круга, этот калькулятор окружности как раз для вас. Уравнения будут приведены ниже, чтобы вы могли видеть, как калькулятор получает значения, но все, что вам нужно сделать, это ввести основную информацию. Калькулятор сделает все остальное.
Окружность аналогична периметру в том смысле, что это общая длина, необходимая для рисования круга.
Заметим длину окружности как c .
c = 2 πr
или
c = πd
17 д )
Давайте рассчитать вручную, например.
Если r = 6 см, длина окружности равна c = 2 π (6) = 12 π см, если писать через π. Если вы предпочитаете числовое значение, ответ, округленный до десятых, будет равен 37,7 см.
Если вы предпочитаете числовое значение, ответ, округленный до десятых, будет равен 37,7 см.
Предположим, вы знаете только диаметр? Если диаметр равен 8 см, то длина окружности равна c = π (8) = 8 π или 25,1 см, округленное до десятых.
Самое замечательное в формулах то, что вы можете манипулировать ими, чтобы найти неизвестное, если вы знаете одну из других величин. Например, если мы знаем длину окружности, но не знаем радиус, можно решить c = 2 πr вместо r и получаем \(r = \frac{c}{2\pi}\). Точно так же, если вам нужен диаметр по окружности, просто возьмите c = πd и найдите d, чтобы получить d = \(\frac{c}{\pi}\).
@mometrixНужна помощь в определении площади круга? Мы вас прикрыли! Ссылка в био. ##math ##mathhelp ##mathematics ##piday ##pi ##mometrix ##area♬ original sound – Подготовка к тесту MometrixНахождение площади:
Пусть a = площадь круга
a = πr²
Если вы знаете диаметр, а не радиус, просто разделите диаметр на 2, чтобы получить радиус, и по-прежнему используйте приведенную выше формулу.
Опять же, формулу можно использовать для вычисления радиуса, если известна площадь. Просто разделите на на π, чтобы получить r², и из полученного результата извлеките квадратный корень из
.
Если вы хотите узнать диаметр по площади, выполните описанную выше процедуру, но удвойте результат, полученный для r . Это потому, что диаметр в два раза больше длины радиуса.
Попробуйте пример вручную, чтобы получить площадь.
Предположим, что r = 5 дюймов
a = πr²
a = π(25) = 25π
90,7 десятых дюймов в квадрате.Если вы знаете диаметр, просто разделите на 2, чтобы получить радиус, и используйте ту же формулу, что и выше.
Конечно, вам не нужно выполнять все вычисления вручную, чтобы использовать этот калькулятор. Просто введите информацию, которую вы знаете, и остальные будут рассчитаны для вас почти мгновенно.
Расчет окружности — диаметр окружности площади радиуса
Окружность ﹣ Калькулятор
Здесь все вращается по кругу: определения, формулы и расчеты радиуса, диаметра, длины окружности и площади круга с единицами разной величины завершают тему.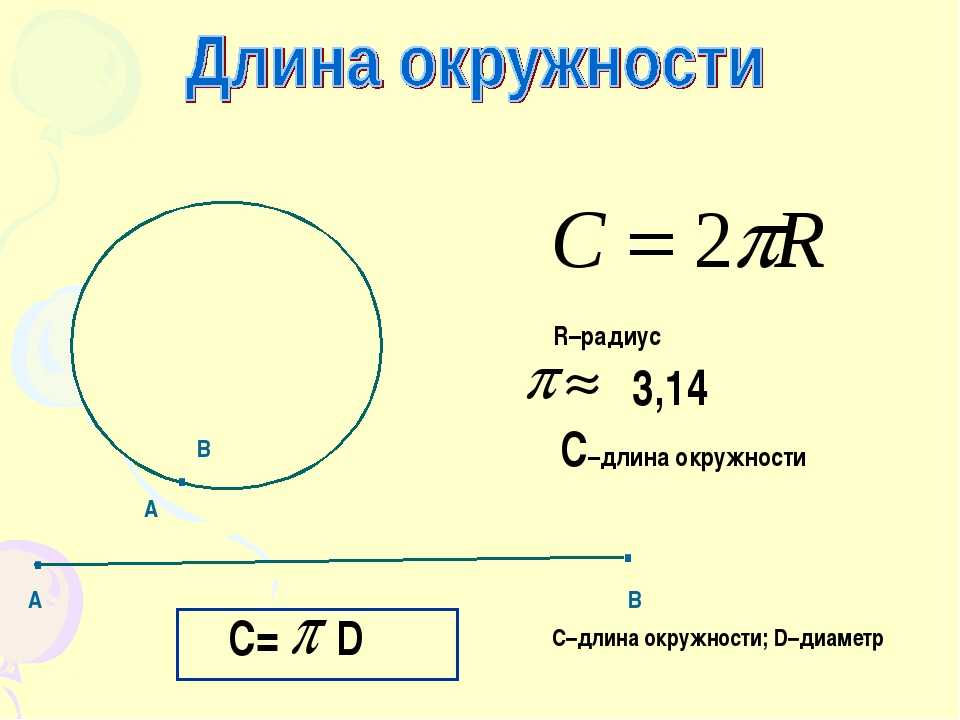 С помощью калькулятора круга вы можете рассчитать наиболее важные свойства круга, т. е. радиус, диаметр, длину окружности и площадь круга. В тексте справки калькулятора кругов каждое преобразование для отдельных свойств круга выводится с использованием соответствующей формулы круга.
С помощью калькулятора круга вы можете рассчитать наиболее важные свойства круга, т. е. радиус, диаметр, длину окружности и площадь круга. В тексте справки калькулятора кругов каждое преобразование для отдельных свойств круга выводится с использованием соответствующей формулы круга.
Содержание
- Определение окружности
- Расчет окружности: формулы
- Справка по вводу данных для калькулятора окружности
- Радиус окружности — определение и формула
- Диаметр окружности — определение и формула Периметр окружности — Определение и формула
- Площадь круга — Определение и формула
- Примеры расчета круга
- Вычисление радиуса круга
- Вычисление диаметра круга
- Расчет длины окружности
- Расчет площади окружности
Калькулятор ↑Содержание ↑
Окружность представляет собой геометрическую фигуру и определяется как множество всех точек на плоскости, находящихся на одинаковом расстоянии от точки М, центра окружности. Это расстояние от каждой точки на линии круга или на краю круга до центра круга называется радиусом. Математически круг является кривой и, следовательно, одномерным. Однако круг обычно интерпретируется как двумерная поверхность или круговой диск, который заключен в линию окружности.
Это расстояние от каждой точки на линии круга или на краю круга до центра круга называется радиусом. Математически круг является кривой и, следовательно, одномерным. Однако круг обычно интерпретируется как двумерная поверхность или круговой диск, который заключен в линию окружности.
К основным свойствам круга относятся радиус, диаметр круга, длина окружности круга и площадь круга. Вычисление этих свойств окружности и их преобразование с использованием формул окружности удобно выполнять с помощью Калькулятора окружности, что более подробно будет рассмотрено ниже.
В связи с расчетами и формулами для круга и расчетом кругов мы неоднократно встречаем Пи или греческую букву π. Число окружности Пи соответствует, независимо от размера окружности, точному отношению длины окружности к диаметру. Пи имеет бесконечное число знаков после запятой и начинается с 3,14159.26. Следовательно, длина окружности всегда примерно в 3,14 раза больше ее диаметра.
Калькулятор ↑Содержание ↑
- Диаметр: d = 2 × r
- Радиус: r = ½ × d
- Окружность: C = 2 × r × π или C = d × π
- Площадь: A = r² × π или A = (d² × π)/4 = ¼ × d² × π
Калькулятор ↑Содержание ↑
Калькулятор для расчета круга содержит несколько полей ввода, которые более подробно описаны ниже:
Выберите здесь соответствующую единицу размера, чтобы отобразить ее для отдельных полей ввода. Вы можете выбрать мм, см, дм, м, км, дюймы, футы, ярды или мили.
Вы можете выбрать мм, см, дм, м, км, дюймы, футы, ярды или мили.
А вот как работает калькулятор: Вы можете заполнить любое поле ввода ниже. Остальные значения затем рассчитываются и заполняются автоматически с использованием формулы для расчета окружности. Справочные тексты для радиуса, диаметра, длины окружности и площади всегда содержат текущий вывод текущего расчета. Как только вы снова измените одно из значений, выполняется новый расчет оставшихся значений и обновление текстов справки для получения нового расчета.
Введите радиус, чтобы рассчитать диаметр, длину окружности и площадь круга. «Справочные тексты» рассчитанных свойств круга будут обновлены, чтобы включить соответствующую формулу круга, а также вывод вычисления из введенного радиуса в соответствующее свойство.
Пожалуйста, введите диаметр, чтобы рассчитать радиус, длину окружности и площадь круга. Затем обновляются справочные тексты рассчитанных свойств окружности, которые содержат соответствующую формулу расчета, а также вывод расчета от введенного диаметра к соответствующему свойству.
Введите длину окружности, чтобы рассчитать радиус, диаметр и площадь круга. Справочные тексты рассчитанных свойств окружности обновляются, и каждый из них содержит конкретный вывод текущего расчета, т. е. от длины окружности до радиуса, до диаметра или до площади окружности.
Введите площадь для расчета радиуса, диаметра и длины окружности. Точно так же при расчете радиуса, диаметра и окружности их справочные тексты обновляются, чтобы можно было понять вывод преобразования в каждом случае.
Эскиз показывает выбранное свойство окружности. Это дает вам представление о том, как определяются радиус, диаметр, длина окружности и площадь круга. Отображение меняется, как только вы нажимаете на поле ввода для свойств круга или выбираете соответствующую кнопку справки.
Калькулятор ↑Содержание ↑
Как уже было сказано, окружность определяется как множество всех точек плоскости, находящихся на равном расстоянии от точки М, центра окружности. Это расстояние от центра круга до края круга называется радиусом.
Это расстояние от центра круга до края круга называется радиусом.
Радиус r или радиус — это расстояние между центральной точкой M окружности и линией окружности.
Калькулятор ↑Содержание ↑
Диаметр окружности d или ⌀ представляет собой длину соединительного расстояния двух точек линии окружности, проходящей через центр окружности M.
Таким образом, диаметр — это максимально возможное расстояние между двумя точками на окружности.
Диаметр d соответствует удвоенному радиусу r
д = 2 × г
Калькулятор ↑Содержание ↑
Длина окружности C равна длине окружности.
Длина окружности C вычисляется путем умножения диаметра d на число Pi (π = 3,1415…).
С = д × π
Калькулятор ↑Содержание ↑
Площадь круга A — это площадь, ограниченная линией окружности.
Площадь круга A вычисляется путем умножения квадрата радиуса r на число Пи (π = 3,1415. ..).
..).
А = г² × π
Видео, демонстрирующее вывод формулы площади круга
Вот еще одно видео на тему «Окружности, окружность и площадь» от Math Antics. В видео формула площади круга получается путем деления круга на множество секторов, которые затем соединяются вместе, образуя прямоугольник. Затем, используя радиус и половину окружности круга, можно получить площадь этого прямоугольника и, в конечном итоге, круг.
Приложение загружается. Пожалуйста, будьте терпеливы.
Если приложение не загружается, это значит, что вы используете наш сайт без рекламы и отслеживания. Пожалуйста дать согласие на использование файлов cookie для активации приложения..
Калькулятор ↑Содержание ↑
Четыре свойства круга, описанные на этой странице, — радиус, диаметр, длина окружности и площадь — можно рассчитать, указав одно значение другого свойства в каждом случае. Например, если вы хотите вычислить площадь круга, это можно сделать, используя одно из трех других свойств в каждом случае, то есть используя радиус, диаметр или длину окружности.
Поэтому ниже мы покажем вам три примера для расчета радиуса, диаметра, длины окружности и площади круга с использованием трех других свойств круга в каждом случае.
Калькулятор ↑Содержание ↑
В следующих трех примерах показано вычисление радиуса с использованием свойств круга диаметра, длины окружности и площади.
Дана окружность с диаметром d 20 в . Ищем радиус r.
Расчет
Радиус r равен половине диаметра d, поэтому r = d / 2 .
Подставляя 20 дюймов, выбранные в примере, вместо диаметра d, радиус окружности равен r = 20 дюймов / 2 = 10 дюймов .
Дан круг с длиной окружности C 30 в . Ищем радиус r.
Расчет
Формула длины окружности: 90 207 C = 2 × r × π 90 208 . Когда мы преобразуем эту формулу в r, мы получаем r = C / π / 2, что составляет половину длины окружности, деленную на Pi (π = 3,1415…), таким образом r = C / π / 2 .
Если мы заменим 30 в выбранном в примере для окружности C, радиус круга r = 30 дюймов / π / 2 = 4,77 дюйма .
Вот еще одно видео на тему «Вычисление длины окружности по заданному радиусу» мистера Дж.: В видео также показано, как преобразовать формулу длины окружности в r, чтобы рассчитать радиус на основе заданной длины окружности. Начиная с 3:09 следуют еще два примера преобразования.
Приложение загружается. Пожалуйста, будьте терпеливы.
Если приложение не загружается, это значит, что вы используете наш сайт без рекламы и отслеживания. Пожалуйста дать согласие на использование файлов cookie для активации приложения.
Дана 90 207 круглая площадь A размером 100 дюймов² 90 208 . Ищем радиус r.
Расчет
Общая формула площади круга A: A = r² × π . Если мы преобразуем эту формулу в r, радиус r будет равен квадратному корню из результата площади круга A, деленному на Pi (π = 3,1415. ..), таким образом r = А / π .
..), таким образом r = А / π .
Если мы вставим 100 дюймов², выбранные в примере для площади A, радиус круга будет r = 100 дюймов / π = 5,64 дюйма .
В целях иллюстрации, вот еще одно видео на тему «Найти радиус» Брайана Маклогана: Здесь также объясняется преобразование формулы площади круга в r, чтобы можно было вычислить соответствующий радиус для заданного круглая площадь.
Приложение загружается. Пожалуйста, будьте терпеливы.
Если приложение не загружается, это значит, что вы используете наш сайт без рекламы и отслеживания. Пожалуйста дать согласие на использование файлов cookie для активации приложения..
Калькулятор ↑Содержание ↑
В следующих примерах показано вычисление диаметра с использованием свойств окружности радиуса, длины окружности и площади.
Дана окружность 90 207 с радиусом r 10 в 90 208 . Ищем диаметр d.
Расчет
Диаметр d соответствует удвоенному радиусу r, то есть d = 2 × r .
Если 10 дюймов, выбранных в примере, используются для радиуса r, диаметр круга равен 90 207 d = 2 × 10 дюймов = 20 в 90 208 .
Дан круг с длиной окружности C 30 в . Ищем диаметр d.
Расчет
Формула длины окружности: C = d × π . Если мы преобразуем эту формулу в d, диаметр d будет равен длине окружности, деленной на число Пи (π = 3,1415…), таким образом d = C / π .
Если мы заменим 30 в выбранном в примере для окружности C, диаметр круга 90 207 d = 30 дюймов / π = 9,55 дюйма 90 208 .
Дан круг с площадью A 100 дюймов² . Ищем диаметр d.
Расчет
Общая формула площади круга A: A = r² × π . Поскольку диаметр d соответствует удвоенному радиусу r, формула поэтому А = (d / 2)² × π .
Если мы преобразуем эту формулу в d, диаметр d будет равен удвоенному квадратному корню из площади круга A, деленному на Pi (π = 3,1415. ..), таким образом d = 2 × A / π .
..), таким образом d = 2 × A / π .
Если мы вставим 100 дюймов², выбранные в примере для площади A, диаметр круга будет d = 2 × 100 дюймов / π = 11,28 дюймов .
Калькулятор ↑Содержание ↑
Следующие примеры иллюстрируют вычисление длины окружности с использованием радиуса, диаметра и площади окружности.
Дана окружность 90 207 с радиусом r, равным 10, в 90 208 . Ищем окружность С.
Расчет
Окружность C соответствует удвоенному радиусу r, умноженному на число Pi (π = 3,1415…), таким образом C = 2 × r × π .
Если мы вставим 10 в выбранный в примере радиус r, длина окружности будет равна C = 2 × 10 дюймов × π = 62,83 дюйма 90 208 .
Дана окружность 90 207 диаметра d, равная 20 в . Ищем окружность С.
Расчет
Длина окружности C соответствует диаметру d, умноженному на число Pi (π = 3,1415…), таким образом C = d × π .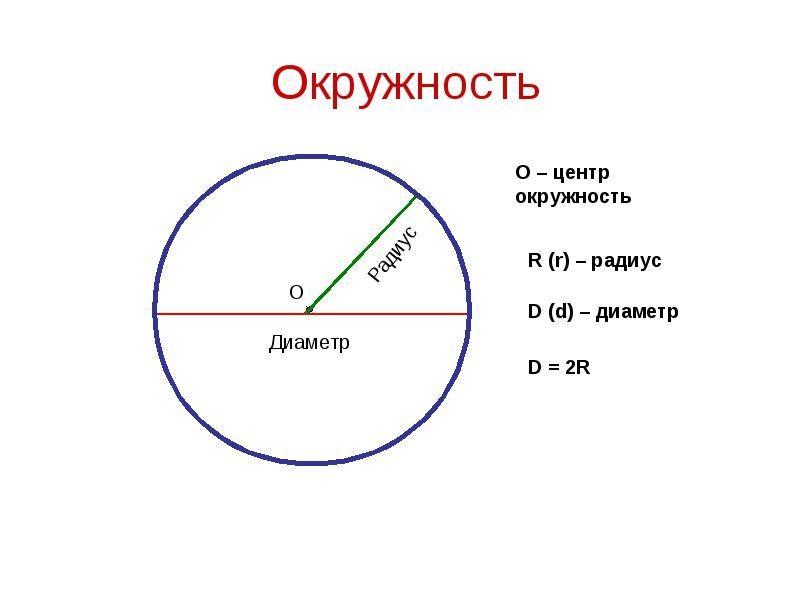
Если мы подставим выбранное в примере 20 вместо диаметра d, длина окружности будет равна C = 20 дюймов × π = 62,83 дюйма .
Дана 90 207 круглая площадь A размером 100 дюймов² 90 208 . Ищем окружность С.
Расчет
Общая формула площади круга A: A = r² × π . Теперь, используя эту формулу, радиус r можно рассчитать, сначала преобразовав формулу в r. Радиус r равен квадратному корню из площади круга A, деленному на Pi (π = 3,1415…), таким образом r = А / π .
Если мы вставим 100 дюймов², выбранные в примере для площади A, радиус круга будет r = 100 дюймов / π = 5,64 дюйма .
Используя рассчитанный таким образом радиус, теперь можно использовать общую формулу расчета длины окружности: длина окружности C равна удвоенному радиусу r, умноженному на число Pi (π = 3,1415…), таким образом C = 2 × r × π .
Если мы вставим ранее рассчитанное значение радиуса r, длина окружности будет равна C = 2 × 5,64 дюйма × π = 35,45 дюйма .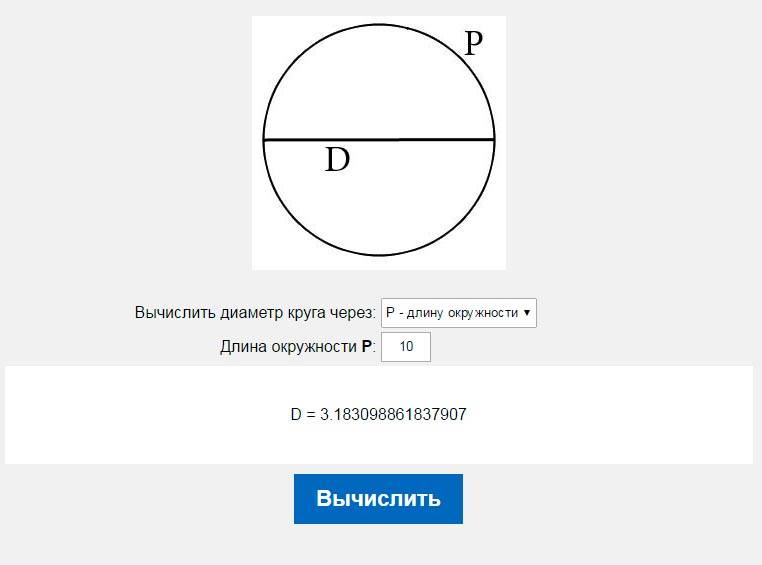
Калькулятор ↑Содержание ↑
Следующие примеры иллюстрируют вычисление площади круга с использованием радиуса, диаметра и длины окружности.
Дана окружность с радиусом r 10 в . Найдем площадь круга А.
Расчет
Площадь круга A равна квадрату радиуса, т. е. r², умноженному на число Pi (π = 3,1415…), и, следовательно, A = r² × π .
Если 10 дюймов, выбранных в примере, используются для радиуса r, площадь круга будет следующей: A = (10 дюймов)² × π = 314,16 дюйм² .
Дана окружность с диаметром d 20 в . Найдем площадь круга А.
Расчет
Площадь A равна половине диаметра в квадрате, т. е. (d / 2)², умноженному на число Pi (π = 3,1415…), и, таким образом, A = (d / 2)² × π .
Если вместо диаметра d подставить выбранные в примере 20, то площадь круга будет равна A = (20 дюймов / 2)² × π = 314,16 дюйм² .
Дан круг с длиной окружности C 30 в .


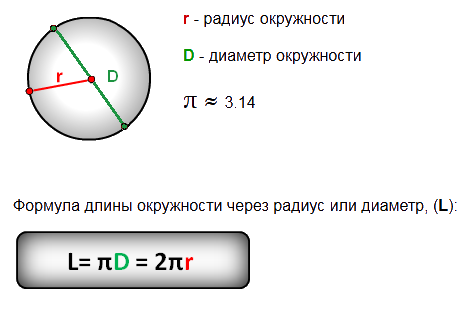
 Несмотря на то, что число π известно с древних времен, греческой буквой пи его стали обозначать совсем недавно — с середины XVIII века. π — иррациональное и трансцендентное число. Это означает, что его нельзя точно представить в виде простой дроби и оно не является корнем любого многочлена с рациональными коэффициентами. Есть много чисел, которые являются иррациональными, но не являются трансцендентными. Например, √2 — иррациональное, но не трансцендентное число, так как оно является корнем уравнения x² — 2 = 0. Интересно отметить, что поскольку точное значение π определить невозможно, значит невозможно найти и точное значение длины окружности или площади любого круга.
Несмотря на то, что число π известно с древних времен, греческой буквой пи его стали обозначать совсем недавно — с середины XVIII века. π — иррациональное и трансцендентное число. Это означает, что его нельзя точно представить в виде простой дроби и оно не является корнем любого многочлена с рациональными коэффициентами. Есть много чисел, которые являются иррациональными, но не являются трансцендентными. Например, √2 — иррациональное, но не трансцендентное число, так как оно является корнем уравнения x² — 2 = 0. Интересно отметить, что поскольку точное значение π определить невозможно, значит невозможно найти и точное значение длины окружности или площади любого круга.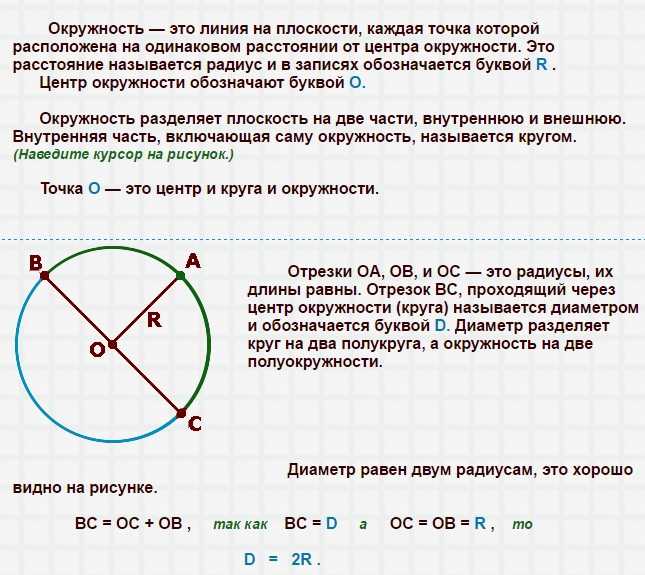 Но ничего, так уж сложилось и англоговорящие люди привыкли к этой неточности.
Но ничего, так уж сложилось и англоговорящие люди привыкли к этой неточности. Окружности и сферы можно найти практически в любой культуре, религии или системе верований в качестве магических знаков или символов. Многие культовые здания и сооружения являются окружностями в плане — например, буддийские ступы в форме полусферы или Стоунхендж.
Окружности и сферы можно найти практически в любой культуре, религии или системе верований в качестве магических знаков или символов. Многие культовые здания и сооружения являются окружностями в плане — например, буддийские ступы в форме полусферы или Стоунхендж. Они могут иметь совершенную сферическую форму, как римские и византийские купола или могут плавно заостряться на вершине, и тогда купол становится похожим на луковицу, как в православных храмах или в архитектурных стилях Великих Моголов.
Они могут иметь совершенную сферическую форму, как римские и византийские купола или могут плавно заостряться на вершине, и тогда купол становится похожим на луковицу, как в православных храмах или в архитектурных стилях Великих Моголов. Другие спрятаны в компьютерах, стиральных и посудомоечных машинах, холодильниках, турбинах и другом оборудовании.
Другие спрятаны в компьютерах, стиральных и посудомоечных машинах, холодильниках, турбинах и другом оборудовании.