Перевод чисел в степени: Возведение в степень | Онлайн калькулятор

Системы счисления. Перевод из одной системы в другую.

1. Порядковый счет в различных системах счисления.

В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».

Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.

Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100.

И так далее.

Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):

0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30

Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):

0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

 

 
2.Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.

Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.

Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

Это и есть десятичная запись нашего числа, т. е.

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.

Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:

Таблицу соответствия мы научились строить в п.1.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т. е.

Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.

Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:

Благодарим за то, что пользуйтесь нашими статьями. Информация на странице «Системы счисления. Перевод из одной системы в другую.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам. Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена: 08.05.2023

Перевод чисел между системами счисления, основания которых равно степени числа 2

Перевод чисел между системами счисления, основания которых равны значениям степеней числа 2 (т. е. P = 2 ⁿ), можно произвести по более простым алгоритмам. Получим эти правила.

Перевод между двоичной и восьмеричной системами счисления

Определим информационный вес двоичной цифры. Так как алфавит двоичной системы содержит две цифры (0 и 1), то используя формулу Хартли, имеем:
N = 2 ⁱ, 2 = 2 ⁱ, откуда i = 1 бит

Аналогично для восьмеричной цифры:
N = 2 ⁱ, 8 = 2 ⁱ, 2 ³ = 2 ⁱ, откуда i = 3 бит

Нетрудно заметить, что информационный вес восьмеричной цифры в три раза больше двоичного. Поэтому каждой восьмеричной цифре можно поставить в соответствие группу из трех двоичных разрядов (триаду):

0 – 000, 1 – 001, 2 – 010, 3 – 011, 4 – 100, 5 – 101, 6 – 110, 7 – 111

Последнее утверждение позволяет сформулировать алгоритм перевода двоичного числа в восьмеричную систему счисления

:

1. Разбить двоичное число на триады, справа налево.
2. Если в правой группе меньше трех цифр, то добавить ведущие нули.
3. Каждую триаду перевести в восьмеричную систему счисления.
4. Записать полученные цифры в соответствующих разрядах восьмеричного числа.

Пример. Перевести двоичное число 1011101110₂ в восьмеричную систему счисления.

Для решения задачи воспользуемся выше приведенным алгоритмом:

1. 1.011.101.110
2. 001.011.101.110
3. 1 3 5 6
4. 1011101110₂ = 1356₈

Ответ. 1356

Алгоритм перевода восьмеричного числа в двоичную систему счисления:

1. Разбить двоичное число на триады, справа налево.
2. Поставить в соответствие каждой восьмеричной цифре двоичную триаду.
3. Соединить триады и записать двоичное число.
4. Удалить (если существуют) незначащие нули.

Пример. Перевести восьмеричное число 257₈ в двоичную систему счисления.

Используем алгоритм, приведенный выше:

1. 010.101.111
2. 010101111
3. 10101111

Таким образом, 257₈ = 10101111₂

Ответ. 10101111

Перевод между двоичной и шестнадцатеричной системами счисления

Определим информационный вес шестнадцатеричной цифры:

N = 2 ⁱ, 16 = 2 ⁱ, 2 ⁴ = 2 ⁱ, откуда i = 4 бит

Итак, информационный вес шестнадцатеричной цифры в четыре раза больше двоичного. Значит, каждой цифре шестнадцатеричной системы счисления можно поставить в соответствие группу из четырех двоичных разрядов (тетраду):

0 – 000, 1 – 001, 2 – 010, 3 – 011, 4 – 100, 5 – 101, 6 – 110, 7 – 111
8 – 0111, 9 – 1001, A – 1010, B – 1011, C – 1100, D – 1101, E – 1110, F – 1111

Алгоритм перевода двоичного целого числа в шестнадцатеричную систему счисления:

1. Разбить двоичное число на тетрады, справа налево.
2. Если в правой группе меньше четырех цифр, то добавить ведущие нули.
3. Каждую тетраду перевести в шестнадцатеричную систему счисления.
4. Записать полученные цифры в соответствующих разрядах шестнадцатеричного числа.

Пример. Перевести двоичное число 10011011102 в шестнадцатеричную систему счисления.

Воспользуемся выше приведенным алгоритмом:

1. 10.0110.1110
2. 0010.0110.1110
3. 2 6 E
4. 1001101110₂ = 26E₁₆

Ответ. 26E

Алгоритм перевода шестнадцатеричного числа в двоичную систему счисления:

1. Поставить в соответствие каждой шестнадцатеричной цифре двоичную тетраду.
2. Соединить тетрады и записать двоичное число.
3. Удалить (если существуют) незначащие нули.

Пример. Перевести шестнадцатеричное число 3AC₁₆ в двоичную систему счисления.

Используем алгоритм, приведенный выше:

1. 0011.1010.1100
2. 001110101100
3. 1110101100

Таким образом, 3AC₁₆ = 1110101100₂

Ответ. 1110101100

Почему существуют научные обозначения? Как это работает?

Основные правилаNegativeEng. Not’nFractional

Purplemath

Что такое научная запись?

Научное представление — это метод преобразования громоздких чисел, будь то огромных или крошечных, в более удобный формат. Это преобразование выполняется с использованием показателей степени; формат преобразованного значения будет следующим: a.bcdef…×10 ⁿ , где a, b, c, d, e, f и т. д. – цифры, а n – положительное или отрицательное целое число.

Содержание продолжается ниже

MathHelp.com

Научное обозначение

Почему существует научное обозначение?

Ученые часто работают с очень большими и очень маленькими числами. Вместо того, чтобы записывать все число, научная запись позволяет сокращать выражения. Например, вместо того, чтобы говорить, что молекула воды имеет диаметр около 0,00000000000275 метров, мы можем сказать, что ее ширина составляет около 2,75×10 ⁻¹² метров.

В повседневной жизни большинство людей не сталкиваются с гигантскими или крошечными числами. Научная нотация была изобретена, чтобы облегчить жизнь ученым, которые часто имеют дело с астрономическими числами (в буквальном смысле измерения расстояний между звездами) и микроскопическими числами (в буквальном смысле нуждаются в каком-то микроскопе, чтобы увидеть, что они измеряют). . Научная нотация упрощает работу.

Как работает научная запись?

Формат записи числа в экспоненциальном представлении довольно прост: (первая [ненулевая] цифра числа), затем (десятичная точка), а затем (все остальные цифры числа), умноженное на ( 10, возведенные в соответствующую степень).

Чтобы преобразовать большое число в экспоненциальное представление, выполните следующие действия:

1. Возьмите исходное значение и переместите десятичную точку после последней цифры в позицию после первой цифры. Например, возьмем 7 375,49.8 555 и переместите (понятную) десятичную точку после последних 5 до 7, чтобы получить 7,375498555.
2. Подсчитайте количество позиций, на которые была перемещена десятичная точка. В этом примере точка переместилась на 9 мест.
3. Умножьте преобразованное число на 10, возведенное в степень, на сколько мест была перемещена точка. В этом примере экспоненциальное представление равно 7,375498555×10 ⁹ .

Процесс преобразования небольшого числа в экспоненциальное представление аналогичен:

1. Возьмите исходное значение и переместите десятичную точку из исходного положения сразу после первой ненулевой цифры. Например, возьмите 0,00000000000275 и переместите десятичную точку после первого нуля сразу после 2, чтобы получить 2,75.
2. Подсчитайте количество позиций, на которые была перемещена десятичная точка. В этом примере точка переместилась на 12 мест.
3. Умножьте преобразованное число на 10, возведенное в отрицательную степень, на сколько мест была перемещена точка. В этом примере экспоненциальное представление равно 2,75×10 ⁻¹² .

Независимо от того, преобразуете ли вы большие или маленькие числа в экспоненциальное представление, часть, предшествующая «умножить на 10 в некоторой степени», называется коэффициентом; 10 — основа; а сила есть сила.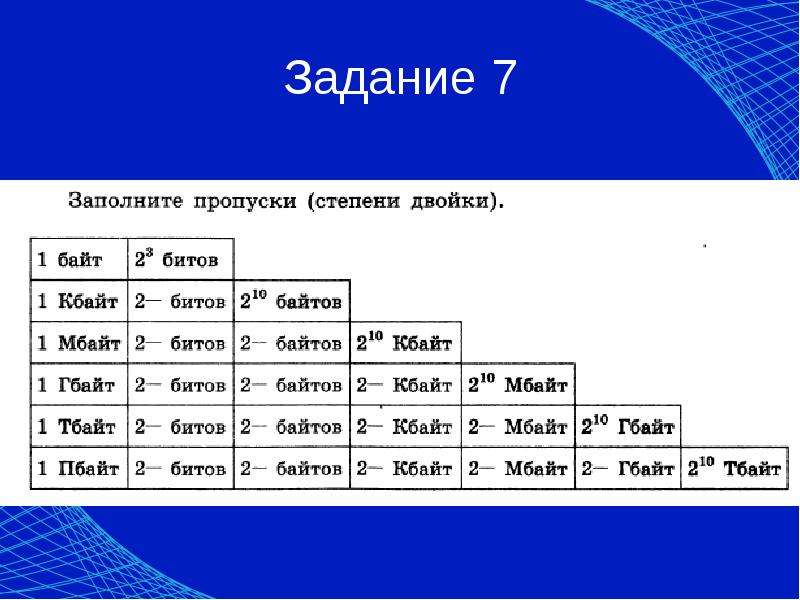

Откуда вы знаете, какой знак использовать для степени 10?

Большое число будет состоять из 10 до некоторого положительного значения, например 10 ⁷ , что составляет 1 000 000. Небольшое число будет содержать от 10 до некоторого отрицательного значения, например 10 ⁻⁷ , что равно 0,0000001. Так что ожидайте положительных степеней, когда вы конвертируете большие числа в экспоненциальную запись, и отрицательных степеней, когда вы конвертируете маленькие числа.

На практике процесс преобразования довольно прост.

• Запишите 124 в экспоненциальном представлении.

Это не очень большое число, но оно прекрасно подойдет для примера преобразования в экспоненциальное представление.

Чтобы преобразовать это в научное представление, я сначала преобразую «124» в «1,24». Это не то число, которое мне дали, но у меня будет такое же значение, как только я добавлю базу и мощность.

Чтобы преобразовать 1,24 обратно в 124, я умножил бы на 100: (1,24)(100) = 124. И 100 = 10 ² .

Тогда в экспоненциальном представлении 124 записывается как:

1,24 × 10 ²

В приведенном выше примере я использовал математические рассуждения, чтобы объяснить, почему степень 10 должна равняться 2. Но преобразование между «обычной» записью и экспоненциальной записью еще проще, чем я только что показал, потому что все, что вам действительно нужно сделать, это посчитать десятичные разряды. Чтобы выполнить преобразование для предыдущего примера, я бы подсчитал количество знаков после запятой, на которые я передвинул десятичную точку. Поскольку я переместил его на два места, я имел бы дело со степенью 2 на 10. Но должна ли она быть положительной или отрицательной степенью 2? Поскольку исходное число (124) было больше преобразованной формы (1,24), то мощность должна быть положительной.

• Запись в десятичной системе счисления: 3,6 × 10 ¹²

Поскольку показатель степени 10 положительный, я знаю, что они ищут БОЛЬШОЕ число, поэтому мне нужно переместить десятичную точку вправо, чтобы сделать число БОЛЬШЕ. Поскольку показатель степени 10 равен 12, мне нужно переместить десятичную точку на двенадцать разрядов.

Во-первых, я перенесу десятичную точку на двенадцать разрядов. Я делаю маленькие петли, когда считаю места, чтобы отслеживать:

Затем я заполняю циклы нулями:

Итак, мой ответ:

3 600 000 000 000

…или 3,6 триллиона.

Идиоматическое примечание: «Триллион» означает тысячу миллиардов, то есть тысячу тысяч миллионов, на американском языке; британско-английский термин для американского «миллиарда» будет «миллиардом», поэтому американский «триллион» (выше) будет британским «тысяча миллиардов».

---

• Запишите 0,000 000 000 043 6 в экспоненциальном представлении.

(Примечание. Пробелы между каждой тройкой цифр после запятой служат для облегчения чтения числа. Они не имеют математического значения, так же как и запятые в больших числах «не означают» что-либо. .)

В экспоненциальном представлении коэффициент (т.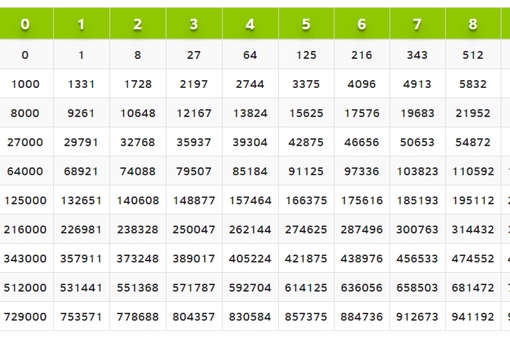 е. числовая часть, а не десятичная часть в степени) будет равен «4,36». Итак, я посчитаю, на сколько знаков десятичная точка должна переместиться, чтобы попасть из того места, где она сейчас, туда, где она должна быть:

Тогда степень числа 10 должна быть равна −11: «одиннадцать», потому что именно на столько знаков нужно переместить десятичную точку, и «минус», потому что я имею дело с МАЛЕНЬКИМ числом.

Итак, в экспоненциальном представлении данное число записывается как:

4,36 × 10 ⁻¹¹

---

• Преобразовать 4,2 × 10 ⁻⁷ в десятичную систему счисления.

Поскольку показатель степени 10 отрицателен, я ищу небольшое число. Поскольку показатель степени равен семи, я буду перемещать десятичную точку на семь знаков. Поскольку мне нужно переместить точку, чтобы получить небольшое число, я буду перемещать ее влево.

Тогда мой ответ:

0,000 000 42

---

• Преобразовать 0,000 000 005 78 в экспоненциальное представление.

Это небольшое число, поэтому показатель степени 10 будет отрицательным. Первая «интересная» (т. е. ненулевая) цифра в этом числе — 5, так что именно там должна стоять десятичная точка. Чтобы перейти от того места, где оно находится, сразу после 5, десятичная точка должна будет переместиться на девять знаков вправо. (Пересчитайте их, если не уверены!)

Тогда степень числа 10 будет равна отрицательной 9, и мой ответ таков:

5,78 × 10 ⁻⁹

---

• Преобразуйте 93 000 000 в экспоненциальную запись.

Это большое число, поэтому показатель степени 10 будет положительным. Первая «интересная» цифра в этом числе — ведущая 9, так что именно там должна быть десятичная точка. Чтобы перейти от того места, где оно находится, сразу после 9, десятичная точка должна будет переместиться на семь знаков влево.

Тогда степень числа 10 будет положительной 7, и мой ответ:

9,3 × 10 ⁷

---

Помните: на сколько делений вы переместили десятичную дробь, это степень числа 10. Если у вас небольшой число в десятичной форме (меньше 1 по модулю), тогда степень отрицательна для научной записи; если это большое десятичное число (больше 1 по абсолютной величине), то показатель степени положителен для научного представления.

Предупреждение: Отрицательное значение показателя степени и отрицательное значение числа означает два очень разные вещи ! Например:

−0,00036 = −3,6 × 10 ⁻⁴
0,00036 = 3,6 × 10 ⁻⁴
36 000 = 3,6 × 10 ⁴
−36 000 = −3,6 × 10 ⁴

Не путайте!

Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в преобразовании обычного числа в экспоненциальное представление. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)

Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.

(Нажмите здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)

Вас могут попросить умножить и разделить числа в экспоненциальном представлении. Я никогда не видел смысла в этом, так как в «реальной жизни» вы бы имели дело с этими беспорядочными числами, используя калькулятор, но вот процесс, если вам нужно «показать свою работу»:

• Упростите и выразите в научной записи: (2,6 × 10 ⁵ ) (9,2 × 10 ⁻¹³ )

Поскольку я умножаю, я могу легко перемещать вещи и упрощать некоторые из них:

(2,6 × 10 ⁵ ) (9,2 × 10 ⁻¹³ )
= (2.6) (10 ⁵ ) (9.2) (10 ⁻¹³ )
= (2,6) (9,2) (10 ⁵ ) (10 ⁻¹³ )
= (2.6) (9.2) (10 ⁵⁻¹³ )
= (2,6) (9,2) (10 ⁻⁸ )

Хорошо; Я упростил десятую часть. Теперь мне нужно иметь дело с 2,6 умножить на 9,2, не забывая перевести произведение в экспоненциальное представление:

2,6 × 9,2 = 23,92 = 2,392 × 10 = 2,392 × 10 ¹

Собрав все вместе, я получил:

90 002 (2,6 × 10 ⁵ ) (9,2 × 10 ⁻¹³ )
= (2,6) (9,2) (10 ⁻⁸ )
= (2,392 × 10 ¹ ) (10 ⁻⁸ )
= (2,392)(10 ¹ ) (10 ⁻⁸ )
= (2,392) (10 ¹⁻⁸ )
= 2,392 × 10 ⁻⁷

Тогда (2,6 × 10 ⁵ ) (9,2 × 10 ⁻¹³ ) = 2,392 × 10 ⁻⁷

901 06

Деление чисел в экспоненциальном представлении работает примерно так же.

• Упростите и выразите в экспоненциальном представлении: (1,247 × 10 ⁻³ ) ÷ (2,9 × 10 ⁻² )

Во-первых, я разберусь со степенями десяти:

(1,247 × 10 ⁻³ ) ÷ (2,9 × 10 ⁻² )
= (1,247 ÷ 2,9) (10 ⁻³ ÷ 10 ⁻² )
= (1,247 ÷ 2,9) (10 ⁻³ × 10 ² )
= (1,247 ÷ 2,9) (10 ⁻¹ )

Теперь займусь делением:

1,247 ÷ 2,9 = 0,43 = 4,3 × 10 ⁻¹

Сложив все вместе, я получаю:

(1,247 × 10 ⁻³ ) ÷ (2,9 × 10 ^{− 2} )
= (1,247 ÷ 2,9) (10 ⁻¹ )
= (4,3 × 10−1) (10 ⁻¹ )
= (4.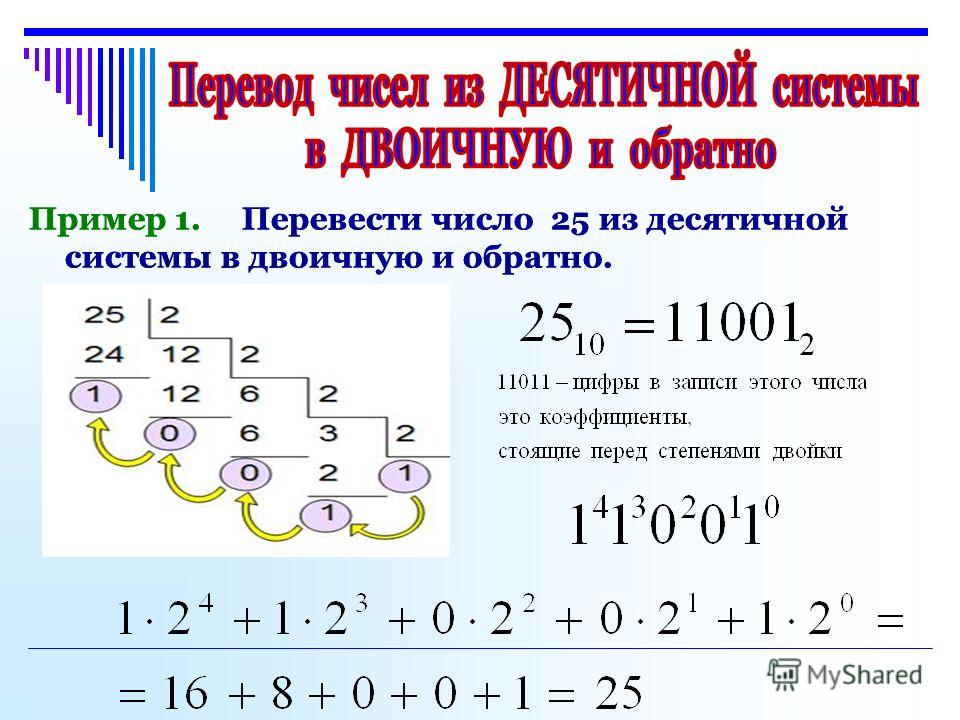 3) (10 ⁻¹ ) (10 ⁻¹ )
= (4.3) (10 ⁻² )
= 4,3 × 10 ⁻²

Таким образом, ответ: (1,247 × 10 ⁻³ ) ÷ (2,9 × 10 ⁻² ) = 4,3 × 10 ⁻²

---

, если вам нужно решать проблемы, помните, что вы всегда можете проверить свои ответы в калькуляторе. Например, если ввести «1,247 EE −3 ÷ 2,9 EE –2» на моем калькуляторе, получится «0,043», что равно 4,3 × 10  ^-2  в экспоненциальном представлении.

Если вам приходится решать много таких задач, может оказаться полезным настроить калькулятор на отображение всех значений в экспоненциальном представлении. Инструкции см. в руководстве пользователя.

---

URL: https://www.purplemath.com/modules/exponent3.htm

Стр. 1 Стр. 2 Стр. 4 Стр. 0033 Определение десятичных и экспоненциальных представлений

Преобразование экспоненциального представления в десятичное представление

Преобразование десятичной записи в экспоненциальную

Определение научного представления

Помните работу с разрядным значением для целых чисел и десятичных дробей? Наша система счисления основана на степенях [латекс]10[/латекс]. {-3}\hfill \end{array}[/latex]

Когда число записывается как произведение двух чисел, где первый множитель представляет собой число больше или равное единице, но меньше [латекс]10[/латекс], а второй множитель представляет собой степень [латекс] 10[/latex], записанный в экспоненциальной форме, говорят, что это научных обозначений.

Прежде чем мы сможем преобразовать экспоненциальную и десятичную систему счисления, нам нужно знать разницу между ними. S научная нотация используется учеными, математиками и инженерами при работе с очень большими или очень маленькими числами. Используя экспоненциальную запись, большие и маленькие числа можно записать так, чтобы их было легче читать.

Когда число записывается в экспоненциальном представлении, показатель степени говорит вам, является ли член большим или маленьким числом. Положительный показатель степени указывает на большое число, а отрицательный показатель указывает на малое число, которое находится между [латекс]0[/латекс] и [латекс]1[/латекс]. Трудно понять, насколько велики миллиард или триллион. Вот способ, который поможет вам подумать об этом.

9{n}[/latex], где коэффициент a  равен [latex]1\leq{a}<10[/latex], а n  – целое число.

В научных обозначениях принято использовать [латекс]\раз [/латекс] в качестве знака умножения, хотя мы избегаем использования этого знака в других местах алгебры.

Посмотрите на числа ниже. Какое из чисел записывается в экспоненциальном представлении?

Ворд	Сколько тысяч	Номер

Номер

Научное обозначение?

{3}[/латекс]

нет

10 не < 10

Преобразование из десятичной записи в экспоненциальную

Теперь давайте сравним некоторые числа, выраженные как в экспоненциальной, так и в стандартной десятичной системе счисления, чтобы понять, как преобразовать из одной формы в другую. Взгляните на таблицы ниже.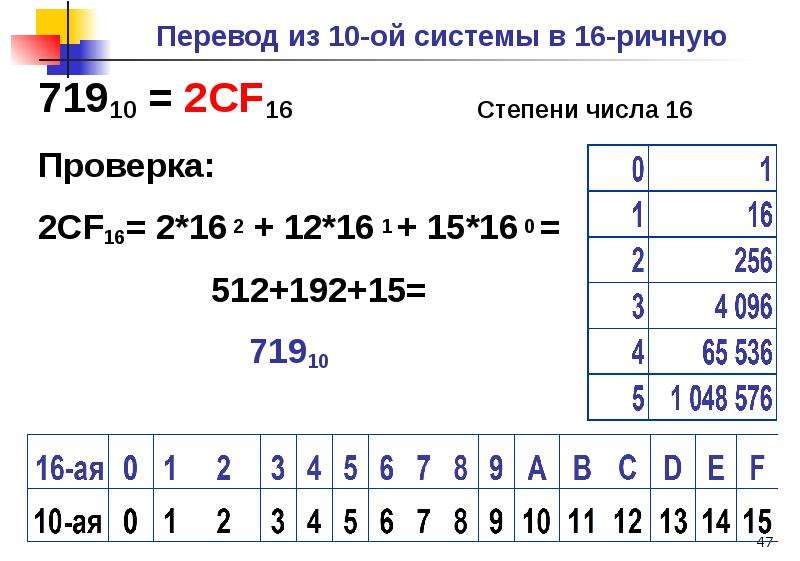 Обратите особое внимание на показатель степени в экспоненциальном представлении и положение десятичной точки в десятичном представлении.

9{-10}[/латекс]

Если мы посмотрим, что происходит с десятичной точкой, мы увидим метод простого преобразования десятичной записи в экспоненциальную.

В обоих случаях десятичная дробь была перемещена [latex]3[/latex] разряда, чтобы получить первый множитель, [latex]4[/latex], сам по себе.

Чтобы записать большое число в экспоненциальном представлении, переместите десятичную точку влево, чтобы получить число между [латекс]1[/латекс] и [латекс]10[/латекс]. Поскольку перемещение десятичной точки изменяет значение, вам нужно умножить десятичную дробь на степень [latex]10[/latex], чтобы выражение имело то же значение. 9{5}\end{array}[/latex]

Обратите внимание, что десятичная точка была перемещена на [latex]5[/latex] позиций влево, а показатель степени равен [latex]5[/latex].

В примерах, показанных ниже, мы будем следовать этой общей стратегии преобразования десятичных чисел в экспоненциальное представление:

Преобразование десятичного представления в экспоненциальное представление

1. Переместите десятичную точку так, чтобы первый множитель был больше или равен [латекс]1[/латекс], но меньше [латекс]10[/латекс]. 9{-n}[/латекс].
2. Чек.

В приведенных ниже примерах мы преобразовываем большие десятичные значения в экспоненциальное представление.

пример

Напишите [латекс]37,000[/латекс] в экспоненциальном представлении.

Решение

Шаг 1 : Переместите десятичную точку так, чтобы первый множитель был больше или равен [латекс]1[/латекс], но меньше [латекс]10[/латекс].
{4}[/латекс]

Пример

Запишите следующие числа в экспоненциальном представлении.

1. [латекс]920 000 000[/латекс]
2. [латекс]10 200 000[/латекс]
3. [латекс]100 000 000 000[/латекс]

Показать решение

попробуйте

 

Теперь давайте рассмотрим преобразование очень маленького десятичного числа в экспоненциальное представление. Чтобы записать небольшое число (от [latex]0[/latex] до [latex]1[/latex]) в экспоненциальном представлении, вы перемещаете десятичную дробь до 9.{-5}\end{array}[/latex]

Вы можете заметить, что десятичная точка была перемещена на пять знаков вправо , пока вы не дошли до числа 4, которое находится между [latex]1[/latex] и [латекс]10 [/латекс]. Показатель степени равен [латекс]−5[/латекс].

пример

Запишите в экспоненциальном представлении: [латекс]0,0052[/латекс]

Показать решение

Пример

Запишите следующие числа в экспоненциальном представлении.

1. [латекс]0,0000000000035[/латекс]
2. [латекс]0.0000000102[/латекс]
3. [латекс]0. 000000000000000793[/латекс]

Показать решение

попробуй

В следующем видео представлены примеры преобразования больших и малых чисел из десятичной записи в экспоненциальную.

Преобразование из экспоненциального представления в десятичное

Как преобразовать экспоненциальное представление в десятичное? Давайте посмотрим на два числа, записанные в экспоненциальном представлении, и посмотрим. 9{-4}\hfill \\ 9,12\times 10,000\hfill & & & 9,12\times 0,0001\hfill \\ 91,200\hfill & & & 0,000912\hfill \end{array}[/latex]

Если мы посмотрим на расположение десятичной точки, мы можем увидеть простой способ преобразования числа из экспоненциального представления в десятичную форму.

В обоих случаях десятичная точка переместилась на 4 разряда. Когда показатель степени был положительным, десятичная дробь сдвигалась вправо. Когда показатель степени был отрицательным, десятичная точка перемещалась влево. 9{-8}=\underset{\longleftarrow}{0.00000005.}=0.00000005\end{массив}[/latex]

Для каждой степени f[latex]10[/latex] вы перемещаете десятичную точку на одно место. Будьте осторожны и не увлекайтесь нулями — количество нулей после запятой всегда будет [latex]1[/latex] меньше, чем показатель степени на , потому что он занимает одну степень [latex]10[ /latex], чтобы сдвинуть первое число слева от десятичной дроби.

Практикуя преобразование экспоненциальной системы счисления в десятичную форму, мы будем выполнять следующие шаги:

Преобразовать экспоненциальное представление в десятичную форму

1. Определить показатель степени [латекс]n[/латекс] для множителя [латекс]10[/латекс].
2. Переместите десятичные [латекс]n[/латекс] разрядов, при необходимости добавив нули.
   • Если показатель степени положительный, переместите десятичную точку [latex]n[/latex] знаков вправо.
   • Если показатель степени отрицательный, переместите десятичную точку на [латекс]|n|[/латекс] разрядов влево.
3. Чек.

Начнем с преобразования большого числа в экспоненциальном представлении в десятичную форму. 9{6}[/латекс] Показать решение

 

Подумайте об этом

Чтобы лучше понять взаимосвязь между знаком экспоненты и относительным размером числа, записанного в экспоненциальном представлении, ответьте на следующие вопросы. Вы можете использовать текстовое поле, чтобы написать свои идеи, прежде чем раскрыть решение.

1. Вы пишете число, которое больше, чем [latex]1[/latex] в экспоненциальном представлении. Будет ли ваш показатель положительным или отрицательным?

2. Вы пишете число между [латекс]0[/латекс] и [латекс]1[/латекс] в экспоненциальном представлении. Будет ли ваш показатель положительным или отрицательным?

3. Какую мощность нужно приложить к [латексу]10[/латексу], чтобы получить результат [латекс]1[/латекс]?

Показать решение

 

В следующем видео вы увидите, как преобразовать число, записанное в экспоненциальном представлении, в десятичное представление.