Перевод в градусы в радианы: Онлайн калькулятор: Перевод градусов в радианы

Как перевести градусы в радианы в excel

Как перевести градусы в радианы в excel

В этой статье описаны синтаксис формулы и использование функции РАДИАНЫ в Microsoft Excel.

Описание

Преобразует градусы в радианы.

Синтаксис

Аргументы функции РАДИАНЫ описаны ниже.

Угол Обязательный. Величина угла в градусах, которую требуется преобразовать.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Разберем как перевести градусы в радианы (и наоборот) с помощью стандартных функций Excel, а также узнаем как это можно сделать без применения функций.

В повседневной жизни мы привыкли оперировать градусами, как основной единицей измерения углов.
Однако не всегда градусы удобно использовать в расчетах, к примеру, в математическом анализе при работе с тригонометрическими функциями аргумент по умолчанию считается выраженным в радианах.

Вдобавок в тригонометрических функциях в Excel, таких как SIN (синус), COS (косинус), TAN (тангенс), в качестве аргумента указывается угол в радианной мере, поэтому для корректной работы с данными формулами необходимо предварительно перевести его в радианы.
И наоборот, в обратных тригонометрических функциях в Excel, таких как ASIN (арксинус), ACOS (арккосинус), ATAN (арктангенс), уже возвращаемое значение выражается в радианной мере, поэтому при необходимости результат нужно будет переводить уже в градусы.

Перед тем как перевести угол из градусной меры в радианную вспомним, что радиан — это угол, соответствующий дуге, длина которой равна ее радиусу. Из определения следует, что один полный оборот в 360° составляет 2π радиан, откуда можно получить формулу перевода угла из одной системы измерения в другую:

В Excel есть две стандартные функции, которые позволяют перевести градусы в радианы и наоборот.
Давайте подробно остановимся на особенностях применения каждой из них.

Функция РАДИАНЫ в Excel

Синтаксис и описание:

РАДИАНЫ(угол)
Преобразует градусы в радианы.

• Угол(обязательный аргумент) — угол в градусной мере, преобразуемый в радианы.

В качестве аргумента задаем угол в градусной мере, в результате преобразования получаем радианную:

Функция ГРАДУСЫ в Excel

Синтаксис и описание:

ГРАДУСЫ(угол)
Преобразует радианы в градусы.

• Угол(обязательный аргумент) — угол в радианной мере, преобразуемый в градусы.

Функция по сути аналогична описанной выше, но в данном случае на входе мы задаем радианы, а на выходе получаем градусы:

Альтернативный способ перевода

Перевести угол из градусной меры в радианную можно и без использования стандартных формул перевода углов в Excel.
Действительно, мы уже выяснили, что в развернутом угле (180°) содержится π радиан, поэтому умножая угол выраженный в градусах на коэффициент π/180 (с помощью константы Пи) получим радианную меру угла:

Аналогично умножая на обратный коэффициент 180/π можно сделать перевод из радианной меры в градусную:

Функции Excel для перевода из РАДИАНЫ в ГРАДУСЫ и обратно

Функция РАДИАНЫ (на английском RADIANS) – это одна из математических и тригонометрических функций, которая часто применяется для инженерных расчетов. Данная функция в Excel легко преобразует градусы в радианы – угол, соответствующий дуге, а длина этой дуги равна ее радиусу.

Как работает функция индекс в Excel?

ПРИМЕР 1. Для инженерных расчетов связанных с движением по окружности зачастую необходимо вычислять угловые скорости и переводить градусы в радианы и радианы в градусы. В Excel для этого предусмотрены специальные функции. Для упрощения математических расчетов может потребоваться выразить в одной и второй величине.

Нам необходимо найти сколько будет в Радианах 180°. Нажимаем кнопку fx возле строки формул для вызова окна выбора функций «Вставка функции» (SHIFT+F3) и в окне поиска вводим функцию «РАДИАНЫ». Выбираем высветившуюся нужную функцию, как показано на ниже рисунке.

Появляется окно, в которое нужно ввести аргументы функции. Вводим значение 180, так как нам нужно найти сколько будет радиан в 180 градусах. Жмем ОК.

В 180 градусах будет 3,1415 радиан.

Найдем радианы для угла в 90°. Откроем окно функций и введем функцию, что необходимо вычислить. Находим ее в окне мастера функций и выбираем аргумент 90.

ОК. В 90 градусах будет 1,5707 радиан.

В следующих примерах рассмотрим, как конвертировать эти единицы измерения углов в обоих направлениях.

Как перевести Радианы в Градусы средствами Excel

ПРИМЕР 2. Иногда нужно единицу измерения углов rad перевести в значение gradus° . Для этого предусмотрена функция ГРАДУСЫ. Она позволяет перевести значения выраженные в радианах в градусы в десятичном исчислении.

Нам нужно найти сколько будет в градусах 4,1 радианы. Нажимаем кнопку fx для вызова окна выбора функции и в окне поиска вводим соответствующее название функции.

Появляется окно в которое нужно ввести аргументы функции. Вводим значение 4,1, так как нам следует найти сколько будет gradus° в 4,1 rad . Нажимаем ОК.

Для исходного значения 4,1 получаем ровно 235 градусов.

Таким образом выполняется перевод из радиан в градусы в Excel.

Сколько радиан в нескольких значениях градуса?

ПРИМЕР 3. Иногда нужно определить сколько радиан в сразу нескольких значениях градуса и вводить тогда каждый раз аргумент очень долго. В таком случае можно воспользоваться немного иным способом конвертирования величин для измерения углов.

Требуется найти сколько будет в Радианах 45, 67, 23, 12, 57 градусов. Нажимаем кнопку fx (SHIFT+F3) для вызова окна выбора функции и в окне поиска вводим необходимо функцию как показано ниже на рисунке.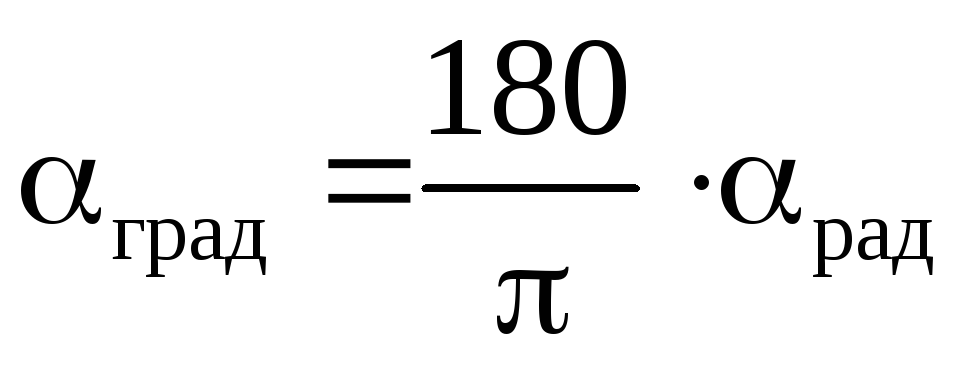 Указываем на высветившуюся функцию.

Выбираем диапазон градусов (А3 по А7) и нажимаем на кнопку ОК.

Протягиваем строку вниз для того, чтобы мы могли узнать сколько радиан во всех приведенных градусах, не вызывая функцию по несколько раз.

Получаем сразу значения всех радиан:

Для 45 градусов – это 0,7853, для 67 градусов – это 1,1693, для 23 градусов – это 0,4014, для 12 градусов – это 0,2094, для 57 градусов – это 0,9948 в радианах.

Преобразование градусов в радианы с помощью Numpy в Python

Арулиус Савио / 28 ноября 2022 г. 28 января 2023 г.

Геометрия — увлекательный предмет для занятий. Все эти формы и фигуры обладают таинственной для невооруженного глаза основой, которую, однако, можно разгадать с помощью математики. Не зря его называют Королевой всех наук . В этой статье речь пойдет об одном таком свойстве, связанном с геометрией, — углах!

Как и любой показатель, угол также может быть измерен с помощью определенной единицы измерения. Воспоминание о старых добрых школьных днях поможет нам вспомнить время, когда мы использовали транспортир для рисования угловых фигур и что было выгравировано на транспортире, чтобы помочь нам нарисовать угол. Да, это градусов !

Точно так же, как мили в километрах, градусы также имеют синонимичный показатель, который можно использовать для измерения угла —

Различные способы преобразования градусов в радианы с помощью Numpy

Теперь, когда у нас есть обзор того, что есть что, давайте сразу перейдем к программной части. Мы начнем с импорта библиотеки NumPy в Python, используя следующий код.

 импортировать numpy как np
 

Ниже приведены различные методы, которые можно использовать для преобразования градусов в радианы с помощью Python.

• с использованием numpy.radians ()
• с использованием numpy.deg2rad ()
• с использованием Pi (π)

 np.радиан(180)
 

Из приведенного выше видно, что возвращаемое значение 3,141592… равно пи (π), поскольку 180 градусов — это то же самое, что пи радиан.

Хотя можно также преобразовать отдельный объект с помощью функции deg2rad() из библиотеки numpy , то же самое можно сделать и для массива. Итак, мы продемонстрируем преобразование массива значений градусов в радианы, используя deg2rad() функция. Это верно и для описанной выше техники, и процедура такая же, как описана ниже.

 ar1 = [[10, 50, 120],
       [150, 180, 266]]
np.deg2rad(ar1)
 

В этом методе используется базовый принцип, на основе которого радианы преобразуются из градусов; та самая математическая основа, которую использует все программное обеспечение, включая Python. Некоторые вещи лучше показать, чем рассказать, так что вот она, формула перевода градусов в радианы.

В предыдущем методе было указано, что π равно 180 градусам в радианах. Таким образом, любой угол нужно умножить на π, а затем разделить на 180 градусов, чтобы получить его эквивалент в радианах.

Хорошо, что мы сделаем то же самое и в Python! Но нам нужно импортировать другую библиотеку, чтобы получить точное значение pi, , а не использовать приближение 3,14. Мы будем использовать следующий код для импорта math 9Библиотека 0006 на Python.

 импорт математики
из математического импорта пи
 

 усл = пи/180
 

Затем мы можем использовать функцию multiple() из библиотеки numpy для преобразования, как показано ниже. Заключение0005 библиотека numpy в Python. Вот еще одна статья, в которой подробно рассказывается, как разделить объекты с помощью numpy в Python. В AskPython есть множество других интересных и не менее информативных статей, которые могут быть очень полезны тем, кто хочет повысить свой уровень в Python. Пока вы наслаждаетесь этим, адиос !

Математическая задача: Градусы в радианы

Преобразование величины угла α = 502°47’25» в радианы:

Правильный ответ:

Пошаговое объяснение:

α=180π​(502+6047​+360025​)=8,78 рад

Нашли ошибку или неточность? Не стесняйтесь

. Спасибо!

Советы по использованию соответствующих онлайн-калькуляторов

Попробуйте перевести единицы измерения угла в градусы, минуты, секунды, радианы, грады.

Для решения этой задачи по математике вам необходимо знать следующие знания:

Единицы физических величин:

• Совместное преобразование
• Угол

Стал слов Проблема:

• Практика для 12 -летнего возраста
• Практика для 13 -летнего возраста
• ARC
  CONVER TO ARC DORDS): 919
  • ARC
    CONVERT ARC. запишите как кратное π
  • Радиан
    Преобразуйте 324° в радианы. Запишите результат как кратное числу π.
  • В треугольнике
    В треугольнике ABC величина внутреннего угла гамма равна одной трети угла альфа. Размер угла бета на 80 градусов больше размера угла гамма. Вычислите величины внутренних углов треугольника ABC.
  • Одна четверть 13953
    Вычислите величину внутренних углов треугольника ABC, если альфа = две пятых бета и альфа = одна четверть гамма.
  • Вычислить 8059
    Вычислить величину третьего внутреннего угла в треугольнике ABC при альфа = 30°, бета = 60°
  • Остаток 25441
    Равнобедренный треугольник имеет величину углов при основании альфа = бета = 34 градуса 34 минут. Вычислите величину угла при оставшейся вершине треугольника в градусах и минутах.
  • Параллелограмм
    Найдите периметр параллелограмма, где основание a = 8 см, высота v = 3 см и угол α = 35° — величина угла при вершине A.
  • Величины 24271
    В треугольнике ABC величина внутреннего угла бета составляет одну треть величины угла альфа и на 20° больше величины угла гамма. Определить величины внутренних углов этого треугольника.
  • Дуга окружности
    Рассчитайте длину дуги окружности, если диаметр d = 20 см и угол альфа = 142 °
  • Радианы треугольника
    Величина двух внутренних углов треугольника ABC равна α=6/18π и β=7/18π. Вычислить размер третьего угла.
  • Прямоугольный 81150
    В прямоугольном треугольнике ABC (прямой угол при вершине C) отношение углов равно α : β = 5 : 3.

    No related posts.