Квадрат. Формулы и свойства квадрата
Навигация по странице: Определение квадрата Основные свойства квадрата Диагональ квадрата Периметр квадрата Площадь квадрата Окружность описанная вокруг квадрата Окружность вписанная в квадрат
Определение.
Квадрат — это четырехугольник у которого все четыре стороны и углы одинаковы. Квадраты отличаются между собой только длиной стороны, но все четыре угла у них прямые, то есть по 90°.
| Рис.1 | Рис.2 |
Основные свойства квадрата
Квадратом также могут быть параллелограмм, ромб или прямоугольник если они имеют одинаковые длины диагоналей, сторон и одинаковые углы.
1. Все четыре стороны квадрата имеют одинаковую длину, то есть они равны:
AB = BC = CD = AD
2. Противоположные стороны квадрата параллельны:
AB||CD, BC||AD
Все четыре угла квадрата прямые:∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
4. Сумма углов квадрата равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
5. Диагонали квадрата имеют одинаковой длины:
AC = BD
6. Каждая диагональ квадрата делит квадрат на две одинаковые симметричные фигуры
7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам:
| AC┴BD | AO = BO = CO = DO = | d | |
| 2 |
8. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности
9. Каждая диагональ делит угол квадрата пополам, то есть они являются биссектрисами углов квадрата:
ΔABC = ΔADC = ΔBAD = ΔBCD
10.
Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные и прямоугольные:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Диагональ квадрата
Определение.
Диагональю квадрата называется любой отрезок, соединяющий две вершины противоположных углов квадрата.
Диагональ любого квадрата всегда больше его стороны в√2 раз.
Формулы определения длины диагонали квадрата
1. Формула диагонали квадрата через сторону квадрата:
d = a·√2
2. Формула диагонали квадрата через площадь квадрата:
d = √2S
3. Формула диагонали квадрата через периметр квадрата:
| d = | P |
| 2√2 |
4. Формула диагонали квадрата через радиус описанной окружности:
d = 2R
5.
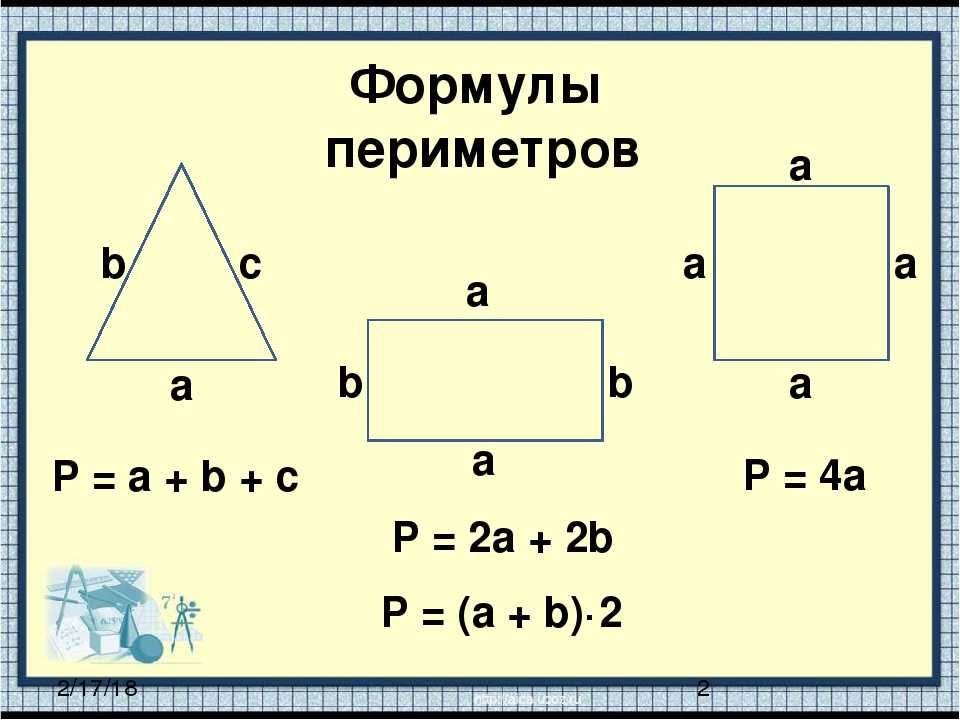Формула диагонали квадрата через диаметр описанной окружности:
d = Dо
6. Формула диагонали квадрата через радиус вписанной окружности:
d = 2r√2
7. Формула диагонали квадрата через диаметр вписанной окружности:
d = Dв√2
8. Формула диагонали квадрата через длину отрезка l:
| d = l | 2√10 |
| 5 |
Периметр квадрата
Определение.
Периметром квадрата называется сумма длин всех сторон квадрата.
Формулы определения длины периметра квадрата
1. Формула периметра квадрата через сторону квадрата:
P = 4a
2. Формула периметра квадрата через площадь квадрата:
P = 4√S
3. Формула периметра квадрата через диагональ квадрата:
P = 2d√2
4.
Формула периметра квадрата через радиус описанной окружности:
P = 4R√2
5. Формула периметра квадрата через диаметр описанной окружности:
P = 2Dо√2
6. Формула периметра квадрата через радиус вписанной окружности:
P = 8r
7. Формула периметра квадрата через диаметр вписанной окружности:
P = 4Dв
8. Формула периметра квадрата через длину отрезка l:
| P = l | 8 |
| √5 |
Площадь квадрата
Определение.
Площадью квадрата называется пространство, ограниченное сторонами квадрата, то есть в пределах периметра квадрата.
Площадь квадрата больше площади любого четырехугольника с таким же периметром.
Формулы определения площади квадрата
1. Формула площади квадрата через сторону квадрата:
S = a2
2.
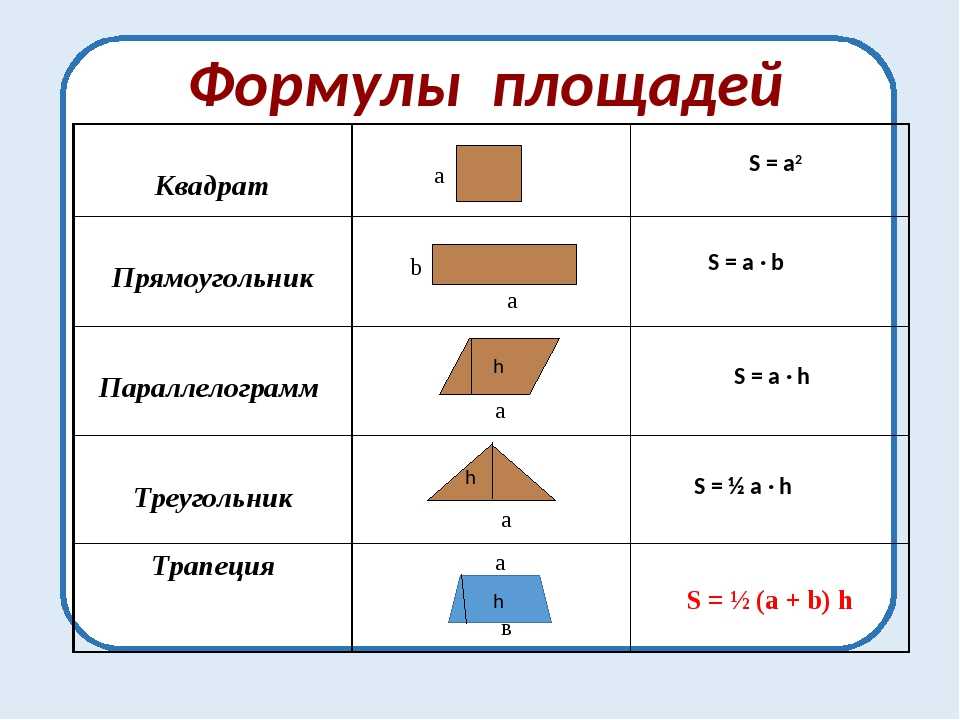Формула площади квадрата через периметр квадрата:
| S = | P2 |
| 16 |
3. Формула площади квадрата через диагональ квадрата:
| S = | d2 |
| 2 |
4. Формула площади квадрата через радиус описанной окружности:
S = 2R2
5. Формула площади квадрата через диаметр описанной окружности:
| S = | Do2 |
| 2 |
6. Формула площади квадрата через радиус вписанной окружности:
S = 4r2
7. Формула площади квадрата через диаметр вписанной окружности:
S = Dв2
8. Формула площади квадрата через длину отрезка l:
| S = l 2 | 16 |
| √5 |
Окружность описанная вокруг квадрата
Определение.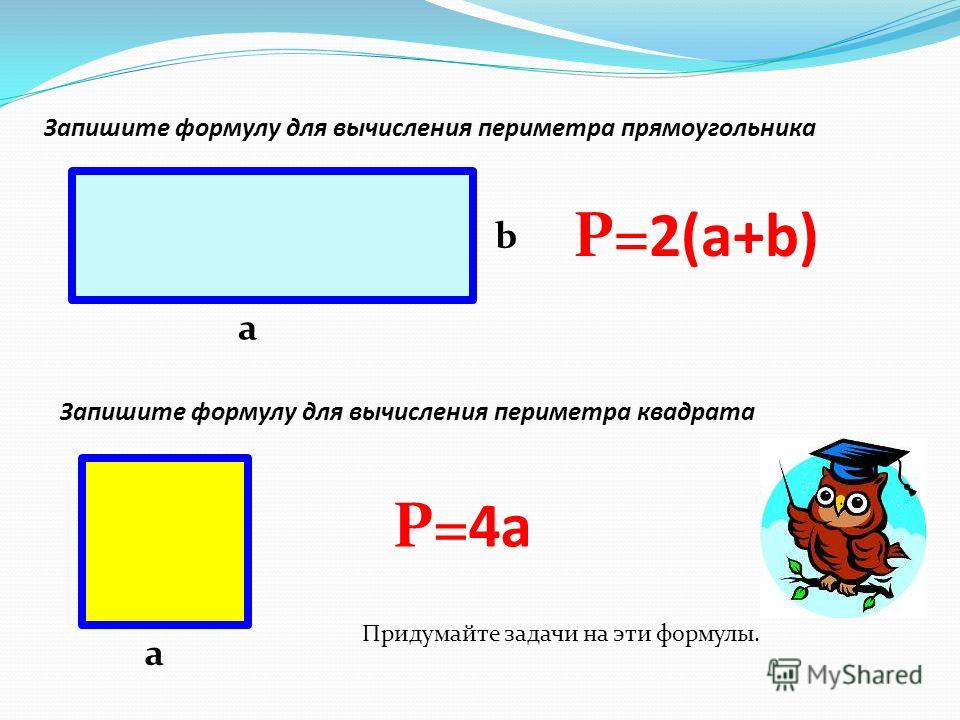
Кругом описанным вокруг квадрата называется круг проходящий через четыре вершины квадрата и имеющий центр на пересечении диагоналей квадрата.
Радиус окружности описанной вокруг квадрата всегда больше радиуса вписанной окружности в√2 раз.
Радиус окружности описанной вокруг квадрата равен половине диагонали.
Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.
Формулы определения радиуса окружности описанной вокруг квадрата
1. Формула радиуса окружности описанной вокруг квадрата через сторону квадрата:
| R = a | √2 |
| 2 |
2. Формула радиуса окружности описанной вокруг квадрата через периметр квадрата:
| R = | P |
| 4√2 |
3. Формула радиуса окружности описанной вокруг квадрата через площадь квадрата:
| R = | √2S |
| 2 |
4.
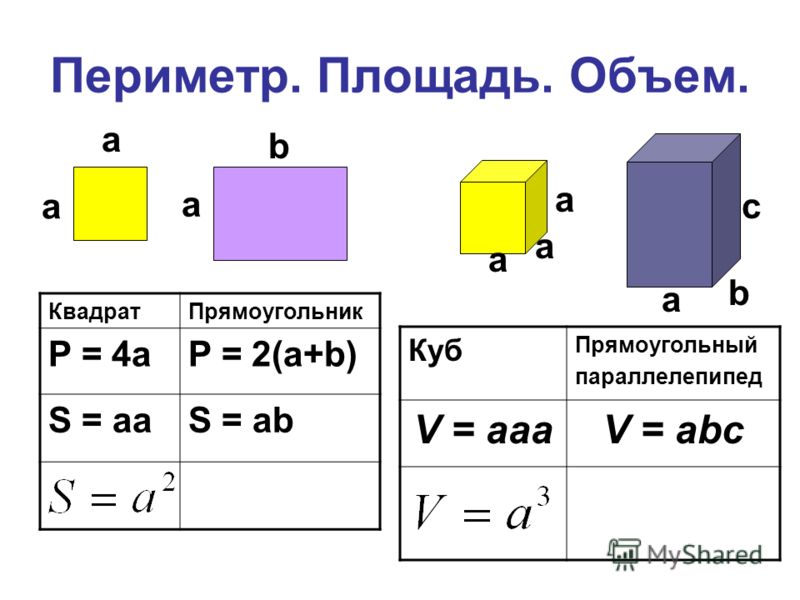Формула радиуса круга описанного вокруг квадрата через диагональ квадрата:
| R = | d |
| 2 |
5. Формула радиуса круга описанного вокруг квадрата через диаметр описанной окружности:
| R = | Dо |
| 2 |
6. Формула радиуса круга описанного вокруг квадрата через радиус вписанной окружности:
R = r √2
7. Формула радиуса круга описанного вокруг квадрата через диаметр вписанной окружности:
| R = Dв | √2 |
| 2 |
8. формула радиуса круга описанного вокруг квадрата через длину отрезка l:
| R = l | √10 |
| 5 |
Окружность вписанная в квадрата
Определение.
Кругом вписанным в квадрат называется круг, который примыкает к серединам сторон квадрата и имеет центр на пересечении диагоналей квадрата.
Радиус вписанной окружности равен половине стороны квадрата.
Площадь круга вписанного в квадрат меньше площади квадрата в π/4 раза.
Формулы определения радиуса круга вписанного в квадрат
1. Формула радиуса круга вписанного в квадрат через сторону квадрата:
| r = | a |
| 2 |
2. Формула радиуса круга вписанного в квадрат через диагональ квадрата:
| r = | d |
| 2√2 |
3. Формула радиуса круга вписанного в квадрат через периметр квадрата:
| r = | P |
| 8 |
4. Формула радиуса круга вписанного в квадрат через площадь квадрата:
| r = | √S |
| 2 |
5. Формула радиуса круга вписанного в квадрат через радиус описанной окружности:
| r = | R |
| √2 |
6.
Формула радиуса круга вписанного в квадрат через диаметр, описанной окружности:
| r = | Dо |
| 2√2 |
7 Формула радиуса круга вписанного в квадрат через диаметр вписанной окружности:
| r = | Dв |
| 2 |
8. Формула радиуса круга вписанного в квадрат через длину отрезка l:
| r = | l |
| √5 |
Формулы по геометрии Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции — Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции — Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Формулы площади геометрических фигур Формулы периметра геометрических фигур Формулы объема геометрических фигур Формулы площади поверхности геометрических фигур
Все таблицы и формулы
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
как найти, формула, через диагональ
Содержание:
- Квадрат
-
Нахождение площади квадрата
- Через длину стороны
- Через диагональ
- Через радиус вписанной окружности
- Через радиус описанной окружности
- Через периметр
Содержание
- Квадрат
-
Нахождение площади квадрата
- Через длину стороны
- Через диагональ
- Через радиус вписанной окружности
- Через радиус описанной окружности
- Через периметр
Квадрат
Определение
Квадрат — геометрическая фигура, являющаяся правильным четырехугольником.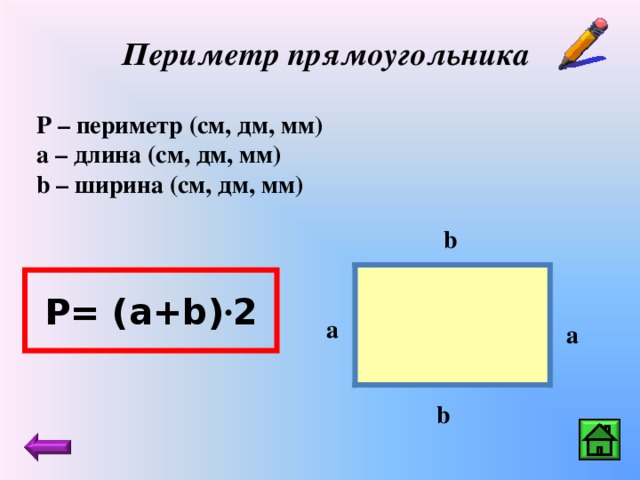
2}{16}\)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Как найти площадь квадрата?
Площадь квадрата можно определить по тому, сколько пространства занимает внутри него квадрат. Проще говоря, пространство, находящееся в пределах границы квадрата, известно как площадь квадрата. В этой статье вы узнаете основные параметры квадрата. Кроме того, вы узнаете, как найти площадь квадрата, площадь формулы квадрата и площадь поверхности квадратной пирамиды.
Все ли мы знаем, что такое квадрат? Квадрат – это замкнутый четырехугольник. Четырехугольники – это фигуры, имеющие 4 стороны. Таким образом, квадрат — это четырехсторонняя фигура, у которой все четыре стороны равны. Если одна сторона квадрата равна 10 см, то и другие стороны равны 10 см.
Давайте сначала изучим некоторые математические термины и понятия, связанные с квадратом:
- У квадрата все стороны равны. Отсюда следует, что противолежащая и прилежащая стороны квадрата равны друг другу.
- Противоположные стороны квадрата параллельны, что делает его параллелограммом.
- Смежные стороны квадрата перпендикулярны друг другу. Это означает, что любые две смежные стороны имеют между собой угол 90 градусов.
- Квадрат разделен на два равных прямоугольных треугольника.
- Квадрат — это частный случай прямоугольника.
- Периметр квадрата: Расстояние, пройденное границами квадрата, называется периметром квадрата. Он сформулирован как:
Периметр (квадрат) = s + s + s + s = 4 x s = 4s {где s — сторона квадрата}
В нашей повседневной жизни мы можем встретить квадраты повсюду. От наших домов до наших школ квадраты присутствуют на каждом углу. Плитка на вашей кухне квадратная. Шахматная доска представляет собой квадрат, состоящий из 64 черных и белых меньших квадратов.
Самый простой пример — кубик Рубрика. Каждая поверхность кубика Рубика квадратная.
Другие измерения, такие как диагональ и периметр квадрата, также могут использоваться для вычисления площади квадрата. В этой статье мы попытаемся узнать больше о площади квадрата.
Площадь квадрата
Площадь квадрата определяется как количество квадратных единиц, необходимых для заполнения этой формы. Другими словами, при вычислении площади квадрата мы учитываем длину его стороны. Поскольку все стороны фигуры равны, ее площадь равна произведению двух сторон. Наиболее распространенными единицами измерения площади квадрата являются квадратные метры, квадратные футы, квадратные дюймы и квадратные сантиметры.
Площадь квадрата также можно вычислить, используя другие измерения, такие как диагональ и периметр квадрата. На этой странице мы попытаемся узнать больше о площади квадрата.
Какова площадь квадрата?
Квадрат — это двумерная замкнутая фигура, имеющая четыре равные стороны и четыре равных угла.
Четыре угла при вершинах образованы четырьмя сторонами квадрата. Периметр квадрата — это сумма длин его сторон, а площадь квадрата — это площадь, занимаемая фигурой. Он обладает следующими свойствами четырехугольника.
Две стороны параллельны.
- Все четыре стороны одинаковые.
- Все углы 90 o .
Квадраты можно найти повсюду. Вот несколько примеров часто встречающихся объектов квадратной формы. Квадрат представлен шахматной доской, часами, доской и плиткой.
Иллюстрация: Рассмотрим квадрат длины 4 единицы. Теперь рассмотрим меньшие квадраты длиной 1 единица каждый. Как мы видим на рисунке ниже, 4 квадрата по 1 единице заполняют первый ряд большего квадрата. Аналогично по 4 квадрата 1 единицы заполняют второй, третий и четвертый ряд. Теперь большой квадрат заполнен. Если мы посчитаем количество меньших квадратов, то получим, что 16 квадратов из 1 единицы заполняют квадрат из 4 единиц.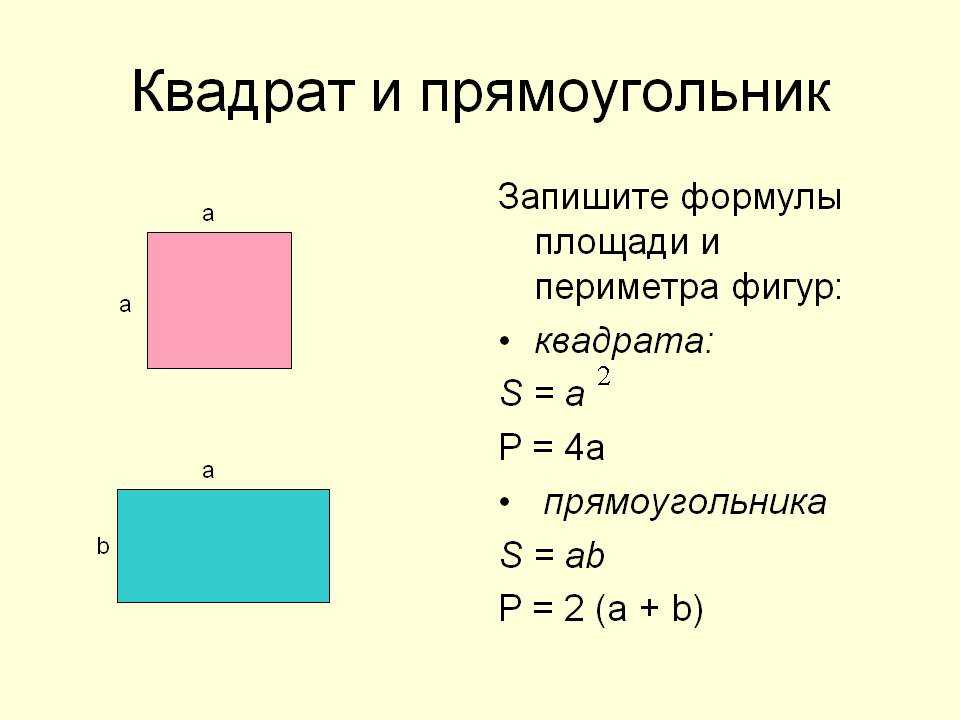
Следовательно, 16 единиц — это площадь квадрата.
Из этого мы можем сделать вывод, что площадь квадрата равна произведению двух его сторон. Как мы знаем, 16 = 4 х 4, а 4 единицы составляют одну сторону квадрата. В следующем разделе мы изучим и выведем формулу площади квадрата.
Формула площади квадрата
Из приведенного выше рисунка мы узнаем, что площадь квадрата равна произведению сторон. Это можно записать как «сторона х сторона». Следовательно, формула для любого квадрата с любой длиной стороны задается как
Площадь = (Сторона) 2
Давайте рассмотрим пример, чтобы понять эту формулу:
Пример: Найдите площадь квадрата со стороной 13 см.
Решение: Учитывая длину стороны = 13 см
Площадь квадрата = (Сторона) 2 = (13) 2 = 169 см 4 ,
4
Площадь квадрата всегда выражается в квадратных единицах (квадратный сантиметр, квадратный метр, квадратный дюйм и т.
д.)
Что если нам даны не стороны квадрата, а длина диагонали? Как найти площадь квадрата в этом случае?
Не волнуйтесь! Площадь квадрата можно вычислить, даже если известна длина диагонали. Вы можете найти площадь, используя формулу, написанную ниже:
Площадь квадрата (с использованием диагоналей) = (D) 2 /2, где D представляет собой длину диагонали.
Примечание: Помните, что диагонали квадрата равны, поэтому площадь остается неизменной, если дана любая из диагоналей.
Пример: Найдите площадь квадрата, если длина диагонали равна 13 см.
Решение: Нас дается, диагональ = 13 см
Площадь квадрата = D 2 /2
= (13) 2 /2
= 169/2 см 2
6 = 169/2 см
266 = 169/2 см
26. Как найти площадь квадрата
До сих пор мы выучили 2 формулы, связанные с нахождением площади квадрата.
Давайте узнаем, как вы будете подходить к вопросам, связанным с площадью любого квадрата.
- Если указана чья-либо сторона:
- Шаг 1: Запишите значение стороны, например «а».
- Шаг 2: Подставьте значение an в формулу -> Площадь (со стороной) = (Сторона) 2 = (a) 2
- Шаг 3: Запишите ответ в квадратных единицах.
Пример: Найдите площадь пластика, необходимую для покрытия квадратного стола длиной 8 м.
Решение: Учитывая, что длина стола = 8 м
Следовательно, площадь пластика, необходимая для покрытия стола, = площади стола.
Площадь стола = (сторона) 2 = 8 2 = 64 м
- Шаг 1: Запишите значение длины диагонали, например «d».
- Шаг 2: Подставляем значение d в формулу -> Площадь (с диагональю) = (d) 2 /2 =
- Шаг 3: Запишите результат в квадратных единицах.
Пример: Найдите площадь квадрата с диагональю 4 см
Решение: Учитывая, что длина диагонали = 4 см 16/2 = 8 см 2
Найти площадь квадрата, зная периметр квадрата
В предыдущих разделах мы научились вычислять площадь квадрата, зная сторону или диагональ. Но, предположим, вам не предоставлен ни один из этих параметров, но задан периметр квадрата. Как найти площадь, если известен периметр квадрата? Давайте узнаем:
- Шаг 1: Запишите периметр данного квадрата.
- Шаг 2: Мы знаем, что периметр квадрата равен 4 с. Следовательно, 4s = периметр.
- Шаг 3: Подставьте значение периметра и найдите сторону по формуле s = Периметр/4
- Шаг 4: Теперь мы знаем сторону квадрата. Найдите площадь, используя s2.
- Шаг 5: Запишите ответ в квадратных единицах.
Пример: Квадратный сад имеет периметр 64 см.
Макс хочет посадить цветы и найти площадь этого сада, но не знает, как это сделать? Помогите ему определить площадь сада.
Решение: Мы знаем: Периметр сада = 64 см
Сначала вычислим длину сторон сада.
Используя формулу шага 3
Сторона (s) = периметр/4
= 64/4
= 16 см
Теперь,
Площадь сада = (s) 2
= 16 2
= 256 см 2
Некоторые советы с нашей стороны:
Примите к сведению следующие факторы к сохранению к сохранению факторов к «hore» иметь в виду, когда вы вычисляете площадь квадрата.
При вычислении площади квадрата мы часто ошибаемся, удваивая число. Это не тот случай! Имейте в виду, что площадь квадрата не равна удвоенной стороне. Это всегда либо «сторона х сторона», либо сторона 2 .
Мы должны не забыть указать единицу измерения площади при ее представлении. Площадь квадрата всегда двумерна; следовательно, мы используем квадратные единицы.
Например см 2 , м 2 , дюйм 2 и т. д.
Часто задаваемые вопросы
1. Что такое площадь квадрата в геометрии?
Ответ. Площадь квадрата в геометрии — это измерение поверхности. Он рассчитывается путем умножения длины на ширину.
2. Что такое формула площади квадрата?
Ответ. Формула площади квадрата — это способ вычисления площади квадрата. Формула площади квадрата: A = s2, где s представляет собой длину каждой стороны квадрата.
3. Как вычислить площадь квадрата?
Ответ. Чтобы вычислить площадь квадрата, нужно умножить длину одной стороны на саму себя. Итак, если у вас есть квадрат со сторонами по 10 сантиметров, вы должны сделать: 10 * 10 = 100.
4. Каковы единицы измерения площади квадрата?
Ответ. Единицы измерения площади квадрата – это квадраты. Наиболее распространенной единицей измерения площади являются квадратные метры, но иногда вы также можете встретить квадратные футы или акры.
5. Что такое периметр и площадь квадратных формул?
Ответ. Формула для периметра квадрата: p = 4s
Формула площади квадрата: A = s2
Площадь квадрата: формула и примеры
Квадрат – это фигура с четырьмя равными сторонами. (равносторонний) и четыре равных угла (равноугольный). Это единственный равносторонний и равноугольный четырехугольник. Вот краткое руководство по вычислению площадь квадрата .
Как вычислить площадь квадратаПлощадь фигуры относится к общему количеству заключенного в ней пространства. Чтобы найти площадь квадрата , умножьте Основание на Высоту, как указано в формуле A=BH; однако, так как квадрат имеет равные стороны, мы можем записать формулу как:
A = s • s
где: s = длина одной стороны квадрата
Пример . Найдите площадь ш курица длина 12см .
a = S • S
Let S BE 12 см
A = 12 см • 12 см
A = 144 см 2
. Появление. квадрат.
Хотите узнать больше о нахождении периметра квадрата?
Связанные материалы: Периметр квадрата – формула и примеры
Пример 1. Вычисление
площадь квадрата с а длина из 11 дюймов .Решение для примера № 1:
Замените 11 дюймов на s в формуле площади: A = s • s 4 .
A = 11 в • 11 В
A = 121 в 2
Следовательно, Область — 121 в 2 4495.
Пример 2. Найдите
площадь с курицей длина из 5,5 метра .Решение для примера № 2:
Подставьте 5,5 метра вместо s в формуле периметра: A = s
s
A = 5,5 м • 5,5 M
A = 30,25 M 2
Следовательно, область — 30,25 M 2 445.