| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Как найти периметр призмы
Обновлено 22 декабря 2020 г.
Эллиот Уолш
Вы можете видеть призмы как на уроках математики, так и в повседневной жизни. Кирпич представляет собой прямоугольную призму. Пакет апельсинового сока является своего рода призмой. Коробка для салфеток представляет собой прямоугольную призму. Амбары представляют собой разновидность пятиугольной призмы. Пятиугольник представляет собой пятиугольную призму. Аквариум представляет собой прямоугольную призму. Этот список можно продолжать и продолжать.
Призмы по определению представляют собой твердые объекты с одинаковыми формами концов, одинаковыми поперечными сечениями и плоскими боковыми гранями (без кривых). И хотя большинство математических задач и реальных примеров, касающихся расчетов призм, связаны с формулой объема или формулой площади поверхности, есть один расчет, который вам нужно сначала понять, прежде чем вы сможете это сделать:0009 периметр призмы .
Что такое призма?
Общее определение призмы – это трехмерная объемная форма, которая имеет следующие характеристики:
- Это многогранник (что означает, что это объемная фигура).
- Поперечное сечение объекта одинаково по всей длине объекта.
- Это параллелограмм (4-сторонняя фигура, в которой противоположные стороны параллельны друг другу).
- Грани объекта плоские (без изогнутых граней).
- Две концевые формы идентичны .
Название призмы происходит от формы двух концов, которые известны как основания. Это может быть любая форма (кроме кривых или кругов). Например, призма с треугольными основаниями называется треугольной призмой. Призму с прямоугольным основанием называют прямоугольной призмой. Этот список можно продолжить.
Глядя на характеристики призм, мы исключаем сферы, цилиндры и конусы из числа призм, потому что они имеют криволинейные грани. Это также исключает пирамиды, потому что они не имеют одинаковой формы основания или одинакового поперечного сечения.
Периметр призмы
Говоря о периметре призмы, вы фактически имеете в виду периметр базовой формы.
Периметр основания призмы равен периметру любого поперечного сечения призмы, так как все сечения одинаковы по длине призмы.
Периметр измеряет сумму длин любого многоугольника. Таким образом, для каждого типа призмы вы найдете сумму длин любой формы, являющейся основанием, и это будет периметр призмы.
Формула для нахождения периметра треугольной призмы, например, будет представлять собой сумму трех длин треугольника, образующего основание, или:
\text{Периметр треугольника } = a + b + c
где a , b и c три длины треугольника.
Это будет периметр прямоугольной призмы по формуле:
\text{ Периметр прямоугольника } = 2l + 2w
где l длина прямоугольника и w — ширина.
Примените стандартные расчеты периметра к базовой форме призмы, и вы получите периметр.
Зачем нужно вычислять периметр призмы?
Нахождение периметра призмы не кажется слишком сложным, если вы понимаете, о чем вас спрашивают.
Однако периметр является важным расчетом, который учитывает формулы площади поверхности и объема для некоторых призм.
Например, вот формула для нахождения площади поверхности прямой призмы (прямоугольная призма имеет одинаковые основания и стороны):
\text{Площадь поверхности } = 2b + ph
где b равно площади основания, p равно периметру основания и h равно высоте основания призма. Вы можете видеть, что периметр необходим для нахождения площади поверхности.
Пример задачи: Периметр прямоугольной призмы
Допустим, вам дали задачу с прямоугольной призмой и вас попросили найти периметр. Вам даны следующие значения:
Длина = 75 см
Ширина = 10 см
Высота = 5 см
Чтобы найти периметр, используйте формулу для нахождения периметра прямоугольной призмы, так как имя говорит вам, что основание является прямоугольником:
\ begin{align} \text{Периметр } &= 2l + 2w \\ &= 2(75\text{см}) + 2(10\text{см} ) \\ &= 150\text{см} + 20\ text{ см} \\ &= 170 \text{ см} \end{aligned}
Затем вы можете перейти к нахождению площади поверхности, потому что вам дана высота, периметр основания и известно, что эта призма 92 \end{align}
Калькулятор периметра — Как найти периметр различных форм
Онлайн-калькулятор периметра поможет вам определить периметр для нескольких геометрических фигур с разными параметрами.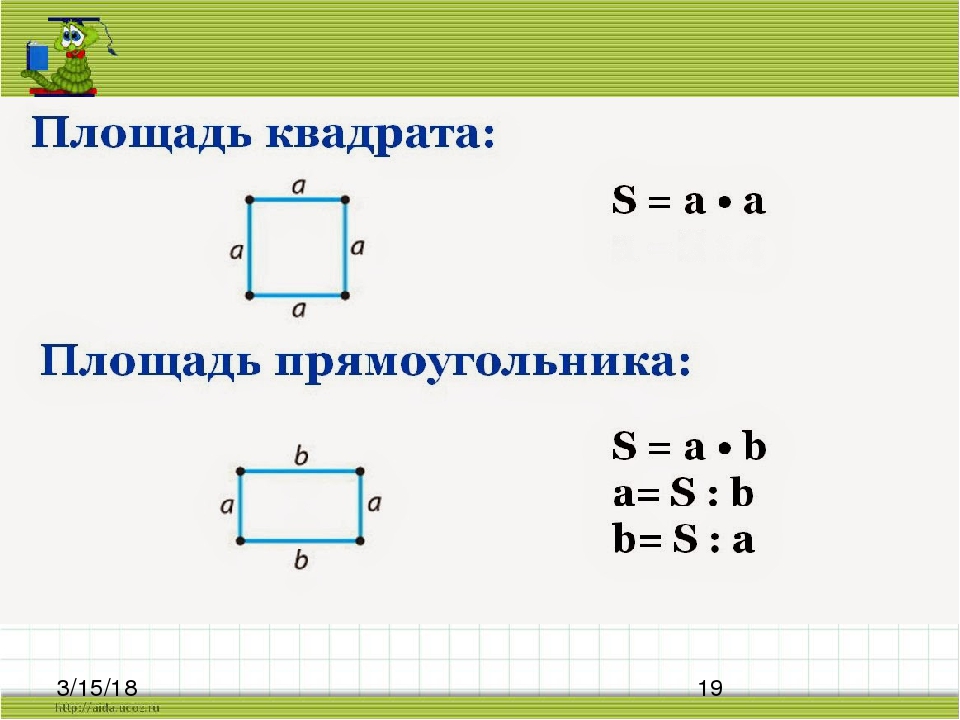
Ну, как найти периметр различных форм не более сложно с нашим бесплатным онлайн-калькулятором периметра в площадь. Начнем с основ.
В математике периметр фигуры определяется как общее расстояние вокруг фигуры. По сути, это длина любой формы, если она расширяется линейно. Диапазон различных форм может быть одинаковым по длине в зависимости от их размера.
Например, если из металлической проволоки длиной L сделать круг, то из той же металлической проволоки можно построить квадрат с той же длиной стороны. Вы можете найти площадь поверхности проволоки перед ее установкой на различные формы.
Как найти периметр? Обычно самым простым и понятным методом является суммирование всех сторон фигуры. Однако иногда ребра отсутствуют (например, эллипсы, окружности и т. д.) или неизвестны одно или несколько ребер. Ниже приведены некоторые уравнения периметра, используемые с калькулятором периметра для определения периметра.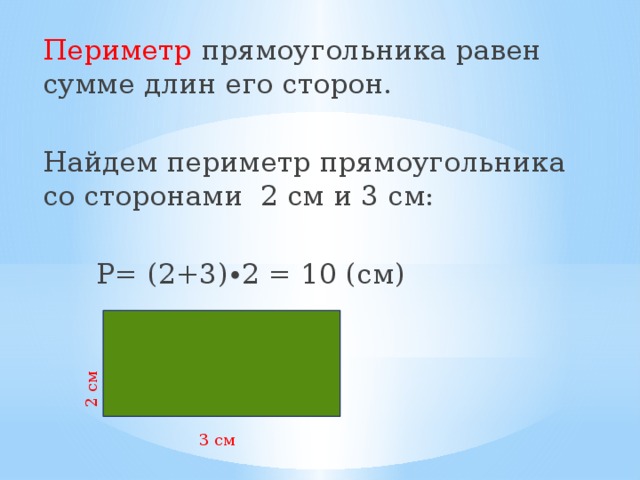
Наш калькулятор периметра использует простую формулу для регулярного периметра полигона:
Полигонный периметр = x * n
, где
n = Номер из полигона. Если вы хотите найти периметр любого многоугольника, то возьмите сумму длин всех его сторон:
Периметр многоугольника = Σ x
, где x₁, x₂, …, xₙ — длины сторон, а «Σ» — сумма (от i = 1 до n) 92 }
с a(n+1) = a(1) и b(n+1) = b(1)
Однако онлайн-калькулятор синуса определит тригнометрические значения синуса для заданного угла в градусах, радианах , или π радиан.
Эллипс:Хотя формула площади эллипса очень проста и легко запоминается, формула длины окружности эллипса самая сложная. Итак, мы решили реализовать аппроксимацию Рамануджана в этом калькуляторе длины окружности эллипса: 92
Периметр эллипса ≈ π * (x + y) * [1 + 3 * h] / [10 + \sqrt {(4 – 3 * h)}]
Трапеция:Для вычисления периметра неправильная трапеция, специальной формулы нет — просто сложите все стороны:
Периметр трапеции = m + n + o + p
Параллелограмм:В этом калькуляторе периметра есть три формулы для периметра параллелограмма :
Сложение всех сторон:
Периметр параллелограмма = x + y + x + y = 2(x + y) 92)}
Высота и любой угол параллелограмма:
Формула периметра для высоты и любого угла параллелограмма
Периметр параллелограмма = 2 * (x + m / sin(α))
Ромб: 9014Периметр ромба равен периметру квадрата!
Периметр ромба = 4x
Ромб с заданными диагоналями
Другой метод: нахождение периметра ромба с длинами диагоналей:
92)} Однако онлайн-калькулятор косинуса помогает вычислить значение косинуса заданного угла в градусах, радианах, милли-радианах и π-радианах.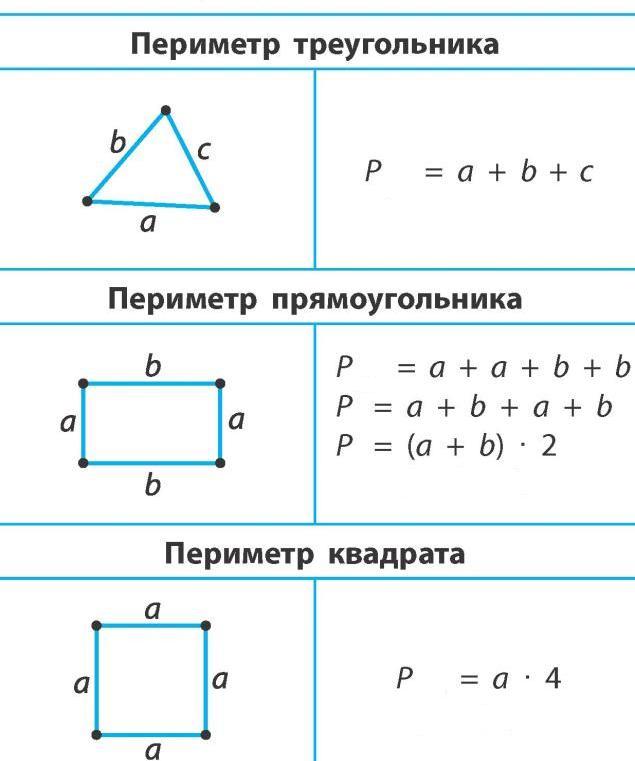
Формула периметра воздушного змея очень проста – просто сложите все стороны вместе:
Периметр воздушного змея = x + x + y + y = 2(x + y)
Кольцо:В кольцо необходимо добавить периметр обеих концентрических окружностей:
= 2π * r + 2π * R
= 2π * (R + r)
Сектор:Вычисление периметра сектора круга кажется сложным: это просто длина дуги или длина дуги плюс два радиуса? Подумайте об определении периметра! Периметр сектора представляет собой сумму длин всех его границ, поэтому последний:
Периметр сектора круга = r * (α + 2)
Где
α в радианах.
Квадрат:У квадрата четыре стороны одинаковой длины. Чтобы найти его периметр, нужно длину стороны умножить на 4:
Периметр квадрата = x + x + x + x = 4x
Прямоугольник: Формула периметра прямоугольника проста как уравнение для периметра квадрата.
Единственная разница в том, что у нас есть две пары сторон одинаковой длины:
Периметр прямоугольника = x + y + x + y = 2x + 2y = 2(x + y)
Треугольник:Формула для определение периметра треугольника — это сложение всех сторон:
Периметр треугольника = x + y + z 92 – 2xy * cos(γ))}
Два угла и сторона:
Если у вас есть одна сторона и два угла, то используйте закон синусов:
y = sin(β) * x / sin(γ + β)
z = sin(γ) * x / sin(γ + β)
Итак, периметр треугольника можно представить как:
Периметр треугольника = x + (x / (sin(β) + sin(γ) * sin(β + γ)))
Круг:Периметр круга также известен как длина окружности. Формула периметра круга использует одну переменную: 92
А = 22/7 × 9 × 9
А = 1782 кв.см.
Нахождение периметра круга:
Длина окружности = 2πr
C = 2 x 22/7 x 9 = 57 см
Как работает калькулятор периметра?Онлайн-калькулятор периметра в площадь находит периметр определенной фигуры, выполнив следующие действия:
Ввод:- Сначала выберите геометрическую фигуру из раскрывающегося списка.
- Теперь калькулятор отображает форму выбранного тела.
- Затем подставьте значения в соответствующие поля.
- Нажмите кнопку расчета, чтобы увидеть результаты.
- Решатель периметра мгновенно вычисляет периметры квадрата, прямоугольника, треугольника, круга, полукруга, эллипса, сектора круга, трапеции, параллелограмма, ромба, воздушного змея, кольца и правильного многоугольника.
Площадь — это область, окруженная фигурой или фигурой, а периметр — это расстояние, пройденное внешним краем фигуры.
Единица площади выражается в квадрате, а единица измерения периметра совпадает с единицей измерения.
Каковы периметр и площадь круга? Длина окружности равна длине ее внешней границы. Это означает, что длина окружности равна ее периметру.