Периметр прямоугольника измеряется в чем: Как найти периметр прямоугольника, формула ⬅️

В чем измеряется периметр. Периметр

Подписаться на сайт

Ребята, мы вкладываем душу в сайт. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте

Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».

Как вычислить периметр

Периметр обозначается латинской буквой P . Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».

Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).

Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см.

Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.

Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.

Периметр и площадь квадрата

Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:

P= a+a+a+a

Например, перед нами квадрат со стороной 10 см.

Ответ: 40 см

P = 10+10+10+10

P =40

Ответ: 40 см

Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.

Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:

S – это площадь, а – сторона квадрата.

Например, в задаче указано, что длина стороны квадрата составляет 10см.

S= 100 см 2

Ответ: 10 0 см 2

Периметр и площадь прямоугольника

Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:

P= (a+b)*2

Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.

Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.

P = (6+2) * 2

P = 16

Ответ: 16 см

Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:

Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.

S = 5*2

S =10см 2

Ответ: 10 см 2

Периметр круга (длина окружности)

Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.

Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:

L = 2πr

L – длина окружности

π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.

π = 3.141 592 653 589 793 238 462 643 383 279 502

Для удобства вычислений обычно используют значение 3.14

R – это радиус окружности

D – Диаметр окружности

Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то

Например, перед нами круг с радиусом 3 см. Найдем его периметр.

L = 2*3,14*3

L =6 π

L=6*3.14

L = 18.84 см

P к = 18,84 см

Ответ: 18.84 см

Отличие периметра от площади

Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ.

Площадь всегда измеряется в квадратных единицах (см 2 , м 2 , мм 2). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.

Существует несколько понятий периметра.

Геометрическое: всякая замкнутая плоскость имеет длину своих границ. И из области безопасности. То есть, периметром называют собственно охраняемую границу или территорию охраняемого объекта. Поскольку тема эта из рубрики «Обучение», а не из рубрики «Законы и безопасность», следует остановиться на геометрическом понятии периметра.

Итак, что такое периметр?

Этот вопрос почему-то ставит в тупик некоторых молодых людей. Они что, не учили этого в школе? Если какие-то математические (геометрические) формулы, которыми пичкают школяров, никогда не пригодятся в жизни, то знать, что такое периметр – просто необходимо, и это знание, можете не сомневаться, будет востребованным.

Каков периметр вашего дачного дома? А участка? От периметра зависит площадь и того, и другого. А если ваш огород, поле, сад имеет овальную форму или множество углов? Как вы узнаете их периметр?

Для начала следует заглянуть в словари и энциклопедии. И уяснить для себя, что включает в себя понятие «периметр».

Большой энциклопедический словарь дает такое определение периметру: это длина контура, который замкнут. Сумма длин сторон геометрической фигуры, к примеру, всех пяти сторон пятиугольника.

Скажем, имеется земельный участок, представляющий пятиугольник. Одна сторона простирается на 20 метров, другая – на 16, третья – на 4, четвертая – на 11 и пятая – на 6 метров. Каков периметр земельного участка? Простым арифметическим действием сложения мы вычисляем периметр земельного участка: 20 + 16 + 4 + 11 + 6 = 57 метров.

Словарь Ушакова дает такое объяснение понятию «периметр»: это сумма длин всех сторон плоской фигуры. Что мы уже и проиллюстрировали на вышеприведенном примере.

А как же окружность? Она ведь тоже плоская. Каков ее периметр, и как его вычислить?

Существует формула вычисления периметра (длины) окружности. Но для этого сначала надлежит вспомнить, что такое окружность, и какие она имеет элементы. А окружность – есть кривая, которая не только плоская и замкнутая, но еще и все ее точки расположены на одинаковом удалении от заданной точки, зовущейся центром.

Отрезок прямой, соединяющий этот центр с какой-либо точкой окружности, есть радиус (R).

Отрезок прямой, проходящий через центр окружности и соединяющий ее две точки, наиболее удаленные друг от друга, есть диаметр (D). Диаметр равен двум радиусам.

Отношение длины окружности к ее диаметру одинаково для любой окружности и равно постоянному числу 3, 14… Число это обозначается буквой π (пи).

Вот теперь можно и дать формулу вычисления периметра (длины) окружности: P = 2πR или π D.

Скажем, нам известен радиус окружности: 5 метров. Чему будет равен ее периметр?

Действия здесь будут следующие: диаметр (10 метров) умножаем на 3, 14. И получаем периметр окружности, равный 31, 4 метра.

Встречаются и более сложные фигуры, периметр которых необходимо узнать. Здесь для расчета периметра применяются методы математического анализа, что требует уже специальных знаний…

Урок и презентация на тему: «Периметр и площадь прямоугольника»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»

Что такое прямоугольник и квадрат

Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.

Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:

P ABCD = 2 * (AB + BС)

P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: P ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P ABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P ABCD = 4 * AB

Пример.

Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P ABCD = 4 * AB

3. Подставим в формулу наши данные:

P ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1. Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры.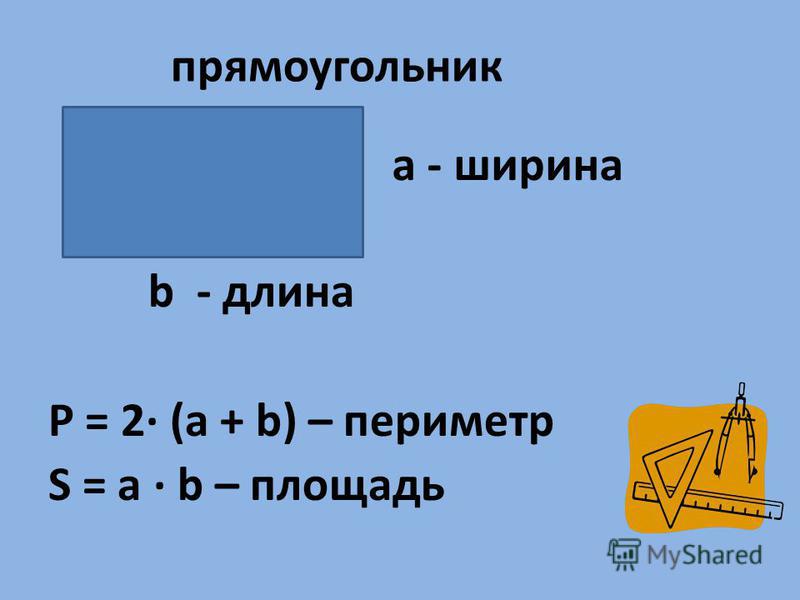 Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S AKMO = AK * KM

Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Сегодня у нас речь пойдет о том, как вычислить периметр многоугольника . Но сначала поговорим о многообразии фигур. Посмотрите на рисунок. Какие фигуры мы здесь видим? Это прямоугольник и квадрат – многоугольники, которые имеют по четыре стороны, а также треугольник, имеющий три стороны, и пятиугольник с пятью сторонами.

И как же найти периметр этих фигур?

Для того, чтобы найти периметр многоугольника надо сложить длины всех его сторон .

Периметр обозначается заглавной латинской буквой Р .

Давайте рассмотрим несколько примеров.

Вычислим периметр многоугольника О. Как мы говорили ранее, периметр многоугольника – это сумма длин всех его сторон. Сложим все стороны нашего многоугольника:

Р = 15 + 17 + 10 + 10 + 20 + 15 = 87

Но можно вычислить периметр и другим способом, используя умножение. Мы видим, что некоторые стороны многоугольника одинаковы. У нас две стороны по 15 условных единиц и еще две по 10. Запишем выражение:

Р = 15 × 2 + 10 × 2 + 17 + 20 = 87

Теперь поговорим об особенностях вычисления периметра некоторых многоугольников.

Прямоугольник – это такой четырехугольник, у которого противоположные стороны равны. Например, чтобы вычислить А со сторонами а и б , надо сложить эти стороны и умножить полученный результат на 2 :

Р(прямоугольника) = (а + б) × 2

То есть, если сторона прямоугольника а = 5 см , а сторона прямоугольника б = 3 см , то периметр прямоугольника будет:

Р = (5 + 3) × 2 = 16 см

А как найти неизвестные стороны прямоугольника, если известен его периметр и только одна из сторон?

Р(прямоугольника) = 2 × а + 2 × б

а = (Р – 2 × б) ÷ 2 или б = (Р – 2 × а) ÷ 2

Пример: Периметр прямоугольника 16 см, сторона а = 5 см.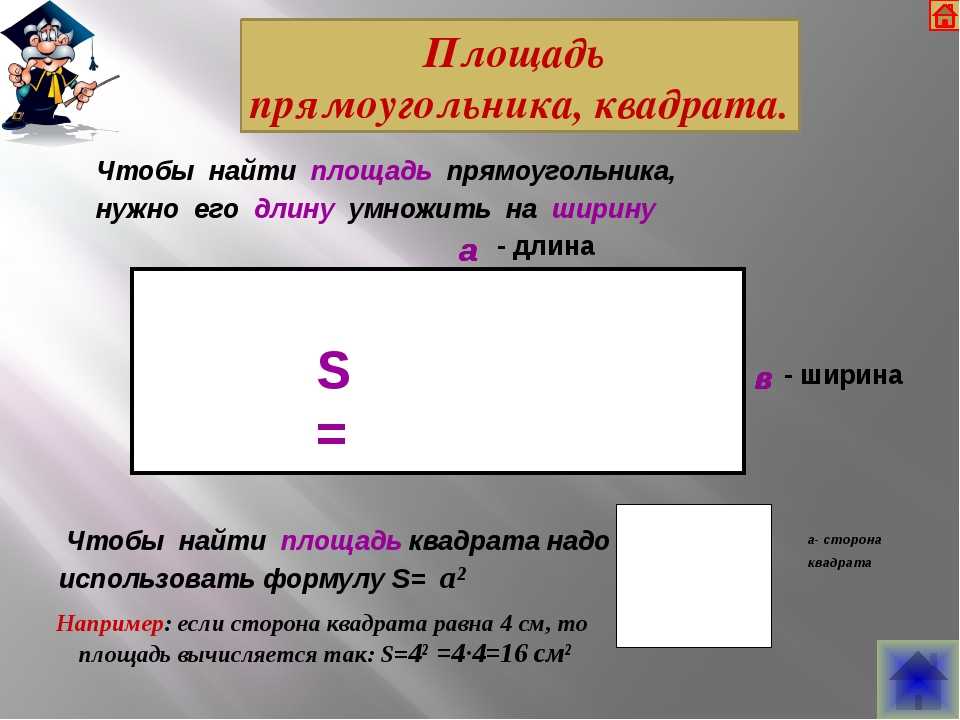 Чему равны остальные стороны прямоугольника?

Если мы знаем одну сторону прямоугольника, значит длины двух, из четырех сторон нам известны. Найдем остальные две стороны. То есть найдем одну, а вторая будет ей равна.

сторона б = (16 – 2 × 5) ÷ 2 = 3 см

Ответ: у прямоугольника две стороны по 5 см и две по 3 см.

Квадрат – это прямоугольник, у которого все стороны равны. Чтобы вычислить надо длину одной стороны умножить на 4:

Р(квадрата) = а × 4

Например, у квадрата В сторона а = 5 см. Чтобы найти его периметр:

Р(В) = 5 × 4 = 20 см

А если известен периметр квадрата, как найти длины его сторон? Очень просто, надо его периметр разделить на четыре:

а = Р ÷ 4

Пример: Периметр квадрата 24 см. Чему равны его стороны?

а = 24 ÷ 4 = 6

Ответ: Стороны квадрата равны 6 см.

По подобию вычисления периметра квадрата вычисляется периметр всех равносторонних многоугольников . То есть равен длине одной его стороны умноженной на количество сторон.

Если длина одной стороны многоугольника равна а , а число его сторон равно n , то его периметр будет равен:

Р(равностороннего многоугольника) = а × n

Например, у пятиугольника Д сторона а = 6 см . Найдем его периметр:

Р(Д) = 6 × 5 = 30 см

Ну а если известен периметр равностороннего многоугольника, то вычислить длины его сторон очень просто, надо разделить его периметр на количество сторон.

Инструкция

Источники:

• как найти периметр abcd

Периметр – это сумма длин сторон какой-либо геометрической фигуры. Иными словами, если взять нить и выложить с ее помощью на столе, например, квадрат, а потом измерить длину этой нити, то полученная цифра и будет периметром данного квадрата. Все знают, что такое периметр, но не каждый может сразу сообразить, как его рассчитать.
Для измерения периметра разных фигур существуют различные способы.

Инструкция

Квадрат. Общеизвестно, что у квадрата есть 4 стороны и они . Поэтому для вычисления его периметра так:

где а – это длина одной стороны данной фигуры.

Проще говоря, измерьте одну из сторон квадрата и умножьте эту цифру на количество сторон, то есть на 4. В нашем случае равен 16 см (4*4).

Прямоугольник и ромб. У этих двух фигур только параллельные друг другу стороны равны, соответственно периметр определяется следующим образом:

где а и b – соприкасающиеся стороны. Таким образом, на нашем примере периметр прямоугольника равен 24 см (2*(8+4)).

Треугольник. Поскольку треугольники бывают совершенно разными – равнобедренными, неправильными, с углами, то единственным верным способом периметр такой фигуры является формула:

То есть для вычисления периметра треугольника просто измерьте длины всех трех сторон и сложите полученные цифры. В нашем случае периметр треугольника равен 10,7 см (2+5+3,7).

Периметр называют длиной окружности, которая вычисляется по особой формуле:

где d – это окружности, а 3,14 – это число «пи», которое специально выведено учеными для определения периметра данной геометрической фигуры. Наш круг (см.) имеет 3 см, то есть периметр окружности равен 9,42см (3*3,14).

Источники:

• как находить длину окружности

Ом в общем случае называют длину линии, которая ограничивает замкнутую фигуру. Для многоугольников периметром является сумма всех длин сторон. Эту величину можно измерить, а для многих фигур и просто рассчитать, если известны длины соответствующих элементов.

Вам понадобится

• — линейка или рулетка;
• — прочная нить;
• — роликовый дальномер.

Инструкция

Чтобы измерить произвольного многоугольника, измерьте при линейки или другим измерительным прибором все его стороны, а затем найдите их сумму. Если дан четырехугольник со сторонами 5, 3, 7 и 4 см, которые измерены линейкой, найдите периметр, сложив их вместе Р=5+3+7+4=19 см.

Если же фигура произвольная и включает в себя не только прямые линии, то измерьте ее периметр обычной веревкой или ниткой. Для этого расположите ее так, она точно повторяла все линии, ограничивающие фигуру, и сделайте на ней отметку, если можно, просто обрежьте ее чтобы избежать путаницы. Затем при помощи рулетки или линейки, измерьте длину нитки, она и будет равна периметру данной фигуры. Обязательно следите за тем, чтобы нить максимально точно повторяла линию для большей точности результата.

Периметр сложной геометрической фигуры измеряйте роликовым дальномером (курвиметром). Для этого не линии намечается точка, в которую устанавливается ролик дальномера и прокатывается по ней, до возвращения в исходную точку. Дистанция, измеренная роликовым дальномером, и будет равна периметру фигуры.

Периметр некоторых геометрических фигур вычисляйте. Например, чтобы найти периметр любого правильного многоугольника (выпуклого многоугольника, стороны которого ), длину стороны умножьте на количество углов или сторон (они равны). Чтобы найти периметр правильного треугольника со стороной 4 см умножьте это на 3 (Р=4∙3=12 см).

Чтобы найти периметр , сложите длины всех его сторон. Если не даны все стороны, а есть углы ними, найдите их по теореме синуса или косинуса. Если известны две стороны прямоугольного треугольника, третью найдите по теореме Пифагора и найдите их сумму. Например, если известно, что катеты прямоугольного треугольника равны 3 и 4 см, то гипотенуза будет равна √(3²+4²)=5 см. Тогда периметр Р=3+4+5=12 см.

Источники:

• периметру

Для решения этой задачи методами векторной алгебры, вам необходимо знать следующие понятия: геометрическая векторная сумма и скалярное произведение векторов, а также следует помнить свойство суммы внутренних углов четырехугольника.

Вам понадобится

• — бумага;
• — ручка;
• — линейка.

Инструкция

Вектор – это направленный отрезок, то есть величина, считающаяся заданной полностью, если задана его длина и направление (угол) к заданной оси. Положение вектора больше ничем не ограничено. Равными считаются два вектора, обладающие длинами и одним направлением. Поэтому при использовании координат векторы изображают радиус-векторами точек его конца (начало в начале координат).

По определению: результирующим вектором геометрической суммы векторов называется вектор, исходящий из начала первого и имеющего конец второго, при условии, что конец первого, совмещен с началом второго. 2))=1/(sqrt2sqrt5), ф3=arcos(-1/sqrt(10))=п-ф1.
В соответствии с замечанием 2 — ф4=2п- ф1 — ф2- ф3=п/4.

Видео по теме

Обратите внимание

Замечание 1. В определении скалярного произведения используется угол между векторами. Здесь, например, ф2 — это угол между АВ и ВС, а между a и b этот угол п-ф2. сos(п- ф2)=- сosф2. Аналогично для ф3.
Замечание 2. Известно, что сумма углов четырехугольника равна 2п. Поэтому ф4=2п- ф1 — ф2- ф3.

Любая выпуклая и плоская геометрическая фигура имеет ограничивающую ее внутреннее пространство линию — периметр. У многоугольников он состоит из отдельных отрезков (сторон), сумма длин которых определяет протяженность периметра. Участок плоскости, ограниченный этим периметром, тоже может быть выражен через длины сторон и углы в вершинах фигуры. Ниже приведены соответствующие формулы для одного из видов многоугольников — параллелограмма.

Инструкция

Если в задачи даны длины двух смежных сторон параллелограмма (a и b) и величина угла между ними (γ), то этого будет достаточно для вычисления обоих параметров. Для расчета периметра (P) четырехугольника сложите длины сторон и вдвое увеличьте полученное значение: P = 2*(a+b). Вычислять (S) фигуры придется с помощью тригонометрической функции — синуса. Перемножьте длины сторон, а результат умножьте на известного угла: S = a*b*sin(γ).

Если известна длина лишь одной из сторон (a) параллелограмма, но есть данные о (h) и величине угла (α) в любой из вершин , то это позволит и периметр (P) (S). Сумма всех углов в любом равна 360°, а в параллелограмме те из них, что лежат в противоположных вершинах, одинаковы. Поэтому для нахождения величины оставшегося неизвестным угла отнимите от 180° величину известного. После этого рассмотрите треугольник, составленный из высоты и лежащего напротив него угла, величины которых известны, а также неизвестной пока стороны. Примените к нему теорему синусов, и выясните, что длина стороны будет равна отношению высоты к синусу угла, лежащего напротив нее: h/sin(α).

После проведения предварительных расчетов предыдущего шага составьте нужные . Подставьте полученное выражение в формулу из первого шага и получите равенство: P = 2*(a+h/sin(α)). В том случае, если высота соединяет две противоположные стороны параллелограмма, длина которых дана в исходных условиях, для нахождения площади просто перемножьте эти два значения: S=a*h. Если же это условие не соблюдено, то подставьте в формулу выражение для другой стороны, полученное в предыдущем шаге: S=a*h/sin(α).

Видео по теме

Среди основных задач аналитической геометрии на первом месте стоит представление геометрических неравенством, уравнением или системой тех или других. Это возможно благодаря применению координат. Опытный математик, только взглянув на уравнение, без труда скажет, какую геометрическую фигуру можно начертить.

Инструкция

Уравнением F (x, y) можно задать кривую или прямую линию при выполнении двух условий: если координаты точки, которая не принадлежит заданной линии, не удовлетворяют уравнению; если каждая точка искомой линии со координатами удовлетворяет этому уравнению.

Уравнение вида x+√(y(2r-y))=r arccos (r-y)/r задает в декартовых координатах циклоиду – траекторию, которая описывается точкой на окружности c радиусом r. При этом окружность не по оси абсцисс, а катится. Какая при этом получается фигура, смотрите на рисунке 1.

Фигура, координаты точек которой задаются следующими уравнениями:
x=(R+r) cosφ — rcos (R+r)/r φ
y=(R+r) sinφ — rsin (R-r)/r φ,
называется эпициклоидой. Она траекторию, которую описывает точка на окружности с радиусом r. Эта окружность катится по другой окружности, имеющей радиус R, с внешней стороны. То, эпициклоида, смотрите на рисунке 2.

Что такое периметр

Периметр — один из математических, а точнее — геометрических терминов, применяется в основном для вычисления сторон фигуры.

Из нашей статьи вы узнаете, что такое периметр и как он измеряется на примере основных геометрических фигур.

Определение периметра

Периметром называют общую длину всех сторон или окружности той или иной фигуры.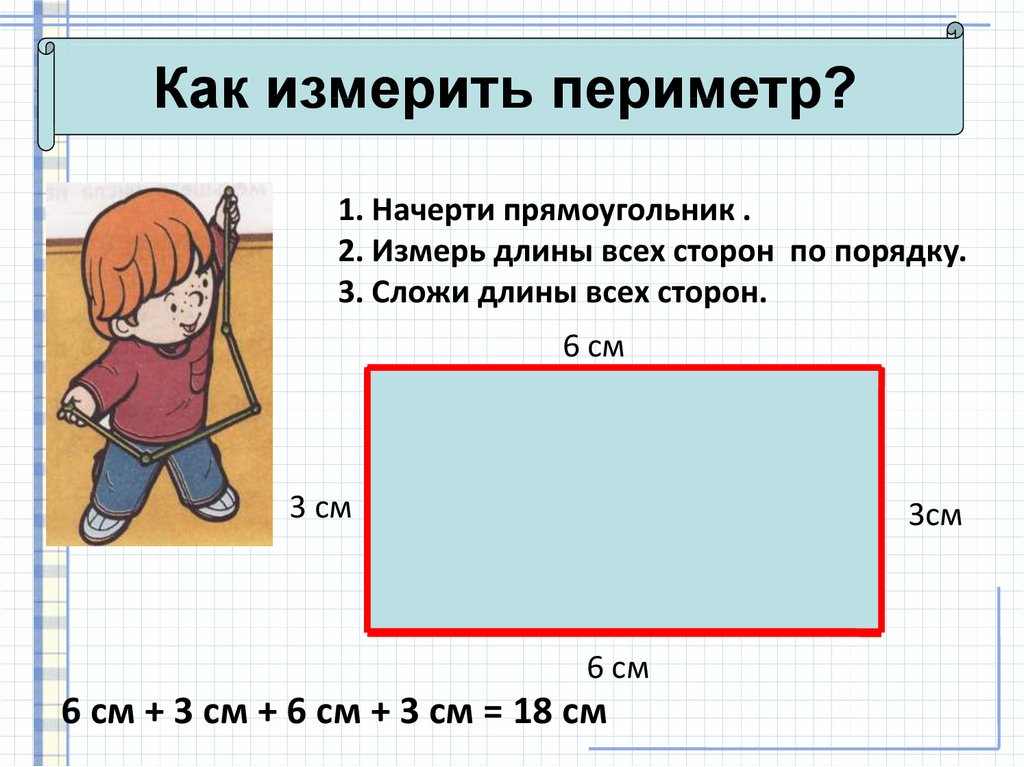 Обозначается периметр большой буквой «Р», а измерять его можно в различных единицах длины, таких как миллиметры (мм), сантиметры (см), метры (м) и т. д. Для различных фигур существуют различные формулы для нахождения периметра. Ниже мы приведем несколько примеров, как узнать периметр у прямоугольника и некоторых других фигур.

Измеряем периметр

Если вам необходимо узнать периметр у сложной фигуры (к таким фигурам можно отнести фигуры с неровными линиями), то для этого вам понадобится веревка или нитка. При помощи этих вещей необходимо описать точный контур фигуры, а чтобы не запутаться, вы можете на веревке сделать отметки карандашом. Или же можно просто ее обрезать, а после приложить все части к линейке. Таким образом, вы узнаете, чему равен периметр практически у любой сложной фигуры.

Существует еще одно приспособление для вычисления периметра у сложных фигур: его называют курвиметр (роликовый дальномер). С его помощью вам нужно установить ролик в любую точку фигуры и описать роликом контур фигуры.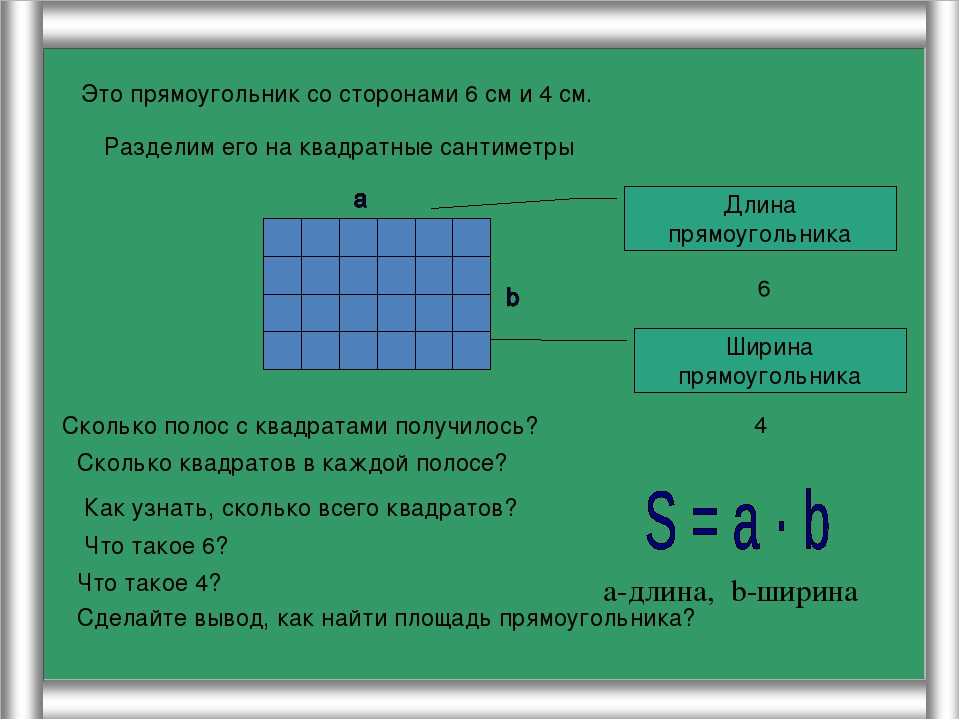 Полученное число и будет равно периметру. О нахождении периметра у других геометрических фигур вы сможете узнать из нашей статьи . Ну а мы расскажем ещё о нескольких способах изменения периметра для разных фигур.

Круг, квадрат, равносторонний треугольник

Давайте также рассмотрим, как узнать периметр круга. Это довольно-таки просто: достаточно лишь определить длину окружности, а сделать это можно, умножив радиус «r» на число π≈3,14 и затем на 2 (P=L=2∙π∙r).

Одним из базовых понятий математики является периметр прямоугольника. На эту тему существует множество задач, при решении которых не обойтись без формулы периметра и навыков его вычисления.

Основные понятия

Прямоугольник – это четырехугольник, у которого все углы прямые, а противоположные стороны попарно равны и параллельны. В нашей жизни многие фигуры имеют форму прямоугольника, например, поверхность стола, тетрадь и прочее.

Рассмотрим пример: по границам земельного участка необходимо поставить забор.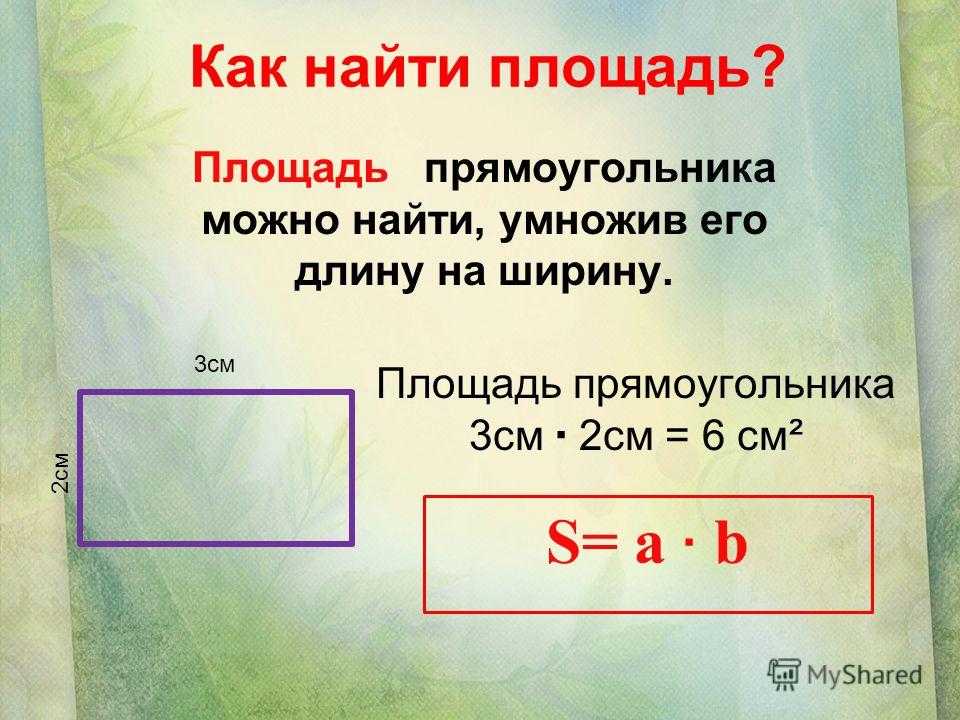 Для того чтобы узнать длину каждой из сторон необходимо их измерить.

Рис. 1. Земельный участок формой прямоугольника.

Земельный участок имеет стороны длиной 2 м., 4 м., 2 м., 4 м. потому чтобы общую узнать длину забора необходимо сложить длины всех сторон:

2+2+4+4= 2·2+4·2 =(2+4)·2 =12 м.

Именно эта величина в общем случае и называется периметром. Таким образом, для нахождения периметра необходимо сложить все стороны фигуры. Для обозначения периметра используют букву P.

Для вычисления периметра прямоугольной фигуры не нужно разделять её на прямоугольники, нужно измерить линейкой (рулеткой) лишь все стороны данной фигуры и найти их сумму.

Периметр прямоугольника измеряется в мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одинаковую систему измерения.

Периметр прямоугольника измеряется в различных единицах: мм., см., м., км и так далее. При необходимости, данные в задании, переводят в одну систему измерения.

Формула периметра фигуры

Если принять к вниманию тот факт, что противоположные стороны прямоугольника равны, то можно вывести формула периметра прямоугольника:

$P = (a+b) * 2$, где а, b – стороны фигуры.

Рис. 2. Прямоугольник, с обозначенными противоположными сторонами.

Существует и другой способ найти периметр. Если в задание дано лишь одну сторону и площадь фигуры, можно использовать выразить другую сторону через площадь. Тогда формула будет выглядеть следующим образом:

$P = {{2S + 2a2}\over{a}}$, где S – площадь прямоугольника.

Рис. 3. Прямоугольник с сторонами a, b .

Задание : Вычислить периметр прямоугольника, если его стороны равны 4 см. и 6 см.

Решение:

Используем формулу $P = (a+b)*2$

$P = (4+6)*2=20 см$

Таким образом, периметр фигуры $P = 20 см$.

Так как периметр – это сумма все сторон фигуры, то полупериметр это сумма только одной длины и ширины. Чтобы получить периметр необходимо полупериметр умножить на 2.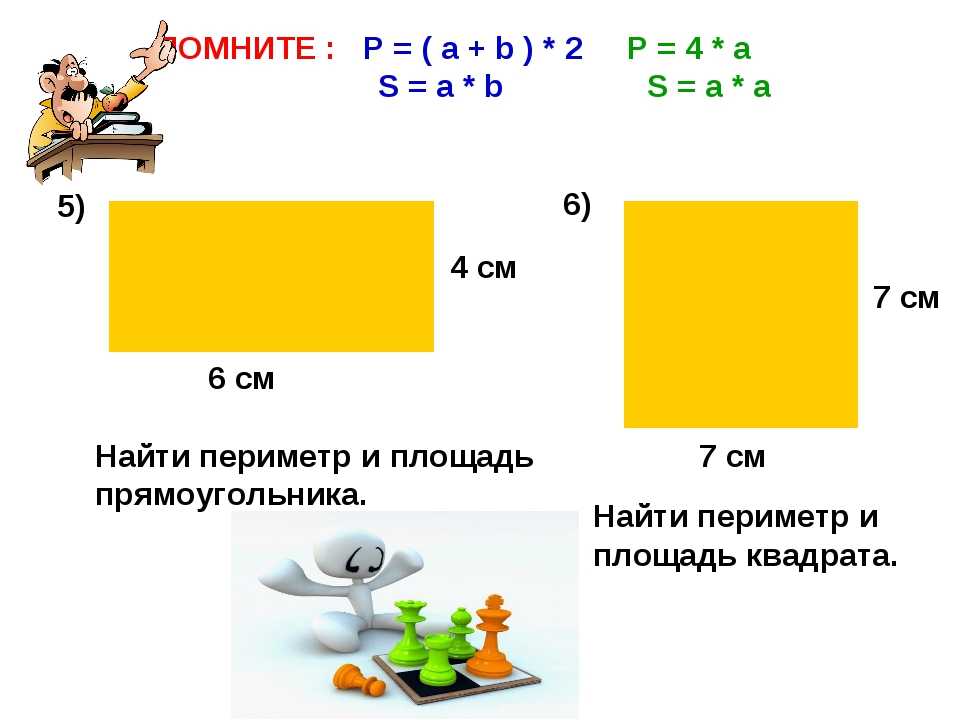

Площадь и периметр – это два основных понятия измерения любой фигуры. Их нельзя путать, хоть они и связаны между собой. Если увеличить, либо уменьшить площадь, то, соответственно, увеличится либо уменьшится его периметр.

Инструкция

Если измеряемый многоугольник правильный, то есть у него все стороны и углы равны, то для нахождения периметра измерьте длину одной из его сторон с помощью линейки. Затем посчитайте количество , которое равно количество его сторон. Получившееся число умножьте на длину стороны фигуры. Это будет многоугольника.

Если многоугольник симметричный и имеет 2 или 4 пары равного набора сторон, то измерьте сначала длину сторон на одном из повторяющихся участков. Затем сложите полученные значения и для получения периметра фигуры умножьте эту сумму на количество повторяющихся частей в многоугольнике.

Источники:

• единица измерения периметра

Нахождение периметра пятиугольника — задача, требующая обширных теоретических знаний, пространственного и логического мышления. Важно также и правильно оформить решение.

Вам понадобится

• — Тетрадь;
• — линейка;
• — карандаш;
• — ручка;
• — калькулятор.

Инструкция

Пятиугольник – это многоугольник с . Пятиугольники правильными и неправильными. Правильный пятиугольник — это выпуклый многоугольник, у которого все стороны и все углы равны между собой.

Неправильный пятиугольник – это многоугольник, стороны и углы которого не равны. В базовом курсе чаще рассматриваются правильные пятиугольники.

Если в задаче дано, что сторона правильного пятиугольника АВСDF равна 5 см, то периметр его будет равен:

В данном случае вы просто умножаете длину стороны пятиугольника на количество сторон, т.к. все они равны между собой (Рис.1).

Если же в задании вам встретился неправильный пятиугольник, то вы должны сначала найти длину каждой его стороны, а потом сложить их.

К , в задаче говорится, что ВО = 8, ОF = 4, ВС = 7, угол ВОА = 90, угол ОАМ = 45, ОМ = 3, АВ = DF, ВС = СD. 2 = 64 + 16

АВ = DF = 8,94.

Затем рассмотрите треугольник АОF. АО = ОF = 4, ОМ = 3. Угол АОВ = DОF = 90 (как накрест лежащие). Следовательно, АОМ = ВОD (как накрест лежащие), и АОМ + ВОD = 360 — АОВ + DОF = 180. АОМ = 90.

Отсюда следует, что треугольник АОF – прямоугольный.

Значит угол АМО = АОМ – ОАМ,

АМО = 90 – 45, АМО = 45.

Следовательно, треугольник АОF – равнобедренный. А в равнобедренных треугольниках напротив углов лежат равные стороны. Значит АМ = ОМ = 3.

Отсюда АF = 2АМ = 6.

Теперь вы можете вычислить периметр пятиугольника АВСDF.

Р = 8,94*2+7*2+6

Многоугольник состоит из нескольких отрезков, соединенных между собой и образующих замкнутую линию. Все фигуры этого класса делятся на простые и сложные. К простым относятся треугольник и четырехугольник, а к сложным — многоугольники с большим количеством сторон , а также звездчатые многоугольники.

Инструкция

Наиболее часто в задачах встречается правильный треугольник со сторон ой a. 2α=xtgα.Отсюда найдите основание:c=2xtgα.

Квадрат представляет собой , сторон ы которого вычисляются несколькими способами. Ниже рассмотрен каждый из них.Первый способ предлагает нахождение сторон ы квадрата. Поскольку все углы у квадрата прямые, данная их пополам таким образом, что образуются два прямоугольных треугольника с углами 45 градусов при . Соответственно, сторон а квадрата равна:a=b=c=f=d*cosα=d√2/2, где d — квадрата.Если квадрат вписан в окружность, то зная радиус этой окружности, найдите его сторон у:a4=R√2, где R — радиус окружности.

У многосторон них многоугольников сторон у вычисляйте последним из способов — путем вписывания многоугольника в окружность. Для этого начертите правильный многоугольник с произвольными сторон ами, а вокруг него окружность с заданным радиусом R.Представьте себе, что в задаче дан некоторый произвольный n-угольник. Если окружность описана около этого многоугольника , то для нахождения сторон ы примените формулу:an=2Rsinα/2.

Видео по теме

Периметром многоугольника называют замкнутую ломаную линию, составленную из всех его сторон. Нахождение длины этого параметра сводится к суммированию длин сторон. Если все отрезки, образующие периметр такой двухмерной геометрической фигуры, имеют одинаковые размеры, многоугольник называется правильным. В этом случае вычисление периметра значительно упрощается.

Инструкция

В самом простом случае, когда известны длина стороны (а) правильного многоугольника и число вершин (n) в нем, для вычисления длины периметра (Р) просто перемножьте эти две величины: Р = а*n. Например, длина периметра со стороной в 15 см должна быть равна 15*6=90 см.

Вычислить периметр такого многоугольника по известному радиусу (R) описанной около него окружности тоже возможно. Для этого сначала выразить длину стороны с использованием радиуса и количества вершин (n), а затем умножить полученную величину на число сторон. Чтобы рассчитать длину стороны умножьте радиус на синус числа Пи, поделенного на количество вершин, а результат удвойте: R*sin(π/n)*2. Если вам удобнее вычислять тригонометрическую функцию в , замените число Пи на 180°: R*sin(180°/n)*2. Периметр вычислите умножением полученной величины на число вершин: Р = R*sin(π/n)*2*n = R*sin(180°/n)*2*n. Например, если шестиугольник вписан в круг с радиусом 50 см, его периметр будет иметь длину 50*sin(180°/6)*2*6 = 50*0,5*12 = 300 см.

Схожим способом можно периметр, не зная длины стороны правильного многоугольника , если он около окружности с известным радиусом (r). В этом случае для вычисления размера стороны фигуры будет отличаться от предыдущей лишь задействованной тригонометрической функцией. Замените в формуле синус на тангенс, чтобы

В следующих тестовых заданиях требуется найти периметр фигуры, изображенной на рисунке.

Найти периметр фигуры можно разными способами. Можно преобразовать исходную фигуру таким образом, чтобы периметр новой фигуры можно было бы легко вычислить (например, перейти к прямоугольнику).

Другой вариант решения — искать периметр фигуры непосредственно (как сумму длин всех её сторон). Но в этом случае нельзя полагаться только на рисунок, а находить длины отрезков, исходя из данных задачи.

Хочу предупредить: в одном из заданий среди предложенных вариантов ответов я не нашла того, который получился у меня.

C) .

Перенесем стороны маленьких прямоугольников с внутренней области во внешнюю. В результате большой прямоугольник замкнулся. Формула для нахождения периметра прямоугольника

В данном случае, a=9a, b=3a+a=4a. Таким образом, P=2(9a+4a)=26a. К периметру большого прямоугольника прибавляем сумму длин четырех отрезков, каждый из которых равен 3a. В итоге, P=26a+4∙3a=38a .

C) .

После переноса внутренних сторон маленьких прямоугольников во внешнюю область, получаем большой прямоугольник, периметр которого равен P=2(10x+6x)=32x, и четыре отрезка, два — диной по x, два — по 2x.

Итого, P=32x+2∙2x+2∙x=38x .

?) .

Перенесем 6 горизонтальных «ступенек» из внутренней части во внешнюю. Периметр полученного большого прямоугольника равен P=2(6y+8y)=28y. Осталось найти сумму длин отрезков внутри прямоугольника 4y+6∙y=10y. Таким образом, периметр фигуры равен P=28y+10y=38y .

D) .

Перенесем вертикальные отрезки из внутренней области фигуры влево, во внешнюю область. Чтобы получить большой прямоугольник, перенесём одни из отрезков длиной 4x в нижний левый угол.

Периметр исходной фигуры найдём как сумму периметра этого большого прямоугольника и длин оставшихся внутри трёх отрезков P=2(10x+8x)+6x+4x+2x=48x .

E) .

Перенеся внутренние стороны маленьких прямоугольников во внешнюю область, получим большой квадрат. Его периметр равен P=4∙10x=40x. Чтобы получить периметр исходной фигуры, нужно у периметру квадрата прибавить сумму длин восьми отрезков, каждый длиной 3x. Итого, P=40x+8∙3x=64x .

B) .

Перенесём все горизонтальные «ступеньки» и вертикальные верхние отрезки во внешнюю область. Периметр полученного прямоугольника равен P=2(7y+4y)=22y. Чтобы найти периметр исходной фигуры, нужно к периметру прямоугольника прибавить сумму длин четырех отрезков, каждый длиной y: P=22y+4∙y=26y .

D) .

Перенесем из внутренней области во внешнюю все горизонтальные линии и передвинем две вертикальные внешние линии в левом и правом углах, соответственно, на z левее и правее. В результате получим большой прямоугольник, периметр которого равен P=2(11z+3z)=28z.

Периметр исходной фигуры равен сумме периметра большого прямоугольника и длин шести отрезков по z: P=28z+6∙z=34z .

B) .

Решение полностью аналогично решению предыдущего примера. После преобразования фигуры находим периметр большого прямоугольника:

P=2(5z+3z)=16z. К периметру прямоугольника прибавляем сумму длин оставшихся шести отрезков, каждый из которых равен z: P=16z+6∙z=22z .

Что такое периметр в математике

Вам, как родителю, может быть интересно, что такое периметр в математике.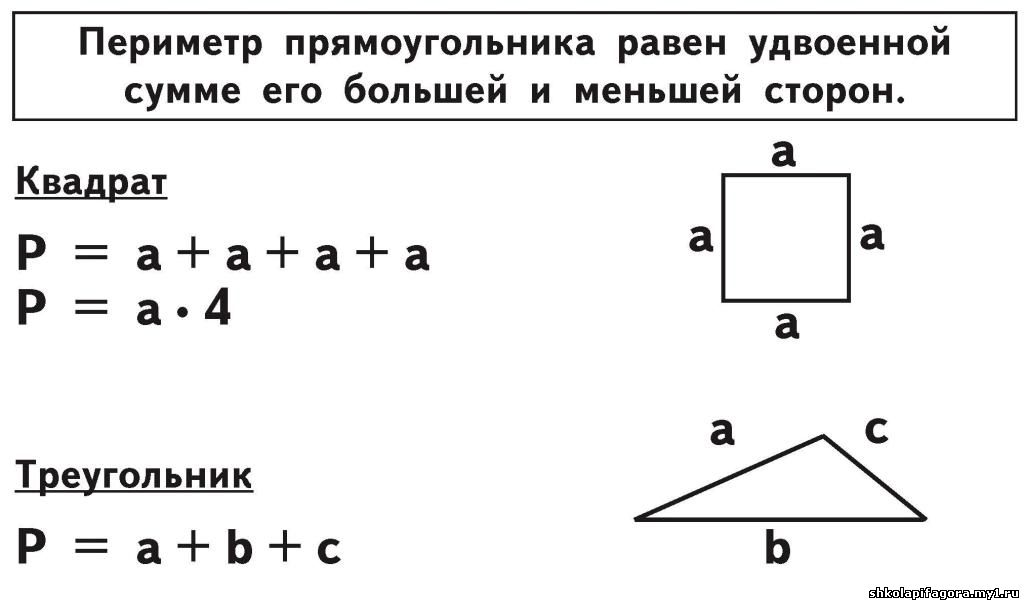 Периметр — это измерение расстояния вокруг внешней стороны фигуры. Студенты должны знать, что такое периметр, чтобы они могли определить размер и размеры различных предметов и областей.

В этом руководстве мы более подробно рассмотрим концепцию периметра и дадим советы о том, как помочь вашему ребенку лучше ее понять.

Периметр — это расстояние вокруг внешней стороны фигуры

Периметр — это базовое математическое понятие, которое можно использовать в реальных ситуациях, таких как приготовление пищи, садоводство и инженерное дело.

Поначалу периметр может показаться пугающим, но понять его довольно просто. Он определяется как общее расстояние по всему краю формы или фигуры, которое может быть выражено в таких единицах, как сантиметры или дюймы.

В зависимости от формы вычисление периметра обычно включает сложение нескольких сторон и/или кривых, чтобы получить ответ. Периметр позволяет нам быстро измерять, сравнивать и определять размер чего-либо без необходимости измерять каждую сторону по отдельности.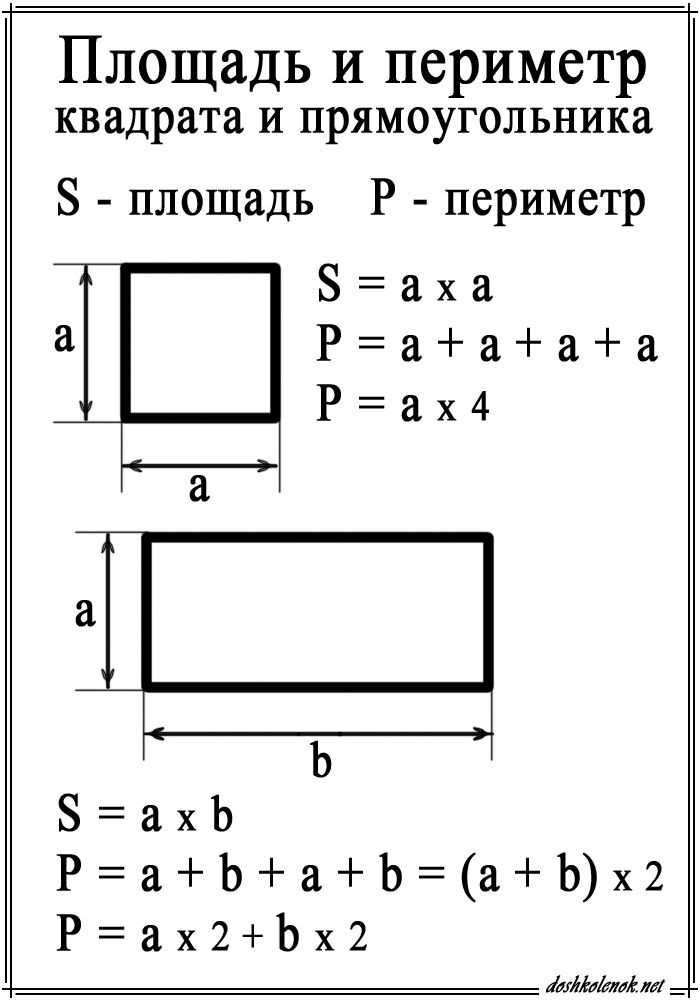

Например, если вы ищете периметр квадрата, все, что вам нужно сделать, это сложить длины каждой стороны. Если длина каждой стороны 10 сантиметров, то периметр будет 40 сантиметров (10 + 10 + 10 + 10).

Для других фигур могут потребоваться более сложные расчеты, но независимо от того, какая это форма, периметр может помочь нам определить общую длину сторон фигуры. Зная периметр, мы можем определить, сколько материала (например, ткани, бумаги или дерева) потребуется для построения фигуры с заданным периметром.

Мы также можем использовать его, чтобы найти площадь фигуры, разделив периметр на четыре и найдя квадратный корень из этого результата.

Как найти периметр прямоугольника

Определение периметра прямоугольника — простая задача, но важно понять, как правильно это сделать. Чтобы найти периметр прямоугольника, просто возьмите измерения длины и ширины и сложите их вместе.

Это даст вам общую длину вокруг четырех сторон вашего прямоугольника.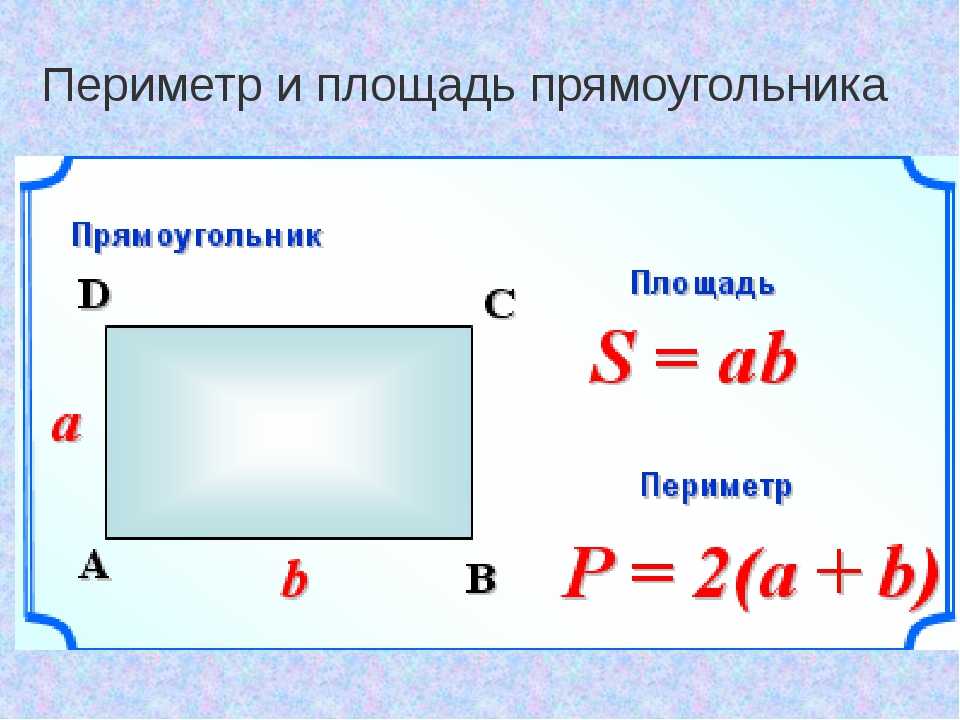 Важно помнить, что если у вас изогнутая или неправильная форма, этот прием не сработает, и вам нужно будет подходить к нему по-другому.

Понимая, какие измерения используются и как они сочетаются для определения периметра, вы сможете быстро и точно найти ответ, который ищете.

Например, если у вас есть прямоугольник шириной 4 см и длиной 7 см, периметр можно рассчитать путем сложения длины и ширины. В этом случае 4 + 7 = 11 см, поэтому ваш периметр будет 11 см.

Когда дело доходит до обучения детей нахождению периметра прямоугольника, лучше всего начать с рисования фигуры на бумаге. Затем попросите их измерить и записать длину и ширину каждой стороны. После того, как они измерили все четыре стороны, попросите их сложить все измерения, чтобы получить периметр. Вы также можете использовать линейку, чтобы измерить стороны прямоугольника.

Вы можете помочь детям больше узнать о периметре, дав им простые словесные задачи на нахождение периметра прямоугольника.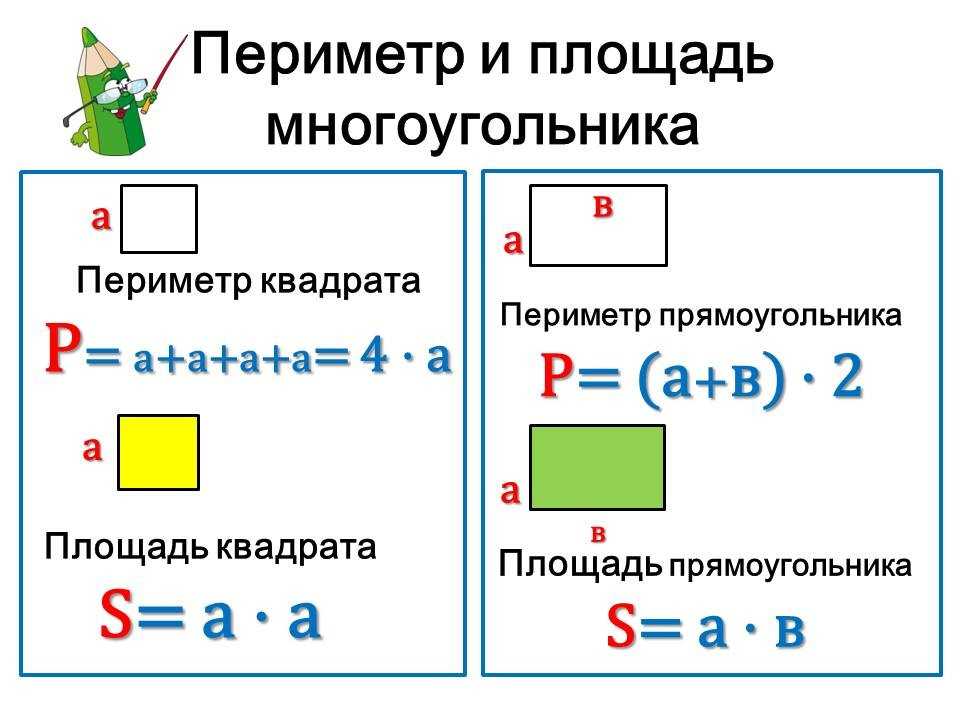 Попросите их прочитать задачу, вычислить ее по формуле, а затем объяснить, как они пришли к своему ответу.

Вы также можете попросить их нарисовать фигуру, описанную в задаче, измерить и записать стороны, а затем сложить все измерения, чтобы получить ответ. Это поможет им научиться лучше измерять и считать, а также больше узнать о периметре.

Формула для нахождения периметра 

Формула для нахождения периметра прямоугольника: P = 2(L + W). Для его применения нужно знать длину (L) и ширину (W) прямоугольника, которые можно измерить линейкой.

Затем нужно умножить длину на два и прибавить к удвоенной ширине; это даст вам ответ. Знание того, как рассчитать периметр прямоугольника, невероятно полезно во многих повседневных ситуациях, например, при определении того, сколько материалов для ограждения или стен вам понадобится для вашего сада.

Давайте применим это на практике. Предположим, длина прямоугольника 8 см, а ширина 4 см. Периметр будет рассчитан следующим образом:

P = 2(8 + 4)

P = 2(12)

P = 24 см

Итак, периметр нашего прямоугольника равен 24 см. Также возможно вычислить периметр неправильного прямоугольника, сложив длины каждой стороны. Это даст вам общую длину, и вы можете удвоить ее, чтобы узнать периметр.

Как периметр обычно используется в математике?

Периметр используется для расчета площади различных фигур. Например, формула для нахождения площади прямоугольника: A = l x w, где l и w — длина и ширина прямоугольника соответственно. Тот же принцип применим и к другим формам, таким как треугольники и круги. Зная периметр фигуры, можно точнее вычислить ее площадь.

Также периметр можно использовать для решения задач с измерением расстояния и окружности.

Например, если вы знаете радиус круга и его периметр, вы можете использовать их для расчета диаметра. Периметр также можно использовать для определения длины дуги, площади сектора и других подобных измерений.

Наконец, периметр можно использовать для нахождения площади неправильной формы, такой как треугольник или многоугольник. Разделив периметр на равные длины, а затем умножив эти длины друг на друга, вы можете относительно легко вычислить площадь фигуры.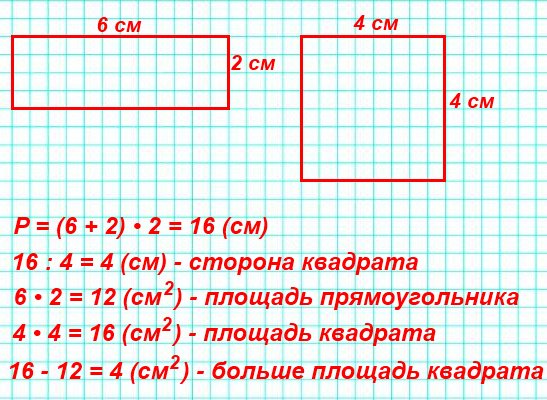

Короче говоря, периметр — это основное математическое понятие, которое можно использовать для измерения фигур и определения их размеров. Он часто используется в сочетании с другими математическими понятиями, такими как площадь или радиус формы, для решения более сложных задач.

Периметр можно использовать для решения проблем в реальной жизни

Использование периметра в решении проблем имеет далеко идущие последствия, поскольку это жизненно важный инструмент для измерения и определения различных параметров, необходимых в повседневной жизни.

От расчета размера фундамента здания до понимания того, сколько ограждений необходимо для ограждения территории, периметр имеет множество практических применений в различных секторах.

Хотя чаще всего понятие периметра используется в архитектуре, его универсальность также позволяет применять его к задачам, связанным с сельским хозяйством, строительством садов и парков, измерением дорог и других территорий.

На самом деле, каждый раз, когда необходимо установить или точно измерить границу ограждения, периметр можно использовать в качестве эмпирического правила для определения необходимой длины.

Как помочь ребенку понять математику

Чтобы найти периметр прямоугольника, достаточно знать формулу и подставить числа. Формула P = 2L + 2W, где P — периметр, а L и W — длина и ширина прямоугольника.

Например, если прямоугольник имеет длину 4 дюйма и ширину 3 дюйма, то его периметр будет рассчитываться следующим образом:

P = 2(4) + 2(3) = 14 дюймов

Если у вашего ребенка проблемы с математикой и ему нужна дополнительная помощь, свяжитесь с нами сегодня, чтобы нанять репетитора. Мы будем рады объединить вас с кем-то, кто сможет оказать вам помощь, необходимую для достижения успеха.

Репетиторство по математике — это эффективный способ укрепить уверенность и развить навыки, необходимые вам или вашему ребенку для достижения успеха. Не стесняйтесь обращаться к нам в Learner сегодня!

Как найти периметр прямоугольника

Как

Пратик — 7 февраля 2023 г.

6

Нахождение периметра прямоугольника — простой процесс. Все, что вам нужно, это линейка, и вы сможете определить длину и площадь прямоугольника. Вы даже можете узнать сумму всех четырех сторон прямоугольника. Очень важно знать, как найти периметр прямоугольника, потому что он используется во многих различных математических уравнениях.

Содержание

Периметр прямоугольника — это мера общего расстояния, которое прямоугольник проходит от внутренней части конструкции до внешней. Он часто измеряется в метрических единицах, таких как сантиметры или метры.

В отличие от круга, прямоугольник имеет четыре стороны, каждая из которых имеет определенную длину и ширину. Квадрат, с другой стороны, является четырехугольником с четырьмя равными сторонами.

Существует несколько формул для вычисления периметра прямоугольника. Одним из наиболее распространенных является уравнение P = (a + b) + a+ b. Это вычисляется путем умножения длины и ширины прямоугольника на два и заключения результатов в круглые скобки.

В качестве альтернативы вы можете использовать компьютерную программу, которая вычисляет периметр прямоугольника с помощью ваших входных данных. Как и следовало ожидать, компьютерная программа имеет ряд возможных входных данных, и вы можете выбрать наиболее подходящий для вашей задачи. Например, если вы хотите узнать периметр прямоугольника с 16 сторонами, вы должны ввести длину и ширину 16 сторон, и компьютерная программа выдаст ответ в квадратных единицах.

Если вы хотите вычислить длину прямоугольника, не измеряя каждую сторону, попробуйте использовать длину веревки, туго обернутой вокруг многоугольника. В этом случае длина струны будет 22 дюйма. Однако правильная длина будет зависеть от размера многоугольника, поэтому лучше придерживаться самого простого метода.

Длина прямоугольника

Длина прямоугольника является математически значимой мерой. Он представляет собой самую длинную сторону фигуры. Однако параллелограмм не является прямоугольником.

Если вы хотите найти длину прямоугольника, есть два основных метода: теорема Пифагора и калькулятор. Используя теорему Пифагора, вы обнаружите, что если у вас есть две пары одинаковых измерений на каждой из сторон, длина прямоугольника равна сумме квадратов двух измерений. Другими словами, если ширина в два раза больше высоты, длина составляет половину высоты. Это также верно, если одна из пар длиннее другой.

Формула длины прямоугольника довольно проста. Для расчета вам нужно знать высоту, длину, ширину, угол и количество единиц. Вы можете использовать калькулятор для преобразования этих измерений в длину, площадь и периметр.

Во-первых, угол. Угол является мерой относительной длины сторон. Углы обычно измеряются в 90 градусов. В общем случае все углы прямоугольника равны 90 градусов.

Длина прямоугольника равна сумме длин всех его сторон. Например, прямоугольник с длиной АВ, шириной ВС и высотой ВС равен 4 м.

Наконец, площадь прямоугольника равна квадрату длины и ширины. Существует несколько геометрических фигур, но наиболее распространенными являются квадраты. Каждый квадрат имеет четыре стороны, равные по длине, и каждая имеет площадь в один квадратный дюйм.

Сумма всех четырех сторон

Прямоугольник — это двумерная плоская замкнутая фигура с четырьмя сторонами. Для того, чтобы измерить периметр прямоугольника, нужно сначала вычислить его длину и ширину.

Один из способов сделать это — использовать формулу периметра. Формула периметра используется для измерения общего расстояния вокруг сторон любой формы. Обычно периметр измеряется в сантиметрах, но может быть выражен и в большем количестве единиц.

Периметр прямоугольника рассчитывается как P = 2 x (l + b). Это уравнение используется для определения общего расстояния, пройденного при полном обходе сторон прямоугольника.

Читайте также: Как найти площадь прямоугольника

Формула периметра квадрата отличается от формулы прямоугольника. Чтобы измерить периметр квадрата, нужно измерить длину стороны и ширину стороны. Если сторона и ширина стороны равны, то сумма всех других сторон также должна быть равна.

Длина и ширина четырехугольника также равны. Однако противоположных углов нет. Также необходимо учитывать диагонали четырехугольника. Диагонали прямоугольника являются биссектрисами и не образуют прямых углов в центре прямоугольника.

Составной прямоугольник

Если вы хотите узнать, как найти периметр составного прямоугольника, есть два разных способа. Первый — разделить фигуру на два прямоугольника. Второй способ заключается в перемножении длины и ширины прямоугольника.

Есть две основные формы, которые можно разбить на два прямоугольника: треугольник и составную форму. Если разбить фигуру на два прямоугольника, то потребуется также измерить длину и ширину другой стороны прямоугольника. Затем вам нужно будет сложить эти два измерения вместе, чтобы получить периметр.