Периметр треугольника 3 класс формула: Как найти периметр треугольника 🔺 формула нахождения

Содержание

Как найти периметр сложной фигуры. Умение применять знания в нахождении периметра и площади геометрических фигур. Как найти периметр прямоугольника – онлайн-ресурсы

Построение урока:

Организация и мотивация учащихся к деятельности на уроке.
Организация восприятия нового материала на основе наглядного материала
Организация осмысления.
Первичная проверка понимания нового материала.
Организация первичного закрепления и самостоятельный анализ учебной информации.
Применение полученных знаний на практикуме.

Цели урока:

Обучающая. Обеспечить усвоение учащимися нахождения площади и периметра геометрических фигур;

визуального восприятия материала на уроке; осмыслено понимать, что такое площадь и периметр.

2. Развивающая. Использовать на уроке развивающие упражнения, активизировать

мыслительную деятельность школьников.

3. Воспитательная. Обеспечить развитие ценностно-смысловой культуры учащихся;

мотивации на умение правильно достигать поставленной цели —

совпадение ожидания и результата.

Оборудование:

М.И.Моро и др. “Математика” — учебник для 3 класса начальной школы, 1 часть.
Рабочая тетрадь по математике.
Ручка, линейка, простой карандаш, треугольник, ножницы.
Модели геометрических фигур для нахождения площади.
Над доской плакаты с формулами нахождения площади и периметра.

Средства обучения:

Дидактический материал.
Наглядные пособия.

Приемы обучения:

Сравнение предметов.
Сопоставления способов нахождения площади одной и той же фигуры.

Ход урока.

1. Организационный момент и сообщение темы урока.

Учитель: Здравствуйте, ребята.

Сегодня мы продолжим изучение большой темы под названием “Площадь и периметр”. Тема нашего урока сегодня:“Умение применять знания в нахождении периметра и площади сложной фигуры”. Сложная фигура – это геометрическая фигура, состоящая из нескольких простейших фигур. Сначала, повторим то, что мы с вами изучили на прошлых уроках.

II. Устный счет.

Задачи на развитие.

Учитель: Найдите площадь данной фигуры, если сторона квадрата 1 см.

Фигура изображена на доске.

Ученик: Если 1 квадрат имеет площадь 1 см 2 , а квадратов изображено 5, то площадь этой фигуры равна 5 см 2 .

Учитель: Правильно. Следующее задание. Уберите 3 палочки, чтобы осталось 3 таких квадрата.

Ученик выходит к доске и убирает 3 палочки.

Учитель: Уберите 4 палочки, чтобы осталось 3 таких же квадрата.

Ученик выходит к доске и убирает 4 палочки. Решение.

III. Работа по теме урока

Учитель: Какие геометрические фигуры вы уже знаете?

Ученик: Прямоугольник.

Ученик: Квадрат.

Учитель: Правильно. Что мы знаем о квадрате?

Ученик: У квадрата 4 стороны и 4 угла.

Учитель: Правильно. Каким свойством обладают стороны квадрата?

Ученик: Они равны.

Учитель: Правильно. А какие углы у квадрата?

Ученик: Они прямые.

Учитель: С помощью чего мы можем построить прямой угол?

Ученик: С помощью треугольника.

Учитель: Давайте построим квадрат со стороной 4 см в вашей тетради. С помощью каких инструментов мы будем чертить квадрат?

Ученик: С помощью линейки, карандаша и треугольника.

Ученики в тетрадях строят квадрат и раскрашивают его.

Учитель: Эта геометрическая фигура. Как найти периметр и площадь этого квадрата?

Ученик: Периметр – это сумма всех его сторон. Сторон у квадрата 4. Значит, 4 сложим 4 раза.

Учитель: Как это записать?

Ученики делают запись в тетради: “Найти площадь фигуры F1”.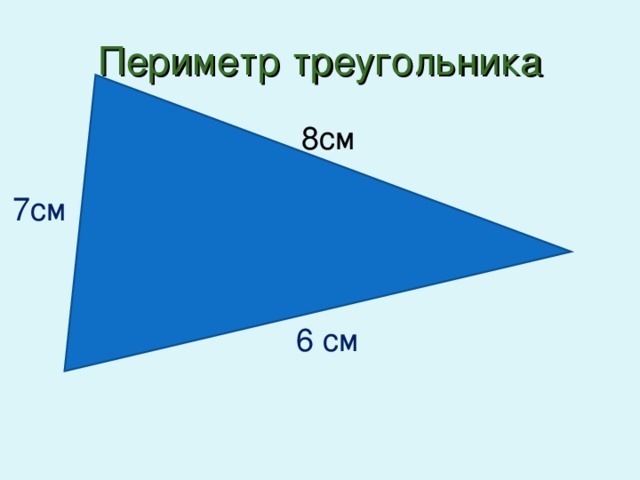

Ученика вызывают к доске, и он пишет: Р = 4 + 4 + 4 + 4 = 16 (см)

Ученики делают запись в тетради.

Учитель: В каких единицах еще измеряется периметр?

Ученик: В сантиметрах, в миллиметрах, в метрах, в дециметрах, в километрах.

Учитель: Молодец! Как еще можно записать периметр?

Ученик: С помощью умножения.

Ученик записывает на доске: Р = 4 · 4 = 16 (см)

Ученики записывают в тетради.

Учитель: А чему равна площадь квадрата?

Ученик: Длину квадрата умножаем на его ширину. Так как стороны у квадрата равны, то

S = 4 · 4 = 16 (см 2)

Ученики делают запись в тетрадке и записывают — “Ответ: S = 16 см 2 ”.

Учитель: Какие еще единицы измерения площади вы знаете?

Ученик: квадратный сантиметр, квадратный дециметр, квадратный метр, квадратный миллиметр.

Учитель: А теперь усложним задачу.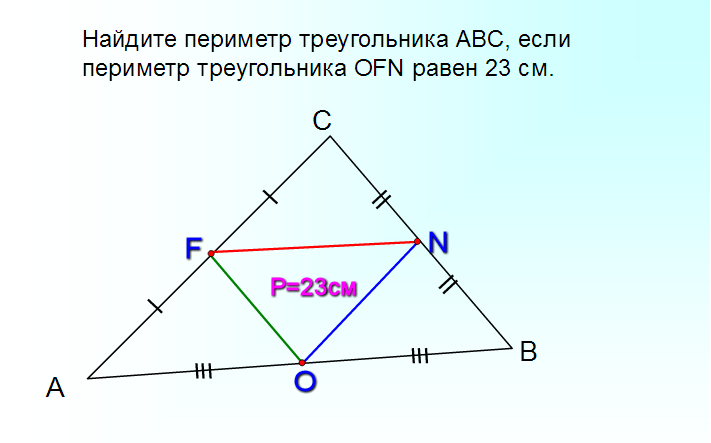 Перед вами лежит карточка.

На этой карточке изображен квадрат такой же, что и у вас в тетрадке. В середине этого квадрата — еще один квадрат со стороной 2 см. Сейчас вы возьмете ножницы и вырежете аккуратно этот маленький квадрат.

Ученики выполняют эту работу и делают запись в тетрадке: “Найти площадь фигуры F2”.

Учитель: У нас получилась фигура “с окошком” — F2. Как можно найти площадь этой интересной фигуры? Площадь квадрата уже известна и равна 16 см 2 .

Ученик: Нужно найти площадь маленького квадратика со стороной 2 см.

Ученик выходит к доске и записывает – S2 = 2 · 2 = 4 (см 2)

Ученики делают запись в тетрадке

Ученик: Из площади большого квадратика вычесть площадь маленького.

Учитель: Правильно.

Ученик записывает на доске – S = S1 – S2 = 16 – 4 = 12 (см 2)

Ученики делают запись в тетрадке.

Учитель: Внимательно посмотрите на эту фигурку и скажите, как еще можно измерить площадь? Можно ли эту фигуру как-то разрезать, чтобы получить фигуры, уже знакомые вам?

Ученики думают и говорят разные варианты.

Один из вариантов оказался очень интересным.

Ученик: Можно так разрезать, чтобы получились прямоугольники и показывает на доске, как это можно сделать.

Ученики разрезают фигуру, как показано на доске.

Учитель: А как находится площадь прямоугольника?

Ученик: Нужно длину умножить на ширину.

Учитель: У вас получилось четыре фигуры. Что можно сказать про них?

Ученик: Две фигурки, как близнецы – одинаковые, и вторые две – тоже одинаковые.

Можно найти площадь одной фигуры и умножить на 2.

Ученик решает на доске: S1 = 1 · 4 = 4 (см 2)

S2 = 1 · 2 = 2 (см 2)

S = 2 · S1 + 2 · S2 = 2 · 4 + 2 · 2 = 8 + 4 = 12(см 2)

Учитель: Молодец! У нас получилась то же значение площади, что и раньше.

Ученики пишут в тетрадке – “Ответ: S = 12 см 2 .”

Учитель: Вы, наверное, устали?

Настало время отдыхать.

Предлагаю усталость

Физкультминуткой снять.

IV. Физкультминутка.

Каждый день по утрам
Делаем зарядку (ходьба на месте).
Очень нравится нам делать по порядку:
Весело шагать (ходьба),
Руки поднимать (руки вверх),
Приседать и вставать (приседание 4-6 раз),
Прыгать и скакать (10 прыжков).

Учитель: А теперь сели за парты и

посмотрите на следующую модель. Фигура F3

Как найти площадь этой интересной фигуры?

Ученик: Треугольник, который выступает

можно отрезать и подставить в ту часть, где

треугольник “уходит” внутрь.

Учитель: Давайте возьмем ножницы, отрежем треугольник и подставим в верхнюю часть.

Что за фигура у нас получилась?

Ученик: Прямоугольник!

Учитель: Как найти площадь этого прямоугольника,

Если стороны нам неизвестны.

Ученик: Мы можем взять линейку и измерить

длину и ширину прямоугольника.

Ученики делают запись – “Найти площадь фигуры F3”.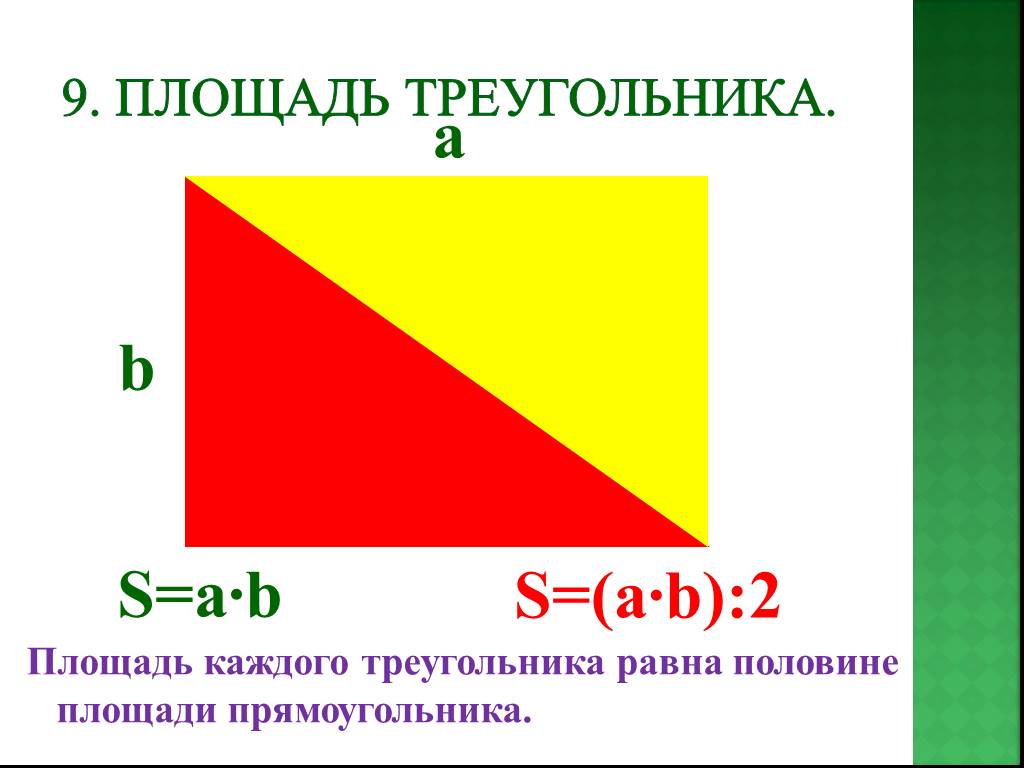

Ученики линейкой измеряют длину и ширину. Получается длина, а = 6 см, ширина в = 2 см.

Ученик: Площадь данной фигуры равна S = 6 · 2 = 12 (см 2).

Ученики делают запись в тетрадке и записывают – “Ответ: S = 12 см 2 .

Учитель: Но это еще не все. Перед вами следующая фигура. Необходимо найти ее площадь.

Что за фигура перед вами?

Ученик: Треугольник. Но площадь треугольника

мы не умеем находить!

Учитель: Это правда. Из этого треугольника

сделаем прямоугольник. Я вам подскажу. Фигура F4

Сначала мы этот треугольник сложим пополам

Ученики: Мы поняли! Правую

сторону переворачиваем.

Получится прямоугольник.

Ученик: С помощью линейки измеряем

длину а и ширину в, и по S = а· в,

находим площадь.

Учитель: Если мы при измерении, мы

получим, что длина

будет выражена в мм, а ширина в см,

что нам делать?

Ученик: Обязательно длину и ширину перевести в одну единицу измерения.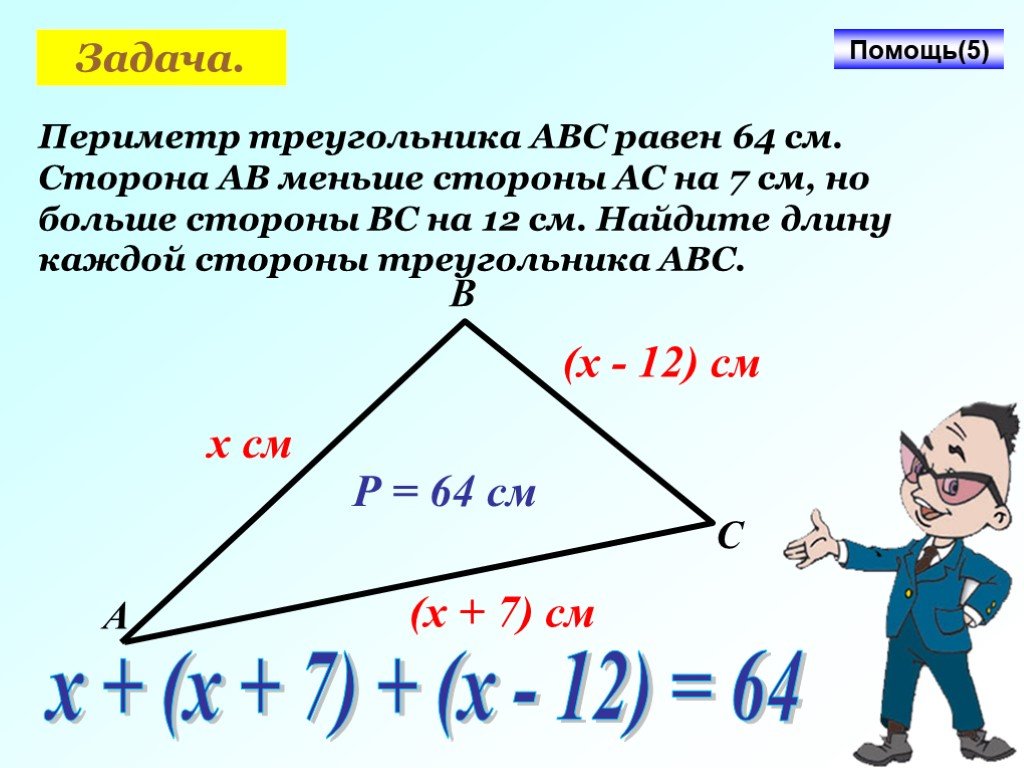

Ученики записывают в тетрадке: “Найти площадь фигуры F4”.

V. Работа в парах.

Учитель: А теперь я предлагаю поработать в паре. Вас за партой двое. Один ученик (I вариант) находит периметр данной фигуры, а второй (II вариант)- площадь.

Для этого начертим в тетради эту фигуру. После того, как вы выполните задание, поменяетесь тетрадями и проверите результаты друг у друга.

Ученики выполняют задание и результаты

записывают в тетрадь.

Учитель: Что у вас получилось?

Ученик: Квадрат со стороной 3 см. Р = 3 · 4 = 12(см)

S = 3 · 3 = 9 (см 2) 3 см

Ученики записывают: “Ответ: P = 12 см, S = 9 см 2 .

Учитель: Молодцы! А теперь я вам предлагаю поработать самостоятельно.

Найти площадь следующей фигуры. Она лежит перед вами.

VI. Самостоятельная работа по закреплению изученного материала.

Учитель раздает заранее заготовленные фигуры.

Ученики самостоятельно, без помощи учителя, разрезают эту фигуры, получают три прямоугольника.

Ученики делают запись: “ Найти площадь фигуры F5”.

Ученики находят S1 = 4 · 3 = 12(см 2), S2 = 2 · 1 = 2(см 2), потом находят площадь данной фигуры: S = S1 + S2 + S2 = 12 + 2 + 2 = 16 (см 2) и делают запись в тетради, затем

записывают: “Ответ: S = 16 см 2 ”.

Учитель: Понравился урок?

Ученики: Да.

Учитель: Что вы нового узнали на этом уроке?

Ученик: Мы научились находить площадь и периметр сложных фигур. Это оказалось очень просто. Нужно немного подумать и эту фигуру перестроить или переделать в ту, периметр и площадь, которой, мы уже умеем находить.

Учитель: Я очень рада, что вам понравилось. Дома еще раз повторить формулы нахождения периметра и площади квадрата и прямоугольника; вспомнить, как переводить одну единицу

в другую. Сегодня хорошо отвечали следующие ученики. . .

Учитель выставляет оценки.

VII. Домашнее задание: учебник стр. 77 № 8.

Знания о том, как найти периметр, учащиеся получают еще в начальной школе. Потом эта информация постоянно используется на протяжении всего курса математики и геометрии.

Общая для всех фигур теория

Стороны принято обозначать латинскими буквами. Причем их можно обозначать как отрезки. Тогда букв потребуется по две для каждой стороны и записанные большими. Или ввести обозначение одной буквой, которая обязательно будет маленькой.
Буквы всегда выбирают по алфавиту. Для треугольника они будут первыми тремя. У шестиугольника их будет 6 — от а до f. Это удобно для введения формул.

Теперь о том, как найти периметр. Он является суммой длин всех сторон фигуры. Количество слагаемых зависит от ее вида. Обозначается периметр латинской буквой Р. Единицы измерения совпадают с теми, которые даны для сторон.

Формулы периметров разных фигур

Для треугольника: Р=а+в+с. Если он равнобедренный, то формула преобразуется: Р=2а+в. Как найти периметр треугольника, если он равносторонний? Поможет такая: Р=3а.

Для произвольного четырехугольника: Р=а+в+с+d. Его частным случаем является квадрат, формула периметра: Р=4а. Есть еще прямоугольник, тогда требуется такое равенство: Р=2(а+в).

Как быть, если неизвестна длина одной или нескольких сторон треугольника?

Воспользоваться теоремой косинусов, если среди данных есть две стороны и угол между ними, который обозначается буквой А. Тогда до того, как найти периметр, придется посчитать третью сторону. Для этого пригодится такая формула: с² = а² + в² — 2 ав cos(А).

Частным случаем указанной теоремы является сформулированная Пифагором для прямоугольного треугольника. В ней значение косинуса прямого угла становится равным нулю, а значит, последнее слагаемое просто исчезает.

Бывают ситуации, когда узнать, как найти периметр треугольника, можно по одной стороне. Но при этом известны еще и углы фигуры. Здесь на помощь приходит теорема синусов, когда отношения длин сторон к синусам соответствующих противолежащих углов равны.

В ситуации, когда периметр фигуры нужно узнать по площади, пригодятся другие формулы. Например, если известен радиус вписанной окружности, то в вопросе о том, как находить периметр треугольника, пригодится следующая формула: S=р*r, здесь р — полупериметр. Его нужно вывести из данной формулы и умножить на два.

Примеры задач

Условие первой. Узнать периметр треугольника, стороны у которого 3, 4 и 5 см.
Решение. Нужно воспользоваться равенством, которое указано выше, и просто подставить в него данные в задаче значения. Расчеты легки, они приводят к числу 12 см.
Ответ. Периметр треугольника равен 12 см.

Условие второй. Одна сторона треугольника равна 10 см. Известно, что вторая на 2 см больше первой, а третья в 1,5 раза больше первой. Требуется вычислить его периметр.
Решение . Для того чтобы его узнать, потребуется сосчитать две стороны. Вторая определится как сумма 10 и 2, третья равна произведению 10 и 1,5. Потом останется только сосчитать сумму трех значений: 10, 12 и 15. Результатом будет 37 см.
Ответ. Периметр равняется 37 см.

Условие третьей. Имеются прямоугольник и квадрат. Одна сторона прямоугольника равна 4 см, а другая на 3 см больше. Нужно вычислить значение стороны квадрата, если его периметр меньше на 6 см, чем у прямоугольника.
Решение. Вторая сторона прямоугольника равна 7. Зная это, легко вычислить его периметр. Расчет дает 22 см.
Чтобы узнать сторону квадрата, нужно сначала вычесть 6 из периметра прямоугольника, а потом разделить полученное число на 4. В результате имеем число 4.
Ответ. Сторона квадрата 4 см.

В следующих тестовых заданиях требуется найти периметр фигуры, изображенной на рисунке.

Найти периметр фигуры можно разными способами. Можно преобразовать исходную фигуру таким образом, чтобы периметр новой фигуры можно было бы легко вычислить (например, перейти к прямоугольнику).

Другой вариант решения — искать периметр фигуры непосредственно (как сумму длин всех её сторон). Но в этом случае нельзя полагаться только на рисунок, а находить длины отрезков, исходя из данных задачи.

Хочу предупредить: в одном из заданий среди предложенных вариантов ответов я не нашла того, который получился у меня.

C) .

Перенесем стороны маленьких прямоугольников с внутренней области во внешнюю. В результате большой прямоугольник замкнулся. Формула для нахождения периметра прямоугольника

В данном случае, a=9a, b=3a+a=4a. Таким образом, P=2(9a+4a)=26a. К периметру большого прямоугольника прибавляем сумму длин четырех отрезков, каждый из которых равен 3a. В итоге, P=26a+4∙3a=38a .

C) .

После переноса внутренних сторон маленьких прямоугольников во внешнюю область, получаем большой прямоугольник, периметр которого равен P=2(10x+6x)=32x, и четыре отрезка, два — диной по x, два — по 2x.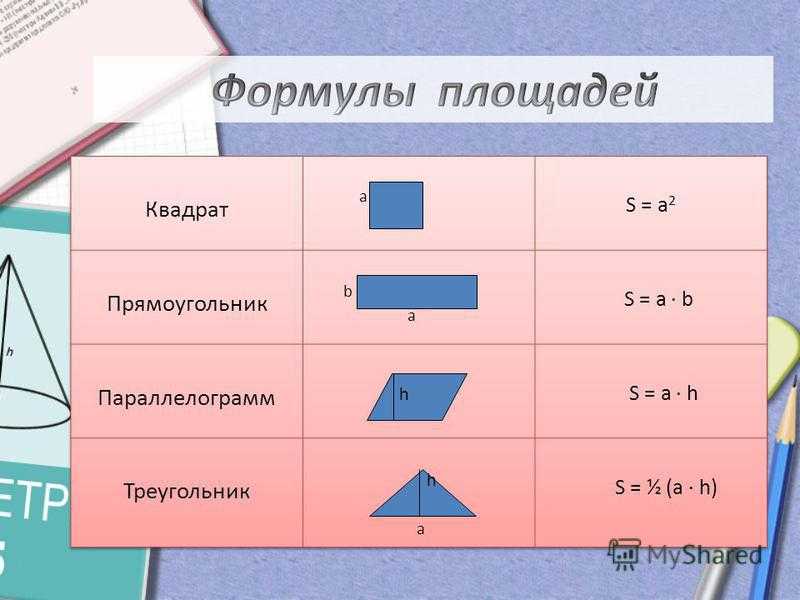

Итого, P=32x+2∙2x+2∙x=38x .

?) .

Перенесем 6 горизонтальных «ступенек» из внутренней части во внешнюю. Периметр полученного большого прямоугольника равен P=2(6y+8y)=28y. Осталось найти сумму длин отрезков внутри прямоугольника 4y+6∙y=10y. Таким образом, периметр фигуры равен P=28y+10y=38y .

D) .

Перенесем вертикальные отрезки из внутренней области фигуры влево, во внешнюю область. Чтобы получить большой прямоугольник, перенесём одни из отрезков длиной 4x в нижний левый угол.

Периметр исходной фигуры найдём как сумму периметра этого большого прямоугольника и длин оставшихся внутри трёх отрезков P=2(10x+8x)+6x+4x+2x=48x .

E) .

Перенеся внутренние стороны маленьких прямоугольников во внешнюю область, получим большой квадрат. Его периметр равен P=4∙10x=40x. Чтобы получить периметр исходной фигуры, нужно у периметру квадрата прибавить сумму длин восьми отрезков, каждый длиной 3x.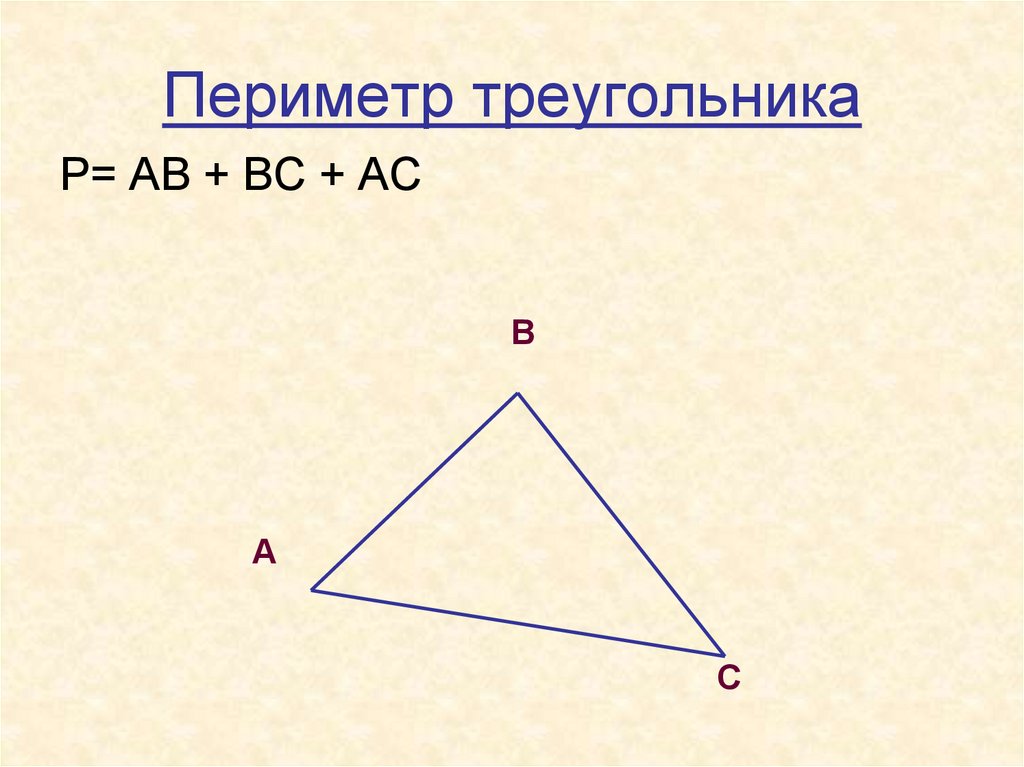 Итого, P=40x+8∙3x=64x .

B) .

Перенесём все горизонтальные «ступеньки» и вертикальные верхние отрезки во внешнюю область. Периметр полученного прямоугольника равен P=2(7y+4y)=22y. Чтобы найти периметр исходной фигуры, нужно к периметру прямоугольника прибавить сумму длин четырех отрезков, каждый длиной y: P=22y+4∙y=26y .

D) .

Перенесем из внутренней области во внешнюю все горизонтальные линии и передвинем две вертикальные внешние линии в левом и правом углах, соответственно, на z левее и правее. В результате получим большой прямоугольник, периметр которого равен P=2(11z+3z)=28z.

Периметр исходной фигуры равен сумме периметра большого прямоугольника и длин шести отрезков по z: P=28z+6∙z=34z .

B) .

Решение полностью аналогично решению предыдущего примера. После преобразования фигуры находим периметр большого прямоугольника:

P=2(5z+3z)=16z. К периметру прямоугольника прибавляем сумму длин оставшихся шести отрезков, каждый из которых равен z: P=16z+6∙z=22z .

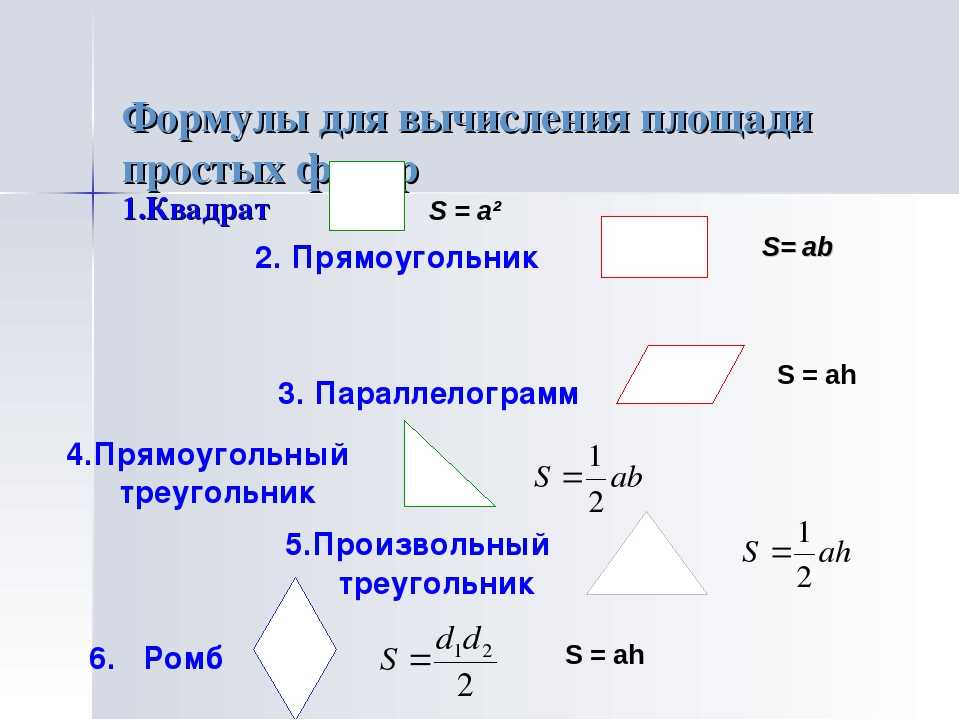
Достаточно узнать длину всех ее сторон и найти их сумму. Периметром называется совокупная длина границ плоской фигуры. Иными словами, это сумма длин ее сторон. Единица измерения периметра должна соответствовать единице измерения его сторон. Формула периметра многоугольника имеет вид Р = a + b + c…+ n, где Р — периметр, а вот а, b, с и n — длина каждой из сторон. Иначе вычисляется (или периметр круга): используется формула р = 2 * π * r, где r — радиус, а π — постоянное число, приблизительно равное 3,14. Рассмотрим несколько простых примеров, наглядно демонстрирующих, как найти периметр. В качестве образца возьмем такие фигуры как квадрат, параллелограмм и окружность.

Как найти периметр квадрата

Квадратом называется правильный четырехугольник, у которого равны все стороны и углы. Так как все стороны квадрата равны, сумму длин его сторон можно вычислить по формуле Р = 4 * a, где а — длина одной из сторон. Таким образом, со стороной 16,5 см равен Р = 4 * 16,5 = 66 см. Так же можно вычислить периметр равностороннего ромба.

Как найти периметр прямоугольника

Прямоугольник — это четырехугольник, все углы которого равны 90 градусам. Известно, что в такой фигуре, как прямоугольник, длины сторон равны попарно. Если ширина и высота прямоугольника имеют одинаковую длину, то он называется квадратом. Обычно длиной прямоугольника называют наибольшую из сторон, а шириной — наименьшую. Таким образом, чтобы получить периметр прямоугольника, необходимо удвоить сумму его ширины и высоты: P = 2 * (а + b), где а — высота, а b — ширина. Имея в наличии прямоугольник, одна сторона которого является длиной и равна 15 см, а другая шириной с установленным значением в 5 см, мы получим периметр, равный Р = 2 * (15 + 5) = 40 см.

Как найти периметр треугольника

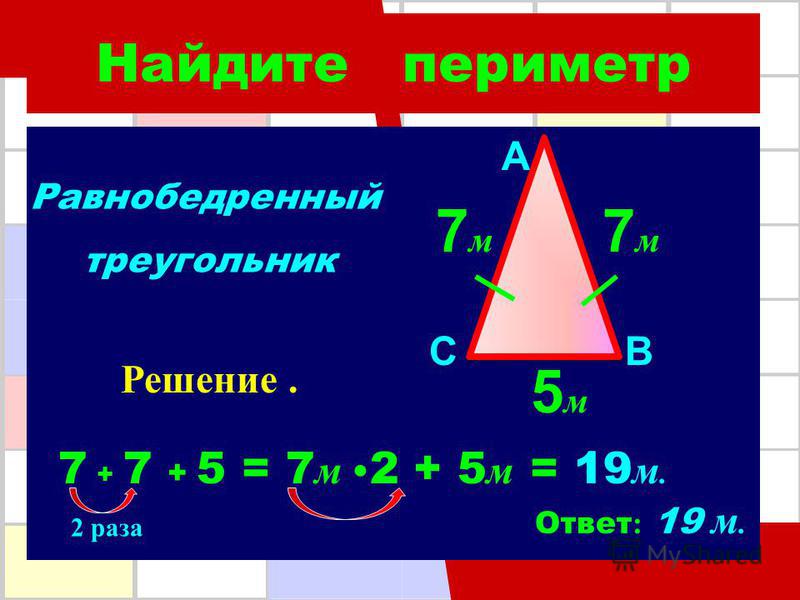
Треугольник образован тремя отрезками, которые соединяются в точках (вершинах треугольника), не лежащих на одной и той же прямой. Треугольник называется равносторонним, если равны все три его стороны, и равнобедренным, если равных сторон две. Чтобы узнать периметр необходимо длину его стороны умножить на 3: Р = 3 * a, где а — одна из его сторон. Если стороны треугольника не равны между собой, необходимо провести операцию сложения: Р = а + b + с. Периметр равнобедренного треугольника со сторонами 33, 33 и 44 соответственно будет равен: P = 33 + 33 + 44 = 110 см.

Как найти периметр параллелограмма

Параллелограмм — это четырехугольник с попарно параллельными противоположными сторонами. Квадрат, ромб и прямоугольник являются частными случаями фигуры. Противоположные стороны любого параллелограмма равны, поэтому для вычисления его периметра воспользуемся формулой P = 2 (а + b). В параллелограмме со сторонами 16 см и 17 см сумма сторон, или периметр, равна Р = 2 * (16 + 17) = 66 см.

Как найти длину окружности

Окружность является замкнутой прямой, все точки которой расположены на равном удалении от центра. Длина окружности и ее диаметр всегда имеют одинаковое отношение. Это отношение выражено константой, записывается при помощи буквы π и равняется примерно 3,14159. Узнать периметр круга можно по произведению радиуса на 2 и на π. Получается, что длина окружности с радиусом в 15 см будет равна Р = 2 * 3,14159 * 15 = 94,2477

Задания на нахождения периметра и площади. Задачи на нахождение периметра и сторон геометрических фигур материал по математике (2 класс)

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.

Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»

Что такое прямоугольник и квадрат

Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.

Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.

Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …

Пример.

Читается так: четырёхугольник ABCD; квадрат EFGH.

Что такое периметр прямоугольника? Формула расчета периметра

Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.

Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.

Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.

Запишем формулу периметра четырехугольника ABCD:

P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)

Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .

Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:

P ABCD = 2 * (AB + BС)

P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см

Ответ: P ABCD = 16 см.

Формула расчета периметра квадрата

У нас есть формула для определения периметра прямоугольника.

P ABCD = 2 * (AB + BC)

Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:

P ABCD = 4 * AB

Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.

Решение.
1. Нарисуем квадрат ABCD с исходными данными.

2. Вспомним формулу расчета периметра квадрата:

P ABCD = 4 * AB

3. Подставим в формулу наши данные:

P ABCD = 4 * 6 см = 24 см

Ответ: P ABCD = 24 см.

Задачи на нахождение периметра прямоугольника

1. Измерь ширину и длину прямоугольников. Определи их периметр.

2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.

3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.

Где используется расчет периметра прямоугольника?

1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?

В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.

2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.

Что такое площадь прямоугольника?

Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .

Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.

S AKMO = AK * KM

Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?

S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .

Ответ: 14 см 2 .

Формула вычисления площади квадрата

Площадь квадрата можно определить, умножив сторону саму на себя.

Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.

S AВСО = AB * BC = AB * AB

Пример.
Определи площадь квадрата AKMO со стороной 8 см.

S AKMО = AK * KM = 8 см * 8 см = 64 см 2

Ответ: 64 см 2 .

Задачи на нахождение площади прямоугольника и квадрата

1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.

2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.

Прежде, чем решать задачи на нахождение периметра и площади геометрических фигур, напомню, что….

I уровень

1.Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь.

2.Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.

3.У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.

4.Найдите периметр и площадь прямоугольника со сторонами 6 см и 8 см.

5.Длина прямоугольника 8 дм, ширина 5 дм. Найди его площадь.

6. Вычисли площадь прямоугольника, длины сторон которого равны 6 мм и 8 мм.

7.Ширина прямоугольника 7 дм, а длина 12 дм. Вычисли площадь.

8.Длина прямоугольника 9 дм, ширина 7 см. Найди его площадь.

9.Длина стороны квадрата 6 см. Узнай площадь.

10.Вычисли периметр квадрата со стороной 4 см.

11.Ширина прямоугольника равна 9 дм, а длина на 6 дм больше. Найдите его площадь.

12.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.

13.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 3 раза больше. Найди его периметр и площадь.

14.Начерти прямоугольник, длина одной стороны которого 6 см, а длина другой в 2 раза больше. Найди его периметр и площадь.

15.Начерти прямоугольник, ширина которого равна 2 см, а длина на 3 см больше. Вычисли его периметр.

16.Сторона квадрата равна 3 см. Чему равен периметр?

17.Лист бумаги имеет квадратную форму. Его сторона равна 10 см.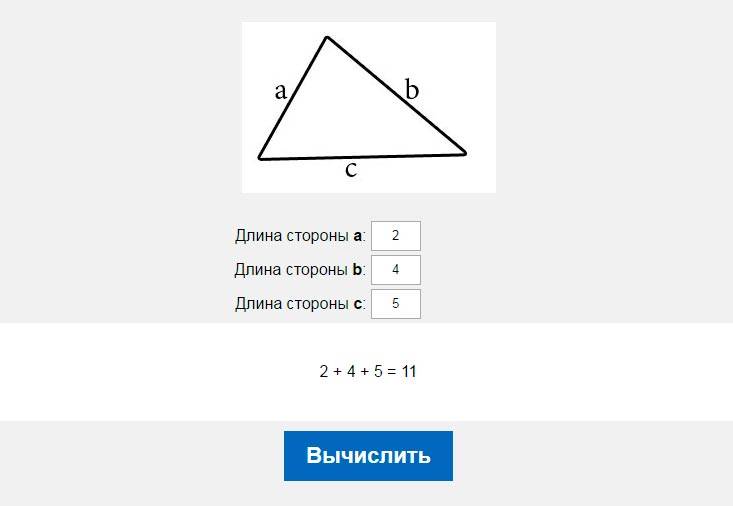 Чему равен периметр?

18.Начерти квадрат со стороной 6 см. Найдите его периметр. Периметр квадрата равен 28 см. Чему равна его сторона?

19.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.

20.Ширина прямоугольника 4 дм, а длина в 5 раз больше ширины. Найди площадь прямоугольника.

21.Площадь прямоугольника 36 см², его длина 9 см. Чему равна ширина прямоугольника?

II уровень

1.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 4 раза больше. Найди его периметр и площадь.

2.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.

3.Дано: прямоугольник, а = 8 дм, в — на 2 см меньше. Найди Р и S.

4.Длина прямоугольника 12 см, а его ширина на 2 см меньше. Найдите площадь и периметр прямоугольника.

5.Сумма двух сторон квадрата 12 дм. Найдите периметр и площадь квадрата.

6.Найдите длину прямоугольника по его ширине – 8 дм и периметру–30 дм.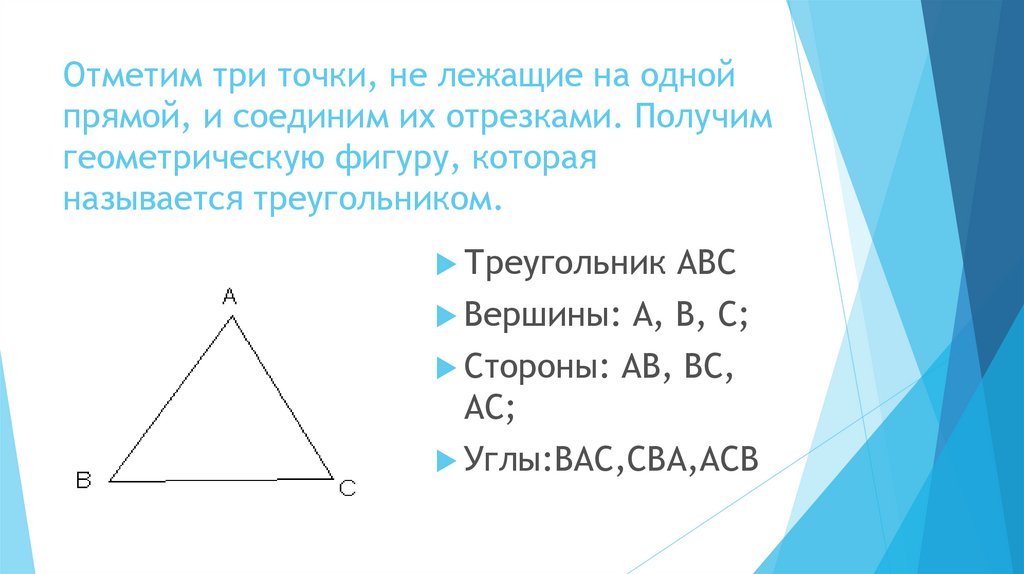

7.Периметр квадрата равен 32 см. Чему равна его сторона?

8.Периметр треугольника 21 см. Надите длину третьей стороны этого треугольника, если длины двух сторон 7 см и 8 см.

9.Периметр прямоугольника 20 см. Длина его стороны 6 см. Узнайте ширину прямоугольника и начертите его.

10.Площадь прямоугольника равна 270 кв.см, его длина 9 дм. Найдите периметр этого прямоугольника.

11.Периметр прямоугольника равен 54 м . Найдите площадь этого прямоугольника, если одна его сторона равна 18 м.

12. Найдите площадь квадрата, периметр которого равен 360 мм.

13. Периметр прямоугольника 40 см. Одна сторона 5 см.Чему равна его площадь?

14. Начерти квадрат, периметр которого равен периметру прямоугольника со сторонами 2 см и 6 см.

15. Дачный участок прямоугольной формы имеет длину 20 м и ширину 12 м. Какой длины забор надо поставить вокруг участка?

16. Периметр квадрата равен периметру треугольника со сторонами 6 см, 3 см и 7 см. Чему равна длина стороны квадрата?

17. У какой фигуры площадь больше и на сколько: у квадрата со стороной 4см или у прямоугольника со сторонами 2 см и 6 см?

18. Периметр прямоугольника равен 54 м. Найди площадь этого прямоугольника, если одна его сторона равна 18 м.

19. Периметр квадратной песочницы 12 м. Найдите площадь этой песочницы.

20. Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 24 см.

Составила К ислова Людмила Борисовна

Разделы: Начальная школа

Построение урока:

Организация и мотивация учащихся к деятельности на уроке.
Организация восприятия нового материала на основе наглядного материала
Организация осмысления.
Первичная проверка понимания нового материала.
Организация первичного закрепления и самостоятельный анализ учебной информации.
Применение полученных знаний на практикуме.

Цели урока:

Обучающая. Обеспечить усвоение учащимися нахождения площади и периметра геометрических фигур;

визуального восприятия материала на уроке; осмыслено понимать, что такое площадь и периметр.

2. Развивающая. Использовать на уроке развивающие упражнения, активизировать

мыслительную деятельность школьников.

3. Воспитательная. Обеспечить развитие ценностно-смысловой культуры учащихся;

мотивации на умение правильно достигать поставленной цели —

совпадение ожидания и результата.

Оборудование:

М.И.Моро и др. “Математика” — учебник для 3 класса начальной школы, 1 часть.
Рабочая тетрадь по математике.
Ручка, линейка, простой карандаш, треугольник, ножницы.
Модели геометрических фигур для нахождения площади.
Над доской плакаты с формулами нахождения площади и периметра.

Средства обучения:

Дидактический материал.
Наглядные пособия.

Приемы обучения:

Сравнение предметов.
Сопоставления способов нахождения площади одной и той же фигуры.

Ход урока.

1. Организационный момент и сообщение темы урока.

Учитель: Здравствуйте, ребята. Сегодня мы продолжим изучение большой темы под названием “Площадь и периметр”. Тема нашего урока сегодня:“Умение применять знания в нахождении периметра и площади сложной фигуры”. Сложная фигура – это геометрическая фигура, состоящая из нескольких простейших фигур. Сначала, повторим то, что мы с вами изучили на прошлых уроках.

II. Устный счет.

Задачи на развитие.

Учитель: Найдите площадь данной фигуры, если сторона квадрата 1 см.

Фигура изображена на доске.

Ученик: Если 1 квадрат имеет площадь 1 см 2 , а квадратов изображено 5, то площадь этой фигуры равна 5 см 2 .

Учитель: Правильно. Следующее задание. Уберите 3 палочки, чтобы осталось 3 таких квадрата.

Ученик выходит к доске и убирает 3 палочки.

Учитель: Уберите 4 палочки, чтобы осталось 3 таких же квадрата.

Ученик выходит к доске и убирает 4 палочки. Решение.

III. Работа по теме урока

Учитель: Какие геометрические фигуры вы уже знаете?

Ученик: Прямоугольник.

Ученик: Квадрат.

Учитель: Правильно. Что мы знаем о квадрате?

Ученик: У квадрата 4 стороны и 4 угла.

Учитель: Правильно. Каким свойством обладают стороны квадрата?

Ученик: Они равны.

Учитель: Правильно. А какие углы у квадрата?

Ученик: Они прямые.

Учитель: С помощью чего мы можем построить прямой угол?

Ученик: С помощью треугольника.

Ученик: С помощью линейки, карандаша и треугольника.

Ученики в тетрадях строят квадрат и раскрашивают его.

Учитель: Эта геометрическая фигура. Как найти периметр и площадь этого квадрата?

Ученик: Периметр – это сумма всех его сторон. Сторон у квадрата 4. Значит, 4 сложим 4 раза.

Учитель: Как это записать?

Ученики делают запись в тетради: “Найти площадь фигуры F1”.

Ученика вызывают к доске, и он пишет: Р = 4 + 4 + 4 + 4 = 16 (см)

Ученики делают запись в тетради.

Учитель: В каких единицах еще измеряется периметр?

Ученик: В сантиметрах, в миллиметрах, в метрах, в дециметрах, в километрах.

Учитель: Молодец! Как еще можно записать периметр?

Ученик: С помощью умножения.

Ученик записывает на доске: Р = 4 · 4 = 16 (см)

Ученики записывают в тетради.

Учитель: А чему равна площадь квадрата?

Ученик: Длину квадрата умножаем на его ширину. Так как стороны у квадрата равны, то

S = 4 · 4 = 16 (см 2)

Ученики делают запись в тетрадке и записывают — “Ответ: S = 16 см 2 ”.

Учитель: Какие еще единицы измерения площади вы знаете?

Ученик: квадратный сантиметр, квадратный дециметр, квадратный метр, квадратный миллиметр.

Учитель: А теперь усложним задачу. Перед вами лежит карточка.

Ученики выполняют эту работу и делают запись в тетрадке: “Найти площадь фигуры F2”.

Ученик: Нужно найти площадь маленького квадратика со стороной 2 см.

Ученик выходит к доске и записывает – S2 = 2 · 2 = 4 (см 2)

Ученики делают запись в тетрадке

Ученик: Из площади большого квадратика вычесть площадь маленького.

Учитель: Правильно.

Ученик записывает на доске – S = S1 – S2 = 16 – 4 = 12 (см 2)

Ученики делают запись в тетрадке.

Ученики думают и говорят разные варианты.

Один из вариантов оказался очень интересным.

Ученик: Можно так разрезать, чтобы получились прямоугольники и показывает на доске, как это можно сделать.

Ученики разрезают фигуру, как показано на доске.

Учитель: А как находится площадь прямоугольника?

Ученик: Нужно длину умножить на ширину.

Учитель: У вас получилось четыре фигуры. Что можно сказать про них?

Ученик: Две фигурки, как близнецы – одинаковые, и вторые две – тоже одинаковые.

Можно найти площадь одной фигуры и умножить на 2.

Ученик решает на доске: S1 = 1 · 4 = 4 (см 2)

S2 = 1 · 2 = 2 (см 2)

S = 2 · S1 + 2 · S2 = 2 · 4 + 2 · 2 = 8 + 4 = 12(см 2)

Учитель: Молодец! У нас получилась то же значение площади, что и раньше.

Ученики пишут в тетрадке – “Ответ: S = 12 см 2 .”

Учитель: Вы, наверное, устали?

Настало время отдыхать.

Предлагаю усталость

Физкультминуткой снять.

IV. Физкультминутка.

Учитель: А теперь сели за парты и

посмотрите на следующую модель. Фигура F3

Как найти площадь этой интересной фигуры?

Ученик: Треугольник, который выступает

можно отрезать и подставить в ту часть, где

треугольник “уходит” внутрь.

Учитель: Давайте возьмем ножницы, отрежем треугольник и подставим в верхнюю часть.

Что за фигура у нас получилась?

Ученик: Прямоугольник!

Учитель: Как найти площадь этого прямоугольника,

Если стороны нам неизвестны.

Ученик: Мы можем взять линейку и измерить

длину и ширину прямоугольника.

Ученики делают запись – “Найти площадь фигуры F3”.

Ученики линейкой измеряют длину и ширину. Получается длина, а = 6 см, ширина в = 2 см.

Ученик: Площадь данной фигуры равна S = 6 · 2 = 12 (см 2).

Ученики делают запись в тетрадке и записывают – “Ответ: S = 12 см 2 .

Учитель: Но это еще не все. Перед вами следующая фигура. Необходимо найти ее площадь.

Что за фигура перед вами?

Ученик: Треугольник. Но площадь треугольника

мы не умеем находить!

Учитель: Это правда. Из этого треугольника

сделаем прямоугольник. Я вам подскажу. Фигура F4

Сначала мы этот треугольник сложим пополам

Ученики: Мы поняли! Правую

сторону переворачиваем.

Получится прямоугольник.

Ученик: С помощью линейки измеряем

длину а и ширину в, и по S = а· в,

находим площадь.

Учитель: Если мы при измерении, мы

получим, что длина

будет выражена в мм, а ширина в см,

что нам делать?

Ученик: Обязательно длину и ширину перевести в одну единицу измерения.

Ученики записывают в тетрадке: “Найти площадь фигуры F4”.

V. Работа в парах.

Ученики выполняют задание и результаты

записывают в тетрадь.

Учитель: Что у вас получилось?

Ученик: Квадрат со стороной 3 см. Р = 3 · 4 = 12(см)

S = 3 · 3 = 9 (см 2) 3 см

Ученики записывают: “Ответ: P = 12 см, S = 9 см 2 .

Учитель: Молодцы! А теперь я вам предлагаю поработать самостоятельно.

Найти площадь следующей фигуры. Она лежит перед вами.

VI. Самостоятельная работа по закреплению изученного материала.

Учитель раздает заранее заготовленные фигуры.

Ученики самостоятельно, без помощи учителя, разрезают эту фигуры, получают три прямоугольника.

Ученики делают запись: “ Найти площадь фигуры F5”.

записывают: “Ответ: S = 16 см 2 ”.

Учитель: Понравился урок?

Ученики: Да.

Учитель: Что вы нового узнали на этом уроке?

в другую. Сегодня хорошо отвечали следующие ученики. . .

Учитель выставляет оценки.

VII. Домашнее задание: учебник стр. 77 № 8.

3 КЛАСС

1) Сторона квадрата равна 3 см. Чему равен периметр?

2) Длина прямоугольника 5 см, а ширина 4 см. Чему равен периметр?

3) Крышка стола имеет прямоугольную форму. Длина 90 см, а ширина 60 см. Чему равен периметр?

4) Начертите квадрат со стороной 6 см. Найдите его периметр.

5) Лист бумаги имеет квадратную форму. Его сторона равна 10 см. Чему равен периметр?

6) Огород прямоугольной формы имеет границу в 1000 м. Какие размеры могут иметь длина и ширина огорода? (Привести несколько решений в целых числах. )

7) Сторона прямоугольника а = 4 см, а b — на 2 см длиннее. Чему равен периметр?

8) Сторона квадрата равна 6 см. Чему равен периметр?

9) Начертите прямоугольник шириной 4 см, а длиной в два раза больше. Найдите его периметр.

10) Сторона прямоугольника а = 4 см, а периметр равен 14 см. Чему равна сторона b?

11) Периметр квадрата равен 24 см. Чему равна его сторона?

12) Одна сторона прямоугольника 1 дм, это на 3 см больше его другой стороны. Узнайте периметр и начертите прямоугольник.

13) Сторона прямоугольника а = 7 см, а b — на 2 см короче. Чему равен периметр прямоугольника?

14) Сторона прямоугольника а = 5 см, Р = 16 см. Чему равна сторона b?

15) Периметр прямоугольника 20 см. Длина его стороны 6 см. Узнайте ширину прямоугольника и начертите его.

16) Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 24 см.

17) Периметр квадрата равен 28см. Чему равна его сторона?

18) Участок земли имеет форму прямоугольника, длина которого 69 м, а ширина 31 м. Какой длины забор окружает этот участок?

19) Начертите квадрат со стороной 5 см. Найдите его периметр.

20) Чему равна сторона классной доски, если её периметр 10 м, а ширина 20 дм?

21) Периметр прямоугольника 64 см. Найдите его длину, если ширина 14 см.

22) Чему равен периметр треугольника со сторонами 10 см, 18 см и 9 см?

23) В парке прямоугольной формы длиной 160 м и шириной 80 м на расстоянии 2 м от ограды сделана аллея. Найдите ее длину.

24) Узнайте периметр хоккейной коробки, если её длина 15 м, а ширина 90 дм.

25) Участок земли имеет форму прямоугольника, ширина которого 28 м, а длина на 14 м больше. Он обнесён проволокой в 7 рядов. Сколько метров проволоки потребовалось?

26) Сколько тесьмы нужно купить для обшивки ковра длиной 2 м и шириной 15 дм?

27) Длина и ширина 1 листа кровельной стали вместе составляют 2130 мм. Какова длина и ширина листа, если длина в два раза больше ширины?

28) Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 36 см (в целых числах).

29) Начертите прямоугольник длиной 6 см, а шириной в два раза меньше. Чему равен его периметр?

30) Какой участок земли имеет большую ограду: квадратный со стороной 40 м или прямоугольный со сторонами 40 м и 30 м?

31) Сумма сторон треугольника с тремя равными сторонами 27 дм. Чему равна его сторона?

32) Найдите периметр прямоугольника длиной 5 дм, шириной 7 см.

33) Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 48 см (в целых числах).

34) Комната имеет 8 м длину и 4 м ширину. Сколько нужно кусков бордюра для оклейки комнаты? Длина куска бордюра 12 м.

{module Адаптивный блок Адсенс в конце статьи}

Периметр треугольника Формула

Периметром любой двумерной фигуры является расстояние, измеренное вокруг нее. Складывая длины каждой из сторон, мы можем измерить диаметр любой замкнутой формы. В этой статье вы узнаете определение периметра и как вычислить периметр различных типов треугольников, когда определены длины всех сторон. Учащиеся могут найти диаметр прямоугольного треугольника, если известны длины только двух сторон. Наконец, учащиеся узнают, как использовать закон косинусов для нахождения периметра любого треугольника, для которого они знают длины двух сторон и вычисление угла между ними («треугольник SAS»).

Окружность треугольника — это полная длина внешней границы треугольника. Или, другими словами, длина окружности треугольника равна количеству его трех сторон. Периметр измеряется так же, как измеряются стороны треугольника.

Если ABC — треугольник, где AB, BC и AC — длины его сторон, то периметр треугольника по формуле ABC определяется по формуле:

Формула для нахождения периметра треугольника = AB + BC + AC

In Кроме того, длина окружности треугольника имеет ту же единицу, что и длины его ребер. Если длины его сторон измеряются в отдельных единицах, сначала переведите их в одну и ту же единицу.

Треугольники делятся на три группы в зависимости от длины их сторон:

Две равные стороны и два равных внутренних угла определяют равнобедренный треугольник. Если известны основание и стороны равнобедренного треугольника, можно вычислить его диаметр.

Формула периметра равнобедренного треугольника

[Изображение будет загружено в ближайшее время]

Периметр равнобедренного треугольника = a + b + c

Поскольку стороны AB и AC имеют одинаковую длину, мы можем записать формулу следующим образом.

Формула периметра равнобедренного треугольника = a + a + c или b + b + c

Это также может быть записано как 2a + c или 2b + c или 2 x равные стороны + c

Полупериметр треугольника

Полупериметр треугольника определяется как половина его периметра. Обозначается с.

Формула полупериметра треугольника с длинами сторон a, b и c определяется как

\[s=\frac{a+b+c}{2}\]

Полупериметр чаще всего используется для треугольники.

Периметр равностороннего треугольника Формула

Равносторонний треугольник — это треугольник с равными сторонами и равным углом с обеих сторон. Внутренние углы равностороннего треугольника почти одинаковы и составляют 60 градусов.

[Изображение будет загружено в ближайшее время]

Где

a — сторона равностороннего треугольника.

h — высота равностороннего треугольника.

Периметр равностороннего треугольника равен a + b + c.

Длины сторон равностороннего треугольника равны.

В результате периметр равностороннего треугольника рассчитывается как a + a + a= 3a.

Эту формулу также можно записать так:

Периметр равностороннего треугольника = 3 x сторона

Как найти периметр треугольника, зная длины всех трех сторон?

Когда даны только две стороны, мы можем измерить периметр треугольника в прямоугольных треугольниках.

[Изображение скоро будет загружено]

Для этого используется теорема Пифагора. Прямоугольный треугольник — это тот, у которого есть одна 90 ^o угол.

Катеты треугольника, обозначенные буквами a и b, образуют угол 90 ^o. Гипотенуза — это сторона треугольника, которая разделяет два катета и лежит напротив угла 90 ^o. Гипотенуза, или самая длинная сторона треугольника, обозначается буквой с.

Следующие формулы можно использовать для нахождения недостающей стороны прямоугольного треугольника, только когда известны две другие стороны:

a ² + b ² = c ² 9{2}}\]

После того, как мы найдем недостающую сторону, мы можем использовать формулу периметра для вычисления периметра треугольника.

Когда мы знаем длины двух сторон треугольника, а также угол, который существует между ними, мы можем использовать закон косинусов, чтобы найти недостающую сторону, когда мы знаем сторону-угол-сторону (SAS).

[Изображение будет загружено в ближайшее время]

Каждая сторона треугольника соответствует углу, непосредственно противоположному ей, когда она обозначена таким образом. Мы можем использовать следующие формулы, чтобы найти недостающие стороны в любом треугольнике с учетом информации SAS, если мы тщательно разметим наш треугольник:

A ² = B ² + C ² — 2BC.COSA

B ² = A ² + C ² — 2AC.COSB

C ² = A ^{= A ^{= A ^{= A ^{= A ^{= A ^{= A ^{= A ^{= A ^{= A ^{= A ^{= A ^{= A ^{= A ^{= A ^{= A} =} =} =} — 2AC.COSB}}}}}}}}}}}

C ² = — 2AC.COSB

C ² — 2 . + b ² — 2ab.cosC

После того, как мы вычислили правую часть уравнения, нам нужно возвести в квадрат обе стороны, чтобы получить окончательную длину недостающей стороны. Периметр треугольника можно рассчитать по формуле периметра.

Решенные примеры:

1.Вычислите длину окружности треугольника со сторонами 6 см, 8 см и 12 см.

Ответ: Дано,

a = 6 см

b = 8 см

c = 12 см

Формула периметра треугольника = a + b + c

= 6 + 8 + 12

9003 900 см

2. Вычислите периметр равностороннего треугольника со стороной 5 см.

Ответ: Мы знаем, что в равностороннем треугольнике все стороны равны.

Таким образом, a = 5

Формула периметра равностороннего треугольника = 3a

= 3 x a

= 3 x 5

= 15 см

3. Найдите периметр равнобедренного треугольника с равными сторонами по 4 см. Длина третьей стороны равна 7 см.

Ответ: Мы знаем, что в равнобедренном треугольнике две стороны равны.

Дано, a = 4, b = 4 и c = 7

Формула для вычисления периметра равнобедренного треугольника = a +b + c = a + a + c = 2a + c

= 2 x 4 + 7

= 8 + 7

= 25 см

Заключение

Мы обсудили, как найти периметр треугольника, когда стороны известны, а также когда одна из сторон отсутствует.

Периметр треугольника определяется следующими способами:

Суммарная длина сторон треугольника называется его периметром. Стороны треугольника могут быть равными или разными.
Равносторонний треугольник – это треугольник с одинаковой длиной всех трех сторон.
Если две стороны равны, то треугольник равнобедренный.

Периметр треугольника – формула, определение и примеры

Содержание

Периметр треугольника

Периметр треугольника равен P= a+b+c, где a,b,c — стороны треугольников. Периметр любой двумерной фигуры определяется как расстояние вокруг нее. Комбинируя длины каждой из сторон, мы можем вычислить периметр любой замкнутой формы. В этом уроке вы узнаете, что такое периметр и как вычислить периметр различных типов треугольников, когда известны длины всех сторон. Кроме того, решенные примеры помогут вам получить дополнительные точки зрения на предмет.

Площадь параллелограмма – формула, определение, примеры

Периметр треугольника — определение

Периметр любого многоугольника равен сумме длин его сторон.

Периметр = сумма трех сторон треугольника

В своем окончательном ответе всегда упоминайте единицы измерения. Если стороны треугольника измеряются в сантиметрах, конечный результат также должен быть в сантиметрах.

Площадь ромба – формула и примеры для класса 8

Периметр треугольника- Формула

В большинстве случаев периметр замкнутой фигуры равен длине внешней линии фигуры. В результате периметр треугольника равен сумме трех его сторон. Если треугольник имеет три стороны, a, b и c, то

Периметр, P = a + b +c

Периметр различных видов треугольников

Периметр треугольника можно рассчитать, сложив длины трех сторон треугольника. Но существуют и разные методы вычисления периметра треугольников разных типов.

Периметр равнобедренного треугольника

Поскольку две стороны равнобедренного треугольника равны, а одна сторона имеет другую длину, чем две другие, поэтому периметр равнобедренного треугольника также можно рассчитать по формуле:

Периметр, P= (2 × A) + B

Где A — длина двух равных сторон, а B — длина третьей стороны.

Периметр равностороннего треугольника

Поскольку все стороны равностороннего треугольника равны друг другу, периметр равностороннего треугольника также можно вычислить по формуле:

Периметр, P= 3 × L

Где L длина сторон треугольника.

Периметр разностороннего треугольника

Поскольку все стороны разностороннего треугольника имеют разную длину, его можно вычислить только по обычной формуле:

Периметр, P = A + B С

Где A, B, C длины сторон треугольника.

Периметр треугольника – Примеры

Пример 1: Найдите периметр треугольника, стороны которого равны 7 см, 8 см и 5 см.

Решение : Поскольку все три стороны не равны, следовательно, это разносторонний треугольник, и мы можем вычислить периметр только обычным методом. т.е. Р=А+В+С.

A = 7 см

B = 8 см

C = 5 см

Периметр = сумма всех сторон = A + B + C = 7 + 8 + 5 = 20

Следовательно, ответ 20 см.

Пример 2 : Найдите периметр треугольника, каждая сторона которого равна 15 см.

Решение : Поскольку все три стороны равны по длине, данный треугольник является равносторонним, и, следовательно, периметр можно рассчитать по формуле: P = 3 × L.

Здесь L = 15 см

Следовательно, периметр = 3 × 15 = 45

Следовательно, периметр данного треугольника равен 45 см.

Пример 3 : Какова длина третьей стороны треугольника, периметр которого равен 50 см, а две стороны равны 15 см и 12 см?

Решение : Дано,

Периметр, P = 50 см

По формуле: P = A + B + C

A = 15 см

B = 12 см

903 C + 1 + 1

C = 50 – 27 = 23

Длина недостающей стороны 23 см.

Пример 4. Вычислите периметр прямоугольного треугольника с основанием 6 см и высотой 8 см.

Во-первых, используя теорему Пифагора, мы можем вычислить гипотенузу прямоугольного треугольника.

h =√(base ² + height ² )

h = √(6 ² +8 ² )

h = √(36 + 64)

h = √100

Или h = 10 см

Итак, периметр треугольника = 6 + 8 + 10 = 24 см.

Связанный пост:

Единица силы — Что такое единица силы СИ и СГС?
Полная форма CNG в науке и медицине
Штукатурка — Формула, Применение
формула отбеливающего порошка и химическое название

Формула периметра треугольника – часто задаваемые вопросы

Что означает периметр треугольника?

Общее расстояние вокруг сторон треугольника называется его периметром.

Общая для всех фигур теория

Формулы периметров разных фигур

Как быть, если неизвестна длина одной или нескольких сторон треугольника?

Примеры задач

Как найти периметр квадрата

Как найти периметр прямоугольника

Как найти периметр треугольника

Как найти периметр параллелограмма

Как найти длину окружности

Задания на нахождения периметра и площади. Задачи на нахождение периметра и сторон геометрических фигур материал по математике (2 класс)

Что такое прямоугольник и квадрат

Что такое периметр прямоугольника? Формула расчета периметра

Формула расчета периметра квадрата

Задачи на нахождение периметра прямоугольника

Где используется расчет периметра прямоугольника?

Что такое площадь прямоугольника?

Формула вычисления площади квадрата

Задачи на нахождение площади прямоугольника и квадрата

I уровень

II уровень

Периметр треугольника Формула

Полупериметр треугольника

Периметр равностороннего треугольника Формула

Как найти периметр треугольника, зная длины всех трех сторон?

Решенные примеры:

Заключение

Периметр треугольника – формула, определение и примеры

Периметр треугольника

Добавить комментарий Отменить ответ