Период колебаний пружинного маятника – формула для свободных и незатухающих колебаний
4.7
Средняя оценка: 4.7
Всего получено оценок: 78.
4.7
Средняя оценка: 4.7
Всего получено оценок: 78.
Одной из простейших колебательных систем, удобных для изучения, является пружинный маятник. Рассмотрим его подробнее, получим формулу периода колебаний.
Пружинный маятник
Идеальный пружинный маятник представляет собой некоторую точечную массу $m$, которая закреплена на одном конце пружины с постоянной жесткостью $k$, а другой конец пружины – закреплен к неподвижной опоре. Больше никакие силы на пружинный маятник не действуют, и он способен к совершению свободных незатухающих колебаний.
Рис. 1. Горизонтальный пружинный маятник.Уравнение движения пружинного маятника
Пусть начало координат находится в точке покоя маятника. Тогда, если маятник выведен из состояния равновесия на расстояние $x$, со стороны пружины на него начинает действовать сила $F=-kx$.
$$a=-{kx\over m}$$
Скорость – это производная координаты. А ускорение – производная скорости. Следовательно, ускорение – это вторая производная координаты. Получим уравнение:
$$x”=-{k\over m}x$$
То есть, вторая производная координаты пропорциональна самой координате, взятой с противоположным знаком. Это дифференциальное уравнение, и в высшей математике доказывается, что единственная функция, являющаяся его решением – это круговая функця (синус или косинус).
Полное же решение данного уравнения выглядит следующим образом:$$x(t)=A cos \sqrt{k\over m}t$$
Если взять вторую производную этой функции, то можно убедиться, что она равна самой себе, с противоположным знаком и необходимым коэффициентом.
Период колебаний маятника
Сравним полученное уравнение с уравнением гармонических колебаний:
$$x(t)=A cos( \omega t+\varphi)$$
Можно видеть, что фаза $\varphi$ в уравнении координаты движения маятника равна нулю, а коэффициент $\sqrt {k\over m}$ представляет собой круговую частоту.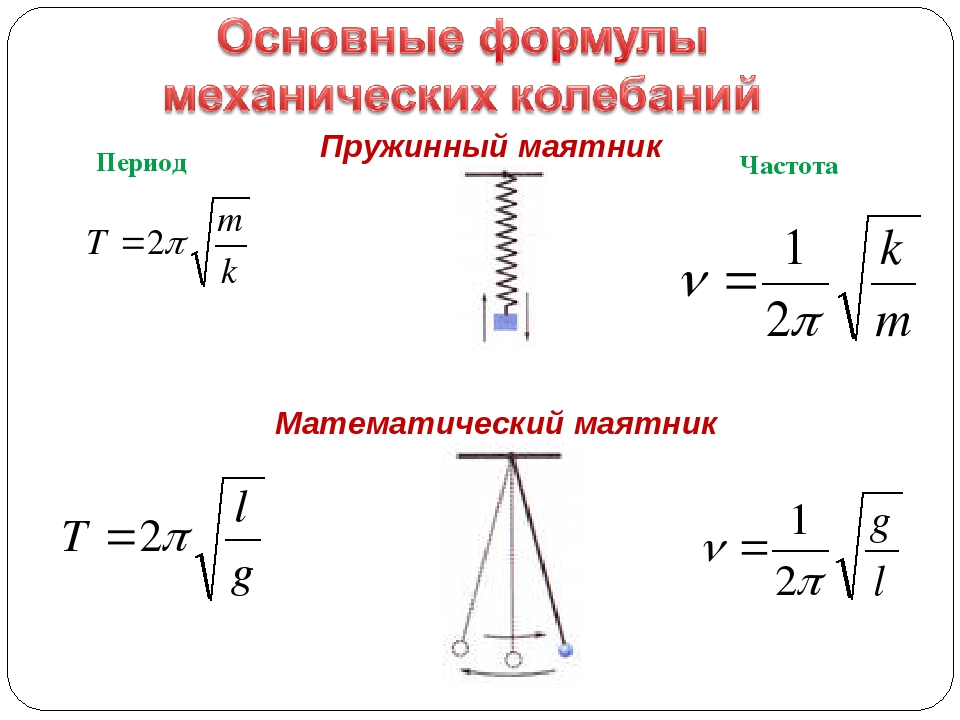
Учитывая формулу, связывающей круговую частоту и период, получим формулу периода колебаний пружинного маятника:
$$T={2\pi \over \omega}=2\pi\sqrt {m\over k}$$
Действительно, чем больше масса пружинного маятника, тем дольше будут совершаться колебания. А чем больше жесткость пружины, тем период колебаний будет меньше. Но величины эти связаны с периодом не прямо, а через коренную зависимость, то есть, для увеличения периода маятника вдвое, надо либо увеличить массу маятника вчетверо, либо во столько же раз уменьшить жесткость пружины.
Рис. 2. Период колебаний пружинного маятника.В реальности на маятник всегда действует сила тяжести, кроме того, в нем происходят потери, связанные с трением и нагревом пружины. Поэтому, его колебания будут затухающими, а их период будет немного отличаться от расчетного. Наиболее близким к идеальному пружинному маятнику является механизм часового балансира.
Что мы узнали?
Пружинный маятник – это точечная масса, двигающая под воздействием пружины постоянной жесткости.
Период колебаний пружинного маятника пропорционален корню из отношения его массы к жесткости пружины.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.7
Средняя оценка: 4.7
Всего получено оценок: 78.
А какая ваша оценка?
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
-
2.
4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
-
4. 4 Электромагнитные колебания и волны
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
-
6. 1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
-
6.
- 7 Общие темы
- 8 Новые страницы
4 Статика
4 Электромагнитные колебания и волны
1 Атомная физика. Квантовая теория
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
домашнее задание и упражнения — Влияние магнитного поля на период времени пружинного маятника
спросил
Изменено 3 года, 9 месяцев назад
Просмотрено 742 раза
$\begingroup$
Предположим, что у нас есть пружинный маятник, а рядом магнит.
Если предположить, что пружина притягивается к магниту, уменьшается ли период?
Формула периода времени = 2𝜋√m/k Будет ли магнитное поле иметь тот же эффект, что и увеличение g?
- домашние задания и упражнения
- экспериментальная физика
- гармонический осциллятор
$\endgroup$
5
$\begingroup$
Нетехническая версия: магнит тянет груз вниз, и величина этой силы увеличивается по мере растяжения пружины. Пружина тянет массу вверх, и величина этой силы также увеличивается по мере растяжения пружины. Таким образом, действие магнита заключается в уменьшении эффективной жесткости пружины, поскольку магнит действует против пружины. Чистая сила, действующая на массу от пружины и магнита вместе, увеличивается медленнее, чем сила от одной только пружины; Другими словами, добавление магнита в основном эквивалентно замене оригинальной пружины менее жесткой.
Техническая версия: Пусть $z$ — вертикальная координата массы, положительная величина $z$ отсчитывается от вниз на от нерастянутого положения пружины. На массу будут воздействовать три силы:
- Гравитация, где $F_g = +mg$;
- Сила пружины, при $F_s = — k z$; и
- Сила $F_m(z)$ со стороны магнита. Эта сила будет (предположительно) направлена вниз для всех значений $z$ и, как правило, будет возрастать по мере увеличения $z$: $dF_m/dz > 0$.
Пусть $z_0$ — координата, в которой система находится в равновесии. В этот момент чистые силы, действующие на массу, должны компенсироваться:
$$
F_g + F_s + F_m = mg — k z_0 + F_m(z_0)= 0.
$$
Теперь представим перемещение массы на небольшое расстояние $\epsilon$ от положения равновесия; другими словами, $z = z_0 + \epsilon$.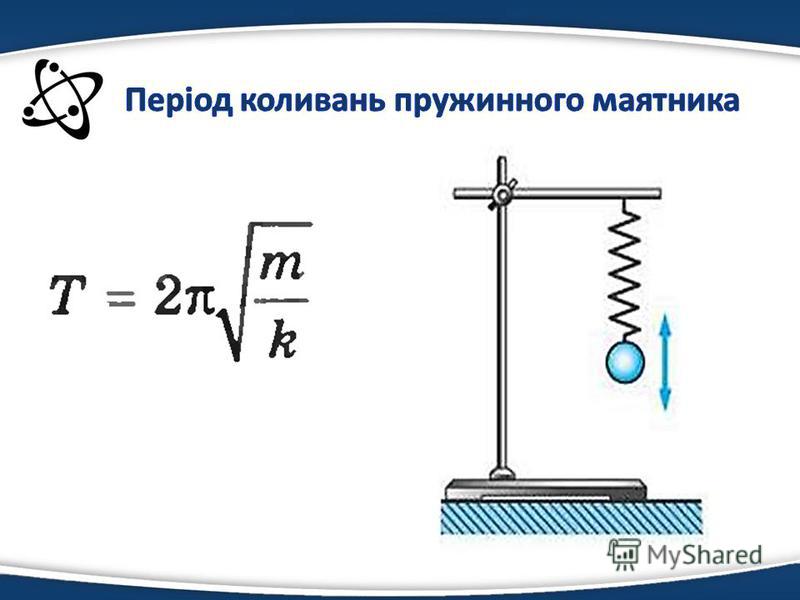
Поскольку $\ddot{z} = \ddot{\epsilon}$, второй закон Ньютона принимает вид:
\начать{выравнивать}
м \ddot{\epsilon} &= F_g + F_s + F_m \\
&= mg — k(z_0 + \epsilon) + F_m(z_0 + \epsilon) \\
&\приблизительно мг — k z_0 — k \epsilon + F_m(z_0) + F_m'(z_0) \epsilon
\end{выравнивание}
где мы разложили $F_m(z_0 + \epsilon)$ в ряд Тейлора на последнем шаге. Тогда из условия равновесия это сводится к
$$
m \ddot{\epsilon} = -(k — F_m'(z_0)) \epsilon
$$
и поэтому частота колебаний
$$
\omega = \sqrt{ \frac{k — F_m'(z_0)}{m}} < \sqrt{\frac{k}{m}}.
$$
Поскольку угловая частота массы в отсутствие магнита равна $\sqrt{k/m}$, заключаем, что период колебаний
(Все это предполагает, что $F_m'(z_0) < k$. Если бы это было не так, то положение равновесия было бы неустойчивым.)
$\endgroup$
2
Зарегистрируйтесь или войдите
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
ньютоновская механика — Почему ускорение $g$ под действием силы тяжести не влияет на период вертикально установленной пружины?
спросил
Изменено 4 года, 3 месяца назад
Просмотрено 33 тысячи раз
$\begingroup$
Для вертикальной пружины я искал формулу $ T= 2\pi \sqrt{m/k}$ для периода. Почему гравитационное ускорение $g$ не учитывается?
- ньютоновская механика
- ньютоновская гравитация
- гармонический осциллятор
- пружина
- осцилляторы
$\endgroup$
92}$, потому что производная константы ($mg/k$) равна нулю, а в правой части после распределения получается $-kx’$.
2} (yy_0) + \ tfrac {k} {m} (yy_0) = g.
$$
Квадрат частоты определяется коэффициентом $y-y_0$, в данном случае $\frac{k}{m}$, который, как вы заметите, не включает $g$.
$\endgroup$
$\begingroup$
Период колебаний зависит от возвращающей силы и инерции (массы), которая колеблется.
Гравитация — постоянная сила. Когда масса находится в положении равновесия, эта сила уравновешивается силой пружины. При отклонении массы от равновесия сила тяжести не меняется, изменяется только сила пружины. Возвращающая сила создается только усилием пружины.
Хотя гравитация влияет на то, каким будет равновесное удлинение, она не является восстанавливающей силой, поэтому не влияет на период колебаний массы на пружине.
Однако гравитация влияет на период маятника. Сила тяжести, действующая на массу маятника, постоянна и не зависит от смещения, но момент этой силы, заставляющий струну маятника вращаться обратно к положению равновесия, непостоянен.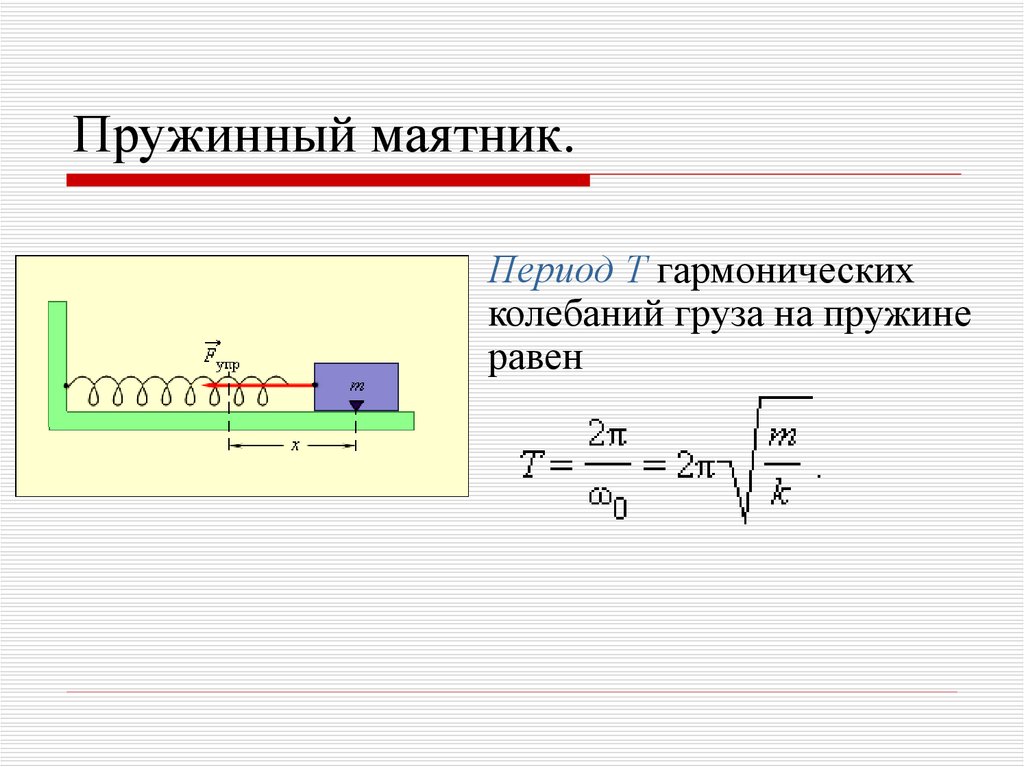
Она увеличивается с угловым смещением. Возвращающий момент (крутящий момент) зависит от силы тяжести, поэтому сила тяжести влияет на период маятника.
$\endgroup$
$\begingroup$
Когда мы подвешиваем пружинный маятник, то результирующая сила на этом маятнике равна нулю, то есть одна сила является силой тяжести, а другая сила противодействует гравитации. Таким образом, мы можем установить, что маятник находится в равновесии, потому что результирующая сила теперь равна нулю, если мы приложим внешнюю усилие на маятник, то он сдвинется на некоторое смещение и запустится СГМ.
$\endgroup$
$\begingroup$ 92$.
Анализ размерностей утверждает, что произвольной математической функции можно передать только выражение, не имеющее единиц измерения; вы найдете все способы объединить ваши базовые параметры в безразмерные параметры $\beta_{1,2,\dots}$, а затем любая другая величина, которую вы хотите рассчитать, должна иметь форму $\alpha~f(\beta_1,\beta_2,\ dots)$ вообще, где $\alpha$ — некоторая комбинация исходных параметров, имеющая правильные единицы измерения.