Интегралы для чайников с примерами решения
Содержание:
- Первообразная и неопределенный интеграл
- Пример с решением:
- Таблица интегралов
- Некоторые свойства неопределенного интеграла
- Постановка задачи. Нижняя и верхняя интегральные суммы
- Определенный интеграл. Теорема о существовании определенного интеграла
Я рассматривала такую задачу: дана функция требуется найти ее производную, т. е. функцию
В этой главе мы будем рассматривать обратную задачу: дана функция требуется найти такую функцию производная которой равна
Определение 1. Функция называется первообразной от функции на отрезке если во всех точках этого отрезка выполняется равенство
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Пример с решением:
Найти первообразную от функции
Из определения первообразной следует, что функция является первообразной, так как
Легко видеть, что если для данной функции существует первообразная, то эта первообразная не является единственной. Так, в предыдущем примере можно было взять в качестве первообразных следующие функции: или вообще (где — произвольная постоянная), так как С другой стороны, можно доказать, что функциями вида исчерпываются все первообразные от функции
Так, в предыдущем примере можно было взять в качестве первообразных следующие функции: или вообще (где — произвольная постоянная), так как С другой стороны, можно доказать, что функциями вида исчерпываются все первообразные от функции
Это вытекает из следующей теоремы.
Теорема. Если — две первообразные от функции на отрезке то разность между ними равна постоянному числу.
Доказательство. В силу определения первообразной имеем
при любом значении на отрезке
Обозначим
Тогда на основании равенств (1) будет или при любом значении на отрезке Но из равенства следует, что есть постоянная.
Действительно, применим теорему Лагранжа (см. § 2 гл. IV) к функции которая, очевидно, непрерывна и дифференцируема на отрезке Какова бы ни была точка на отрезке мы имеем в силу теоремы Лагранжа где
Так как , или
Таким образом, функция в любой точке отрезка сохраняет значение а это и значит, что функция является постоянной на отрезке Обозначая постоянную через из равенств (2) и (3) получаем
Из доказанной теоремы следует, что если для данной функции найдена какая-нибудь одна первообразная тo любая другая первообразная для имеет вид где
Определение 2. Если функция является первообразной для то выражение называется неопределенным интегралом от функции и обозначается символом
Если функция является первообразной для то выражение называется неопределенным интегралом от функции и обозначается символом
Таким образом, по определению, если При этом функцию называют подынтегральной функцией, — подынтегральным выражением, знак — знаком интеграла.
Таким образом, неопределенный интеграл представляет собой семейство функций
С геометрической точки зрения неопределенный интеграл представляет совокупность (семейство) кривых, каждая из которых получается путем сдвига одной из кривых параллельно самой себе вверх или вниз, т. е. вдоль оси
Естественно возникает вопрос: для всякой ли функции существуют первообразные (а значит, и неопределенный интеграл)? Оказывается, что не доя всякой. Заметим, однако, без доказательства, что если функция непрерывна на отрезке то для этой функции существует первообразная (а значит, и неопределенный интеграл).
Выяснению методов, с помощью которых находятся первообразные и неопределенные интегралы от некоторых классов элементарных функций, посвящён этот раздел статьи. |
Нахождение первообразной для данной функции называется интегрированием функции
Заметим следующее: если производная от элементарной функции всегда является элементарной функцией, то первообразная от элементарной функции может оказаться и не представимой с помощью конечного числа элементарных функций. К этому вопросу мы вернемся в конце данной главы.
Возможно вам будут полезны данные страницы:
Вычислить определенный интеграл |
Найти общий интеграл дифференциального уравнения |
Найти неопределённый интеграл: пример решения |
Таблица интегралов |
Из определения 2 следует:
1. Производная от неопределенного интеграла равна подынтегральной функции, т. е. если то и
Последнее равенство нужно понимать в том смысле, что производная от любой первообразной равна подынтегральной функции.
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:
Это получается на основании формулы (4).
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:
Справедливость последнего равенства легко проверить дифференцированием (дифференциалы от обеих частей равенства равный
Таблица интегралов
Прежде чем приступить к изложению методов интегрирования, приведем таблицу интегралов от простейших функций.
Непосредственно из определения 2 § 1 и таблицы производных (§ 15 гл. III) вытекает таблица интегралов. (Справедливость написанных в ней равенств легко проверить дифференцированием, т. е. установить, что производная от правой части равняется подынтегральной функции.)
1. (Здесь и и последующих формулах под понимается произвольная постоянная.)
Замечание. В таблице производных (§ 15 гл. Ill) нет формул, соответствующих формулам 7, 8, 1Г, 12, 13′ и 14. Однако справедливость последних также легко устанавливается с помощью дифференцирования.
Однако справедливость последних также легко устанавливается с помощью дифференцирования.
В случае формулы 7 имеем
следовательно,
В случае формулы 8
следовательно,
В случае формулы 12
следовательно,
Отметим, что последняя формула будет следовать также из общих результатов § 9. В случае формулы 14
следовательно,
Эта формула также будет следовать из общих результатов § 10.
Некоторые свойства неопределенного интеграла
Теорема 1. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов:
Для доказательства найдем производные от левой и правой частей этого равенства. На основании равенства (4) § 1 находим
Таким образом, производные от левой и правой частей равенства (1) равны между собой, т. е. производная от любой первообразной, стоящая в левой части, равняется производной от любой функции, стоящей в правой части равенства.
Следовательно, по теореме § 1 любая функция, стоящая в левой части равенства (1), отличается от любой функции, стоящей в правой части равенства (1), на постоянное слагаемое. В этом смысле и нужно понимать равенство (1).
Теорема 2. Постоянный множитель можно выносить за знак интеграла, т. е. если то
Для доказательства равенства (2) найдем производные от левой и правой его частей:
Производные от правой и левой частей равны, следовательно, как и в равенстве (1), разность двух любых функций, стоящих слева и справа, есть постоянная. В этом смысле и следует понимать равенство (2).
При вычислении неопределенных интегралов бывает полезно иметь в виду следующие правила.
1. Если
то
Действительно, дифференцируя левую и правую части равенства (3), получим
Производные от правой и левой частей равны, что и требозалось доказать.
II. Если
то
Если
то
Равенства (4) и (5) доказываются дифференцированием правой и левой частей равенств.
Пример 1.
Пример 2.
Пример 3.
Пример 4.
Пример 5.
Постановка задачи. Нижняя и верхняя интегральные суммы
Мощным средством исследования в математике, физике, механике и других дисциплинах является определенный интеграл—одно из основных понятий математического анализа. Вычисление площадей, ограниченных кривыми, длин дуг, объемов, работы, скорости, пути, моментов инерции и т. д. сводится к вычислению определенного интеграла.
Пусть на отрезке задана непрерывная функция (рис. 210 и 211). Обозначим через и ее наименьшее и наибольшее значения на этом отрезке. Разобьем отрезок на частей точками деления причем
и положим Обозначим, далее, наименьшее и наибольшее значения функции на отрезке через и на отрезке через и ..на отрезке через и Составим суммы
Сумму называют нижней интегральной суммой, а сумму —верхней интегральной суммой.
Если то нижняя инте;ральная сумма численно равняется площади «вписанной ступенчатой фигуры» ограниченной «вписанной» ломаной, верхняя интегральная сумма численно равняется площади «описанной ступенчатой фигуры»
ограниченной «описанной» ломаной.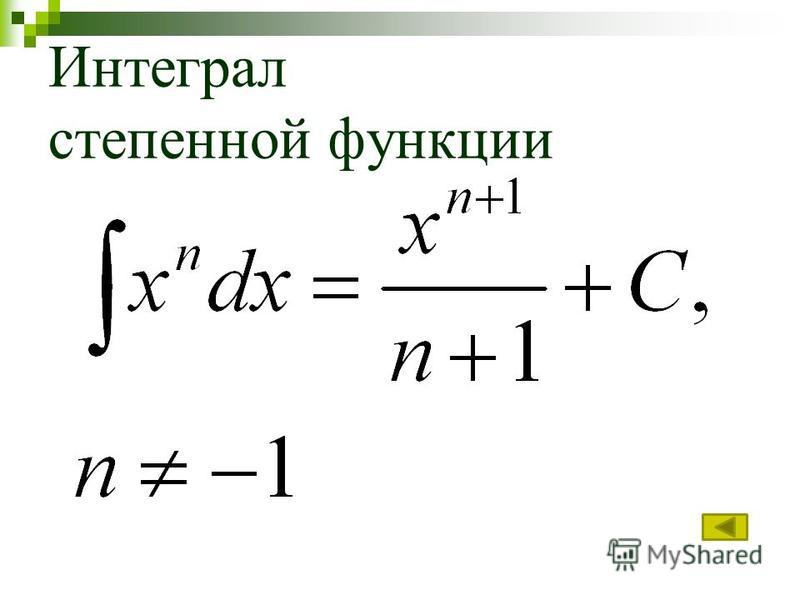
Отметим некоторые свойства верхних и нижних интегральных сумм.
а) Так как для любого то на основании формул (1) и (2) имеем
(Знак равенства будет только в случае, если
б) Так как где —наименьшее значение на то
Итак,
в) Так как где — наибольшее значение на то
Итак,
Соединяя вместе полученные неравенства, имеем
Если то последнее неравенство имеет простой геометрический смысл (рис. 212), так как произведения и соответственно численно равны площадям «вписанного» прямоугольника и «описанного» прямоугольника
Определенный интеграл. Теорема о существовании определенного интеграла
Продолжим рассмотрение вопроса предыдущего параграфа. В каждом из отрезков возьмем по точке, которые обозначим
в каждой из этих точек вычислим значение функции Составим сумму
Эта сумма называется интегральной суммой для функции на отрезке Так как при произвольном принадлежащем отрезку будет и все то
следовательно,
или
Геометрический смысл последнего неравенства при состоит в том, что фигура, площадь которой равна ограничена ломаной, заключенной между «вписанной» ломаной и «описанной» ломаной.
Сумма зависит от способа разделения отрезка на отрезки и от выбора точек внутри получающихся отрезков.
Обозначим теперь через наибольшую из длин отрезков Рассмотрим различные разбиения отрезка на отрезки такие, что — Очевидно, что при этом число отрезков в разбиении стремится к бесконечности. Для каждого разбиения, выбрав соответствующие значения можно составить интегральную сумму
Рассмотрим пекоторую последовательность разбиений, при которых при этом При каждом разбиении выбираем значения Предположим, что эта последовательность интегральных сумм*) стремится к некоторому пределу
Теперь мы можем сформулировать следующее
Определение 1. Если при любых разбиениях отрезка таких, что и при любом выборе точек на отрезках интегральная сумма
стремится к одному и тому же пределу то этот предел называют определенным интегралом от функции на отрезке и обозначают
Таким образом, по определению
Число называется нижним пределом интеграла, —верхним пределом интеграла. Отрезок называется отрезком интегрирования, —переменной интегрирования.
Отрезок называется отрезком интегрирования, —переменной интегрирования.
Определение 2. Если для функции предел (6) существует, то функцию называют интегрируемой на отрезке
Заметим, что нижняя интегральная сумма и верхняя интегральная сумма являются частными случаями интегральной суммы (5), поэтому если интегрируема, то нижняя и верхняя интегральные суммы стремятся к тому же пределу и потому на основании равенства (6) можем написать
Если построить график подынтегральной функции то в случае интеграл
будет численно равен площади так называемой криволинейной трапеции, ограниченной указанной кривой, прямыми и осью (рис. 214).
Поэтому если требуется вычислить площадь криволинейной трапеции, ограниченной кривой прямыми и осью то эта площадь вычисляется с помощью интеграла:
Докажем следующую важную теорему.
Теорема 1. Если функция непрерывна на отрезке то она интегрируется на этом отрезке.
Доказательство. Снова разобьем отрезок на отрезки Составим нижнюю и верхнюю интегральные суммы:
Для дальнейшего установим некоторые свойства верхних и нижних интегральных сумм.
Свойство 1. При увеличении числа отрезков, на которые мы разбиваем отрезок путем добавления новых точек деления, нижняя интегральная сумма может только возрастать, а верхняя интегральная сумма только убывать.
Доказательство.
Пусть отрезок разбит на отрезков путем добавления новых точек Если какой-то отрезок будет разбит на несколько отрезков, например, на отрезков, то в новой нижней интегральной сумме отрезку будет соответствовать слагаемых, которые~мы обозначим через . В сумме этому отрезку соответствует одно слагаемое Но для суммы и величины справедливо неравенство, аналогичное неравенству (4) § 1. Мы можем написать
Написав соответствующие неравенства для каждого отрезка и суммируя левые и правые части, получим
Свойство 1 доказано.
Свойство 2. Нижняя интегрируемая сумма (9) и верхняя интегральная сумма (10) при неограниченном увеличении числа отрезков путем добавления новых точек деления стремятся к некоторым пределам
Доказательство.
На основании неравенства (6) § 1 можем написать:
т. е. ограничена при всех На основании свойств монотонно возрастает при возрастании Следовательно, на основании теоремы 7 о пределах (см. § 5 гл. II) эта переменная величина имеет предел; обозначим его через
Аналогично устанавливается, что ограничена снизу и монотонно убывает. Следовательно, имеет предел, который мы обозначим через
Свойство 3. Если функция непрерывна на замкнутом отрезке то пределы и определенные в свойстве 2 при условии, что равны.
Этот общий предел обозначим через
Свойство 3. Если функция непрерывна на замкнутом отрезке то пределы и определенные в свойстве 2 при условии, что равны.
Этот общий предел обозначим через
Доказательство. Рассмотрим разность верхней и нижней интегральной суммы:
Обозначим через наибольшую из разностей -— при данном разбиении:
Можно доказать (на чем мы останавливаться не будем), что если функция непрерывна на замкнутом отрезке, то при любом
способе разбиения отрезка если только
Свойство непрерывной функции на замкнутом отрезке, выражаемое равенством (15), называется равномерной непрерывностью функции.
Итак, мы будем пользоваться теоремой: Непрерывная функция на замкнутом отрезке равномерно непрерывна на этом отрезке.
Вернемся к равенству (14). Каждую разность в правой части заменим не меньшей величиной Получаем неравенство
Переходя к пределу при получаем
т. e.
или что и требовалось доказать.
Свойство 4. Пусть —нижняя и верхняя интегральные суммы, соответствующие разбиениям отрезка на и соответственно на отрезков. Тогда имеет место неравенство
Тогда имеет место неравенство
при любых
Доказательство. Рассмотрим разбиение отрезка на отрезков, где точками деления будут точки деления первого и второго разбиений.
На основании неравенства (3) § 1 имеем
На основании свойства имеем
Пользуясь соотношениями (20) и (21), можно расширить неравенство (19):
что и требовалось доказать.
Свойство 5. Если функция непрерывна на отрезке то при любой последовательности разбиений отрезка на отрезки не обязательно путем присоединения новых
точек деления, если только нижняя интегральная сумма и верхняя интегральная сумма стремятся к пределу определенному в свойстве 3.
Доказательство. Рассмотрим последовательность разбиений последовательности верхних интегральных сумм определенных в свойстве 2. При любых значениях (на основании неравенства (18)) можем написать
Переходя к пределу при на основании (15) можем написать
Аналогичным способом докажем Итак,
или
Рассмотрим предел разности Так как функция непрерывна на замкнутом отрезке то (так же как и при доказательстве свойства 3) докажем (см. равенство (16)), что
равенство (16)), что
Перепишем последнее соотношение так:
На основании (22) каждая из разностей, стоящих в квадратных скобках, неотрицательна. Следовательно,
и окончательно получаем
что и требовалось доказать.
Теперь можно доказать и сформулированную выше теорему. Пусть непрерывна на отрезке Рассмотрим произвольную последовательность интегральных сумм такую, что — произвольная точка отрезка
Для данной последовательности разбиений рассмотрим соответствующие последовательности верхних и нижних интегральных сумм и Для каждого разбиения будут справедливы соотношения (2):
Переходя к пределу при и пользуясь равенствами (23) и теоремой 4 § 5 гл. II, получаем где предел, определенный в свойстве 3.
Этот предел, как уже говорилось выше, и называется определенным интегралом Итак, если непрерывна на отрезке то
Отметим, что среди разрывных функций есть как интегрируемые, Так и: неинтегрируемые.
Пример 10.
Вычислим интеграл
Решение:
Геометрически задача эквивалентна вычислению площади трапеции, ограниченной линиями (рис. 215).
Функция стоящая под знаком интеграла, непрерывна. Следовательно, для вычисления определенного интеграла мы вправе, как это было замечено выше, произвести разбиение отрезка произвольным способом и произвольно выбрать промежуточные точки Результат вычисления определенного интеграла не зависит от способа построения интегральной суммы — лишь бы шаг разбиения стремился к нулю.
Делим отрезок на равных отрезков.
Длина каждого частичного отрезка равна это число и будет
шагом разбиения. Точки деления имеют координаты В качестве точек возьмем левые концы каждого отрезка: Составим интегральную сумму (I). Так как
где Учитывая что (как сумма геометрической прогрессии), получим
Так как Итак,
Площадь (рис. 215) легко вычислить методами элементарной геометрии.
Результат получится тот же.
Пример 11.
Вычислить
Решение:
Данный интеграл равен площади криволинейной трапеции, ограниченной параболой ординатой и прямой (рис. 216).
Разобьем отрезок на равных частей точками
За точки возьмем крайние правые точки каждого из отрезков. Составим интегральную сумму:
Как известно, поэтому
Пример 12. Вычислить
Решение:
Пример 13.
Вычислить
Решение:
Снова разделим отрезок на равных частей: За точки возьмем левые крайние точки. Составим интегральную сумму:
Выражение в скобках есть геометрическая прогрессия со знаменателем и первым членом 1 поэтому Далее имеем ( По правилу Лопиталя Таким образом: т.е.
Замечание.
Только что рассмотренные примеры показывают, что непосредственное вычисление определенных интегралов как пределов интегральных сумм связано с большими трудностями. Даже в тех случаях, когда подынтегральные функции являются эчень простыми этот способ требует громоздких подсчетов. Нахождение же определенных интегралов от более сложных функций приводит к еще большим трудностям. Поэтому естественно возникает задача: найти практически удобный метод вычисления определенных интегралов. Этот метод, открытый Нью-гоном и Лейбницем, использует глубокую связь, существующую между интегрированием и дифференцированием.
Даже в тех случаях, когда подынтегральные функции являются эчень простыми этот способ требует громоздких подсчетов. Нахождение же определенных интегралов от более сложных функций приводит к еще большим трудностям. Поэтому естественно возникает задача: найти практически удобный метод вычисления определенных интегралов. Этот метод, открытый Нью-гоном и Лейбницем, использует глубокую связь, существующую между интегрированием и дифференцированием.
как решать, правила вычисления, объяснение Интеграл его виды и свойства
Данные свойства используются для осуществления преобразований интеграла с целью его приведения к одному из элементарных интегралов и дальнейшему вычислению.
1. Производная неопределенного интеграла равна подынтегральной функции:
2. Дифференциал неопределенного интеграла равен подынтегральному выражению:
3. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
4.
 Постоянный множитель можно выносить за знак интеграла:
Постоянный множитель можно выносить за знак интеграла:Причем a ≠ 0
5. Интеграл суммы (разности) равен сумме (разности) интегралов:
6. Свойство является комбинацией свойств 4 и 5:
Причем a ≠ 0 ˄ b ≠ 0
7. Свойство инвариантности неопределенного интеграла:
Если , то
8. Свойство:
Если , то
Фактически данное свойство представляет собой частный случай интегрирования при помощи метода замены переменной , который более подробно рассмотрен в следующем разделе.
Рассмотрим пример:
Сначала мы применили свойство 5, затем свойство 4, затем воспользовались таблицей первообразных и получили результат.
Алгоритм нашего онлайн калькулятора интегралов поддерживает все перечисленные выше свойства и без труда найдет подробное решение для вашего интеграла.
В этой статье мы перечислим основные свойства определенного интеграла. Большинство этих свойств доказываются на основе понятий определенного интеграла Римана и Дарбу .
Вычисление определенного интеграла очень часто проводится с использованием первых пяти свойств, так что мы будем при надобности на них ссылаться. Остальные свойства определенного интеграла, в основном, применяются для оценки различных выражений.
Прежде чем перейти к основным свойствам определенного интеграла , условимся, что a не превосходит b .
Для функции y = f(x) , определенной при x = a , справедливо равенство .
То есть, значение определенного интеграла с совпадающими пределами интегрирования равно нулю. Это свойство является следствием определения интеграла Римана, так как в этом случае каждая интегральная сумма для любого разбиения промежутка и любого выбора точек равна нулю, так как , следовательно, пределом интегральных сумм является ноль.
Для интегрируемой на отрезке функции выполняется .
Другими словами, при перемене верхнего и нижнего пределов интегрирования местами значение определенного интеграла меняется на противоположное. Это свойство определенного интеграла также следует из понятия интеграла Римана, только нумерацию разбиения отрезка следует начинать с точки x = b
.
Это свойство определенного интеграла также следует из понятия интеграла Римана, только нумерацию разбиения отрезка следует начинать с точки x = b
.
для интегрируемых на отрезке функций y = f(x) и y = g(x) .
Доказательство.
Запишем интегральную сумму функции для данного разбиения отрезка и данного выбора точек :
где и — интегральные суммы функций y = f(x)
и y = g(x)
для данного разбиения отрезка соответственно.
Переходя к пределу при получим , что по определению интеграла Римана равносильно утверждению доказываемого свойства.
Постоянный множитель можно выносить за знак определенного интеграла. То есть, для интегрируемой на отрезке функции y = f(x) и произвольного числа k справедливо равенство .
Доказательство этого свойства определенного интеграла абсолютно схоже с предыдущим:
Пусть функция y = f(x) интегрируема на интервале X , причем и , тогда .
Это свойство справедливо как для , так и для или .
Доказательство можно провести, опираясь на предыдущие свойства определенного интеграла.
Если функция интегрируема на отрезке , то она интегрируема и на любом внутреннем отрезке .
Доказательство основано на свойстве сумм Дарбу: если к имеющемуся разбиению отрезка добавить новые точки, то нижняя сумма Дарбу не уменьшится, а верхняя – не увеличиться.
Если функция y = f(x) интегрируема на отрезке и для любого значения аргумента , то .
Это свойство доказывается через определение интеграла Римана: любая интегральная сумма для любого выбора точек разбиения отрезка и точек при будет неотрицательной (не положительной).
Следствие.
Для интегрируемых на отрезке
функций y = f(x)
и y = g(x)
справедливы неравенства:
Это утверждение означает, что допустимо интегрирование неравенств. Этим следствием мы будем пользоваться при доказательстве следующих свойств.
Пусть функция y = f(x)
интегрируема на отрезке
, тогда справедливо неравенство .
Доказательство.
Очевидно, что . В предыдущем свойстве мы выяснили, что неравенство можно почленно интегрировать, поэтому, справедливо . Это двойное неравенство можно записать как .
Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке и для любого значения аргумента , тогда , где и .
Доказательство проводится аналогично. Так как m и M – наименьшее и наибольшее значение функции y = f(x) на отрезке , то . Домножение двойного неравенства на неотрицательную функцию y = g(x) приводит нас к следующему двойному неравенству . Интегрируя его на отрезке , придем к доказываемому утверждению.
Следствие.
Если взять g(x) = 1 , то неравенство примет вид .
Первая формула среднего значения.
Пусть функция y = f(x) интегрируема на отрезке , и , тогда существует такое число , что .
Следствие.
Если функция y = f(x) непрерывна на отрезке , то найдется такое число , что .
Первая формула среднего значения в обобщенной форме.
Пусть функции y = f(x) и y = g(x) интегрируемы на отрезке , и , а g(x) > 0 для любого значения аргумента . Тогда существует такое число , что .
Вторая формула среднего значения.
Если на отрезке функция y = f(x) интегрируема, а y = g(x) монотонна, то существует такое число , что справедливо равенство .
В дифференциальном исчислении решается задача:под анной функции ƒ(х) найти ее производную (или дифференциал). Интегральное исчисление решает обратную задачу: найти функцию F(x), зная ее производную F » (x)=ƒ(х) (или дифференциал). Искомую функцию F(x) называют первообразной функции ƒ(х) .
Функция F(x) называетсяпервообразной функции ƒ(х) на интервале (а; b), если для любого х є (а;b) выполняется равенство
F » (x)=ƒ(x) (или dF(x)=ƒ(x)dx).
Например , первообразной функции у=х 2 , х є R, является функция, так как
Очевидно, что первообразными Будут также любые функции
где С — постоянная, поскольку
Tеоpeмa 29. 1. Если
функция F(x) является первообразной функции ƒ(х) на (а;b), то
множество всех первообразных для ƒ(х) задается формулой F(x)+С,
где С — постоянное число.
1. Если
функция F(x) является первообразной функции ƒ(х) на (а;b), то
множество всех первообразных для ƒ(х) задается формулой F(x)+С,
где С — постоянное число.
▲ Функция F(x)+С является первообразной ƒ(х).
Действительно, (F(x)+C) » =F » (x)=ƒ(x).
Пусть Ф(х) — некоторая другая, отличная от F(x), первообразная функции ƒ(х) , т. е. Ф » (x)=ƒ(х). Тогда для любого х є (а;b) имеем
А это означает (см. следствие 25. 1), что
где С — постоянное число. Следовательно, Ф(х)=F(x)+С.▼
Множество всех пepвoобpaзныx функций F(x)+С для ƒ(х) называетсянеопределенным интегралом от функции ƒ(х) и обозначается символом∫ ƒ(х) dx.
Таким образом, по определению
∫ ƒ(x)dx= F(x)+C.
Здесь ƒ(х) называетсяподынтегральнoй функцией , ƒ(x)dx — подынтегральным выражением, х —переменной интегрирования , ∫ —знаком неопределенного интеграла .
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых у=F(x)+C (каждому числовому значению С соответствует определенная кривая семейства) (см. рис. 166). График каждой первообразной (кривой) называетсяинтегральной кривой .
Для всякой ли функции существует неопределенный интеграл?
Имеет место теорема, утверждающая, что «всякая непрерывная на (а;b) функция имеет на этом промежутке первообразную», а следoвaтельно, и неопределенный интеграл.
Отметим ряд свойств неопределенного интеграла, вытекающих из его определения.
1.
Дифференциал
от неопределенного интеграла равен подынтегральному выражению, а
производная неопределенного интеграла равна подынтегральной функции:
d(∫ ƒ(x)dx)=ƒ(x)dх, (∫ ƒ(x)dx) » =ƒ(х).
Дeйcтвительнo, d(∫ ƒ(х) dx)=d(F(x)+С)=dF(x)+d(C)=F » (x) dx =ƒ(х) dx
(∫ ƒ (x) dx) » =(F(x)+C)»=F»(x)+0 =ƒ (x).
Блaгoдapя этому свойству правильность интегрирования проверяется дифференцированием. Например, равенство
Например, равенство
∫(3x 2 + 4) dx=х з +4х+С
верно, так как (х 3 +4х+С)»=3x 2 +4.
2. Hеопpедeлeнный интеграл от диффepeнциaла некоторой функции равен сумме этой функции и произвольной постоянной:
∫dF(x)= F(x)+C.
Действительно,
3. Постоянный множитель можно выносить за знак интеграла:
α ≠ 0 — постоянная.
Действительно,
(положили С 1 /а=С.)
4. Неопределенный интеграл от aлгeбpaическoй суммы конечного числа непрерывных функций равен aлгебpaичecкoй сумме интегралов от слагаемых функций:
Пусть F»(x)=ƒ(х) и G»(x)=g(x). Тогда
где С 1 ±С 2 =С.
5. (Инвариантность формулы интегрирования).
Если, где u=φ(х) — произвольная функция, имеющая непрерывную производную.
▲ Пусть х — независимая переменная, ƒ(х) — непрерывная функция и F(x) — ее пepвoобpaзнaя. Тогда
Положим теперь
u=ф(х), где ф(х) — непрерывно-дифференцируемая функция. Рассмотрим
сложную функцию F(u)=F(φ(x)). В силу инвараинтности формы первого
дифференциала функции (см. с. 160) имеем
с. 160) имеем
Отсюда▼
Таким образом, формула для неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.
Так, из формулыпутем замены х на u (u=φ(х))получаем
В частности,
Пример 29.1. Найти интеграл
где С=C1+С 2 +С 3 +С 4 .
Пример 29.2. Найти интеграл Решение:
- 29.3. Таблица основных неопределенных интегралов
Пользуясь тем, что интегрирование есть действие, обратное дифференцированию, можно получить таблицу основных интегралов путем обращения соответствующих формул диффepeнциaльнoгo исчисления (таблица дифференциалов) и использования свойств неопределенного интеграла.
Например , так как
d(sin u)=cos u . du,
Вывод ряда формул таблицы будет дан при рассмотрении основных методов интегрирования.
Интегралы в приводимой
ниже таблице называются табличными. Их следует знать наизусть. В
интегральном исчислении нет простых и универсальных правил отыскания
первообразных от элементарных функций, как в дифференциальном
исчислении. Методы нахождения пepвoобpaзных (т. е. интегрирования
функции) сводятся к указанию приемов, приводящих данный (искомый)
интеграл к табличному. Следовательно, необходимо знать табличные
интегралы и уметь их узнавать.
Их следует знать наизусть. В
интегральном исчислении нет простых и универсальных правил отыскания
первообразных от элементарных функций, как в дифференциальном
исчислении. Методы нахождения пepвoобpaзных (т. е. интегрирования
функции) сводятся к указанию приемов, приводящих данный (искомый)
интеграл к табличному. Следовательно, необходимо знать табличные
интегралы и уметь их узнавать.
Отметим, что в таблице основных интегралов переменная интегрирования и может обозначать как независимую переменную, так и функцию от независимой переменной (coгласнo свойству инвариантности формулы интeгpиpoвания).
В справедливости приведенных ниже формул можно убедиться, взяв диффepeнциaл правой части, который будет равен подынтегральному выражению в левой части формулы.
Докажем, например, справедливость формулы 2. Функция 1/u определена и непрерывна для всех значений и, отличных от нуля.
Если u > 0, то ln|u|=lnu, тогда Поэтому
Eсли u Значит
Итак, формула 2 верна. Aнaлoгичнo, провepим формулу 15:
Таблица оснoвныx интегралов
Друзья! Приглашаем вас к обсуждению. Если у вас есть своё мнение, напишите нам в комментарии.
Если у вас есть своё мнение, напишите нам в комментарии.
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Изучаем понятие « интеграл»
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных , необходимые и для понимания интегралов, уже есть у нас в блоге.
Сведения о пределах и производных , необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x) .
Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции f(x) .
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:
Точки а и b называются пределами интегрирования.
« Интеграл»
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
- Производная от интеграла равна подынтегральной функции:
- Константу можно выносить из-под знака интеграла:
- Интеграл от суммы равен сумме интегралов. Верно также для разности:
Свойства определенного интеграла
- Линейность:
- Знак интеграла изменяется, если поменять местами пределы интегрирования:
- При любых точках a , b и с :
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл… Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?
Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.
Изучаем понятие « интеграл»
Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась.
Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц , но суть вещей не изменилась.
Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о , необходимые и для понимания интегралов, уже есть у нас в блоге.
Неопределенный интеграл
Пусть у нас есть какая-то функция f(x) .
Неопределенным интегралом функции f(x) называется такая функция F(x) , производная которой равна функции f(x) .
Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как читайте в нашей статье.
Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.
Процесс нахождения интеграла называется интегрированием.
Простой пример:
Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.
Полная таблица интегралов для студентов
Определенный интеграл
Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.
В качестве примера представим себе график какой-нибудь функции.
Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:
Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:
Точки а и b называются пределами интегрирования.
« Интеграл»
Кстати! Для наших читателей сейчас действует скидка 10% на
Правила вычисления интегралов для чайников
Свойства неопределенного интеграла
Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.
- Производная от интеграла равна подынтегральной функции:
- Константу можно выносить из-под знака интеграла:
- Интеграл от суммы равен сумме интегралов. Верно также для разности:
Свойства определенного интеграла
- Линейность:
- Знак интеграла изменяется, если поменять местами пределы интегрирования:
- При любых точках a , b и с :
Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:
Примеры решения интегралов
Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.
Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.
Старинный кованый медный чайник XIX века, кофейник для продажи на 1stDibs
Старинный английский медный латунный чайник Ручка носика кофейного кувшина № 3 c. 1900
Старинный французский заварочный чайник из латуни и меди с гусиной шеей, 13 дюймов
Старинный английский медный латунный чайник, кофейный кувшин Ручка носика #1 c. 1900
Старинный турецкий чеканный медный чайник на «гусиной шее» Кофейник
Чайник с прямой ручкой
1 из 13 выгравированный рисунок на ручке. Размеры: 7″.
Размеры: 7″.
Детали
Размеры
Высота: 13,34 см (5,25 дюйма) Ширина: 13,34 см (5,25 дюйма) Глубина: 18,42 см (7,25 дюйма)
Стиль
Примитива (в стиле)
Материалы и методы
Медная
ПЕРИОД
19055
Дата
Износ соответствует возрасту и использованию. В целом хорошо — некоторые вмятины, следы износа/пятна/царапины.
Местонахождение продавца
Дейтон, Огайо
Справочный номер
Продавец: 357341STDIBS: LU5343231189152
View INTOICE
СОВЕТСТВЕННЫЙ И ВОЗВРАЩАЕТСЯ
1STDIBS Гарантировано с вами. правильно. Узнайте больше
О продавце
Расположен в Дейтоне, штат Огайо
Платиновый продавец
Эти проверенные экспертами продавцы являются самыми опытными продавцами 1stDibs и имеют самые высокие оценки наших клиентов.
Установлен в 2010 году
1stdibs Seller с 2020
676 Продажи на 1stdibs
Типичное время отклика: <1 час
Подробнее от этого Sellerview All
Античный французский
Расположен в Дейтоне, штат Огайо
Старинный медный чайник XIX века с изогнутым носиком и фиксированной латунной ручкой
Категория
Старинные чайные сервизы XIX века викторианской эпохи
Материалы
Латунь, медь
Старинный французский заварочный чайник из латуни и меди с гусиной шеей, 13 дюймов чайник с крышкой и точеной деревянной ручкой. Размеры: 13 дюймов x 9 дюймов x 9,5 дюйма / высота ручки – 4,75 дюйма (ширина x глубина x высота).
Категория
Старинный викторианский стиль XIX века Еще Рестораны и развлечения
Материалы
Медь
Старинный турецкий чеканный медный чайник на гибкой шее Кофейник
Старинный медный кофейник XIX века Корабль для костра Чайник Банка для воды
Находится в Дейтоне, штат Огайо.
 открытого огня в конце 19 века. Размеры: 14 дюймов.
открытого огня в конце 19 века. Размеры: 14 дюймов.Категория
Старинные деревенские чайные сервизы конца XIX века
Материалы
Медь
Старинный медный чайник XIX века Костровый чайник Корабль Банка с водой
Старинный медный чайник Кофейник с прямым носиком Деревенская деревянная ручка
Расположен в Дейтоне, штат Огайо
Очень блестящий старинный медный чайник с прямым носиком и деревянной ручкой. Размеры: 13 дюймов.
Категория
Викторианская эпоха начала 20-го века Еще столовая и развлечения
Материалы
Медь
Старинный медный чайник Кофейник с прямым носиком Деревенская деревянная ручка 9
Расположен в Дейтоне, Огайо. Размер: 9 дюймов.
Категория
Старинные исламские чайные сервизы конца XIX века
Материалы
Латунь, медь
Старинная медь в форме ласточкина хвоста Латунь с гравировкой Чайник Кофейник Чайник Бонсай Гусиная шея
3 Старинные египетские кованые медные кувшины для воды Кувшины Бонсай Гусиная шея
Находится в Дейтоне, Огайо
Три различных чеканных медных кувшина различного дизайна и стиля с геральдическими лилиями, ребристыми вставками и прокручивающимися ручками.
 Один из них имеет носик бонсай «гусиная шея». Ста…
Один из них имеет носик бонсай «гусиная шея». Ста…Категория
Старинные египетские кувшины XIX века
Материалы
Медь
3 Старинные египетские чеканные медные кувшины для воды Кувшины Бонсай Гусиная шея
235 $ / комплект
Люди также просматривали
Старинная коллекция из трех медных чайников
Находится в Норидже, Великобритания. Размеры: 23 х 26 х 17 см 25 х 24 х 19 см 15 х 14 х 11 см …
Категория
Старинные английские чайные сервизы 1860-х годов
Материалы
Медь
Старинная коллекция из трех медных чайников
Старинный медный сосуд XIX века с железными ручками Котел для воды Чайник Котел
Находится в Дейтоне, Огайо
Монументальный чеканный медный сосуд или кувшин для хранения воды.
 Круглый с коническим основанием и ручками из железного кольца. Имеет чеканный железный обод.
Круглый с коническим основанием и ручками из железного кольца. Имеет чеканный железный обод.Категория
Старинные вазоны и жардиньеры Викторианской эпохи XIX века
Материалы
Медь, железо
Антиквариат 19Медный сосуд с железными ручками
Большой французский медный чайник с крышкой конца XIX века, около 1900 года
Расположен в Фейетвилле, штат Арканзас клепаная ручка и крышка с латунной ручкой. Чайник имеет размеры 16 дюймов в высоту и 11 дюймов.0005
Латунь, медь
Большой французский медный чайник с крышкой, конец XIX века, около 1900 года
Италия, Тоскана, кухонный медный чайник XIX века Флоренция Тоскана, Италия, около 1890 года. Выгравирована флорентийская лилия. Медный чайник имеет все признаки времени, но он …
Категория
Старинные итальянские деревенские тарелки и сервировочная посуда конца XIX века
Материалы
Латунь, медь
Италия 19-го века тускана кухня медная вода для водного чайника
$ 1 859
Гранд Медный Радж Период.

Большой медный чайник эпохи Радж в англо-индийском вкусе с декоративными накладками из латуни. Ремонт старого носика. Конец 19 века. Мы являемся основным поставщиком…
Категория
Античный конец 19-го века Индийский англо-индийский чайные наборы
Материалы
Медная
Гранд-медь Радж период чай Латунный чайник для чая Ручка для кофейного кувшина № 2 C. 1900
Находится в Тайлере, штат Техас
ОЧАРОВАТЕЛЬНЫЙ Старинный английский медный чайник для чая или кофе с носиком, крышкой с круглой ручкой и медной ручкой № 2~~c. 1900. Свежий лак Размеры: 12 дюймов в высоту до верха ручки. 1…
Категория
Антикварные английские британские колониальные кувшины конца 19 века
Материалы
Латунь, медь
Старинная английская медь Латунь Чайник Чайник Кофейный кувшин Ручка #2 C.
 19002 Ручка носика кофейного кувшина чайника #3 c. 1900
19002 Ручка носика кофейного кувшина чайника #3 c. 1900Расположен в Тайлере, штат Техас.
очаровательный старинный английский медный чайник для чая или кофе с носиком, крышкой и медной ручкой #3~~c. 1900-1920-е годы Наконечник «Желудь»~~свежий лак
Категория
Старинные английские британские колониальные кувшины конца XIX века
Материалы
Латунь, медь
Старинный английский медный латунный чайник с носиком для кофейного кувшина № 1 c. 1900 Наконечник «Желудь»~~свежий лак 12 дюймов в высоту до верхней части ручки 13 дюймов шириной от…
Категория
Старинные английские британские колониальные кувшины конца XIX века
Материалы
Латунь, медь
Старинная английская медь Чайник из латуни Ручка для кофейного кувшина #1 9 c.
 1900 3 Чайник с ручкой
1900 3 Чайник с ручкой19 -й век. в прекрасно отполированном состоянии. Его можно использовать как на плите, так и в качестве украшения на полке. Подпись на ручке O.S.THORIN -MARSTRAND -2.
Категория
Антиквариат 19Бельгийская чайная набор Adirondack. Изготовлен в середине века, около 1950 года. Подлинное изделие ручной работы в очень хорошем оригинальном состоянии с прекрасной патиной.
Категория
Винтажные австрийские чайные сервизы середины века модерн 1950-х годов
Материалы
Медная
чайный чайник, медный латунный бамбук, 1950S
Расположен в Нью-Йорке, штат Нью-Йорк
Чайник с прямой ручкой, хорошо серебристый, с ручкой из красного дерева.0005
Категория
Античный американские примитивные кувшины 19 -го века
Материалы
Металл
Прямой обработка чайного чайника
Недавно просмотр
Просмотреть большеОбещание 1STDIBS
Узнайте больше
ОПЕРЬЕ.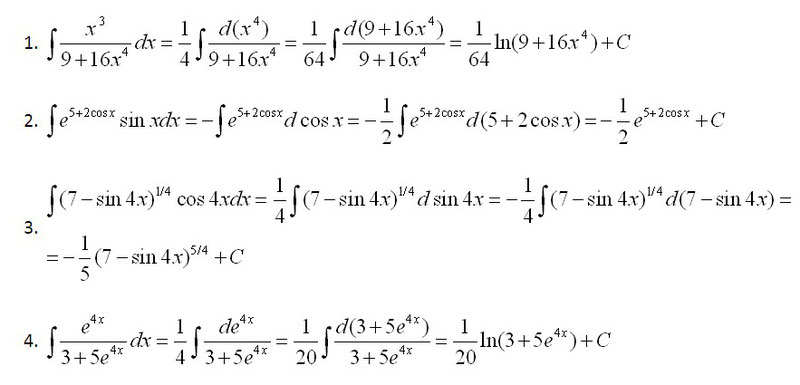
Исключительная поддержка
Защита покупателя
Надежная доставка по всему миру
Дополнительные способы поиска
Старинный медный кофе
Старинный чайник
антикварные медные чайные чайники
Античный медный чайный чай
Старинный медный кофейник
Просмотреть все популярные поисковые запросы кувшинов
Кухня, чайники, диски из коричневого сахара, размягченный сахар, чай — Метка «Примитивная» — Olde Church Emporium
content_copy
Кухня, чайники, диски из коричневого сахара, размягченный сахар, чай – Tagged «Primitive» – Olde Church Emporium
Продажа
Скатерть Park Design Harper Plaid Table Runner, 15 x 72 дюймов, фермерский дом, кантри, хижина
Дизайн парков
Обычная цена 23,00 $ Цена продажи
$18. 00
00
Настольная дорожка Park Design Paradise с пальмовым принтом, 15 x 72 дюйма, пляжная, береговая, прибрежная
Дизайн парков
Обычная цена 50,00 $ Цена продажи
$28.00
Кухонное полотенце Park Design Sturbridge Home Faith Family Friends с аппликацией 18 x 28 дюймов
Дизайн парков
Обычная цена $13.00
Park Design Sturbridge Home Faith Family Friends Квадратная прихватка 8 x 8 дюймов
Дизайн парков
Обычная цена
$14. 00
00
Park Design Sturbridge Home Felt Primitive Table Runner 13 x 36 дюймов Фермерский дом, кантри, хижина
Парк Дизайн
Обычная цена $56.00
ПродажаСпециальная настольная дорожка Park Design, 15 x 72 дюйма, 2 стиля, сланец и стерлинговый фермерский дом, кантри, хижина
Дизайн парков
Обычная цена 23,00 $ Цена продажи
$18.00
Кольца для салфеток Park Folk Rooster — металл, рустик, примитив, кантри
Дизайн парков
Обычная цена
$9.


 открытого огня в конце 19 века. Размеры: 14 дюймов.
открытого огня в конце 19 века. Размеры: 14 дюймов. Один из них имеет носик бонсай «гусиная шея». Ста…
Один из них имеет носик бонсай «гусиная шея». Ста… Круглый с коническим основанием и ручками из железного кольца. Имеет чеканный железный обод.
Круглый с коническим основанием и ручками из железного кольца. Имеет чеканный железный обод.
 19002 Ручка носика кофейного кувшина чайника #3 c. 1900
19002 Ручка носика кофейного кувшина чайника #3 c. 1900 1900
1900