Вычисление производных и первообразных функций. Исследование функции на монотонность – StudyWay
Данная тема часто встречается в заданиях ЕГЭ по математике базового уровня, поэтому рассмотрим её более подробно, вспоминая ранее изученные материалы в школьной программе.
Понятие функции в математике является одной из основных тем в математике. Говорят, что математика начинается именно с графиков и функций.
Ведь с помощью производной в ЕГЭ по математике функции находят минимальные и максимальные точки на графике, а также промежутки, на которых функция является убывающей либо возрастающей. Таким образом, получается с большой точностью построить графики. Основное правило, которое следует помнить – производная является скоростью изменения функции.
В данной статье подробно рассмотрены следующие темы:
– Вычисление производных и первообразных функций;
– Исследование функции на монотонность;
– Нахождение наибольшего и наименьшего значения функции.
При решении подобных заданий в ЕГЭ по математике нужно применять графики для наглядности. Тема производной в математике считается одной из наиболее сложных.
На этом рисунке
(рис. 1) изображены три функции. Быстрее других двух функций растёт третья, а это значит, что у неё наибольшая производная. Здесь нужно смотреть какая функция является крутой, то есть стремительно поднимается вверх, как изменяется при этом х. Производную обычно пишут как:
Рассмотрим как найти производную функции на примере графика
(рис. 2).
Представлен график у = а (х ). Отметим на графике точку А, её абсцисса – х0. Проводим через эту точку касательную на графике. Оцениваем, как круто возрастает функция. Для этого находим тангенс наклона касательной. Производная данной функции в х0 равна тангенсу наклона касательной, которая проведена на графике через эту точку.
Следует обратить внимание, что углом наклона касательной считается угол, находящийся меж касательной, также важно найти направление оси ОХ, которое является положительным.
Найдём тангенс а. Имеем в виду, что тангенс угла в прямоугольнике, являющемся прямоугольным, равен отношению катета, лежащего напротив.
Следует, что треугольник AMN: f ( х ) = tg a = AN /MN.
Так мы нашли производную, пользуясь помощью графика. Не применяя приэтот формулу. Такие задания часто можно встретить в заданиях ЕГЭ по математике.
Прямую задают с помощью уравнения: y = kx + b. K в данном уравнении является коэффициентом угла прямой. К равно тангенсу наклона прямой к х. Получается: f ( х0 ) = tg а = k.
Следует запомнить данную формулу, так как она является смыслом производной. Производная в х0 равняется коэффициенту угла касательной, которая проведена через эту точку на графике. Иначе говоря, производная равняется тангенсу наклона касательной к данному углу. У функции в различных точках возможна различная производная.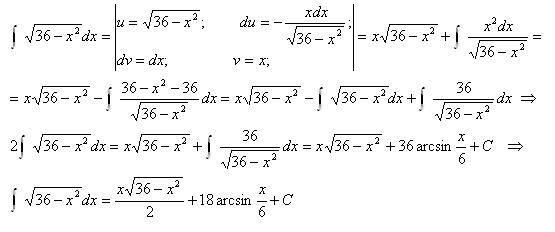
Первообразная функций в их сумме будет равняться сумме их первообразных.
Первообразная у = kf ( x ), где k – постоянный множитель, равняется произведению k на первообразную f ( x ), то есть kF ( х).
Неопределённым интегралом считают различные первообразные у функции. Это записывают в следующем виде: f ( x ) dx = F ( x ) + C.
Исследование функции на монотонность
В данной теме нужно придерживаться двух основных теорий:
- Если в промежутке х, а именно во всех его точках присутствует f ( х ) больше или равное нулю, то функция у = f ( х ) возрастает на этом промежутке. При этом следует учитывать, что данное равенство подлежит выполнению исключительно в определенных точках графика и не может выполняться ни на одном промежутке, являющемся сплошным.
На данном графике
| Функция f ( x ) | Первообразная F ( x ) |
| 0 | С (константа) |
| 1 | x + C |
| x | ( x^2 / 2 ) + C |
| x^n, n не равняется -1 | ( x^n ) + ( 1 / n ) + C |
| 1 / х | In | x | |
| sin x | – cos x + C |
| cos x | sin x + C |
| e^x | е^x + C |
(рис.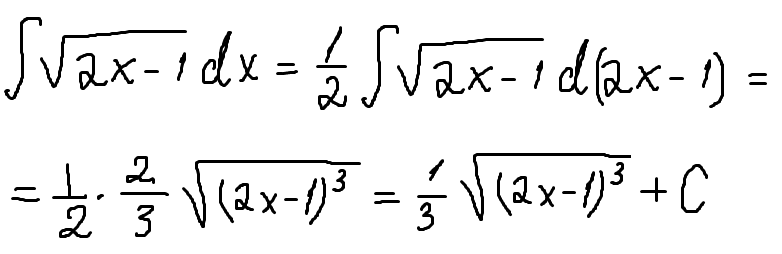
4) детально показана первая теорема.
- Если в промежутке х, а именно во всех его точках можно выполнить неравенство f ( х ) меньше или равно нулю, значит, функция у = f ( х ) будет убывающей в промежутке х. При этом следует учитывать то, что f ( х ) = 0 может выполняться исключительно в некоторых точках и не выполняется ни на одном промежутке, являющимся сплошным.
Рассмотрим пример
(рис. 5). На данном рисунке функция рассмотрена наглядно.
Наибольшее и наименьшее значения функции на отрезке
Рассмотрим более подробно данную тему на примере
(рис. 6).
На первом графике изображена функция, которая имеет наибольшее и наименьшее значения в определённых точках. Данные точки расположены на отрезке от -6 до 6, то есть [−6;6].
На втором графике рассмотрим отрезок от 1 до 6. Здесь наименьшее значение функции принадлежит стационарной точке, а наибольшее – в точке в правой стороне интервала.
Третий рисунок указывает на точки, находящиеся на границе отрезка [−3;2].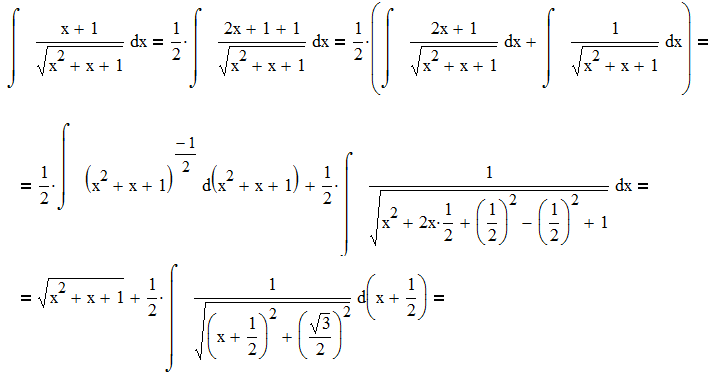
Они равны наибольшему и наименьшему значениям.
Сразу же вспомним определение стационарной точки – это определённое значение, при нём будет нулевой.
Итак, для чего нужны стационарные точки? Существует теорема Ферма, согласно которой функция имеет экстремум (то есть минимальное и максимальное значения) в определённой точке. Данная точка будет стационарной.
Наибольшее и наименьшее на интервале
Рассмотрим пример
(рис. 7).
На данном рисунке функция максимального и минимального значения на открытом интервале от -6 до 6, то есть (-6; 6). Эти значения достигаются в стационарных точках.
На втором графике рассмотрена часть от 1 до 6 [1; 6), здесь наибольшее значение невозможно узнать, наименьшее – в стационарной точке.
На последнем графике наименьшее значение достигнуто в интервале (-3; 2], наибольшее значение неизвестно.
Наибольшее и наименьшее значения на бесконечности
Рассмотрим на примере графика
(рис. 8).
Здесь максимальное значение функции достигается в стационарной точке, её абсцисса равна единице.