тригонометрия — Сумма синуса значений от $0$ до $\pi/2$ с некоторым расстоянием между углами.
Задавать вопрос
спросил
Изменено 8 лет, 1 месяц назад
Просмотрено 282 раза 9{\pi/(2\delta)}\sin n\delta$$
Где мы суммируем по всем числам от $0$ до $\pi/2$, при этом некоторое $\delta$ описывает расстояние между ними.
Например, если $\delta=0,001$, как найти значение $$\sin(0) + \sin(0,001) + \sin(0,002) + \dots + \sin(1,570)$$
- тригонометрия
$\endgroup$
7
$\begingroup$
Взяв ваш пример с $\delta = 0,001$, мы должны оценить
$$\sum_{n=0}^{N}\sin(n \delta)$$
где $N = \text{этаж}(\pi/(2\delta)) = 1570$.
{iN\delta/2}) \\
& = \ frac {\ sin ((N + 1) \ delta / 2) \ sin (N \ delta / 2)} {\ sin (\ delta / 2)} \\
&= \ frac {1} {2} \ frac {\ cos (\ delta/2) — \ cos ((N + 1/2) \ delta)} {\ sin (\ delta/2)}
\end{выравнивание}$$
при условии, что я не сделал никаких ошибок в расчетах. 🙂 9{\pi/2} \sin(x) dx = 1$$
как упоминалось в ответе Майкла Харди.
$\endgroup$
2
$\begingroup$
До редактирования вопрос вроде был о сумме
$$
\sum \{ \sin x : 0\le \frac \pi 2 \le x\}.
$$
Значение этой суммы равно $\infty$ по одному разумному определению: все числа неотрицательны. В этой ситуации можно определить сумму как наименьшее число, которое никогда не может быть больше суммы конечного числа чисел в наборе. 9{\pi/2} \sin x\,dx$? Представьте, что величина растет в $\sin x$ раз быстрее, чем растет $x$, когда $x$ растет от $0$ до $\pi/2$. Тогда этот интеграл равен тому, насколько он растет.
$\endgroup$
Калькулятор — sin(x+pi/2) — Solumaths
Sin, расчет онлайн
Резюме:
Тригонометрическая функция sin для вычисления синуса угла в радианах, градусов или градианов.
sin online
Описание :
Калькулятор позволяет использовать большинство из тригонометрических функций , есть возможность вычислить синус , косинус и касательная угла через одноименные функции.
Тригонометрическая функция синус отметил синус , позволяет вычислить синус угла онлайн , можно использовать разные угловые единицы: градус, градус и радианы, которые по умолчанию являются угловыми единицами.
- Расчет синуса
- Таблица специальных синусоидальных значений
- Основные свойства
Вычисление синуса угла в радианах
Калькулятор синуса позволяет с помощью функции sin вычислить онлайн синус синус угла в радианах, сначала нужно
выберите нужную единицу, нажав на кнопку параметров расчетного модуля.
После этого можно приступать к расчетам.
К вычислить синус онлайн из `pi/6`, введите sin(`pi/6`), после вычисления результат `1/2` возвращается.
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и делать расчеты со специальными связанными значениями в точной форме.
Вычислить синус угла в градусах
Чтобы вычислить синус угла в градусах, необходимо сначала выбрать нужную единицу измерения нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 90, введите sin(90). результат 1 возвращается.
Вычислить синус угла в градусах
Чтобы вычислить синус угла в градианах, необходимо сначала выбрать нужную единицу измерения
нажав на кнопку модуля расчета параметров. После этого можно приступать к вычислениям.
Чтобы вычислить синус 50, введите sin(50), после вычисления, возвращается результат `sqrt(2)/2`.
Обратите внимание, что функция синуса способна распознавать некоторые специальные углы и выполнять исчисление со специальными ассоциированными точными значениями.
Синус допускает некоторые специальные значения, которые калькулятор может определить в точных формах. Вот таблица значения общего синуса :
| sin(`2*pi`) | `0` |
| sin(`pi`) | `0` |
| sin(`pi/2`) | `1` |
| sin(`pi/4`) | `sqrt(2)/2` |
| `sqrt(3)/2` | |
| sin(`pi/6`) | `1/2` |
| sin(`2*pi/3`) | `sqrt(3)/2` |
| sin(`3*pi/4`) | `sqrt(2)/2` |
| sin(`5*pi/6`) | ` 1/2` |
| sin(`0`) | `0` |
| sin(`-2*pi`) | `0` |
| sin(`-pi`) | `0` |
| sin(`90-3`3`) 1` | |
| sin(`-pi/4`) | `-sqrt(2)/2` |
| sin(`-pi/3`) | `-sqrt(3)/2` |
| sin(`-pi/6`) | `-1/2` |
| sin(`-2*pi/3`) | `-sqrt(3)/2` |
| sin(`-3*pi/4`) | `-sqrt(2)/2` |
| sin(`-5*pi/6`) | `-1/2` |
`AA x в RR, k в ZZ`,
- `sin(-x)= -sin(x)`
- `sin(x+2*k*pi)=sin(x)`
- `sin(pi-x)=sin(x) `
- `sin(pi+x)=-sin(x)`
- `sin(pi/2-x)=cos(x)`
- `sin(pi/2+x)=cos(x) `
Производная синуса равна cos(x).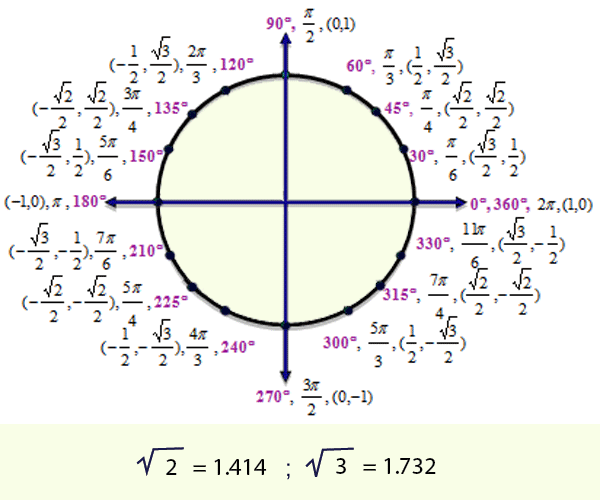
Первообразная синуса равна -cos(x).
Функция sine является нечетной функцией, для каждого действительного x `sin(-x)=-sin(x)`. Следствием для кривой, представляющей синусоидальную функцию, является то, что она допускает начало отсчета как точку симметрии.
Калькулятор имеет решатель, который позволяет решать уравнение с синусом формы cos(x)=a . Расчеты для получения результата детализированы, поэтому можно будет решать уравнения типа `грех(х)=1/2` или `2*sin(x)=sqrt(2)` с этапами расчета.
Синтаксис:
sin(x), где x — мера угла в градусах, радианах или градах.
Примеры:
sin(`0`), возвращает 0
Производный синус:
можно использовать калькулятор производной, который позволяет вычислить производную функции синуса
производная sin(x) is производная(`sin(x)`)=`cos(x)`
Первообразная синуса :
Калькулятор первообразной позволяет вычислить первообразную функции синуса.
Первопроизводная sin(x) является первообразной(`sin(x)`)=`-cos(x)`
Предел синуса :
Калькулятор предела позволяет вычислить пределы функции синуса.
Предел sin(x) равен limit(`sin(x)`)
Обратная функция синуса :
обратная функция синуса представляет собой функцию арксинуса, отмеченную арксинусом.
График синуса :
Графический калькулятор может отображать синусоидальную функцию в заданном интервале.
Свойство функции синуса:
Функция синуса является нечетной функцией.
Расчет онлайн с синусом
См. также
Список связанных калькуляторов:
-
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса. - Арксинус : арксинус. Функция arcsin позволяет вычислить арксинус числа. Функция arcsin является обратной функцией функции синуса.
- Арктангенс: арктангенс. Функция арктангенса позволяет вычислить арктангенс числа. Функция арктангенса является обратной функцией функции тангенса.
- Тригонометрический калькулятор: simple_trig. Калькулятор, который использует тригонометрическую формулу для упрощения тригонометрического выражения.
- Косинус: cos. Кос-тригонометрическая функция вычисляет косинус угла в радианах, градусов или градианов.
- Косеканс: косеканс. Тригонометрическая функция sec позволяет вычислить секанс угла, выраженного в радианах, градусах или градусах.
- Котангенс : котанг. Тригонометрическая функция котана для вычисления котана угла в радианах, градусов или градианов.
- Тригонометрическое расширение: expand_trigo.
Функция arccos позволяет вычислять арккосинус числа.
Функция arccos является обратной функцией функции косинуса.