Прямоугольный параллелепипед. Пирамида. / Геометрия / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Геометрия
- Прямоугольный параллелепипед. Пирамида.
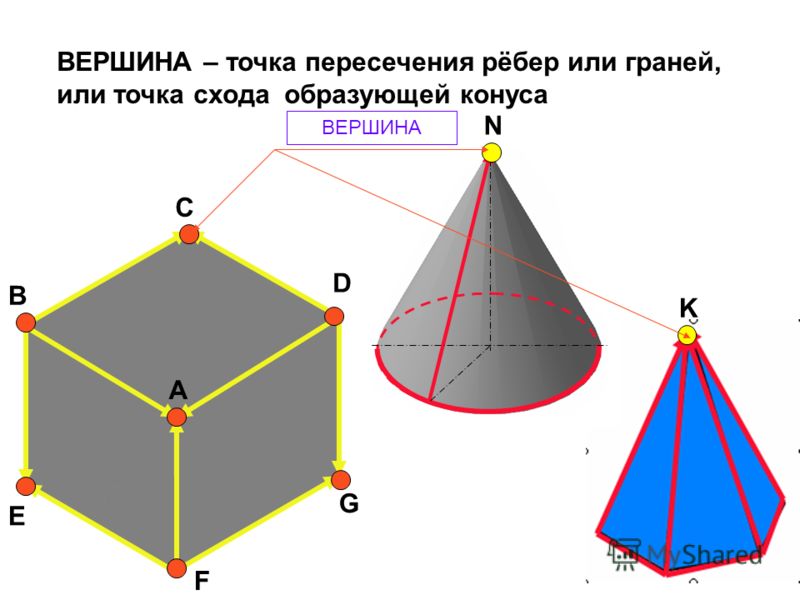
Многогранник — это поверхность, составленная из многоугольников. Грани многогранника — это многоугольники, из которых он составлен. При этом никакие две соседние грани многогранника не лежат в одной плоскости. Стороны граней — это рёбра многогранника, а их концы — это его вершины. На рисунке ниже изображены многогранники.
Один из самых простых многогранников — это прямоугольный параллелепипед. Он составлен из шести прямоугольников, т.е. он ограничен шестью гранями.
ABCDA1B1C1D1 — прямоугольный параллелепипед.
Грани прямоугольного параллелепипеда, которые не имеют общих вершин, называют противолежащими (в нашем случае это пары: ABB1A1 и DCC1D1, ABCD и A1B1C1D1, ADD1A1 и ВСС1В1). Противолежащие грани параллелепипеда равны.| Площадью поверхности параллелепипеда называют сумму площадей всех его граней. |
Измерения прямоугольного параллелепипеда — это длина трех рёбер, имеющих общую вершину. Например, ребра ВВ1
Измерения имеют названия: длина, ширина, высота.
Данные названия введены, чтобы различать измерения:
Диагональ параллелепипеда — это отрезок, соединяющий две его вершины, не принадлежащие одной грани. Например, AC1 — диагональ ABCDA1B1C1D1:
Частным случаем прямоугольного параллелепипеда является куб. Куб — это прямоугольный параллелепипед, все измерения которого равны:
EFHGE1F1H1G1 — куб, его высота, ширина и длина равны. Гранями куба являются 6 равных квадратов.
Рассмотрим следующую фигуру:
Данная фигура состоит из шести прямоугольников, которые попарно равны (выделены одним цветом). Если мы согнём по линиям данную фигуру и склеим, то получим модель прямоугольного параллелепипеда, противоположные грани которого будут одного цвета.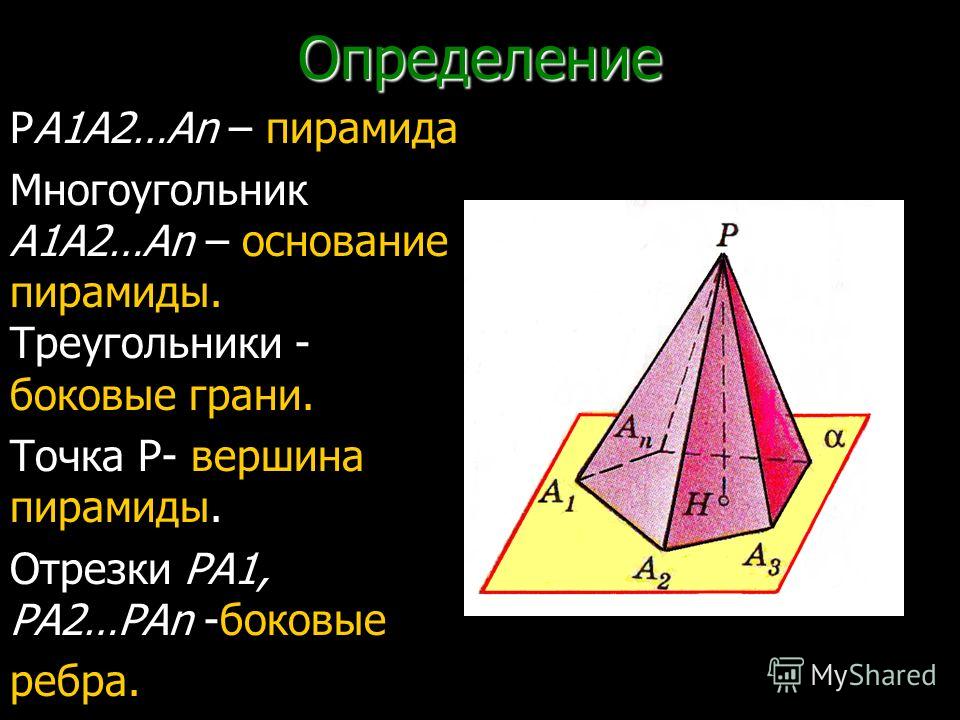
Рассматриваемую фигуру называют развёрткой прямоугольного параллелепипеда. Как сказано выше, куб состоит из 6 равных квадратов, значит, его развертка будет иметь следующий вид:
В данном случае куб «разрезали» по 6 горизонтальным ребрам и 1 вертикальному, при этом противоположные грани выделены одним цветом. Таким образом, «разрезая» любой многогранник по ребрам так, чтобы
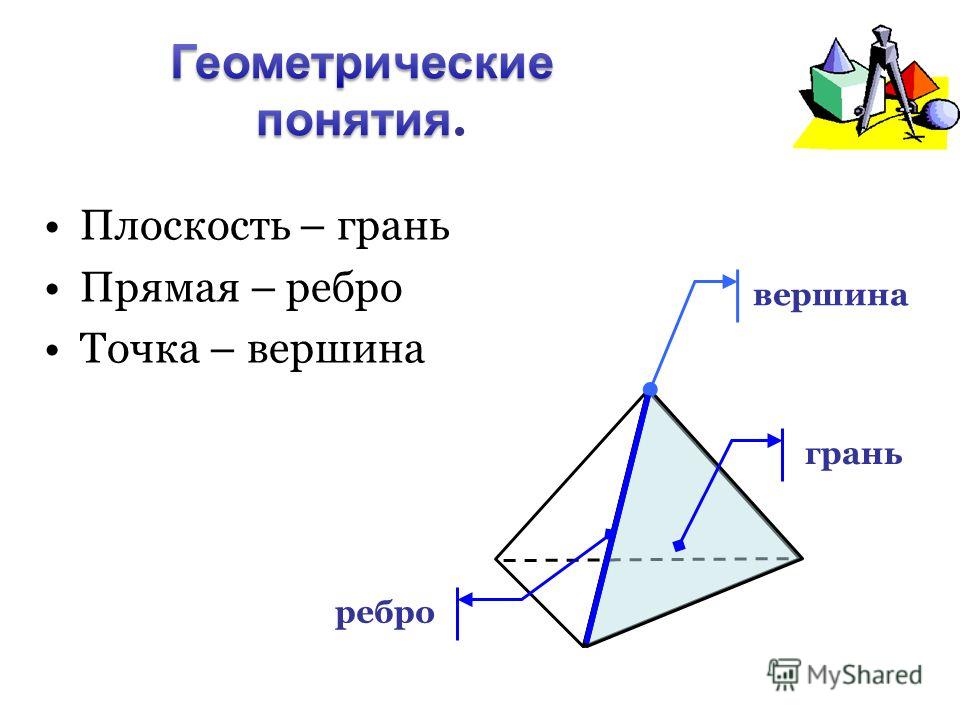
Вторым многогранником, который мы рассмотрим, является пирамида. Пирамида — это многогранник, в основании которого лежит многоугольник, а боковые грани являются треугольниками, имеющими общую вершину, которая является вершиной пирамиды.
Рёбра основания пирамиды — это стороны основания пирамиды.
Боковые рёбра пирамиды — это стороны боковых граней, которые не принадлежат основанию. Пирамида называется в соответствии с числом сторон многоугольника, который является его основанием. Например, на рисунке ниже изображены треугольная пирамида (тетраэдром) и пятиугольная пирамида.
Если мы «разрежем» по боковым рёбрам пятиугольную пирамиду, то получим следующий многоугольник, который будет являться развёрткой данной пирамиды:
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отрезок
Ломаная
Четырехугольники
Единицы измерения площадей. Свойства площадей
Прямоугольник, его периметр и площадь. Ось симметрии фигуры
Квадрат. Периметр и площадь квадрата.
Многоугольники. Правильные многоугольники. Равенство фигур.
Плоскость
Прямая
Луч
Шкалы и координаты
Объем прямоугольного параллелепипеда
Куб. Площадь поверхности куба
Куб.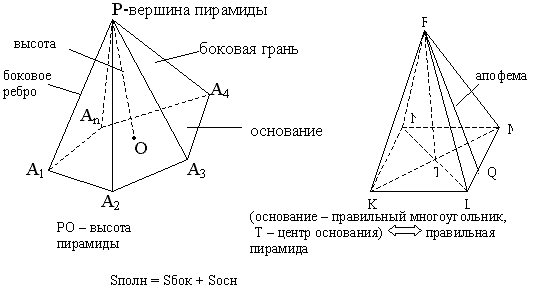
Объем куба
Угол. Обозначение углов
Прямой и развернутый угол
Чертежный треугольник
Измерение углов. Транспортир. Виды углов
Треугольник и его виды
Окружность, круг, шар
Цилиндр, конус
Отрезок-xx
Геометрия
Правило встречается в следующих упражнениях:
5 класс
Задание 792, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 794, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 842, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Задание 9, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 1
Номер 6, Мерзляк, Полонский, Якир, Учебник
Номер 628, Мерзляк, Полонский, Якир, Учебник
Номер 631, Мерзляк, Полонский, Якир, Учебник
Номер 637, Мерзляк, Полонский, Якир, Учебник
Номер 1107, Мерзляк, Полонский, Якир, Учебник
Номер 1201, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 539, Мерзляк, Полонский, Якир, Учебник
Номер 673, Мерзляк, Полонский, Якир, Учебник
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 7, Мерзляк, Полонский, Якир, Учебник
Номер 1, Мерзляк, Полонский, Якир, Учебник
Задание 443, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 476, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 519, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 834, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1036, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 230, Мерзляк, Полонский, Якир, Учебник
Номер 757, Мерзляк, Полонский, Якир, Учебник
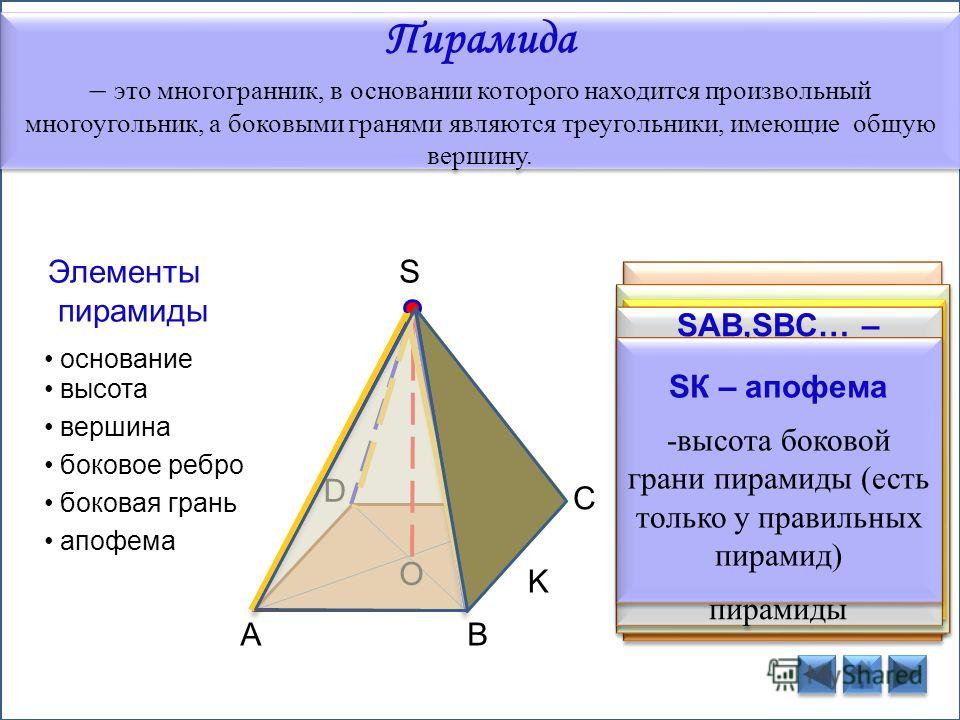
Пирамида, её основание, вершина, боковые рёбра, высота, боковая поверхность
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас.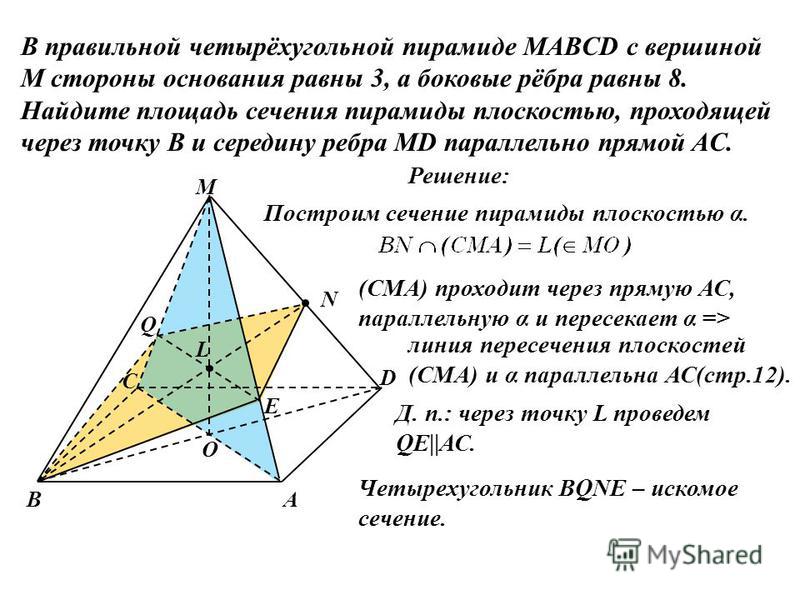
Узоры и орнаменты на посуде»Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Пирамида, её основание,
вершина, боковые рёбра, высота,
боковая поверхность.
Правильная пирамида, апофема,
площадь боковой поверхности
правильной пирамиды.
Повторение
1.
2.
3.
4.
5.
6.
Что такое призма?
Что может являться в основании призмы?
Что является боковой стороной призмы?
Призма имеет n граней. Какой многоугольник лежит в её основании?
Какая призма называется прямой?
перпендикулярны к плоскости основания?
7.
В какой призме боковые рёбра параллельны и равны её высоте?8. Какая призма называется правильной?
9. Является ли призма правильной, если все её рёбра равны друг другу?
10.Может ли высота одной из боковых граней наклонной призмы являться
и высотой призмы?
11.Чему равна диагональ параллелепипеда?
12.Как найти площадь боковой поверхности призмы?
13.Как найти площадь полной поверхности призмы?
Задача № 1.
Основание прямой призмы – треугольник со сторонами 5 см и 3
см и углом в 120° между ними. Наибольшая из площадей
боковых граней равна 35 см². Найдите площади боковой и
полной поверхности призмы.
Изучение нового материала
Рассмотрим многоугольник А1А2А3…Аn
и точку Р, не лежащую в плоскости
этого многоугольника.
Соединим точку Р с вершинами
многоугольника.
Получим n треугольников:
РА1А2, РА2А3, … , РАnА1.
Многогранник, составленный из nугольника А1А2А3…Аn и n
треугольников РА1А2, РА2А3, … , РАnА1
называется пирамидой.
Точка Р – называется вершиной
пирамиды.
Отрезки РА1, РА2, … , Раn называются
боковыми рёбрами пирамиды.
Многоугольник А1А2А3…Аn называется
основанием пирамиды.
Треугольники РА1А2, РА2А3, … , РАnА1
называются боковыми гранями
пирамиды.
Виды пирамид
Четырёхугольная
Шестиугольная
Треугольная
Высота пирамиды.
Высотой пирамиды называется перпендикуляр,
опущенный из вершины пирамиды на
плоскость основания.
Площадь полной поверхности
пирамиды
Площадью полной поверхности пирамиды называется
сумма всех её граней, то есть основания и боковых граней.
S полн S осн S бок
Площадью боковой поверхности
пирамиды называется сумма
площадей её боковых граней.
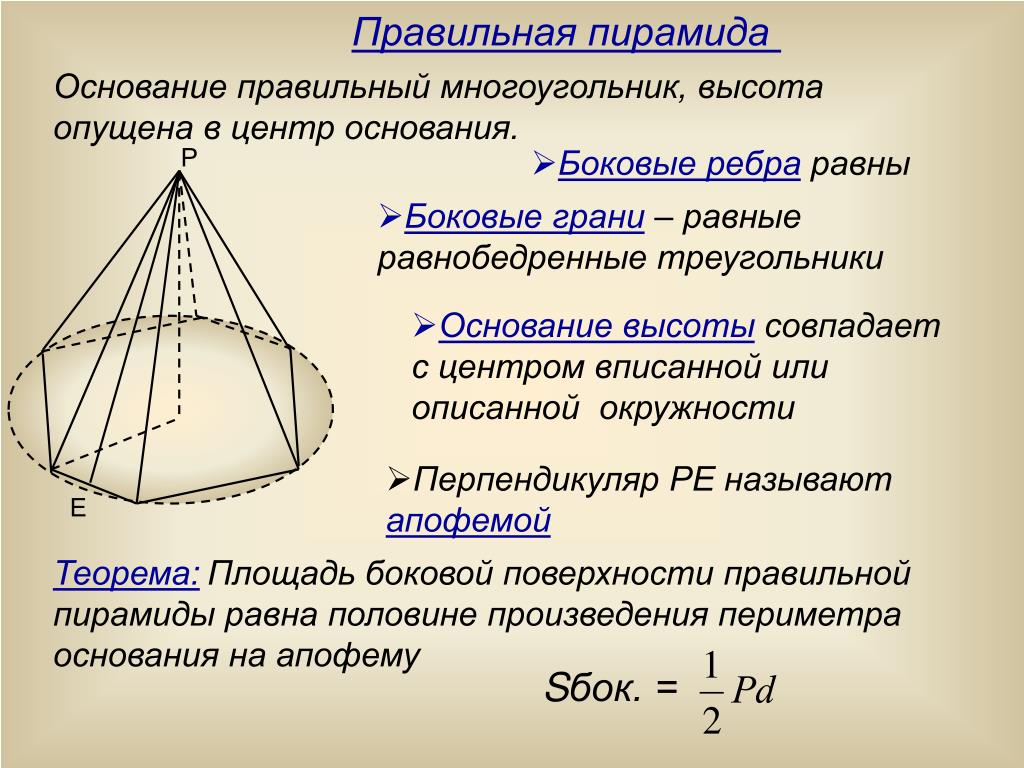
Правильная пирамида
Пирамида называется правильной, если её основание –
правильный многоугольник, а отрезок, соединяющий вершину
пирамиды с центром основания, является её высотой.
Все боковые рёбра правильной пирамиды равны, а боковые
грани являются равными равнобедренными треугольниками.
Теорема
Все боковые рёбра правильной пирамиды равны, а боковые
грани являются равными равнобедренными треугольниками.
Доказательство.
Докажем на примере правильной треугольной
пирамиды SABCD.
1) Рассмотрим треугольники SMA, SMC и SMB.
АМ=ВМ=СМ (как радиусы описанной окружности),
SМ – общая высота, значит, треугольники равны по
двум катетам.
Следовательно, AS=BS=CS.
2) Рассмотрим треугольники SCA, SCB и SAB.
По доказанному выше AS=BS=CS (значит, они
являются равнобедренными), с другой стороны
АС=ВС=АВ (так как в основании правильный
треугольник), следовательно, треугольники SCA,
SCB и SAB равны по трём сторонам.
ЧТД.
Аналогично доказывается для любой правильной пирамиды.
Апофема правильной пирамиды.
Высота боковой грани правильной пирамиды,
проведённая из её вершины, называется апофемой.
Апофема правильной пирамиды.
Площадь боковой поверхности
правильной пирамиды
Теорема. Площадь боковой поверхности правильной пирамиды
равна половине произведения периметра основания на апофему.
1
S Росн l Росн – периметр основания, l – апофема.
2
Доказательство.
Докажем на примере произвольной пирамиды
РА1А2…Аn.
1) Рассмотрим боковую грань РА1А2. Это
равнобедренный треугольник с основанием А1А2.
Площадь этого треугольника равна:
S
1
РК А1 А2 , где РК – апофема,
2
А1А2 – сторона основания.
Аналогично площади других граней будут
вычисляться по формуле
S
1
апофема Ат Ап
2
Площадь боковой поверхности
правильной пирамиды
Теорема. Площадь боковой поверхности правильной пирамиды
равна половине произведения периметра основания на апофему.
1
S Росн l Росн – периметр основания, l – апофема.
2
Доказательство (продолжение).
Sбок S РА1 А2 S РА2 А3 … S РАп 1 Ат
1
1
1
l А1 А2 l А2 А3 … l Ап 1 Ап
2
2
2
1
1
l А1 А2 A2 A3 … An 1 An l P
2
2
ЧТД
Закрепление
1.
2.
3.
4.
5.
6.
7.
8.
Что такое пирамида?
Что такое основание пирамиды?
Что может лежать в основании пирамиды?
Из какой фигуры всегда состоит боковая грань пирамиды?
Что такое высота пирамиды?
Чему равна площадь полной поверхности пирамиды?
Какая пирамида называется правильной?
Каким свойством обладают боковые рёбра и грани
правильной пирамиды?
9.
Как называется отрезок, соединяющий вершину пирамиды ссерединой стороны основания правильной пирамиды?
10. Как найти площадь боковой поверхности правильной
пирамиды?
11. Решить задачу № 240.
Задача № 240.
Основанием пирамиды является параллелограмм,
стороны которого равны 20 см и 36 см, а площадь равна
360 см². Высота пирамиды проходит через точку
пересечения диагоналей основания и равна 12 см.
Найдите площадь боковой поверхности пирамиды.
Дано: SABCD – пирамида,
АВСD – параллелограмм,
АВ=36 см, АD =20 см, SABCD=360 см²,
SO – высота, SO =12 см.
Найти: Sбок.
Задача № 240.
Найдите угол А и угол D.
Найдите ВD.
Найдите SD и SB.
Найдите АС.
Найдите SA и SC.
по формуле Герона
найдите площади
боковых граней
(подумайте, какие из них
одинаковые).
7. Найдите площадь полной
поверхности.
1.
2.
3.
4.
5.
6.
Домашнее задание
1) Прочитать пункты 32 – 33, выучить все определения и
две теоремы с доказательствами.
2) Решить задачи № 239, 241.
English Русский Правила
Вершины, ребра и грани — Математика для 2 класса
Вам когда-нибудь дарили подарочную коробку или праздничный колпак? 🎁
Все трехмерные фигуры.
Трехмерные фигуры состоят из вершин , ребер и граней !
Вершины — это заостренные биты или углы , где встречаются ребра.
Ребра — это линии вокруг фигуры.
Грани — это плоские стороны , к которым вы прикасаетесь, когда держите форму.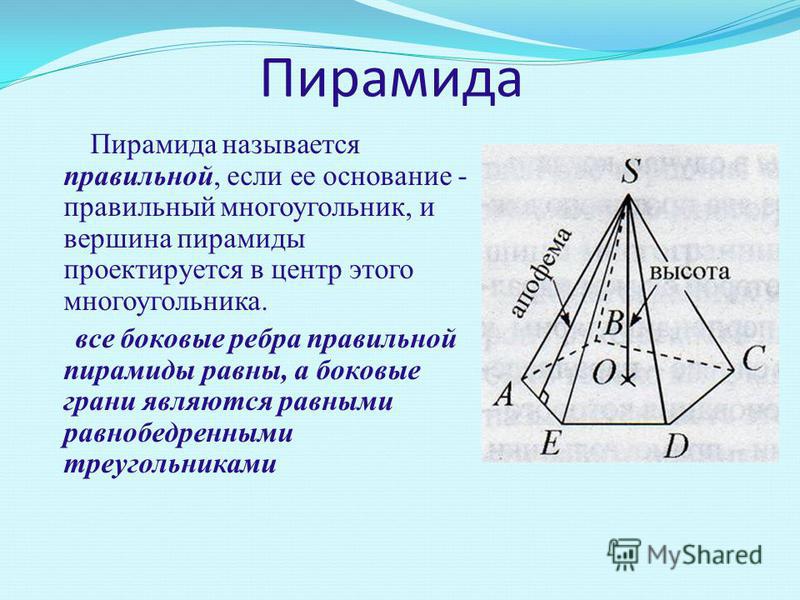
Давайте посмотрим, сколько вершин, ребер и граней имеют разные трехмерные фигуры. 👇
Кубики
Кубики имеют 6 квадрат граней .
Если склеить 6 квадратных граней вместе, они станут кубом с 8 вершинами и 12 ребрами.
Прямоугольные призмы
Подарочная коробка прямоугольной формы:
Она состоит из 6 прямоугольный грани .
Когда вы соедините стороны вместе, он станет прямоугольным призмой с 8 вершинами и 12 ребрами.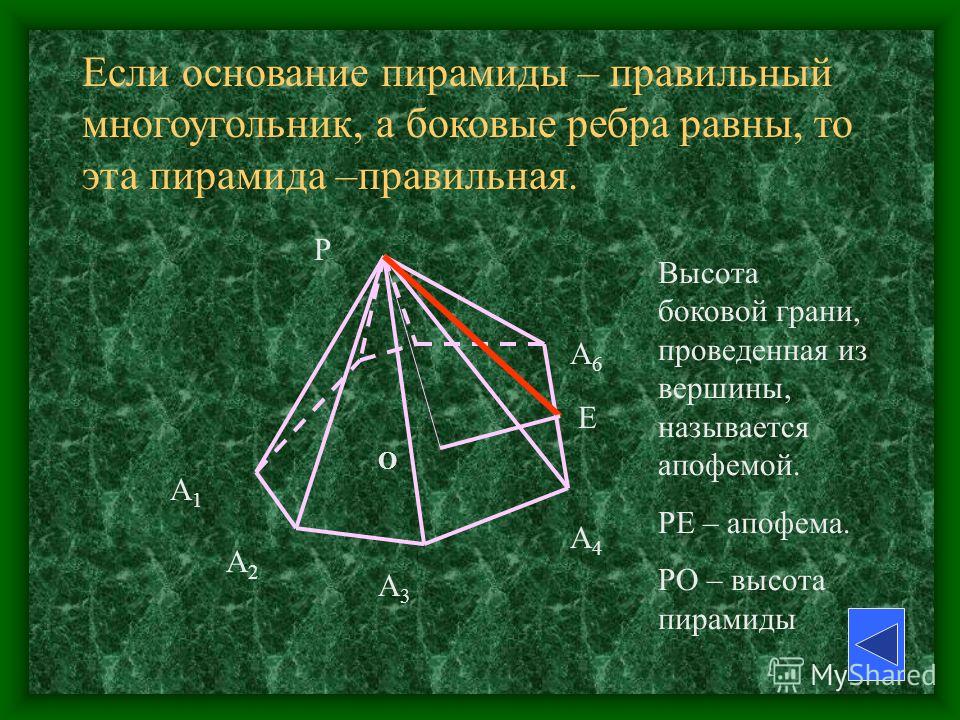
Совет: Все кубов являются прямоугольными призмами, но не все прямоугольные призмы являются кубами.
Это похоже на то, что все квадраты являются прямоугольниками, но не все прямоугольники являются квадратами.
Треугольные призмы
Вот треугольная подарочная коробка:
Она состоит из 5 граней (2 треугольника, 3 прямоугольника).
Треугольные призмы имеют 6 вершины и 9 ребра ! Вы можете их сосчитать?
Пирамиды
Пирамиды состоят из 5 граней (4 треугольника, 1 квадрат).
Когда вы соединяете грани вместе, получается квадрат — на основе пирамида с 5 вершинами и 8 ребрами !
Цилиндр
Цилиндры имеют 2 круглые поверхности и 1 изогнутые поверхность .
Изогнутые поверхности не считаются гранями. Лица плоские .
Когда вы оборачиваете поверхность вокруг кругов, она становится цилиндром с 2 ребрами и 0 вершинами .
В цилиндре нет острых заостренных частей!
Конусы
Конусы, подобные этой шляпе, состоят из 1 поверхности и 1 круглой поверхности поверхности.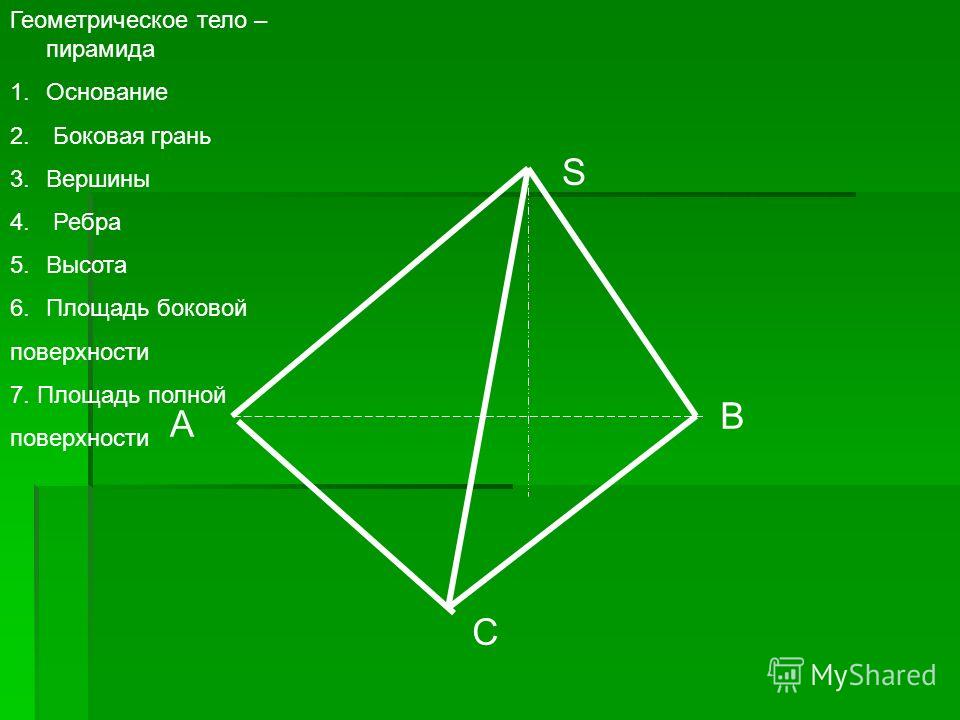
Конусы имеют 1 вершину и 1 ребро .
Сферы
Сферы имеют 0 грани , 0 ребра и 0 вершины .
Как бы вы упаковали шар в подарок? Трудно без мятой бумаги.
Отличная работа! Теперь вы знаете все о вершинах, гранях и ребрах!
Теперь завершите практику. Это поможет вам узнать больше и помнить дольше.
Грани, вершины и ребра прямоугольной пирамиды
Прямоугольные пирамиды представляют собой трехмерные фигуры, образованные основанием и боковыми гранями.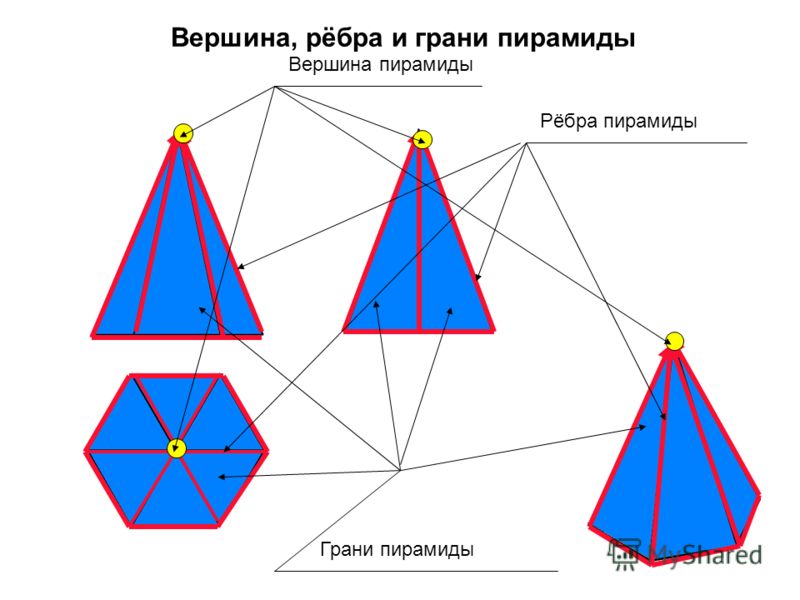
Основание имеет прямоугольную форму, а боковые грани – треугольники. Прямоугольные пирамиды имеют 5 граней, 8 ребер и 5 вершин. Эти фигуры неправильные, так как у их основания стороны разной длины. Однако противоположные лица одинаковы.
Здесь мы более подробно узнаем о гранях, вершинах и ребрах прямоугольных пирамид. Мы облегчим понимание концепций с помощью диаграмм.
ГЕОМЕТРИЯ
Актуально для …
Изучение граней, вершин и ребер прямоугольных пирамид.
См. грани
Содержание
ГЕОМЕТРИЯ
Актуально для …
Изучение граней, вершин и ребер прямоугольных пирамид.
См. грани
Грани прямоугольной пирамиды
Грани прямоугольной пирамиды – это плоские поверхности, образованные на границах пирамиды. Все пирамиды состоят из основания и боковых треугольных граней. В случае прямоугольной пирамиды у нас есть прямоугольное основание и четыре боковые треугольные грани.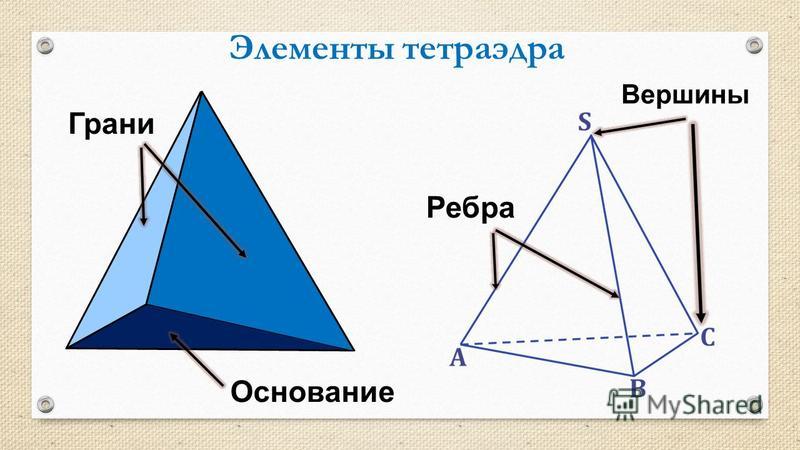
Это означает, что у этих пирамид всего 5 граней.
Поскольку основание представляет собой прямоугольник, не все треугольные грани имеют одинаковую форму. Однако противоположные грани имеют одинаковую форму, поскольку противоположные стороны прямоугольника имеют одинаковую длину.
Важной характеристикой этих пирамид является то, что четыре боковые грани сходятся в одной верхней точке, называемой вершиной.
Площадь поверхности пирамид находится путем сложения площадей всех их граней. Основание представляет собой прямоугольник, поэтому его площадь равна произведению длины основания на длину его ширины. С другой стороны, боковые грани треугольные, поэтому их площадь равна половине длины его основания, умноженной на длину его высоты.
Вершины прямоугольной пирамиды
Вершины прямоугольной пирамиды — это точки, в которых сходятся три или четыре ребра. В общем случае вершины — это точки, в которых встречаются два или более отрезка прямой. Вершины в основании прямоугольной пирамиды образованы пересечением трех ребер, а верхняя вершина образована пересечением четырех ребер.