Векторное произведение векторов.
Векторное произведение векторов.Навигация по странице:
- Определение векторного произведения векторов
- Формулы вычисления векторного произведения векторов
- Свойства векторного произведения векторов
- Примеры задач на вычисления векторного произведения векторов
Онлайн калькулятор. Векторное произведение векторов.
Упражнения на тему векторное произведение векторов.
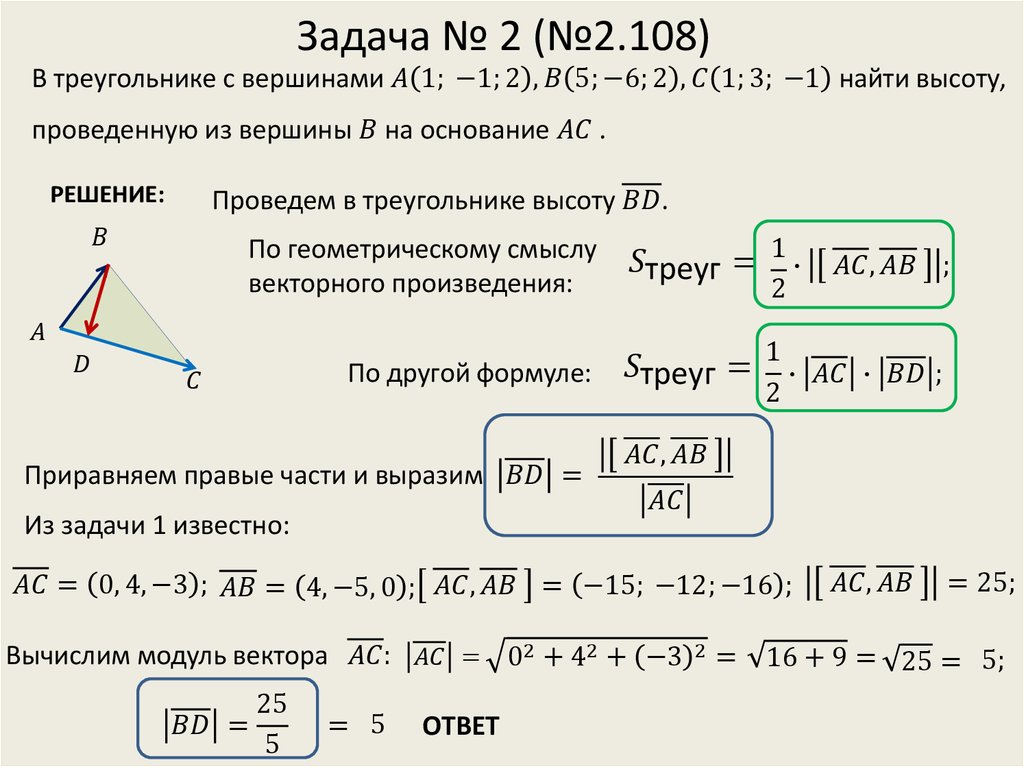
Определение. Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c (рис. 1).
| рис. 1 |
Формулы вычисления векторного произведения векторов
Векторное произведение
a × b = ijkaxayazbxbybz = i (aybz — azby) — j (axbz — azbx) + k (axby — aybx)
a × b = {aybz — azby; azbx — axbz; axby — aybx}
Свойства векторного произведения векторов
Геометрический смысл векторного произведения.

Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:
Sпарал = [a × b]
Геометрический смысл векторного произведения.
Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:
SΔ = 1 |a × b| 2 Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.
Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.
a × b = -b × a
(k a) × b = a × (k b) = k (a × b)
(a + b) × c = a × c + b × c
Примеры задач на вычисления векторного произведения векторов
Пример 1. Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.
Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.
Решение:
| a × b = | i | j | k | = |
| 1 | 2 | 3 | ||
| 2 | 1 | -2 |
= i(2 · (-2) — 3 · 1) — j(1 · (-2) — 2 · 3) + k(1 · 1 — 2 · 2) =
= i(-4 — 3) — j(-2 — 6) + k(1 — 4) = -7i + 8j — 3k = {-7; 8; -3}
Пример 2. Найти площадь треугольника образованного векторами a = {-1; 2; -2} и b = {2; 1; -1}.
Решение: Найдем векторное произведение этих векторов:
| a × b = | i | j | k | = |
| -1 | 2 | -2 | ||
| 2 | 1 | -1 |
= i(2 · (-1) — (-2) · 1) — j((-1) · (-1) — (-2) · 2) + k((-1) · 1 — 2 · 2) =
= i(-2 + 2) — j(1 + 4) + k(-1 — 4) = -5j — 5k = {0; -5; -5}
Из свойств векторного произведения:
SΔ =
12|a × b| =
12√02 + 52 + 52 =
12√25 + 25 =
12√50 =
5√22 = 2.
Ответ: SΔ = 2.5√2.
Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису
Онлайн калькуляторы с векторами
Онлайн упражнения с векторами на плоскости
Онлайн упражнения с векторами в пространстве
Нахождение площади треугольника по векторам. Векторное произведение векторов
Контрольная работа №1
Векторы. Элементы высшей алгебры
Элементы высшей алгебры
1-20. Известны длины векторов и и; – угол между этими векторами.
Вычислить: 1) и, 2) .3) Найти площадь треугольника, построенного на векторах и.
Сделать чертеж.
Решение. Используя определение скалярного произведения векторов:
И свойства скалярного произведения: ,
1) находим скалярный квадрат вектора:
то есть, Тогда .
Рассуждая аналогично, получаем
то есть, Тогда .
По определению векторного произведения: ,
с учетом того, что
Площадь треугольника построенного на векторах и равна
21-40. Известны координаты трех вершин A, B, D параллелограмма ABCD . Средствами векторной алгебры требуется:
A (3;0;-7), B (2;4;6), D (-7;-5;1)
Решение.
Известно, что диагонали
параллелограмма в точке пересечения
делятся пополам. Поэтому координаты
точки  Обозначая их через x E ,y E , z E получим, что
Обозначая их через x E ,y E , z E получим, что
Получаем .
Зная координаты точки E — середины диагонали BD и координаты одного из его концов A (3;0;-7), по формулам определяем искомые координаты вершины С параллелограмма:
Итак, вершина .
2) Чтобы найти проекцию вектора на вектор , найдем координаты этих векторов: ,
аналогично . Проекцию вектора на вектор , находим по формуле:
3) Угол между диагоналями параллелограмма находим как угол между векторами
И по свойству скалярного произведения:
тогда
4) Площадь параллелограмма находим как модуль векторного произведения:
5) Объем пирамиды находим как одну шестую модуля смешанного произведения векторов , где О(0;0;0), тогда
Тогда искомый объем (куб.ед.)
41-60. Даны матрицы:
В ·С -1 +3A T
Обозначения:
Сначала
находим обратную матрицу к матрице С.
Для этого находим ее определитель:
Определитель отличен от нуля, следовательно, матрица является невырожденной и для нее можно найти обратную матрицу С -1
Найдем алгебраические дополнения по формуле , где — минор элемента :
Тогда , .
61–80. Решите систему линейных уравнений:
Методом Крамера; 2. Матричным методом.
Решение.
а) метод Крамера
Найдем определитель системы
Так как , то система имеет единственное решение.
Найдем определители и , заменив в матрице коэффициентов соответственно первый, второй, третий столбцы столбцом свободных членов.
По формулам Крамера:
б) матричный метод (с помощью обратной матрицы).
Данную систему запишем в матричной форме и решим с помощью обратной матрицы.
Пусть А – матрица коэффициентов при неизвестных; X – матрица-столбец неизвестных x , y , z и Н – матрица-столбец из свободных членов:
Левую
часть системы (1) можно записать в виде
произведения матриц
, а
правую в виде матрицы Н . Следовательно имеем матричное уравнение
Следовательно имеем матричное уравнение
Так как определитель матрицы А отличен от нуля (пункт «а»), то матрица А имеет обратную матрицу . Умножим обе части равенства (2) слева на матрицу , получим
Так как , где Е – единичная матрица, а , то
Пусть имеем невырожденную матрицу А:
Тогда обратную матрицу находим по формуле:
где A ij — алгебраическое дополнение элемента a ij в определителе матрицы А , которое является произведением (-1) i+j на минор (определитель) n-1 порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А:
Отсюда получаем обратную матрицу:
Столбец X: X=A -1 H
81–100. Решить систему линейных уравнений методом Гаусса
Решение. Запишем систему в виде расширенной матрицы:
Выполняем элементарные преобразования со строками.
Из
2-ой строки вычитаем первую строку,
умноженную на 2. Из строки 3 вычитаем
первую строку, умноженную на 4. Из строки
4 вычитаем первую строку, получаем
матрицу:
Из строки 3 вычитаем
первую строку, умноженную на 4. Из строки
4 вычитаем первую строку, получаем
матрицу:
Далее получаем нуль в первом столбце последующих строк, для этого из второй строки вычитаем третью строку. Из третьей строки вычитаем вторую строку, умноженную на 2. Из четвертой строки вычитаем вторую строку, умноженную на 3. В результате получаем матрицу вида:
Из четвертой строки вычитаем третью.
Поменяем местами предпоследнюю и последнюю строки:
Последняя матрица равносильна системе уравнений:
Из последнего уравнения системы находим .
Подставляя в предпоследнее уравнение, получаем .
Из второго уравнения системы следует, что
Из первого уравнения находим х:
Ответ:
Контрольная работа №2
Аналитическая геометрия
1-20. Даны координаты вершин треугольника АВС. Найти:
1) длину стороны A В ;
2) уравнения сторон АВ и ВС и их угловые коэффициенты;
3) угол В в радианах с точностью до двух знаков;
4) уравнение высоты CD и её длину;
5) уравнение медианы АЕ
высотой CD ;
К параллельно стороне АВ,
7)
сделать чертёж.
А(3;6), В(15;-3), С(13;11)
Решение.
Применяя (1), находим длину стороны АВ :
2) уравнения сторон АВ и ВС и их угловые коэффициенты:
Уравнение прямой, проходящей через точки и , имеет вид
Подставляя в (2) координаты точек А и В , получим уравнение стороны АВ :
(АВ ).
(BC ).
3) угол В в радианах с точностью до двух знаков.
Известно, что тангенс угла между двумя прямыми, угловые коэффициенты, которых соответственно равны и вычисляется по формуле
Искомый угол В образован прямыми АВ и ВС , угловые коэффициенты которых найдены: ; . Применяя (3), получим
; , или
4) уравнение высоты CD и её длина.
Расстояние от точки С до прямой АВ:
5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с
высотой CD .
середина стороны ВС:
Тогда уравнение АЕ:
Решаем систему уравнений:
6) уравнение прямой, проходящей через точку К параллельно стороне АВ :
Так
как искомая прямая параллельна стороне АВ , то ее
угловой коэффициент будет равен угловому
коэффициенту прямой АВ . Подставив в (4) координаты найденной
точки К и
угловой коэффициент
, получим
Подставив в (4) координаты найденной
точки К и
угловой коэффициент
, получим
; (KF ).
Площадь параллелограмма равна 12 кв. ед., две его вершины – точкиА(-1;3) и В(-2;4). Найти две другие вершины этого параллелограмма, если известно, что точка пересечения его диагоналей лежит на оси абсцисс. Сделать чертёж.
Решение. Пусть точка пересечения диагоналей имеет координаты .
Тогда очевидно, что и
следовательно, координаты векторов .
Площадь параллелограмма находим по формуле
Тогда координаты двух других вершин .
В задачах 51-60 даны координаты точек А и В . Требуется:
Составить каноническое уравнение гиперболы, проходящей через данные точкиА и В, если фокусы гиперболы расположены на оси абсцисс;
Найти полуоси, фокусы, эксцентриситет и уравнения асимптот этой гиперболы;
Найти все точки пересечения гиперболы с окружностью с центром в начале координат, если эта окружность проходит через фокусы гиперболы;
Построить
гиперболу, её асимптоты и окружность.
А(6;-2), В(-8;12).
Решение. Уравнение искомой гиперболы в каноническом виде записывается
где a — действительная полуось гиперболы, b — мнимая полуось. Подставляя координаты точек А и В в это уравнение найдем эти полуоси:
– уравнение гиперболы: .
Полуоси а=4,
фокусное расстояние Фокусы (-8,0) и (8,0)
Эксцентриситет
Асиптоты:
Если окружность проходит через начало координат, ее уравнение
Подставляя один из фокусов, находим и уравнение окружности
Находим точки пересечения гиперболы и окружности:
Строим чертеж:
В задачах 61-80 построить график функции в полярной системе координат по точкам, придавая значения через промежуток /8 (0 2). Найти уравнение линии в прямоугольной декартовой системе координат (положительная полуось абсцисс совпадает с полярной осью, а полюс – с началом координат).
Решение. Построим линию по точкам, предварительно
заполнив таблицу значений
и φ.
Номер | φ , | φ, градусы | Номер | φ , рад | градусы | |||
3∙(x 2 +2∙1x + 1) -3∙1 = 3(x+1) 2 — 3 делаем вывод, что данное уравнение определяет эллипс: Даны
точки А, В, С,
D. 1. Уравнение плоскости(Q ), проходящей через точкиА, В, С D в плоскости (Q) ; 2. Уравнение прямой (I), проходящей через точкиВ и D; 3. Угол между плоскостью (Q) и прямой (I) ; 4. Уравнение плоскости (Р), проходящей через точкуА перпендикулярно прямой (I) ; 5. Угол между плоскостями (Р) и (Q ) ; 6. Уравнение прямой (т), проходящей через точку А в направлении ее радиус-вектора; 7. Угол между прямыми (I) и (т). А(9;-8;1), В(-9;4;5), С(9;-5;5), D (6;4;0) 1.
Уравнение плоскости(Q ), проходящей через точки А,
В, С и проверить, лежит ли
точка D в
плоскости
определяется по формуле
Найти
: 1) . 2) Площадь параллелограмма, построенного на и. Методические рекомендации по выполнению контрольных работ для бакалавриата заочной формы обучения по квалификации 080100. 62 по направлениюМетодические рекомендацииПараллелепипеда и объем пирамиды, построенных на векторах , и. Решение: 2-=2(1;1;1)-(2;1;4)= (2;2;2)-(2;1;4)=(0;1;-2).. . . . . 4.ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ Раздел I. Линейная алгебра . 1 – 10. Дана… |
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника.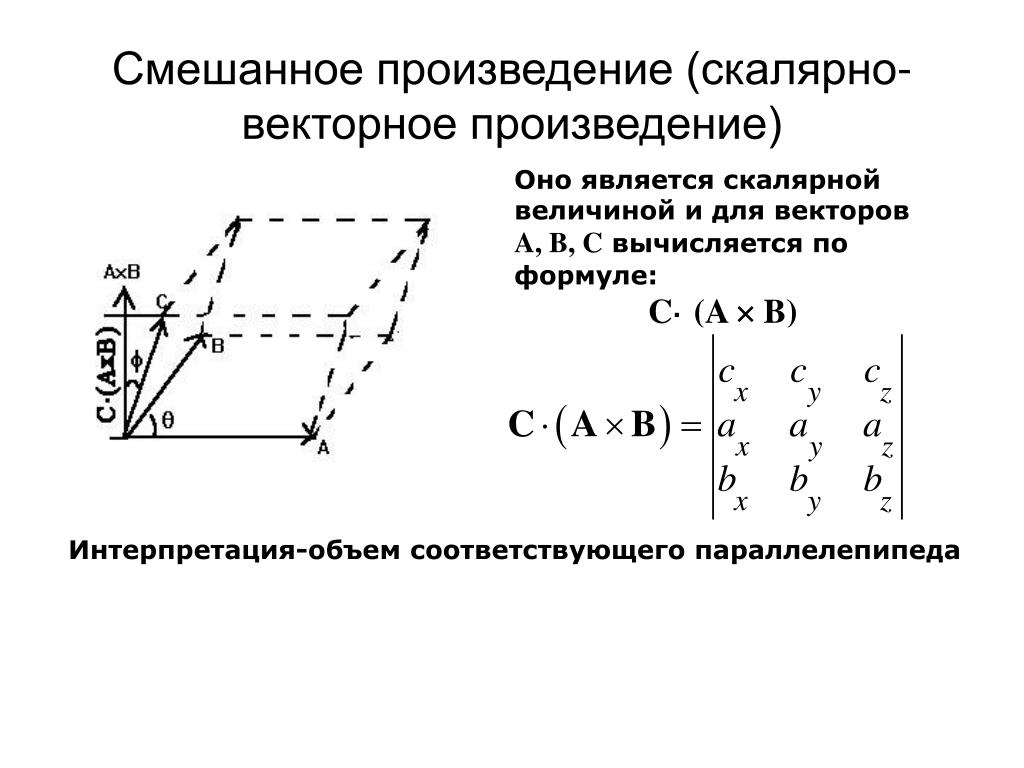 Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то и . Обратите внимание, что само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно тоже равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
В этой статье мы подробно остановимся на понятии векторного произведения двух векторов. Мы дадим необходимые определения, запишем формулу для нахождения координат векторного произведения, перечислим и обоснуем его свойства. После этого остановимся на геометрическом смысле векторного произведения двух векторов и рассмотрим решения различных характерных примеров.
Мы дадим необходимые определения, запишем формулу для нахождения координат векторного произведения, перечислим и обоснуем его свойства. После этого остановимся на геометрическом смысле векторного произведения двух векторов и рассмотрим решения различных характерных примеров.
Навигация по странице.
Определение векторного произведения.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов в трехмерном пространстве.
Отложим векторы от одной точки. В зависимости от направления вектора тройка может быть правой или левой. Посмотрим с конца вектора на то, как происходит кратчайший поворот от вектора к . Если кратчайший поворот происходит против часовой стрелки, то тройка векторов называется правой , в противном случае – левой .
Теперь возьмем два не коллинеарных вектора и . Отложим от точки А
векторы и . Построим некоторый вектор , перпендикулярный одновременно и и . Очевидно, что при построении вектора мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).
В зависимости от направления вектора упорядоченная тройка векторов может быть правой или левой.
Так мы вплотную подошли к определению векторного произведения. Оно дается для двух векторов, заданных в прямоугольной системе координат трехмерного пространства.
Определение.
Векторным произведением двух векторов и , заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор , что
Векторное произведение векторов и обозначается как .
Координаты векторного произведения.
Сейчас дадим второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов и.
Определение.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов и есть вектор , где — координатные векторы.
Это определение дает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты , во второй строке находятся координаты вектора , а в третьей – координаты вектора в заданной прямоугольной системе координат:
Если разложить этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах (при необходимости обращайтесь к статье ):
Следует отметить, что координатная форма векторного произведения полностью согласуется с определением, данным в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны. Доказательство этого факта можете посмотреть в книге, указанной в конце статьи.
Более того, эти два определения векторного произведения эквивалентны. Доказательство этого факта можете посмотреть в книге, указанной в конце статьи.
Свойства векторного произведения.
Так как векторное произведение в координатах представимо в виде определителя матрицы , то на основании легко обосновываются следующие свойства векторного произведения :
Для примера докажем свойство антикоммутативности векторного произведения.
По определению и . Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому, , что доказывает свойство антикоммутативности векторного произведения.
Векторное произведение – примеры и решения.
В основном встречаются три типа задач.
В задачах первого типа заданы длины двух векторов и угол между ними, а требуется найти длину векторного произведения. В этом случае используется формула .
Пример.
Найдите длину векторного произведения векторов и , если известно .
Решение.
Мы знаем из определения, что длина векторного произведения векторов и равна произведению длин векторов и на синус угла между ними, поэтому, .
Ответ:
.
Задачи второго типа связаны с координатами векторов, в них векторное произведение, его длина или что-либо еще ищется через координаты заданных векторов и .
Здесь возможна масса различных вариантов. К примеру, могут быть заданы не координаты векторов и , а их разложения по координатным векторам вида и , или векторы и могут быть заданы координатами точек их начала и конца.
Рассмотрим характерные примеры.
Пример.
В прямоугольной системе координат заданы два вектора . Найдите их векторное произведение.
Решение.
По второму определению векторное произведение двух векторов в координатах записывается как:
К такому же результату мы бы пришли, если бы векторное произведение записали через определитель
Ответ:
.
Пример.
Найдите длину векторного произведения векторов и , где — орты прямоугольной декартовой системы координат.
Решение.
Сначала найдем координаты векторного произведения в заданной прямоугольной системе координат.
Так как векторы и имеют координаты и соответственно (при необходимости смотрите статью координаты вектора в прямоугольной системе координат), то по второму определению векторного произведения имеем
То есть, векторное произведение имеет координаты в заданной системе координат.
Длину векторного произведения находим как корень квадратный из суммы квадратов его координат (эту формулу длины вектора мы получили в разделе нахождение длины вектора):
Ответ:
.
Пример.
В прямоугольной декартовой системе координат заданы координаты трех точек . Найдите какой-нибудь вектор, перпендикулярный и одновременно.
Решение.
Векторы и имеют координаты и соответственно (смотрите статью нахождение координат вектора через координаты точек). Если найти векторное произведение векторов и , то оно по определению является вектором, перпендикулярным и к и к , то есть, является решением нашей задачи. Найдем его
Найдем его
Ответ:
— один из перпендикулярных векторов.
В задачах третьего типа проверяется навык использования свойств векторного произведения векторов. После применения свойств, применяются соответствующие формулы.
Пример.
Векторы и перпендикулярны и их длины равны соответственно 3 и 4 . Найдите длину векторного произведения .
Решение.
По свойству дистрибутивности векторного произведения мы можем записать
В силу сочетательного свойства вынесем числовые коэффициенты за знак векторных произведений в последнем выражении:
Векторные произведения и равны нулю, так как и , тогда .
Так как векторное произведение антикоммутативно, то .
Итак, с помощью свойств векторного произведения мы пришли к равенству .
По условию векторы и перпендикулярны, то есть угол между ними равен . То есть, у нас есть все данные для нахождения требуемой длины
Ответ:
.
Геометрический смысл векторного произведения.

По определению длина векторного произведения векторов равна . А из курса геометрии средней школы нам известно, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними. Следовательно, длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы и , если их отложить от одной точки. Другими словами, длина векторного произведения векторов и равна площади параллелограмма со сторонами и и углом между ними, равным . В этом состоит геометрический смысл векторного произведения.
Примеры как вычислить площадь параллелограмма, построенного на векторах
Вспомним в начале, что такое векторное произведение.
Замечание 1
Векторным произведением для $\vec{a}$ и $\vec{b}$ является $\vec{c}$, представляющий собой некоторый третий вектор $\vec{c}= |[ab]|$, причём этот вектор обладает особенными свойствами:
- Cкаляр полученного вектора — произведение $|\vec{a}|$ и $|\vec{b}|$ на синус угла $\vec{c}= |[ab]|= |\vec{a}| \cdot |\vec{b}|\cdot \sin α \left(1\right)$;
- Все $\vec{a}, \vec{b}$ и $\vec{c}$ образуют правую тройку;
- Полученный вектор ортогонален к $\vec{a}$ и $\vec{b}$.

Если для векторов присутствуют некоторые координаты ($\vec{a}=\{x_1; y_1; z_1\}$ и $\vec{b}= \{x_2; y_2; z_2\}$), то их векторное произведение в декартовой системе координат можно определить по формуле:
$[a \times b] = \{y_1 \cdot z_2 – y_2 \cdot z_1; z_1 \cdot x_2 – z_2 \cdot x_1; x_2 \cdot y_2 – x_2 \cdot y_1\}$
Легче всего запомнить эту формулу записав в форме определителя:
$[ab] = \begin{array} {|ccc|} i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ \end{array}$.
Эта формула весьма удобна для использования, но чтобы понимать, как её использовать, для начала следует ознакомиться с темой матриц и их определителей.
Площадь параллелограмма, стороны которого определяются двумя векторами $\vec{a}$ и $vec{b}$ равна скаляру векторного произведения данных двух векторов.
Это соотношение совсем несложно вывести.
Вспомним формулу для нахождения площади обычного параллелограмма, который можно охарактеризовать образующими его отрезками $a$ и $b$:
$S = a \cdot b \cdot \sin α$
При этом длины сторон равны скалярным значениям векторов $\vec{a}$ и $\vec{b}$, что вполне себе подходит нам, то есть, скаляр векторного произведения данных векторов и будет площадью рассматриваемой фигуры. 2} = \sqrt{1878} ≈ 43, 34$.
2} = \sqrt{1878} ≈ 43, 34$.
Данный ход рассуждений справедлив не только для нахождения площади в 3-хмерном пространстве, но и для двухмерного. Познакомьтесь со следующей задачкой на эту тему.
Пример 2
Вычислить площадь параллелограмма, если его образующие отрезки задаются векторами $\vec{m}$ с координатами $\{2; 3\}$ и $\vec{d}$ с координатами $\{-5; 6\}$.
Решение:
Эта задача представляет собой частный пример задачки 1, решённой выше, но при этом оба вектора лежат в одной плоскости, а это значит, что третью координату, $z$, можно принять за нуль.
Подведём итоги по всему вышесказанному, площадь параллелограмма составит:
$S = \begin{array} {||cc||} 2 & 3\\ -5 & 6 \\ \end{array} = \sqrt{12 + 15} =3 \sqrt3$.
Пример 3
Даны векторы $\vec{a} = 3i – j + k; \vec{b}= 5i$. Определите площадь образуемого ими параллелограмма.
$[ \vec{a} \times \vec{b}] = (3i – j + k) \times 5i = 15 [i \times i] – 5 [j \times i] + [5k\times i]$
Упростим согласно приведённой таблице для единичных векторов:
Рисунок 1. 2} = 5\sqrt{2}$.
2} = 5\sqrt{2}$.
Предыдущие задачи были о векторах, координаты которых заданы в декартовой системе координат, но рассмотрим также случай, если угол между базисными векторами отличается от $90°$:
Пример 4
Вектор $\vec{d} = 2a + 3b$, $\vec{f}= a – 4b$, длины $\vec{a}$ и $\vec{b}$ равны между собой и равны единице, а угол между $\vec{a}$ и $\vec{b}$ равен 45°.
Решение:
Вычислим векторное произведение $\vec{d} \times \vec{f}$:
$[\vec{d} \times \vec{f} ]= (2a + 3b) \times ( a – 4b) = 2 [a \times a] – 8 [a \times b] + 3 [b \times a] – 12 [b \times b]$.
Для векторных произведений согласно их свойствам справедливо следующее: $[a \times a]$ и $[b \times b]$ равны нулю, $[b \times a] = — [a \times b]$.
Используем это для упрощения:
$[\vec{d} \times \vec{f} ]= -8[a \times b] + 3 [b \times a] = -8[a \times b] — 3[a \times b] =-11[a \times b]$.
Теперь воспользуемся формулой $(1)$ :
$[\vec{d} \times \vec{f} ] = |-11 [a \times b]| = 11 \cdot |a| \cdot |b| \cdot \sin α = 11 \cdot 1 \cdot 1 \cdot \frac12=5,5$.
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 07.05.2022
Векторное произведение векторов площадь треугольника. Свойства векторного произведения
Определение. Векторным произведением вектора а (множимое) на не коллинеарный ему вектор (множитель) называется третий вектор с (произведение), который строится следующим образом:
1) его модуль численно равен площади параллелограмма на рис. 155), построенного на векторах т. е. он равен направление перпендикулярно плоскости упомянутого параллелограмма;
3) при этом направление вектора с выбирается (из двух возможных) так, чтобы векторы с составляли правую систему (§ 110).
Обозначение: или
Дополнение к определению. Если векторы коллинеарны, то фигуре считая ее (условно) параллелограммом, естественно приписать нулевую площадь. Поэтому векторное произведение коллинеарных векторов считается равным нуль-вектору.
Поскольку нуль-вектору можно приписать любое направление, это соглашение не противоречит пунктам 2 и 3 определения.
Замечание 1. В термине «векторное произведение» первое слово указывает на то, что результат действия есть вектор (в противоположность скалярному произведению; ср. § 104, замечание 1).
Пример 1. Найти векторное произведение где основные векторы правой системы координат (рис. 156).
1. Так как длины основных векторов равны единице масштаба, то площадь параллелограмма (квадрата) численно равна единице. Значит, модуль векторного произведения равен единице.
2. Так как перпендикуляр к плоскости есть ось то искомое векторное произведение есть вектор, коллинеарный вектору к; а так как оба они имеют модуль 1, то искомое векторное произведение равно либо k, либо -k.
3. Из этих двух возможных векторов надо выбрать первый, так как векторы к образуют правую систему (а векторы левую).
Пример 2. Найти векторное произведение
Решение. Как в примере 1, заключаем, что вектор равен либо k, либо -k. Но теперь надо выбрать -k, так как векторы образуют правую систему (а векторы левую). Итак,
Итак,
Пример 3. Векторы имеют длины, соответственно равные 80 и 50 см, и образуют угол 30°. Приняв за единицу длины метр, найти длину векторного произведения а
Решение. Площадь параллелограмма, построенного на векторах равна Длина искомого векторного произведения равна
Пример 4. Найти длину векторного произведения тех же векторов, приняв за единицу длины сантиметр.
Решение. Так как площадь параллелограмма, построенного на векторах равна то длина векторного произведения равна 2000 см, т. е.
Из сравнения примеров 3 и 4 видно, что длина вектора зависит не только от длин сомножителей но также и от выбора единицы длины.
Физический смысл векторного произведения. Из многочисленных физических величин, изображаемых векторным произведением, рассмотрим только момент силы.
Пусть А есть точка приложения силы Моментом силы относителько точки О называется векторное произведение Так как модуль этого векторного произведения численно равен площади параллелограмма (рис. 157), то модуль момента равняется произведению основания на высоту т. е. силе, умноженной на расстояние от точки О до прямой, вдоль которой действует сила.
157), то модуль момента равняется произведению основания на высоту т. е. силе, умноженной на расстояние от точки О до прямой, вдоль которой действует сила.
В механике доказывается, что для равновесия твердого тела необходимо, чтобы равнялась нулю не только сумма векторов , представляющих силы, приложенные к телу, но также и сумма моментов сил. В том случае, когда все силы параллельны одной плоскости, сложение векторов, представляющих моменты, можно заменить сложением и вычитанием их модулей. Но при произвольных направлениях сил такая замена невозможна. В соответствии с этим векторное произведение определяется именно как вектор, а не как число.
7.1. Определение векторного произведения
Три некомпланарных вектора a , b и с , взятые в указанном порядке, образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму вектору b виден совершающимся против часовой стрелки, и левую, если по часовой (см. рис. 16).
Векторным произведением вектора а на вектор b называется вектор с , который:
1. j
;
j
;
2) |k |=1, но | i x j | = |i | |J | sin(90°)=1;
3) векторы i , j и k образуют правую тройку (см. рис. 16).
7.2. Свойства векторного произведения
1. При перестановке сомножителей векторное произведение меняет знак, т.е. а хb =(b хa ) (см. рис. 19).
Векторы а хb и b ха коллинеарны, имеют одинаковые модули (площадь параллелограмма остается неизменной), но противоположно направлены (тройки а , b , а хb и a , b , b x a противоположной ориентации). Стало быть a xb = -(b xa ).
2. Векторное произведение обладает сочетательным свойством относительно скалярного множителя, т. е. l (а хb ) = (l а ) х b = а х (l b ).
Пусть l >0. Вектор l (а хb ) перпендикулярен векторам а и b . Вектор ( l а )хb также перпендикулярен векторам а и b (векторы а , l а лежат в одной плоскости). Значит, векторы l (а хb ) и ( l а )хb коллинеарны. Очевидно, что и направления их совпадают. Имеют одинаковую длину:
Поэтому l
(a
хb
)=
l
а
хb
.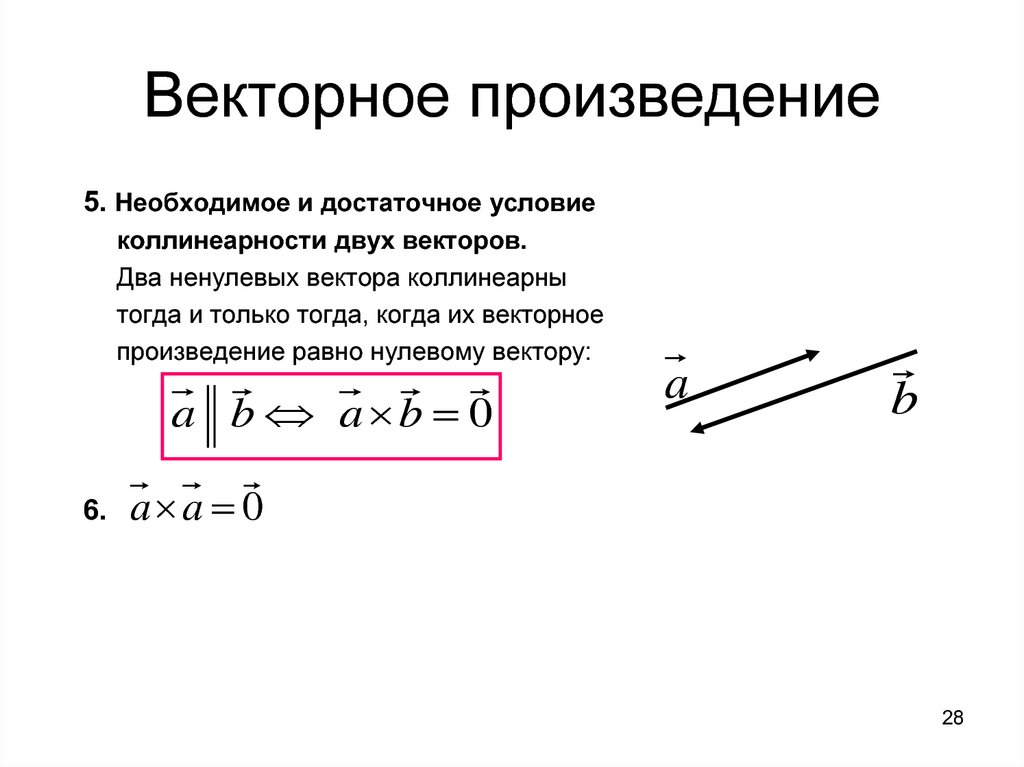 Аналогично доказывается при
l
Аналогично доказывается при
l
3. Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору, т. е. а ||b а хb =0 .
В частности, i *i =j *j =k *k =0 .
4. Векторное произведение обладает распределительным свойством:
(a +b ) хс = а хс +b хс .
Примем без доказательства.
7.3. Выражение векторного произведения через координаты
Мы будем использовать таблицу векторного произведения векторов i , j и k :
если направление кратчайшего пути от первого вектора к второму совпадает с направлением стрелки, то произведение равно третьему вектору, если не совпадает — третий вектор берется со знаком «минус».
Пусть заданы два вектора а =а х i +a y j +a z k и b =b x i +b y j +b z k . Найдем векторное произведение этих векторов, перемножая их как многочлены (согласно свойств векторного произведения):
Полученную формулу можно записать еще короче:
так как правая часть равенства (7.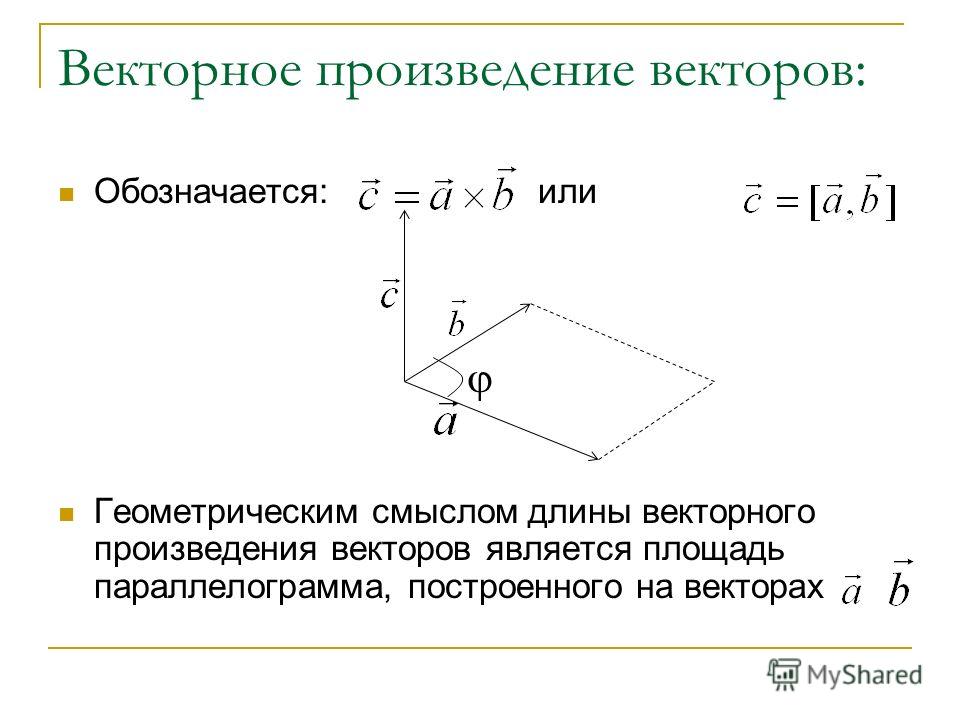 1) соответствует разложению
определителя третьего порядка по элементам первой строки.Равенство (7.2) легко
запоминается.
1) соответствует разложению
определителя третьего порядка по элементам первой строки.Равенство (7.2) легко
запоминается.
7.4. Некоторые приложения векторного произведения
Установление коллинеарности векторов
Нахождение площади параллелограмма и треугольника
Согласно определению векторного произведения векторов а и b |а хb | = |а | * |b |sin g , т. е. S пар = |а х b |. И, значит, D S =1/2|а х b |.
Определение момента силы относительно точки
Пусть в точке А приложена сила F =АВ и пусть О — некоторая точка пространства (см. рис. 20).
Из физики известно, что моментом си лы F относительно точки О называется вектор М , который проходит через точку О и:
1) перпендикулярен плоскости, проходящей через точки О, А, В;
2) численно равен произведению силы на плечо
3) образует правую тройку с векторами ОА
и
A
В
.
Стало быть, М =ОА х F .
Нахождение линейной скорости вращения
Скорость v точки М твердого тела, вращающегося с угловой скоростью w вокруг неподвижной оси, определяется формулой Эйлера v =w хr , где r =ОМ , где О-некоторая неподвижная точка оси (см. рис. 21).
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Определение векторного произведенияСначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства.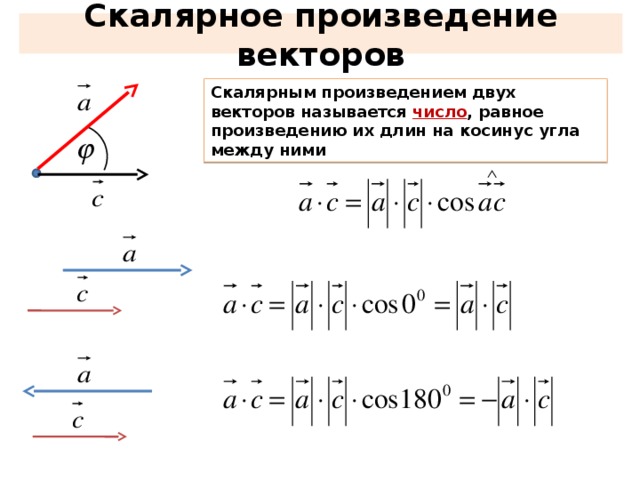 Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом».
Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
В этой статье мы подробно остановимся на понятии векторного произведения двух векторов. Мы дадим необходимые определения, запишем формулу для нахождения координат векторного произведения, перечислим и обоснуем его свойства. После этого остановимся на геометрическом смысле векторного произведения двух векторов и рассмотрим решения различных характерных примеров.
После этого остановимся на геометрическом смысле векторного произведения двух векторов и рассмотрим решения различных характерных примеров.
Навигация по странице.
Определение векторного произведения.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов в трехмерном пространстве.
Отложим векторы от одной точки. В зависимости от направления вектора тройка может быть правой или левой. Посмотрим с конца вектора на то, как происходит кратчайший поворот от вектора к . Если кратчайший поворот происходит против часовой стрелки, то тройка векторов называется правой , в противном случае – левой .
Теперь возьмем два не коллинеарных вектора и . Отложим от точки А векторы и . Построим некоторый вектор , перпендикулярный одновременно и и . Очевидно, что при построении вектора мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).
В зависимости от направления вектора упорядоченная тройка векторов может быть правой или левой.
Так мы вплотную подошли к определению векторного произведения. Оно дается для двух векторов, заданных в прямоугольной системе координат трехмерного пространства.
Определение.
Векторным произведением двух векторов и , заданных в прямоугольной системе координат трехмерного пространства, называется такой вектор , что
Векторное произведение векторов и обозначается как .
Координаты векторного произведения.
Сейчас дадим второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов и.
Определение.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов и есть вектор , где — координатные векторы.
Это определение дает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты , во второй строке находятся координаты вектора , а в третьей – координаты вектора в заданной прямоугольной системе координат:
Если разложить этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах (при необходимости обращайтесь к статье ):
Следует отметить, что координатная форма векторного произведения полностью согласуется с определением, данным в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны. Доказательство этого факта можете посмотреть в книге, указанной в конце статьи.
Более того, эти два определения векторного произведения эквивалентны. Доказательство этого факта можете посмотреть в книге, указанной в конце статьи.
Свойства векторного произведения.
Так как векторное произведение в координатах представимо в виде определителя матрицы , то на основании легко обосновываются следующие свойства векторного произведения :
Для примера докажем свойство антикоммутативности векторного произведения.
По определению и . Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому, , что доказывает свойство антикоммутативности векторного произведения.
Векторное произведение – примеры и решения.
В основном встречаются три типа задач.
В задачах первого типа заданы длины двух векторов и угол между ними, а требуется найти длину векторного произведения. В этом случае используется формула .
Пример.
Найдите длину векторного произведения векторов и , если известно .
Решение.
Мы знаем из определения, что длина векторного произведения векторов и равна произведению длин векторов и на синус угла между ними, поэтому, .
Ответ:
.
Задачи второго типа связаны с координатами векторов, в них векторное произведение, его длина или что-либо еще ищется через координаты заданных векторов и .
Здесь возможна масса различных вариантов. К примеру, могут быть заданы не координаты векторов и , а их разложения по координатным векторам вида и , или векторы и могут быть заданы координатами точек их начала и конца.
Рассмотрим характерные примеры.
Пример.
В прямоугольной системе координат заданы два вектора . Найдите их векторное произведение.
Решение.
По второму определению векторное произведение двух векторов в координатах записывается как:
К такому же результату мы бы пришли, если бы векторное произведение записали через определитель
Ответ:
.
Пример.
Найдите длину векторного произведения векторов и , где — орты прямоугольной декартовой системы координат.
Решение.
Сначала найдем координаты векторного произведения в заданной прямоугольной системе координат.
Так как векторы и имеют координаты и соответственно (при необходимости смотрите статью координаты вектора в прямоугольной системе координат), то по второму определению векторного произведения имеем
То есть, векторное произведение имеет координаты в заданной системе координат.
Длину векторного произведения находим как корень квадратный из суммы квадратов его координат (эту формулу длины вектора мы получили в разделе нахождение длины вектора):
Ответ:
.
Пример.
В прямоугольной декартовой системе координат заданы координаты трех точек . Найдите какой-нибудь вектор, перпендикулярный и одновременно.
Решение.
Векторы и имеют координаты и соответственно (смотрите статью нахождение координат вектора через координаты точек). Если найти векторное произведение векторов и , то оно по определению является вектором, перпендикулярным и к и к , то есть, является решением нашей задачи. Найдем его
Найдем его
Ответ:
— один из перпендикулярных векторов.
В задачах третьего типа проверяется навык использования свойств векторного произведения векторов. После применения свойств, применяются соответствующие формулы.
Пример.
Векторы и перпендикулярны и их длины равны соответственно 3 и 4 . Найдите длину векторного произведения .
Решение.
По свойству дистрибутивности векторного произведения мы можем записать
В силу сочетательного свойства вынесем числовые коэффициенты за знак векторных произведений в последнем выражении:
Векторные произведения и равны нулю, так как и , тогда .
Так как векторное произведение антикоммутативно, то .
Итак, с помощью свойств векторного произведения мы пришли к равенству .
По условию векторы и перпендикулярны, то есть угол между ними равен . То есть, у нас есть все данные для нахождения требуемой длины
Ответ:
.
Геометрический смысл векторного произведения.

По определению длина векторного произведения векторов равна . А из курса геометрии средней школы нам известно, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними. Следовательно, длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы и , если их отложить от одной точки. Другими словами, длина векторного произведения векторов и равна площади параллелограмма со сторонами и и углом между ними, равным . В этом состоит геометрический смысл векторного произведения.
Единичный вектор — это вектор , абсолютная величина (модуль) которого равен единице. Для обозначения единичного вектора мы будем использовать нижний индекс е. Так, если задан вектор а , то его единичным вектором будет вектор а е. Этот единичный вектор направлен туда же, куда направлен и сам вектор а , и его модуль равен единице, то есть а е = 1.
Очевидно, а = а·а е (а — модуль вектора а) . Это следует из правила, по которому выполняется операция умножения скаляра на вектор .
Это следует из правила, по которому выполняется операция умножения скаляра на вектор .
Единичные векторы часто связывают с координатными осями системы координат (в частности, с осями декартовой системы координат). Направления этих векторов совпадают с направлениями соответствующих осей, а их начала часто совмещают с началом системы координат.
Напомню, что декартовой системой координат в пространстве традиционно называется тройка взаимно перпендикулярных осей, пересекающихся в точке, которая называется началом координат. Координатные оси обычно обозначают буквами X , Y , Z и называют соответственно осью абсцисс, осью ординат и осью аппликат. Сам Декарт пользовался только одной осью, на которой откладывались абсциссы. Заслуга использования системы осей принадлежит его ученикам. Поэтому фраза декартова система координат исторически ошибочна. Лучше говорить прямоугольная система координат или ортогональная система координат . Тем не менее, изменять традиции мы не станем и в дальнейшем будем считать, что декартова и прямоугольная (ортогональная) системы координат — это одно и то же.
Тем не менее, изменять традиции мы не станем и в дальнейшем будем считать, что декартова и прямоугольная (ортогональная) системы координат — это одно и то же.
Единичный вектор , направленный вдоль оси Х, обозначается i , единичный вектор , направленный вдоль оси Y , обозначается j , а единичный вектор , направленный вдоль оси Z, обозначается k . Векторы i , j , k называются ортами (рис. 12, слева), они имеют единичные модули, то есть
i = 1, j = 1, k = 1.
Оси и орты прямоугольной системы координат в некоторых случаях имеют другие названия и обозначения. Так, ось абсцисс X может называться касательной осью, а ее орт обозначается τ (греческая строчная буква тау), ось ординат — осью нормали, ее орт обозначается n , ось аппликат — осью бинормали, ее орт обозначается b . Зачем менять названия, если суть остается той же?
Дело в том, что, например, в механике при изучении движения тел прямоугольная система координат используется очень часто. Так вот, если сама система координат неподвижна, а изменение координат движущегося объекта отслеживается в этой неподвижной системе, то обычно оси обозначают X, Y, Z, а их орты соответственно i , j , k .
Так вот, если сама система координат неподвижна, а изменение координат движущегося объекта отслеживается в этой неподвижной системе, то обычно оси обозначают X, Y, Z, а их орты соответственно i , j , k .
Но нередко, когда объект движется по какой-то криволинейной траектории (например, по окружности) бывает удобнее рассматривать механические процессы в системе координат, движущейся с этим объектом. Именно для такой движущейся системы координат и используются другие названия осей и их ортов. Просто так принято. В этом случае ось X направляют по касательной к траектории в той ее точке, в которой в данный момент этот объект находится. И тогда эту ось называют уже не осью X, а касательной осью, а ее орт обозначают уже не i , а τ . Ось Y направляют по радиусу кривизны траектории (в случае движения по окружности — к центру окружности). А поскольку радиус перпендикулярен касательной, то ось называют осью нормали (перпендикуляр и нормаль — это одно и то же). Орт этой оси обозначают уже не j , а n . Третья ось (бывшая Z) перпендикулярна двум предыдущим. Это — бинормаль с ортом b (рис. 12, справа). Кстати, в этом случае такую прямоугольную систему координат часто называют «естественной» или натуральной.
Орт этой оси обозначают уже не j , а n . Третья ось (бывшая Z) перпендикулярна двум предыдущим. Это — бинормаль с ортом b (рис. 12, справа). Кстати, в этом случае такую прямоугольную систему координат часто называют «естественной» или натуральной.
Векторное произведение векторов.
Навигация по странице:
- Определение векторного произведения векторов
- Формулы вычисления векторного произведения векторов
- Свойства векторного произведения векторов
- Примеры задач на вычисления векторного произведения векторов
Онлайн калькулятор. Векторное произведение векторов.
Упражнения на тему векторное произведение векторов.
Определение. Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c (рис. 1).
1).
| рис. 1 |
Формулы вычисления векторного произведения векторов
Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя следующие формулы:
| a × b = | i | j | k | = i(aybz — azby) — j(axbz — azbx) + k(axby — aybx) |
| ax | ay | az | ||
| bx | by | bz |
a × b = {aybz — azby; azbx — axbz; axby — aybx}
Свойства векторного произведения векторов
Геометрический смысл векторного произведения.

Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:
Sпарал = [a × b]
Геометрический смысл векторного произведения.
Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:
SΔ = 1 |a × b| 2 Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.
Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.
a × b = -b × a
(k a) × b = a × (k b) = k (a × b)
(a + b) × c = a × c + b × c
Примеры задач на вычисления векторного произведения векторов
Пример 1.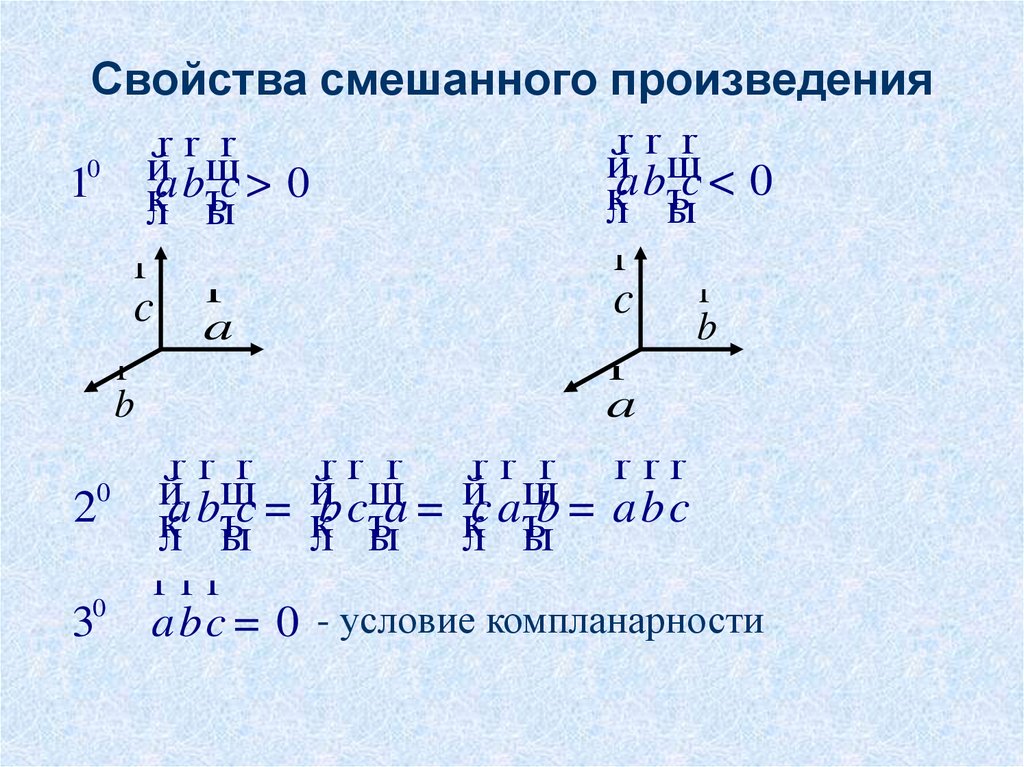 Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.
Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.
Решение:
| a × b = | i | j | k | = |
| 1 | 2 | 3 | ||
| 2 | 1 | -2 |
= i(2 · (-2) — 3 · 1) — j(1 · (-2) — 2 · 3) + k(1 · 1 — 2 · 2) =
= i(-4 — 3) — j(-2 — 6) + k(1 — 4) = -7i + 8j — 3k = {-7; 8; -3}
Пример 2. Найти площадь треугольника образованного векторами a = {-1; 2; -2} и b = {2; 1; -1}.
Решение: Найдем векторное произведение этих векторов:
| a × b = | i | j | k | = |
| -1 | 2 | -2 | ||
| 2 | 1 | -1 |
= i(2 · (-1) — (-2) · 1) — j((-1) · (-1) — (-2) · 2) + k((-1) · 1 — 2 · 2) =
= i(-2 + 2) — j(1 + 4) + k(-1 — 4) = -5j — 5k = {0; -5; -5}
Из свойств векторного произведения:
| SΔ = | 1 | |a × b| = | 1 | √02 + 52 + 52 = | 1 | √25 + 25 = | 1 | √50 = | 5√2 |
| 2 | 2 | 2 | 2 | 2 |
Ответ: SΔ = 2. 5√2.
5√2.
Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису
Онлайн калькуляторы с векторами
Онлайн упражнения с векторами на плоскости
Онлайн упражнения с векторами в пространстве
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
13. Векторное произведение векторов, его свойства. Площадь параллелограмма.
Векторным
произведениемвектора a на вектор b
называется вектор c, длина которого
численно равна площади параллелограмма
построенного на векторах a и b,
перпендикулярный к плоскости этих
векторов и направленный так, чтоб
наименьшее вращение от a к b вокруг
вектора c осуществлялось против часовой
стрелки, если смотреть с конца вектора
c (рис. 1).
1).
рис. 1 |
Формулы вычисления векторного произведения векторов
Векторное произведениедвух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя следующие формулы:
a × b = | i | j | k | = i(aybz — azby) — j(axbz — azbx) + k(axby — aybx) |
ax | ay | az | ||
bx | by | bz |
a × b = {aybz— azby; azbx— axbz; axby— aybx}
Свойства векторного произведения векторов
Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:
Sпарал= a × b]
Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:
SΔ = | 1 | |a × b| |
2 |
Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.

Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.
a × b = -b × a
(k a) × b = a × (k b) = k (a × b)
(a + b) × c = a × c + b × c
14. Смешанное произведение векторов, его свойства. Условие компланарности вектора. Объем параллелепипеда. Объём пирамиды.
Смешанным произведением некомпланарныхвекторов,взятых в данном порядке, называетсяобъём параллелепипеда, построенного на данных векторах, снабжённый знаком «+», если базисправый, и знаком «–», если базислевый.
1. Смешанное произведение не меняется при циклической перестановке его сомножителей (не меняется ни объем параллелепипеда, ни ориентация его ребер): .
2. Смешанное произведение не меняетсязнаков векторного и скалярного умножения:, поэтому смешанное произведение записывают.
3.
Смешанное
произведение меняет свой знак при
перемене любых двух вектор-сомножителей:
,.
4. Смешанное произведение ненулевых векторов ,иравно нулю тогда и только тогда, когда они компланарны:,, – компланарны.
Доказательство. Предположим, что векторы ,и– не компланарны. Тогда можно построить параллелепипед имеющий объем, т.е., но это противоречит условию, согласно которого,. Следовательно, векторы,и– компланарны.
Обратно, пусть ,и– компланарны. Тогда вектори перпендикулярен плоскости, в которой находятся векторы,и, значит, он перпендикулярен любому вектору, лежащему в этой плоскости, напримерЭто значит, что .
Смешанное произведение векторов, заданных своими проекциями в декартовой системе координат.
Пусть векторы заданы своими разложениями по ортам в декартовой системе координат:
, и.
Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:
.
Итак,
.
Приложения смешанного произведения:
1. Определение взаимной ориентации векторов в пространстве.
Если ,и– правая тройка, еслилевая.
2. Установление компланарности векторов:
( (,, – компланарны).
3. Определение объема параллелепипеда и треугольной пирамиды (тетраэдра):
, .
Пример. Компланарны ли векторы ,и, если .
Решение. Вычислим смешанное произведение векторов:
векторы ,ине компланарны.
Пример. Доказать, что векторы ,икомпланарны.
Решение. Рассмотрим матрицу, составленную из координат векторов ,и
,
т. к. определитель матрицы равен нулю,
то векторы линейно зависимы, следовательно
они компланарны.
к. определитель матрицы равен нулю,
то векторы линейно зависимы, следовательно
они компланарны.
Пример. Вычислить объем тетраэдра с вершинами в точках и его высоту, опущенную из вершинына грань, если
Решение. Найдем координаты векторов:
, ,.
Вычислим объем:
.
Поскольку объем тетраэдра , то высота.
Вычислим площадь основания тетраэдра
.
Итак, высота .
Многомерное исчисление. Почему величина перекрестного произведения a и b дает площадь параллелограмма, натянутого на a и b?
спросил
Изменено 11 месяцев назад
Просмотрено 24к раз
$\begingroup$
Я пытался найти это, но многие веб-сайты просто указывают это без доказательств и без интуиции. Я надеюсь изучить его немного лучше, чтобы не забыть, как вычислять якобиан при работе с поверхностными интегралами, где теорема о дивергенции неприменима.
Я надеюсь изучить его немного лучше, чтобы не забыть, как вычислять якобиан при работе с поверхностными интегралами, где теорема о дивергенции неприменима.
Если у вас есть хороший онлайн-справочник, пожалуйста, предоставьте его 🙂
Спасибо,
- многомерное исчисление
- площадь
- перекрестное произведение
- поверхностные интегралы
$\endgroup$
1
$\begingroup$
Выберите координаты так, чтобы два вектора $\vec a, \vec b$ лежали в плоскости $xy$, а $\vec a$ вдоль оси $x$. (Обратите внимание, что пока вы выбрали единицу длины , точное направление, которое вы выберете для осей координат, ничего не меняет. Векторы и их векторное произведение живут в пространстве без координат, просто плавая. Мы просто вводим координаты, чтобы упростить конкретные вычисления. 2} = |a_1b_2|$, очевидно. Но у параллелограмма есть основание $|a_1|$ и высота $|b_2|$, а это значит, что площадь параллелограмма задается точно таким же выражением.
2} = |a_1b_2|$, очевидно. Но у параллелограмма есть основание $|a_1|$ и высота $|b_2|$, а это значит, что площадь параллелограмма задается точно таким же выражением.
$\endgroup$
9
$\begingroup$
Вероятно, потому что ответ прост с точки зрения классической 2D-геометрии.
$||\vec u\times \vec v||=||\vec u||.||\vec v||.\sin(\vec u,\vec v)$
Но площадь параллелограмм, определяемый $\vec u$ и $\vec v$, представляет собой произведение основания на высоту. Если взять $\vec u$ за основу, высота будет $h=||\vec v||.\sin(\vec u,\vec v)$, отсюда и результат…
$\endgroup$
1
$\begingroup$
$|А×В|=|А| ×|B|\sin \theta $, где $\theta$ — угол между A и B. Используя простую тригонометрию, пусть высотой параллелограмма будет буква X
Используя простую тригонометрию, пусть высотой параллелограмма будет буква X
Площадь параллелограмма определяется основанием × высота
$\sin\theta=X/|A|$ Это означает, что $X= |A| \sin\theta $
Следовательно, площадь задается основанием $|B| × |А| \sin\тета $ По сути, это величина перекрестного произведения A и B
$\endgroup$
1
$\begingroup$
Определим $A \times_1 B, A \times_2 B$ как векторы, перпендикулярные $A, B$, с ориентацией, выбранной по правилу правой руки, и величиной $|A||B|sin \theta$ соответственно. абсолютное значение
$$
\begin{vmatrix}
\bf{i} & \bf{j} & \bf{k} \\
а_1 и а_2 и а_3 \\
б_1 и б_2 и б_3
\end{vmatrix}
$$
Простое геометрическое доказательство показывает, что $A \times_1 B$ линейно зависит от $A, B$. А детерминантные свойства показывают, что $A \times_2 B$ линейно зависит также в $A, B$. Остается заметить, что $\times_1, \times_2$ совпадают на базисных векторах $\bf{i}, \bf{j}, \bf{k}$, а значит, как и ожидалось, $\times_1 = \times_2$ .
Остается заметить, что $\times_1, \times_2$ совпадают на базисных векторах $\bf{i}, \bf{j}, \bf{k}$, а значит, как и ожидалось, $\times_1 = \times_2$ .
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.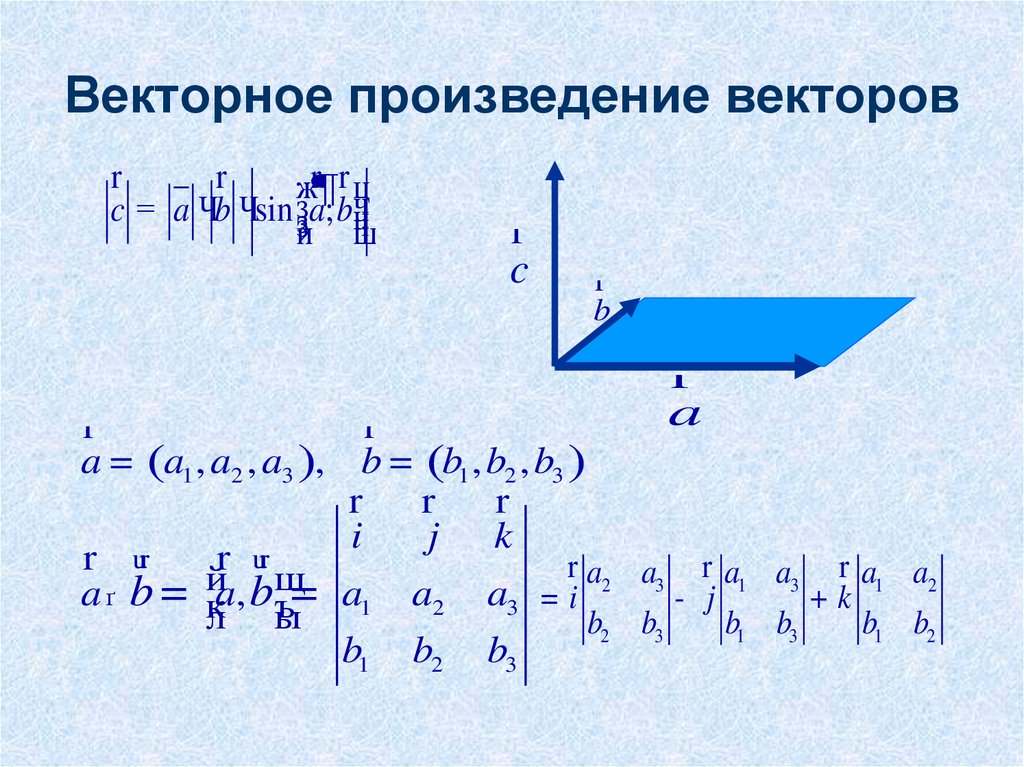
внешняя алгебра — Интуиция за перекрестным произведением и площадью параллелограмма
спросил
Изменено 4 месяца назад
Просмотрено 2к раз
$\begingroup$
Перекрестное произведение в 2D определяется следующим образом: $|(x_1, y_1) \times (x_2, y_2)| = x_1 y_2 — x_2 y_1.$
Я прекрасно понимаю первую часть определения: $x_1 y_2$, которая представляет собой просто площадь прямоугольника:
Я изо всех сил пытаюсь понять вторую часть: $- x_2 y_1.$
Я чувствую, что вторая часть, вероятно, связана с поворотами векторов $(x_1, y_1)$ и $(x_2, y_2)$, потому что при повороте исходного прямоугольника мы должны сохранить площадь и $- x_2 y_1$ каким-то образом компенсирует избыток площади , что мы получаем из первого слагаемого $x_1 y_2$.
Я чувствую, что моей интуиции не хватает многих деталей, и я был бы признателен за объяснение второго члена и его связи с вращениями.
Мой вопрос отличается от Рассуждения о перекрестных произведениях, используемых для нахождения площади, хотя названия почти идентичны. Ортогональность моего вопроса к этому можно увидеть, прочитав эти части вопроса:
У меня нет проблем с вычислением площади между двумя векторами.
Но у меня есть.
… но не почему вместо скалярного произведения используется перекрестное произведение.
Скалярный продукт выходит за рамки моего вопроса.
- площадь
- внешняя алгебра
- перекрестное произведение
$\endgroup$
9
$\begingroup$
Если вы предпочитаете геометрическое видение, зафиксируйтесь на фигуре.
Площадь параллелограмма $OMPN$, очевидно, равна площади розового параллелограмма (то же основание $OM$ и та же высота, потому что противоположные стороны параллельны). Но площадь розового параллелограмма также определяется как: $ \quad Area=|a_1c|$, и мы можем найти $c$ как пересечение в начале координат прямой из $N,P$.
Изучив элементарную аналитическую геометрию, вы обнаружите, что $$ c=\frac{a_1b_2-a_2b_1}{a_1} $$
и это означает, что:
$$ Площадь = |a_1b_2-a_2b_1| $$
, то есть абсолютное значение дермината матрицы, столбцами которой являются два вектора $\overline {OM}$ и $\overline {ON}$, или абсолютное значение векторного произведения тех же двух векторов.
$\endgroup$
$\begingroup$
- Формула отлично работает для стандартных единичных векторов.
- Расширение одного из векторов на константу $c$ должно умножать (ориентированную) площадь на $c$ и действительно умножает векторное произведение на $c$
- Сдвиг вдоль $(x_1,y_1)$, т.
 е. замена $(x_2,y_2)$ на $(x_2+cx_1,y_2+cy_1)$ не меняет ни площадь, ни векторное произведение (дополнительные члены отменить)
е. замена $(x_2,y_2)$ на $(x_2+cx_1,y_2+cy_1)$ не меняет ни площадь, ни векторное произведение (дополнительные члены отменить)
Поскольку любой параллелограмм может быть получен из стандартных единичных векторов с помощью нескольких шагов сдвига/растяжения, векторное произведение сообщает нам ориентированную площадь для всех параллелограммов.
$\endgroup$
$\begingroup$
Перекрестное произведение можно также определить как $a\times b=|a||b|\sin\theta$, где $\theta$ представляет собой угол между $a$ и $b$.
Его можно рассматривать как задающий вектор, перпендикулярный к $a$ и $b$, с длиной $|a||b|\sin\theta$ или как площадь косого прямоугольника (т. е. параллелограмма) с длинами сторон $a$ и $b$ и косой чертой $\theta$.
$\endgroup$
$\begingroup$
Вот представление определителя всех положительных величин, которое может обеспечить понимание связи с площадями на первом уровне.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.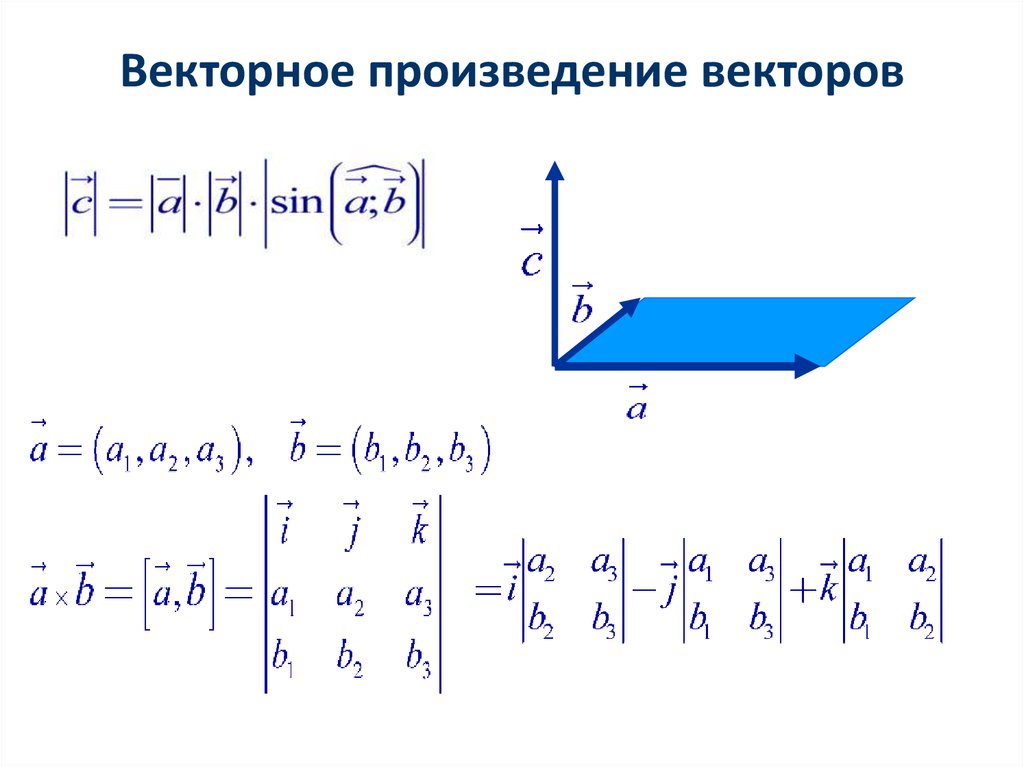
Площадь параллелограмма
Площадь параллелограммаЧасть 3:
Параллелограммы и треугольники Даны два вектора u и v с общим
начальная точка, множество конечных точек векторов s u + t v для 0 £ s , t £ 1 определяется как параллелограмм охватывает u и против .

|
| ||||||
Теорема 3.3: Если q угол, образованный u и v , то
|| u × v || = || и || || против || sin(q)
Рассмотрим два приложения теоремы 3.3. Во-первых, если и и v параллельны, тогда q = 0 и u × v = 0.
Таким образом, площадь параллелограмма, образованного и и и , равна || и |||| против || грех(q) . Действительно, имеем следующее:
Действительно, имеем следующее:
Последний результат следует из того факта, что и — и делит пополам параллелограмм, образованный и и и .
Проверьте правильность чтения: Какова площадь параллелограмма, натянутого на u и против в примере 6?ПРИМЕР 5 Найдите площадь треугольника с вершинами P 1 (2,2) , P 2 (4,4) и P 9 (6,) 3 .
Решение: Легко видеть, что u = б2,2 ñ и v = б 4,-1 с . В качестве векторов в R 3 , мы имеем u = б2,2,0 ñ и v = а 4,-1,0 с . Таким образом, их векторное произведение равно
Так как треугольник имеет половину площади параллелограмма, образованного u и v , площадь треугольника
а 0,0, 2·( -1) -4·2 –
0,0,-10 – ПРИМЕР 6 Найдите площадь треугольника с вершинами P 1 ( 3,0,2) , P 2 ( 4,6,1) , и P 3 09046 3 5,4) .
Область = || u × v || =
0 2 +0 2 +(-10) 2 = 5 единиц 2 Решение: Для этого сначала построим векторы u и против :
В качестве векторов в R 3 мы теперь имеем u = б2,2,0 ñ и v = а 4,-1,0 с .
и = П 1 П 2
= б4-3,6-0,1-2 с = а 1,6,-1 с v = Р 1 Р 3
= В0-3,5-0,4-2 с = б-3,5,2 с Таким образом, их векторное произведение равно
Поскольку треугольник имеет половину площади параллелограмма, образованного 90 233 u 90 234 и 90 233 v 90 234, площадь треугольника равна
.
6·2-5·(-1),(-1)·(-3)-2·1,1·5-(-3)·6 –
17,1,23 –
Область = || u × v || =
17 2 +2 2 +23 2 = 14,335 единиц 2 Рисунок Maple/Javaview
Перекрестное произведение двух векторов
Перекрестное произведение двух векторов — это метод умножения двух векторов. Перекрестное произведение обозначается знаком умножения (x) между двумя векторами. Это бинарная векторная операция, определенная в трехмерной системе. Перекрестное произведение двух векторов — это третий вектор, перпендикулярный двум исходным векторам. Его величина определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. Перекрестное произведение двух векторов также известно как векторное произведение, поскольку результирующая перекрестного произведения векторов является векторной величиной. Здесь мы узнаем больше о векторном произведении двух векторов.
Перекрестное произведение обозначается знаком умножения (x) между двумя векторами. Это бинарная векторная операция, определенная в трехмерной системе. Перекрестное произведение двух векторов — это третий вектор, перпендикулярный двум исходным векторам. Его величина определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. Перекрестное произведение двух векторов также известно как векторное произведение, поскольку результирующая перекрестного произведения векторов является векторной величиной. Здесь мы узнаем больше о векторном произведении двух векторов.
| 1. | Перекрестное произведение двух векторов |
| 2. | Формула перекрестного произведения |
| 3. | Правило правой руки перекрестного произведения |
| 4. | Свойства перекрестного продукта |
5.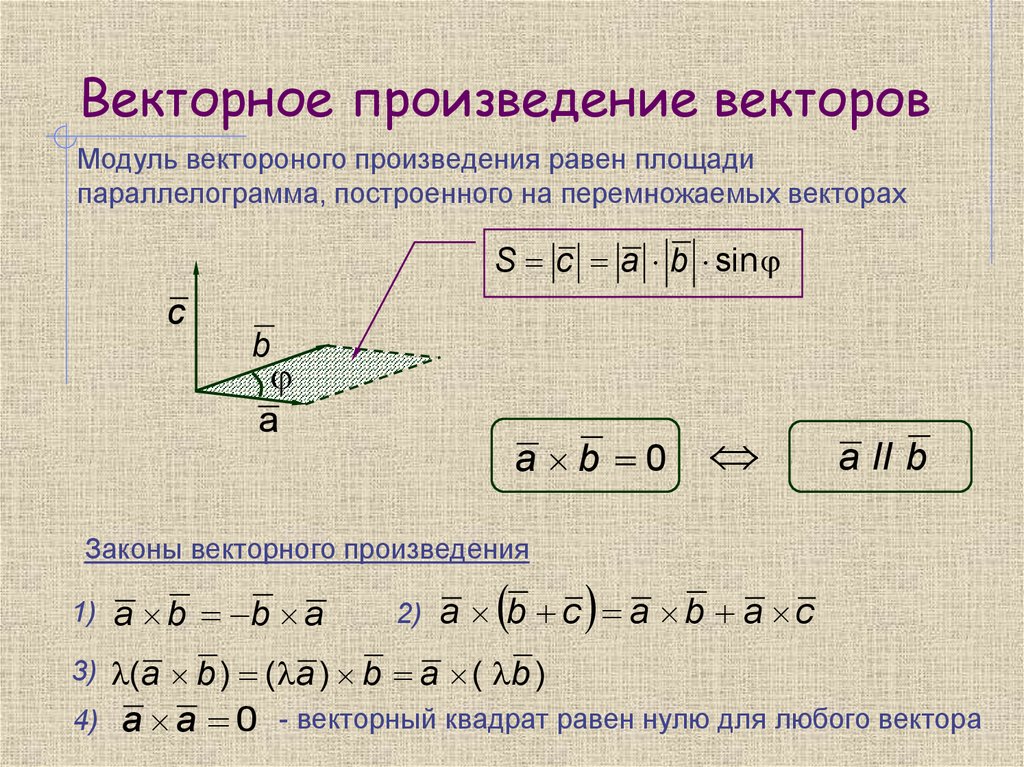 | Продукт тройного креста |
| 6. | Пример перекрестного произведения |
| 7. | Часто задаваемые вопросы о векторном произведении двух векторов |
Перекрестное произведение двух векторов
Перекрестное произведение — это форма умножения векторов, выполняемая между двумя векторами разной природы или вида. Вектор имеет как величину, так и направление. Мы можем умножать два или более векторов на перекрестное произведение и скалярное произведение. Когда два вектора перемножаются друг с другом и произведение векторов также является векторной величиной, то результирующий вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.
Определение векторного произведения
Если A и B — два независимых вектора, то результат векторного произведения этих двух векторов (Ax B) перпендикулярен обоим векторам и нормален к плоскости, содержащей оба вектора. Он представлен:
Он представлен:
А х В = |А| |Б| sin θ
Мы можем понять это на примере, что если у нас есть два вектора, лежащих в плоскости X-Y, то их векторное произведение даст результирующий вектор в направлении оси Z, которая перпендикулярна плоскости XY . Символ × используется между исходными векторами. Векторное произведение или перекрестное произведение двух векторов показано как:
\(\overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c}\)
Где
- \(\overrightarrow{a}\) и \(\overrightarrow{b}\) два вектора.
- \(\overrightarrow{c}\) — результирующий вектор.
Перекрестное произведение двух векторов Значение
Используйте изображение, показанное ниже, и обратите внимание на углы между векторами \(\overrightarrow{a}\) и \(\overrightarrow{c}\) и углы между векторами \(\ overrightarrow{b}\) и \(\overrightarrow{c}\). 9\circ\).т. е. \(\overrightarrow{b}\) и \(\overrightarrow{c}\) являются ортогональными векторами.
Формула перекрестного произведения
Формула перекрестного произведения между любыми двумя векторами дает площадь между этими векторами. Формула векторного произведения дает величину результирующего вектора, который представляет собой площадь параллелограмма, натянутого на два вектора.
Формула перекрестного произведения
Рассмотрим два вектора \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \шляпа i+b_2 \шляпа j+b_3 \шляпа k\). Пусть θ — угол, образованный между \(\overrightarrow{a}\) и \(\overrightarrow{b}\), а \(\hat n\) — единичный вектор, перпендикулярный плоскости, содержащей обе \(\overrightarrow{a }\) и \(\overrightarrow{b}\). Перекрестное произведение двух векторов определяется формулой:
Перекрестное произведение двух векторов определяется формулой:
\(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)
Где
- \(\mid \overrightarrow a \mid\ ) — величина вектора a или длина \(\overrightarrow{a}\),
- \(\mid \overrightarrow b \mid\) — величина вектора b или длина \(\overrightarrow{b}\).
Предположим, что \(\overrightarrow{a}\) и \(\overrightarrow{b}\) — два вектора, такие что \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \ hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \hat i+b_2 \hat j+b_3 \hat k\), то с помощью определителей мы могли бы найти векторное произведение и запишите результат в виде формулы перекрестного произведения, используя матричную запись.
Перекрестное произведение двух векторов также представляется с помощью формулы перекрестного произведения как:
\(\overrightarrow{a} \times \overrightarrow{b} = \hat i (a_2b_3-a_3b_2) \\- \hat j (a_1b_3-a_3b_1)\\+ \hat k (a_1b_2-a_2b_1)\)
Примечание: \( \hat i, \hat j, \text{ и } \hat k \) — единичные векторы в направлении оси x, оси y и оси z соответственно.
Правило правой руки — векторное произведение двух векторов
Мы можем узнать направление вектора, который получается при перекрестном произведении двух векторов по правилу правой руки. Мы следуем следующей процедуре, чтобы узнать направление результата перекрестного произведения двух векторов:
- Направьте указательный палец в направлении первого вектора (\(\overrightarrow{A}\)).
- Совместите средний палец в направлении второго вектора \(\overrightarrow{B}\).
- Теперь большой палец указывает в направлении векторного произведения двух векторов.
Посмотрите на изображение ниже, чтобы понять это лучше.
Свойства перекрестного произведения двух векторов
Свойства перекрестного произведения помогают ясно понять умножение векторов и помогают легко решать все проблемы векторных вычислений. Свойства перекрестного произведения двух векторов следующие:
- Длина векторного произведения двух векторов \(= \overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta)\).

- Антикоммутативное свойство: \(\overrightarrow{a} \times \overrightarrow{b} = — \overrightarrow{b} \times \overrightarrow{a}\)
- Распределительное свойство: \(\overrightarrow{a} \times (\overrightarrow{b} + \overrightarrow{c}) = (\overrightarrow{a}\times \overrightarrow{b} )+ (\overrightarrow{a}\times \overrightarrow{с})\)
- Перемножение нулевого вектора: \(\overrightarrow{a}\times \overrightarrow{0} = \overrightarrow{0}\)
- Перемножение вектора с самим собой: \(\overrightarrow{a}\times \overrightarrow{a} = \overrightarrow{0}\)
- Умножить на скалярную величину: \(\overrightarrow{c}(\overrightarrow{a}\times \overrightarrow{b}) = c\overrightarrow{a}\times \overrightarrow{b} = \overrightarrow{a}\times c\overrightarrow{b}\)
- Перекрестное произведение единичных векторов: \(\overrightarrow{i}\times \overrightarrow{i} =\overrightarrow{j}\times \overrightarrow{j} = \overrightarrow{k}\times \overrightarrow{k} = 0\)
- \(\overrightarrow{i}\times \overrightarrow{j} = \overrightarrow{k}\\ \overrightarrow{j}\times \overrightarrow{k}= \overrightarrow{i}\\\overrightarrow{k}\times \overrightarrow{i} = \overrightarrow{j}\)
- \(\overrightarrow{j}\times \overrightarrow{i} = \overrightarrow{-k}\\ \overrightarrow{k}\times \overrightarrow{j}= \overrightarrow{-i}\\ \overrightarrow{i} \times \overrightarrow{k} = \overrightarrow{-j}\)
Тройное перекрестное произведение
Перекрестное произведение вектора на перекрестное произведение двух других векторов представляет собой тройное перекрестное произведение векторов. Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:
Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:
\((\overrightarrow{a}\times \overrightarrow{b}) \times \overrightarrow{c} = (\overrightarrow{a}\cdot \overrightarrow{c})\overrightarrow{b} -(\overrightarrow{b}\cdot \overrightarrow{c}) \overrightarrow{a}\)
Перекрестное произведение двух векторов Пример
Перекрестное произведение играет решающую роль в нескольких областях науки и техники. Два очень простых примера показаны ниже.
Пример 1: Открытие крана: Мы прикладываем равные и противоположные силы к двум диаметрально противоположным концам крана. В этом случае применяется крутящий момент. В векторной форме крутящий момент представляет собой векторное произведение радиус-вектора (от оси вращения до точки приложения силы) и вектора силы.
т. е. \(\overrightarrow{T} = \overrightarrow{r} \times \overrightarrow{F}\)
Пример 2: Скручивание болта гаечным ключом: длина гаечного ключа равна одному вектору. Здесь направление, в котором мы прикладываем усилие к гаечному ключу (чтобы затянуть или ослабить болт), является другим вектором. Результирующее направление закручивания перпендикулярно обоим векторам.
Важные примечания
- В результате перекрестного произведения двух векторов получается вектор, ортогональный двум заданным векторам.
- Направление векторного произведения двух векторов определяется правилом большого пальца правой руки, а величина определяется площадью параллелограмма, образованного исходными двумя векторами \(\overrightarrow{a}\) и \(\overrightarrow {б}\).
- Перекрестное произведение двух линейных векторов или параллельных векторов является нулевым вектором.
☛ Также проверьте:
- Типы векторов
- Векторные формулы
- Компоненты вектора
- Калькулятор перекрестного произведения
- Сложение векторов
Примеры перекрестного произведения двух векторов
Пример 1: Два вектора имеют скалярную величину как ∣a∣=2√3 и ∣b∣ = 4, а угол между двумя векторами равен 60 ∘ .

Рассчитать векторное произведение двух векторов.
Решение:
Мы знаем, что sin60° = √3/2
Перекрестное произведение двух векторов определяется выражением \(\overrightarrow{a} \times \overrightarrow{b} \) = |a ||b|sin(θ)\( \шляпа n \) = 2√3×4×√3/2 = 12\( \шляпа n \)
Ответ: перекрестное произведение равно 12n.
Вопрос 2: Найдите векторное произведение двух векторов \(\overrightarrow{a}\) = (3,4,5) и \(\overrightarrow{b}\) = (7,8,9)
Решение:
Перекрестное произведение задается как
\(\begin{align}a \times b &=\begin{matrix} \hat i & \hat j & \hat k\\ 3 & 4 & 5\\ 7 & 8 & 9 \end{matrix}\end{align}\)
= [(4×9)−(5×8)] \( \шляпа {i}\) −[(3×9)−(5×7)]\( \шляпа {j} \)+[(3×8)−(4 ×7)] \( \hat {k}\)
= (36−40)\( \hat i\) − (27−35)\( \hat j\) +(24−28) \( \ шляпа k\) = −4\( \hat i\) + 8\( \hat j\) −4\( \hat k\)
Ответ: ∴ \(\overrightarrow{a} \times \overrightarrow{ b} \) = −4\( \hat i\) + 8\( \hat j\) −4\( \hat k\)
Пример 3: Если \(\overrightarrow{a}\) = (2, -4, 4) и \(\overrightarrow{b}\) = (4, 0,3), найдите угол между ними.

Решение
\(\overrightarrow{a}\) = 2i — 4j + 4k
\(\overrightarrow{b}\) = 4i + 0j +3k
Величина \(\overrightarrow{a }\) равно
∣a∣=√(2 2 +4 2 +4 2 ) = √36 = 6
Величина \(\overrightarrow{b}\) равна
∣900 b∣=√(4 2 +0 2 +3 2 ) = √25 = 5
Согласно формуле перекрестного произведения, мы имеем\(\begin{align}\overrightarrow{a}\times \overrightarrow{b} &= \begin{matrix} \hat i & \hat j & \hat k\\ 2 & -4 & 4\\ 4 & 0 & 3 \end{matrix}\\\\&=[(-4\times3) — (4\times0)]\hat i \\ — &[(3\times 2) — (4\times 4)] \hat j \\\\ + &[(2\times 0) -(-4\times 4)]\hat k \\\\&= -12\hat i + 10 \hat j +16 \hat k \\ \overrightarrow{a}\times \overrightarrow{b} &= (-12, 10, 16) \end{align}\)
Длина \(\overrightarrow{c}\) равна
∣c∣=√(−(12) 2 +10 2 +16 2 )
=√0(144+ +256)
=√500
=10√5
\(\begin{align}\overrightarrow{a}\times \overrightarrow{b} &= \mid a \mid \mid b \mid \sin\ тета\\\sin\theta &= \dfrac{\overrightarrow{a}\times \overrightarrow{b}}{\mid a \mid \mid b \mid}\end{align}\)
sinθ = 10√ 5/(5×6)
sinθ = √5/3
θ = sin −1 (√5/3)
θ = sin −1 (0,74)
θ = 48 ∘
Ответ: Угол между векторами равен 904 904 904.

перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных эффектов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Забронировать бесплатный пробный урок
Практические вопросы по перекрестному произведению двух векторов
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о перекрестном произведении двух векторов
Что такое векторное произведение двух векторов?
В результате перекрестного произведения двух векторов при умножении третий вектор перпендикулярен двум исходным векторам. Величина результирующего вектора определяется площадью параллелограмма между ними, а его направление можно определить по правилу правой руки. a × b = c, где c — векторное произведение двух векторов a и b.
Каков результат векторного перекрестного произведения?
Когда мы находим векторное произведение двух векторов, мы получаем другой вектор, выровненный перпендикулярно плоскости, содержащей два вектора. Величина результирующего вектора является произведением греха угла между векторами и величиной двух векторов. а × б = | а | |б| грех θ.
Величина результирующего вектора является произведением греха угла между векторами и величиной двух векторов. а × б = | а | |б| грех θ.
Что такое скалярное произведение и векторное произведение двух векторов?
Векторы можно умножать двумя разными способами, т. е. скалярным произведением и перекрестным произведением. Результаты обоих этих умножений векторов различны. В результате скалярное произведение дает скалярную величину, тогда как векторное произведение дает векторную величину. Скалярное произведение — это скалярное произведение двух векторов, а перекрестное произведение двух векторов — это векторное произведение двух векторов. Скалярное произведение также известно как скалярное произведение, а перекрестное произведение также известно как векторное произведение. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\)
\overrightarrow{b} = |a| |b| \cos(\theta)\)
Как найти векторное произведение двух векторов?
Перекрестное произведение двух векторов определяется по формуле: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)
Где
- |\(\overrightarrow a\)| величина или длина \(\overrightarrow{a}\),
- |\(\overrightarrow b\)| является величиной или длиной \(\overrightarrow{b}\)
Почему перекрестное произведение является синусоидальным?
Поскольку θ — это угол между двумя исходными векторами, используется sin θ, поскольку площадь параллелограмма получается путем перекрестного произведения двух векторов.
Всегда ли положительное произведение двух векторов?
Когда угол между двумя исходными векторами изменяется от 180° до 360°, векторное произведение становится отрицательным. Это связано с тем, что sin θ отрицателен для 180°< θ <360°.
В чем разница между скалярным произведением и перекрестным произведением двух векторов?
При умножении векторов скалярное произведение исходных векторов дает скалярную величину, тогда как перекрестное произведение двух векторов дает векторную величину. Скалярное произведение — это произведение величины векторов и cos угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.
Скалярное произведение — это произведение величины векторов и cos угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.
Что такое формула векторного произведения для двух векторов?
Формула векторного произведения определяет векторное произведение для любых двух заданных векторов, задавая площадь между этими векторами. Формула перекрестного произведения имеет вид \(\overrightarrow{A} × \overrightarrow{B} =|A||B| sinθ\), где |A| = величина вектора A, |B| = величина вектора B, а θ = угол между векторами A и B.
Как найти величину векторного произведения двух векторов?
Перекрестное произведение двух векторов — это еще один вектор, величина которого определяется выражением \(\overrightarrow{a} \times \overrightarrow{b} = \hat i (a_2b_3-a_3b_2) \\- \hat j (a_1b_3-a_3b_1) \\+ \шляпа k (a_1b_2-a_2b_1)\)
Что такое формула перекрестного произведения с использованием матричной записи?
Для двух заданных векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) мы можем найти векторное произведение, используя определители. Например, \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \hat i+b_2 \hat j+b_3 \hat k\), то мы можем записать результат как \(\overrightarrow{a} \times \overrightarrow{b} = \hat i (a_2b_3-a_3b_2) \\- \hat j (a_1b_3- a_3b_1)\\+ \шляпа k (a_1b_2-a_2b_1)\)
Например, \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \hat i+b_2 \hat j+b_3 \hat k\), то мы можем записать результат как \(\overrightarrow{a} \times \overrightarrow{b} = \hat i (a_2b_3-a_3b_2) \\- \hat j (a_1b_3- a_3b_1)\\+ \шляпа k (a_1b_2-a_2b_1)\)
Как использовать формулу перекрестного произведения?
Рассмотрим заданные векторы.
- Шаг 1: Проверьте компоненты векторов |A| = величина вектора A, |B| = модуль вектора B и θ = угол между векторами A и B.
- Шаг 2: Подставьте значения в формулу векторного произведения: \ ((\vec {A × B})=|A||B|\text{Sin}\vec{θ_n}\)
Например, если \(\vec {A}=a\hat{i} + b\hat{j}+c\hat{k}\) и \( \vec{B}=d\hat{i } + e\hat{j}+f\hat{k}\), затем \({\vec{A × B}} = \begin{matrix} \hat{i} & \hat{j} & \hat{ k} \\ a & b & c \\ d & e & f \end{matrix}\)
\({\vec{A × B}} = \шляпа{i}(bf-ce) — \шляпа{j}(af-cd) + \шляпа{k}(ae-bd)\)
Что такое правило большого пальца правой руки для перекрестного произведения двух векторов?
Правило правой руки для векторного произведения двух векторов помогает определить направление результирующего вектора. Если мы направим правую руку в направлении первой стрелки, а пальцы согнем в направлении второй, то наш большой палец окажется в направлении векторного произведения двух векторов. Правило большого пальца правой руки дает формулу векторного произведения для нахождения направления результирующего вектора.
Если мы направим правую руку в направлении первой стрелки, а пальцы согнем в направлении второй, то наш большой палец окажется в направлении векторного произведения двух векторов. Правило большого пальца правой руки дает формулу векторного произведения для нахождения направления результирующего вектора.
Понимание перекрестного произведения – BetterExplained
Взяв два вектора, мы можем записать каждую комбинацию компонентов в сетку:
Эта завершенная сетка представляет собой внешний продукт , который можно разделить на:
Скалярный продукт , взаимодействия между подобными измерениями (
x*x,y*y,z*z)Перекрестное произведение , взаимодействия между различными измерениями (
x*y,y*z,z*xи т.д.)
Скалярное произведение ($\vec{a} \cdot \vec{b}$) измеряет сходство, поскольку оно накапливает взаимодействия только в совпадающих измерениях. Это простой расчет с 3 компонентами.
Это простой расчет с 3 компонентами.
Перекрестное произведение (обозначаемое как $\vec{a} \times \vec{b}$) должно измерять полдюжины «перекрестных взаимодействий». Вычисление выглядит сложным, но концепция проста: суммируйте 6 индивидуальных различий для получения общей разницы.
Вместо того, чтобы думать «Когда мне нужно перекрестное произведение?» подумайте: «Когда мне нужно взаимодействие между разными измерениями?».
Область, например, образована векторами, указывающими в разные стороны (чем ортогональнее, тем лучше). Действительно, перекрестное произведение измеряет площадь, охватываемую двумя трехмерными векторами (источник):
(«Перекрестное произведение» предполагает трехмерные векторы, но концепция распространяется на более высокие измерения.)
Ключевая интуиция щелкнула? Перейдем к деталям.
Определение перекрестного произведения
Скалярное произведение представляет сходство между векторами в виде одного числа:
Например, мы можем сказать, что север и восток сходны на 0%, поскольку $(0, 1) \cdot (1, 0) = 0$. Или что Север и Северо-Восток похожи на 70% ($\cos(45) = 0,707$, помните, что триггерные функции представляют собой проценты.) Сходство показывает количество одного вектора, которое «проявляется» в другом.
Или что Север и Северо-Восток похожи на 70% ($\cos(45) = 0,707$, помните, что триггерные функции представляют собой проценты.) Сходство показывает количество одного вектора, которое «проявляется» в другом.
Должно ли перекрестное произведение, разность между векторами, тоже быть одним числом?
Попробуем. Синус — это разница в процентах, поэтому мы могли бы написать:
К сожалению, нам не хватает некоторых деталей. Допустим, мы смотрим вниз по оси x: и y, и z указывают на 100% от нас. Число вроде «100%» говорит нам о большой разнице, но мы не знаем, в чем она заключается! Нам нужна дополнительная информация, чтобы сказать нам, что «разница между $\vec{x}$ и $\vec{y}$ составляет на » и «разница между $\vec{x}$ и $\vec{z} $ — это , что ».
Итак, давайте представим перекрестное произведение в виде вектора:
Размер перекрестного произведения — это числовая «величина разницы» (с $\sin(\theta)$ в процентах).
 Само по себе это не отличает $\vec{x} \times \vec{y}$ от $\vec{x} \times \vec{z}$.
Само по себе это не отличает $\vec{x} \times \vec{y}$ от $\vec{x} \times \vec{z}$.направление перекрестного произведения основано на обоих входных данных: это направление ортогонально обоим (т. е. не в пользу ни того, ни другого).
Теперь $\vec{x} \times \vec{y}$ и $\vec{x} \times \vec{z}$ имеют разные результаты, каждый с величиной, указывающей, что они на «100%» отличаются от $ \vec{х}$.
(Должно ли скалярное произведение также быть векторным результатом? Ну, мы отслеживаем сходство между $\vec{a}$ и $\vec{b}$. Сходство измеряет перекрытие между направлениями исходного вектора, которое у нас уже есть.)
Геометрическая интерпретация
Два вектора определяют плоскость, и векторное произведение указывает в направлении, отличном от обоих (источник):
Вот проблема: есть два перпендикулярных направления. По соглашению мы предполагаем «правостороннюю систему» (источник):
Если вы держите первые два пальца, как показано на диаграмме, ваш большой палец будет указывать в направлении векторного произведения. Я проверяю правильность ориентации, проводя пальцем от $\vec{a}$ до $\vec{b}$. Когда направление выяснено, величина векторного произведения равна $|a| |б| \sin(\theta)$, который пропорционален величине каждого вектора и «проценту разницы» (синусу).
Я проверяю правильность ориентации, проводя пальцем от $\vec{a}$ до $\vec{b}$. Когда направление выяснено, величина векторного произведения равна $|a| |б| \sin(\theta)$, который пропорционален величине каждого вектора и «проценту разницы» (синусу).
Перекрестное произведение для ортогональных векторов
Чтобы запомнить правило правой руки, напишите xyz закажите дважды: xyzxyz . Затем найдите нужный шаблон:
-
xy => z(xкрестyравноz) -
yz => x(yпересечьzравноx; мы зациклились:yдоzдоx) -
зх => у
Итак, xy и yx имеют противоположные знаки, потому что они идут вперед и назад в нашем 9Настройка 1241 xyzxyz .
Таким образом, без формулы вы сможете вычислить:
Опять же, это потому, что x пересечение y является положительным z в правосторонней системе координат. Я использовал единичные векторы, но мы могли масштабировать термины:
Я использовал единичные векторы, но мы могли масштабировать термины:
Вычисление перекрестного произведения
Отдельный вектор можно разложить на 3 ортогональные части:
компоненты (например, $a_x \times b_y$) голосуют за то, куда должен указывать ортогональный вектор. 6 компонентов, 6 голосов, и их сумма является векторным произведением. (Похоже на градиент, где каждая ось голосует за направление наибольшего увеличения.)
-
xy => zиyx => -z(предположим, что $\vec{a}$ стоит первым, поэтомуxyозначает $a_x b_y$) -
yz => xиzy => -x -
zx => yиxz => -y
xy и yx сражаются в направлении z . Если эти члены равны, например, в $(2, 1, 0) \times (2, 1, 1)$, компонент перекрестного произведения в z 9 отсутствует.1242 направления (2 – 2 = 0).
Окончательная комбинация:
, где $\vec{n}$ — единичный вектор, нормальный к $\vec{a}$ и $\vec{b}$.
Пусть это вас не пугает:
- Всего 6 терминов, 3 положительных и 3 отрицательных
- Два измерения голосуют за третье (поэтому терм
zдолжен иметь только компонентыyиx) - Положительный/отрицательный порядок основан на шаблоне
xyzxyz
Если хотите, есть алгебраическое доказательство того, что формула одновременно ортогональна и имеет размер $|a| |б| \sin(\theta)$, но мне нравится интуитивное «пропорциональное голосование».
Пример времени
Опять же, мы должны произвести в уме простые перекрестные произведения:
Почему? Мы пересекли оси x и y , получив z (или $\vec{i} \times \vec{j} = \vec{k}$, используя эти единичные векторы). Переход в другую сторону дает $-\vec{k}$.
Вот как я рассматриваю более сложные примеры:
- Возьмем последний член, z-компоненту.
 Это (1)(5) минус (4)(2), или 5 – 8 = -3. Сначала я сделал
Это (1)(5) минус (4)(2), или 5 – 8 = -3. Сначала я сделал z, потому что он используетxиy, первые два термина. Попробуйте увидеть (1)(5) как «вперед», когда вы сканируете от первого вектора ко второму, и (4)(2) как назад, когда вы двигаетесь от второго вектора к первому. - Теперь компонент
и: (3)(4) – (6)(1) = 12 – 6 = 6 - Теперь компонент
x: (2)(6) – (5)(3) = 12 – 15 = -3
Итого $(-3, 6, -3)$, что мы можем проверить с помощью Wolfram Alpha.
Вкратце:
- Перекрестное произведение отслеживает все «взаимодействия» между измерениями
- Есть 6 взаимодействий (по 2 в каждом измерении) со знаками, основанными на
xyzxyzпорядке
Приложение
Связь с определителем
Вы можете вычислить векторное произведение, используя определитель этой матрицы:
Здесь есть четкая связь, поскольку определитель («площадь/объем со знаком») отслеживает вклад ортогональных компонентов.
Существуют теоретические причины, по которым векторное произведение (как ортогональный вектор) доступно только в 0, 1, 3 или 7 измерениях. Однако перекрестное произведение как отдельное число по существу является определителем (площадь со знаком, объем или гиперобъем как скаляр).
Соединение с завитком
Изгиб измеряет скручивающую силу, которую векторное поле прикладывает к точке, и измеряется вектором, перпендикулярным поверхности. Всякий раз, когда вы слышите «перпендикулярный вектор», начинайте думать о «перекрестном произведении».
Возьмем «детерминант» этой матрицы:
Вместо умножения взаимодействие берет частную производную. Как и прежде, $\vec{i}$-компонента curl основана на векторах и производных в направлениях $\vec{j}$ и $\vec{k}$.
Связь с теоремой Пифагора
Перекрестное произведение и скалярное произведение подобны ортогональным сторонам треугольника:
Для единичных векторов, где $|a| = |б| = 1$, имеем:
Я немного схитрила в диаграмме сетки, так как мы должны отслеживать квадраты величин (как это делается в теореме Пифагора).
Advanced Math
Перекрестное произведение и друзья расширяются в алгебре Клиффорда и геометрической алгебре. Я все еще изучаю это.
Перекрестное произведение перекрестных произведений
Иногда у вас будет такой сценарий:
Во-первых, перекрестное произведение не ассоциативно: порядок имеет значение.
Далее, вспомним, что делает векторное произведение: находит ортогональные векторы. Если любые две компоненты параллельны ($\vec{a}$ параллельны $\vec{b}$), то нет размерностей, сталкивающих друг друга, и векторное произведение равно нулю (что приводит к $0 \times \vec {с}$).
Но $\vec{a}$ и $\vec{c}$ могут быть параллельны, поскольку они никогда не участвуют напрямую в перекрестном произведении, например:
Ого! Как мы вернулись к $\vec{j}$? Мы запросили направление, перпендикулярное как $\vec{i}$, так и $\vec{j}$, и снова сделали это направление перпендикулярным к $\vec{i}$. Быть «двойным перпендикуляром» означает, что вы вернулись на исходную ось.
Быть «двойным перпендикуляром» означает, что вы вернулись на исходную ось.
Скалярное произведение перекрестных произведений
Теперь, если мы возьмем
, что произойдет? Мы вынуждены сначала выполнить $\vec{a} \times \vec{b}$, потому что $\vec{b} \cdot \vec{c}$ возвращает скаляр (одно число), который нельзя использовать в перекрестном произведении.
Что произойдет, если $\vec{a}$ и $\vec{c}$ параллельны? Итак, $\vec{a} \times \vec{b}$ перпендикулярно $\vec{a}$, что означает, что оно перпендикулярно $\vec{c}$, поэтому скалярное произведение с $\vec{c }$ будет равно нулю.
Я никогда не запоминал эти правила, я должен продумывать взаимодействие.
Другие системы координат
Игровой движок Unity предназначен для левшей, OpenGL (и большинство математических и физических инструментов) — для правшей. Почему?
В компьютерной игре x идет по горизонтали, y по вертикали, а z уходит «в экран». В результате получается левосторонняя система. (Попробуйте: используя правую руку, вы можете увидеть
В результате получается левосторонняя система. (Попробуйте: используя правую руку, вы можете увидеть x креста и должны указывать за пределы экрана).
Применение векторного произведения
- Найдите направление, перпендикулярное двум заданным векторам.
- Найдите область со знаком, натянутую на два вектора.
- Определить, являются ли два вектора ортогональными (хотя проверка скалярного произведения 0, вероятно, выполняется быстрее).
- «Умножение» двух векторов, когда вклад вносят только перпендикулярные перекрестные члены (например, определение крутящего момента).
- С кватернионами (четыре комплексных числа) векторное произведение выполняет работу по вращению одного вектора вокруг другого (еще одна статья в разработке!).
Счастливая математика.
Другие публикации из этой серии
- Векторное исчисление: понимание скалярного произведения
- Векторное исчисление: понимание векторного произведения
- Векторное исчисление: понимание потока
- Векторное исчисление: понимание дивергенции
- Векторное исчисление: понимание циркуляции и завитка
- Векторное исчисление: понимание градиента
- Понимание пифагорейского расстояния и градиента
Как вычислить векторное произведение и площадь прямоугольника за 3 простых шага
15 июня 2021 517 прочтений
Площадь прямоугольника — это количество плоских областей, ограниченных определенной формой. Площадь прямоугольника – это площадь формы и периметра прямоугольника. Вычисление площади в 3 простых шага — это простая процедура, как кусок пирога. Студенты обычно считают, что их очень сложно понять, но это несложно, поскольку с этим вы видите, что вычисление площади и векторного произведения двух векторов можно выполнить всего за три простых шага. Для вычисления площади, с точки зрения формы, прямоугольник считается самым простым.
Площадь прямоугольника – это площадь формы и периметра прямоугольника. Вычисление площади в 3 простых шага — это простая процедура, как кусок пирога. Студенты обычно считают, что их очень сложно понять, но это несложно, поскольку с этим вы видите, что вычисление площади и векторного произведения двух векторов можно выполнить всего за три простых шага. Для вычисления площади, с точки зрения формы, прямоугольник считается самым простым.
@james-johnson
Джеймс ДжонсонЯ исследователь и автор технических материалов. Преподаватель математики с 2007 года. Люблю путешествовать, Любовь
О @james-johnson
Кросс-произведение
Помимо скалярных произведений, существует другой подход к умножению двух векторов. Хотя скалярное произведение двух векторов дает скаляр, результирующий вектор, напротив, является вектором векторных произведений. Таким образом, его масштаб и направление совпадают. Таким образом, векторное произведение векторов выражается в величине и угле двух векторов и записывается как
Оба вектора перпендикулярны направлению векторного произведения. Используется правило правой руки для получения соответствующей ориентации перекрестного произведения. Направьте указательный палец (правой руки) в направлении первого вектора. Затем выровняйте руку по второму вектору так, чтобы ваш средний палец указывал на него. Разверните большой палец. Направление вашего большого пальца указывает направление перекрестного произведения.
Используется правило правой руки для получения соответствующей ориентации перекрестного произведения. Направьте указательный палец (правой руки) в направлении первого вектора. Затем выровняйте руку по второму вектору так, чтобы ваш средний палец указывал на него. Разверните большой палец. Направление вашего большого пальца указывает направление перекрестного произведения.
Для двух векторов сначала нужно гарантировать, что оба вектора являются трехмерными, чтобы получить векторное произведение. Если два вектора даны в 3-х измерениях, то произведение задается как:
Вычисление векторного произведения
Чтобы вычислить векторное произведение двух векторов, используйте стандартные единичные векторы i, j и k для R3.
Если u = (u1, u2, u3) = u1i + u2j + u3k, и v = (v1, v2, v3) = v1i + v2j + v3k, тогда u × v задается как u × v = (u2v3 − u3v2) i + (u3v1 − u1v3) j + (u1v2 − u2v1) k
Площадь прямоугольника
Четырехсторонний многоугольник, в котором каждый угол каждой вершины равен 90° и имеет одинаковую длины противоположных сторон, называется прямоугольником. Таким образом, двухмерный многоугольник представляет собой прямоугольник с четырьмя гранями, четырьмя вершинами и четырьмя прямыми углами. В прямоугольнике две противоположные стороны параллельны. Прямоугольная область – это пространство в форме. Площадь прямоугольника также является периметром прямоугольника. Это отличает площадь прямоугольника от интегрирования, в котором мы вычисляем площадь под кривой.
Таким образом, двухмерный многоугольник представляет собой прямоугольник с четырьмя гранями, четырьмя вершинами и четырьмя прямыми углами. В прямоугольнике две противоположные стороны параллельны. Прямоугольная область – это пространство в форме. Площадь прямоугольника также является периметром прямоугольника. Это отличает площадь прямоугольника от интегрирования, в котором мы вычисляем площадь под кривой.
Для вычисления площади с точки зрения формы прямоугольник считается самым простым. Площадь — это пространство, занимаемое какой-либо формой или предметом. Однако описательно мы можем сказать, что площадь — это количество плоской области, ограниченной определенной формой. Часто используемые типичные единицы площади включают см2 (квадратный сантиметр), м2 (метр в квадрате) и км2 (километр в квадрате) .
Как вычислить площадь прямоугольника за 3 простых шага
Вычисление площади прямоугольника — простая процедура, как кусок пирога. Как известно, площадь прямоугольника равна произведению его ширины на длину. Таким образом, вы наверняка сможете вычислить площадь прямоугольника за три простых шага.
Как известно, площадь прямоугольника равна произведению его ширины на длину. Таким образом, вы наверняка сможете вычислить площадь прямоугольника за три простых шага.
Прямоугольник состоит из 4 сторон, не равных по длине. Однако противоположные стороны равны по длине друг другу. В прямоугольной форме его длинная сторона называется длиной, а более короткая сторона известна как ширина.
Таким образом, чтобы вычислить площадь прямоугольника, мы можем записать его формулу как
A = l x w
Хотя для вычисления в 3 простых шага все, что нам нужно сделать, это:
- Прежде всего, определите равные и противоположные стороны прямоугольника. Затем возьмите одно значение со стороны длины и одно со стороны ширины.
- Запишите их в области формулы прямоугольника. Например, если у нас есть 6 см для длины и 4 см для ширины прямоугольника, мы запишем их как 6x4 .
- Наконец, умножьте оба значения друг на друга, или вы также можете использовать арифметические таблицы для получения произведения обоих значений.


 Требуется найти:
Требуется найти: 3) Объем параллелепипеда, построенного на векторах , и. Контрольная работа по теме «Элементы теории линейных пространств…
3) Объем параллелепипеда, построенного на векторах , и. Контрольная работа по теме «Элементы теории линейных пространств…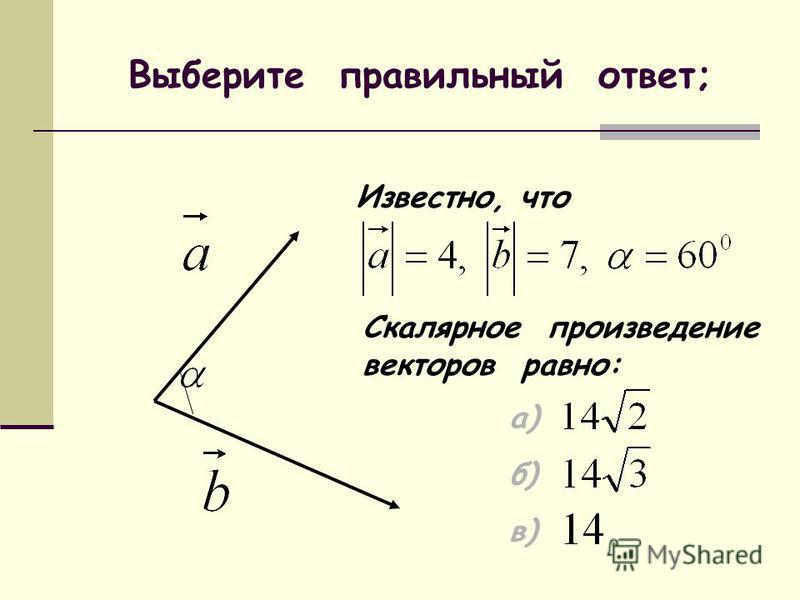
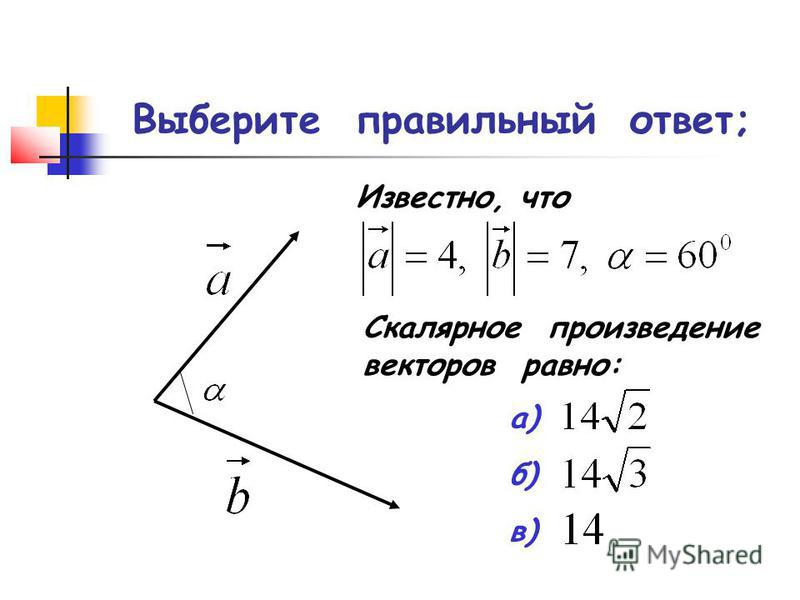

 е. замена $(x_2,y_2)$ на $(x_2+cx_1,y_2+cy_1)$ не меняет ни площадь, ни векторное произведение (дополнительные члены отменить)
е. замена $(x_2,y_2)$ на $(x_2+cx_1,y_2+cy_1)$ не меняет ни площадь, ни векторное произведение (дополнительные члены отменить) 3: Если q угол, образованный u и v , то
3: Если q угол, образованный u и v , то
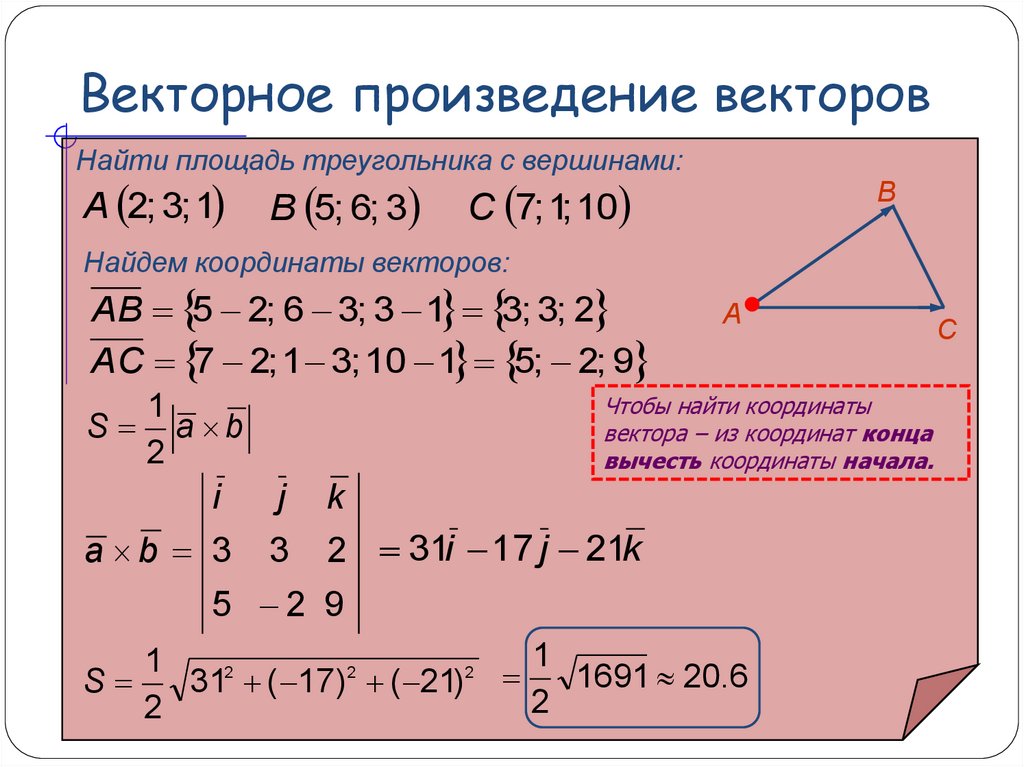 Таким образом, их векторное произведение равно
Таким образом, их векторное произведение равно