Онлайн урок: Площадь. Площадь прямоугольника по предмету Математика 5 класс
В нашей жизни приходится часто вычислять площади различных геометрических фигур. Например, площадь огорода, поля; при покупке жилья — площадь квартиры, дома, комнат; делая ремонт, мы вычисляем площадь стен, пола, окон, строительных материалов и т.д.
Сегодня мы научимся вычислять площади двух геометрических фигур: прямоугольника и квадрата, познакомимся с понятием площади и единицами ее измерения.
Выясним, какими свойствами обладает площадь.
Разберем несколько примеров решения задач.
Прямоугольник, квадрат и другие замкнутые геометрические фигуры имеют некоторую границу (контур), которая делит плоскость на области: область, которая находится снаружи этой границы, и область, которая находится внутри контура.
Площадью называют часть плоскости, ограниченную линией (кривой или ломаной).
Для обозначения площади обычно используют заглавную латинскую букву S.
Площадь различных фигур можно сравнивать.
Площадь будет больше у той фигуры, которая на плоскости занимает больше места.
Например, даны три фигуры №1, №2, №3.
Площадь фигуры №1 больше площади фигуры №2 и №3, а площадь фигуры №2 больше площади фигуры №3.
Невооруженным глазом заметно, какая фигура меньше, а какая больше.
Рассмотрим еще один пример.
Даны две фигуры №1 и №2.
Однозначно сказать, площадь какой фигуры больше, а какой меньше, затруднительно.
Нам известно, что фигуры называют равными, если при наложении одной фигуры на другую они совпадают.
Попробуем сравнить первую и вторую фигуры наложением.
Этот способ сравнения не смог дать нам однозначного ответа, поэтому постараемся найти более точный способ нахождения площади данных фигур.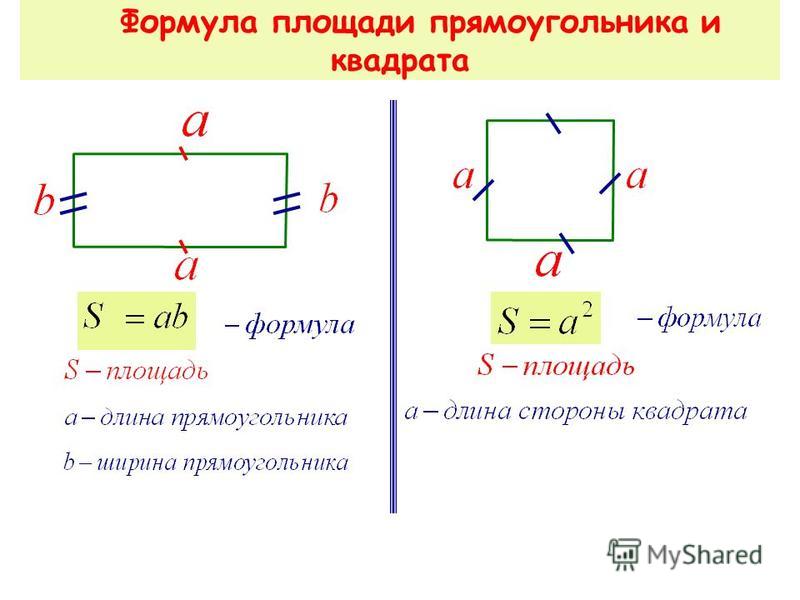
Известно, чтобы определить длину отрезка, его сравнивают с отрезком, принятым за единицу измерения.
В таком случае, чтобы измерить площадь фигуры, необходимо посчитать сколько раз в ней помещается другая фигура, принятая за единицу измерения.
При измерении длины отрезка используют линейные меры длины: 1 мм, 1 см, 1 дм и т.д.
Площадь же измеряют квадратными единицами.
Квадратная единица представляет собой квадрат, стороны которого выражены линейными единицами; другими словами, площадь измеряется квадратными единицами длины.
Квадрат, у которого все стороны равны 1 мм, называется квадратным миллиметром.
Квадрат, у которого все стороны равны 1 см, называется квадратным сантиметром.
Квадрат, у которого все стороны равны
Аналогично определяется квадратный метр и квадратный километр.
Определить площадь фигуры- это значит найти сколько квадратных единиц содержится в данной фигуре.
Обозначают квадратные единицы следующим образом:
1 мм2— один миллиметр квадратный (квадратный миллиметр)
1 см2— один сантиметр квадратный (квадратный сантиметр)
1 дм2— один дециметр квадратный (квадратный дециметр)
1 м2— один метр квадратный (квадратный метр)
1 км2— один километр квадратный (квадратный километр) и т.д.
Если разбить фигуру на n равных квадратов, то ее площадь будет равна n квадратных единиц.
Найдем для нашего примера площадь фигуры №
1 и площадь фигуры №2 и сравним полученные площади. Так мы сможем выяснить, какая из фигур имеет большую площадь.Для этого разобьем эти две фигуры на одинаковые квадраты со сторонами 1 см (т.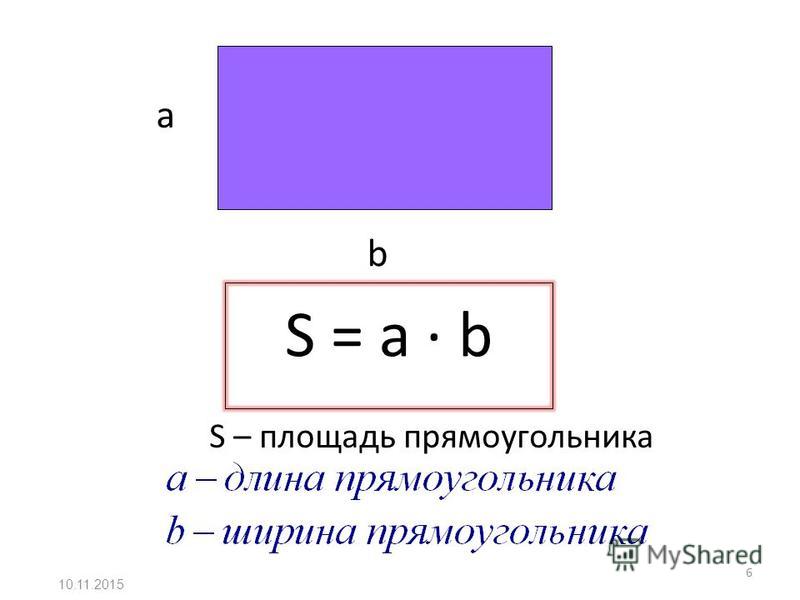
е. на квадратные сантиметры).
Фигура №1 состоит из 12 квадратов, следовательно, данная фигура имеет площадь 12 квадратных единиц, в нашем случае квадратных сантиметров: S1 = 12 см2
Фигура №2 состоит также из 12 квадратов, значит, данная фигура имеет площадь 12 квадратных единиц, в нашем случае квадратных сантиметров: S2 = 12 см2
Сравним площади фигур: так как S1 =
У меня есть дополнительная информация к этой части урока!
Закрыть
В каждом конкретном случае необходимо оценивать, в каких единицах измерения удобней выражать площадь той или иной фигуры.
Если требуется определить площадь фигуры, изображенной на листе бумаги, то целесообразнее измерять площадь в квадратных сантиметрах (см2).
Если же необходимо измерить площадь стены или потолка в комнате, то удобно площадь выражать в квадратных метрах (м2).
Большие значения площадей, такие как площадь Земли, островов, континентов, океанов, государств удобнее выражать в квадратных километрах (км
2).Пройти тест
Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации
Вход Регистрация
Во всех выше рассмотренных примерах мы имели дело с плоскими геометрическими фигурами (прямоугольником и квадратом).
Вспомним, что называют прямоугольником, а что квадратом.
Прямоугольник- это плоская геометрическая фигура, образованная замкнутой ломаной линией, состоящей из четырех звеньев, и плоскостью, которая располагается внутри этой линии.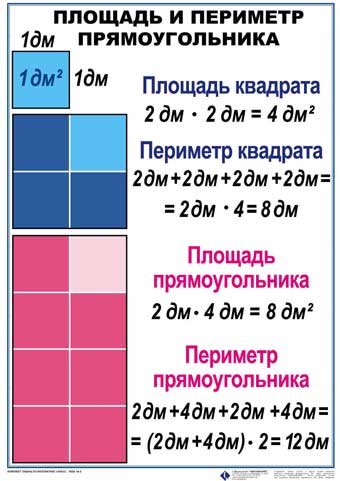
У прямоугольника противоположные стороны равны и все четыре угла одинаковые.
Обычно прямоугольник обозначают четырьмя заглавными латинскими буквами, записывая их по порядку следования.
Пример: прямоугольник
Отрезки АВ, ВD, DC, СА называются сторонами прямоугольника АВDС.
Причем АВ = СD и АС = ВD.
Точки А, В, С, D называют вершинами прямоугольника АВDС.
Углы, образованные сторонами АС и АВ, АВ и ВD, ВD и DC, DC и СА, называют углами прямоугольника АВDС.
Отрезки СВ и АD, соединяющие вершины С и В, А и D, — это диагонали прямоугольника АВDС.
В любом прямоугольнике можно провести две диагонали, и они будут равны СВ = АD.
Диагонали пересекаются в точке пересечения диагоналей (точка О— точка пересечения диагоналей СВ и АD).
Она делит диагонали на равные отрезки:
Точка O делит диагональ СВ на равные отрезки СО и ОB.
Точка O делит диагональ АD на равные отрезки AО и ОD.
Каждая диагональ делит прямоугольник на два равных треугольника.
Диагональ СВ делит прямоугольник АВDС на равные треугольники САВ и СDВ.
Диагональ АD делит прямоугольник АВDС на равные треугольники АСD и АВD.
Квадрат- это прямоугольник, у которого все стороны равны.
Пример:
Квадрат АВDС.
Отрезки АВ, ВD, DC, СА— называются сторонами квадрата АВDС.
Причем АВ = СD = АС = ВD.
Точки А, В, С, D называют вершинами квадрата АВDС.
Углы, образованные сторонами АС и АВ, АВ и ВD, ВD и DC, DC и СА, называют углами квадрата АВDС.
Отрезки СВ и АD, соединяющие вершины С и В, А и D, — это диагонали квадрата
АВDС.Все свойства прямоугольника характерны и для квадрата.
Чтобы найти площадь прямоугольника, можно разделить его на одинаковые единичные квадраты и сосчитать их количество.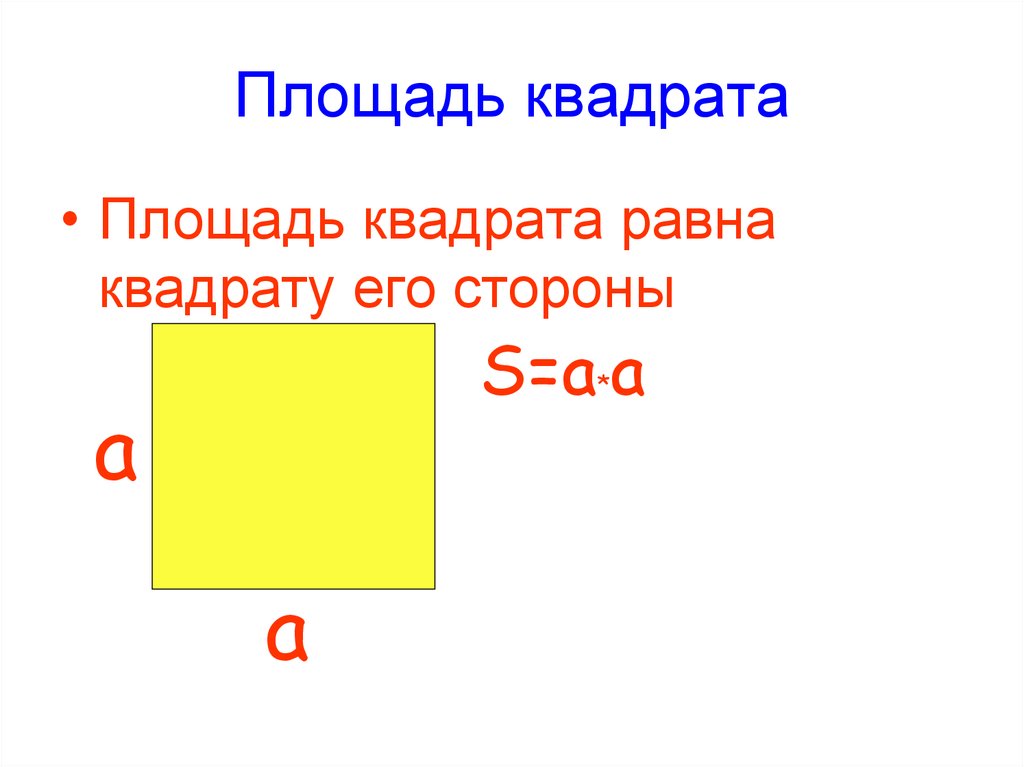
Такой способ нахождения площади фигуры мы рассмотрели ранее.
Пример:
Найдем площадь прямоугольника ABCD.
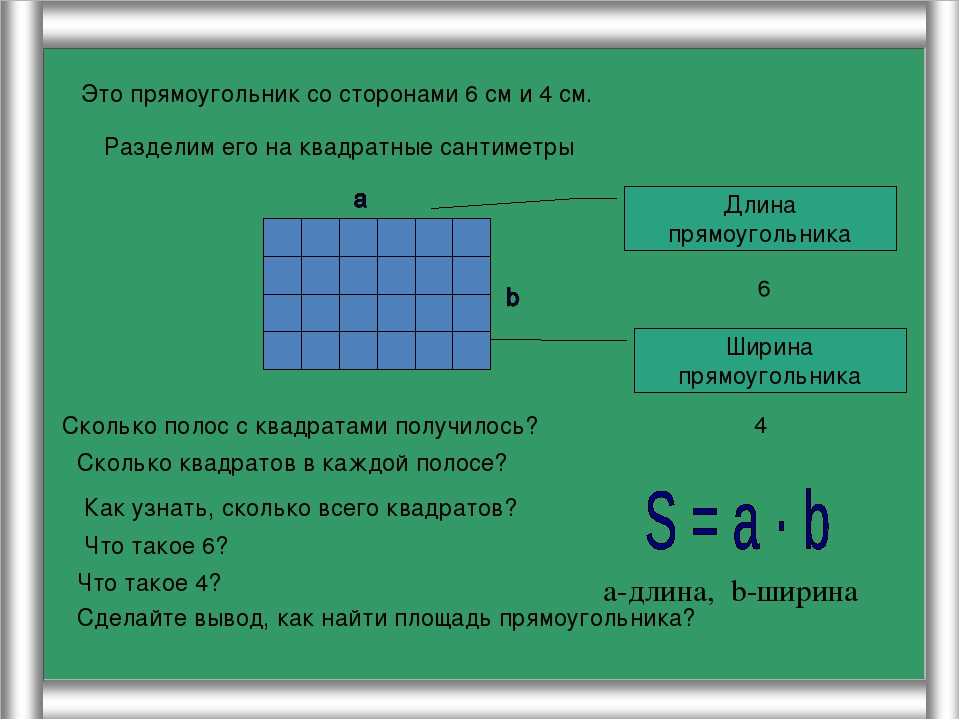
Прямоугольник ABCD разобьем на квадраты со стороной 1 см, значит в нашем случае единицей измерения площади будет квадратный сантиметр (см2).
Посчитаем сколько раз помещается квадратный сантиметр в фигуру ABCD.
В прямоугольнике ABCD содержится 15 квадратов, следовательно, его площадь равна 15 квадратных сантиметров (15 см2).
Если внимательно посмотреть на прямоугольник
Тогда количество таких квадратов в прямоугольнике ABCD можно определить выражением (3 ∙ 5).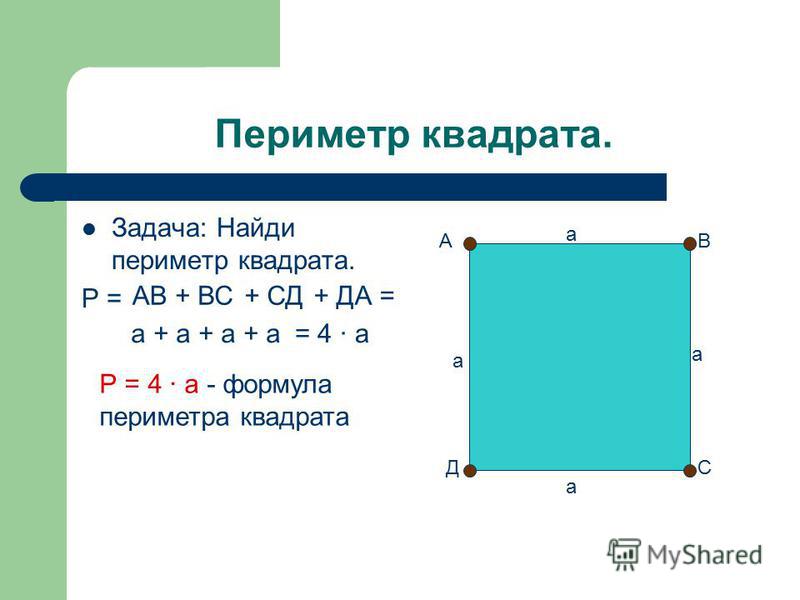
Найдем значение данного выражения:
3 ∙ 5 = 15
Значит площадь прямоугольника ABCD равна 15 см2.
Пересчитав по порядку каждый квадратный сантиметр прямоугольника ABCD, мы получили такой же результат.
Этот же прямоугольник можно разбить на 5 полос по 3 квадрата со сторонами 1 см каждый.
Найдем площадь прямоугольника ABCD.
В этом случае площадь прямоугольника ABCD будет определяться выражением (5 ∙ 3).
Как нам уже известно, от перестановки множителей произведение не изменяется:
5 ∙ 3 = 15.
Площадь прямоугольника получается равной 15 см2 Результат, как мы видим, не изменился.
Важно заметить, что сторона АВ прямоугольника ABCD- это ширина данного прямоугольника (равная 3 см), а сторона ВС — это его длина (равная 5 см).
Таким образом, для того, чтобы найти площадь прямоугольника ABCD, не обязательно разбивать его на квадратные единицы, необходимо просто знать длину и ширину этого прямоугольника.
Правило: чтобы найти площадь прямоугольника, нужно его длину умножить на ширину (в одинаковых единицах).
Единицы измерения длины и ширины должны совпадать.
Если меры не совпадают, их необходимо перевести, т.е. свести к единой единице измерения.
Запишем правило в виде формулы.
Площадь прямоугольника обозначим латинской буквой S, ширину прямоугольника обозначим буквой а, длину буквой b.
Формула площади прямоугольника выглядит так:
Рассмотрим некоторые свойства площади.
1. Площади равных фигур равны.
Периметры таких фигур также равны.
Фигуры, имеющие равные площади называются равновеликими.
У меня есть дополнительная информация к этой части урока!
Закрыть
Не следует путать такие понятия, как периметр и площадь геометрических фигур.
Периметр- это замкнутая ломаная или кривая линия (контур) геометрической фигуры, которая ограничивает внутреннюю область этой фигуры.
По сути, периметр- это длина контура фигуры (для многоугольника это сумма длин всех сторон многоугольника).
Периметр часто обозначают заглавной латинской буквой Р.
Периметр измеряется в линейных единицах длины: мм, см, дм и т.д.
Площадь же- это часть плоскости, которая ограничена периметром.
Площадь измеряется только в квадратных единицах длины: мм2, см2, дм2 и т.д.
Пример:
На рисунке периметр обозначен красной линией, площадь фигуры выделена на рисунке штриховкой.
Р = 2 см + 6 см + 2 см + 6 см = 2 (2 + 6) = 16 (см) периметр фигуры (прямоугольника).
S = 2 см∙ 6 см = 12 (см2) площадь фигуры (прямоугольника)
2. Площадь всей фигуры равна сумме площадей ее частей.
Рассмотрим пример, иллюстрирующий данное свойство.
Разделим прямоугольник ABCD на две части ломаной линией KOMN.
Одна из частей- ABNMОK имеет площадь, равную 10 см2.
S1 = 10 см2.
Вторая часть- KОMNCD имеет площадь 8 см2.
S2 = 8 см2.
Площадь всего прямоугольника равна сумме его частей:
S = S1 + S2
S = 10 см2 + 8 см2 = 18 см2.
Вычислив площадь прямоугольника по формуле S = a ∙ b,
где а = АВ = 3 см, b = ВС = 6 см.
S = 3 ∙ 6 = 18 см2.
Площадь всей фигуры равна 18 см2, такой же результат был получен при сложении площадей двух частей, на которые эта фигура была разделена.
Первое и второе свойства- это основные свойства площадей.
3. Диагональ прямоугольника (квадрата), делит его на два равных треугольника.
Пусть отрезок BD делит прямоугольник ABCD на два равных треугольника:
∆ ABD = ∆ BCD
Сумма площадей каждого треугольника равна площади всего прямоугольника, следовательно, площадь каждого треугольника равна половине площади прямоугольника.
SABD = SABCD ÷ 2.
SBCD = SABCD ÷ 2.
4. Площадь квадрата.
Квадрат- это прямоугольник, у которого все четыре стороны равны.
Изобразим квадрат со стороной 2 см (это выражение означает, что все четыре стороны у квадрата будут 2 см).
Площадь квадрата рассчитывается таким же образом, как и площадь прямоугольника:
S = a ∙ b— произведение длины и ширины прямоугольника.
Известно, что в квадрате все стороны между собой равны, значит, длина квадрата равна ширине этого квадрата.
В таком случае, умножив длину на ширину, получим произведение двух равных по значению множителей, каждый равен длине стороны квадрата (а).
Получаем формулу площади квадрата:
S = a ∙ a
Число, умноженное само на себя, представляет собой квадрат этого числа.
Формула площади квадрата будет выглядеть так:
Число возводится во вторую степень, т.е. возводится в квадрат.
Правило: площадь квадрата равна квадрату его стороны.
Рассмотрим такой пример.
Вычислим площадь квадрата со стороной 4 см.
Решение данной задачи:
Пройти тест
Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации
Вход Регистрация
Теперь, когда нам известны формулы площадей прямоугольника и квадрата и их свойства, рассмотрим решение нескольких задач.
Задача №1
Длина столешницы прямоугольной формы 2 м, а ее ширина 10 дм.
Найдите площадь и периметр столешницы.
Единица измерения ширины столешницы выражена в дециметрах, ее сразу переведем в метры.
Задача №2
Периметр прямоугольного участка земли 80 м, а его длина 30 м.
Чему равна площадь этого участка?
Выясним план решения данной задачи.
Решать задачу будем по действиям.
1. Найдем чему равна половина периметра (Р ÷ 2), т.е. выясним, чему равна сумма двух сторон (ширины и длины) участка.
2. Из полученного значения полупериметра вычтем известное значение длины прямоугольника b; таким образом, мы найдем ширину участка а.
3. Когда будут известны ширина и длина участка, можно будет найти его площадь.
Задача №3
Площадь прямоугольной грядки 7 м2, ширина этой грядки 1 м.
Чему равен периметр грядки?
Задача №4
Девочка вырезала прямоугольник, длина которого получилась равной 5 см, а ширина 2 см, и разрезала этот прямоугольник по диагонали, у нее получились два равных треугольника.
Найдите площадь этих треугольников.
План решения у нас будет следующим.
1. Первым делом найдем площадь вырезанного прямоугольника.
2. Диагональ делит прямоугольник на два равных треугольника, значит, площадь одного треугольника будет в два раза меньше площади прямоугольника.
3. Разделив площадь прямоугольника на два, получим площадь треугольника.
У меня есть дополнительная информация к этой части урока!
Закрыть
Вычислить площадь квадрата легко, зная длину стороны:
S = а ∙ а = а2
Рассмотрим случай, когда длина стороны квадрата не определена, но известна длина диагонали квадрата.
Чтобы рассчитать площадь квадрата на основании длины его диагонали, нужно длину диагонали возвести в квадрат и разделить на два.
В виде формулы данное правило выглядит так:
S = р2 ÷ 2
S— площадь квадрата
p— длина диагонали
Задача №5
Найдите площадь квадрата, диагональ которого равна 4 см.
Площадь квадрата можно найти, если известен его периметр.
Так как все четыре стороны квадрата равны, периметр квадрата находится по формуле
Р = 4 ∙ а
а- это длина стороны квадрата.
Выразим из этой формулы сторону квадрата, для этого разделим периметр на 4.
а = Р ÷ 4
Зная длину стороны квадрата, можно найти площадь квадрата:
S = а2 = Р2 ÷ 42 = Р2 ÷ 16
S = Р2 ÷ 16
Задача №6
Периметр квадратной песочницы 8 м.
Найдите площадь этой песочницы.
Первый способ: решим данную задачу по действиям.
Второй способ: решим данную задачу с помощью формулы S = Р2 ÷ 16.
Решая задачу первым и вторым способом, ответ получили одинаковый: площадь песочницы оказалась равной S = 4 (м2).
Попробуем решить обратную задачу: по известной площади квадрата найдем его периметр.
Задача №7
Площадь квадратной комнаты равна 25 м2.
Найдите периметр этой комнаты.
Пройти тест
Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации
Вход Регистрация
Пройти тест
Формулы периметра геометрических фигур.
Как найти площадь и периметр квадрата и других фигурСодержание
- Основные свойства квадрата
- Как посчитать периметр помещения
- Что необходимо знать о квадрате?
- Как вычислить периметр
- Периметр и площадь прямоугольника
- Свойства квадрата.
- Периметры фигур
- Площадь квадрата
- Формулы определения площади квадрата
- Диагональ квадрата.
- Формулы определения длины диагонали квадрата
- Найти периметр квадрата
- Формула площади квадрата через радиус вписанной окружности
- Пример
- Вывод
Основные свойства квадрата
Квадратом также могут быть параллелограмм, ромб или прямоугольник если они имеют одинаковые длины диагоналей, сторон и одинаковые углы.
1. Все четыре стороны квадрата имеют одинаковую длину, то есть они равны:
AB = BC = CD = AD
2. Противоположные стороны квадрата параллельны:
AB||CD, BC||AD
3.
Все четыре угла квадрата прямые:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
4. Сумма углов квадрата равна 360 градусов:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
5. Диагонали квадрата имеют одинаковой длины:
AC = BD
6. Каждая диагональ квадрата делит квадрат на две одинаковые симметричные фигуры
7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам:
| AC┴BD | AO = BO = CO = DO = | d | |
| 2 |
8. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности
9. Каждая диагональ делит угол квадрата пополам, то есть они являются биссектрисами углов квадрата:
ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°
10.
Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные и прямоугольные:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Как посчитать периметр помещения
Периметр – это длина геометрической фигуры по её внешней границе.
Периметр помещения – это сумма длин сторон помещения. Соответственно для вычисления периметра необходимо суммировать все стороны.
Формула расчета периметра помещения:
P = 2 * (A + B)
А – длина помещения;
В – ширина помещения;
Для помещения произвольной конфигурации используются более сложные формулы расчета и этот расчет быстрее и удобнее выполнить с применением чертежных программных продуктов.
В нашей проектной организации Вы можете заказать расчет периметра помещения на основании технологического или конструкторского задания. Расчет выполним для любой конфигурации по Вашему рисунку с применением самых современных чертежных программ 2D-черчения.
Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы.
Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета периметра помещения. С помощью этого калькулятора в один клик вы можете вычислить периметр помещения, если известны длина и ширина.
Что необходимо знать о квадрате?
Прежде чем приступать к проведению вычислений, необходимо знать некоторые важные сведения об этой фигуре, среди которых:
- все стороны квадрата равны;
- все углы квадрата прямые;
- площадь квадрата – это способ исчисления того, как много места занимает фигура в двухмерном пространстве;
- двухмерное пространство – это лист бумаги или экран компьютера, где нарисован квадрат;
- периметр не является индикатором наполненности фигуры, однако позволяет работать с его сторонами;
- периметр – это сумма всех сторон квадрата;
- подсчитывая периметр, мы оперируем одномерным пространством, что означает фиксацию результата в метрах, а не метрах квадратных (площадь).
Как вычислить периметр
Периметр обозначается латинской буквой P. Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».
Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).
Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.
Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.
Периметр и площадь прямоугольника
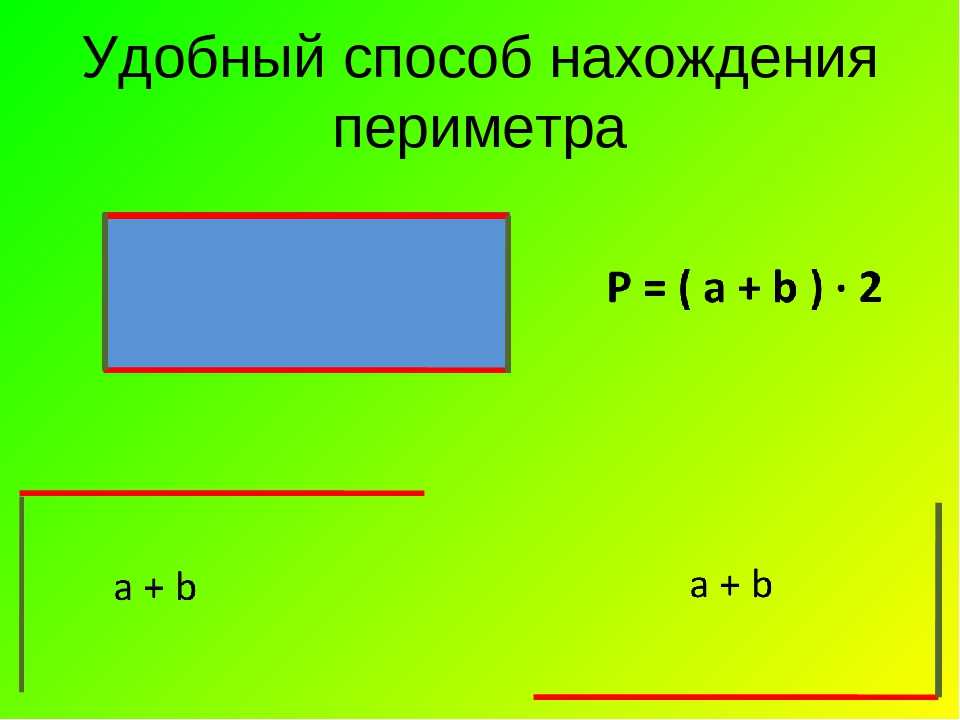
Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b.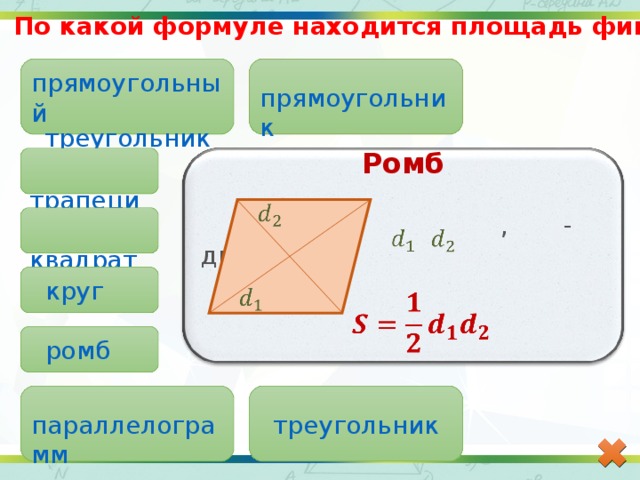
Формула для вычисления периметра прямоугольника выглядит так:
P= (a+b)*2
Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.
Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.
P= (6+2) * 2
P= 16
Ответ: 16 см
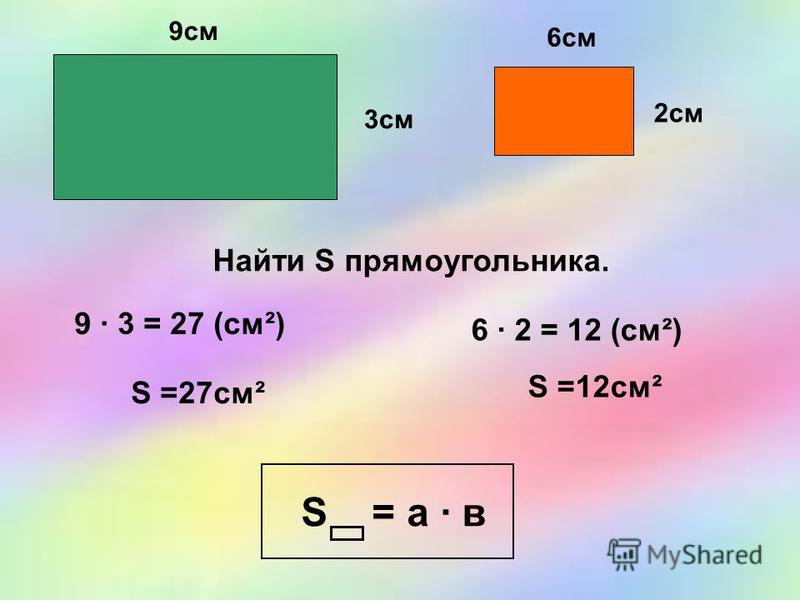
Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:
S= a*b
Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см. Меняем буквы a и b на указанные числа.
S= 5*2
S=10см2
Ответ: 10 см2
Свойства квадрата.
– у всех 4-х сторон квадрата одинаковая длина, т.е. стороны квадрата равны:
AB = BC = CD = AD
– противолежащие стороны квадрата параллельны:
AB||CD, BC||AD
– каждый угол квадрата прямой:
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°
– сумма углов квадрата равна 360°:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
– каждая диагональ квадрата имеет такую же длину, как и другая:
AC = BD
– каждая из диагоналей квадрата делит квадрат на 2 одинаковые симметричные фигуры.
– угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
AC┴BD;AO = BO = CO = DO = d/2
– точку пересечения диагоналей называют центр квадрата и она оказывается центром вписанной и описанной окружностей.
– все диагонали делят угол квадрата на две равные части, таким образом, они оказываются биссектрисами углов квадрата:
ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°
– диагонали делят квадрат на 4 одинаковых треугольника, кроме того, полученные треугольники в одно время и равнобедренные и прямоугольные:
ΔAOB = ΔBOC = ΔCOD = ΔDOA
Периметры фигур
Расчет периметра квадрата, прямоугольника, треугольника, круга (периметры фигур).Периметры фигурПлощадь квадрата
Определение.
Площадью квадрата называется пространство, ограниченное сторонами квадрата, то есть в пределах периметра квадрата.
Площадь квадрата больше площади любого четырехугольника с таким же периметром.
Формулы определения площади квадрата
1. Формула площади квадрата через сторону квадрата:
S = a2
2. Формула площади квадрата через периметр квадрата:
| S = | P2 |
| 16 |
3. Формула площади квадрата через диагональ квадрата:
| S = | d2 |
| 2 |
4. Формула площади квадрата через радиус описанной окружности:
S = 2R2
5. Формула площади квадрата через диаметр описанной окружности:
| S = | Do2 |
| 2 |
6.
Формула площади квадрата через радиус вписанной окружности:
S = 4r2
7. Формула площади квадрата через диаметр вписанной окружности:
S = Dв2
8. Формула площади квадрата через длину отрезка l:
| S = l 2 | 16 |
| √5 |
Диагональ квадрата.
Диагональю квадрата является всякий отрезок, который соединяет 2-е вершины противолежащих углов квадрата.
Диагональ всякого квадрата больше стороны этого квадрата в √2 раз.
Формулы для определения длины диагонали квадрата:
1. Формула диагонали квадрата через сторону квадрата:
2. Формула диагонали квадрата через площадь квадрата:
3. Формула диагонали квадрата через периметр квадрата:
4. Сумма углов квадрата = 360°:
5. Диагонали квадрата одной длины:
6. Все диагонали квадрата делят квадрат на 2-е одинаковые фигуры, которые симметричны:
7.
Угол пересечения диагоналей квадрата равен 90°, пересекая друг друга, диагонали делятся на две равные части:
8. Формула диагонали квадрата через длину отрезка l:
9. Формула диагонали квадрата через радиус вписанной окружности:
R – радиус вписанной окружности;
D – диаметр вписанной окружности;
d – диагональ квадрата.
10. Формула диагонали квадрата через радиус описанной окружности:
R – радиус описанной окружности;
D – диаметр описанной окружности;
d – диагональ.
11. Формула диагонали квадрата через линию, которая выходит из угла на середину стороны квадрата:
C – линия, которая выходит из угла на середину стороны квадрата;
d – диагональ.
Периметр квадрата. Площадь квадрата.
Вписанный круг в квадрат – это круг, примыкающий к серединам сторон квадрата и имеющий центр на пересечении диагоналей квадрата.
Радиус вписанной окружности – сторона квадрата (половина).
Площадь круга вписанного в квадрат меньше площади квадрата в π/4 раза.
Круг, описанный вокруг квадрата – это круг, который проходит через 4-ре вершины квадрата и который имеет центр на пересечении диагоналей квадрата.
Радиус окружности описанной вокруг квадрата больше радиуса вписанной окружности в √2 раз.
Радиус окружности описанной вокруг квадрата равен 1/2 диагонали.
Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.
Формулы определения длины диагонали квадрата
1. Формула диагонали квадрата через сторону квадрата:
d = a·√2
2. Формула диагонали квадрата через площадь квадрата:
d = √2S
3. Формула диагонали квадрата через периметр квадрата:
| d = | P |
| 2√2 |
4.
2.
Запишем в числовом виде: С =√36 + 36. Получили √72, а это 3√8 или 6√2.
А теперь найдем ту же диагональ, но уже по второму способу: С = А√2 или в числовом виде: 6√2
Теперь видно, насколько второй способ быстрее, легче и самое главное – эффективнее, особенно в таких легких задачках, ведь на экзамене дорога каждая минута!
Вывод
Вопросом, как посчитать диагонали квадрата, обычно задаются ученики, пропустившие эту тему в школе. Однако такие фундаментальные правила математики должен знать каждый! Желательно решать как можно быстрее, и для этого необходимы знания сокращенных формул. Все это предельно просто и легко, но вместе с тем является базой, необходимой для решения в дальнейшем гораздо более сложных задач. И важную часть этой базы занимает квадрат.
Источники
- https://ru.onlinemschool.com/math/formula/square/
- https://www.center-pss.ru/math/perimetr/pomeshenie.htm
- http://obvi.ru/science/mathematics/how-to-find-the-area-and-perimeter-of-square/
- https://topkin. ru/voprosy/nauka-voprosy/chto-takoe-perimetr-i-ploshhad/
- https://www.calc.ru/Geometricheskiye-Figury-Kvadrat.html
- https://www.calc.ru/perimetr-pryamougolnika.html
- https://ru.onlinemschool.com/math/assistance/figures_perimeter/square/
- https://mnogoformul.ru/formuly-ploshhadi-kvadrata
- https://1Ku.ru/obrazovanie/65472-kak-poschitat-diagonal-kvadrata-formula-dliny-diagonali-kvadrata/
ru/voprosy/nauka-voprosy/chto-takoe-perimetr-i-ploshhad/Разница между площадью и периметром. Чем отличается периметр от площади
Прежде, чем решать задачи на нахождение периметра и площади геометрических фигур, напомню, что….
I уровень
1.Длина прямоугольника 8 дм, ширина 7 дм. Найди его площадь.
2.Длина стороны квадрата 6 см. Узнайте площадь и периметр квадрата.
3.У прямоугольника длина 7 см, ширина 5 см. Узнайте площадь и периметр прямоугольника.
4.Найдите периметр и площадь прямоугольника со сторонами 6 см и 8 см.
5.Длина прямоугольника 8 дм, ширина 5 дм.
Найди его площадь.
6.Вычисли площадь прямоугольника, длины сторон которого равны 6 мм и 8 мм.
7.Ширина прямоугольника 7 дм, а длина 12 дм. Вычисли площадь.
8.Длина прямоугольника 9 дм, ширина 7 см. Найди его площадь.
9.Длина стороны квадрата 6 см. Узнай площадь.
10.Вычисли периметр квадрата со стороной 4 см.
11.Ширина прямоугольника равна 9 дм, а длина на 6 дм больше. Найдите его площадь.
12.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
13.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 3 раза больше. Найди его периметр и площадь.
14.Начерти прямоугольник, длина одной стороны которого 6 см, а длина другой в 2 раза больше. Найди его периметр и площадь.
15.Начерти прямоугольник, ширина которого равна 2 см, а длина на 3 см больше. Вычисли его периметр.
16.Сторона квадрата равна 3 см. Чему равен периметр?
17.Лист бумаги имеет квадратную форму.
Его сторона равна 10 см. Чему равен периметр?
18.Начерти квадрат со стороной 6 см. Найдите его периметр. Периметр квадрата равен 28 см. Чему равна его сторона?
19.Ширина окна прямоугольной формы 4 дм, а длина в 2 раза больше. Вычисли площадь окна.
20.Ширина прямоугольника 4 дм, а длина в 5 раз больше ширины. Найди площадь прямоугольника.
21.Площадь прямоугольника 36 см², его длина 9 см. Чему равна ширина прямоугольника?
II уровень
1.Начерти прямоугольник, длина одной стороны которого 2 см, а длина другой в 4 раза больше. Найди его периметр и площадь.
2.Длина прямоугольника равна 5 дм, ширина — на 4 см меньше. Найдите Р и S этого прямоугольника.
3.Дано: прямоугольник, а = 8 дм, в — на 2 см меньше. Найди Р и S.
4.Длина прямоугольника 12 см, а его ширина на 2 см меньше. Найдите площадь и периметр прямоугольника.
5.Сумма двух сторон квадрата 12 дм. Найдите периметр и площадь квадрата.
6.Найдите длину прямоугольника по его ширине – 8 дм и периметру–30 дм.
7.Периметр квадрата равен 32 см. Чему равна его сторона?
8.Периметр треугольника 21 см. Надите длину третьей стороны этого треугольника, если длины двух сторон 7 см и 8 см.
9.Периметр прямоугольника 20 см. Длина его стороны 6 см. Узнайте ширину прямоугольника и начертите его.
10.Площадь прямоугольника равна 270 кв.см, его длина 9 дм. Найдите периметр этого прямоугольника.
11.Периметр прямоугольника равен 54 м . Найдите площадь этого прямоугольника, если одна его сторона равна 18 м.
12. Найдите площадь квадрата, периметр которого равен 360 мм.
13. Периметр прямоугольника 40 см. Одна сторона 5 см.Чему равна его площадь?
14. Начерти квадрат, периметр которого равен периметру прямоугольника со сторонами 2 см и 6 см.
15. Дачный участок прямоугольной формы имеет длину 20 м и ширину 12 м. Какой длины забор надо поставить вокруг участка?
16. Периметр квадрата равен периметру треугольника со сторонами 6 см, 3 см и 7 см. Чему равна длина стороны квадрата?
17.
У какой фигуры площадь больше и на сколько: у квадрата со стороной 4см или у прямоугольника со сторонами 2 см и 6 см?
18. Периметр прямоугольника равен 54 м. Найди площадь этого прямоугольника, если одна его сторона равна 18 м.
19. Периметр квадратной песочницы 12 м. Найдите площадь этой песочницы.
20. Напишите все возможные варианты длины и ширины прямоугольника, если его периметр 24 см.
Составила К ислова Людмила Борисовна
Подписаться на сайт
Ребята, мы вкладываем душу в сайт. Cпасибо за то,
что открываете эту красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
Периметр – это геометрический термин, который часто встречается в задачах. Чтобы понять, что такое периметр, следует нарисовать произвольный многоугольник и вооружиться линейкой. В переводе с греческого языка этот термин обозначает «измеряю вокруг».
Как вычислить периметр
Периметр обозначается латинской буквой P .
Его можно измерить в сантиметрах, миллиметрах, метрах или дециметрах. Чтобы узнать периметр, следует измерить длину всех сторон многоугольника. Полученные значения нужно сложить. Итоговая сумма и станет ответом на вопрос: «Чему равен периметр многоугольника».
Периметр – это длина линий, которые ограничивают замкнутую фигуру (квадрат, прямоугольник, треугольник и др.).
Например, перед вами многоугольник со сторонами 10, 12, 13 и 11 см. Складываем вышеназванные числа (10+12+13+11) и получаем сумму 46. Это и есть периметр многоугольника.
Для удобства вычисления периметра в геометрии существует ряд формул. Каждая формула соответствует определенной фигуре.
Периметр и площадь квадрата
Это сумма его четырех сторон. Как мы знаем, все стороны квадрата имеют равный размер. Поэтому мы можем узнать периметр квадрата, умножив длину его стороны на четыре:
P= a+a+a+a
Например, перед нами квадрат со стороной 10 см.
Ответ: 40 см
P = 10+10+10+10
P =40
Ответ: 40 см
Чтобы разобраться, что такое периметр и площадь, следует уяснить, что периметр вычисляет длину контура фигуры, а площадь – размер всей ее поверхности.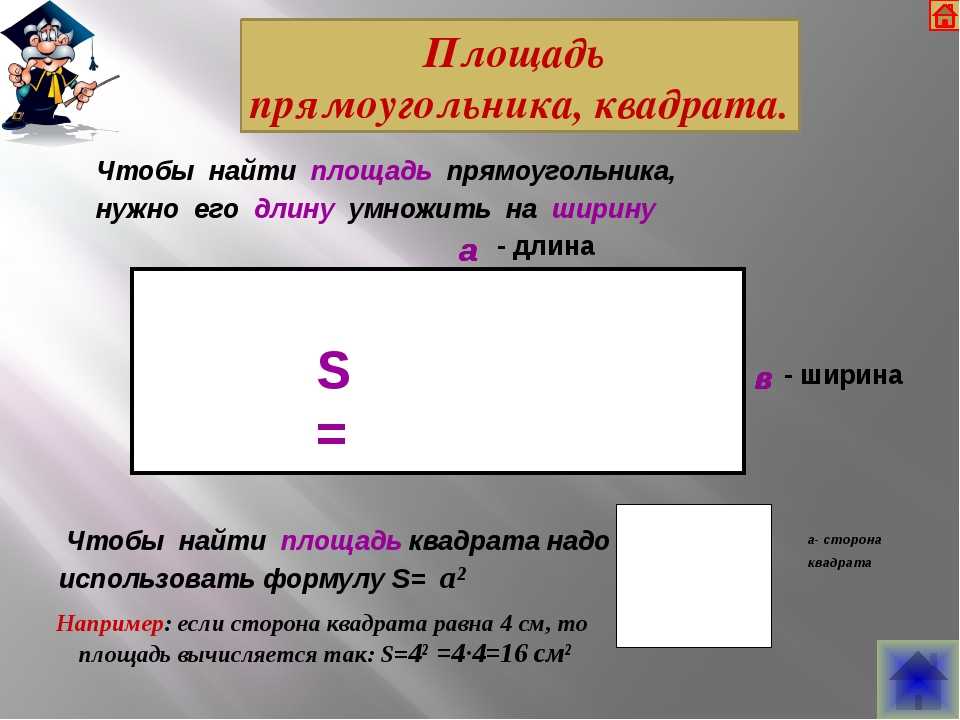
Чтобы узнать площадь квадрата, необходимо воспользоваться простой формулой:
S – это площадь, а – сторона квадрата.
Например, в задаче указано, что длина стороны квадрата составляет 10см.
S= 100 см 2
Ответ: 10 0 см 2
Периметр и площадь прямоугольника
Стороны прямоугольника, находящиеся друг напротив друга и имеющие одинаковую длину, называются противолежащими. Это длина и ширина, они условно обозначаются латинскими буквами a и b. Формула для вычисления периметра прямоугольника выглядит так:
P= (a+b)*2
Используя эту формулу, мы сначала находим сумму ширины и длины, а затем умножаем ее на два.
Например, перед нами прямоугольник, имеющий длину 6 см и ширину 2 см.
P = (6+2) * 2
P = 16
Ответ: 16 см
Чтобы узнать площадь прямоугольника, следует длину умножить на ширину. Формула выглядит так:
Например, в условиях задачи сказано, что прямоугольник имеет длину 5 см и ширину 2см.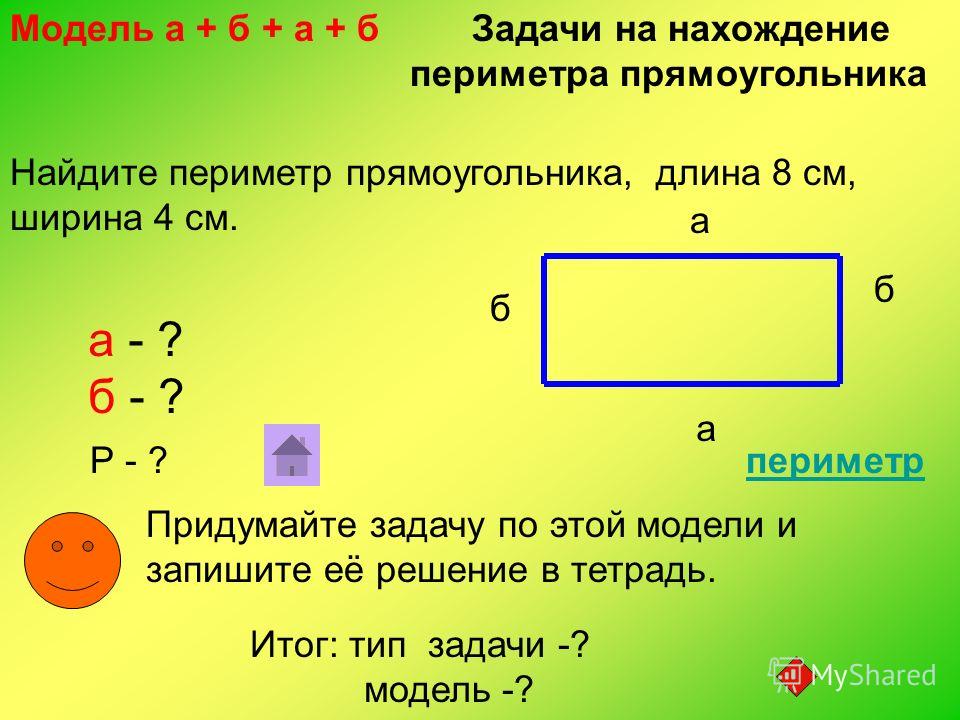
Меняем буквы a и b на указанные числа.
S = 5*2
S =10см 2
Ответ: 10 см 2
Периметр круга (длина окружности)
Каждый круг имеет центр. Расстояние от центра круга до любой точки, расположенной на окружности, имеет название радиус круга. Часто ученики путают понятия «круг» и «окружность» и пытаются определить площадь окружности. Это серьезная ошибка. Следует разделить в голове понятия «круг» и «окружность». У окружности нет и не может быть площади, у нее есть только длина.
Чтобы найти периметр круга, следует вычислить длину его окружности. Существует формула для нахождения длины окружности:
L = 2πr
L – длина окружности
π – это число «пи», математическая константа. Она равна отношению длины окружности к длине ее диаметра. Древнее название числа «пи» – лудольфово число. Это число иррационально, его десятичное представление после точки никогда не заканчивается.
π = 3.
141 592 653 589 793 238 462 643 383 279 502
Для удобства вычислений обычно используют значение 3.14
R – это радиус окружности
D – Диаметр окружности
Итак, чтобы определить периметр круга, надо найти произведение радиуса и 2π. Если в задаче указан диаметр, то
Например, перед нами круг с радиусом 3 см. Найдем его периметр.
L = 2*3,14*3
L =6 π
L=6*3.14
L = 18.84 см
P к = 18,84 см
Ответ: 18.84 см
Отличие периметра от площади
Площадь – это размер поверхности фигуры, а периметр – это сумма ее границ.
Площадь всегда измеряется в квадратных единицах (см 2 , м 2 , мм 2). Периметр измеряется в единицах длины – в сантиметрах, миллиметрах, метрах, дециметрах.
Урок и презентация на тему: «Периметр и площадь прямоугольника»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания.
Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.
Периметр обозначается латинской буквой P . Так как периметр — это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как P ABCD , где А, В, С, D — это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
P ABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим P ABCD .
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
P ABCD = 2 * (AB + BС)
P ABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: P ABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
P ABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
P ABCD = 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
P ABCD = 4 * AB
3. Подставим в формулу наши данные:
P ABCD = 4 * 6 см = 24 см
Ответ: P ABCD = 24 см.
Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1.
Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры.
Площадь измеряется квадратными единицами длины: см 2 , м 2 , дм 2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S .
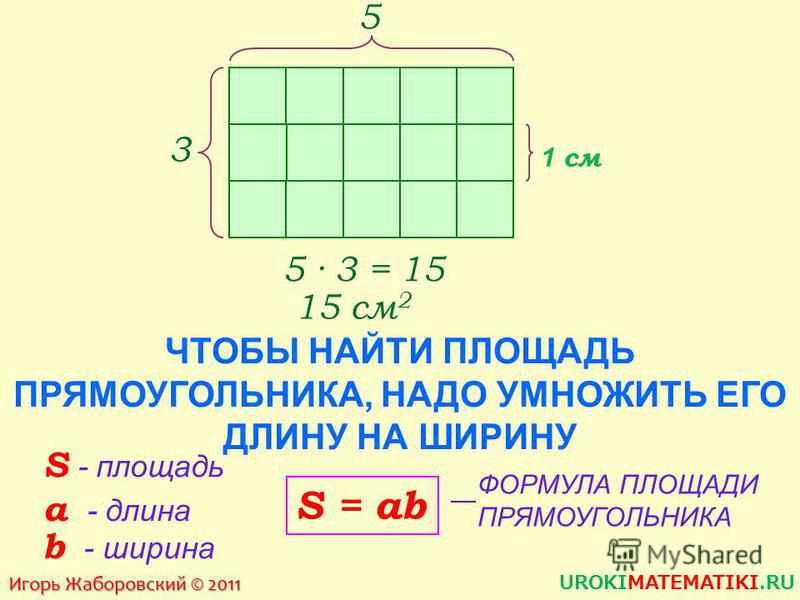
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.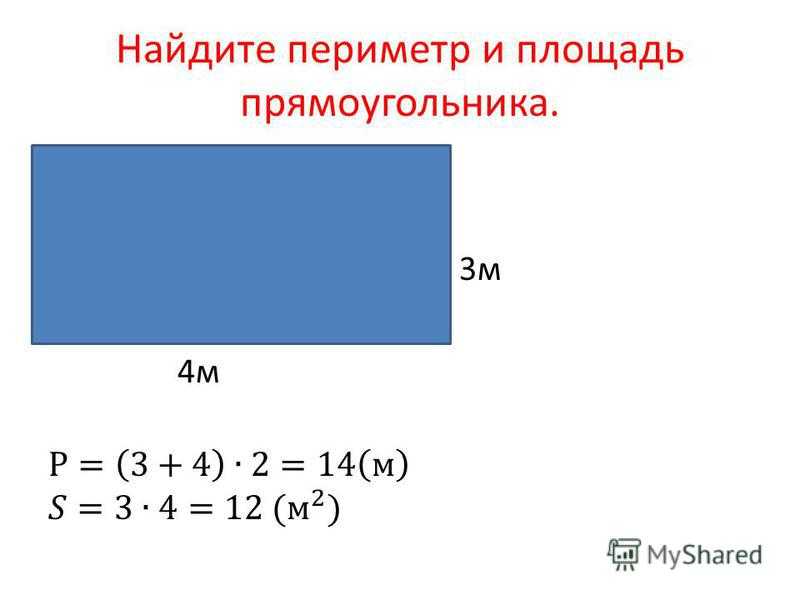
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO = AK * KM = 7 см * 2 см = 14 см 2 .
Ответ: 14 см 2 .
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.
Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см 2
Ответ: 64 см 2 .
Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.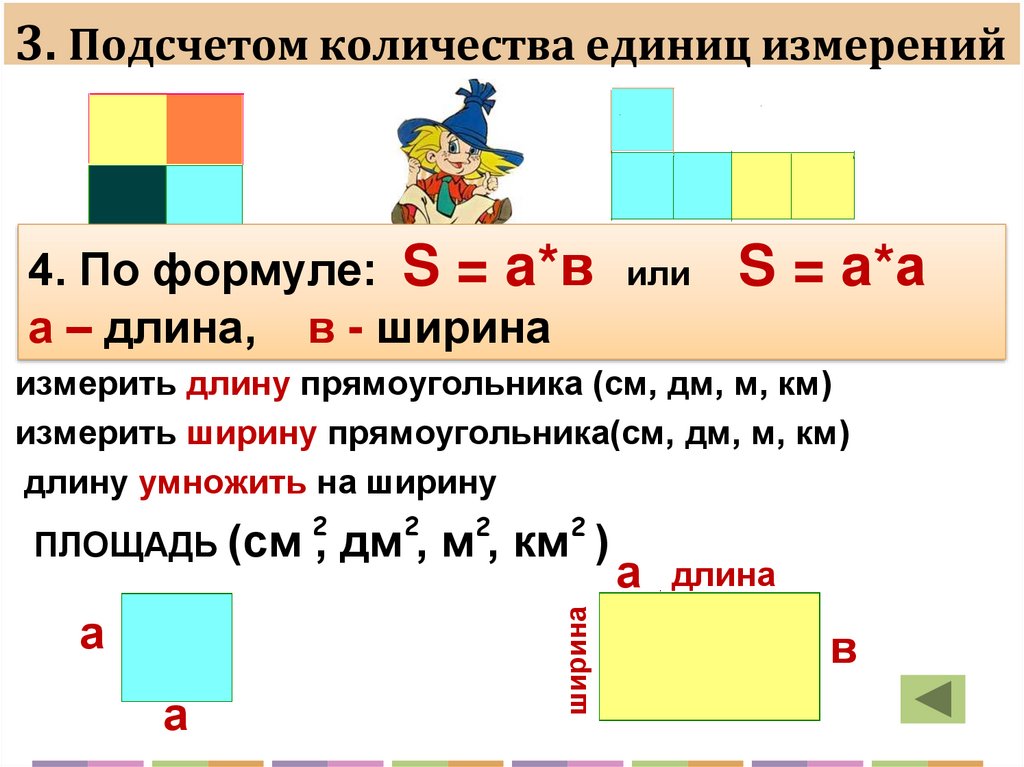
Периметр — это сумма длин всех сторон многоугольника.
- Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
- Периметр измеряется в единицах длины: мм, см, м, км и т.д.
- Прямоугольник – это четырехугольник.
- Все параллельные стороны равны
- Все углы = 90º.
- Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.
Существует 2 способа его нахождения:
- 1 способ. Складываем все стороны. P = a + а + b + b
- 2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.
«a» — длина прямоугольника, более длинная пара его сторон.
«b» — ширина прямоугольника, более короткая пара его сторон.
Пример задачи на подсчет периметра прямоугольника:
Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.
Запомни формулы вычисления периметра прямоугольника!
Полупериметр — это сумма одной длины и одной ширины.
- Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
- Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.
Как найти площадь прямоугольника
Формула площади прямоугольника S= a*b
Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.
- : a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.
Помни!
- Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
- Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)
При решении, необходимо принять во внимание, что решить задачу о нахождении площади прямоугольника только из длины его сторон нельзя .
В этом несложно убедиться. Пусть периметр прямоугольника будет равен 20 см. Это будет верно, если его стороны 1 и 9, 2 и 8, 3 и 7 см. Все эти три прямоугольника будут иметь одинаковый периметр, равный двадцати сантиметрам. (1 + 9) * 2 = 20 точно также как и (2 + 8) * 2 = 20 см.
Как видно, мы можем подобрать бесконечное количество вариантов размеров сторон прямоугольника, периметр которого будет равен заданному значению.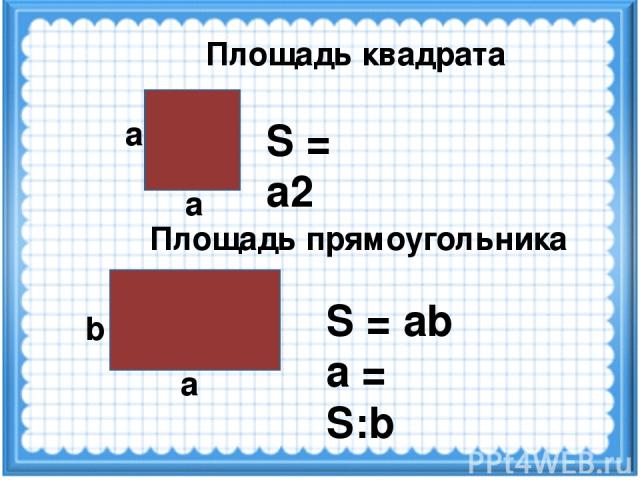
Площадь прямоугольников с заданным периметром 20 см, но с различными сторонами будет различна. Для приведенного примера — 9, 16 и 21 квадратных сантиметров соответственно.
S 1 = 1 * 9 = 9 см 2
S 2 = 2 * 8 = 16 см 2
S 3 = 3 * 7 = 21 см 2
Как видим, вариантов площади фигуры при заданном периметре — бесконечное количество.
Замечание для любознательных . В случае с прямоугольником, у которого задан периметр, максимальную площадь будет иметь квадрат.
Таким образом, для того, чтобы вычислить площадь прямоугольника из его периметра, нужно обязательно знать либо соотношение его сторон, либо длину одной из них. Единственной фигурой, которая имеет однозначную зависимость своей площади от периметра, является круг. Только для круга и возможно решение.
В этом уроке:
- Задача 4. Изменение длины сторон при сохранении площади прямоугольника
Задача 1. Найти стороны прямоугольника из площади
Периметр прямоугольника равен 32 сантиметрам, а сумма площадей квадратов, построенных на каждой из его сторон — 260 квадратных сантиметров.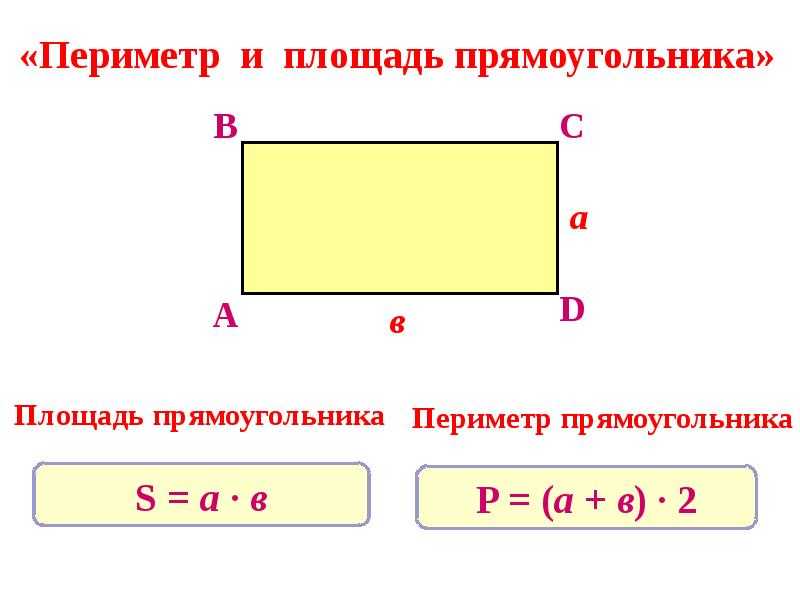
Найдите стороны прямоугольника.
Решение.
2(x+y)=32
Согласно условию задачи, сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, четыре) будет равна
2x 2 +2y 2 =260
x+y=16
x=16-y
2(16-y) 2 +2y 2 =260
2(256-32y+y 2)+2y 2 =260
512-64y+4y 2 -260=0
4y 2 -64y+252=0
D=4096-16×252=64
x 1 =9
x 2 =7
Теперь примем во внимание, что исходя из того, что x+y=16 (см. выше) при x=9, то y=7 и наоборот, если x=7, то y=9
Ответ : Стороны прямоугольника равны 7 и 9 сантиметров
Задача 2. Найти стороны прямоугольника из периметра
Периметр прямоугольника 26 см, а сумма площадей квадратов, построенных на двух его смежных сторонах, равна 89 кв. см. Найдите стороны прямоугольника.
Решение.
Обозначим стороны прямоугольника как x и y.
Тогда периметр прямоугольника равен:
2(x+y)=26
Сумма площадей квадратов построенных на каждой из его сторон (квадратов, соответственно, два и это квадраты ширины и высоты, поскольку стороны смежные) будет равна
x 2 +y 2 =89
Решаем полученную систему уравнений.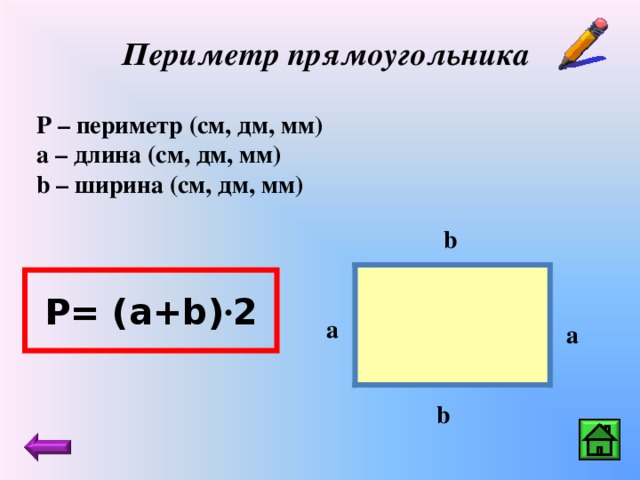
Из первого уравнения выводим, что
x+y=13
y=13-y
Теперь выполняем подстановку во второе уравнение, заменяя x его эквивалентом.
(13-y) 2 +y 2 =89
169-26y+y 2 +y 2 -89=0
2y 2 -26y+80=0
Решаем полученное квадратное уравнение.
D=676-640=36
x 1 =5
x 2 =8
Теперь примем во внимание, что исходя из того, что x+y=13 (см. выше) при x=5, то y=8 и наоборот, если x=8, то y=5
Ответ: 5 и 8 см
Задача 3. Найти площадь прямоугольника из пропорции его сторон
Найти площадь прямоугольника если его периметр равен 26 см а стороны пропорциональны как 2 к 3.
Решение.
Обозначим стороны прямоугольника через коэффициент пропорциональности x.
Откуда длина одной стороны будет равна 2x, другой — 3х.
Тогда:
2(2x+3x)=26
2x+3x=13
5x=13
x=13/5
Теперь, исходя из полученных данных, определим площадь прямоугольника:
2x*3x=2*13/5*3*13/5=40,56 см 2
Длина прямоугольника увеличена на 25%.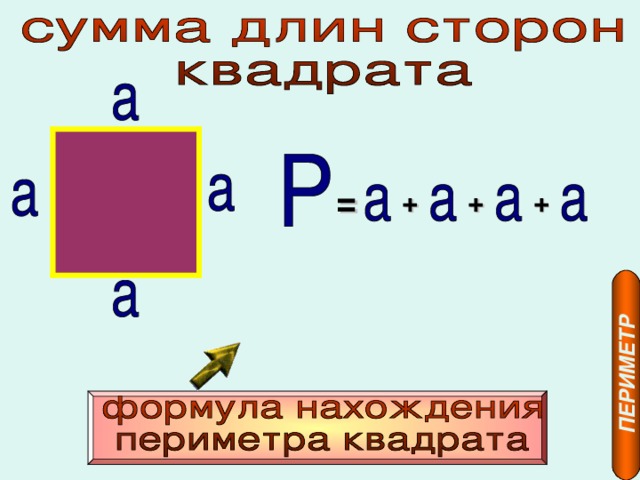
На сколько процентов надо уменьшить ширину, чтобы его площадь не изменилась?
Решение .
Площадь прямоугольника равна
S = ab
В нашем случае один из множителей увеличился на 25%, что означает a 2 = 1,25a . Таким образом, новая площадь прямоугольника должна быть равна
S 2 = 1,25ab
Таким образом, для того, чтобы вернуть площадь прямоугольника к начальному значению, то
S 2 = S / 1.25
S 2 = 1,25ab / 1.25
Поскольку новый размер а изменять нельзя, то
S 2 = (1,25a) b / 1.25
1 / 1,25 = 0,8
Таким образом, величину второй стороны нужно уменьшить на (1 — 0,8) * 100% = 20%
Ответ : ширину нужно уменьшить на 20%.
3 класс, периметр и площадь прямоугольника
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать: Периметр и площадь прямоугольника (PDF)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 3 класса
Тренажер для 3 класса «Правила и упражнения по математике»
Электронное учебное пособие для 3 класса «Математика за 10 минут»
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.
Периметр обозначается латинской буквой P. Так как периметр – это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как PABCD, где А, В, С, D – это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
PABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим PABCD.
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
PABCD = 2 * (AB + BС)
3. Подставим в формулу наши данные:
PABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: PABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
PABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата. Учитывая, что все стороны квадрата равны, получаем:
PABCD= 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
PABCD = 4 * AB
3. Подставим в формулу наши данные:
PABCD = 4 * 6 см = 24 см
Ответ: PABCD = 24 см.Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором.
Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см2, м2, дм2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S.
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO= AK * KM = 7 см * 2 см = 14 см2.
Ответ: 14 см2.Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.
Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см2
Ответ: 64 см2.Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.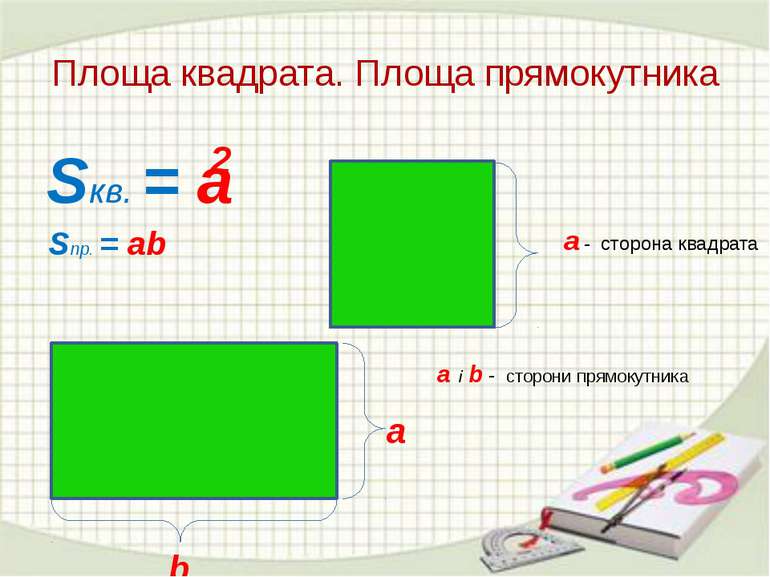
Формулы / Натуральные числа и действия над ними / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Формулы
Буквенные выражения, о которых мы говорили в статье «Числовые и буквенные выражения«, лежат в основе математических формул.
Буквенное выражение — математическое выражение, в котором используются цифры, знаки действий и буквы, также могут быть и скобки.
Математическая формула — совокупность величин, выраженных числами и буквами и соединенных посредством математических знаков.
Примеры математических формул
1) Формула периметра и площади прямоугольника.
Пусть мы имеем прямоугольник, ширина которого равна , а длина равна .
Если — периметр прямоугольника, тогда формула для вычисления периметра прямоугольника: или . Полученную формулу можно использовать для вычисления периметра любого прямоугольника.
Если — площадь прямоугольника, тогда формула для вычисления площади прямоугольника: . Полученную формулу можно использовать для вычисления площади любого прямоугольника.
2) Формула периметра и площади квадрата.
Пусть мы имеем квадрат, сторона которого равна .
Если — периметр квадрата, тогда формула для вычисления периметра квадрата: . Полученную формулу можно использовать для вычисления периметра любого квадрата.
Если — площадь квадрата, тогда формула для вычисления площади квадрата: . Полученную формулу можно использовать для вычисления площади любого квадрата.
3) Формула пути.
Если — пройденный путь (расстояние), — скорость движения, — время, за которое пройден путь , тогда формула пути: .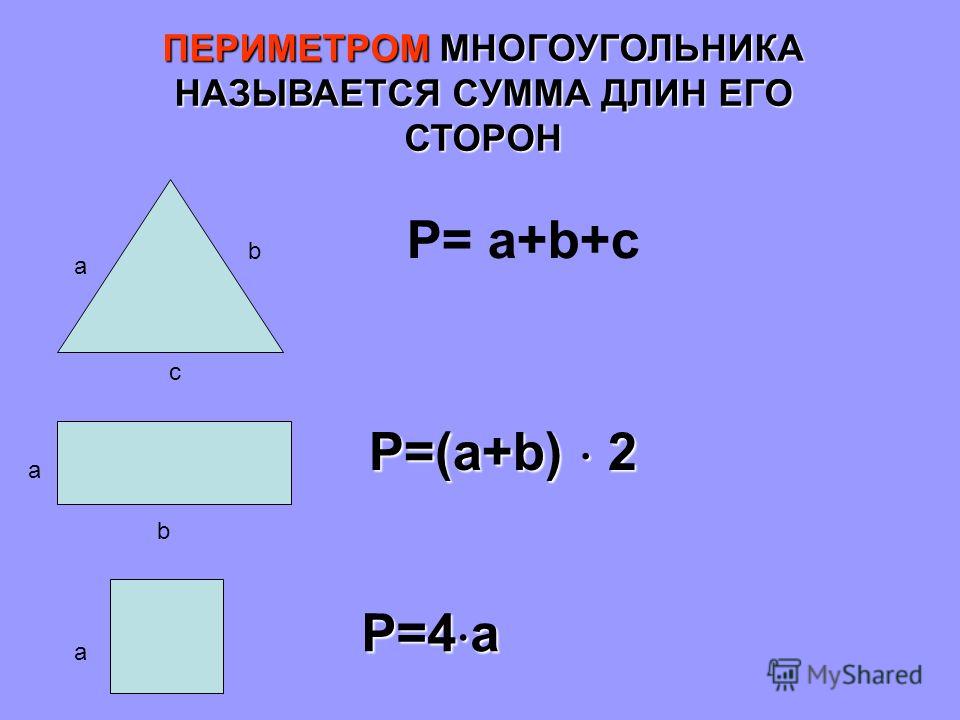
Из данной формулы также можно получить формулы:
- скорости движения: ;
- времени: .
Обратите внимание:
При записи математических формул знак умножения «·» не пишут, что позволяет упростить запись выражения. Так, например, в формуле площади прямоугольника , между буквами и подразумевают знак «·» , но не пишут его.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Степень числа. Квадрат и куб числа
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 309 , Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 311 , Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 702, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 732, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 741, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 796, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 811, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 847, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1557, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 252, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 659, Мерзляк, Полонский, Якир, Учебник
Номер 670, Мерзляк, Полонский, Якир, Учебник
Номер 671, Мерзляк, Полонский, Якир, Учебник
Номер 672, Мерзляк, Полонский, Якир, Учебник
Номер 673, Мерзляк, Полонский, Якир, Учебник
Номер 729, Мерзляк, Полонский, Якир, Учебник
Задание 598, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1168, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1169, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 746, Мерзляк, Полонский, Якир, Учебник
Номер 754, Мерзляк, Полонский, Якир, Учебник
Номер 755, Мерзляк, Полонский, Якир, Учебник
Номер 756, Мерзляк, Полонский, Якир, Учебник
Номер 757, Мерзляк, Полонский, Якир, Учебник
Номер 759, Мерзляк, Полонский, Якир, Учебник
Номер 781, Мерзляк, Полонский, Якир, Учебник
Номер 852, Мерзляк, Полонский, Якир, Учебник
Номер 853, Мерзляк, Полонский, Якир, Учебник
Номер 857, Мерзляк, Полонский, Якир, Учебник
What is the area and perimeter of a square? – Reviews Wiki
Ответ: площадь квадрата равна квадрату длины его стороны, а периметр квадрата в 4 раза больше длины его стороны.
Пусть длина стороны квадрата равна единицам «а».
Аналогично, квадрат периметра прямоугольника? Существуют разные единицы измерения периметра и площади. Периметр имеет те же единицы измерения, что и длина сторон прямоугольника или квадрата, тогда как единица площади возведена в квадрат.
Как найти площадь и периметр квадрата и прямоугольника? Периметр прямоугольника P определяется по формуле P=2l+2w , где l — длина, а w — ширина прямоугольника. Площадь прямоугольника А находится по формуле A = lw, где l — длина, а — ширина.
Какова формула периметра? Формула периметра прямоугольника гласит, что Р = (Д + Ш) × 2, где P обозначает периметр, L обозначает длину, а W обозначает ширину. Когда вам даны размеры прямоугольной формы, вы можете просто подставить значения L и W в формулу, чтобы найти периметр.
Во-вторых, каковы формулы площади и периметра? Формулы площади и периметра
| Форма | Район | Периметр |
|---|---|---|
| Треугольник | А = ½ × b × ч | S = а + Ь + с |
| Квадратный | А = а 2 | Р = 4а |
| Прямоугольные | А = l × w | P = 2 (l + w) |
| Параллелограмм | А = б × ч | Р = 2 (а + б) |
• 7 сентября 2020 г.
Что такое площадь 6см и 4см?
Чтобы вычислить площадь, мы просто умножаем основание (ширину) на высоту (как прямоугольник). Площадь = 6 см x 4 см = 24 см2 = 22cm2 Page 5 Начальная школа Netherbrook 1. На схеме показан прямоугольник, нарисованный на квадратной сетке.
тогда какая формула площади квадрата и прямоугольника? Например, площадь квадрата можно вычислить с помощью 2 где это длина его стороны.
…
Формулы площади.
| цифры | Формула | Переменные |
|---|---|---|
| Прямоугольные | Площадь = l × w | l = длина w = ширина |
| Квадратный | Площадь = а2 | a = стороны квадрата |
| Треугольник | Площадь = 12 кв.ч | b = основание h = высота |
Какова формула периметра всех фигур? Формулы периметра
| Геометрическая форма | Формула периметра | Метрика |
|---|---|---|
| Треугольник | а + б + с | a , b и c — длины сторон |
| Прямоугольные | 2 (длина + ширина) | |
| Квадратный | 4a | a = длина стороны |
| Трапеция | а + б + с + г | a, b, c, d — стороны трапеции |
Как найти периметр всех форм?
Как вы рассчитываете примеры периметра? Объяснение: Разделите площадь прямоугольника на ширину, чтобы получить длину 14 футов.. Периметр — это сумма длин сторон, которая в данном случае составляет 14 футов + 4 фута + 14 футов + 4 фута, или 36 футов.
Чему равна площадь квадрата и прямоугольника?
Квадратный. Площадь = а2. а = длина стороны. Прямоугольник. Площадь = ш × ч.
Как найти площадь и периметр всех форм? Формула площади и периметра
- Формула площади и периметра — это две основные формулы для любой двумерной формы в математике. …
- Площадь Квадрата = а 2 , где а — сторона квадрата.
- Периметр прямоугольника = 2 (L + B) = 2 (6 см + 4 см) = 2 × 10 см = 20 см.
- Формулы периметра для различных геометрических фигур:
Чему равен периметр 8 см и 3 см?
Периметр — это расстояние вокруг прямоугольника.
У прямоугольника 4 стороны: 2 из них будут длиной (8 см) и 2 из них шириной (3 см). Чтобы получить периметр, нужно сложить 2 длины и 2 ширины: 2 х 8 + 2 х 3. Следовательно, ответ таков: 22cm (не забудьте единицы измерения!)
см2 это периметр?
Для квадрата 2 см периметр равен 8 см, а площадь 4 см2. Периметр вдвое больше площади.
Как найти периметр прямоугольника, зная площадь? Чтобы получить периметр из площади квадрата, умножьте квадратный корень из площади на 4 . Периметр всегда измеряется в линейных единицах, которые выводятся из квадратных единиц площади.
Как найти площадь и периметр квадратного треугольника, прямоугольника и круга?
Что такое квадратная формула? В геометрии квадрат — это форма с четырьмя равными сторонами.
Площадь квадрата определяется как количество квадратных единиц, составляющих полный квадрат. Он рассчитывается по формуле площади квадрата Площадь = s × s = s2 в квадратных единицах.
Каков периметр конуса?
Подсказка: чтобы найти криволинейную поверхность конуса, нам дан периметр основания конуса, равный длине окружности, т. е. С = 2πr .
Каков периметр квадрата 3 см?
Пример: если длина стороны квадрата 3 см, то найдите его периметр. Периметр квадрата = 4 х сторона = 4 х 3 = 12 см.
Как посчитать периметр из квадратных метров?
Периметр будет 2 x один фактор + 2 x другой фактор.
Допустим, площадь прямоугольника равна 96 квадратных футов. Тогда прямоугольник может быть 8 футов на 12 футов, поэтому периметр будет равен 2 x 8 футов + 2 x 12 футов, или 40 футов. Но прямоугольник также может быть 6 футов на 16 футов, поэтому периметр будет равен 44.
Какая фигура имеет периметр 34 фута? периметр Прямоугольник 34 фута, а площадь 30 квадратных футов.
Периметр, площадь и объем
Горячая математика1. периметр из многоугольник (или любая другая замкнутая кривая, например круг) — это расстояние вокруг внешней стороны.
2. область из простая, замкнутая, плоская кривая — это объем пространства внутри.
3. объем из твердый 3 Д форма — это количество пространства, вытесненного ею.
Некоторые формулы для общих
2
-мерные плоские фигуры и
3
-мерные тела приведены ниже.
Ответов один, два,
или три измерения; периметр измеряется в линейные единицы , область измеряется в квадратные единицы , а также объем измеряется в кубические единицы .
Форма | Формула | Переменные |
Квадрат | п знак равно 4 с | с
это длина стороны квадрата. |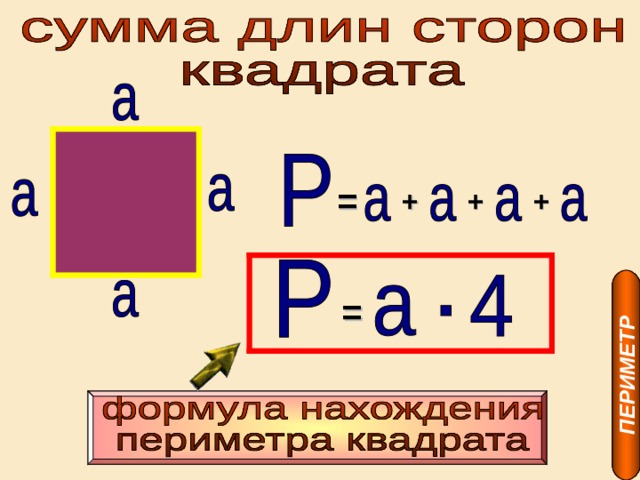
Прямоугольник | п знак равно 2 л + 2 Вт | л а также Вт длины сторон прямоугольника (длина и ширина). |
Треугольник | а + б + с | а , б , а также с являются длинами сторон. |
Прямоугольный треугольник с ножками а а также б (видеть Теорема Пифагора ) | п знак равно а + б + а 2 + б 2 | а а также б это длины двух катетов треугольника |
Круг |
| р
это радиус и
г
это диаметр. |
Форма | Формула | Переменные |
Квадрат |
| с это длина стороны квадрата. |
Прямоугольник |
| л
а также
Вт
длины сторон прямоугольника (длина и ширина). |
Треугольник | А знак равно 1 2 б час | б а также час это основание и высота |
Треугольник | А знак равно с ( с − а ) ( с − б ) ( с − с ) куда с знак равно а + б + с 2 | а , б , а также с это длины сторон и с это полупериметр |
Параллелограмм |
| б
это длина основания и
час
это высота. |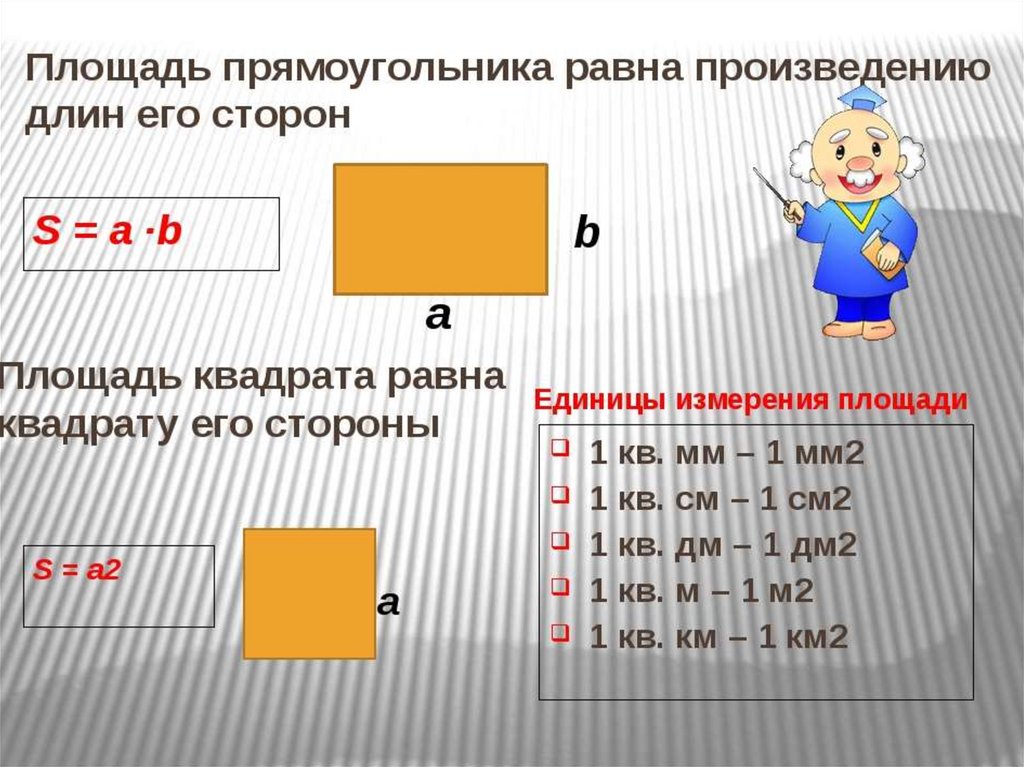
Трапеция | А знак равно б 1 + б 2 2 час | б 1 а также б 2 — длины параллельных сторон и час расстояние (высота) между параллелями. |
Круг | А знак равно π р 2 | р это радиус. |
Форма | Формула | Переменные |
Куб |
| с
это длина стороны. |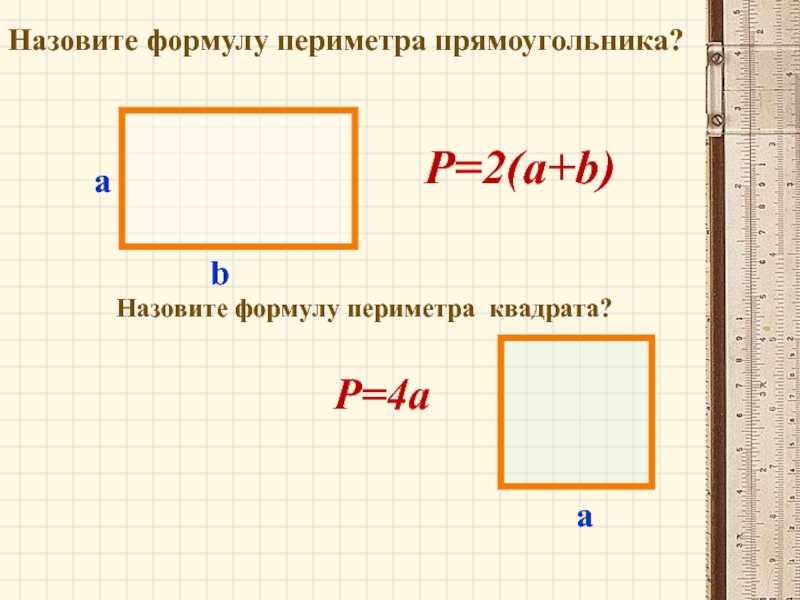
Правая прямоугольная призма |
| л это длина, Вт это ширина и ЧАС это высота. |
Призма или цилиндр | В знак равно А час | А площадь основания, час это высота. |
Пирамида или конус | В знак равно 1 3 А час | А
площадь основания,
час
это высота. |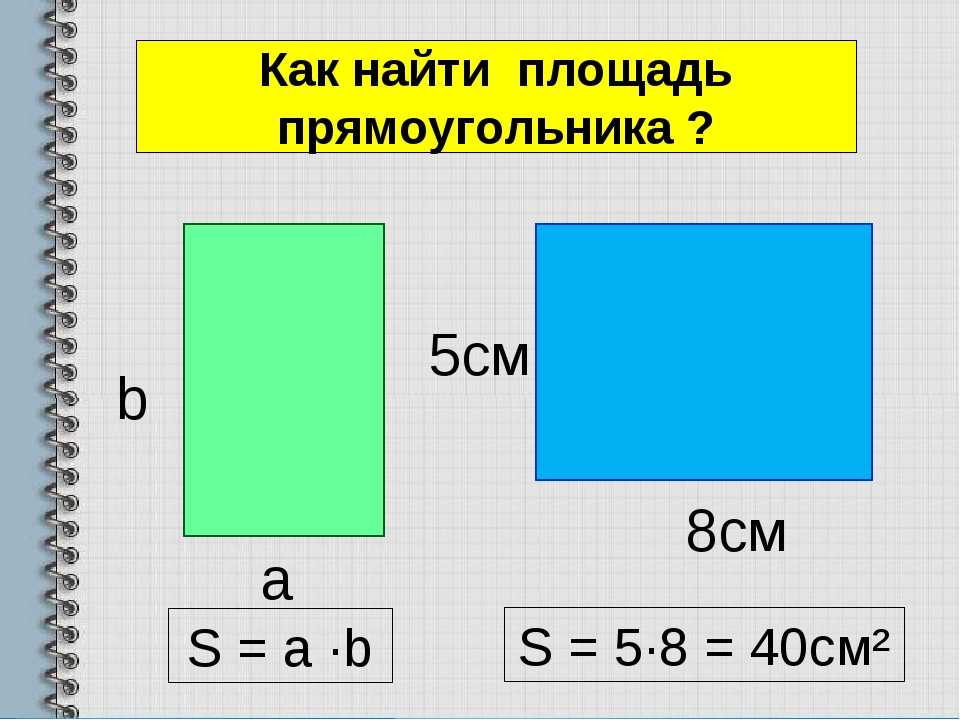
Сфера |
| р это радиус. |
Объяснение урока: Периметр прямоугольников и квадратов
В этом объяснении мы научимся находить периметр прямоугольника или квадрата путем сложения длин всех их сторон или по формуле, используя только целые числа.
Вы уже должны знать определение периметра фигуры.
Определение: периметр
Периметр фигуры — это общая длина ее границы. Он рассчитывается путем добавления вместе длина всех сторон.
Для квадрата со стороной 𝑥 периметр, который мы можем обозначить 𝑃, будет равна сумме длин его сторон: 𝑃=𝑥+𝑥+𝑥+𝑥.
Кроме того, поскольку все стороны равны по длине, периметр вычисляется по формуле
умножая длину одной из сторон на 4: 𝑃=4𝑥.
Это дает нам формулу, описывающую, как найти периметр квадрата, зная его сторону. длина.
Формула периметра квадрата
Периметр 𝑃 квадрата со стороной 𝑥 может быть рассчитывается по следующей формуле: 𝑃=4𝑥.
Теперь, когда мы знаем формулу периметра квадрата, воспользуемся ею для решения некоторых типичные проблемы.
Пример 1. Нахождение периметра квадрата по его длине
Найдите периметр квадрата, длина стороны которого равна 19 см.
Ответ
Нам сказали, что длина каждой стороны квадрата равна длине 19 см.
Итак, чтобы найти периметр 𝑃, нам просто нужно сложить длины из 4 сторон 𝑃=19+19+19+19=76.
В качестве альтернативы мы можем использовать формулу периметра квадрата, которая говорит нам, что периметр равен 4𝑥, где 𝑥 — длина одна из сторон. Следовательно, 𝑃=4×19=76.
Но это не окончательный ответ. Мы должны убедиться, что мы включили правильную длину
единиц при записи периметра фигур.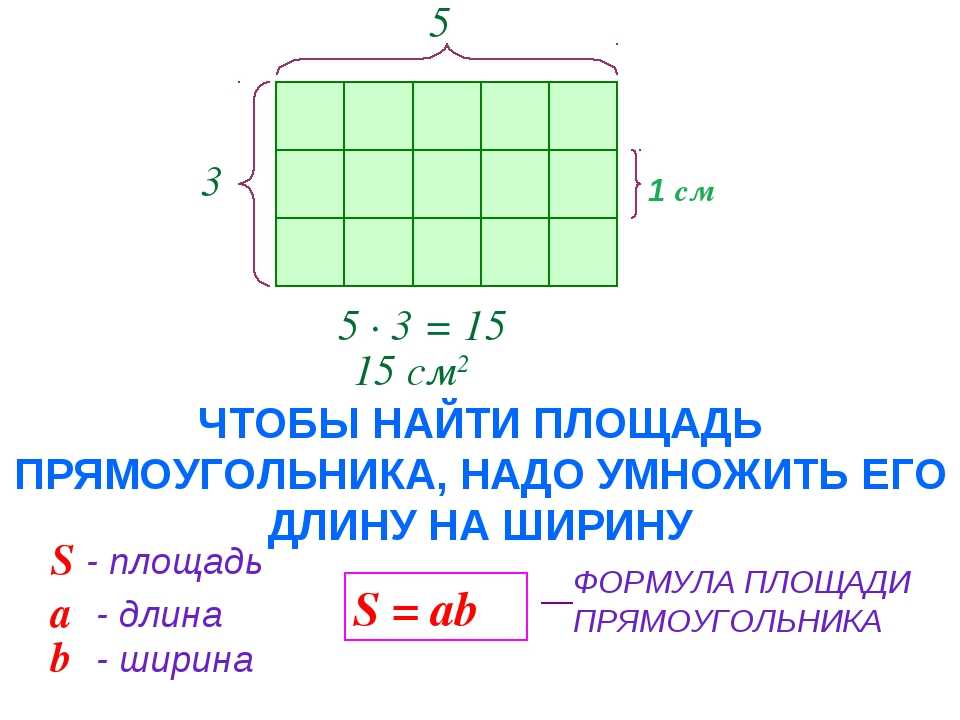
Так как длина стороны измеряется в
см, периметр у нас есть
исчисляется также в сантиметрах. Значит, периметр квадрата
76 см.
Пример 2. Нахождение периметра квадрата и преобразование единиц измерения
Вычислите в см периметр квадрата квадрат со стороной 70 мм.
Ответ
Мы знаем, что периметр 𝑃 квадрата можно вычислить с помощью формула 𝑃=4𝑥, где 𝑥 — длина одной стороны. Мы известно, что 𝑥=70 и, следовательно, 𝑃=4×70=280.
Поскольку длина дана в миллиметрах, мы показали, что периметр квадрат 280 мм.
Обратите внимание, что в вопросе нам предлагается вычислить длину в сантиметрах. Итак, последний шаг — преобразовать 280 мм в сантиметры. Напомним, что есть 10 мм в 1 см, значит, чтобы перевести 280 миллиметров в сантиметры, нужно разделить на десять.
Следовательно, периметр квадрата равен 28010=28 см
В приведенных выше примерах нас попросили найти периметр квадрата, зная его длину; связанный
задача состоит в том, чтобы работать в обратном направлении и найти длину стороны квадрата по его периметру.
Поскольку мы знаем, что 𝑃=4𝑥, мы можем изменить эту формулу, разделив обе стороны на 4, чтобы получить формулу для вычисления длины 𝑥 по периметру 𝑃.
Формула связи длины и периметра квадрата
Длина стороны 𝑥 квадрата с периметром 𝑃 может быть рассчитывается по следующей формуле: 𝑥=𝑃4.
Пример 3. Нахождение длины квадрата по его периметру
Вычислите длину стороны квадрата в метрах, периметр которого равен 24 м.
Ответ
Периметр 𝑃 квадрата равен 24 м, и нас попросили найдите длину стороны 𝑥.
Формулы, связывающие длину и периметр квадрата: 𝑃=4𝑥𝑥=𝑃4.и
Итак, мы вычисляем, что 𝑥=244=6.
Наконец, мы должны проверить, правильно ли мы используем единицы измерения для нашего ответа. Периметр был даны в метрах, и нас попросили найти длину в метрах, чтобы мы сделать вывод, что длина равна 6 м.
Пример 4. Нахождение длины квадрата по его периметру
Если провод длиной 96 см складывается квадрат, какой длины будет каждая сторона?
Ответ
Длина провода 96 см.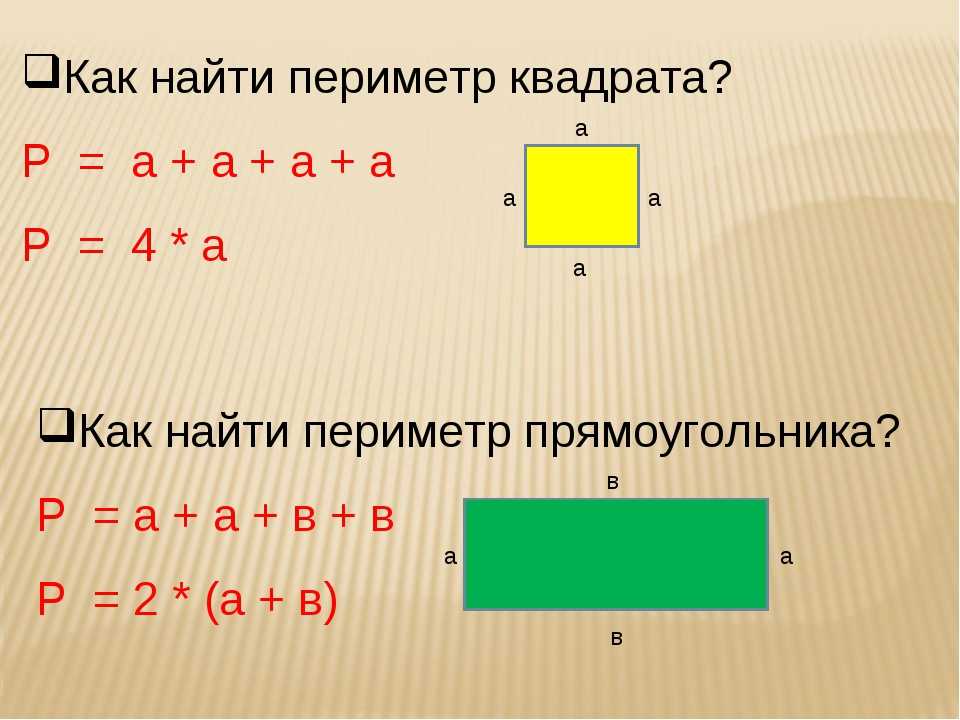
и это равно периметру созданного квадрата.
Поскольку 4 стороны квадрата имеют одинаковую длину, каждая сторона будет равна четверти длина провода.
Итак, чтобы найти длину стороны, мы вычисляем 964=24.
Наконец, мы должны включить правильные единицы в окончательный ответ. Так как провод был измеряется в сантиметрах, мы имеем показано, что длина каждой стороны 24 см.
Пример 5. Решение задач на периметр квадратов
Сумма периметров двух квадратов равна 108 мм. Если длина стороны одного из них 2 мм, найти длина стороны другого квадрата в миллиметрах.
Ответ
Может быть полезно сделать набросок того, что мы знаем, чтобы понять, как ответить на вопрос. Мы знай, что есть два квадрата; назовем их A и B.
Длина сторон одного из квадратов равна
2 мм; мы скажем, что это
Квадрат A. Итак, вопрос заключается в том, чтобы найти длину стороны квадрата B.
Мы будем
обозначим неизвестную длину стороны через 𝑥.
Последняя часть информации, которую нам дают, это сумма периметров, PerimeterofAPerimeterofBmm+=108, а мы знаем, что периметр квадрата в 4 раза больше длина стороны.
Давайте напишем формулу для 𝑥 с этой информацией.
Поскольку периметр квадрата А равен 8 мм и периметр Квадрат B равен 4𝑥, у нас есть следующее уравнение для суммы периметры: 8+4𝑥=108.
Мы можем решить это уравнение, чтобы найти 𝑥.
Сначала вычтите по 8 с обеих сторон: 4𝑥=100.
Теперь разделите обе части на 4, чтобы получить 𝑥=25.
Наконец, не забудьте указать в ответе правильные единицы измерения. Длина стороны квадрата В составляет 25 мм.
Наконец, мы будем использовать то, что мы знаем о периметре квадратов, для решения задач с более шаги.
Вот основные шаги, которые следует помнить при решении задач с длиной и периметром.
Практическое руководство. Решение вопросов, связанных с длиной и периметром квадратов
- Если известна длина стороны 𝑥, можно умножить на 4, чтобы получить периметр 𝑃.
- Если известен периметр, можно разделить его на 4, чтобы получить длину стороны.
- Не забывайте всегда включать единицы измерения длины в свой ответ и проверять, соответствует ли вопрос хочет, чтобы вы использовали одни и те же единицы измерения или конвертировали единицы измерения.
Могут ли квадрат и прямоугольник иметь одинаковую площадь и периметр?
Измерение — это раздел математики, который занимается вычислением таких параметров, как вес, объем, площадь, периметр и т. д. геометрических фигур. Измерение связано с 2D и 3D формами.
В 2D-фигурах объекты имеют два измерения и размещаются на плоской поверхности. Двухмерными будут только длина и ширина объекта. Это не имеет отношения к толщине объекта.
Трехмерные формы объектов имеют три измерения и присутствуют в реальном мире.
Три измерения: высота, ширина и глубина.
Формулы двумерных форм
Некоторые стандартные формулы для расчета параметров некоторых двумерных фигур приведены ниже:
- прямоугольник
Периметр = 2 (длина + ширина)
Область = Длина × Флэкста
- квадрат
квадрат . side)
- Circle
Diameter = 2 × radius
Area = πr 2
- Triangle
Area = 1/2 base × height
Формулы трехмерных форм
Ниже приведены некоторые стандартные формулы для расчета параметров некоторых трехмерных форм: = 4 (сторона) 2
Общая площадь поверхности = 6 (сторона) 2
- Кубоид
Объем = длина × width × hiew
.
Общая площадь поверхности = 2 (LB+LH+BH)
)- Сфера
Том = 4/3πr 3
Площадь поверхности = 4πr 2
.
Объем = 1/3πr 2 h
Общая площадь поверхности = πr(l+радиус)
Могут ли квадрат и прямоугольник иметь одинаковую площадь и периметр?
Вычисление площади квадрата и прямоугольника.
Согласно заданию нам нужно выяснить, равны ли площади двух геометрических фигур квадрата и прямоугольника или нет.
Предположим, есть квадрат со стороной l. И прямоугольник с длиной (l) и шириной (b).
Теперь,
Площадь квадрата = площадь прямоугольника
Используя стандартные формулы,
=>(сторона) 2 = длина × ширина
=>l 2 = l × b
25 l = b
Если b = 4, то l = 4
Расчет площади квадрата и прямоугольника
Площадь квадрата = (сторона) 2
0516 2 = l × l = 4 × 4 = 16
Площадь прямоугольника = l × b
= 4 × 4 = 16
Следовательно, площади квадрата и прямоугольника могут быть одинаковыми.
Таким же способом вычислим периметр квадрата и прямоугольника.
Вычисление периметра квадрата и прямоугольника
Предположим, что у квадрата длина стороны равна l. И прямоугольник с длиной (l) и шириной (b).
Теперь,
Периметр квадрата = периметру прямоугольника
=>4(сторона) = 2(длина+ширина)
=>4l = 2(l+b)
=>4l = 2l+2b
=>4l-2l = 2b
=>2l = 2B
=> L = B
Если L = 4 Then, B = 4
Расчет периметра квадрата = 4 (сторона)
= 4L = 4 × 4 = 16
Расчет периметра прямоугольника = 2 (2 (2 ( l+b)
= 2(4+4) = 2 × 8 = 16
Следовательно, квадрат и прямоугольник могут иметь одинаковую площадь и периметр при определенных условиях.
Примеры вопросов
Вопрос 1. Найдите площадь треугольника с основанием 9 см и высотой 5 см.
Решение:
Дано,
Основание треугольника(b) = 9см
Высота треугольника(h) = 5см 1/2 × (9 × 5)
=>45/2 см 2
Вопрос 2.
, данный,
Длина (L) = 8 см
Область (A) = 48 см 2
СЕЙЧАС,
Область = L × B
=> 48 = 8 × B
= L × B
=> 48 = 8 × B
= = L × B
=> 48 = 8 × B
= L × B
=> 48 = 8 × B 9000
= L × B
=> 48 = 8 × B 9000
= L × B
=> 48 = 8 × B 9000
>b = 48/8
=>b = 6 см
Вопрос 3. Найдите площадь квадрата, сторона которого равна 15 см.
Solution:
Given,
Side(l) = 15cm
Now,
Area = (side) 2
= l 2 = 15 × 15 = 225cm 2
Вопрос 4. Если прямоугольник имеет длину 10см и ширину 5см. Каков будет его периметр?
Решение:
Дано,
Длина (l) = 10 см
Ширина (b) = 5 см
Сейчас,
Периметр = 2(l+b)
=>P = 2(10+5)
=>P = 2 × 15
=>P = 30 см
Периметр и площадь – формулы для всех фигур
Для двумерной фигуры периметр относится к границе или пути вокруг фигуры.
Начнем!
1. Прямоугольник
(Изображение будет загружено в ближайшее время)
Прямоугольник — это фигура, у которой противоположные стороны равны, а все углы прямые (90 градусов).
Периметр прямоугольника = \[2 ( a + b )\]
Площадь прямоугольника = \[ a \times b \]
2. Квадрат
(Изображение будет загружено в ближайшее время)
655 Квадрат – это фигура, у которой все четыре стороны равны, а все углы равны 9.{2} \]
Примечание.
4. Треугольник
(Изображение будет загружено в ближайшее время)
Треугольник – это фигура с тремя углами и тремя прямыми линиями. Треугольники можно разделить на три вида, например:
Равносторонний треугольник
Периметр равностороннего треугольника = 3 a 9{2} \]
Равнобедренный треугольник
Периметр равнобедренного треугольника = 2s + b
Площадь равнобедренного треугольника = \[\frac{1}{2} \times\] b \[\ times\] hb
Разносторонний треугольник
Периметр разностороннего треугольника = a + b + c
Площадь разностороннего треугольника = \[\frac{1}{2} \times b \times h \ ]
5.
(Изображение скоро будет загружено)
Эта фигура представляет собой четырехугольник, противоположные стороны которого параллельны.
Периметр параллелограмма = \[2 ( a + b ) \]
Площадь параллелограмма = \[b \times h\]
Это параллелограмм, стороны которого равны.
Площадь ромба = \[a \times h \]
Периметр ромба = \[4 \times a \]
7. Трапеция
Эта фигура представляет собой четырехугольник, который имеет как минимум 1 пару параллельных сторон .
Периметр трапеции = \[a_1 + a_2 + b_1 + b_2 \]
Площадь трапеции = \[(\frac{( a1 + a2 )}{2}) \times h \]
8. Обычный N-Gon
(Изображение будет загружено в ближайшее время)
Правильным многоугольником называется многоугольник, у которого количество сторон и углов одинаковы.
Площадь правильного n-угольника = \[\frac{1}{2} \times ( a \times n \times s) \]
Периметр правильного n-угольника = \[n \times s \]
92\]
И периметр = \[2 ( l + b ) = 2 ( 10 + 12 ) = 44 м\]
Пример 2. Найдите периметр кругов, радиус которых (i) 14 см (ii) 10 м и (iii) 4 км.
Раствор.
по формуле \]
\[ 2 \pi r = 2 \times 3,14 \times 4 км = 25,12 км \]
9{2} \]
Этот материал в основном предназначен для учащихся, которые относятся к стандарту VII, поэтому здесь приведены только основные формулы. Существуют и другие методы определения периметра и площади специально для таких фигур, как ромб, треугольник и т. д., которые вы изучите в старших классах.
Если вы хотите обратиться к другим решенным примерам площади и периметра, загрузите приложение Vedantu сегодня.
Калькулятор площади прямоугольника
Авторы: Богна Шик и Ханна Памула, кандидат наук
Отзыв от Jack Bowater
Последнее обновление: 14 сентября 2022 г.
Содержание:
- Что такое прямоугольник?
- Как найти площадь прямоугольника?
- Формулы прямоугольника
- Вычисление прямоугольника: найти A (площадь)
- Вычисление прямоугольника: найти P (периметр)
- Вычисление прямоугольника: найти D (диагональ)
- Золотой прямоугольник
- Свойства прямоугольника
- формы. Является ли квадрат прямоугольником?
- Странный забавный факт: какая страна имеет самую прямоугольную форму в мире?
- Прямоугольники
- Прямоугольники в повседневной жизни: прямоугольная форма тела, прямоугольный бассейн, прямоугольная скатерть… прямоугольный бассейн или окно, эта площадь прямоугольного калькулятора решит вашу проблему в мгновение ока!
Все, что вам нужно сделать, это ввести длину и ширину (или диагональ) и позволить этому прямоугольнику вычислить значения P (периметр) и A (площадь).
Продолжайте читать, если вы хотите понять, что такое прямоугольник, вас интересует определение прямоугольника, формулы и свойства прямоугольника… Или вы просто хотите узнать, как найти площадь прямоугольника.
Что такое прямоугольник?
Прямоугольник — это четырехугольник с четырьмя прямыми углами . Мы можем также определить его по-другому: параллелограмм, содержащий прямой угол — если один угол прямой, другие должны быть такими же. При этом каждая сторона прямоугольника имеет ту же длину, что и противоположная ей сторона. Он также имеет неравные смежные стороны, в отличие от квадрата, частного случая прямоугольника.
Если вы немного знаете латынь, название фигуры обычно многое объясняет. Слово прямоугольник происходит от латинского rectangulus . Это комбинация rectus (что означает «правильный, прямой») и angulus (угол), так что это может служить простым базовым определением прямоугольника.
Прямоугольник является примером четырехугольника.
Как найти площадь прямоугольника?
На изображении выше показан типичный прямоугольник. У него четыре стороны и четыре прямых угла. Длины его сторон обозначаются a и b , а длина диагонали обозначается d .
Если все стороны прямоугольника имеют одинаковую длину, мы называем его квадратом .
Площадь прямоугольника — это пространство, ограниченное его сторонами или, другими словами, в пределах периметра прямоугольника. Чтобы найти площадь прямоугольника, достаточно умножить стороны прямоугольника на 9.1085 a и
b:
Площадь = a × bФормулы прямоугольника
В нашем калькуляторе прямоугольников реализованы следующие формулы:
Для площади прямоугольника :
A = a × bДля периметра прямоугольника :
P = 2 × (a + b)Для диагонали прямоугольника :
d² = a² + b²
d = √(a² + b²)Расчет прямоугольника: найти A (площадь)
Поскольку мы знаем формулу площади прямоугольника
A = a × b, покажем на примере, как можно вычислить это свойство:
- Выберите длину прямоугольник – например,
а = 5 см.- Определитесь с шириной прямоугольника – например,
b = 6 см.- Умножьте эти два значения:
A = 5 см × 6 см = 30 см².- Площадь прямоугольника 30 см².
Расчет прямоугольника: найти P (периметр)
Давайте узнаем, как найти периметр прямоугольника. Как обычно, периметр представляет собой сумму всех сторон фигуры:
P = a + b + a + b… что можно записать как:
P = 2 × (a + b )Возьмем для примера тот же прямоугольник:
- Выберите длину прямоугольника –
a = 5 смв нашем случае.- Определите ширину прямоугольника – например,
b = 6 см.- Сложите эти два значения:
a + b = 5 + 6 = 11 см.- Умножьте результат на 2:
P = 2 × 11 = 22 см.- Поехали! Периметр нашего прямоугольника равен 22 см.
Расчет прямоугольника: найти D (диагональ)
Диагональ прямоугольника — это отрезок, соединяющий две противоположные вершины прямоугольника.
- Выберите длину прямоугольника – например,
a = 5 см.- Определитесь с шириной прямоугольника – например,
b = 6 см.- Вычислить
aв степени двойки:a² = 25 см².- Вычислите
bв степени двойки:b² = 36 см².- Сложите эти два значения:
a² + b² = 25 + 36 = 61 см².- Наконец, извлеките квадратный корень из результата:
d = √(a² + b²) = √61 ~ 7,81 см.- Длина диагонали 7,81 см.
Естественно, вместо того, чтобы вычислять все эти значения вручную, вы можете использовать эту область калькулятора прямоугольника. Вы также можете использовать его в обратном порядке — например, для вычисления ширины прямоугольника с известными длиной и периметром.
Золотой прямоугольник
На рисунке выше показан особый тип прямоугольника, называемый золотым прямоугольником (узнайте с помощью нашего калькулятора золотого прямоугольника).
(a + b) / a = a / b = ϕгде φ — золотое сечение, равное 1,618. Узнайте больше об этом особом соотношении с помощью нашего калькулятора золотого сечения.
Как вы, вероятно, помните из калькулятора отношений, отношение — это отношение между двумя величинами, часто представленное в виде дроби.
Знаете ли вы, что золотой треугольник можно построить, используя только линейку и циркуль ? Это всего несколько шагов!
- Нарисуй квадрат.
- Проведите линию от середины одной стороны квадрата до противоположного угла. Наш калькулятор средней точки может помочь вам с этим шагом.
- Нарисуйте круг с радиусом, равным этой линии, с центром в средней точке, как показано на рисунке выше.
- Точка, в которой круг встречается с расширенной стороной квадрата, является следующим углом золотого прямоугольника.
- Найдите последнюю вершину и завершите золотой прямоугольник.
Таадааах! Это было не так сложно, не так ли?
Свойства прямоугольника
Прямоугольники обладают многими интересными свойствами:
- Цикличность – это означает, что все углы лежат на одной окружности.
- Равноугольный – все его углы равны 90 градусам.
- Прямолинейный – его стороны сходятся под прямым углом.
- Две линии отражательной симметрии – вертикальная и горизонтальная через центр.
- Две диагонали, делящие друг друга пополам . Длину диагонали можно найти по теореме Пифагора.
- Противоположные стороны прямоугольника параллельны друг другу и имеют одинаковую длину.
Другие менее известные прямоугольные свойства:
- Пересечение диагоналей — это центр описанной окружности — существует окружность с центром в этой точке, которая проходит через четыре угла.
- В прямоугольнике с разной длиной сторон (попросту говоря, не в квадрате) невозможно провести вписанную окружность.
- Прямые, соединяющие середины сторон прямоугольника, образуют ромб, площадь которого равна половине площади прямоугольника. Стороны фигуры параллельны диагоналям.
Можно придумать и свои собственные свойства, например, о вращении прямоугольника — по стороне или диагонали, чтобы получился цилиндр или конус соответственно.
Прямоугольник по сравнению с другими формами. Является ли квадрат прямоугольником?
TL;DR:
- Является ли квадрат прямоугольником? ДА .
- Является ли прямоугольник параллелограммом? ДА .
- Является ли прямоугольник ромбом? В целом – НЕТ. Только если это квадрат (все углы ромба 90 градусов).
- Является ли ромб прямоугольником? В целом – НЕТ. Только если это квадрат (все стороны прямоугольника равны по длине).
- Является ли прямоугольник четырехугольником? ДА , конечно.
- Является ли прямоугольник трапецией? ДА .
Хотите знать, является ли квадрат прямоугольником или прямоугольником является параллелограмм? Взгляните на рисунок ниже, и у вас больше не должно быть никаких сомнений относительно отношений между четырехугольниками:
Источник: WikimediaКак читать эту диаграмму? Начнем с нашего прямоугольника. Непосредственно к фигуре присоединены три фигуры: квадрат, параллелограмм и равнобедренная трапеция. Итак, если фигура находится выше интересующей нас формы, например, квадрата или прямоугольника, мы можем сказать, что:
- Каждый квадрат является прямоугольником и квадрат является частным случаем прямоугольника .
Для двух других фигур можно сказать аналогично:
- Каждый прямоугольник является параллелограммом и прямоугольник является частным случаем параллелограмма .
- Каждый прямоугольник является трапецией , а прямоугольник является частным случаем трапеции .
Странный забавный факт: какая страна имеет самую прямоугольную форму в мире?
Существует множество различных рейтингов, оценивающих страны по площади, населению, уровню образования или лауреатам Нобелевской премии.
А вы когда-нибудь задумывались, , кто победит в конкурсе на самую прямоугольную страну? Австралийский геостатистик Дэвид Бэрри рассчитал параметр прямоугольности для всех стран мира и составил рейтинг.
Он выяснил, что самой прямоугольной страной является Египет, тогда как титул «наименее прямоугольной страны в мире» достается Мальдивским островам (впрочем, автор допускает, что расчеты для стран, состоящих из множества мелких островов, могут быть ужасно неверными). Взгляните на таблицу ниже и проверьте первые десять стран, а также наименее прямоугольные.
Наивысшие баллы по рейтингу прямоугольности.
Ранг
Страна
Круглость
Изображение
1
Египет
0,955
2
Ватикан
0,948
3
Синт-Мартен
0,937
4
Лесото
0,936
5
Йемен
0,928
6
Гана
0,924
7
Македония
0,921
8
Кот-д’Ивуар
0,919
9
Польша
0,919
10
Науру
0,917
.
169
США
0,735
…
206
Тувалу
0,240
207
Маршалловы Острова
0,201
208
Мальдивы
0,018
Египет — лидер, но это не должно никого удивлять, проверяя форму этой страны на карте. США находится в середине рейтинга, в основном из-за неординарности Аляски и Гавайев. Смущает то, что 2-я самая прямоугольная страна – Ватикан – одновременно является 4-й страной по круглости, а Польша , 5-я в классификации округлости, является 9-й в рейтинге прямоугольности.
Как вообще возможно быть прямоугольным и круглым одновременно?! Как вы можете догадаться, все дело в определении прямоугольности и округлости, которое может быть неадекватным для сложных или разбросанных форм — и такими примерами обычно являются границы стран, содержащие острые края, маленькие острова или колонии где-то на другой стороне.
Если вам интересна эта тема, вы можете ознакомиться с этим объяснением и обсуждением результатов. Кроме того, в калькуляторе кругов вы найдете специальный параграф о круглости стран с аналогичной таблицей и примерами.
Можно подумать, что мир было бы легче рисовать, если бы каждая страна была прямоугольником… Или нет?
Шаблоны прямоугольников
Форма прямоугольника используется во многих периодических шаблонах мозаики. Его можно использовать для стен из кирпича, напольной плитки, тротуара или различной мозаики. Ниже вы найдете несколько популярных шаблонов:
- Укладка в стопку – самый распространенный и простой способ укладки плитки, так как плитка укладывается прямыми линиями.
- Текучая связка – типична для дорожных покрытий, плитки и кирпичной кладки.
- Елочка – с таким рисунком хорошо смотрятся деревянные полы.
- Корзиночная ткань – часто используется для коридоров или дорожек на улице.
Конечно, плитка бывает всех форм и размеров – довольно популярны шестиугольные и восьмиугольные с квадратами. Для пятиугольника форма должна быть неправильной, чтобы образовался мозаичный узор.
Прямоугольники в повседневной жизни: прямоугольное телосложение, прямоугольный бассейн, прямоугольная скатерть…
Телосложение типа — одна из самых популярных проблем, связанных с прямоугольниками. Все, что вам нужно сделать, это измерить свой бюст, талию, бедра и высоту бедер и ввести значения в инструмент. Тогда вы получите информацию о том, какая у вас форма тела.
Например, прямоугольная фигура определяется как «мальчишеский» тип телосложения — ваши бедра, талия и бюст примерно одного размера. Ваше тело имеет правильные пропорции и спортивный вид.
Удивительно, но нас окружают прямоугольные предметы. Вот почему наш калькулятор прямоугольников может быть полезен не только на уроках математики, но и в решении повседневных задач.
Прямоугольные скатерти – учитывая размер вашего стола, вы можете узнать, какая скатерть нужна или сколько кружева или подшивочной ленты вам нужно использовать.
Двери или оконное стекло – шторм или мяч для гольфа разбили ваше оконное стекло? Рассчитайте площадь и оцените стоимость ремонта, учитывая цену за кв.м или кв.м.
Экраны электронных устройств — планшетов, смартфонов, телевизоров — используйте этот калькулятор площади прямоугольника, чтобы оценить, сколько места на стене займет ваш экран — или насколько большой экран телефона, который вы хотите купить.
Доски, зеркала, рамы, холст, листы бумаги, блокноты, конверты, деньги, флажки, прямоугольные бассейны.
Посмотрите. Можете ли вы найти больше прямоугольных объектов вокруг вас? Что вы можете!
FAQ
Как найти периметр и площадь прямоугольника?
Чтобы найти периметр, нужно сложить все стороны прямоугольника:
P = a + b + a + bЧтобы найти площадь прямоугольника, нужно умножить меньшую и длинную стороны :
A = a × bКакова площадь прямоугольника размером 3 фута на 4 дюйма?
Это 144 квадратных дюйма ! Чтобы найти площадь этого прямоугольника, вам нужно:
- Преобразовать футов в дюймы. 3 фута равны 36 дюймам.
- Умножьте на ширину и длину прямоугольника. Площадь равна 4 умножить на 36.
- Проверьте свой результат в нашем калькуляторе площади прямоугольника!
Как определить, является ли фигура прямоугольником?
Фигура является прямоугольником, если:
- Она имеет два измерения – длину и ширину.
- У него четыре стороны, образующие четыре угла.
- Все углы прямые (90°).
- Противоположные стороны прямоугольника параллельны друг другу и имеют одинаковую длину.
Богна Шик и Ханна Памула, кандидаты наук
Длина (a)
Ширина (b)
Площадь (A)
Периметр (P)
Диагональ (d)0005
Посмотрите 21 похожий калькулятор 2D-геометрии 📏
ПлощадьПлощадь полумесяцаЦентр масс… Еще 18
Открыть учебники | Siyavula
Загрузите наши открытые учебники в различных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См. различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителей
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителей
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.
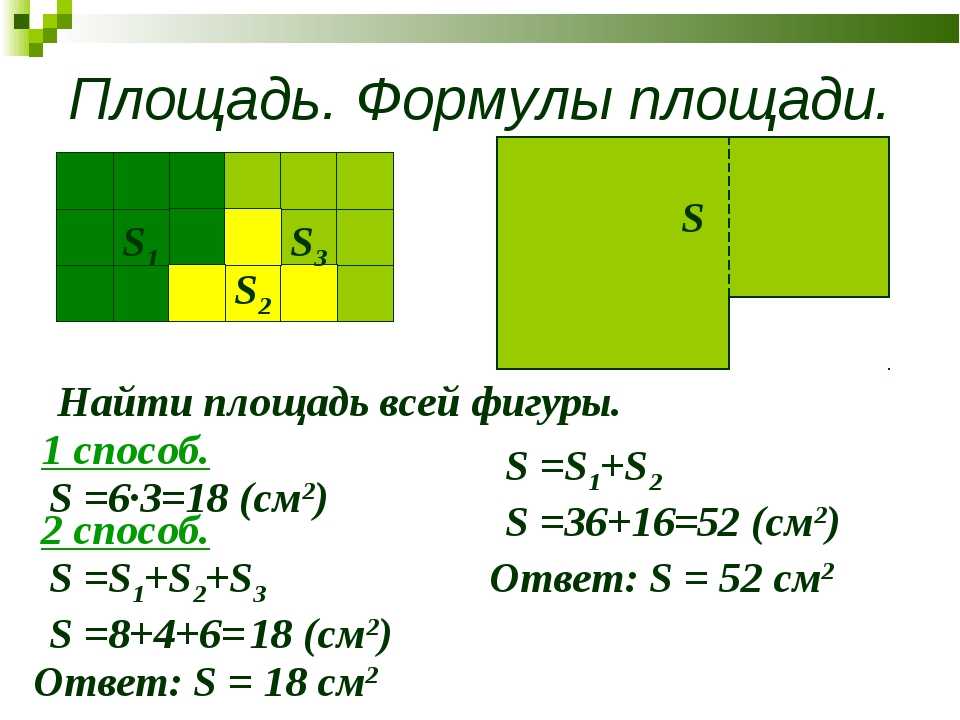
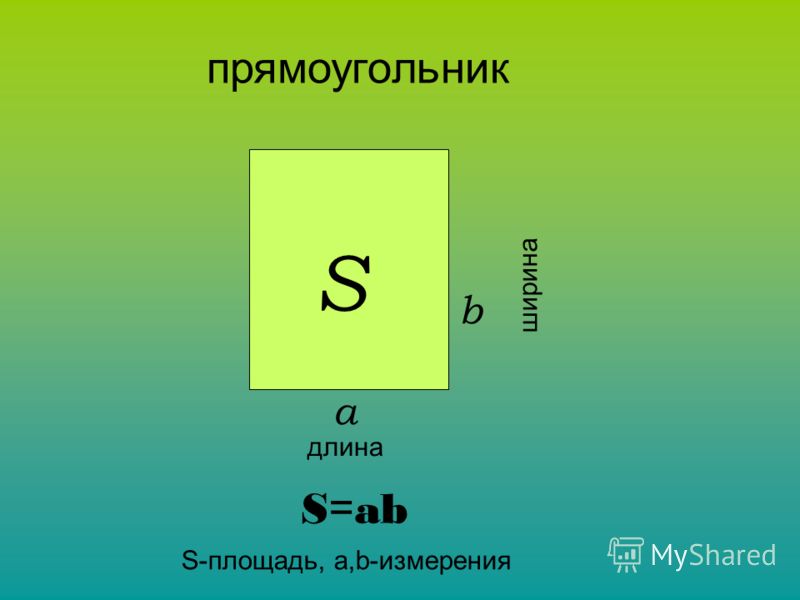Площадь прямоугольника 48см 2 . Если его длина 8 см, найдите его ширину. 
С другой стороны, площадь двумерной фигуры — это пространство, занимаемое на поверхности фигуры. Существуют различные типы фигур, но наиболее распространенными являются квадрат, прямоугольник, треугольник, круг и т. д. В этом содержании вы сможете узнать периметр и площадь основных фигур.
Здесь значение числа пи равно \[\frac{22}{7} \] или 3,14. Вы можете использовать любой из них, если он не указан в вопросе.
Параллелограмм
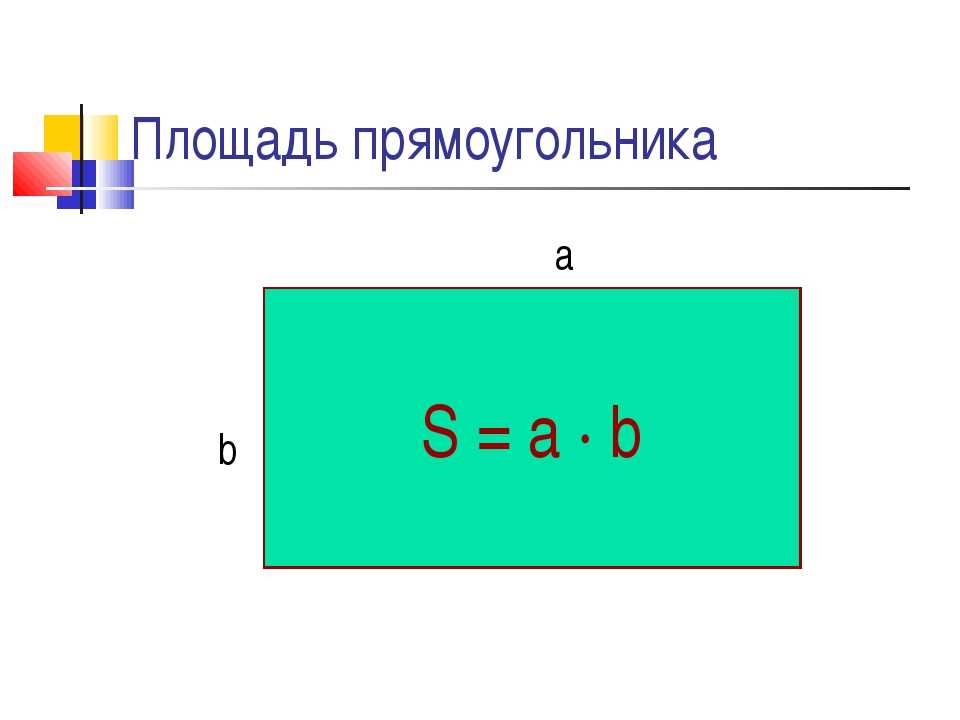Вы можете использовать наш четырехугольник калькулятор, чтобы найти площадь других типов четырехугольника.
Вычислим длину диагонали примерного прямоугольника:
Такой прямоугольник удовлетворяет следующему условию: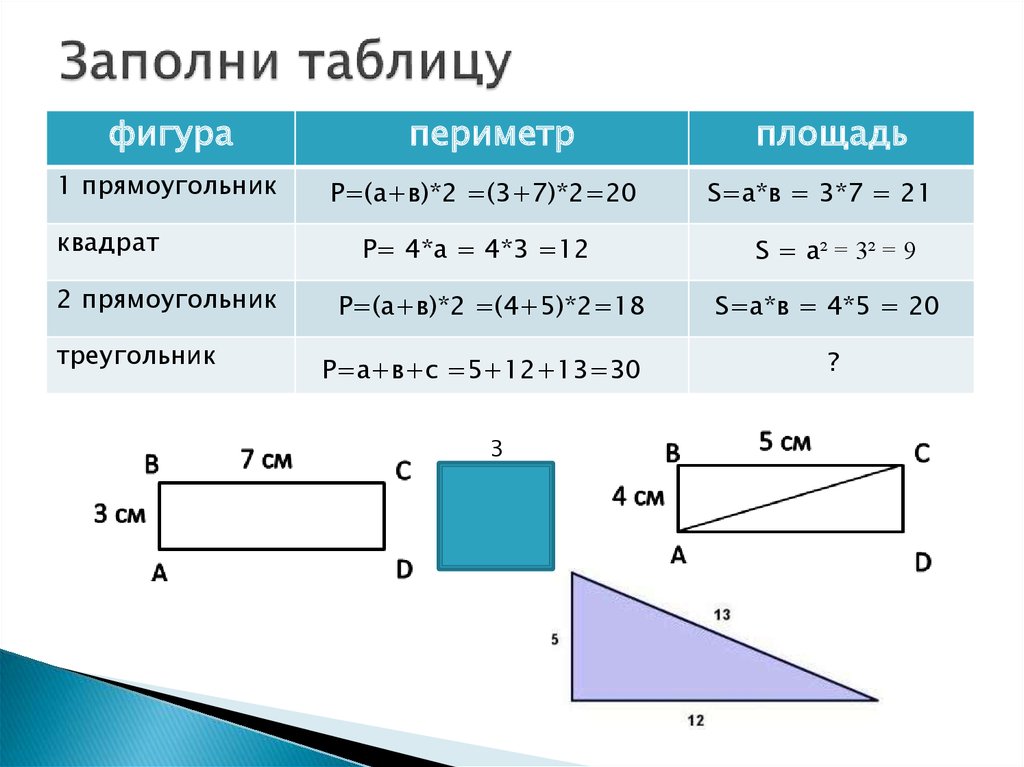
Индекс 1 — идеальный прямоугольник, 0 — бесконечное число бесконечно малых островков. Таблица адаптирована с веб-страницы г-на Барри как изображение мира ниже.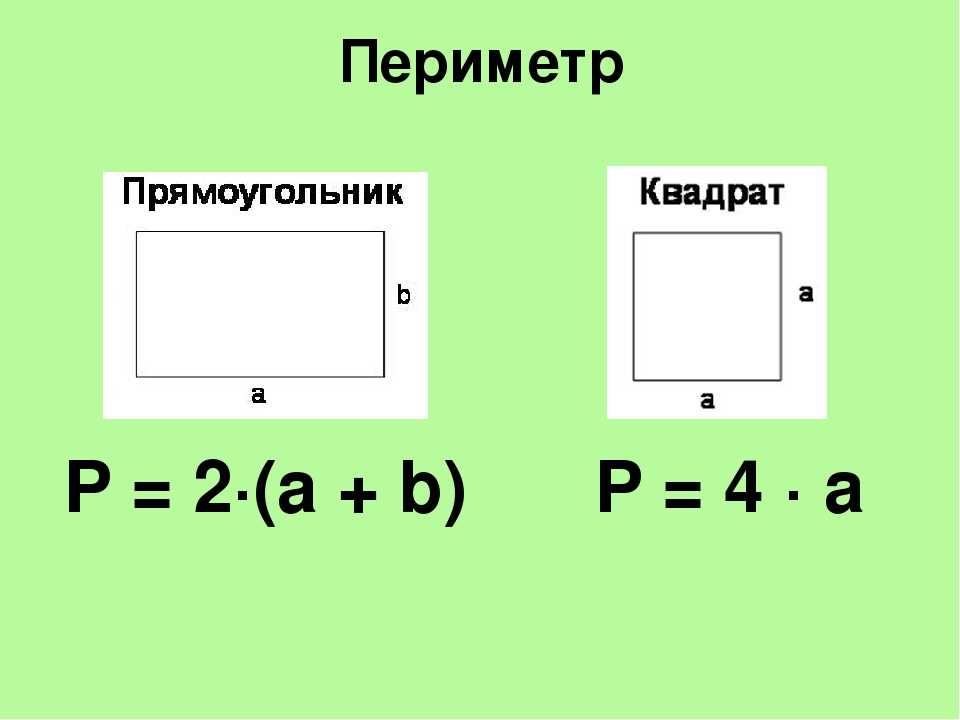
..
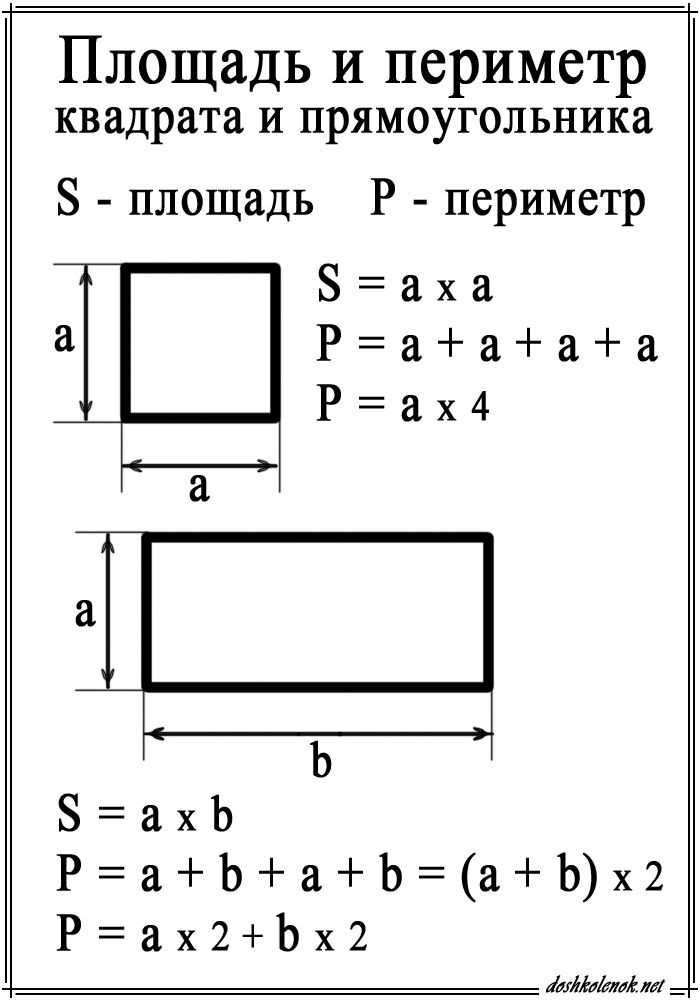земного шара.
Конечно, идеального прямоугольника в реальности не найти, так как он всегда имеет третье измерение; но если оно мало по сравнению с двумя другими измерениями, приближение достаточно хорошее.
.. Это бесконечный список!
