Площадь кольца формула: Формулы площади круга worksheet

2)}

Найти площадь кольца

через радиусы через диаметры

Внешний радиус R

ммсмдммкмдюймы (in)футы (ft)

Внутренний радиус r

ммсмдммкмдюймы (in)футы (ft)

Результат в

мм²см²дм²м²км²кв. дюймы (in²)кв. футы (ft²)

Виджет

Ссылка на расчет

Сообщить об ошибке

Сохранить расчет

Печатать

С помощью приведенных калькулятора и формул можно рассчитать площадь кольца через радиусы или диаметры онлайн.

Кольцо — плоская геометрическая фигура, ограниченная двумя концентрическими окружностями.

Содержание:

1. калькулятор площади кольца
2. формула площади кольца через радиусы
3. формула площади кольца через диаметры
4. примеры задач

Формула площади кольца через радиусы

{S = \pi (R^2 — r^2)}

R — внешний радиус кольца

r — внутренний радиус кольца

Формула площади кольца через диаметры

{S= \dfrac{\pi}{4}(D^2 — d^2)}

D — внешний диаметр кольца

d — внутренний диаметр кольца

Примеры задач на нахождение площади кольца

Задача 1

Найдите площадь кольца ограниченного двумя окружностями с общим центром и радиусами 3 см и 7 см. 2

Проверка .

Формула площади кольца

Кольцо, это геометрическая фигура, которая имеет внешний радиус R и внутренний радиус r с общим центром. В повседневной жизни с кольцами приходится встречаться не так уж и редко, поскольку они являются необходимыми элементами многих технических устройств, которыми пользуются практически все. Еще чаще с кольцами имеют дело инженеры и конструкторы, создающие всевозможные машины, узлы и агрегаты.

Расчет площади кольца

 

Найти площадь кольца можно по формуле:

 

S = π ( R2− r2)

 

R – радиус внешней окружности

r – радиус внутренней окружности

S – площадь кольца

π – 3.14

Форму колец имеют шайбы, являющимися элементами крепежа, которые устанавливаются между головками болтов или гаек и скрепляемых изделий для того, чтобы увеличить площадь прилегания, а также для того, чтобы предотвратить самопроизвольное отвинчивание. Если требуется в том или ином случае рассчитать или подобрать для установки в изделие именно ту шайбу, которая необходима, конструкторам нужно, помимо всего прочего, найти площадь кольца. Эти детали чаще всего изготавливаются из стали, цветных металлов или пластмасс и могут иметь как плоскую, так и специальную поверхность. Во втором случае шайбы производятся из пружиненной стали, называемые гроверными шайбами которые служат для предотвращения ослабления резьбовых соединений при тряске и вибрациях.

Большое распространение в технике получили также и уплотнительные кольца. Они предназначаются для того, чтобы обеспечить герметизацию соединений в трубопроводах, по которым производится транспортировка газов или жидкостей, а также в пневматических и гидравлических агрегатах. Устанавливаются они в местах соединений различных деталей и благодаря своей эластичности очень плотно прилегают к поверхностям, между которыми располагаются. Наиболее распространенным материалом для изготовления уплотнительных колец является резина различных сортов и составов, а также некоторые специальные виды пластических масс.

Практически все современные двигатели внутреннего сгорания имеют в своей конструкции такие важные элементы, как поршневые кольца. Эти детали нужны для того, чтобы достичь необходимой степени компрессии в камере сгорания и располагаются между поршнями и стенками цилиндров. Поскольку при работе силовых агрегатов они испытывают постоянное трение, то со временем изнашиваются и требуют замены. Изготавливаются поршневые кольца чаще всего из высококачественного серого чугуна.

Еще одной разновидностью колец являются стопорные кольца. Они используются для фиксации различных механических деталей и почти всегда устанавливаются в специально проточенных для них канавках. Чаще всего стопорные кольца можно встретить на валах, однако нередко они располагаются и в корпусах деталей. В зависимости от местонахождения они подразделяются на те, которые предназначены для вала и те, которые монтируются в отверстиях, а что касается материала изготовления этих деталей, то им чаще всего является сталь.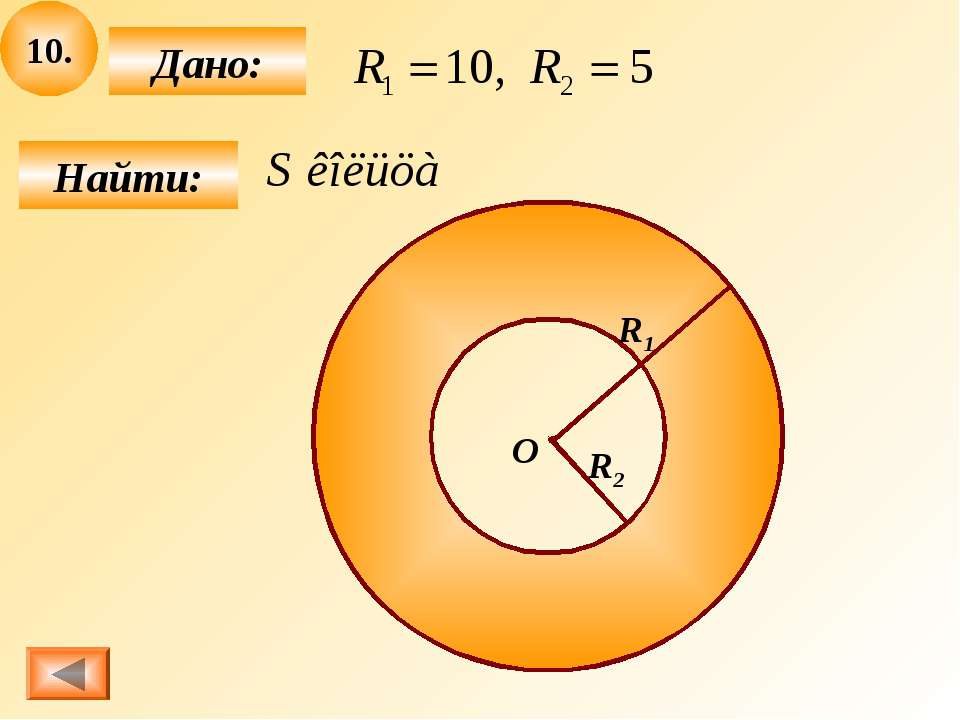 После установки на свое «законное» место стопорное кольцо обычно немного разжимается и своими торцевыми поверхностями препятствует смещению деталей друг относительно друга.

Калькулятор площади кругового кольца

1. Преобразователь Кайла >
2. Калькуляторы >
3. Геометрия >
4. Зона кругового кольца

Расчет площади кругового кольца:

Пожалуйста, поделитесь, если вы нашли этот инструмент полезным:

Формула площади кругового кольца

Область кругового кольца — это область между двумя концентрическими окружностями, эта область также известна как кольцо. Площадь между двумя концентрическими окружностями можно рассчитать, используя радиус внешней окружности, обозначаемый как R, R1 или r ₁ и радиус внутренней окружности, обычно обозначаемый r или r ₂ .

А = π(R1 ² — r2 ² )

Площадь кругового кольца или расчет кольца

Переменные площади кругового кольца

Площадь можно вычислить, зная радиусы двух концентрических окружностей.

Радиус 1 (R1)

Радиус большего внешнего круга. Радиус большего круга должен быть равен 1, чтобы формула работала.

Радиус 2 (r2)

Радиус меньшего внутреннего круга. Радиус меньшего круга нужно вычесть из радиуса большего круга, два радиуса не взаимозаменяемы в формуле.

Зона (А)

Область между двумя концентрическими окружностями, также известная как кольцо. В квадратных единицах.

Решение для круглого кольца

Как рассчитать площадь круглого кольца с внешним радиусом 3 и внутренним радиусом 2?

org/HowToStep»>
• А = π(R1 ² — r2 ² )
• Формула для расчета площади

• A = π(3 ² — 2 ² )
• Подставить значения радиусов

• A = π(9 — 4)
• Вычислить степени

• A = π(5)
• Вычитание в скобках

org/HowToStep»>
• A = 3,14159(5)
• Используйте значение 3,14159 для π

• A = 15,70795
• Окончательное умножение и результат

• 15,70795 квадратных единиц

Площадь между концентрическими окружностями радиусом 3 и радиусом 2 составляет 15,70795 квадратных единиц, используя приближение 3,14159 как π.

Пример области круглого кольца

Какова площадь кольцевого пространства между трубой радиусом 10,5 дюймов и трубой 6 дюймов? Предположим, что трубы не имеют толщины, или мы измеряем снаружи меньшей трубы внутрь большей трубы.

• А = π(R1 ² — r2 ² )
• А = π(10,5 ² — 6 ² )
• А = π(110,25 — 36)
• А = 3,14159(74,25)
• 233.2630575

Внешняя труба с радиусом 10,5 дюймов и внутренняя труба с радиусом 6 дюймов имеют кольцевое пространство около 233,26 квадратных дюймов.

Конвертер квадратных дюймов

Преобразование квадратных дюймов в другие единицы измерения

Кольцо – определение, формула и примеры

Кольцо представляет собой плоскую кольцеобразную структуру, состоящую из 2 кругов. Другой способ взглянуть на это — круглое кольцо с круглым отверстием в нем. Математически это площадь между двумя окружностями, имеющими общий центр (концентрические окружности), лежащими в одной плоскости. Кольцевое пространство выражается в квадратных единицах, таких как м ² , см ² , ² и ² футов .

Термин «аннулус» (множественное число — аннулы) происходит от латинского слова, означающего «маленькое кольцо». Некоторыми реальными примерами кольца являются пончик и кольцо на пальце.

Ниже показано кольцо, в котором меньший круг лежит внутри большего с буквой «О» в центре.

Кольцо

Площадь

Площадь кольца можно получить, найдя площадь внешнего круга и площадь внутреннего круга, а затем вычтя площадь внутреннего круга из внешней.

Формула для расчета площади кольца приведена ниже:

Площадь кольца

Вывод

Пусть,

Площадь внешнего круга = πR ² , здесь R = радиус внешней окружности

Площадь внутренней окружности = πr ² , здесь r = радиус внутренней окружности

∴ Площадь (A) кольца = πR ² – πr ²

= π(R ² – r ² )

Приведенное выше уравнение также можно записать в виде

Площадь ( A ) 5(R ) 4(R ) R-r)

Таким образом, площадь кольца определяется уравнением ( A ) = π(R ² – r ² ) или π(R+r)(R-r)

Давайте решим несколько примеров, чтобы лучше понять концепцию.

Найдите площадь кольца с внешним радиусом 16 см и внутренним радиусом 8 см?

Решение:

Как мы знаем,
Площадь (A) = π(R ² – r ² ), здесь π = 3,141, R = 16 см, r = 8 см 4 1 (= 16. ² – 8 ² )
= 3,141(256 – 64)
 = 3,141 × 192
 = 603,072 см ²

внешние круги. (Используйте π = 3,141)

Решение:

Как мы знаем, внутренний радиус равен r, а внешний радиус равен R
Согласно задаче,
Ширина (w) = R – r, здесь w = 2 дюйма
=> 2 = R – r
=> R = 2 + r
Теперь,
Площадь (A) = π(R ² – r ² )
=> 883 = π(R + r)(R – r)
 => 883 = 3,141(2 + r + r)(2)
 => 2 +2r = 883/3,141 × 2
 => 2 +2r = 883/6,282
 => 2 +2r = 140,56
=> 2r =140,56 – 2
=> 2r = 2r = 138,56
=> 8 дюймы
Таким образом, радиус (r) внутренней окружности равен 69,28 дюйма
Теперь радиус (R) внешней окружности = (2 + 69,28) дюйма
 = 71,28 дюйма

Периметр

Периметр кольца равен общее расстояние, пройденное вокруг границы внешнего и внутреннего круга.