Площадь конуса формула через высоту: Формула площади конуса по радиусу и высоте, расчет в см2, м2

Содержание

Как найти площадь поверхности прямого кругового конуса: боковую, основания, полную

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение площади поверхности конуса: формула и задачи

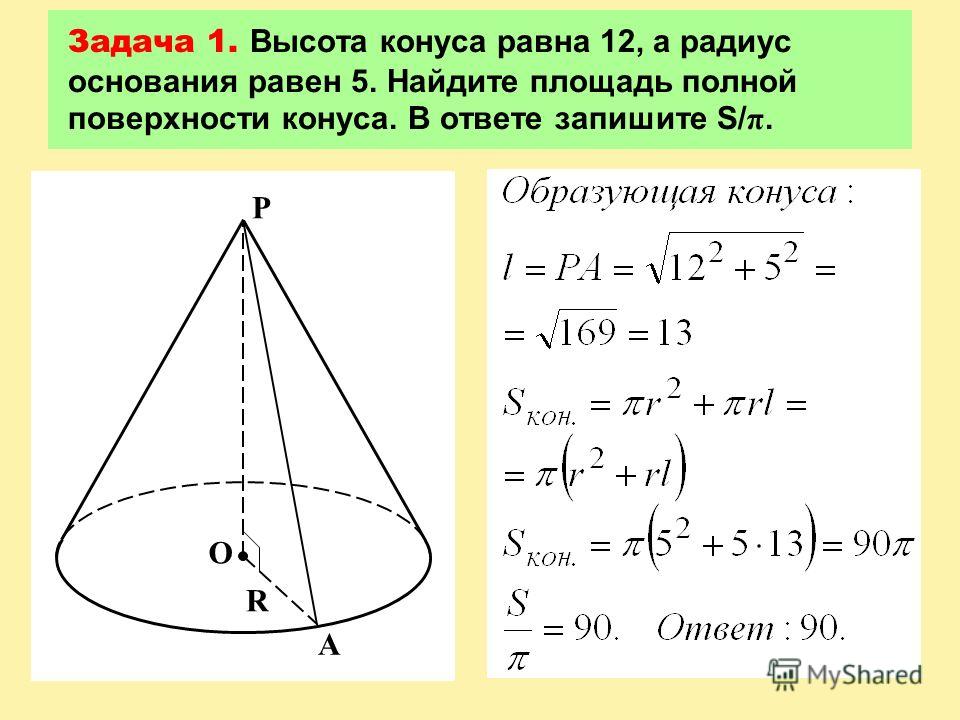
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности прямого кругового конуса (боковую, полную и основания), а также разберем примеры решения задач для закрепления материала.

Формула вычисления площади конуса
- 1. Боковая поверхность
- 2. Основание
- 3. Полная площадь
Примеры задач

Формула вычисления площади конуса

1. Боковая поверхность

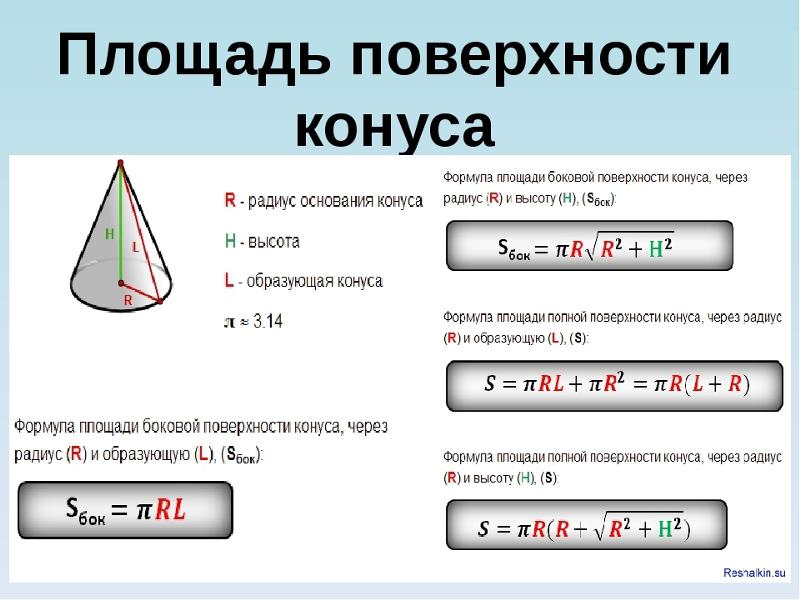
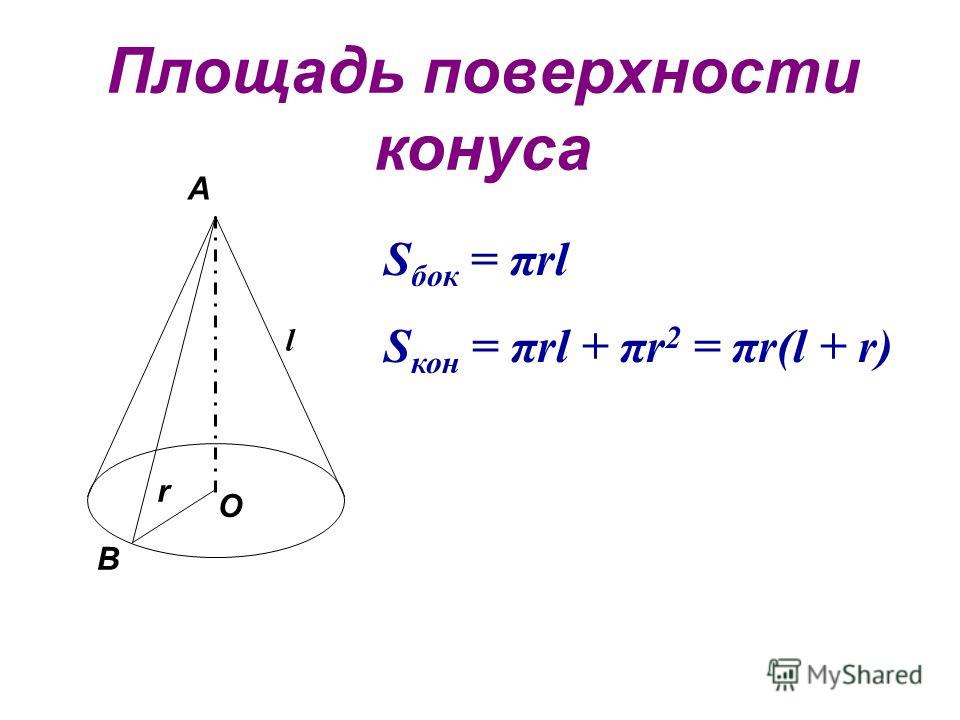
Площадь (S) боковой поверхности конуса равняется произведению числа π на радиус основания и на длину образующей.

S_бок. = πRl

Образующая (l) соединяет вершину конуса и границу основания, другими словами, точку на окружности.

Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание

Основанием конуса является круг, площадь которого вычисляется так:

S_осн. = πR²

Учитывая то, что диаметр круга равняется двум его радиусам (d = 2R), данную формулу можно представить в виде:

S_осн. = π(d/2)²

3. Полная площадь

Для вычисления суммарной площади конуса следует сложить площади боковой поверхности и основания:

S_полн. = πRl + πR² = πR(l + R)

Примеры задач

Задание 1
Вычислите площадь боковой поверхности конуса, если известно, что его радиус равен 16 см, а длина образующей – 5 см.

Решение:
Используем соответствующую формулу с известными нам величинами:
S = 3,14 ⋅ 16 см ⋅ 5 см = 251,2 см².

Задание 2
Высота конуса равна 4 см, а его радиус – 3 см. Найдите суммарную площадь поверхности фигуры.

Решение:
Если рассмотреть конус в сечении, то можно заметить, что его высота, радиус и образующая представляют собой прямоугольный треугольник. Следовательно, воспользовавшись теоремой Пифагора, можно найти длину образующей (является гипотенузой):
l² = (4 см)² + (3 см)² = 25 см².
l = 5 см.

Осталось только использовать найденное и известные по условиям задачи значения, чтобы рассчитать площадь:
S = 3,14 ⋅ 3 см ⋅ (5 см + 3 см) = 75,36 см².

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Площадь поверхности конуса — формулы, пример расчета

Пусть α– плоскость, точка S– точка, не лежащая в этой плоскости. Возьмем на плоскости произвольный круг с радиусом R. Соединим произвольную точку A этого круга с точкой S отрезком AS. Если точка А будет описывать круг с радиусом R, то отрезки AS будут заполнять некоторое тело. Это тело называют

круговым конусом.

Границей конуса является круг радиуса R и боковая поверхность конуса.
Боковую поверхность описывает отрезок AS , когда точка A описывает круг.
Точка S является вершиной конуса. Множество отрезков AS, соединяющих вершину с окружностью основания являются направляющими конуса.Если перпендикуляр, опущенный из точки S, совпадает с центром основания, то конус называется прямым.Очень часто говорят, что прямой конус образуется в результате вращения прямоугольного треугольника вокруг оси, содержащий его катет.
На данном рисунке прямой конус получился в результате вращения прямоугольного треугольника AOS вокруг катета SO. Тогда говорят, что

Катет SO –это высота конуса;
Гипотенуза AS –образующая конуса;
Катет AO – радиус конуса.

Площадь боковой поверхности конуса через его радиус и направляющую

Пусть дан конус с радиусом R и образующей L
AS=L, AO=R

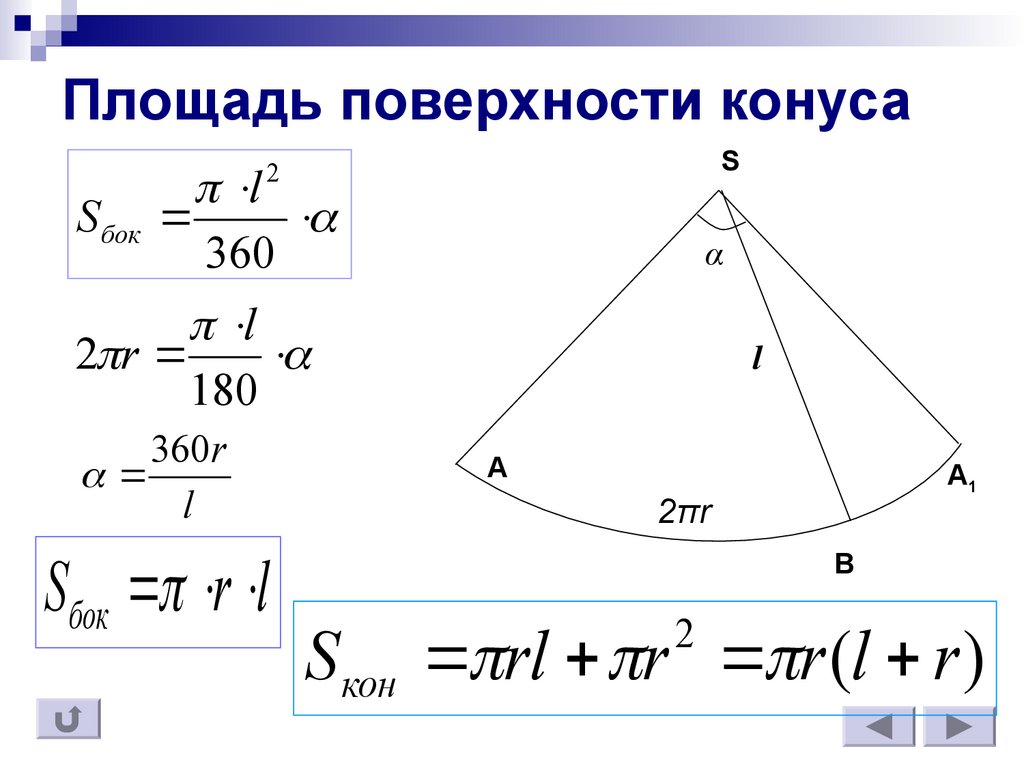
Разрежем конус по образующей L и развернем его боковую поверхность.
В результате получим криволинейный треугольник ASA` , где AS=L, A`S=L.
Дуга AA` -это вытянутая окружность основания конуса с радиусом R. Следовательно, длина дуги AA` будет равна 2πR
Площадь боковой поверхности будет равна площади сектора круга с радиусом R.
Если угол α – радиальная мера угла, то:
где α=∠{ASA`}
Чтобы найти угол ∠{ASA`} воспользуемся формулой длины дуги, которая стягивает данный угол:
Но с другой стороны:
Приравняем правые части равенств. Имеем:
Выразим α:
Подставим полученное выражение в формулу площади сектора:
Следовательно, боковая поверхность конуса равна произведению числа π на радиус конуса и его образующую.
Формула боковой поверхности конуса будет иметь следующий вид:

Пример расчета площади боковой поверхности конуса, если известны его радиус и направляющая
Найти площадь боковой поверхности конуса с радиусом равным 3 см, образованным направляющей равной 7 см
По условию задачи L = 5см, R=3см
Формула боковой поверхности конуса:

Подставив в формулу значения из условия задачи, имеем:

Площадь боковой поверхности конуса через его радиус и высоту

Очень часто в задачах на вычисление площади боковой поверхности конуса известна высота конуса вместо его направляющей.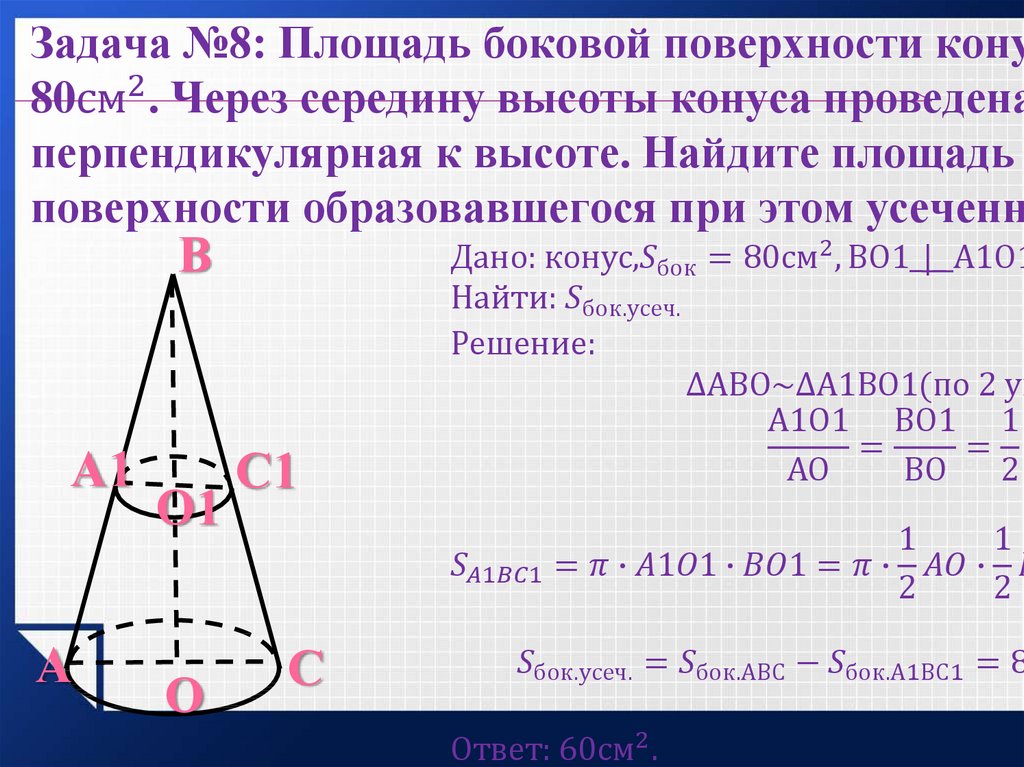
Так как конус прямой, то треугольник AOS – прямоугольный, где AO и OS – катеты, а AS –гипотенуза. Воспользовавшись теоремой Пифагора, получаем:
Отсюда:
Но
Тогда:
Подставим данное выражение в формулу площади боковой поверхности конуса:
Боковая поверхность конуса равна произведению числа на радиус конуса и корень квадратный из суммы квадратов радиуса и высоты конуса

Пример расчета площади боковой поверхности конуса, если известны его радиус и высота.
Найти площадь боковой поверхности конуса с радиусом равным 1 см и высотой, равной 5 см
По условию задачи Н = 5см, R=1см
Формула боковой поверхности конуса:

Подставив в формулу значения из условия задачи, имеем:

Полная поверхность конуса

Полная поверхность конуса – это сумма площади его боковой поверхности и площади основания конуса:

Основанием конуса является круг с радиусом R. Его площадь равна произведению числа π на квадрат его радиуса:
Площадь боковой поверхности вычисляется по формуле: или
Тогда площадь полной поверхности конуса равна:
или
Таким образом, площадь полной поверхности конуса равна произведению числа {pi} на радиус конуса и сумму направляющей и радиуса.
Формула имеет следующий вид:
Площадь полной поверхности конуса равна произведению числа π на радиус конуса и сумму корня квадратного из суммы квадратов радиуса и высоты конуса и радиуса конуса.
Формула имеет следующий вид:

Объем и площадь поверхности правильного круглого конуса (видео и практика)

Привет, ребята! Добро пожаловать в сегодняшнее видео, где мы поговорим об объеме и площади поверхности конуса. Мы знаем, что конус на самом деле очень похож на пирамиду. В то время как у пирамиды есть квадратное основание, которое соединяется с заостренным концом на противоположном конце, основание конуса вместо этого представляет собой круг.

Прежде чем углубляться в детали, давайте убедимся, что вы знакомы с понятиями объема и площади поверхности. Это две ключевые особенности, которыми обладают все \(3\)-мерные фигуры. Объем — это пространство внутри \(3D\) объекта, а площадь поверхности — это просто так! Это общая площадь поверхности фигуры. Думайте об объеме как о количестве жидкости, которой вы можете заполнить объект, а о площади поверхности — как о том, сколько бумаги вы можете обернуть вокруг этого объекта. Каждый куб, сфера, цилиндр, конус (разумеется) и т. д. имеют объем и площадь поверхности; и формулы, используемые для нахождения этих измерений, различны для каждой формы.

В случае конуса наша формула объема выглядит так: 9{2}+\pi rl\)

Где \(r\), \(h\) и \(l\) представляют разные измерения на конусе. Но какие измерения представляют эти буквы (или, как мы называем их в «математическом мире», переменных )?

\(r\) представляет собой радиус круглого основания конуса.

\(h\) обозначает высоту конуса. Точнее, это длина воображаемой линии, которая проходит от центра круглого основания до самого кончика конуса.

Наконец, \(l\) представляет наклонную высоту. Думайте об этом как о прямой линии, идущей от кончика конуса к краю его основания.

Итак, чтобы решить уравнения объема и площади поверхности, мы просто подставим размеры конуса в соответствующие переменные.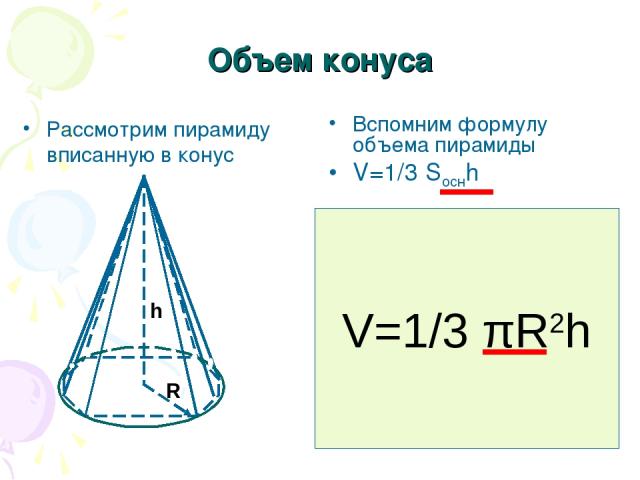 {2}+\pi rl\) 9{2}+\pi (3)(5)\)

Итак:

\(SA=\pi(9)+\pi (15)\)

Что равно \( 24\пи\). В конце концов, мы бы сказали, что площадь поверхности равна \(24\pi\) (или примерно \(75,4\)) квадратных единиц. Обратите внимание на то, как это измеряется! Поскольку мы говорим о площади, мы используем квадратные единицы.

Довольно просто подставить значения для \(r\), \(h\) и \(l\), верно? А что, если бы мы захотели выяснить, какого размера рожок мороженого нам понадобится, чтобы в него поместилось \(30\) кубических дюймов мягкой порции? 9{2}\)

Тогда все, что нам нужно сделать, это извлечь квадратный корень из обеих частей. Таким образом, когда мы это делаем, мы получаем:

\(r=\frac{3}{\sqrt{\pi }}\приблизительно 1,7\)

Фактически, поскольку линейные размеры конуса измеряются в дюймах, мы знаем, что \(r\) приблизительно равно \(1,7\text{дюймы}\).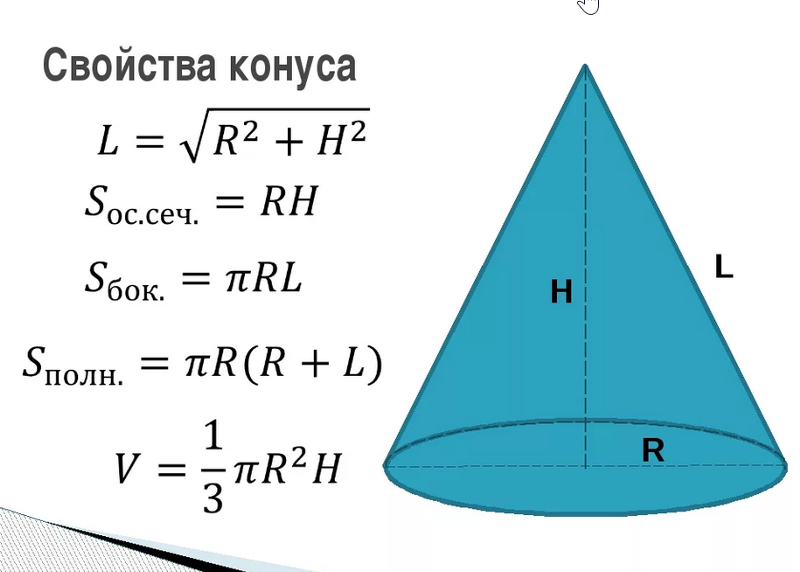

Ладно, круто! Так что, если мы хотим вычислить площадь поверхности того конуса, о котором мы только что говорили? Теперь мы знаем три важных параметра этого конуса: объем, высоту и радиус основания. Помните, что в нашем уравнении площади поверхности нам нужны как радиус, так и наклонная высота конуса, чтобы найти площадь поверхности. Хотите верьте, хотите нет, но мы можем рассчитать наклонную высоту, используя значение \(h\), которое нам дали, и значение \(r\), которое мы только что нашли. Нам просто нужно использовать теорему Пифагора. 9{2}ч\). Но помните, нам дан диаметр круглого основания, а не его радиус. Мы не могли просто подставить \(10\) вместо \(r\) в этом уравнении. Вместо этого мы используем то, что знаем о связи между диаметром и радиусом: радиус круга равен \(\frac{1}{2}\) его диаметра. Таким образом, радиус этого конуса на самом деле составляет \(5\) футов; и теперь найти объем довольно просто.

Итак, если мы подставим известные нам переменные, мы получим:

\(V=\frac{1}{3}\pi (5)^{2}(12)\) 92)}\), где \(r\) представляет радиус круглого основания, а \(h\) представляет высоту или высоту конуса.
Q
В чем разница между высотой и наклонной высотой?
A
«Высота» конуса и «наклонная высота» конуса — это не одно и то же. Высота конуса считается вертикальной высотой или высотой конуса. Это перпендикулярное расстояние от вершины конуса до центра круглого основания. наклонная высота конуса — это расстояние от вершины конуса вниз по стороне конуса до края круглого основания.
Q
Как найти вертикальную высоту конуса, зная радиус и наклонную высоту?
A
Вертикальная высота, радиус и наклонная высота конуса образуют три линии, образующие прямоугольный треугольник. Это означает, что теорему Пифагора можно использовать для определения пропущенного значения, если известны как минимум два значения. Например, можно рассчитать вертикальную высоту, если заданы радиус и наклонная высота. Если конус имеет радиус \(92\), что упрощается до \(r=3\).
Практические вопросы
Вопрос № 1:

Чему равен объем конуса высотой 14 дюймов и радиусом 6 дюймов с точностью до ближайшего целого числа?
535 в ³
582 в ³
528 в ³
498 в ^{3 903 34}
Показать Ответ
Ответ:
Правильный ответ: 528 в ³ . 2h\), и подставьте 6 вместо 9.3\)
Скрыть ответ
Вопрос №2:

Чему равен объем пи конуса высотой 12 см и радиусом 9 см?
324π см ³
346π см ³
445π см ³
389π см ³
Показать ответ
Ответ:
Правильный ответ: 324π см ³ . Начните с формулы объема конуса и подставьте 9 вместо 9.3\)
Скрыть Ответ
Вопрос №3:

Найдите объем конуса, имеющего радиус 6 метров и высоту 11 метров. Выразите ответ через число пи.
227π м ³
432π м ³
145π м ³
132π м ³
Показать ответ
Ответ:
Правильный ответ: 132π m ³ . Начните с формулы объема конуса и подставьте 6 вместо 9.3\)
Скрыть Ответ
Вопрос №4:

Найдите объем конуса, имеющего диаметр 18 м и высоту 30 м. Выразите ответ до ближайшего целого числа.
2 676 м ³
2 304 м ³
2 499 м ³
2 545 м 903 33 3
Показать ответ
Ответ:
Правильный ответ: 2545 м ³ . Если диаметр 18 метров, то диаметр 93\)
Скрыть ответ
Вопрос №5:

Найдите объем конуса, имеющего радиус 6 м и высоту 10 м. Выразите ответ до ближайшего целого числа.
488 ярдов ³
377 ярдов ³
366 ярдов ³
411 ярдов 903 33 3
Показать ответ
Ответ:
Правильный ответ: 377 ярдов ³ . Начните с формулы объема цилиндра и подставьте 6 вместо 9.3\)
Скрыть ответ
Формула высоты конуса — Что такое формула высоты конуса? Примеры
Конус представляет собой трехмерную форму, образованную набором отрезков или линий, которые соединяются в общей точке, называемой вершиной или вершиной, со всеми точками круглого основания (которое не содержит вершина). Мы также можем определить конус как пирамиду с круглым поперечным сечением, в отличие от пирамиды с треугольным поперечным сечением. Изучим формулу высоты конуса на решённых примерах в конце страницы.
Что такое формула высоты конуса?
Формула высоты конуса помогает вычислить расстояние от вершины конуса до основания конуса. Высоту конуса можно рассчитать, используя либо объем куба и радиус, либо наклонную высоту и радиус конуса.
Формула высоты конуса
Формула высоты конуса для конуса может быть выражена как
Формула 1: h = 3V/πr ²
где,
V = Объем конуса
r = радиус конуса
Эта формула получена из формулы объема конуса.
Формула 2: h = √l ² — r ²
где,
l = высота наклона конуса
r = радиус конуса
Эта формула получена с использованием теоремы Пифагора.
Рассмотрим применение формулы высоты конуса в следующем разделе.
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций с помощью Cuemath.

Записаться на бесплатный пробный урок
Примеры с использованием формулы высоты конуса
Пример 1: Шапочка на день рождения имеет коническую форму, объем 20 единиц ³, а радиус ее основания составляет 5 единиц. Какая высота шапки?
Решение:
Чтобы найти: Высота конуса.
Дано:
объем = 20 единиц ³
Радиус = 5 единиц
Используя формулу высоты конуса,
h = 3V/πr ²
= (3 × 20)/π × 5 ²
= (60)/(π × 25)
= 0,76 единицы

Ответ: Высота конуса 0,76 единицы
Пример 2: Что такое высота конуса с радиусом = 3 единицы и объем = 50 кубических единиц?
Решение:
Найти: Высота конуса.
Дано:
Объем = 50 кубических единиц
Радиус = 3 единицы
Используя формулу высоты конуса,
h = 3V/πr 50)/π × 3 ²
= (150)/(π × 9)
= 5,305 единицы
Ответ: Высота конуса равна 5,305 единицы.
Пример 3: Определить высоту конуса с радиусом = 5 единиц и наклонной высотой = 13 единиц?

Решение:
Найти: Высота конуса.
Дано:
Наклонная высота = 13 единиц
Радиус = 5 единиц
Используя формулу высоты конуса,
h = √l ² — r ²
= √(13) ² — ( 5) ²
= √169-25
= √144
= 12 единиц
Ответ: Высота конуса равна 12 единицам.
No related posts.