Площадь круга (окружности): онлайн калькулятор, формулы, примеры решений
Фигура {$ main.figures[data.figure] $}
Рассчитываем {$ main.types[data.type] $}
Радиусили диаметр
Стороныили диагонали
Введите 2 величины
Сторона A
Сторона B
Диагонали
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Сторона A
Сторона B
Сторона C
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Угол γ{$ main.angles[data.angle] $}
Введите 2 величины
Сторона A
Сторона B
Сторона C
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 2 величины
Сторона
Высота
Диагональ 1
Диагональ 2
Угол α{$ main.
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Сторона A
Сторона B
Высота ha
Высота hb
Диагональ 1
Диагональ 2
Угол α{$ main.angles[data.angle] $}
Угол β{$ main.angles[data.angle] $}
Введите 3 величины
Основание A
Основание C
Высота H
Дополните боковые стороны для поиска периметра
Сторона B
Сторона D
Введите 1 величину
Сторона A
Радиус описанной окружности (R)
Радиус вписанной окружности (r)
Количество сторон многоугольника
Введите 1 величину
Сторона A
Радиус описанной окружности (R)
Радиус вписанной окружности (r)
Введите 1 величину
Сторона A = радиусу описанной окружности (R)
Радиус вписанной окружности (r)
Результат расчёта
- Периметр: {$ result.
 p|number:4 $}
p|number:4 $} - Площать: {$ result.s|number:4 $}
Круг — это часть плоскости, ограниченная окружностью. В свою очередь окружность — замкнутая кривая, которая состоит из бесконечного количества равноудаленных от некоторого центра точек. Круг занимает важное место в жизни человека, и во многих ситуациях вам может понадобиться узнать площадь круга.
Геометрия круга
Круг — заданное множество точек плоскости, которые удалены от центра круга на расстояние, не превышающее его радиус. Окружность — внешняя граница круга, но в случае, если радиус окружности равен нулю, то фигура превращается в точку. Круг и прямая, как и циркуль с линейкой — самые важные инструменты для геометра, ведь при помощи них легко построить любое, даже самое сложное геометрическое тело. Круг всегда очаровывал людей, и с самой древности фигура считалась символом бесконечного космоса, пространства и времени. Математики шутят, что круг — это многоугольник с бесконечным количеством углов.
Круги чрезвычайно эффективны: такие фигуры охватывают максимальную площадь для заданного периметра, соответственно, имеют минимальный периметр при охвате определенной области. Благодаря этому свойству в природе существует множество круглых объектов, которые в трехмерном пространстве преобразуются в шары или сферы. К примеру, благодаря минимизации периметра образуются такие природные объекты, как капли воды, снежные комья или целые планеты.
Большое значение в геометрии круга имеет число Пи, которое отображает отношение длины окружности к диаметру круга. Это соотношение известно геометрам с древних времен: изначально люди полагали, что неизменное для любого круга значение равно примерно 3,1. Древние вавилоняне считали, что данное соотношение равняется 25/8, а Архимед пришел к выводу, что Пи можно выразить в виде дроби 22/7. Впрочем, в Древней Греции число Пи не имело названия. До работы Леонарда Эйлера число Пи называли лудольфовым числом.
Площадь круга
Площадь круга выражается одной из самых простых математических формул:
S = pi R2
Для подсчета площади вам необходимо узнать только радиус окружности или ее диаметр.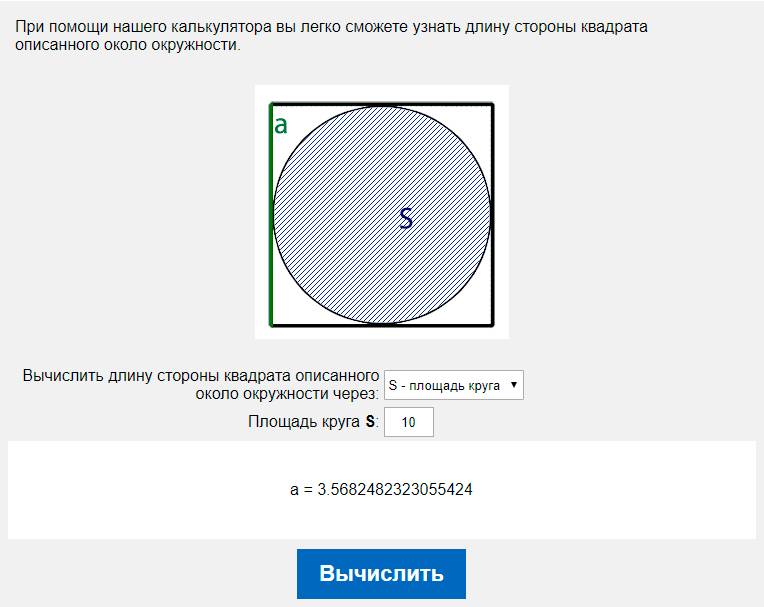 В последнем случае формула несколько изменится:
В последнем случае формула несколько изменится:
S = (pi/4) D2
Круг довольно часто встречается в реальной жизни. В инженерии машин и механизмов используются детали, сечения которых — круг. К примеру, в технике распространены такие цилиндрические детали, как валы, цилиндры, конденсаторы, поршни, оси и тому подобное. Круги также можно встретить в строительстве, производстве мебели, микропроцессорной технике или архитектуре, поэтому инженеры используют в своих расчетах простые формулы для определения площади круга. Рассмотрим пару абстрактных примеров.
Примеры из реальной жизни
DVD-диск
Сегодня DVD-диски утратили звание самого популярного носителя информации, но это не мешает нам измерить площадь болванки. Стандартный диск имеет отверстие диаметром 15 мм, а сама болванка имеет диаметр 120 мм. Таким образом, площадь диска Sd составит:
Sd = Sb – So,
где So – площадь пустого отверстия.
Введем данные в форму онлайн-калькулятора и получим такие результаты:
Sb = 376,9 и So = 47,12
Выполняем несложный расчет и получаем:
Sd = 376,9 — 47,12 = 328,79
Таким образом, площадь стандартного DVD-диска составляет 328,79 квадратных миллиметров.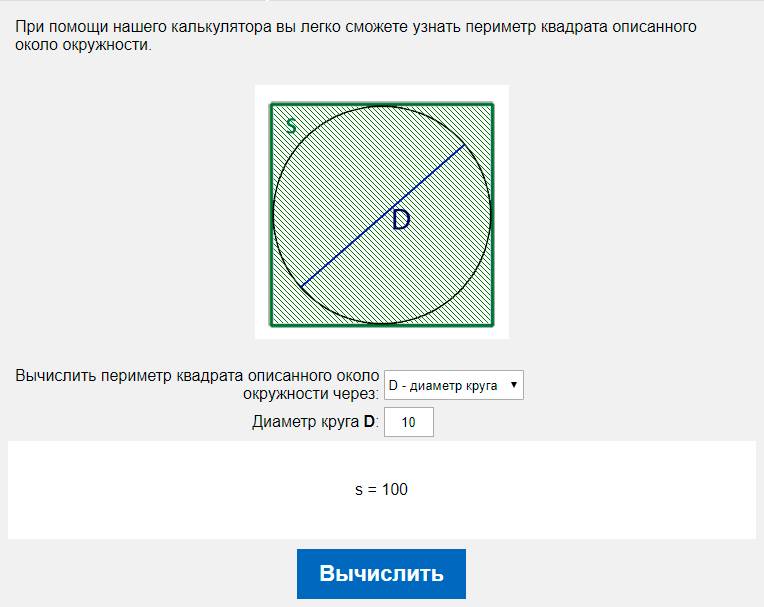
Основание конуса
Все мы знаем, что в основании объемного конуса лежит круг. Коническую форму имеют многие реальные объекты, к примеру, обычный дорожный конус. Если вы хотите узнать площадь основания такой фигуры, то вам достаточно замерить радиус конуса и ввести эти данные в форму калькулятора. Допустим, радиус выбранной фигуры составляет 15 см. Тогда площадь круга, лежащего в основании, будет равна:
S =94,24
Это означает, что площадь основания дорожного конуса составляет 94,24 квадратных сантиметров.
Заключение
Круг — фигура на плоскости, поэтому в реальной жизни круги встречаются как составные части объемных объектов, к примеру, основания цилиндрических или конических деталей, а также «плоские» объекты, как медали, диски или блинчики. Если вам необходимо подсчитать площадь круга, зная его радиус или диаметр, воспользуйтесь нашим онлайн-калькулятором, который быстро и точно предоставит вам результат.
Калькулятор площади круга
Калькулятор площади кругаДанный онлайн-калькулятор поможет рассчитать площадь круга по диаметру, через радиус или длину окружности, даже если известно только что-то одно. Формула даёт расчёт в квадратных метрах (м
Формула даёт расчёт в квадратных метрах (м
ДиаметрРадиусДлина окружности
ДлинаРазмерность
СантиметрыМетрыМиллиметрыКилометры
РаcсчитатьСкопировать:
ссылку link
код code
Формула (формулы) площади круга
Найти площадь круга можно разными способами, в зависимости от известных данных.
По радиусу
Если дан только радиус, то площадь составит произведение константы Пи на квадрат радиуса. Расчёт будет по формуле (где r – радиус, а π – константа, равная 3,1415…):
Например, если радиус равен 2 метра, то площадь круг можно вычислить так S = 3,14 × 22 = 3,14 × 4 = 12,56 м2 (квадратных метров).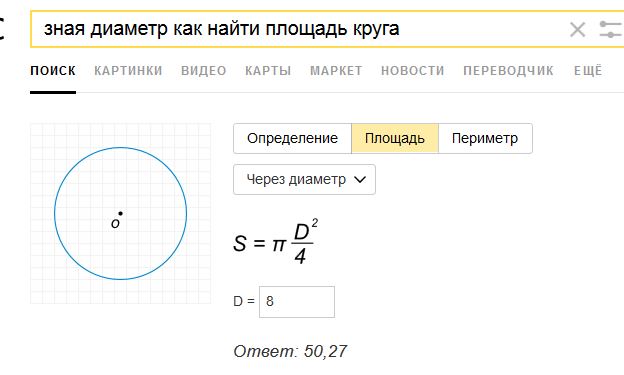
Через диаметр
Если известен диаметр, то площадь круга будет равняться одной четвёртой произведения Пи и квадрата диаметра. Формула площади круга будет такой (где d — диаметр, а π – константа, равная 3,1415…):
К примеру, если диаметр круга (площадь поверхности пиццы) составляет 35 сантиметров, то площадь такого круга будет равна S = ¼ × 3,14 × 352 = ¼ × 3,14 × 1225 = 962 см2 (квадратных сантиметра).
Через длину окружности
Если мы знаем только длину окружности (периметр круга), то рассчитать площадь фигуры можно по формуле (где L — длина окружности, а π – константа, равная 3,1415…):
Например, если длинна окружности составляет 120 мм, тогда площадь круга будет равна S = 1202 / (4 × 3,14) = 14 400 / (4 × 3,14) = 1146,5 мм2 (квадратных миллиметров).
Какие термины используются для поиска площади круга?
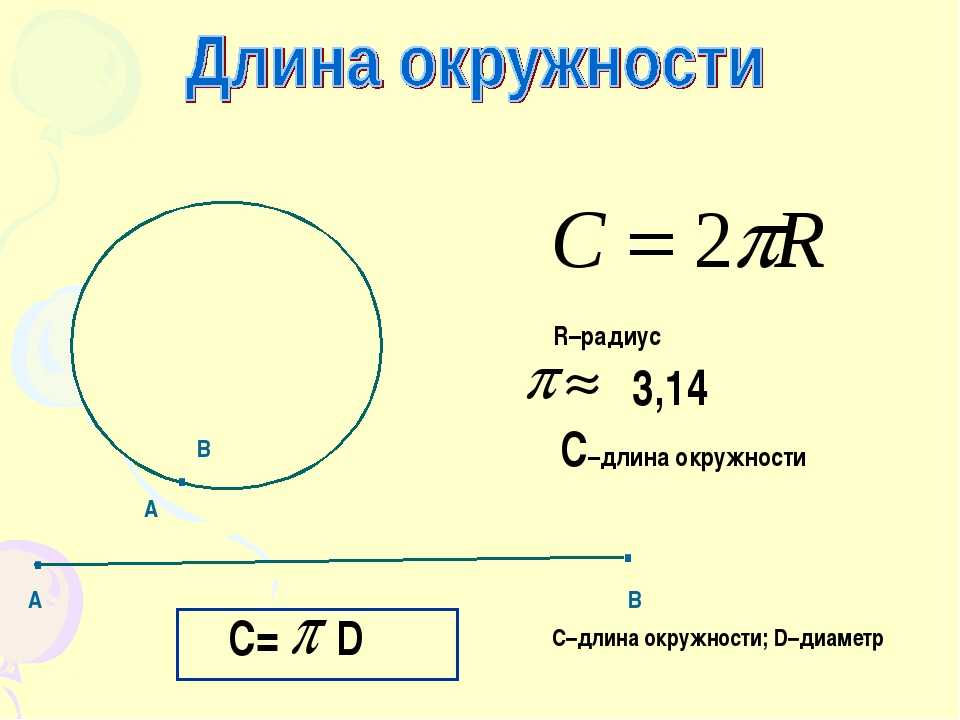
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра.
Круг — множество точек на плоскости, которые удалены от центра на расстоянии, не превышающем радиус.
Диаметр — отрезок, соединяющий две точки на окружности и проходящий через центр окружности. Диаметр равен двум радиусам.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Число π (пи) — математическая постоянная, равная отношению длины окружности к её диаметру. Пи равняется примерно 3,14.
Площадь круга и размеры пицц
Люди не всегда верно сопоставляют площадь круга и диаметры. К примеру, сможете ли вы ответить:
Что больше: 2 пиццы диаметром 25 см или 1 пицца диаметром 40 см?
Интуитивно кажется, что 2 пиццы, так как в сумме их радиусы дают 50 сантиметров, что больше, чем 40. Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
Однако это неправильный вывод, так как сравнивать нужно не сумму диаметров, а сумму квадратов диаметров. То есть:
- 252 + 252 = 625 + 625 = 1250
- 402 = 1600
Так как ¼π является константой, то можно сравнивать только квадраты диаметров. Получается, что пицца 40 см больше, чем даже 2 пиццы размером 25 см. А вот если диаметр пиццы составляет 35 см, то 352 = 1225, и в этом случае 2 пиццы по 25 см будут иметь бОльшую площадь.
Площади усеченных частей круга
А также полезно знать следующие геометрические элементы, связанные с кругами и окружностями:
Хорда — отрезок, соединяющий любые две точки окружности.
Сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Сектор является частью круга, а его площадь относится к площади круга так же, как и длина окружности сектора к длине всей окружности. Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Поэтому площадь сектора равна площади круга, умноженной на отношение длинны окружности сектора к длине окружности всего круга.
Но площадь сектора можно вычислить и по более простой формуле. Она равна длине дуги сектора, умноженной на половину радиуса:
S = sr/2
где S — площадь сектора, r — радиус круга.
Сегмент — это часть круга, ограниченная дугой и стягивающей её хордой.
Площадь сегмента можно найти по формулам:
S = r2sinα/ 2
где S — площадь сегмента, sinα — синус угла двух между радиусов до концов хорды, r — радиус круга.
Часто задаваемые вопросы о площади круга?
И конечно, стоит ответить на некоторые вопросы, которые возникают во время расчетов.
Входит ли окружность (периметр) в площадь круга?
Да, входит, ведь кругом являются все точки, удаленные от центра круга на расстояние, которое не превышает радиус.
Какие есть ещё калькуляторы для круга у вас на сайте?
У нас есть разнообразные калькуляторы, в частности калькуляторы: длины окружности, диаметра и площади круга. Для последней калькулятор находится на данной странице.
Хватит ли только диаметра, только радиуса или только длинны окружности для расчета площади круга?
Да, хватит чего-то одного, так как все 3 сущности можно вывести одну из другой, например, диаметр равен двум радиусам, а длина окружности – это диаметр, умноженный на число Пи.
Почему Пи равняется 3,1415926…, а не является «ровным» числом?
Число Пи – это отношение длины окружности к диаметру. После его вычисления математики выяснили, что оно является иррациональным числом: то есть его значение не может быть точно выражено в виде дроби m/n, где m — целое число, а n — натуральное. Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Следовательно, его десятичное представление никогда не заканчивается и не является периодическим. На июнь 2022 года известны первые 100 триллионов знаков числа «пи» после запятой. И получается, что именно с такой точностью можно рассчитать площадь круга. Если у квадрата и треугольника площадь точная, то у круга всегда приблизительная.
Кто впервые научился вычислять площадь круга?
Гиппократ Хиосский (не тот, в честь которого назвали клятву) первым сформулировал, что площадь круга пропорциональна квадрату его диаметра. Евдокс Книдский в IV веке до н. э. строго доказал это утверждение. А Архимед в III веке до н. э. нашёл число Пи и продемонстрировал, что оно чуть меньше, чем 3 и 1/7.
Есть что добавить?
Поделитесь комментарием или этой страницей в соцсетях.
Площадь круга | Онлайн калькулятор
Расчет площади круга — это не только учебная задача для школьников шестого класса.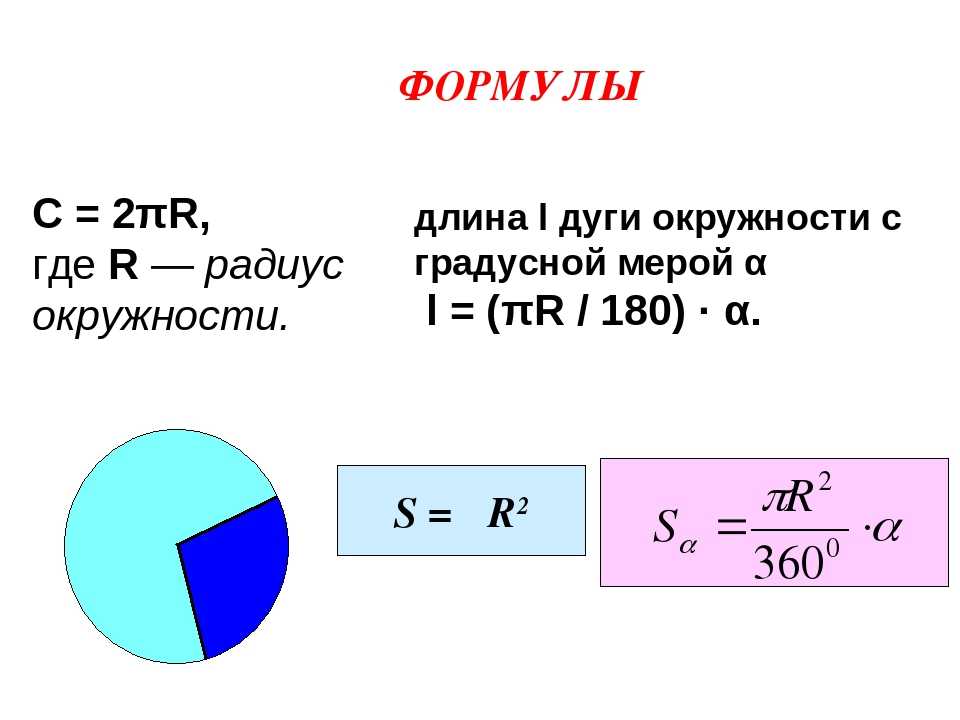 Круглых предметов довольно много и в реальной жизни, а необходимость посчитать их площадь хотя и не так часто, но возникает. Например, это может потребоваться для определения количества краски для ремонта круглой столешницы или для расчета площади остекления дома, спроектированного и построенного в готическом стиле.
Круглых предметов довольно много и в реальной жизни, а необходимость посчитать их площадь хотя и не так часто, но возникает. Например, это может потребоваться для определения количества краски для ремонта круглой столешницы или для расчета площади остекления дома, спроектированного и построенного в готическом стиле.
Сложность вычисления площади круга связана с тем, что практически во всех формулах встречается иррациональное число пи, которое в обычных расчетах принимается равным 3,14. Даже если вы с детства неплохо владеете устным счетом, вычислить в уме площадь круга, радиус которого выражается дробным числом, будет довольно затруднительно. Но теперь это и не нужно, поскольку мы разработали для вас удобный сервис, который сделает все расчеты за несколько мгновений. Причем необязательно пересчитывать известные вам размеры конструкции так, чтобы получить значение радиуса в явном виде. Наш калькулятор умеет считать площадь круга практически по всем параметрам, которые могут быть известны на практике.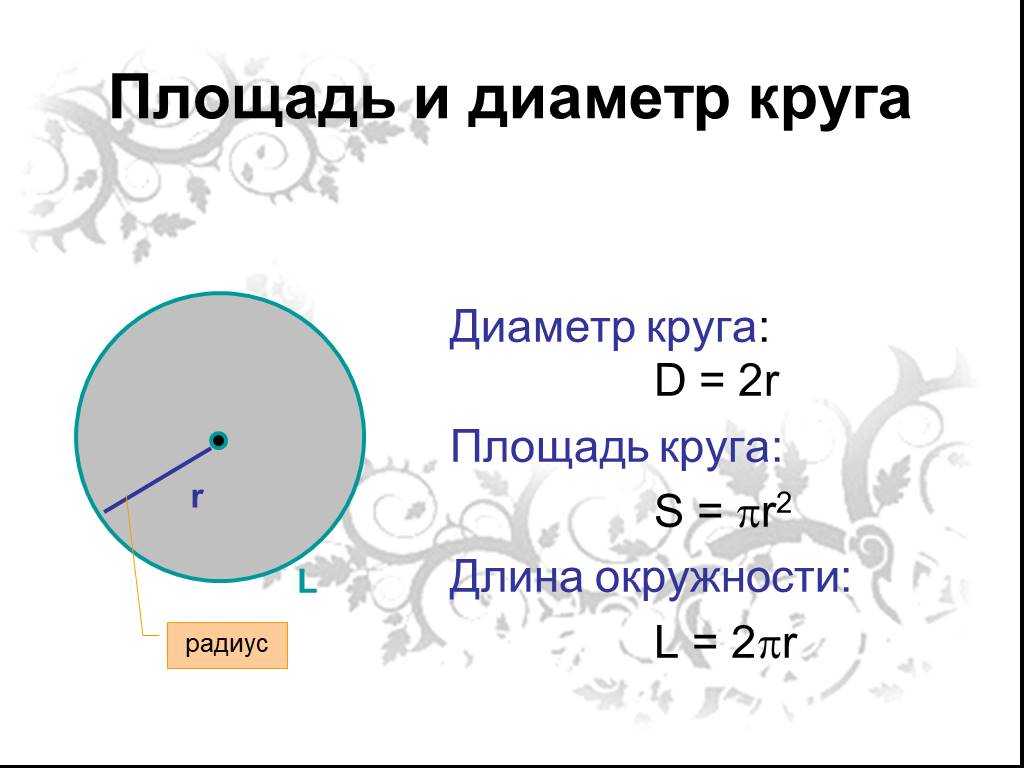
Расчет площади круга по его радиусу
Начнем с классической формулы: S = π · R2, где S — площадь круга, R — его радиус, а π — то самое число пи. В нашем онлайн-калькуляторе оно задано с точностью до пяти знаков после запятой, поэтому он выполняет немного более точные вычисления. Если вы знаете радиус круга, введите его в соответствующем окне на первой вкладке. Результат будет выведен сразу же под ним.
Формула площади круга через диаметр
Если вам известен диаметр круга, можно разделить его пополам и подставить в предыдущую формулу. Но можно поступить еще проще. Перейдите на вторую вкладку и введите диаметр D в качестве исходных данных. Калькулятор использует формулу S = π · D2 / 4 и рассчитывает площадь круга прямо в процессе вашего ввода. Если после вывода результата вы измените значение диаметра, результат пересчитается автоматически.
Площадь круга через длину окружности
Для начала на всякий случай определимся с терминологией: окружность — это линия, каждая точка которой удалена на одинаковое расстояние от центра, а круг — это все, что находится внутри нее. Таким образом, окружность представляет собой внешнюю границу круга. Ее длина равна
Таким образом, окружность представляет собой внешнюю границу круга. Ее длина равна 2 · π · R (за R по-прежнему обозначаем радиус круга и окружности). Теоретически отсюда можно вычислить радиус и посчитать площадь круга по классической формуле. Но, опять же, есть более простой способ: воспользоваться нашим онлайн-калькулятором и ввести известную длину окружности, не выполняя ненужных промежуточных действий. Результат, как и всегда, будет выведен мгновенно.
Расчет площади круга по стороне вписанного квадрата
Эта задача может встретиться при разработке дизайн-проекта или при необходимости закрыть предмет квадратного сечения кругом минимальной площади. Известная сторона квадрата также довольно легко переводится в радиус описанного вокруг него круга, но калькулятор считает его площадь так, чтобы вам не пришлось делать никаких промежуточных вычислений. Для справки: используется формула S = π · a2 / 2, где a — сторона квадрата.
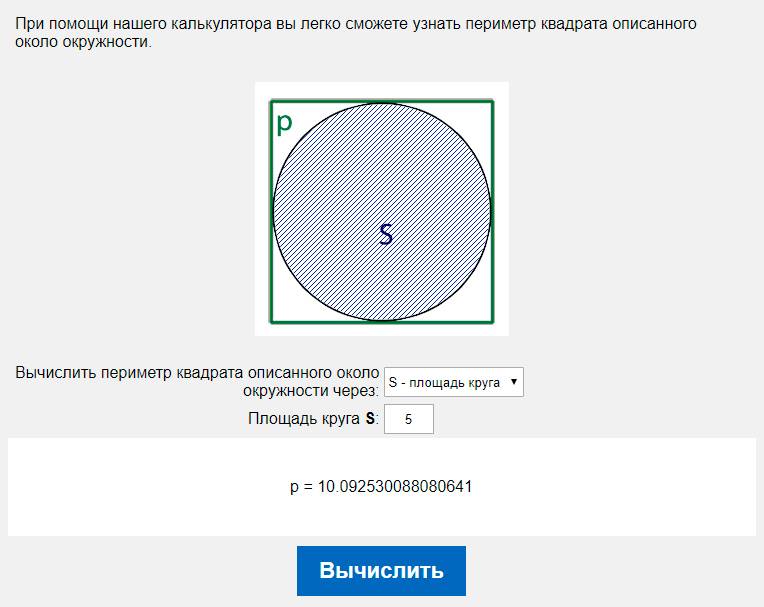
Как найти площадь круга, если известна сторона описанного вокруг него квадрата
Предположим, вы хотите купить бассейн, под который у вас выделен квадратный участок известных размеров. Вполне закономерно желание поставить резервуар максимальной емкости, которая определяется его высотой и площадью. То есть нужно найти площадь круга максимального радиуса, вписанного в квадрат, что и приводит к необходимости ее расчета через сторону этого квадрата. Нетрудно заметить, что задача сводится к вычислению площади круга по известному диаметру, так как сторона описанного вокруг него квадрата как раз и есть его диаметр. Но мы сделали для этого варианта отдельную вкладку, чтобы не заставлять вас запоминать ненужную информацию. Просто вводите длину стороны квадрата и получайте результат точно так же, как и во всех предыдущих случаях.
Вполне закономерно желание поставить резервуар максимальной емкости, которая определяется его высотой и площадью. То есть нужно найти площадь круга максимального радиуса, вписанного в квадрат, что и приводит к необходимости ее расчета через сторону этого квадрата. Нетрудно заметить, что задача сводится к вычислению площади круга по известному диаметру, так как сторона описанного вокруг него квадрата как раз и есть его диаметр. Но мы сделали для этого варианта отдельную вкладку, чтобы не заставлять вас запоминать ненужную информацию. Просто вводите длину стороны квадрата и получайте результат точно так же, как и во всех предыдущих случаях.
Вычисление площади круга через диагональ описанного квадрата
Если в условиях предыдущего примера вы знаете не сторону квадрата, а его диагональ d, вам тоже не потребуется ничего пересчитывать. В калькулятор уже заложена формула S = π · d2 / 8, в соответствии с которой он покажет результат, как только вы введете длину диагонали на нужной вкладке.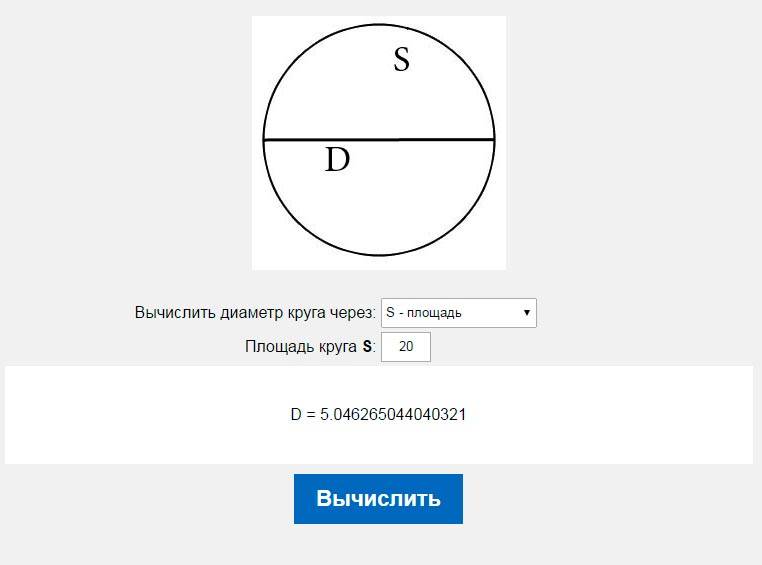 Как всегда, площадь круга вычисляется автоматически и выводится заново каждый раз, когда вы меняете значение диагонали.
Как всегда, площадь круга вычисляется автоматически и выводится заново каждый раз, когда вы меняете значение диагонали.
Расчет площади круга по площади описанного вокруг него квадрата
Как наиболее рационально использовать квадратную заготовку известной площади для изготовления круглой детали? Очевидно, что необходимо вырезать из нее круг максимального диаметра. Площадь такого круга вы можете посчитать с помощью нашего калькулятора, задав на соответствующей вкладке известную площадь квадрата. Формула расчета имеет вид: Sкр = Sкв · π / 4.
Условия использования онлайн-калькулятора расчета площади круга
Вы можете пользоваться данным сервисом совершено бесплатно. Количество расчетов не ограничено, калькулятор запускается из любого браузера, ничего устанавливать на ваш компьютер не нужно. Если наш сайт оказался полезным для вас, напишите об этом в комментариях и не забудьте сохранить его в закладках, чтобы иметь возможность выполнять любые математические вычисления, не отходя от компьютера.
Matrix Calculator — Примеры, Online Matrix Calculator
Matrix Calculator вычисляет результирующую матрицу, когда к двум заданным матрицам применяются определенные арифметические операции. В математике матрица — это функция сетки или прямоугольный массив, в котором числа расположены в упорядоченных строках и столбцах.
Что такое матричный калькулятор?
Калькулятор матриц — это онлайн-инструмент, который помогает выполнять различные матричные операции с матрицами 2 × 2, т. е. сложение матриц, вычитание матриц и умножение матриц. Матрица, имеющая одинаковое количество строк и столбцов, называется квадратной матрицей. Чтобы использовать это Матричный калькулятор , введите числа в поле ввода.
Калькулятор матриц
ПРИМЕЧАНИЕ. Введите не более трех цифр.
Как пользоваться матричным калькулятором?
Выполните следующие действия, чтобы найти окончательную матрицу с помощью онлайн-калькулятора матриц:
- Шаг 1: Перейдите к онлайн-калькулятору матриц Cuemath.

- Шаг 2: Введите значение матрицы 2 × 2 в поля ввода и выберите операцию, которую необходимо выполнить, из раскрывающегося списка.
- Шаг 3: Нажмите кнопку «Вычислить» , чтобы найти результирующую матрицу.
- Шаг 4: Нажмите кнопку «Сброс» , чтобы очистить поля и ввести новые значения.
Как работает матричный калькулятор?
Размеры матрицы обычно представляются как m x n. Здесь m обозначает количество строк, а n представляет количество столбцов в этой матрице. Таким образом, матрица 2×2 будет иметь 2 строки и 2 столбца. С матрицами можно выполнять вычитание, сложение и умножение. Методы вычисления результата для этих арифметических операций приведены ниже:
1. Сложение матриц — Если две матрицы имеют одинаковое количество строк и столбцов, то можно выполнить сложение. Чтобы сложить две матрицы, элементы каждой строки и столбца одной матрицы добавляются к соответствующим элементам другой матрицы.
A + B = \(\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} +\begin{bmatrix} b_{11} & b_ {12} \\ b_{21} & b_{22} \end{bmatrix} =\begin{bmatrix} a_{11} + b_{11} & a_{12} + b_{12}\\ a_{21} + b_{21}& a_{22} + b_{22} \end{bmatrix}\)
2. Вычитание матриц — Подобно сложению, мы можем вычесть две матрицы, только если они имеют одинаковое количество строк и столбцов. Вычитаем элементы каждой строки и столбца одной матрицы из соответствующих элементов предыдущей матрицы.
A — B = \(\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} -\begin{bmatrix} b_{11} & b_ {12} \\ b_{21} & b_{22} \end{bmatrix} =\begin{bmatrix} a_{11} — b_{11} & a_{12} — b_{12}\\ a_{21} — b_{21}& a_{22} — b_{22} \end{bmatrix}\)
3. Умножение матриц — Для умножения двух матриц количество столбцов в первой матрице должно быть равно количеству строк во второй матрице. Умножение матриц можно выполнить следующим образом:
A × B = \(\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} \times \begin {bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix} =\begin{bmatrix} a_{11}b_{11} + a_{12}b_{21 } & a_{11}b_{12} + a_{12}b_{22}\\ a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{ 22}b_{22} \end{bmatrix}\)
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.
Записаться на бесплатный пробный урок
Решенные примеры на калькуляторе матриц
Пример 1:
Сложите две матрицы \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\) & \(\begin{bmatrix} 2 & 1 \\ 4 & 2 \end{bmatrix}\) и проверьте это с помощью калькулятора матриц.
Решение:
Матрица 1 + Матрица 2 = \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 2 & 1\\ 4 & 2 \end {bmatrix} = \begin{bmatrix} 3 & 3 \\ 7 & 6 \end{bmatrix}\)
Пример 2:
Вычтите две матрицы \(\begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\) & \(\begin{bmatrix} 2 & 1 \\ 4 & 2 \end{bmatrix}\) и проверьте это с помощью калькулятора матриц.
Решение:
Матрица 1 — Матрица 2 = \(\begin{bmatrix} 1 и 2 \\ 3 и 4 \end{bmatrix} + \begin{bmatrix} 2 и 1\\ 4 & 2 \end{bmatrix} = \ begin{bmatrix} -1 & 1 \\ -1 & 2 \end{bmatrix}\)
Точно так же вы можете попробовать матричный калькулятор для сложения, вычитания и умножения следующих матриц:
- Matrices = \(\begin {bmatrix} 2 и 1 \\ 4 и 2 \end{bmatrix}\) & \(\begin{bmatrix} 3 и 3 \\ 7 и 6 \end{bmatrix}\)
- Матрицы = \(\begin{bmatrix} 5 и 8 \\ 10 и 16 \end{bmatrix}\) & \(\begin{bmatrix} 8 и 2 \\ 1 и 3 \end{bmatrix}\)
- Матрицы
- Добавление матриц
Калькулятор площади круга — Расчет круга: найти r, a, c, d
Введите информацию
Решите для Выберите optionAreaRadiusDiameterCircumference
Учитывая
Результат
Использование калькулятора:
Чтобы использовать этот калькулятор, выполните следующие действия:
• Выберите значение, которое вы хотите рассчитать. т. е. площадь, радиус и т. д.
т. е. площадь, радиус и т. д.
• Выберите имеющееся у вас значение из раскрывающегося списка.
• Введите требуемые значения в указанные поля ввода.
• Нажмите кнопку вычислить , чтобы выполнить вычисление.
В появившейся панели с правой стороны вы получите результаты расчета вместе с формулой и всеми этапами расчета.
Получить Специально созданный калькулятор для вашего веб-сайта
Получить сейчас
ИЛИ
Получить Калькулятор площади круга Для вашего сайта
Получить сейчас
Содержание:
| 1 | Калькулятор площади круга |
| 2 | Что такое круг? |
| 3 | Формула площади круга |
| 4 | Как вычислить площадь круга? |
| 5 | Каталожные номера: |
Калькулятор площади круга
Калькулятор площади круга – это онлайн-инструмент, который используется для расчета нескольких значений, связанных с кругом.
Калькулятор круга может рассчитать:
• Площадь круга
• Радиус круга
• Диаметр круга
• Длина окружности
После вычисления площади круга вы также можете вычислить сектор круга с помощью наш калькулятор площади сектора.
Что такое круг?
Академия Хана определяет круг следующим образом:
Круг – это фигура, расстояние от центра до края которой всегда одинаково. У каждого круга есть центр, то есть точка, лежащая в центре круга.
Радиус: Расстояние от центра круга до его границы называется радиусом круга. Обозначается р.
Диаметр : Расстояние или линия от центра круга, которая касается границы круга с двух сторон, называется диаметром круга. Обозначается д. Диаметр ровно в два раза больше радиуса.
Окружность : Расстояние по окружности называется окружностью окружности. Обозначается буквой C.
Формула площади круга
Формула площади круга очень проста для интерпретации и использования. Если мы возьмем квадрат радиуса круга и умножим его на число пи (пипипи), то получим площадь круга.
Если мы возьмем квадрат радиуса круга и умножим его на число пи (пипипи), то получим площадь круга.
Формула площади круга может быть выражена следующим образом:0003
Где:
A представляет площадь круга,
r — радиус круга,
и π — математическая константа, равная 13,1415.
Как вычислить площадь круга?
Калькулятор площади поверхности круга выше может быть использован для расчета площади круга с большим удобством.
Однако, если вам нужно найти площадь круга вручную, вы можете выполнить следующие шаги:
• Определите радиус круга и запишите его.
• Запишите формулу площади круга.
• Подставьте значения в формулу и рассчитайте площадь.
Давайте попробуем этот метод на примере.
Пример:
Если радиус круга равен 20 см , найдите площадь этого круга?
Решение:
Шаг 1 : Определите радиус круга и запишите его.
г = 202020 92πr2
Шаг 3 :
Подставьте значения в формулу и рассчитайте площадь.
A = 3,1415 × 2023,1415 \ Times 2023.1415 × 202
A = 1256,6 см 2
SO, область круга с 20 см Radius будет 1256,6 CM2 .
Каталожные номера:
Учебник по греческой математике | источник HEATH THOMAS L (2003)
Объяснение площади круга | источник с Wikipedia.com
Окружность и площадь круга — Периметр и площадь — Национальный 4 Применение математики | BBC.CO.UK
Другие языки
Рейтинги пользователей
- Всего отзывов 1
- Общий рейтинг 5/5
- Звезды
Спасибо! Для вашего рассмотрения
Ваш отзыв скоро появится.
Отправить свой отзыв Закрыть
Отзывы
Пожалуйста, заполните 1 строку
Обратная связь
Отправьте нам свой отзыв!
Нужна помощь? Вы можете связаться с нами в любое время.
Калькулятор площади полукруга
Калькулятор площади полукруга специально разработан для расчета площади полукруга. Не только это, но и этот калькулятор полукруга также позволит вам определить различные параметры, связанные с этой конкретной геометрической фигурой.
Итак, не теряя времени, давайте приступим к статье, в которой подробно рассмотрим теорию полукруга.
Сосредоточься!
Что такое полукруг?
С точки зрения геометрии:
«Полукруг — это фигура, являющаяся половиной любого круга»
Как построить полукруг?
Здесь вам нужно разрезать круг на две равные половины. Это можно сделать, если разрезать его по центру круга. Остальное, когда дело доходит до анализа полукруга, то это можно сделать с помощью этого калькулятора площади полукруга. 9{2}}{2} $$
Если вам интересно найти площадь полного круга, вы также можете быстро сделать это с помощью нашего калькулятора другого круга.
Периметр полукруга:
$$ \text{Perimeter_{semicircle}} = \left(\frac{Circumference}{2}\right) + 2*radius $$
$$ \text{Perimeter_{semicircle} } = \frac{2*\pi*r}{2} + 2*r $$
$$ \text{Perimeter_{semicircle}} = \pi*r + 2*r $$
Принимая r за общий:
$$ \text{Периметр_{полукруг}} = r*\left(\pi + 2\right) $$
Это же выражение также используется в вычислителе периметра полукруга, а также для определения этого важного объекта.
Диаметр полукруга:
Обычно в полукруге диаметр является его основанием. И вы можете рассчитать, используя следующее выражение:
$$ Диаметр = 2*Радиус $$
И когда мы разделим диаметр на коэффициент 2, мы получим радиус полукруга, как показано ниже:
$ $ Радиус = \frac{Диаметр}{2} $$ 9{\text{o}}} $$
Кроме этого, вы можете определить длину дуги для всего круглого тела, используя наш другой Калькулятор длины дуги.
Как найти площадь полукруга?
Эта конкретная часть чтения заполнена несколькими примерами задач, которые позволят вам прочно усвоить концепцию. Давайте двигаться к ним сейчас!
Давайте двигаться к ним сейчас!
Пример № 01:
Как найти площадь полукруга с радиусом 23 ?
9{2}}{2} $$
$$ \text{Area_{semicircle}} = \frac{180*529}{2} $$
$$ \text{Area_{semicircle}} = \frac{ 95220}{2} $$
$$ \text{Area_{semicircle}} = 47610 $$
Этот бесплатный калькулятор площади полукруга также позволяет найти те же результаты, но экономит ваше драгоценное время.
Пример #02:
Определить периметр полукруга радиусом 2.
Решение:
Здесь имеем:
$$ \text{Периметр_{полуокружность}} = r*\left(\pi + 2\right) $$
$$ \text{Периметр_{полукружность}} = 2*\left(\pi + 2\ справа) $$
$$ \text{Периметр_{полукруг}} = 2*\pi + 2*2 $$
$$ \text{Периметр_{полукруг}} = 2*\pi + 4 $$
$$ \text{Периметр_{полукруг}} = 2*\влево(\пи + 2\вправо) $$
Вы также можете проверить результаты с помощью этого онлайн-калькулятора периметра полукруга за несколько секунд.
Как работает калькулятор площади полукруга?
Всплывающее окно, чтобы узнать, как работает этот калькулятор площади полукруга, с помощью руководства, организованного как:
Ввод:
- Прежде всего, выберите параметр, который вы хотите определить, из первого раскрывающегося списка
- После того, как вы сделаете выбор, перейдите к извлечению связанных запрошенных объектов в назначенных им полях
- После того, как вы закончите, нажмите кнопку расчета
Вывод:
Бесплатный калькулятор полукруга отображает следующие результаты на экране вашего устройства:
- Диаметр полукруга
- Радиус полукруга
- Площадь полукруга
- Длина дуги полукруга
- Периметр полукруга
Часто задаваемые вопросы:
Что такое угол полуокружности?
Если говорить об угле, который образует треугольник внутри полукруга, то этот угол будет равен 90 градусов. Это прямой угол, и его можно определить с помощью нашего калькулятора треугольников.
Это прямой угол, и его можно определить с помощью нашего калькулятора треугольников.
Сколько полукругов в круге?
Полукруг — это полукруг, поэтому в полном круге два полукруга.
Как называется четверть круга?
Четверть круга можно назвать квадрантом.
Какая самая длинная хорда в полуокружности?
Самая длинная хорда в окружности — это ее диаметр. Вы должны помнить, что все хорды никогда не могут быть названы диаметром. Но с другой стороны, все диаметры можно считать хордами.
Как обычно называют окружность?
Обычно круг называют по его центральной точке. Другие параметры, которые используются для его определения, включают диаметр, радиус, хорду и длину дуги.
Какая часть круга самая короткая?
Самая короткая часть любого круга или полукруга получается, когда он пересекается отрезком в любом месте.
Какая польза от полукруга?
Полуокружность помогает вычислить среднее геометрическое и арифметическое двух линий.

 p|number:4 $}
p|number:4 $}