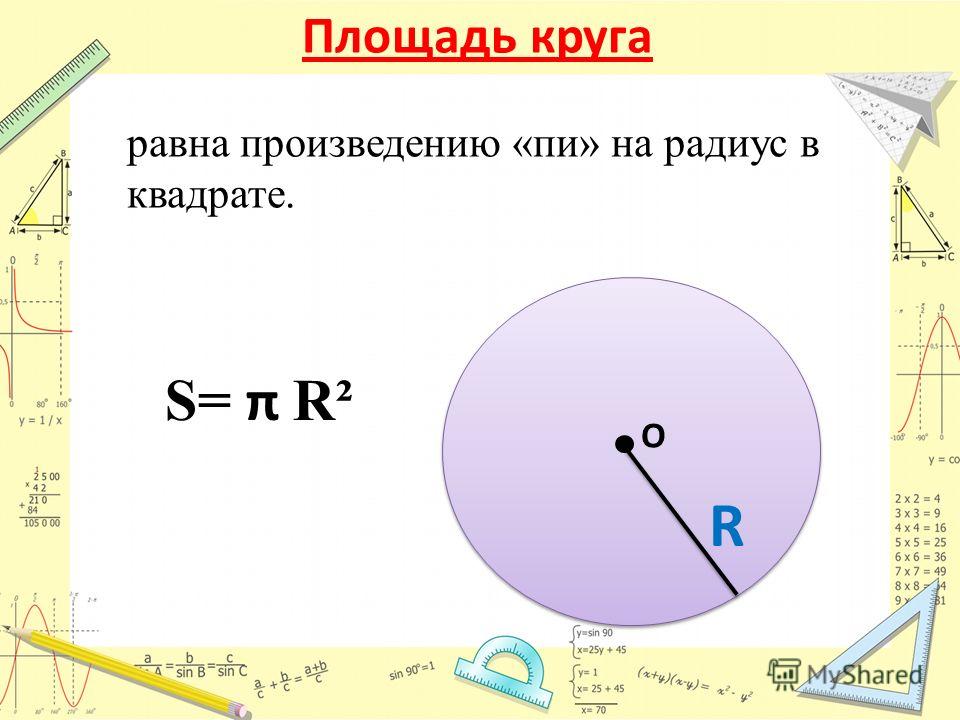
Площадь круга по диаметру онлайн калькулятор. Как найти площадь круга
- Длину диаметра – отрезка, проходящего через центр круга и соединяющего две противоположные точки окружности, либо радиуса – отрезка, одна из крайних точек которого находится в центре круга, а вторая – на дуге окружности. Таким образом, диаметр равен длине радиуса, умноженной на два.
- Значение числа π. Эта величина представляет собой константу – иррациональную дробь, не имеющую конца. При этом она не является периодической. Данное число выражает соотношение длины окружности к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.
Формулы для нахождения площади круга, его сегмента или сектора
В зависимости от специфики условий геометрической задачи применяются две формулы нахождения площади круга:
Чтобы определить, как найти площадь круга проще всего, нужно тщательно проанализировать условия задания.
Школьный курс геометрии также включает в себя задачи на расчет площади сегментов или секторов, для которых применяются специальные формулы:
- Сектор представляет собой часть круга, ограниченную окружностью и углом с вершиной, расположенной в центре. Площадь сектора рассчитывается по формуле: S = (π*r 2 /360)*А;
- r – радиус;
- А – величина угла в градусах.
- r – радиус;
- р – длина дуги.
- Сегмент – представляет собой часть, ограниченную сечением круга (хордой) и окружностью. Его площадь можно найти по формуле S=(π*r 2 /360)*А± S ∆ ;
Также существует второй вариант S = 0,5*р*r;
- r – радиус;
- А – величина угла в градусах;
- S ∆ – площадь треугольника, сторонами которого являются радиусы и хорда круга; при этом одна из его вершин располагается в центре круга, а две других – в точках соприкосновения дуги окружности с хордой. Важный момент – знак “минус” ставится в том случае, если значение А меньше 180 градусов, а знак “плюс” – если больше 180 градусов.

Чтобы упростить решение геометрической задачи, можно вычислить площадь круга он-лайн . Специальная программа быстро и безошибочно сделает расчет за пару секунд. Как рассчитать он-лайн площадь фигур? Для этого необходимо известные ввести исходные данные: радиус, диаметр, величину угла.
Инструкция
Используйте число Пи для нахождения радиуса по известной площади круга. Эта константа задает пропорцию между диаметром круга и длиной его границы (окружности). Длина окружности максимальную площадь плоскости, которую возможно с ее помощью охватить, а диаметр равняется двум радиусам, поэтому и площадь с радиусом тоже соотносятся друг с другом с пропорцией, которую можно выразить через число Пи. Эта константа (π) определяется как площади (S) и возведенного в квадрат радиус (r) круга. Из этого вытекает, что радиус можно выразить, как квадратный корень из частного от деления площади на число Пи: r=√(S/π).
Долгое время Эрастофен возглавлял Александрийскую библиотеку, самую знаменитую библиотеку древнего мира.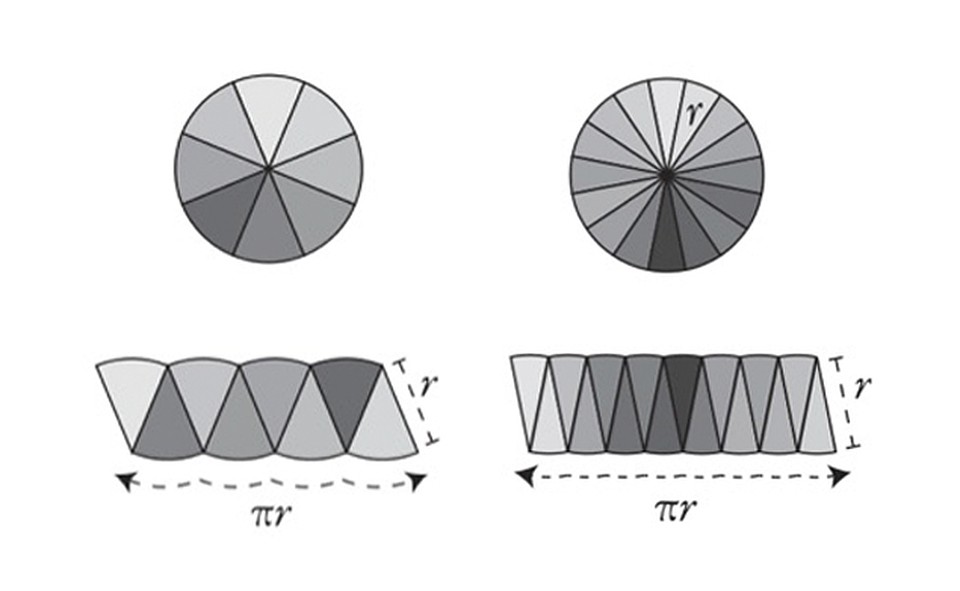 Помимо того, что он вычислил размер нашей планеты, сделал еще ряд важных изобретений и открытий. Изобрел нехитрый метод определять простые числа, называемый теперь «решето Эрастофена».
Помимо того, что он вычислил размер нашей планеты, сделал еще ряд важных изобретений и открытий. Изобрел нехитрый метод определять простые числа, называемый теперь «решето Эрастофена».
Нарисовал «карту мира», в которой показал все части света, известные на тот момент древним грекам. Карта считалась одной из лучших для своего времени. Разработал систему долготы и широты и календарь, включавший високосные годы. Изобрел армиллярную сферу, механическое устройство, используемое ранними астрономами, чтобы демонстрировать и предсказывать видимое движение звезд на небе. Также составил звездный каталог, включавший в себя 675 звезд.
Источники:
- Греческий ученый Эратосфен Киренский впервые в мире вычислил радиус Земли
- Eratosthenes» Calculation of Earth»s Circumference
- Eratosthenes
В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом.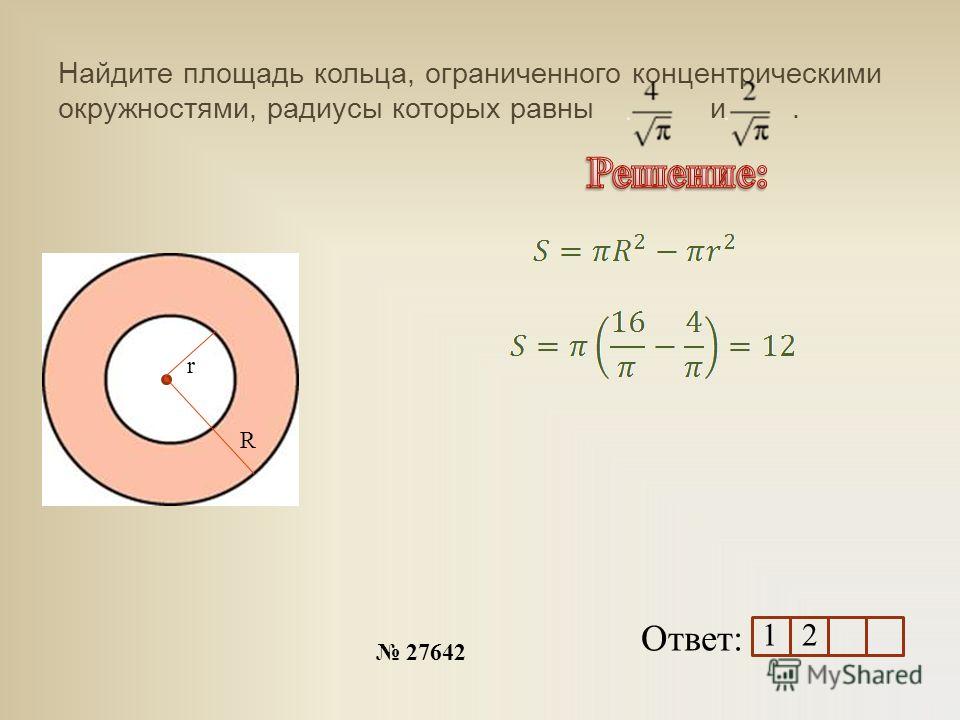 При этом внешней границей круга является окружность , а в том случае, если длина радиуса равна нулю, круг вырождается в точку.
При этом внешней границей круга является окружность , а в том случае, если длина радиуса равна нулю, круг вырождается в точку.
Определение площади круга
При необходимости площадь круга можно вычислить по формуле:
| S | πr 2 | D 2 |
r — радиус круга
D — диаметр круга
S — площадь круга
π — 3.14
Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно

Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга , а впервые они стали строиться еще во времена античности. Само слово « circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.
Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна. Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол », которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.
– это плоская фигура, которая представляет собой множество точек равноудаленных от центра. Все они находятся на одинаковом расстоянии и образуют собой окружность.
Все они находятся на одинаковом расстоянии и образуют собой окружность.
Отрезок, который соединяет центр круга с точками его окружности, называется радиусом . В каждой окружности все радиусы равны между собой. Прямая, соединяющая две точки на окружности и проходящая через центр называется диаметром . Формула площади круга рассчитывается с помощью математической константы – числа π..
Это интересно : Число π. представляет собой соотношение длины окружности к длине ее диаметра и является постоянной величиной. Значение π = 3,1415926 получило применение после работ Л. Эйлера в 1737 г.
Площадь окружности можно вычислить через константу π. и радиус окружности. Формула площади круга через радиус выглядит так:
Рассмотрим пример расчета площади круга через радиус. Пусть дана окружность с радиусом R = 4 см. Найдем площадь фигуры.
Площадь нашей окружности будет равна 50,24 кв. см.
Существует формула площади круга через диаметр .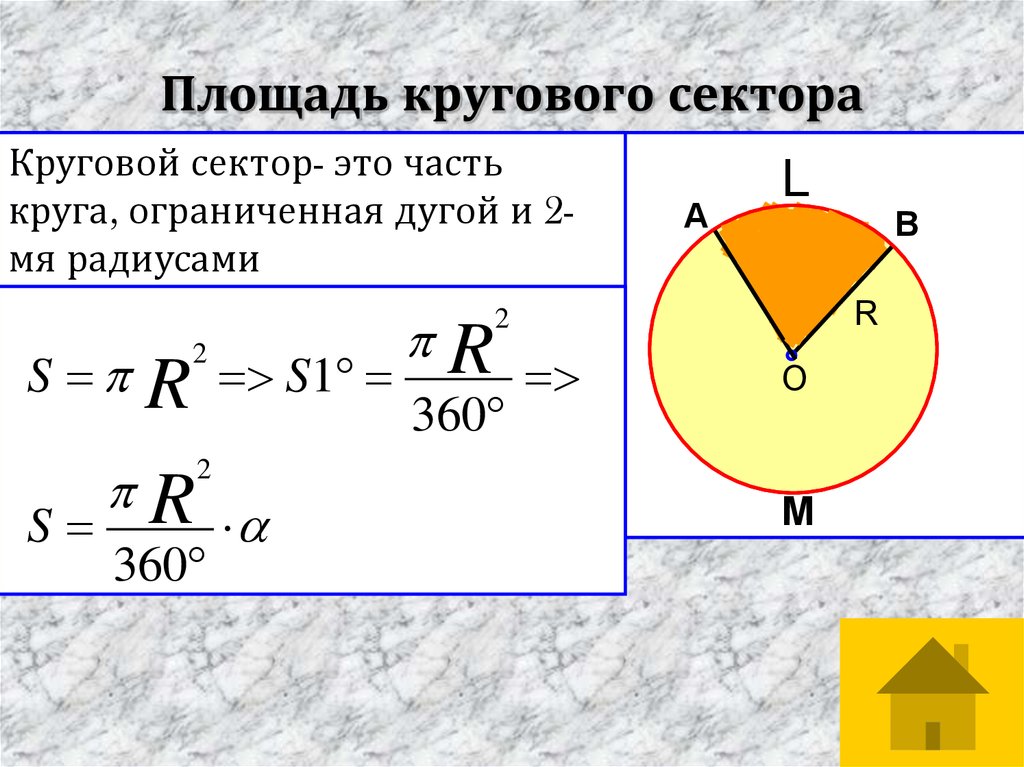
Рассмотрим пример расчета площади круга через диаметр, зная его радиус. Пусть дана окружность с радиусом R = 4 см. Для начала найдем диаметр, который, как известно, в два раза больше радиуса.
Теперь используем данные для примера расчета площади круга по приведенной выше формуле:
Как видим, в результате получаем тот же ответ, что и при первых расчетах.
Знания стандартных формул расчета площади круга помогут в дальнейшем легко определять площадь секторов и легко находить недостающие величины.
Мы уже знаем, что формула площади круга рассчитывается через произведение постоянной величины π на квадрат радиуса окружности. Радиус можно выразить через длину окружности и подставить выражение в формулу площади круга через длину окружности:
Рассмотрим пример расчета площади круга через длину окружности. Пусть дана окружность с длиной l
= 8 см. Подставим значение в выведенную формулу:
Пусть дана окружность с длиной l
= 8 см. Подставим значение в выведенную формулу:
Итого площадь круга будет равна 5 кв. см.
Площадь круга описанного вокруг квадрата
Очень легко можно найти площадь круга описанного вокруг квадрата.
Для этого потребуется только сторона квадрата и знание простых формул. Диагональ квадрата будет равна диагонали описанной окружности. Зная сторону a
ее можно найти по теореме Пифагора: отсюда .
После того, как найдем диагональ – мы сможем рассчитать радиус: .
И после подставим все в основную формулу площади круга описанного вокруг квадрата:
Круг – это видимая совокупность множества точек, которые находятся на одинаковом расстоянии от центра. Чтобы найти его площадь, необходимо знать, что такое радиус, диаметр, число π и окружность.
Величины, участвующие в расчете площади круга
Расстояние, ограниченное центральной точкой круга и любой из точек окружности, называется радиусом этой геометрической фигуры. 2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.
2. Другими словами диаметр во 2 степени равен стороне квадрата во 2 степени, умноженной на 2.
Вычислив значение длины диаметра круга, можно узнать и его радиус, после чего воспользоваться одной их формул определения площади круга.
Площадь сектора круга
Сектор – это часть круга, ограниченная 2 радиусами и дугой между ними. Чтобы узнать его площадь, нужно измерить угол сектора. После этого необходимо составить дробь, в числителе которой будет значение угла сектора, а в знаменателе – 360. Чтобы высчитать площадь сектора, значение, полученное в результате деления дроби, нужно умножить на площадь круга, вычисленную по одной из вышеперечисленных формул.
| 1 | Оценить с использованием заданного значения | квадратный корень из 50 | |
| 2 | Оценить с использованием заданного значения | квадратный корень из 45 | |
| 3 | Вычислить | 5+5 | |
| 4 | Вычислить | 7*7 | |
| 5 | Разложить на простые множители | 24 | |
| 6 | Преобразовать в смешанную дробь | 52/6 | |
| 7 | Преобразовать в смешанную дробь | 93/8 | |
| 8 | Преобразовать в смешанную дробь | 34/5 | |
| 9 | График | y=x+1 | |
| 10 | Оценить с использованием заданного значения | квадратный корень из 128 | |
| 11 | Найти площадь поверхности | сфера (3) | |
| 12 | Вычислить | 54-6÷2+6 | |
| 13 | График | y=-2x | |
| 14 | Вычислить | 8*8 | |
| 15 | Преобразовать в десятичную форму | 5/9 | |
| 16 | Оценить с использованием заданного значения | квадратный корень из 180 | |
| 17 | График | y=2 | |
| 18 | Преобразовать в смешанную дробь | 7/8 | |
| 19 | Вычислить | 9*9 | |
| 20 | Risolvere per C | C=5/9*(F-32) | |
| 21 | Упростить | 1/3+1 1/12 | |
| 22 | График | y=x+4 | |
| 23 | График | y=-3 | |
| 24 | График | x+y=3 | |
| 25 | График | x=5 | |
| 26 | Вычислить | 6*6 | |
| 27 | Вычислить | 2*2 | |
| 28 | Вычислить | 4*4 | |
| 29 | Вычислить | 1/2+(2/3)÷(3/4)-(4/5*5/6) | |
| 30 | Вычислить | 1/3+13/12 | |
| 31 | Вычислить | 5*5 | |
| 32 | Risolvere per d | 2d=5v(o)-vr | |
| 33 | Преобразовать в смешанную дробь | 3/7 | |
| 34 | График | y=-2 | |
| 35 | Определить наклон | y=6 | |
| 36 | Перевести в процентное соотношение | 9 | |
| 37 | График | y=2x+2 | |
| 38 | График | y=2x-4 | |
| 39 | График | x=-3 | |
| 40 | Решить, используя свойство квадратного корня | x^2+5x+6=0 | |
| 41 | Преобразовать в смешанную дробь | 1/6 | |
| 42 | Преобразовать в десятичную форму | 9% | |
| 43 | Risolvere per n | 12n-24=14n+28 | |
| 44 | Вычислить | 16*4 | |
| 45 | Упростить | кубический корень из 125 | |
| 46 | Преобразовать в упрощенную дробь | 43% | |
| 47 | График | x=1 | |
| 48 | График | y=6 | |
| 49 | График | y=-7 | |
| 50 | График | y=4x+2 | |
| 51 | Определить наклон | y=7 | |
| 52 | График | y=3x+4 | |
| 53 | График | y=x+5 | |
| 54 | График | 3x+2y=6 | |
| 55 | Решить, используя свойство квадратного корня | x^2-5x+6=0 | |
| 56 | Решить, используя свойство квадратного корня | x^2-6x+5=0 | |
| 57 | Решить, используя свойство квадратного корня | x^2-9=0 | |
| 58 | Оценить с использованием заданного значения | квадратный корень из 192 | |
| 59 | Оценить с использованием заданного значения | квадратный корень из 25/36 | |
| 60 | Разложить на простые множители | 14 | |
| 61 | Преобразовать в смешанную дробь | 7/10 | |
| 62 | Risolvere per a | (-5a)/2=75 | |
| 63 | Упростить | x | |
| 64 | Вычислить | 6*4 | |
| 65 | Вычислить | 6+6 | |
| 66 | Вычислить | -3-5 | |
| 67 | Вычислить | -2-2 | |
| 68 | Упростить | квадратный корень из 1 | |
| 69 | Упростить | квадратный корень из 4 | |
| 70 | Найти обратную величину | 1/3 | |
| 71 | Преобразовать в смешанную дробь | 11/20 | |
| 72 | Преобразовать в смешанную дробь | 7/9 | |
| 73 | Найти НОК | 11 , 13 , 5 , 15 , 14 | , , , , |
| 74 | Решить, используя свойство квадратного корня | x^2-3x-10=0 | |
| 75 | Решить, используя свойство квадратного корня | x^2+2x-8=0 | |
| 76 | График | 3x+4y=12 | |
| 77 | График | 3x-2y=6 | |
| 78 | График | y=-x-2 | |
| 79 | График | y=3x+7 | |
| 80 | Определить, является ли полиномом | 2x+2 | |
| 81 | График | y=2x-6 | |
| 82 | График | y=2x-7 | |
| 83 | График | y=2x-2 | |
| 84 | График | y=-2x+1 | |
| 85 | График | y=-3x+4 | |
| 86 | График | y=-3x+2 | |
| 87 | График | y=x-4 | |
| 88 | Вычислить | (4/3)÷(7/2) | |
| 89 | График | 2x-3y=6 | |
| 90 | График | x+2y=4 | |
| 91 | График | x=7 | |
| 92 | График | x-y=5 | |
| 93 | Решить, используя свойство квадратного корня | x^2+3x-10=0 | |
| 94 | Решить, используя свойство квадратного корня | x^2-2x-3=0 | |
| 95 | Найти площадь поверхности | конус (12)(9) | |
| 96 | Преобразовать в смешанную дробь | 3/10 | |
| 97 | Преобразовать в смешанную дробь | 7/20 | |
| 98 | Преобразовать в смешанную дробь | 2/8 | |
| 99 | Risolvere per w | V=lwh | |
| 100 | Упростить | 6/(5m)+3/(7m^2) |
Площадь круга 200 мм.
 Площадь круга: формула
Площадь круга: формулаИнструкция
Используйте число Пи для нахождения радиуса по известной площади круга. Эта константа задает пропорцию между диаметром круга и длиной его границы (окружности). Длина окружности максимальную площадь плоскости, которую возможно с ее помощью охватить, а диаметр равняется двум радиусам, поэтому и площадь с радиусом тоже соотносятся друг с другом с пропорцией, которую можно выразить через число Пи. Эта константа (π) определяется как площади (S) и возведенного в квадрат радиус (r) круга. Из этого вытекает, что радиус можно выразить, как квадратный корень из частного от деления площади на число Пи: r=√(S/π).
Долгое время Эрастофен возглавлял Александрийскую библиотеку, самую знаменитую библиотеку древнего мира. Помимо того, что он вычислил размер нашей планеты, сделал еще ряд важных изобретений и открытий. Изобрел нехитрый метод определять простые числа, называемый теперь «решето Эрастофена».
Нарисовал «карту мира», в которой показал все части света, известные на тот момент древним грекам. Карта считалась одной из лучших для своего времени. Разработал систему долготы и широты и календарь, включавший високосные годы. Изобрел армиллярную сферу, механическое устройство, используемое ранними астрономами, чтобы демонстрировать и предсказывать видимое движение звезд на небе. Также составил звездный каталог, включавший в себя 675 звезд.
Карта считалась одной из лучших для своего времени. Разработал систему долготы и широты и календарь, включавший високосные годы. Изобрел армиллярную сферу, механическое устройство, используемое ранними астрономами, чтобы демонстрировать и предсказывать видимое движение звезд на небе. Также составил звездный каталог, включавший в себя 675 звезд.
Источники:
- Греческий ученый Эратосфен Киренский впервые в мире вычислил радиус Земли
- Eratosthenes» Calculation of Earth»s Circumference
- Eratosthenes
Как найти площадь круга? Сначала найдите радиус. Учитесь решать простые и сложные задачи.
Круг — это замкнутая кривая. Любая точка на линии окружности будет находиться на одинаковом расстоянии от центральной точки. Круг — это плоская фигура, поэтому решать задачи с нахождением площади просто. В этой статье мы рассмотрим, как найти площадь круга, вписанного в треугольник, трапецию, квадрат, и описанного около этих фигур.
Чтобы найти площадь данной фигуры, нужно знать, что такое радиус, диаметр и число π.
Радиус R — это расстояние, ограниченное центром окружности. Длины всех R-радиусов одной окружности будут равными.
Диаметр D — это линия между двумя любыми точками окружности, которая проходит через центральную точку. Длина этого отрезка равна длине R-радиуса, умноженной на 2.
Число π — это неизменная величина, которая равна 3,1415926. В математике обычно это число округляется до 3,14.
Формула нахождения площади круга через радиус:Примеры решения заданий по нахождению S-площади круга через R-радиус:
Задача: Найдите площадь окружности, если ее радиус равен 7 см.
Решение: S=πR², S=3,14*7², S=3,14*49=153,86 см².
Ответ: Площадь окружности равна 153,86 см².
Формула нахождения S-площади круга через D-диаметр:Примеры решения заданий по нахождению S, если известен D:
————————————————————————————————————————-
Задача: Найдите S круга, если его D равен 10 см.
Решение: P=π*d²/4, P=3,14*10²/4=3,14*100/4=314/4=78,5 см².
Ответ: Площадь плоской круглой фигуры равна 78,5 см².
Нахождение S круга, если известна длина окружности:
Сначала находим, чему равен радиус. Длина окружности рассчитывается по формуле: L=2πR, соответственно радиус R будет равен L/2π. Теперь находим площадь круга по формуле через R.
Рассмотрим решение на примере задачи:
———————————————————————————————————————-
Задача: Найдите площадь круга, если известна длина окружности L — 12 см.
Решение: Сначала находим радиус: R=L/2π=12/2*3,14=12/6,28=1,91.
Теперь находим площадь через радиус: S=πR²=3,14*1,91²=3,14*3,65=11,46 см².
Ответ: Площадь круга равна 11,46 см².
Найти площадь круга, вписанного в квадрат просто. Сторона квадрата — это диаметр круга. Чтобы найти радиус, нужно сторону разделить на 2.
Формула нахождения площади круга, вписанного в квадрат:
Примеры решения задач по нахождению площади круга, вписанного в квадрат:
———————————————————————————————————————
Задача №1: Известна сторона квадратной фигуры, которая равна 6 сантиметров. Найдите S-площадь вписанной окружности.
Найдите S-площадь вписанной окружности.Решение: S=π(a/2)²=3,14(6/2)²=3,14*9=28,26 см².
Ответ: Площадь плоской круглой фигуры равна 28,26 см².
————————————————————————————————————————
Задача №2 : Найдите S круга, вписанного в квадратную фигуру и его радиус, если одна сторона равна a=4 см.Решайте так : Сначала найдем R=a/2=4/2=2 см.
Теперь найдем площадь окружности S=3,14*2²=3,14*4=12,56 см².
Ответ: Площадь плоской круглой фигуры равна 12,56 см².
Немного сложнее находить площадь круглой фигуры, описанной около квадрата. Но, зная формулу, можно быстро подсчитать данное значение.
Формула нахождения S круга, описанного около квадратной фигуры:
Примеры решения заданий по нахождению площади окружности, описанной около квадратной фигуры:
Задача
Окружность, которая вписана в треугольную фигуру — это круг, который касается всех трех сторон треугольника. В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
В любую треугольную фигуру можно вписать круг, но только один. Центром круга будет точка пересечения биссектрис углов треугольника.
Формула нахождения площади круга, вписанного в равнобедренный треугольник:
Когда будет известен радиус, площадь можно вычислить по формуле: S=πR².
Формула нахождения площади круга, вписанного в прямоугольный треугольник:
Примеры решения заданий:
Задача №1
Если в этой задаче нужно найти еще и площадь круга с радиусом 4 см, то сделать это можно по формуле: S=πR²
Задача №2
Решение:
Теперь, когда известен радиус, можно найти площадь круга через радиус. Формулу смотрите выше по тексту.
Задача №3
Площадь круга, описанного около прямоугольного и равнобедренного треугольника: формула, примеры решения задач
Все формулы по нахождению площади круга сводятся к тому, что сначала нужно найти его радиус. Когда известен радиус, то найти площадь просто, как было описано выше.
Когда известен радиус, то найти площадь просто, как было описано выше.
Площадь круга, описанного около прямоугольного и равнобедренного треугольника находится по такой формуле:
Примеры решения задач:
Вот еще пример решения задачи с использованием формулы Герона.
Решать подобные задачи сложно, но их можно осилить, если знать все формулы. Такие задачи школьники решают в 9 классе.
Площадь круга, вписанного в прямоугольную и равнобедренную трапецию: формула, примеры решения задач
У равнобедренной трапеции две стороны равны. У прямоугольной трапеции один угол равен 90º. Рассмотрим, как найти площадь круга, вписанного в прямоугольную и равнобедренную трапецию на примере решения задач.
Например, в равнобедренную трапецию вписана окружность, которая в точке касания делит одну сторону на отрезки m и n.
Для решения этой задачи нужно использовать такие формулы:
Нахождение площади окружности, вписанной в прямоугольную трапецию, производится по следующей формуле:
Если известна боковая сторона, то можно найти радиус через это значение.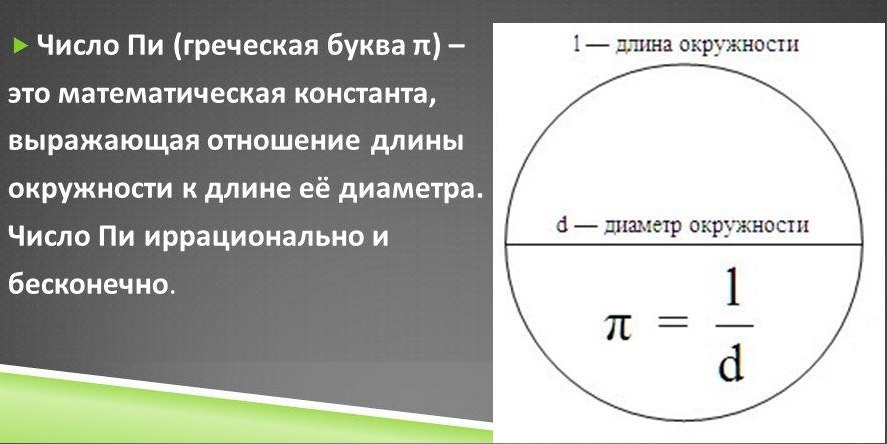 Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Высота боковой стороны трапеции равна диаметру окружности, а радиус — это половина диаметра. Соответственно, радиус равен R=d/2.
Примеры решения задач:
Трапецию можно вписать в окружность, когда сумма ее противолежащих углов равна 180º. Поэтому вписать можно только равнобокую трапецию. Радиус для вычисления площадь круга, описанного около прямоугольной или равнобедренной трапеции, рассчитывается по таким формулам:
Примеры решения задач:
Решение: Большое основание в данном случае проходит через центр, так как в окружность вписана равнобедренная трапеция. Центр делит это основание ровно пополам. Если основание АВ равно 12, тогда радиус R можно найти так: R=12/2=6.
Ответ: Радиус равен 6.
В геометрии важно знать формулы. Но все их невозможно запомнить, поэтому даже на многих экзаменах разрешается пользоваться специальным формуляром. Однако важно уметь находить правильную формулу для решения той или иной задачи. Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Тренируйтесь в решении разных задач на нахождение радиуса и площади окружности, чтобы уметь правильно подставлять формулы и получать точные ответы.
Видео: Математика | Вычисление площадей круга и его частей
В геометрии кругом называется некоторое множество всех точек на плоскости, которые удалены от одной точки, называемой его центром, на расстояние, не большее заданного, называемого его радиусом. При этом внешней границей круга является окружность , а в том случае, если длина радиуса равна нулю, круг вырождается в точку.
Определение площади круга
При необходимости площадь круга можно вычислить по формуле:
| S | πr 2 | D 2 |
r — радиус круга
D — диаметр круга
S — площадь круга
π — 3.14
Эта геометрическая фигура очень часто встречается как в технике, так и в архитектуре. Конструкторы машин и механизмов разрабатывают различные детали, сечения многих из которых представляют собой именно круг . К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг . Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.
К примеру, таковыми являются валы, штоки, тяги, цилиндры, оси, поршни и так далее. При изготовлении этих деталей используются заготовки из различных материалов (металлов, древесины, пластических масс), их сечения также представляют собой именно круг . Само собой разумеется, что разработчикам нередко приходится вычислять площадь круга через диаметр или радиус, используя для этой цели несложные математические формулы, открытые еще в глубокой древности.
Именно тогда круглые элементы стали активно и широко использоваться в архитектуре. Один из самых ярки тому примеров – цирк, представляющий собой разновидность строений, предназначенных для проведения в них различных зрелищных мероприятий. Их арены имеют форму круга , а впервые они стали строиться еще во времена античности. Само слово «circus » в переводе с латинского языка означает «круг ». Если в древности в цирках шли театральные постановки и проводились бои гладиаторов, то сейчас они служат местом, где практически исключительно проводятся цирковые представления с участием дрессировщиков, акробатов, фокусников, клоунов и т. д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.
д. Стандартный диаметр цирковой арены составляет 13 метров, причем это совершенно не случайно: дело в том, что именно он обеспечивает минимально необходимые геометрические параметры манежа, по которому цирковые лошади могут бегать по кругу галопом. Если вычислить площадь круга через диаметр, то получится, что для цирковой арены эта величина составляет 113,04 квадратных метра.
Архитектурными элементами, которые могут принимать форму круга, являются окна. Конечно, в большинстве случаев они прямоугольные или же квадратные (причем во многом благодаря тому, что это проще как для зодчих, так и для строителей), но в некоторых зданиях можно встретить и круглые окна. Более того, в таких транспортных средствах, как воздушные, морские и речные суда они чаще всего именно такие.
Отнюдь не является редкостью использование круглых элементов для производства мебели, например столов и стульев. Существует даже понятие «круглый стол », которое подразумевает конструктивную дискуссию, в ходе которой происходит всестороннее обсуждение различных важных проблем и вырабатывается пути их решения. Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.
Что касается изготовления самих столешниц, имеющих круглую форму, то для их производства применяются специализированные инструменты и оборудование, при условии участия рабочих с довольно высокой квалификацией.
- Длину диаметра – отрезка, проходящего через центр круга и соединяющего две противоположные точки окружности, либо радиуса – отрезка, одна из крайних точек которого находится в центре круга, а вторая – на дуге окружности. Таким образом, диаметр равен длине радиуса, умноженной на два.
- Значение числа π. Эта величина представляет собой константу – иррациональную дробь, не имеющую конца. При этом она не является периодической. Данное число выражает соотношение длины окружности к ее радиусу. Для вычисления площади круга в заданиях школьного курса используется значение π, приведенное с точностью до сотых – 3,14.
Формулы для нахождения площади круга, его сегмента или сектора
В зависимости от специфики условий геометрической задачи применяются две формулы нахождения площади круга:
Чтобы определить, как найти площадь круга проще всего, нужно тщательно проанализировать условия задания.
Школьный курс геометрии также включает в себя задачи на расчет площади сегментов или секторов, для которых применяются специальные формулы:
- Сектор представляет собой часть круга, ограниченную окружностью и углом с вершиной, расположенной в центре. Площадь сектора рассчитывается по формуле: S = (π*r 2 /360)*А;
- r – радиус;
- А – величина угла в градусах.
- r – радиус;
- р – длина дуги.
- Сегмент – представляет собой часть, ограниченную сечением круга (хордой) и окружностью. Его площадь можно найти по формуле S=(π*r 2 /360)*А± S ∆ ;
Также существует второй вариант S = 0,5*р*r;
- r – радиус;
- А – величина угла в градусах;
- S ∆ – площадь треугольника, сторонами которого являются радиусы и хорда круга; при этом одна из его вершин располагается в центре круга, а две других – в точках соприкосновения дуги окружности с хордой. Важный момент – знак “минус” ставится в том случае, если значение А меньше 180 градусов, а знак “плюс” – если больше 180 градусов.

Чтобы упростить решение геометрической задачи, можно вычислить площадь круга он-лайн . Специальная программа быстро и безошибочно сделает расчет за пару секунд. Как рассчитать он-лайн площадь фигур? Для этого необходимо известные ввести исходные данные: радиус, диаметр, величину угла.
Окружности требуют более аккуратного подхода и встречаются в заданиях B5 гораздо реже. Вместе с тем, общая схема решения даже проще, чем в случае с многоугольниками (см. урок «Площади многоугольников на координатной сетке »).
Все, что требуется в таких заданиях — это найти радиус окружности R . Затем можно вычислить площадь круга по формуле S = πR 2 . Из этой формулы также следует, что для решения достаточно найти R 2 .
Чтобы найти указанные величины, достаточно указать на окружности точку, лежащую на пересечении линий сетки. А затем воспользоваться теоремой Пифагора. Рассмотрим конкретные примеры вычисления радиуса:
Задача. Найти радиусы трех окружностей, изображенных на рисунке:
Выполним дополнительные построения в каждой окружности:
В каждом случае точка B выбрана на окружности таким образом, чтобы лежать на пересечении линий сетки. Точка C в окружностях 1 и 3 дополняют фигуру до прямоугольного треугольника. Осталось найти радиусы:
Точка C в окружностях 1 и 3 дополняют фигуру до прямоугольного треугольника. Осталось найти радиусы:
Рассмотрим треугольник ABC в первой окружности. По теореме Пифагора: R 2 = AB 2 = AC 2 + BC 2 = 2 2 + 2 2 = 8.
Для второй окружности все очевидно: R = AB = 2.
Третий случай аналогичен первому. Из треугольника ABC по теореме Пифагора: R 2 = AB 2 = AC 2 + BC 2 = 1 2 + 2 2 = 5.
Теперь мы знаем, как искать радиус окружности (или хотя бы его квадрат). А следовательно, можем найти площадь. Встречаются задачи, где требуется найти площадь сектора, а не всего круга. В таких случаях легко выяснить, какую часть круга составляет этот сектор, и таким образом найти площадь.
Задача. Найти площадь S закрашенного сектора. В ответе укажите S /π .
Очевидно, сектор составляет одну четверть круга. Следовательно, S = 0,25 · S круга.
Остается найти S круга — площадь круга. Для этого выполним дополнительное построение:
Треугольник ABC
— прямоугольный. По теореме Пифагора имеем: R
2 = AB
2 = AC
2 + BC
2 = 2 2 + 2 2 = 8.
По теореме Пифагора имеем: R
2 = AB
2 = AC
2 + BC
2 = 2 2 + 2 2 = 8.
Теперь находим площади круга и сектора: S круга = πR 2 = 8π ; S = 0,25 · S круга = 2π .
Наконец, искомая величина равна S /π = 2.
Площадь сектора при неизвестном радиусе
Это совершенно новый тип задач, ничего подобного в 2010-2011 годах не было. По условию, нам дан круг определенной площади (именно площади, а не радиуса!). Затем внутри этого круга выделяется сектор, площадь которого и требуется найти.
Хорошая новость состоит в том, что подобные задачи — самые легкие из всех задач на площади, которые бывают в ЕГЭ по математике. К тому же, круг и сектор всегда помещается на координатную сетку. Поэтому, чтобы научиться решать такие задачи, просто взгляните на картинку:
Пусть исходный круг имеет площадь S
круга = 80. Тогда его можно разделить на два сектора площадью S
= 40 каждый (см. 2 шаг). Аналогично, каждый из этих секторов-«половинок» можно снова разделить пополам — получим четыре сектора площадью S
= 20 каждый (см. 3 шаг). Наконец, можно разделить каждый из этих секторов еще на два — получим 8 секторов-«ошметков». Площадь каждого из этих «ошметков» составит S
= 10.
3 шаг). Наконец, можно разделить каждый из этих секторов еще на два — получим 8 секторов-«ошметков». Площадь каждого из этих «ошметков» составит S
= 10.
Обратите внимание: более мелкого разбиения ни в одной задаче ЕГЭ по математике нет! Таким образом, алгоритм решения задачи B-3 следующий:
- Разрезать исходный круг на 8 секторов-«ошметков». Площадь каждого из них составляет ровно 1/8 часть площади всего круга. Например, если по условию круг имеет площадь S круга = 240, то «ошметки» имеют площадь S = 240: 8 = 30;
- Выяснить, сколько «ошметков» помещается в исходном секторе, площадь которого требуется найти. Например, если в нашем секторе помещается 3 «ошметка» площадью 30, то площадь искомого сектора равна S = 3 · 30 = 90. Это и будет ответ.
Вот и все! Задача решается практически устно. Если все равно что-то непонятно, купите пиццу и порежьте ее на 8 кусков. Каждый такой кусок будет тем самым сектором-«ошметком», которые можно объединить в более крупные куски.
А теперь разберем примеры из пробного ЕГЭ:
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 40. Найдите площадь заштрихованной фигуры.
Итак, площадь круга равна 40. Разделим его на 8 секторов — каждый площадью S = 40: 5 = 8. Получим:
Очевидно, закрашенный сектор состоит ровно из двух секторов-«ошметков». Следовательно, его площадь равна 2 · 5 = 10. Вот и все решение!
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 64. Найдите площадь заштрихованной фигуры.
Снова разделим весь круг на 8 равных секторов. Очевидно, что площадь одного их них как раз и требуется найти. Следовательно, его площадь равна S = 64: 8 = 8.
Задача. На клетчатой бумаге нарисован круг, площадь которого равна 48. Найдите площадь заштрихованной фигуры.
Опять разделим круг на 8 равных секторов. Площадь каждого из них равна S
= 48: 8 = 6. В искомом секторе помещается ровно три сектора-«ошметка» (см. рисунок). Следовательно, площадь искомого сектора равна 3 · 6 = 18.
рисунок). Следовательно, площадь искомого сектора равна 3 · 6 = 18.
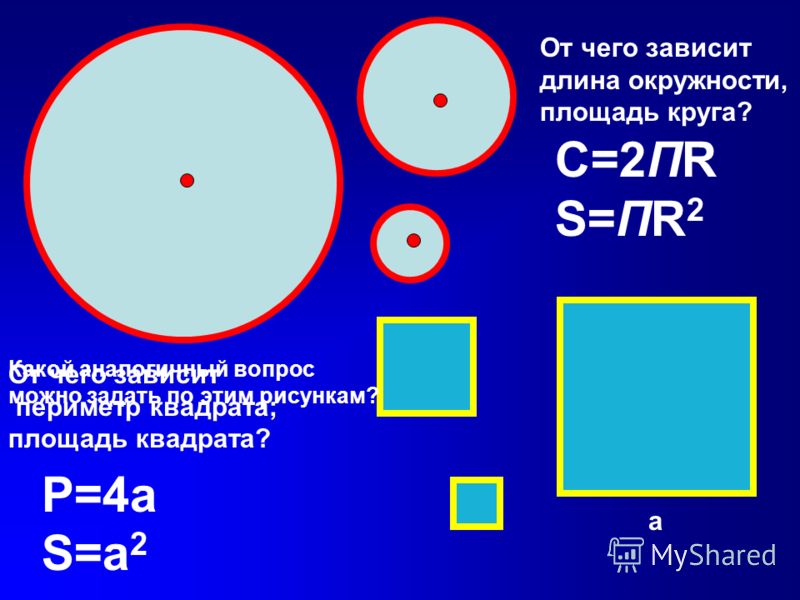
что такое пи? как вычисляется площадь круга?
Площадь круга
Ганга Б.
спросил 04.01.14диаметр колеса автомобиля 77см. сколько оборотов он сделает, чтобы преодолеть расстояние 72,6 м?
Подписаться І 7
Подробнее
Отчет
6 ответов от опытных наставников
Лучший Новейшие Самый старыйАвтор: Лучшие новыеСамые старые
Стив С. ответил 04.01.14
Репетитор
5 (3)
Обучение предварительному исчислению, тригонометрическому исчислению и дифференциальному исчислению
См. таких репетиторов
Смотрите таких репетиторов
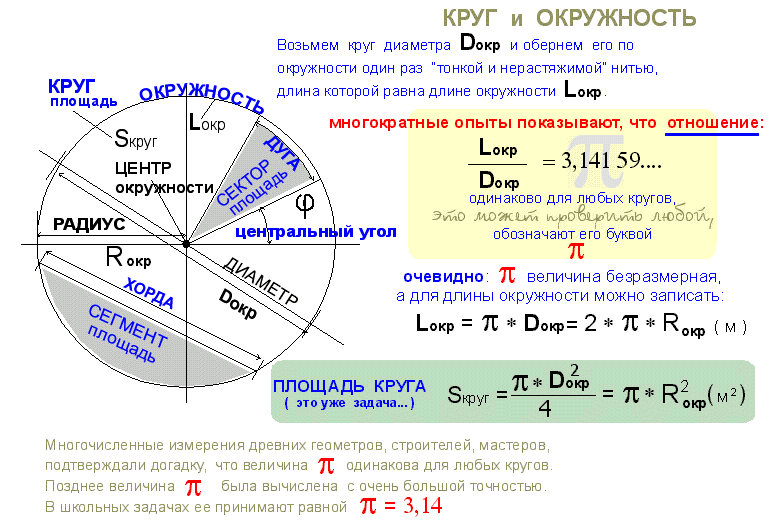
Все круги имеют одинаковую форму, но разные размеры. Фигуры, имеющие одинаковую форму, «подобны», а их соответствующие части «пропорциональны». Для всех кругов это означает, что их отношение длины окружности к диаметру равно:
Фигуры, имеющие одинаковую форму, «подобны», а их соответствующие части «пропорциональны». Для всех кругов это означает, что их отношение длины окружности к диаметру равно:
C_1 / D_1 = C_2 / D_2 = C_3 / D_3 = C_4 / D_4 = … = C_n / D_n := π или pi.
Как указано, это обыкновенное отношение определяется (:=) как число π или pi. Обратите внимание, что хотя число пи определяется как отношение чисел, оно НЕ является рациональным, поскольку не является отношением целых чисел; либо C_i, либо D_i ДОЛЖНЫ быть иррациональными.
Окружность можно аппроксимировать правильным многоугольником с n сторонами длины s и внутренним радиусом r (кратчайшее расстояние между центром и одной стороной). Площадь такого правильного многоугольника (просто сложите все треугольники): 92
=====
Автомобильное колесо диаметром D = 77 см = 0,77 м имеет окружность C = π D = π * 0,77 м.
Чтобы преодолеть расстояние 72,6 м, колесо должно будет повернуться 72,6 м / (π * 0,77 м) ≈ 30,01207498304312 ≈ 30,0 раз.
Голосовать за 0 голос против
Подробнее
Отчет
Парвиз Ф. ответил 04.01.14 92).
C = 77 π = 241,9 см / Расстояние, пройденное за
один оборот.
(7260 см)/(241,9 см/оборот) = 30 оборотов.
Голосовать за 0 голос против
Подробнее
Отчет
Уильям С. ответил 04.01.14
Репетитор
4.4 (10)
Опытный ученый, математик и преподаватель — Уильям
Смотрите таких репетиторов
Смотрите таких репетиторов
Если диаметр колеса 77см, то его окружность 77см*pi = 241,903см или 242см.
Число оборотов = 72,6 м/242 см
Преобразовать числитель в см (7260)
Количество оборотов = 7260 см/242 см = 30,012 или 30 оборотов
Голосовать за 0 голос против
Подробнее
Отчет
Ирина С. ответил 04.01.14
Репетитор
5 (1)
Математика и естествознание (репетитор со стажем)
Смотрите таких репетиторов
Смотрите таких репетиторов
Сначала вам нужна окружность или периметр круга. Вам не нужна площадь, потому что колесо вращается на краю.
C=pi×d, поэтому 3,14×77=241,78 см
1 метр равен 100 см, поэтому 241,78/100=2,4178 м, и это расстояние за один оборот в метрах.
72,6÷2,4178=30,02 или около 30 полных оборотов на заданном расстоянии.
fyi: площадь круга A=pi×r 2
Голосовать за 0 голос против
Подробнее
Отчет
Артур Д. ответил 04.01.14
Репетитор
4.9 (133)
Репетитор по математике со степенью магистра математики
Об этом репетиторе ›
Об этом репетиторе ›
сначала нужно найти длину окружности колеса
C=pi*d где pi=3,14159265…и d=77 см
C=3,14159265*77
C=241, см см, где 1 м=100 см
72,6 м=7260 см
теперь разделим 7260 на 241,; 7260/241,=30,012076 оборотов
кстати пи это отношение длины окружности к ее диаметру которое одинаково для все круга
пи — иррациональное число; бесконечное, неповторяющееся десятичное число
мы используем приближения для пи, такие как 3,14, 3,14159, 3,1416 и 22/7
Голосовать за 0 голос против
Подробнее
Отчет
Вивиан Л. ответил 04.01.14
ответил 04.01.14
Репетитор
3 (1)
Microsoft Word/Excel/Outlook, составление эссе, математика; Я ЛЮБЛЮ УЧИТЬ
Смотрите таких репетиторов
Смотрите таких репетиторов
Привет Ганга;
диаметр=77 см
расстояние=72,6 м
Наш главный приоритет касается того факта, что оба эти числа выражены в разных единицах: см и м. Преобразуем один. Случайно выбираю первое. Один метр равен 100 см.
диаметр=0,77 м
расстояние=72,6 м
Длина окружности равна расстоянию, умноженному на пи, 3,14.
окружность=(0,77 м)(3,14)
расстояние=72,6 м=(окружность)(x)
x=количество оборотов
72,6 м=(0,77 м)(3,14)(x)
9000 м2 72,6 =(2.42 )(x)Разделим обе части на 2,42…
30,0=x
Голосовать за 0 Голосовать против
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.

Задайте вопрос бесплатно
Получите бесплатный ответ на быстрый вопрос.
Ответы на большинство вопросов в течение 4 часов.
ИЛИ
Найдите онлайн-репетитора сейчас 92 | Сделай сам
Твиттер Инстаграм Фейсбук Пинтерест
Окружность – это замкнутая двумерная фигура с центром, где все точки плоскости равноудалены. Некоторыми примерами кругов являются колеса, пицца, круглая земля и т. д. Формула площади круга полезна для измерения площади, занимаемой круглым полем или участком.
Допустим, у вас есть участок для его ограждения, тогда формула площади поможет вам проверить, сколько требуется ограждения. Или предположим, что вам нужно купить скатерть, то сколько порций ткани нужно, чтобы полностью ее покрыть.
Но почему площадь круга равна пи, умноженному на квадрат радиуса? Обычное определение числа пи — это отношение длины окружности к ее диаметру, так что длина окружности равна пи, умноженному на диаметр, или двум пи, умноженным на радиус.
Этот удивительный проект «Сделай сам» показывает, что круг можно разрезать и переставить так, чтобы он напоминал параллелограмм с высотой r и основанием, равным pi, умноженному на r, путем разделения круга на части. Если вы сделаете больше срезов, аппроксимация, полученная таким образом, будет еще лучше. Кстати, есть еще один прекрасный способ понять математику площади круга! Вы можете проверить это здесь.
Впервые эта идея пришла мне в голову из прекрасной книги Стивена Строгаца «Бесконечные силы » об истории исчисления, когда я учился в колледже.
Ингредиенты:
- Карандаш
- Маркеры
- Лист бумаги
- Compass
- Scissors
- RULER
- Pen
- 18.

- .
Шаг 2
ВЫРЕЗАЙТЕ КРУГ: Используйте циркуль, чтобы нарисовать круг на бумаге. Вырежьте его, сложите пополам и с помощью линейки проведите линию вдоль сгиба.Шаг 3
РАЗРЕЗАТЬ НА СЕГМЕНТЫ: снова сложите пополам и с помощью линейки проведите линию вдоль сгиба. Повторите еще дважды, пока у вас не будет 8 равных секторов, отмеченных в круге…Шаг 4
Затем раскрасьте половину секторов, прежде чем вырезать их все. Теперь у вас должно быть 8 секторов.Шаг 5
СДЕЛАЙТЕ ПАРАЛЛЕЛОГРАМ: Переставьте сектора так, чтобы четыре были внизу и четыре наверху, чтобы получилась фигура, немного похожая на параллелограмм.Шаг 6
ПРЯМОУГОЛЬНИК πr x r : Сложите крайний сектор пополам и разрежьте вдоль сгиба, чтобы получились два полусектора. Поместите по одному на каждый конец, чтобы сформировать форму, близкую к прямоугольнику…Шаг 7
.высота прямоугольника равна радиусу окружности, или сокращенно r. Его основание почти точно соответствует изогнутым внешним сторонам цветных секторов или половине окружности круга. Итак, если длина окружности равна 2πr, основание должно быть равно πr.
Итак, если длина окружности равна 2πr, основание должно быть равно πr.Шаг 8
Площадь прямоугольника равна основанию x высоте. Итак, если основание равно πr, а высота равна r, площадь прямоугольника равна πr x r. Другой способ записать это — π r², потому что r x r = r². СОВЕТ: π чуть больше 3, поэтому площадь круга примерно равна 3 x r².Шаг 9
Быстрый способ запомнить площадь круга — представить себе квадрат размером r x r. Его площадь равна r x r = r². Теперь, если вы представите, что этот квадрат разрезается по диагонали, вы увидите, что площадь круга больше 2 r². Но меньше 4 r². Так примерно 3 r².Детали для самостоятельной сборки
Источник
BBC Bitesize
Ср. Продолжительность
30 мин
Получить Abakcus прямо на ваш почтовый ящик
Порекомендуйте это своими руками
Похожие самоделки
Похожие самоделки
Как сделать бумажный микроскоп за 5 долларов?
Хотите иметь собственный микроскоп всего за 5 долларов? Foldscope — это бумажный микроскоп, который поможет вам получить классный научный инструмент!
Научный эксперимент Attarctive Nails
Attractive Nails — это красивый инженерный проект «сделай сам».
 Когда вы закончите с этим, вы можете сделать свой собственный электромагнит.
Когда вы закончите с этим, вы можете сделать свой собственный электромагнит.Как сделать перископ?
Сделать перископ из картона и нескольких кусочков зеркала проще, чем вы думаете. Вот планы и инструкции для перископа.
Как сделать картофельную силу?
Знаете ли вы, что скромная картошка может питать лампочку? Вот так! Ваша любимая еда — это мини-батарейка! Вот как!
Как сделать самодельную водяную бомбу?
Хотите весело провести время дома с детьми? Вот совершенно интересный сделай сам инженерный проект для тебя!
Научный эксперимент с горящим пудингом
Хочешь увидеть что-нибудь интересное? Вот научный эксперимент своими руками, который вы и ваши дети можете провести дома.
Крепкий орешек для научного эксперимента
Вот веселый и полезный научный эксперимент! Вы можете использовать бразильские орехи и крекер для орехов, чтобы открыть скорлупу, не повредив орех.
Как построить компас?
Хотите сделать самодельный компас с помощью иглы и магнита? Это очень простой и забавный эксперимент о магнетизме.

Научный эксперимент с желатином и маслом
Этот красивый инженерный проект покажет вам, почему масло используется в двигателях, чтобы обеспечить легкое скольжение движущихся частей друг относительно друга.
Abakcus — лучший сайт только для математики и естественных наук. Мы делаем тяжелую работу и отбираем лучшие статьи, книги, инструменты, продукты, видео и проекты.
Твиттер Facebook-f Инстаграм Пинтерест
Категории
© Все права защищены
Сделано с ❤ Али Кая
Дизайн Хусейн Эркмен
Abakcus участвует в партнерской программе Amazon Services LLC, чтобы получать комиссионные за подключение к Amazon. Другими словами, это означает, что всякий раз, когда вы покупаете что-то на Amazon по ссылке здесь, мы получаем небольшой процент от его цены.
Что такое число Пи? | Живая наука
Живая наука поддерживается своей аудиторией. Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию.
Рукописные числа Пи на зеленой доске. (Изображение предоставлено: domin_domin через Getty Images) Вот почему вы можете доверять нам.
Вот почему вы можете доверять нам.Пи — это число, которое связывает длину окружности с ее диаметром. Пи — это иррациональное число , что означает, что это действительное число, которое не может быть выражено простой дробью. Это потому, что пи — это то, что математики называют «бесконечным десятичным числом» — после запятой цифры продолжаются вечно.
Студенты обычно знакомятся с числом пи, имеющим приблизительное значение 3,14 или 3,14159.. Хотя это иррациональное число, некоторые люди используют рациональные выражения, такие как 22/7 или 333/106, для оценки числа пи. (Эти рациональные выражения точны только до пары знаков после запятой.)
Математики и энтузиасты математики заинтересованы в вычислении числа пи с максимально возможным числом знаков. Рекорд по произнесению большинства цифр числа «пи» принадлежит Сурешу Кумару Шарме из Индии, который в 2015 году произнес число «пи» с точностью до 70 030 знаков после запятой, согласно мирового рейтинга числа пи (открывается в новой вкладке).
 Между тем, некоторые компьютерные программы рассчитали значение pi до поразительных 62,8 триллионов цифр, ранее сообщалось Live Science о . Подобные расчеты часто публикуются в День Пи, псевдопраздник, который отмечается каждый год 14 марта (14 марта).
Между тем, некоторые компьютерные программы рассчитали значение pi до поразительных 62,8 триллионов цифр, ранее сообщалось Live Science о . Подобные расчеты часто публикуются в День Пи, псевдопраздник, который отмечается каждый год 14 марта (14 марта).Похожие: 11 чисел, которые круче, чем число Пи
Каковы первые 100 цифр числа Пи?
The first 100 digits of pi are:
3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 7067
На веб-сайте piday.org (открывается в новой вкладке) число пи указано до первого миллиона цифр.
Откуда взялось число Пи?
Некоторые уравнения геометрии кругов (Изображение предоставлено Барри Барнсом через Shutterstock)По определению, пи — это отношение длины окружности к ее диаметру. Другими словами, пи равно длине окружности, деленной на диаметр (π = c/d). И наоборот, длина окружности равна пи, умноженному на диаметр (c = πd).
 Независимо от того, насколько большой или маленький круг, число Пи всегда будет одним и тем же. Пи (π) — это 16-я буква греческого алфавита, которая используется для обозначения широко известной математической константы.
Независимо от того, насколько большой или маленький круг, число Пи всегда будет одним и тем же. Пи (π) — это 16-я буква греческого алфавита, которая используется для обозначения широко известной математической константы.Кто изобрел число Пи?
Число Пи известно уже почти 4000 лет и было открыто древними вавилонянами. Табличка, датируемая где-то между 1900 г. до н.э. и 1680 г. до н.э. обнаружил, что число пи равно 3,125, согласно Exploratorium в Сан-Франциско (открывается в новой вкладке). Люди в Древнем Египте делали подобные открытия, о чем свидетельствует папирус Райнда 1650 г. до н.э. В этом документе египтяне рассчитали площадь круга по формуле, дающей число Пи приблизительно равное 3,1605. Есть даже библейский стих, в котором, по-видимому, число «пи» было приблизительно равно 9.0500 к переписке, опубликованной в 1999 году в журнале Nature :
И он сделал расплавленное море, десять локтей от одного края до другого: оно было кругом, а высота его была пять локтей; и окружала его линия в тридцать локтей.
 — I Царств 7:23 (версия короля Иакова)
— I Царств 7:23 (версия короля Иакова)Одно из первых вычислений числа пи было выполнено греческим математиком Архимедом Сиракузским (287 г. до н. э. — 212 г. до н. э.), согласно Exploratorium (откроется в новой вкладке). Архимед использовал теорему Пифагора, чтобы найти площади двух многоугольников. Архимед аппроксимировал площадь круга на основе площади правильного многоугольника, вписанного в круг, и площади правильного многоугольника, внутри которого описан круг. Многоугольники в том виде, в каком их нанес на карту Архимед, давали верхнюю и нижнюю границы площади круга, и он приблизил число пи между 3 1/7 и 3 10/71.
Гравюра, изображающая последние мгновения жизни греческого математика и изобретателя Архимеда (ок. 287–212 до н. э.), когда он размышлял над математической диаграммой незадолго до своей смерти от рук римских солдат, вторгшихся в Сиракузы, Сицилия, в 212 г. до н. э. (Изображение предоставлено: Stock Montage через Getty Images)Ранее китайский математик и астроном Цзу Чунчжи (429–501 гг.
 2 = 28,27 см. Потому что кругов часто встречаются в природе и часто используются в других математических уравнениях, число пи окружает нас повсюду и используется постоянно.
2 = 28,27 см. Потому что кругов часто встречаются в природе и часто используются в других математических уравнениях, число пи окружает нас повсюду и используется постоянно.Пи проник даже в литературный мир. Пилиш — это форма письма на английском языке, в которой количество букв в последовательных словах следует за цифрами числа пи, согласно автору Майку Киту (открывается в новой вкладке). Кит использовал Пилиша в своей книге « Not A Wake. » Вот пример из книги: « Сейчас я падаю, усталый пригородник в жидкости под деревьями, Дрейфующий вдоль лесов, кипящих красным в сумерках над Европой.»
«Сейчас» состоит из 3 букв, « I» состоит из 1 буквы, « осень» состоит из 4 букв, « a» имеет 1 письмо и т. д.
Эта статья была обновлена 19 октября 2018 г. старшим автором Live Science Брэндоном Спектором. Она была обновлена еще раз 3 марта 2022 г. участником Live Science Адамом Манном
Дополнительно ресурсы
- Узнайте больше о числе Пи, его истории и значении из piday.
 org (открывается в новой вкладке)
org (открывается в новой вкладке) - Смейтесь (или вздыхайте) над этими шутками и каламбурами, связанными с числом пи (открывается в новой вкладке) с образовательного сайта The Nine Planets
Библиография
Exploratorium. (н.д.). Краткая история pi . Получено 3 марта 2022 г. с https://www.exploratorium.edu/pi/history-of-pi (открывается в новой вкладке)
Кейт, М. (2010). Не поминки. Винкулум Пресс. Получено 3 марта 2022 г. с http://www.cadaeic.net/notawake.htm (открывается в новой вкладке)
Кит М. (без даты). Написание по-филисски . Получено 3 марта 2022 г. с http://www.cadaeic.net/pilish.htm (открывается в новой вкладке)
Подготовка к тесту Mometrix. (без даты) 1 миллион цифр числа пи . Получено 3 марта 2022 г. с https://www.piday.org/million (открывается в новой вкладке)
Peil, N. (1999). Библейский ответ на приготовление пи. Природа 399 (522).

- Узнайте больше о числе Пи, его истории и значении из piday.


 Итак, если длина окружности равна 2πr, основание должно быть равно πr.
Итак, если длина окружности равна 2πr, основание должно быть равно πr. Когда вы закончите с этим, вы можете сделать свой собственный электромагнит.
Когда вы закончите с этим, вы можете сделать свой собственный электромагнит.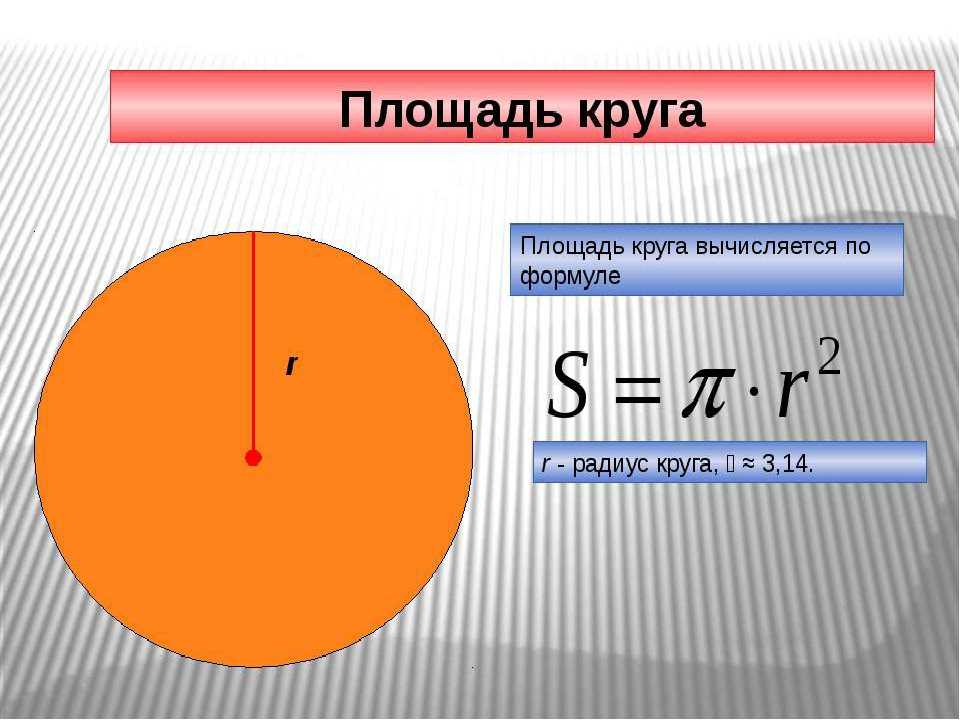
 Вот почему вы можете доверять нам.
Вот почему вы можете доверять нам. Между тем, некоторые компьютерные программы рассчитали значение pi до поразительных 62,8 триллионов цифр, ранее сообщалось Live Science о . Подобные расчеты часто публикуются в День Пи, псевдопраздник, который отмечается каждый год 14 марта (14 марта).
Между тем, некоторые компьютерные программы рассчитали значение pi до поразительных 62,8 триллионов цифр, ранее сообщалось Live Science о . Подобные расчеты часто публикуются в День Пи, псевдопраздник, который отмечается каждый год 14 марта (14 марта). Независимо от того, насколько большой или маленький круг, число Пи всегда будет одним и тем же. Пи (π) — это 16-я буква греческого алфавита, которая используется для обозначения широко известной математической константы.
Независимо от того, насколько большой или маленький круг, число Пи всегда будет одним и тем же. Пи (π) — это 16-я буква греческого алфавита, которая используется для обозначения широко известной математической константы. — I Царств 7:23 (версия короля Иакова)
— I Царств 7:23 (версия короля Иакова) 2 = 28,27 см. Потому что кругов часто встречаются в природе и часто используются в других математических уравнениях, число пи окружает нас повсюду и используется постоянно.
2 = 28,27 см. Потому что кругов часто встречаются в природе и часто используются в других математических уравнениях, число пи окружает нас повсюду и используется постоянно. org (открывается в новой вкладке)
org (открывается в новой вкладке)