Расчет характеристик полого прямоугольного сечения
- Подробности
Калькулятор онлайн рассчитывает геометрические характеристики (площадь, моменты инерции, моменты сопротивления изгибу, радиусы инерции) плоского сечения в виде полого прямоугольника (прямоугольной трубы) по известным линейным размерам и выводит подробное решение.
| Исходные данные: | ||
| Наружная ширина b, мм | ||
| Наружная высота h, мм | ||
| Толщина горизонтальной стенки sh, мм | ||
| Толщина вертикальной стенки sb, мм | ||
| Определение вспомогательных данных: | ||
| Внутренняя ширина, мм | расчет внутренней ширины полого прямоугольника | |
| Внутренняя высота, мм | расчет внутренней высоты полого прямоугольника | |
| Решение: | ||
| Площадь сечения, мм2 | расчет площади сечения полого прямоугольника | |
| Осевые моменты инерции относительно центральных осей, мм4 | расчет момента инерции полого прямоугольника относительно оси ОХ расчет момента инерции полого прямоугольника относительно оси ОY | |
| Моменты сопротивления изгибу, мм3 | расчет момента сопротивления изгибу полого прямоугольника относительно оси ОХ расчет момента сопротивления изгибу полого прямоугольника относительно оси ОY | |
| Радиусы инерции сечения, мм | расчет радиуса инерции полого прямоугольника относительно оси ОХ расчет радиуса инерции полого прямоугольника относительно оси ОY | |
I.
Порядок действий при расчете характеристик полого прямоугольного сечения:
- Для проведения расчета требуется ввести ширину сечения b, высоту сечения h и соответствующие толщины стенок Sh и Sb.
- По введенным данным программа автоматически вычисляет внутреннюю ширину сечения b1 и высоту сечения h1.
- Результаты расчета площади, моментов сопротивления изгибу, моментов и радиусов инерции полого прямоугольного сечения выводятся автоматически.
- На рисунке справа приведены необходимые размеры элементов сечения.
II. Примечание:
- Блок исходных данных выделен желтым цветом, блок промежуточных вычислений выделен голубым цветом, блок решения выделен зеленым цветом.
Расчет прогиба балки онлайн калькулятор. Площадь поперечного сечения профиля. Расчет на прочность. • AST3D
Skip to content
 Главная › Инфо › Расчет прогиба балки онлайн калькулятор.
Площадь поперечного сечения профиля. Расчет на прочность.
При проектировании и изготовлении конструкций из металла и других материалов очень важно соблюдать и выполнять физико-механические расчеты на прочность, одним из которых является расчет балок на изгиб (прогиб). Выполнять расчет прогиба балки онлайн — очень удобно и быстро. Поэтому специалисты нашего предприятия подготовили онлайн калькулятор для расчетов.
Расчет прогиба балки онлайн
Профиль
Материал
СтальЧугунАлюминийДеревоФанераМедьФторопластАкрилПоликарбонат
Способ фиксации
Шарнир-Шарнир (распределенная) Шарнир-Шарнир (точечная) Заделка-Шарнир (распределенная) Заделка-Шарнир (точечная) Заделка-Заделка (распределенная) Заделка-Заделка (точечная) Свободный конец (распределенная) Свободный конец (точечная)Схема фиксации
Значения
Выберите профиль
Результаты расчетов
Площадь поперечного сечения профиля:
—
Расчетный вес профиля (балки):
—
Прогиб балки F
—
Описание
При выборе схемы с распределенной нагрузкой, приложенная «Нагрузка Q» указывается как относительная «килограмм на метр».
Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].
Использование калькулятора «Расчет прогиба балки онлайн» значительно сократит время и послужит залогом надежных инженерных конструкций.
Калькулятор разработан исключительно по формулам Сопромата и справочным данным для каждого типа материала и сечения балки. Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий.
Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.
Сделать расчет вала ЧПУ на прогиб также можно произвести на данном калькуляторе. Следовательно Вы будете знать предварительные прочностные показатели перед сборкой ЧПУ станка.
Для быстрого доступа к расчетам необходимого профиля добавьте калькулятор в избранное (CTRL+D на ПК или значек «звездочка» справа вверху браузера)
Ключевые слова: расчет балки на прогиб, расчет балки на прочность, расчет балки на двух опорах, расчет балки на изгиб, расчет балки онлайн бесплатно, расчет балки перекрытия, расчет балки на прогиб пример, расчет балки онлайн, расчет прогиба деревянной балки, расчет прогиба балки, расчет прогиба профильной трубы онлайн, расчет прогиба балки на двух опорах, расчет прогиба плиты перекрытия, расчет прогиба швеллера, beam deflection calculator, free, calculator online, Free Online Beam Calculator, Elastic beam deflection calculator, расчет прогиба металлической балки, расчет прогиба листа, расчет прогиба фанеры, расчет на прочность онлайн, расчет на прочность при изгибе, расчет на прогиб деревянной балки, расчет на прогиб металлической балки, расчет на прогиб, расчет на прогиб уголка
Редакция AST3D 17.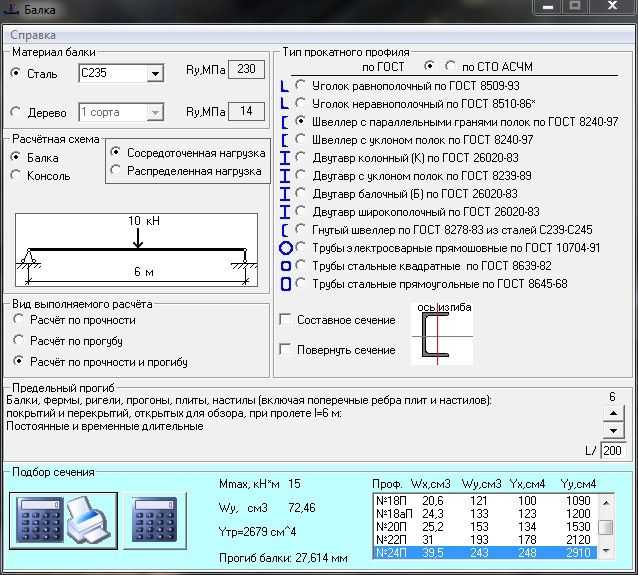
09.2018 11:11
Калькулятор свойств прямоугольного полого профиля
Калькулятор свойств прямоугольного полого сечения для площадь поперечного сечения, вес, второй момент площади, модуль сечения и радиус расчет вращения полого прямоугольного сечения.
| ВХОДНЫЕ ПАРАМЕТРЫ | ||
| Параметр | Значение | |
| Высота [В] | ||
| Ширина [В] | ||
| Внутренняя высота [ч] | ||
| Внутренняя ширина [b] | ||
| Длина [л] | 93 | |
| | ||
| РЕЗУЛЬТАТЫ | ||
| Параметр | Значение | |
| Площадь поперечного сечения (А) | — 92 | |
| Масса (М) | — | кгфунтов |
| Второй момент площади (Ixx) | — | 93|
| Модуль сечения (Syy) | — | |
| Радиус вращения (rx) | — | |
| Радиус вращения (ry) | — | |
| Расстояние CoG в направлении x (xcog) | — | |
| Расстояние CoG в направлении Y (ycog) | — | |
Примечание.
Используйте точку «.» как десятичный разделитель.
Второй момент площади: расстояние от оси, на котором площадь тела можно считать равной сосредоточена, а площадь второго момента этой конфигурации равна площадь второго момента фактического тела относительно той же оси.
Модуль сечения: Момент инерция площади поперечного сечения элемента конструкции, деленная на расстояние от центра тяжести до самой дальней точки сечения; а мера прочности балки на изгиб.
Труба прямоугольного сечения | calcresource
Содержание
— Геометрия
— Момент инерции
-Elastic Modulus
-Пластиковый модуль
-около x оси
-около оси Y
-Радиус круга
-прямоугольная сечтная формула
-Связанные страницы
Геометрия
.
внешний периметр P_\textit{out} и внутренний периметр P_\textit{in} прямоугольного сечения трубы можно найти по следующим формулам:
\begin{split} & A & = b h — b_i h_i\\ & P_ {out} & = 2(b+h)\\ & P_{in} & = 2(b_i+h_i) \end{split}
где b, h внешние стороны прямоугольного сечения трубы и b_i, h_i соответствующие внутренние стороны. Последние составляют:
- b_i=b-2t внутренняя ширина
- h_i=h-2t внутренняя высота
где t толщина стен.
Момент инерции
Момент инерции (второй момент площади) прямоугольного сечения трубы относительно оси x, проходящей через ее центр тяжести и параллельной ее основанию b, можно найти по следующему выражению: 93}{12}
Момент инерции (второй момент или площадь) используется в теории балок для описания жесткости балки при изгибе. Изгибающий момент M, приложенный к поперечному сечению, обычно связан с моментом инерции поперечного сечения следующим уравнением:
M = E\times I \times \kappa
свойство материала, а \kappa кривизна балки из-за приложенной нагрузки.
Таким образом, из предыдущего уравнения видно, что при приложении определенного изгибающего момента M к поперечному сечению балки развиваемая кривизна обратно пропорциональна моменту инерции I.
Полярный момент инерции описывает жесткость поперечного сечения по отношению к моменту кручения, так же как описанные выше плоские моменты инерции связаны с изгибом. Расчет полярного момента инерции I_z вокруг оси z (перпендикулярной сечению) можно выполнить с помощью теоремы о перпендикулярных осях:
I_z = I_x + I_y
, где I_x и I_y — моменты инерции вокруг осей x и y, взаимно перпендикулярных z-z и встречающихся в общем начале координат. 94 .
Модуль упругости
Модуль упругого сечения S_x любого поперечного сечения вокруг его центральной оси x описывает реакцию сечения на упругий изгиб вокруг той же оси. Он определяется как:
S_x = \frac{I_x}{Y}
, где I_x — момент инерции сечения вокруг оси x, а Y — расстояние от центра тяжести волокна сечения, параллельного той же оси.
Обычно представляет интерес более удаленное волокно. Если поперечное сечение симметрично (прямоугольная труба) вокруг оси (например, по центроиду x) и его размер, перпендикулярный этой оси, равен h, тогда Y=h/2, и приведенная выше формула принимает вид:
S_x = \frac{2I_x}{h}
Аналогично, для модуля сечения S_y вокруг оси y, которая также является осью симметрии, приведенные выше определения записываются как:
S_y = \frac{ I_y}{X} \Rightarrow S_y = \frac{2 I_y}{b}
Если изгибающий момент M_x приложен вокруг оси x-x, сечение будет реагировать нормальными напряжениями, линейно изменяющимися с расстоянием от нейтральной оси (которое в упругом режиме совпадает с центральной осью x). Над нейтральной осью напряжения равны нулю. Абсолютный максимум \сигма будет иметь место в самом удаленном волокне, величина которого определяется формулой: 93 .
Модуль пластичности
Модуль упругости аналогичен модулю упругости, но определен с учетом полной пластической текучести поперечного сечения вследствие изгибного изгиба.
В этом случае все сечение разделено на две части, одну на растяжение и одну на сжатие, каждая из которых находится под однородным полем напряжений. Для материалов с равными напряжениями текучести при растяжении и сжатии это приводит к разделению сечения на две равные области, A_t при растяжении и A_c при сжатии, разделенные нейтральной осью. Это результат уравновешивания внутренних сил в поперечном сечении при пластическом изгибе. В самом деле, сжимающая сила будет равна A_cf_y, если предположить, что предел текучести равен f_y при сжатии, и что материал по всей площади сжатия поддался (таким образом, напряжения везде равны f_y). Точно так же растягивающая сила будет равна A_t f_y, если использовать те же предположения. Обеспечение равновесия:
A_cf_y = A_t f_y\Rightarrow
A_c= A_t
Ось называется пластической нейтральной осью , а для несимметричных сечений не совпадает с упругой нейтральной осью (которая снова является центроидальной).
Вокруг оси x
Модуль пластического сечения задается общей формулой (при условии изгиба вокруг оси x):
Z_x = A_c Y_c + A_t Y_t
где Y_c, расстояние от центра масс области сжатия A_c, от пластической нейтральной оси, и Y_t, соответствующее расстояние от центра тяжести области растяжения A_t.
В случае прямоугольного поперечного сечения трубы пластическая нейтральная ось проходит через центр тяжести, разделяя всю площадь на две равные части. Используя преимущество симметрии, это: Y_c=Y_t. Найти эти центроиды несложно. Мы будем рассматривать часть над нейтральной осью (предполагаемой при сжатии). Центр тяжести этой детали расположен на расстоянии Y_c от нейтральной пластической оси. Удобно предположить, что вся часть эквивалентна разности внешнего прямоугольника с размерами b и h/2 за вычетом внутреннего прямоугольника с размерами b-2t и h/2-t. Затем находят центр тяжести всей детали, делая статический момент инерции (первый момент площади) всей детали равным разности двух ее прямоугольных площадей. Помните, что рассматриваемая деталь имеет половину общей площади сечения: 92 \over 4}\right)
где:
- b_i=b-2t, внутренняя ширина поперечного сечения трубы, и
- h_i=h-2t, внутренняя высота поперечного сечения трубы
Принимая во внимание, что Y_c=Y_t (из-за симметрии) и учитывая, что A_c=A_t, модуль пластического сечения прямоугольной трубы вокруг оси x находится:
Z_x = A_c Y_c + A_t Y_t \Rightarrow
Z_x = 2 A_c Y_c \Rightarrow
Z_x = 2 {A\over2} {1\over A} \left({b h^2 \over 4} -{b_i h_i^2 \over 4}\вправо) \стрелка вправо 92\over4}
Тогда всю прямоугольную трубу можно рассматривать как разность между внешним прямоугольником с размерами b и h и внутренним прямоугольником с размерами b_i и h_i, как показано на следующем рисунке.
Оба прямоугольника имеют одну и ту же центральную ось x (иначе мы не смогли бы продолжить). С учетом этого вышеприведенная формула выводится естественным образом, как разность модулей пластичности между этими двумя прямоугольниками.
Вокруг оси y
Следуя аналогичной процедуре, модуль пластического сечения вокруг оси y находится по следующей формуле: 92}{4}
Обратите внимание, что последняя формула аналогична формуле для модуля пластичности Z_x, но с заменой местами размеров высоты и ширины.
Радиус вращения
Радиус вращения R_g поперечного сечения относительно оси определяется по формуле:
R_g = \sqrt{\frac{I}{A}}
где I момент инерции поперечного сечения вокруг той же оси и A его площади. Размеры радиуса вращения [Длина]. Он описывает, насколько далеко от центра тяжести распределена область. Малый радиус указывает на более компактное сечение. Круг – это форма с минимальным радиусом вращения по сравнению с любым другим сечением с такой же площадью А.