Урок математики по теме:»Площадь многоугольника»
Цели:
- обучающие: научить учащихся находить площадь многоугольника, используя выбранные ими способы, сформировать начальные представления
- многоугольнике, графические и измерительные навыки;
- развивающие: развитие способов умственной деятельности учащихся при выполнении заданий от наблюдения, расчетов до выяснения закономерностей вычисления площади многоугольника;
- воспитывающие: раскрытие субъективного опыта учащихся, поощрение действий, стремлений учащихся как основы воспитания положительных качеств личности;
- методическая: создание условий для проявления познавательной активности учащихся.
Оснащение урока:
- Оформление доски: слева — фигуры многоугольника,
справа — чистое полотно доски для записи на уроке,
в центре – многоугольник-прямоугольник.

- Листок “К исследованию”.
- Инструментарии учителя и учащихся (мел, указка, линейка, листок исследования, фигуры, ватман, маркер).
Метод урока:
- По взаимодействию учителя и учащихся – диалог-общение;
- По способу решения задач – частично-поисковый;
- По способу умственной деятельности — (СУД) развивающее обучение.
Форма урока — фронтальная, в парах, индивидуальная.
Тип урока — урок усвоения новых знаний, умений и навыков.
Структура урока — постепенное углубление в тему, гибкая, диалогическая.
Ход урока
Приветствие.
Урок прекрасен и приносит радость, когда мы мыслим, дружно работаем. Сегодня мы будем рассматривать фигуры, определять их названия, думать, искать и находить решения. Пожелаем друг другу успешной работы.
Актуализация знаний.
Рассмотрите фигуры (на доске многоугольники).
Они все вместе. Почему? Какой у них общий признак? (Многоугольники).
Назовите этот многоугольник (5-угольник, 6-угольник…)
Может быть, вы знаете, что такое площадь многоугольника?
Тогда покажите на одной из фигур.
(Обобщение учителем: площадь — часть плоскости внутри замкнутой геометрической фигуры.)
В русском языке это слово имеет несколько значений.
(Ученик по словарю знакомит со значениями.)
- Часть плоскости внутри замкнутой геометрической фигуры.
- Большое незастроенное и ровное место.
- Помещение для какой-либо цели.
Какое из значений используется в математике?
В математике используется первое значение.
(На доске фигура).
Назовите фигуру по-другому. Прямоугольник.
Покажи длину, ширину.
Как найти площадь многоугольника?
Запишите при помощи букв и знаков формулу.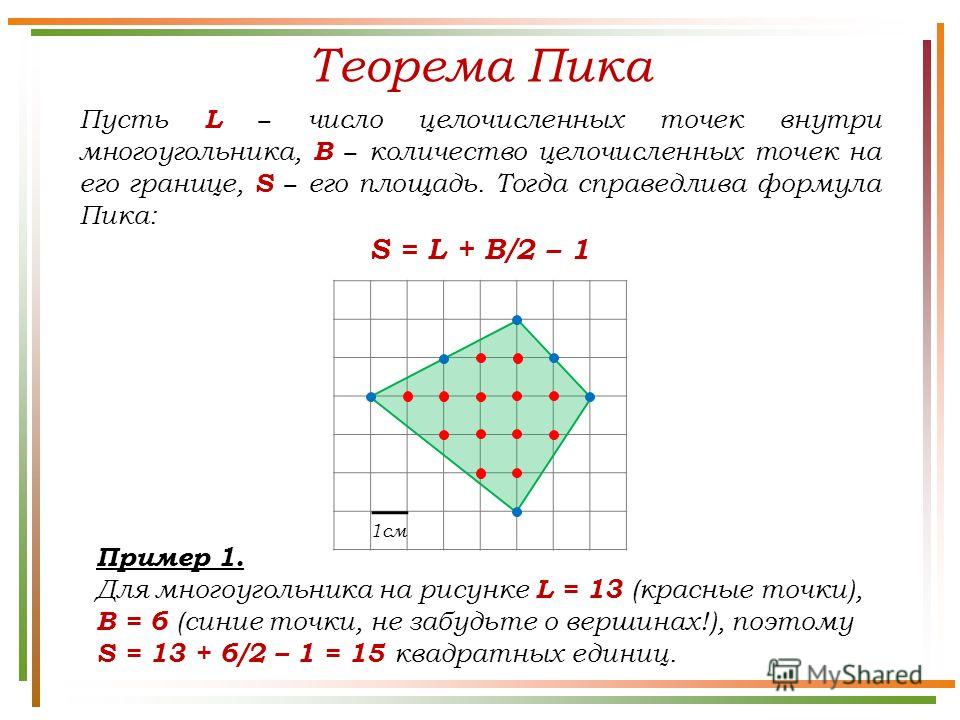
S = а * в
Если длина нашего прямоугольника 20 см, ширина 10см. Чему равна площадь?
Площадь равна 200 см2
Подумайте, как приложить линейку, чтобы фигура разделилась на:
- Два треугольника
- Два четырехугольника
- Треугольник и четырехугольник
- Треугольник и пятиугольник
Увидели, из каких частей состоит фигура? А теперь, наоборот, по частям соберем целое.
( Части фигуры лежат на партах. Дети собирают из них прямоугольник ).
Сделайте вывод по наблюдениям.
Целую фигуру можно разделить на части и из частей составить целую.
Дома на основе треугольников и четырехугольников составляли фигуры, силуэты. Вот какие они получились.
(Демонстрация рисунков, выполненных дома учащимися. Одна из работ анализируется).
Какие фигуры использовал? У тебя получился сложный многоугольник.
Постановка учебной задачи.
На уроке мы должны ответить на вопрос: как найти площадь сложного многоугольника?
Для чего человеку нужно находить площадь?
(Ответы детей и обобщение учителем).
Задача определения площади возникла из практики.
(Показывается план школьного участка).
Для того чтобы построить школу, сначала создали план. Потом разбивалась территория на участки определенной площади, размещались строения, клумбы, стадион. При этом участок имеет определенную форму — форму многоугольника.
Решение учебной задачи.
(Раздаются листы для исследования).
Перед вами фигура. Назовите ее.
Многоугольник, шестиугольник.
Найдем площадь многоугольника. Что для этого надо делать?
Разделить на прямоугольники.
(При затруднении будет другой вопрос: “Из каких фигур состоит многоугольник?”).
Из двух прямоугольников.
С помощью линейки и карандаша разделите фигуру
на прямоугольники. Обозначьте цифрами 1 и 2
полученные части.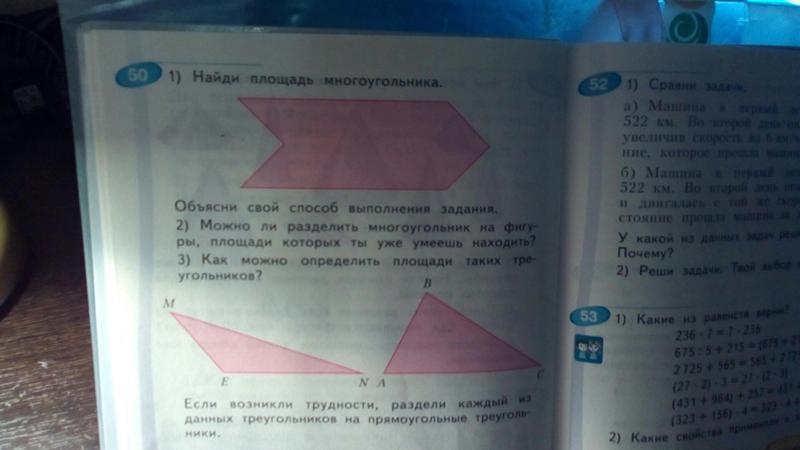
Проведем измерения.
Найдем площадь первой фигуры.
(Учащиеся предлагают следующие варианты решений и записывают их на доске).
1способ:
- S1 = 5 ? 2 = 10 см2
- S2 = 5 ? 1 = 5 см2
Зная площадь частей, как найти площадь целой фигуры?
S = 10 + 5 = 15 см2
2 способ:
- S1 = 6 ? 2 = 12 см 2
- S2 = 3 ? 1 = 3 см2
- S = 12 + 3 = 15 см2.
Сравните результаты и сделайте вывод.
Проследим наши действия
Как находили площадь многоугольника?
Составляется и записывается на плакате алгоритм:?
1. Делим фигуру на части
2. Находим площади частей этих многоугольников ( S1, S2 ).
3. Находим площадь целого многоугольника ( S1 + S 2 ).
Проговорить алгоритм.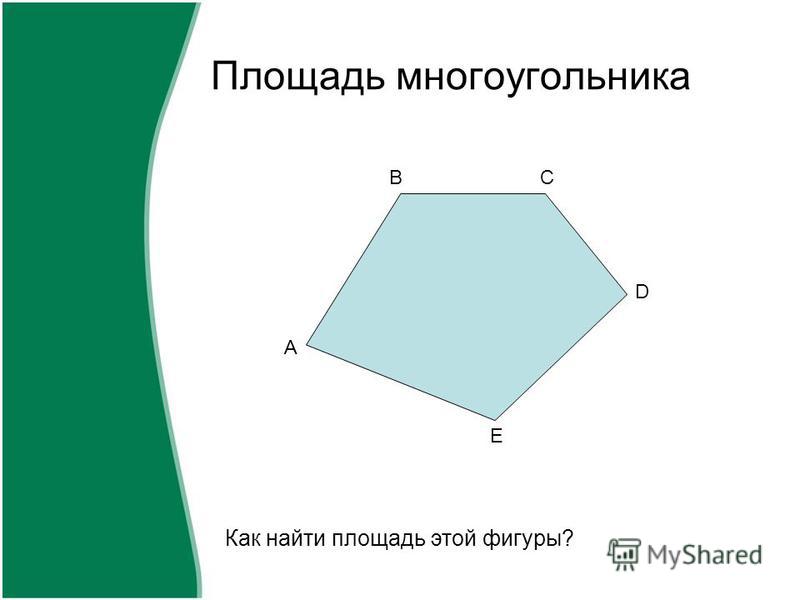
( Несколько учащихся проговаривают алгоритм).
Мы нашли два способа, а может, есть еще?
А можно фигуру достроить.
Сколько прямоугольников получилось?
Два.
Обозначим части 1 и 2. Проведем измерения.
Найдите площадь каждой части многоугольника.
- S1=6? 5=30см2
- S2= 5 ? 3 = 15 см2
Как найти площадь нашего шестиугольника?
S = 30 – 15 = 15 см2
Составим алгоритм:
Достроили фигуру до прямоугольника
Нашли S1 и S2.
Нашли разность S1 – S2.
Сравните два алгоритма. Сделайте вывод. Какие действия одинаковые? Где разошлись наши действия?
Закройте глазки, опустите головки. Мысленно повторите алгоритм.
Мы провели исследовательскую работу, рассмотрели разные способы и теперь можем находить площадь любого многоугольника.
Проверка результативности.
Проверьте себя.
Перед вами многоугольники.
Найти площадь одной фигуры по выбору, при этом можете пользоваться разными способами.
Работа выполняется самостоятельно. Дети выбирают фигуру. Находят площадь одним из способов. Проверка – ключ на доске.
Что можно сказать о форме? ( Форма разная)
А какова площадь этих многоугольников? ( Площади этих многоугольников равны)
Оценивают результаты.
У кого правильно – поставь “+”.
У кого сомнения, затруднения – “?”
Консультанты оказывают помощь ребятам, ищут ошибки, помогают исправить.
Домашнее задание:
Составить свои листки исследования, вычислить площадь многоугольника разными способами.
Итог урока.
Итак, ребята, что вы расскажите родителям, о том как найти площадь геометрической фигуры – многоугольника.
Определение площади многоугольника | Методическая разработка по математике (4 класс) по теме:
Математика.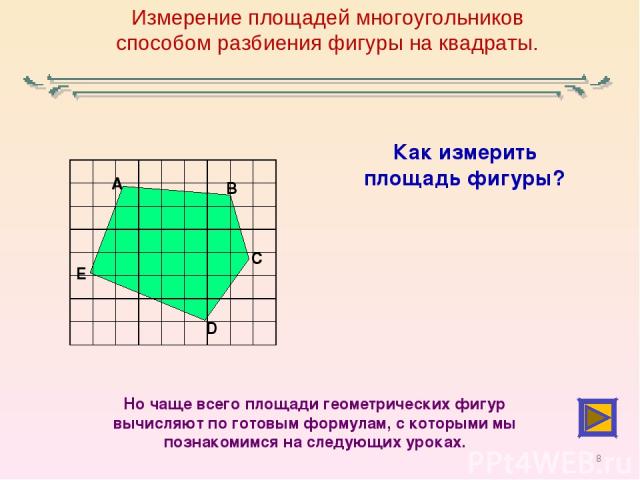
Тема: Определение площади многоугольника.
Цели:
Специальные :
-выделение существенных признаков прямоугольника и квадрата;
— учить находить границы площади фигур;
— развивать способность к восприятию формы;
— закрепить знания о свойствах диагоналей прямоугольника и квадрата;
— продолжить работу с именованными числами;
Общеучебные:
— развивать умение осознавать и принимать учебную цель;
— проверять по ходу работы и после работы ее правильность;
— работать самостоятельно и вместе с товарищами;
— развивать умения анализировать, сравнивать, обобщать, классифицировать и систематизировать;
— делать вывод.
Оборудование:
Тетради; танграмм; цветовые геометрические фигуры; цветовые жетоны для высказывания своего мнения об уроке.
Ход урока.
I.Орг. момент.
II. Постановка темы и целей.
Есть о математике молва,
Что она в порядок ум приводит,
Потому хорошие слова
Часто говорят о ней в народе.
Сегодня мы научимся определять площадь многоугольника. Чтобы это сделать, нам придется слушать, делать вывод, проверять правильность работы, конструировать, помогать друг другу.
IIIПодготовка к основному этапу урока.
Запишите математический диктант:
— Ширина огорода 12 метров, а длина в 3 раза больше. Найдите длину. (36 м)
— Окно имеет форму квадрата со стороной 40 сантиметров. Чему равен периметр? (1600 см)
— Площадь поля 72 квадратных метра.1\2 площади засеяли пшеницей. Чему равна незасеянная площадь? (36 м2)
— Какой длины потребуется проволока для прямоугольной рамки, если длина рамки 25 сантиметров, а ширина 5 сантиметров? (60 см)
¿Один ученик выполняет работу у доски.
Сравнение записи на доске с записью в тетради.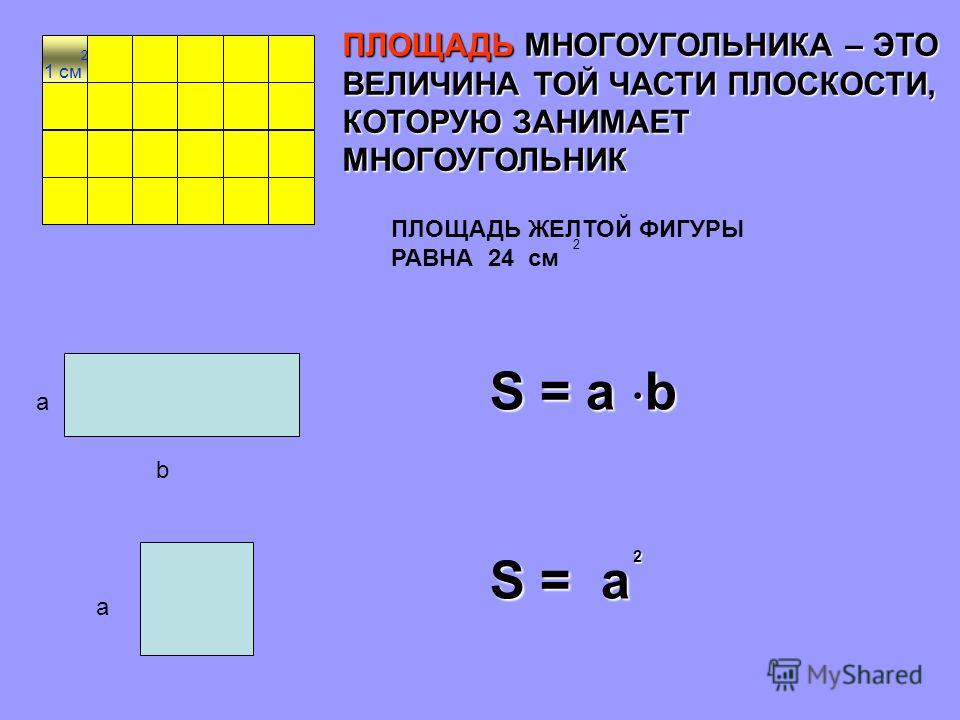
IY. Актуализация знаний учащихся.
¿На доске закреплены цветовые различные геометрические фигуры.
В геометрии встречаются различные фигуры.
— Назовите фигуры, которые вы видите. (прямоугольник, треугольник, квадрат, круг, трапеция, параллелограмм)
— Какая фигура на ваш взгляд является лишней? (круг)
— Почему? ( у круга нет углов)
¿Круг убирается с доски.
— Среди оставшихся фигур выберите те, площадь которых вы умеете находить.
¿Дети называют прямоугольник, треугольник и квадрат. Данные фигуры вывешиваются отдельно.
Данные фигуры вывешиваются отдельно.
— Под каждой фигурой напишите соответствующую формулу нахождения площади.
¿Трое учащихся выполняют работу на доске. Остальные проверяют правильность написания формул. Если работа выполнена правильно, то фигура разворачивается. На обратной стороне фигуры записана формула нахождения площади.
— В каких единицах измеряется площадь? (см2, м2, дм2 и т.д.)
— Вернемся к математическому диктанту.
— Какое число повторилось дважды? (36)
— Какое значение из математического диктанта может выражать площадь? (36м2)
— Может ли данное значение быть площадью квадрата?(да)
— При каких значениях длины стороны квадрата? (6м)
— Почему? (длины сторон квадрата равны).
— Может ли данное значение быть площадью прямоугольника? (да).
— При каких значениях длин сторон прямоугольника?
(36м и 1м; 18м и 2м; 9м и 4м).
— Чему будет равна площадь прямоугольного треугольника, если провести диагональ в квадрате и прямоугольнике с равными площадями? (половине их площади, в данном случае 18м2).
Y. Усвоение новых знаний.
— А что делать с остальными фигурами? Как найти их площади? На этот вопрос нам предстоит ответить. Будем учиться находить площадь таких фигур.
¿Из двух цветовых треугольников и цветового прямоугольника на доске составляется трапеция.
— Назовите фигуру. (трапеция)
— Как найти площадь данной фигуры? (Найти границы известных фигур)
— Какие фигуры вы нашли? (два прямоугольных треугольника и прямоугольник).
— Какой можно сделать вывод по определению площади многоугольника?
Вывод: чтобы найти площадь многоугольника, нужно разделить его на известные фигуры. Найти их площади, а затем значения сложить.
YI. Динамическая пауза.
Потрудились – отдохнем.
Встанем, глубоко вздохнем.
Руки в стороны, вперед,
Влево, вправо поворот.
Три хлопка и прямо встать.
Руки вниз и вверх поднять.
Руки плавно опустили,
Всем улыбки подарили.
YII. Проблемная ситуация.
¿У каждого учащего на парте лежит цветовой танграмм. Все танграммы различной величины.
— Обратимся к танграмму. Поменяйтесь со своим соседом танграммом.
— Выложите из танграмма фигуру и найдите ее площадь.
¿Работа проводится самостоятельно. Производится запись в тетради с расчетами.
— Поменяйтесь тетрадями и произведите проверку правильности выполненной работы.
¿Проверку работы дети выполнят быстро и правильно, т.к. на обороте каждой фигуры уже сделаны вычисления по нахождению площади.
YIII.Домашнее задание.
На уроке мы работали с известными вам геометрическими фигурами. Дома составьте многоугольник и найдите его площадь.
IX. Подведение итогов.
— Чему был посвящен урок? (нахождению площади многоугольника).
— Каждый человек имеет право избирать и быть избранным. Прошу выбрать утверждение, соответствующее вашему мнению об уроке и проголосовать с помощью жетонов, лежащих у вас на столе.
¿На доске вывешивается «ТАБЛИЦА МНЕНИЙ»
Запись «Было скучно, неинтересно» — красного цвета;
«Узнал для себя кое-что познавательное»-желтого цвета;
«Очень понравился урок!»-зеленого цвета.
Было скучно, неинтересно |
Узнал для себя кое-что познавательное |
Очень понравился урок |
былоБб
¿Результаты «Таблицы мнений » дают учителю информацию о правильности выбора приемов и методов на данном уроке.
— Что вам напоминает сочетание этих цветов? (светофор)
— На какой сигнал светофора можно переходить дорогу? (на зеленый)
-Верно! Ребята, спасибо вам за работу. Без помощи и поддержки друг друга вы не смогли бы достичь цели. Молодцы!
Как найти площадь многоугольника
Все математические ресурсы ACT
14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept
ACT Math Help » Геометрия » Плоская геометрия » Другие полигоны » Как найти площадь многоугольника
Длина определенного прямоугольника в 4 раза больше его ширины. Предположим, что длина и ширина этого прямоугольника разделены пополам. Площадь первого прямоугольника во сколько раз больше площади второго прямоугольника?
Возможные ответы:
Правильный ответ:
Объяснение:
Этот вопрос на самом деле содержит много лишней информации, которая вам не понадобится для решения проблемы.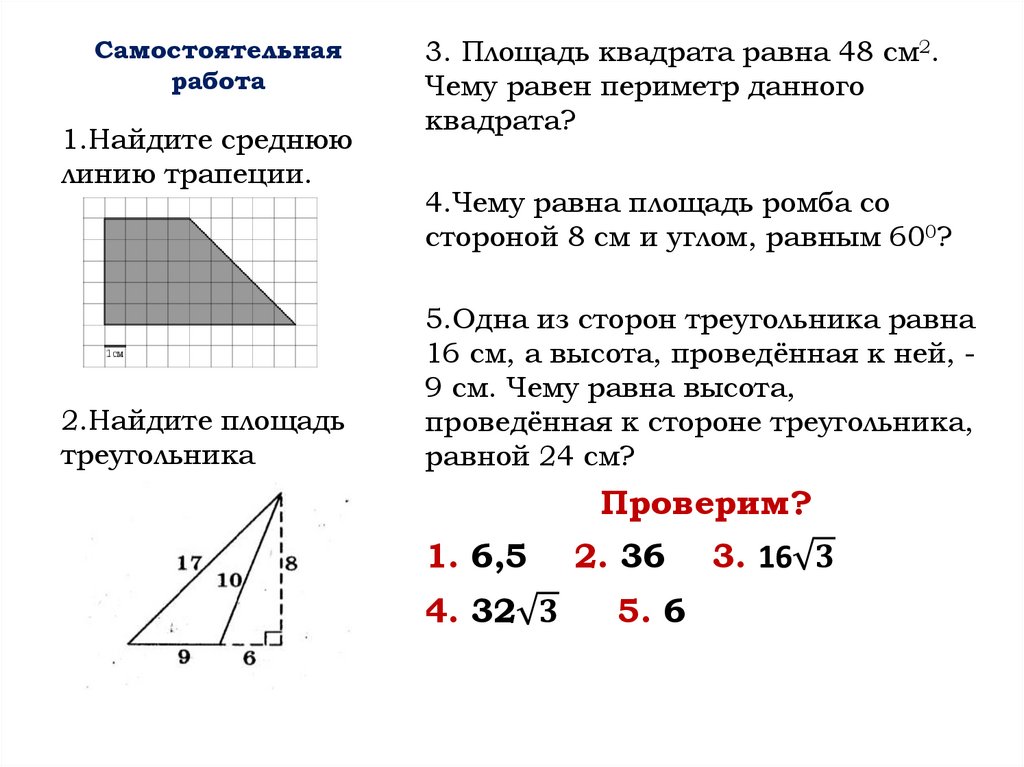 При уменьшении размеров любого прямоугольника вдвое площадь полученного прямоугольника всегда будет равна исходной.
При уменьшении размеров любого прямоугольника вдвое площадь полученного прямоугольника всегда будет равна исходной.
Еще один способ решить эту проблему — вычислить площадь первого прямоугольника. В этом случае пусть будет ширина, а будет длина.
Следовательно, площадь равна:
Для второго прямоугольника ширина равна , а длина равна
Таким образом, площадь этого прямоугольника равна:
Следовательно, площадь первого прямоугольника в 4 раза больше площади прямоугольника два.
Сообщить об ошибке
Садовник ухаживает за садом в форме правильного восьмиугольника. Его апофема — футы. Какова площадь сада?
Возможные ответы:
Недостаточно информации
Правильный ответ:
5
55
Объяснение:
В этом типе проблем первым шагом является определение того, какая информация вам не хватает, что мешает вам решить проблему как есть? Учитывая , что формула для нахождения площади правильного многоугольника выглядит следующим образом , где a – апофема, а P – периметр, можно сделать вывод, что информация о длине каждой стороны восьмиугольника отсутствует. Однако предоставляется достаточно информации для расчета этой части информации с использованием прямоугольных треугольников.
Однако предоставляется достаточно информации для расчета этой части информации с использованием прямоугольных треугольников.
Чтобы продолжить, необходимо вычислить внутренние углы правильного восьмиугольника. Стрелка указывает на внутренний угол. Это можно решить с помощью уравнения: , где n — количество сторон. Внутренний угол рассчитывается как . При создании прямоугольного треугольника, как показано на предыдущем рисунке, внутренний угол делится пополам. В результате треугольник можно увидеть как:
. Теперь, используя тригонометрические функции, можно вычислить основание треугольника. Поскольку основание треугольника составляет лишь половину общей длины одной из сторон восьмиугольника, это число нужно умножить на 2.
9.94 будет использоваться для вычисления периметра восьмиугольника:
Теперь осталось подставить в полученные числа апофему и периметр, чтобы определить площадь:
Сообщить об ошибке
Внутри вписаны два круга прямоугольника и находятся рядом. Чему равна площадь заштрихованной области?
Чему равна площадь заштрихованной области?
Возможные ответы:
Правильный ответ:
Объяснение:
Пытаясь найти площадь пространства между двумя фигурами, найдите площадь обеих фигур и вычтите площадь меньшей фигуры (в данном случае кругов) из большей фигуры (прямоугольника).
Для этого мы должны сначала вычислить площадь данных кругов.
Когда окружность вписана внутрь квадрата или прямоугольника (другими словами, она будет касаться всех сторон фигуры, диаметр окружности будет таким же, как у квадрата. В этом случае, поскольку фигура прямоугольник, ширина которого равна диаметру одного круга, а длина равна диаметру обоих кругов.0005
Используйте это, чтобы найти площадь кругов:
Площадь каждого круга равна 50,24 кв. прямоугольника:
Затем вычтите два, чтобы найти площадь заштрихованного пространства.
Сообщить об ошибке
Третьеклассник Сэмми нарисовал дом, нарисовав квадрат с равносторонним треугольником наверху. Нижняя часть квадрата длинная. Сэмми хотел бы знать площадь дома, чтобы раздобыть мелок подходящего размера, чтобы раскрасить его.
Что из следующего ближе всего к площади дома в квадратных сантиметрах?
Возможные ответы:
Правильный ответ:
Пояснение:
Площадь дома состоит из площади квадратного основания и треугольной крыши. У квадрата есть длина стороны, поэтому площадь квадрата равна , а площадь равносторонней треугольной крыши определяется как , где – основание треугольника, .
Основание треугольника лежит на вершине квадрата, поэтому его длина одинакова, .
Высота равностороннего треугольника равна .
Его можно найти, разделив равносторонний треугольник на два прямоугольных треугольника (точнее, на прямоугольные треугольники).
В совокупности площадь квадрата и треугольника составляет
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы ACT Math
14 диагностических тестов
767 практических тестов
Вопрос дня
Карточки
Учитесь по концепции
Как найти площадь правильного многоугольника?
Геометрия — раздел математики, который включает в себя расчет различных параметров плоских и объемных форм. В этой статье мы обсудили формулы для расчета таких параметров, как площадь, периметр и объем различных форм, а также кратко описали правильные многоугольники и формулы для расчета их площади вместе с некоторыми примерами решений для лучшего понимания.
Некоторые основные формулы для плоских фигур
Прямоугольник
- Площадь = длина × ширина
- Периметр = 2 (длина+ширина)
квадрат
- Область = (сторона)
6 2
- = (сторона)
6 2
- = (сторона)
6 2
- .

Circle
- Diameter = 2 × radius
- Area = π × (radius)2
Triangle
- Area = 1/2 breadth × height
Solid shapes
Cube
- Volume = (side) 3
- Lateral surface area = 4 × (side) 2
- Total surface area = 6 × (side) 2
Cuboid
- Объем = длина × ширина × высота
- Площадь боковой поверхности = 2 × высота (l+b)
- Общая площадь поверхности = 2 (lb+lh+hb)
Сфера
- Объем = 4/3πr 3
- Площадь поверхности = 4πr 2
Конус
- Объем = 1/3πr 2 h
- Общая площадь поверхности = πr (l+радиус)
9 900 Что такое правильный многоугольник? Правильный многоугольник включает плоские формы, имеющие стороны одинаковой длины с равными внутренними углами. Ромб, квадрат, равносторонний треугольник, прямоугольник — вот некоторые основные примеры правильных многоугольников. Любой другой многоугольник, имеющий неравные стороны или внутренние углы, известен как неправильный многоугольник, который включает разносторонний треугольник, трапецию и т. д.
Ромб, квадрат, равносторонний треугольник, прямоугольник — вот некоторые основные примеры правильных многоугольников. Любой другой многоугольник, имеющий неравные стороны или внутренние углы, известен как неправильный многоугольник, который включает разносторонний треугольник, трапецию и т. д.
Свойства правильного многоугольника
- У правильного многоугольника все стороны и внутренние углы равны.
- Биссектрисы правильного многоугольника пересекаются в центре при движении от внутренних углов.
- Расстояние между центром и вершинами правильного многоугольника одинаково.
- Длина перпендикуляра, проведенного из центра к вершинам правильного многоугольника, всегда равна.
Площадь правильного многоугольника
Все правильные многоугольники можно рассматривать как циклический многоугольник и касательный многоугольник, поскольку все вершины правильного многоугольника лежат на описанной окружности, а именно. у них есть конциклические точки, и у них также есть вписанная окружность, которая касается каждой стороны, лежащей в средней точке соответственно. поскольку многоугольник имеет равные стороны и равные углы, обычно для вычисления площади правильного многоугольника используется апофема.
у них есть конциклические точки, и у них также есть вписанная окружность, которая касается каждой стороны, лежащей в средней точке соответственно. поскольку многоугольник имеет равные стороны и равные углы, обычно для вычисления площади правильного многоугольника используется апофема.
Апофема — это отрезок, соединяющий центр многоугольника с серединами сторон и проведенный перпендикулярно сторонам.
Площадь правильного многоугольника можно записать как
где
l длина стороны
n количество сторон
Пример задачи
4 Расчет площади
4 пятиугольника со стороной 4 см.
Решение:
Заданы параметры:
l = 4 см и n = 5
Формула для нахождения площади.
=>
=>A = (4) 2 × 5/4tan(180/5)
=>A = 80/4 × 0,7265
=>A = 27,53 см 2
90,0 площадь шестиугольника со стороной 10 см.
 Однако предоставляется достаточно информации для расчета этой части информации с использованием прямоугольных треугольников.
Однако предоставляется достаточно информации для расчета этой части информации с использованием прямоугольных треугольников. Чему равна площадь заштрихованной области?
Чему равна площадь заштрихованной области?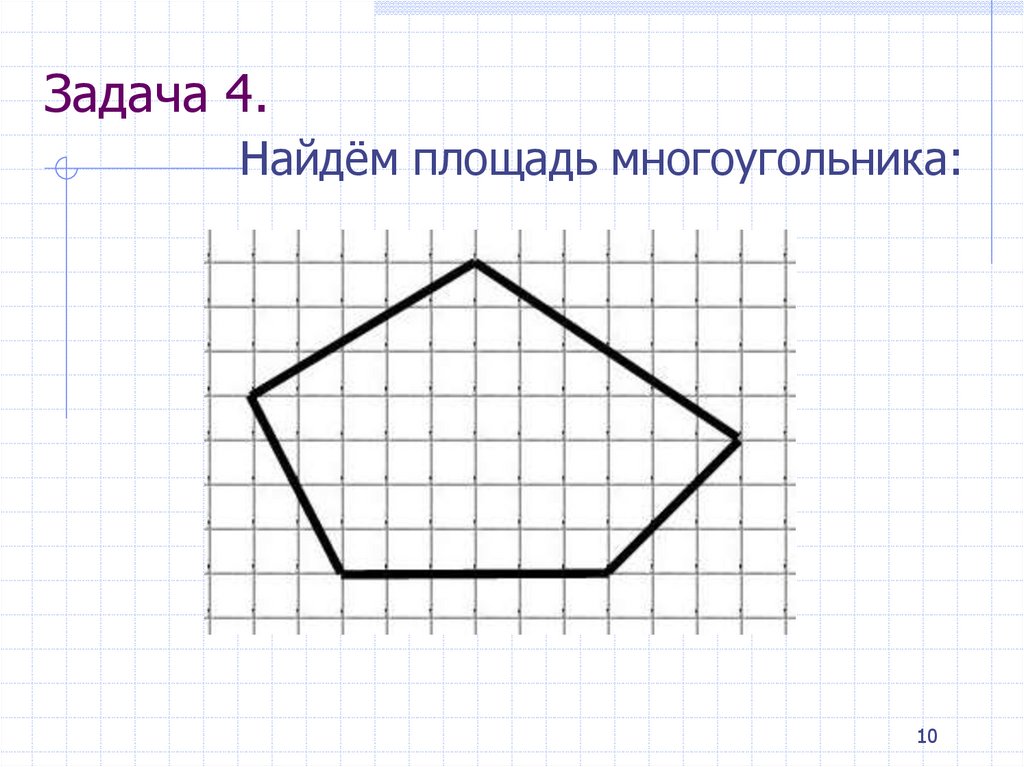
6 2
- = (сторона)
6 2
- = (сторона)
6 2
- .

Circle
- Diameter = 2 × radius
- Area = π × (radius)2
Triangle
- Area = 1/2 breadth × height
Solid shapes
Cube
- Volume = (side) 3
- Lateral surface area = 4 × (side) 2
- Total surface area = 6 × (side) 2
Cuboid
- Объем = длина × ширина × высота
- Площадь боковой поверхности = 2 × высота (l+b)
- Общая площадь поверхности = 2 (lb+lh+hb)
Сфера
- Объем = 4/3πr 3
- Площадь поверхности = 4πr 2
Конус
- Объем = 1/3πr 2 h
- Общая площадь поверхности = πr (l+радиус) 9 900 Что такое правильный многоугольник?
- У правильного многоугольника все стороны и внутренние углы равны.
- Биссектрисы правильного многоугольника пересекаются в центре при движении от внутренних углов.
- Расстояние между центром и вершинами правильного многоугольника одинаково.
- Длина перпендикуляра, проведенного из центра к вершинам правильного многоугольника, всегда равна.
Правильный многоугольник включает плоские формы, имеющие стороны одинаковой длины с равными внутренними углами.
 Ромб, квадрат, равносторонний треугольник, прямоугольник — вот некоторые основные примеры правильных многоугольников. Любой другой многоугольник, имеющий неравные стороны или внутренние углы, известен как неправильный многоугольник, который включает разносторонний треугольник, трапецию и т. д.
Ромб, квадрат, равносторонний треугольник, прямоугольник — вот некоторые основные примеры правильных многоугольников. Любой другой многоугольник, имеющий неравные стороны или внутренние углы, известен как неправильный многоугольник, который включает разносторонний треугольник, трапецию и т. д.Свойства правильного многоугольника
Площадь правильного многоугольника
Все правильные многоугольники можно рассматривать как циклический многоугольник и касательный многоугольник, поскольку все вершины правильного многоугольника лежат на описанной окружности, а именно.
 у них есть конциклические точки, и у них также есть вписанная окружность, которая касается каждой стороны, лежащей в средней точке соответственно. поскольку многоугольник имеет равные стороны и равные углы, обычно для вычисления площади правильного многоугольника используется апофема.
у них есть конциклические точки, и у них также есть вписанная окружность, которая касается каждой стороны, лежащей в средней точке соответственно. поскольку многоугольник имеет равные стороны и равные углы, обычно для вычисления площади правильного многоугольника используется апофема.Апофема — это отрезок, соединяющий центр многоугольника с серединами сторон и проведенный перпендикулярно сторонам.
Площадь правильного многоугольника можно записать как
где
l длина стороны
n количество сторон
Пример задачи
4 Расчет площади
4 пятиугольника со стороной 4 см.
Решение:
Заданы параметры:
l = 4 см и n = 5
Формула для нахождения площади.
=>
=>A = (4) 2 × 5/4tan(180/5)
=>A = 80/4 × 0,7265
=>A = 27,53 см 2
90,0 площадь шестиугольника со стороной 10 см.

- .
- = (сторона)


 Ромб, квадрат, равносторонний треугольник, прямоугольник — вот некоторые основные примеры правильных многоугольников. Любой другой многоугольник, имеющий неравные стороны или внутренние углы, известен как неправильный многоугольник, который включает разносторонний треугольник, трапецию и т. д.
Ромб, квадрат, равносторонний треугольник, прямоугольник — вот некоторые основные примеры правильных многоугольников. Любой другой многоугольник, имеющий неравные стороны или внутренние углы, известен как неправильный многоугольник, который включает разносторонний треугольник, трапецию и т. д. у них есть конциклические точки, и у них также есть вписанная окружность, которая касается каждой стороны, лежащей в средней точке соответственно. поскольку многоугольник имеет равные стороны и равные углы, обычно для вычисления площади правильного многоугольника используется апофема.
у них есть конциклические точки, и у них также есть вписанная окружность, которая касается каждой стороны, лежащей в средней точке соответственно. поскольку многоугольник имеет равные стороны и равные углы, обычно для вычисления площади правильного многоугольника используется апофема.