Площадь многоугольника. Площадь квадрата и прямоугольника 8 класс онлайн-подготовка на Ростелеком Лицей
Тема 2: Площадь
- Видео
- Тренажер
- Теория
Заметили ошибку?
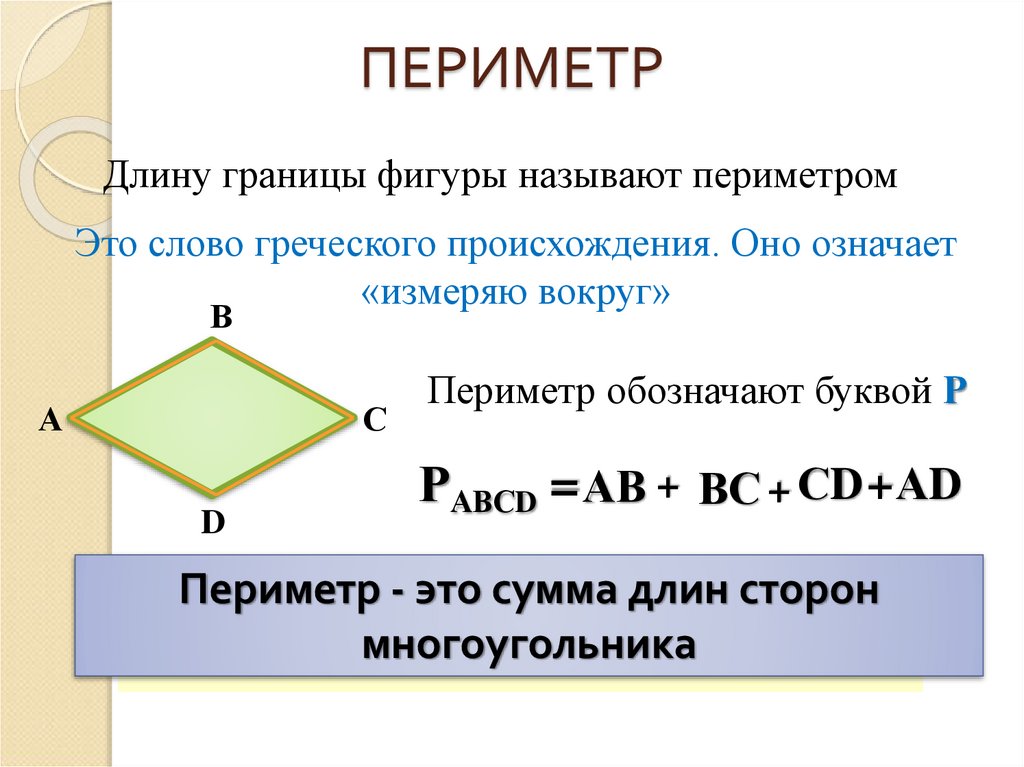
Площадь многоугольника. Площадь квадрата и прямоугольника.
Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
За единицу измерения площадей принимают квадрат, сторона которого равна единице измерения отрезков.
Например, единица измерения отрезков 1 мм, а единица измерения площади 1 мм2 – квадратный миллиметр.
1 см – единица измерения отрезков, а единица измерения площади 1 см2 – квадратный сантиметр.
1 м – единица измерения отрезков, а 1 м2 – единица площади – квадратный метр.
При выбранной единице измерения площадей площадь каждого многоугольника выражается положительным числом. Это число показывает, сколько раз единица измерения и ее части укладываются в данном многоугольнике.
Если форма многоугольника сложная, то данный процесс усложняется, и на практике неудобен. Поэтому обычно измеряют некоторые отрезки, связанные с многоугольником, и затем вычисляют площадь многоугольника по специальным формулам.
Вывод этих формул основан на свойствах площадей.
-
Равные многоугольники имеют равные площади.
-
Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
Площадь первой фигуры равна сумме площадей двух маленьких фигур, из которых состоит эта фигура.
Площадь второй фигуры равна сумме площадей трех маленьких фигур, из которых состоит эта фигура.
Эти два свойства называют основными свойствами площадей.
-
Площадь квадрата равна квадрату его стороны.

-
Площадь прямоугольника равна произведению длины на ширину.
S = ab
В геометрии, когда нужно сравнить площади фигур, используют следующие понятия: равновеликие многоугольники и равносоставленные.
Равновеликие многоугольники – это многоугольники, которые имеют равные площади.
Равносоставленные многоугольники – это многоугольники, которые составлены из многоугольников, имеющих равные площади. На следующем рисунке изображены два равносоставленных многоугольника.
Любые два равносоставленных многоугольника – равновеликие.
Верно и обратное утверждение: если два многоугольника равновеликие, то они равносоставленные.
Заметили ошибку?
Расскажите нам об ошибке, и мы ее исправим.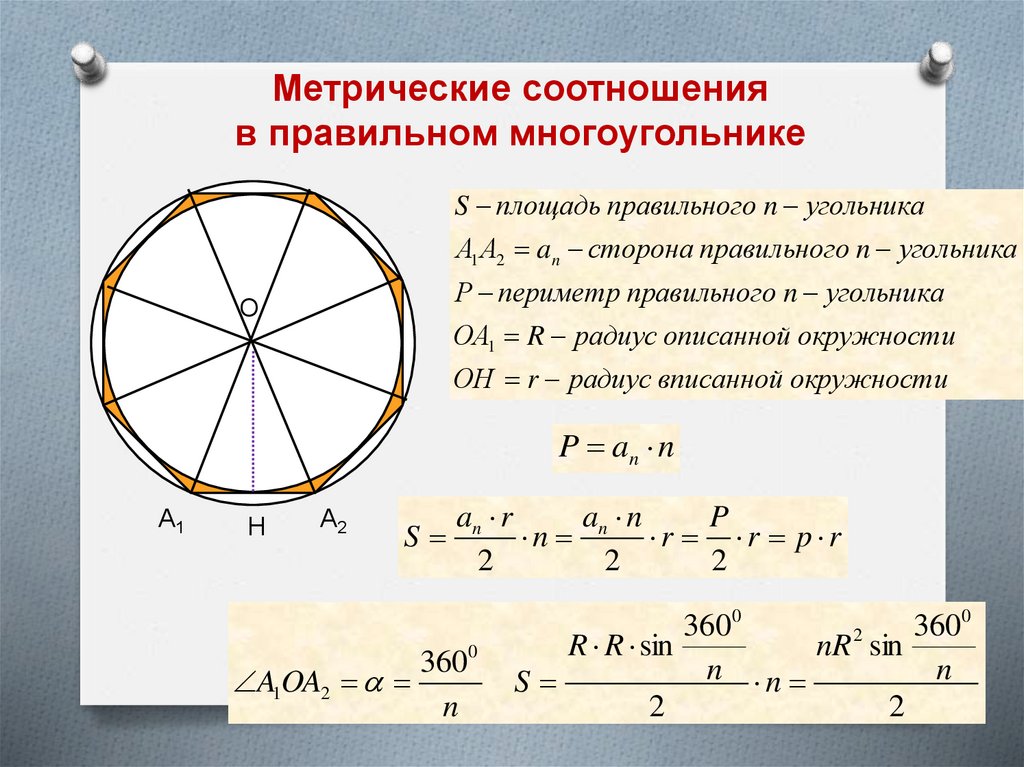 2 \Rightarrow
S_{\text{пр-к}}=ab \end{multline*}\)
2 \Rightarrow
S_{\text{пр-к}}=ab \end{multline*}\)Определение
Высота параллелограмма — это перпендикуляр, проведенный из вершины параллелограмма к стороне (или к продолжению стороны), не содержащей эту вершину.
Например, высота \(BK\)
падает на сторону \(AD\)
, а высота \(BH\)
— на продолжение стороны \(CD\)
:
Теорема: площадь параллелограмма
Площадь параллелограмма равна произведению высоты и стороны, к которой проведена эта высота.
Доказательство
Проведем перпендикуляры \(AB»\) и \(DC»\) , как показано на рисунке. Заметим,что эти перпендикуляры равны высоте параллелограмма \(ABCD\) .
Тогда \(AB»C»D\) – прямоугольник, следовательно, \(S_{AB»C»D}=AB»\cdot AD\) .
Заметим, что прямоугольные треугольники \(ABB»\) и \(DCC»\) равны. Таким образом,
\(S_{ABCD}=S_{ABC»D}+S_{DCC»}=S_{ABC»D}+S_{ABB»}=S_{AB»C»D}=AB»\cdot AD.\)
\[{\Large{\text{Площадь треугольника}}}\]
Определение
Будем называть сторону, к которой в треугольнике проведена высота, основанием треугольника.
Теорема
Площадь треугольника равна половине произведения его основания на высоту, проведенную к этому основанию.
Доказательство
Пусть \(S\) – площадь треугольника \(ABC\) . Примем сторону \(AB\) за основание треугольника и проведём высоту \(CH\) . Докажем, что \ Достроим треугольник \(ABC\) до параллелограмма \(ABDC\) так, как показано на рисунке:
Треугольники \(ABC\) и \(DCB\) равны по трем сторонам (\(BC\) – их общая сторона, \(AB = CD\) и \(AC = BD\) как противоположные стороны параллелограмма \(ABDC\) ), поэтому их площади равны. Следовательно, площадь \(S\) треугольника \(ABC\) равна половине площади параллелограмма \(ABDC\) , то есть \(S = \dfrac{1}{2}AB\cdot CH\) .
Теорема
Если два треугольника \(\triangle ABC\) и \(\triangle A_1B_1C_1\) имеют равные высоты, то их площади относятся как основания, к которым эти высоты проведены.
Следствие
Медиана треугольника делит его на два треугольника, равных по площади.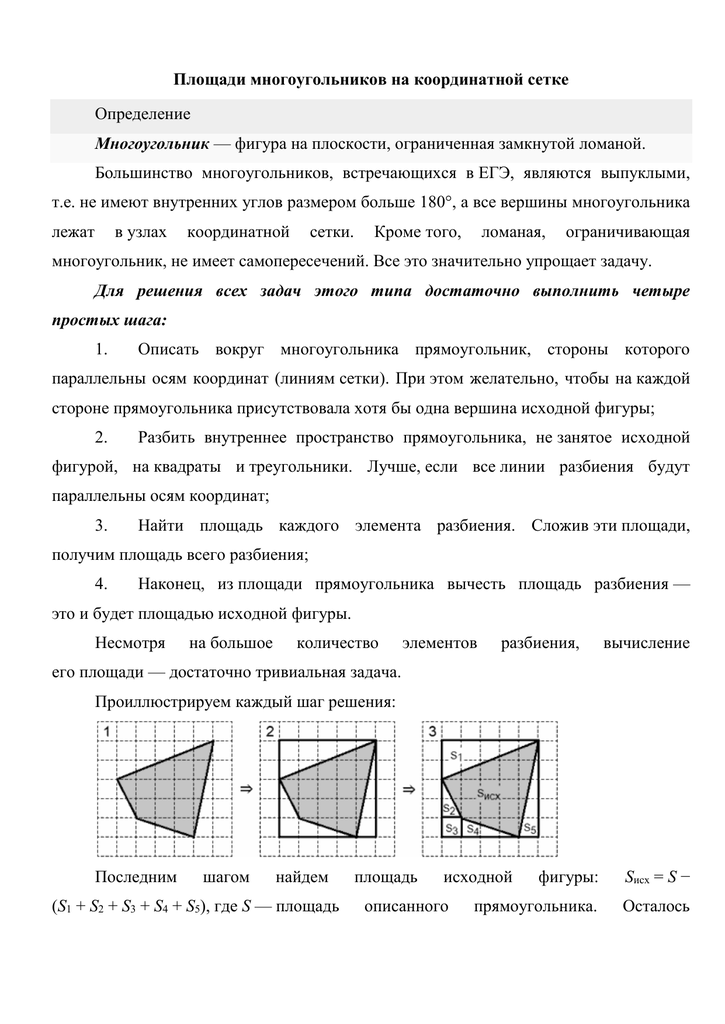
Теорема
Если два треугольника \(\triangle ABC\) и \(\triangle A_2B_2C_2\) имеют по равному углу, то их площади относятся как произведения сторон, образующих этот угол.
Доказательство
Пусть \(\angle A=\angle A_2\) . Совместим эти углы так, как показано на рисунке (точка \(A\) совместилась с точкой \(A_2\) ):
Проведем высоты \(BH\) и \(C_2K\) .
Треугольники \(AB_2C_2\) и \(ABC_2\) имеют одинаковую высоту \(C_2K\) , следовательно: \[\dfrac{S_{AB_2C_2}}{S_{ABC_2}}=\dfrac{AB_2}{AB}\]
Треугольники \(ABC_2\) и \(ABC\) имеют одинаковую высоту \(BH\) , следовательно: \[\dfrac{S_{ABC_2}}{S_{ABC}}=\dfrac{AC_2}{AC}\]
Перемножая последние два равенства, получим: \[\dfrac{S_{AB_2C_2}}{S_{ABC}}=\dfrac{AB_2\cdot AC_2}{AB\cdot AC} \qquad \text{ или } \qquad \dfrac{S_{A_2B_2C_2}}{S_{ABC}}=\dfrac{A_2B_2\cdot A_2C_2}{AB\cdot AC}\]
Теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
Верно и обратное: если в треугольнике квадрат длины одной стороны равен сумме квадратов длин других двух сторон, то такой треугольник прямоугольный.
Теорема
Площадь прямоугольного треугольника равна половине произведения катетов.
Теорема: формула Герона
Пусть \(p\) – полупериметр треугольника, \(a\) , \(b\) , \(c\) – длины его сторон, тогда его площадь равна \
\[{\Large{\text{Площадь ромба и трапеции}}}\]
Замечание
Т.к. ромб является параллелограммом, то для него верна та же формула, т.е. площадь ромба равна произведению высоты и стороны, к которой проведена эта высота.
Теорема
Площадь выпуклого четырехугольника, диагонали которого перпендикулярны, равна половине произведения диагоналей.
Доказательство
Рассмотрим четырехугольник \(ABCD\) . Обозначим \(AO=a, CO=b, BO=x, DO=y\) :
Заметим, что данный четырехугольник составлен из четырех прямоугольных треугольников, следовательно, его площадь равна сумме площадей этих треугольников:
\(\begin{multline*} S_{ABCD}=\frac12ax+\frac12xb+\frac12by+\frac12ay=\frac12(ax+xb+by+ay)=\\ \frac12((a+b)x+(a+b)y)=\frac12(a+b)(x+y)\end{multline*}\)
Следствие: площадь ромба
Площадь ромба равна половине произведения его диагоналей: \
Определение
Высота трапеции – это перпендикуляр, проведенный из вершины одного основания к другому основанию.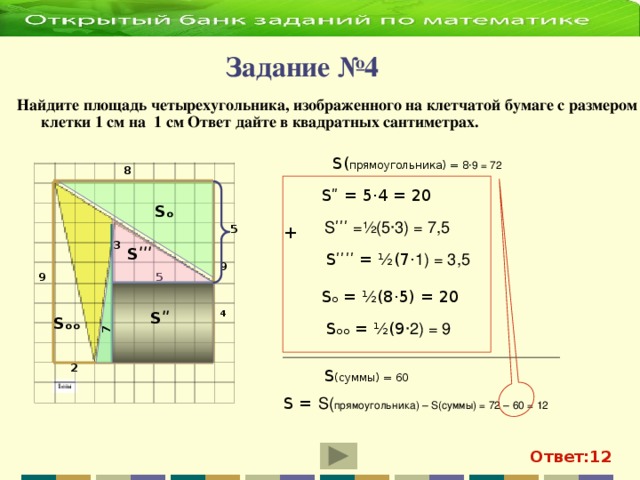
Теорема: площадь трапеции
Площадь трапеции равна произведению полусуммы оснований на высоту.
Доказательство
Рассмотрим трапецию \(ABCD\) с основаниями \(BC\) и \(AD\) . Проведем \(CD»\parallel AB\) , как показано на рисунке:
Тогда \(ABCD»\) – параллелограмм.
Проведем также \(BH»\perp AD, CH\perp AD\) (\(BH»=CH\) – высоты трапеции).
Тогда \(S_{ABCD»}=BH»\cdot AD»=BH»\cdot BC, \quad S_{CDD»}=\dfrac12CH\cdot D»D\)
Т.к. трапеция состоит из параллелограмма \(ABCD»\) и треугольника \(CDD»\) , то ее площадь равна сумме площадей параллелограмма и треугольника, то есть:
\ \[=\dfrac12 CH\left(BC+AD»+D»D\right)=\dfrac12 CH\left(BC+AD\right)\]
Каждый, кто изучал в школе математику и геометрию, хотя бы поверхностно знает эти науки. Но со временем, если в них не практиковаться, познания забываются. Многие даже считают, что только зря потратили своё время, изучая геометрические расчёты. Однако они ошибаются. Технические работники выполняют повседневную работу, связанную с геометрическими расчётами. Что касается расчета площади многоугольника, то и эти знания находят своё применение в жизни. Понадобятся они хотя бы для того, чтобы рассчитать площадь земельного участка. Итак, давайте узнаем, как найти площадь многоугольника.
Технические работники выполняют повседневную работу, связанную с геометрическими расчётами. Что касается расчета площади многоугольника, то и эти знания находят своё применение в жизни. Понадобятся они хотя бы для того, чтобы рассчитать площадь земельного участка. Итак, давайте узнаем, как найти площадь многоугольника.
Определение многоугольника
Сначала определимся с тем, что такое многоугольник. Это плоская геометрическая фигура, которая образовалась в результате пересечения трех или более прямых. Другое простое определение: многоугольник — это замкнутая ломаная. Естественно, при пересечении прямых образуются точки пересечения, их количество равно количеству прямых, образовывающих многоугольник. Точки пересечения называют вершинами, а отрезки, образованные от прямых, — сторонами многоугольника. Смежные отрезки многоугольника находятся не на одной прямой. Отрезки, являющиеся несмежными, — это те, которые не проходят через общие точки.
Сумма площадей треугольников
Как находить площадь многоугольника? Площадь многоугольника — это внутренняя часть плоскости, которая образовалась при пересечении отрезков или сторон многоугольника. Поскольку многоугольник — это сочетание таких фигур, как треугольник, ромб, квадрат, трапеция, то универсальной формулы для вычисления его площади просто нет. На практике наиболее универсальным является метод разбиения многоугольника на более простые фигуры, нахождение площади которых не вызывают затруднений. Сложив суммы площадей этих простых фигур, получают площадь многоугольника.
Поскольку многоугольник — это сочетание таких фигур, как треугольник, ромб, квадрат, трапеция, то универсальной формулы для вычисления его площади просто нет. На практике наиболее универсальным является метод разбиения многоугольника на более простые фигуры, нахождение площади которых не вызывают затруднений. Сложив суммы площадей этих простых фигур, получают площадь многоугольника.
Через площадь окружности
В большинстве случаев многоугольник имеет правильную форму и образует фигуру с равными сторонами и углами между ними. Рассчитать площадь в этом случае очень просто при помощи вписанной или описанной окружности. Если известна площадь окружности, то её необходимо умножить на периметр многоугольника, а затем полученное произведение поделить на 2. В итоге получается формула расчёта площади такого многоугольника: S = ½∙P∙r., где P — площадь окружности, а r — периметр многоугольника.
Метод разбиения многоугольника на «удобные» фигуры — самый популярный в геометрии, он позволяет быстро и правильно найти площадь многоугольника. 4 класс средней школы обычно изучает такие методы.
4 класс средней школы обычно изучает такие методы.
В данной статье речь пойдёт о том, как выразить площадь многоугольника, в который можно вписать окружность, через радиус этой окружности. Сразу стоит отметить, что не во всякий многоугольник можно вписать окружность. Однако, если это возможно, то формула, по которой вычисляется площадь такого многоугольника, становится очень простой. Дочитайте эту статью до конца или посмотрите прилагающийся видеоурок, и вы узнаете, как же выразить площадь многоугольника через радиус вписанной в него окружности.
Формула площади многоугольника через радиус вписанной окружности
Нарисуем многоугольник A 1 A 2 A
Мы взяли здесь для примера 5-угольник. Но на самом деле это не имеет существенного значения, поскольку дальнейшее доказательство справедливо и для 6-угольника и для 8-угольника и вообще для любого сколь угодно «угольника».
Если соединить центр вписанной окружности со всеми вершинами многоугольника, то он разобьётся на столько треугольников, сколько вершин в данном многоугольнике. В нашем случае: на 5 треугольников. Если же соединить точку O со всеми точками касания вписанной окружности со сторонами многоугольника, то получится 5 отрезков (на рисунке снизу это отрезки OH 1 , OH 2 ,
Как же найти площадь нашего описанного многоугольника? Ответ прост. Нужно сложить площади всех полученных в результате разбиения треугольников:
Рассмотрим, чему равна площадь треугольника . На рисунке снизу он выделен жёлтым цветом:
Она равна половине произведения основания A 1 A 2 на высоту OH 1 , проведённую к этому основанию. Но, как мы уже выяснили, эта высота равна радиусу вписанной окружности. То есть формула площади треугольника принимает вид: , где r — радиус вписанной окружности. Аналогично находятся площади всех оставшихся треугольников. В результате искомая площадь многоугольника оказывается равна:
Но, как мы уже выяснили, эта высота равна радиусу вписанной окружности. То есть формула площади треугольника принимает вид: , где r — радиус вписанной окружности. Аналогично находятся площади всех оставшихся треугольников. В результате искомая площадь многоугольника оказывается равна:
Видно, что во всех слагаемых этой суммы ест общий множитель , который можно вынести за скобки. В результате получится вот такое выражение:
То есть в скобках осталась просто сумма всех сторон многоугольника, то есть его периметр P . Чаще всего в этой формуле выражение заменяют просто на p и называют эту букву «полупериметром». В результате, окончательная формула принимает вид:
То есть площадь многоугольника, в который вписана окружность известного радиуса, равна произведению этого радиуса на полупериметр многоугольника. Это и есть тот результат, в которому мы стремились.
Отметит напоследок, что в треугольник, который является частным случаем многоугольника, всегда можно вписать окружность. Поэтому для треугольника эту формулу можно применять всегда. Для остальных многоугольников, с количеством сторон большим 3, сперва нужно убедиться, что в них можно вписать окружность. Если это так, можно смело использовать эту простую формулу и находить по ней площадь этого многоугольника.
Поэтому для треугольника эту формулу можно применять всегда. Для остальных многоугольников, с количеством сторон большим 3, сперва нужно убедиться, что в них можно вписать окружность. Если это так, можно смело использовать эту простую формулу и находить по ней площадь этого многоугольника.
Материал подготовил , Сергей Валерьевич
Конвертер единиц расстояния и длины Конвертер единиц площади Присоединяйтесь © 2011-2017 Довжик Михаил Копирование материалов запрещено. В онлайн калькуляте можно использовать величины в одинаквых единицах измерения! Если у вас возниели трудности с преобразованием едениц измерения воспользуйтесь конвертером единиц расстояния и длины и конвертером единиц площади. Дополнительные возможности калькулятора вычисления площади четырехугольника
- Между полями для ввода можно перемещаться нажимая клавиши «вправо» и «влево» на клавиатуре.
Теория. Площадь четырехугольника Четырёхугольник — геометрическая фигура, состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Четырёхугольник называется выпуклым, если отрезок соединяющий любые две точки этого четырехугольника, будет находиться внутри него.
Четырёхугольник называется выпуклым, если отрезок соединяющий любые две точки этого четырехугольника, будет находиться внутри него.
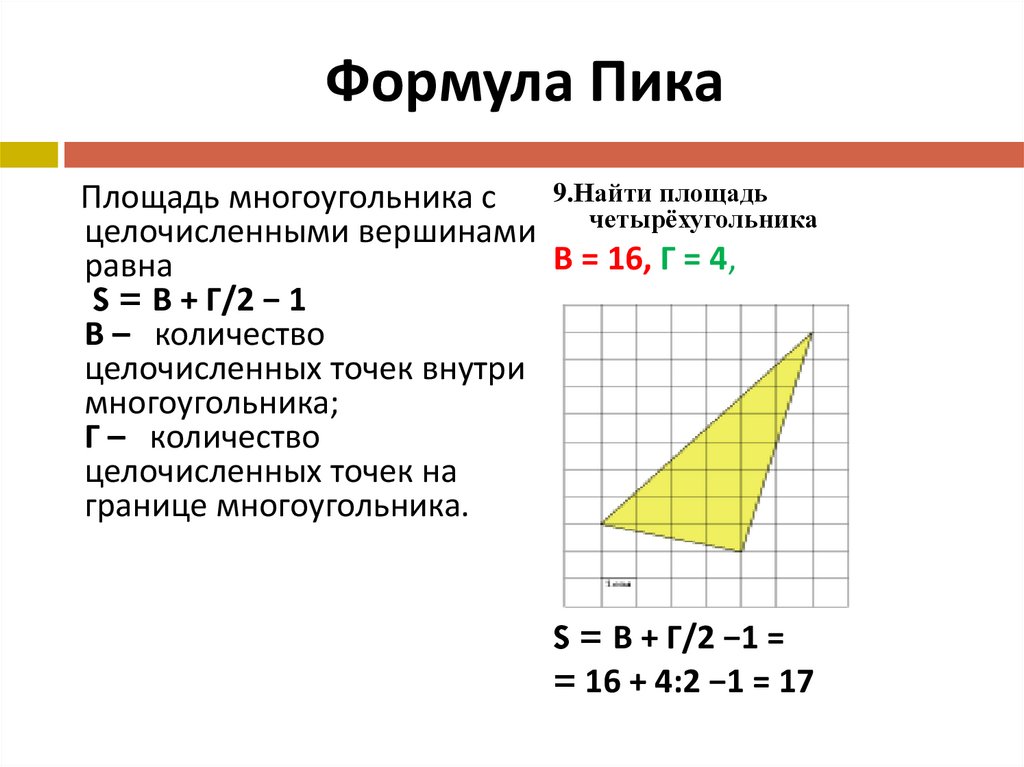
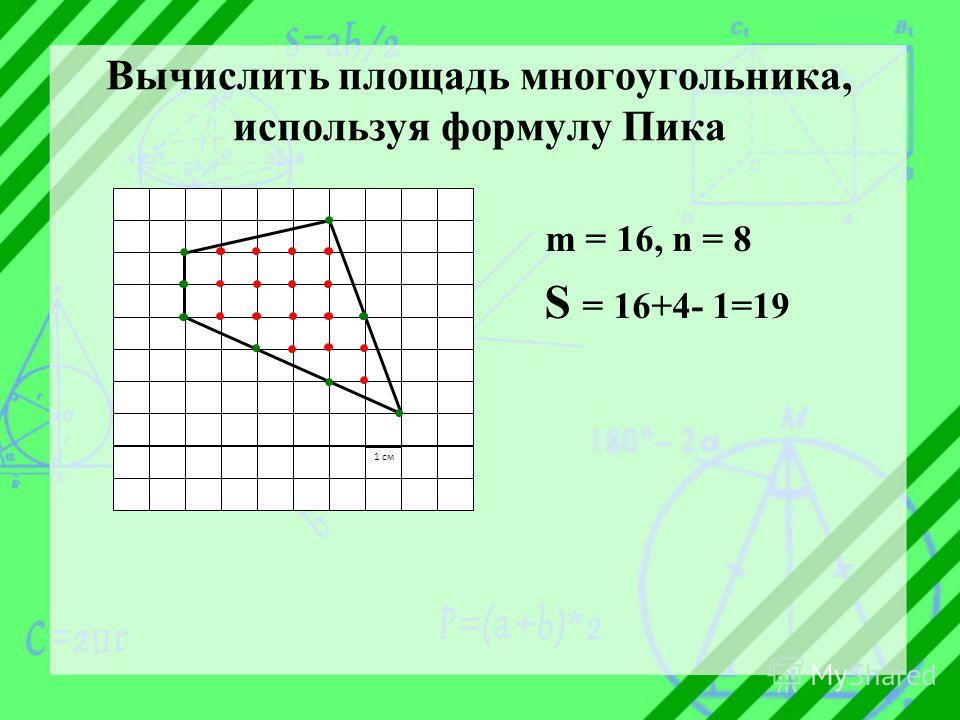
Как узнать площадь многоугольника?
Формула определения площади определяется путем взятия каждого ребра многоугольника АВ, и вычисления площади треугольника АВО с вершиной в начале координат О, через координаты вершин. При обходе вокруг многоугольника, образуются треугольники, включающие внутреннюю часть многоугольника и расположенные снаружи его. Разница между суммой этих площадей и есть площадь самого многоугольника.
Поэтому формула называется формулой геодезиста, так как «картограф» находится в начале координат; если он обходит участок против часовой стрелки, площадь добавляется если она слева и вычитается если она справа с точки зрения из начала координат. Формула площади действительна для любого самонепересекающегося (простого) многоугольника, который может быть выпуклым или вогнутым. Содержание
- 1 Определение
- 2 Примеры
- 3 Более сложный пример
- 4 Объяснение названия
- 5 См.

Площадь многоугольника
Внимание
Это может быть:
- треугольник;
- четырехугольник;
- пяти- или шестиугольник и так далее.
Такая фигура непременно будет характеризоваться двумя положениями:
- Смежные стороны не принадлежат одной прямой.
- У несмежных отсутствуют общие точки, то есть они не пересекаются.
Чтобы понять, какие вершины являются соседними, потребуется посмотреть, принадлежат ли они одной стороне. Если да, то соседние. В противном случае их можно будет соединить отрезком, который необходимо назвать диагональю. Их можно провести только в многоугольниках, у которых больше трех вершин.
Какие их виды существуют? Многоугольник, у которого больше четырех углов, может быть выпуклым или вогнутым. Отличие последнего в том, что некоторые его вершины могут лежать по разные стороны от прямой, проведенной через произвольную сторону многоугольника.
Как найти площадь правильного и неправильного шестиугольника?
- Зная длину стороны, умножим её на 6 и получим периметр шестиугольника:10 см х 6 = 60 см
- Подставим полученные результаты в нашу формулу: Площадь = 1/2*периметр*апофему Площадь = ½*60см*5√3 Решаем: Теперь осталось упростить ответ, чтобы избавиться от квадратных корней, а полученный результат укажем в квадратных сантиметрах: ½ * 60 см * 5√3 см =30 * 5√3 см =150 √3 см =259.
 8 см² Видео о том, как найти площадь правильного шестиугольника Существует несколько вариантов определения площади неправильного шестиугольника:
8 см² Видео о том, как найти площадь правильного шестиугольника Существует несколько вариантов определения площади неправильного шестиугольника:- Метод трапеции.
- Метод расчета площади неправильных многоугольников при помощи оси координат.
- Метод разбивания шестиугольника на другие фигуры.
В зависимости от исходных данных, которые вам будут известны, подбирается подходящий метод.
Важно
Некоторые неправильные шестиугольники состоят из двух параллелограммов. Для определения площади параллелограмма следует умножить его длину на ширину и затем сложить две уже известные площади. Видео о том, как найти площадь многоугольника Равносторонний шестиугольник имеет шесть равных сторон и является правильным шестиугольником.
Площадь равностороннего шестиугольника равняется 6 площадям треугольников, на которые разбита правильная шестиугольная фигура. Все треугольники в шестиугольнике правильной формы равны, поэтому для нахождения площади такого шестиугольника достаточно будет знать площадь хотя бы одного треугольника. Для нахождения площади равностороннего шестиугольника используется, конечно же, формула площади правильного шестиугольника, описанная выше.
Для нахождения площади равностороннего шестиугольника используется, конечно же, формула площади правильного шестиугольника, описанная выше.
404 not found
Украшение жилища, одежды, рисование картин способствовало процессу формирования и накопления сведений в области геометрии, которые люди тех времён добывали опытным путем, по крупицам и передавали из поколения в поколение. Сегодня знания геометрии необходимы и закройщику, и строителю, и архитектору и каждому простому человеку в быту. Поэтому нужно учиться рассчитывать площадь различных фигур, и помнить, что каждая из формул может пригодиться впоследствии на практике, в том числе, и формула правильного шестиугольника.
Шестиугольником называется такая многоугольная фигура, общее количество углов которой равно шести. Правильным шестиугольником называют шестиугольную фигуру, которая имеет равные стороны. Углы у правильного шестиугольника также между собой равны.
В повседневной жизни мы часто можем встретить предметы, имеющие форму правильного шестиугольника.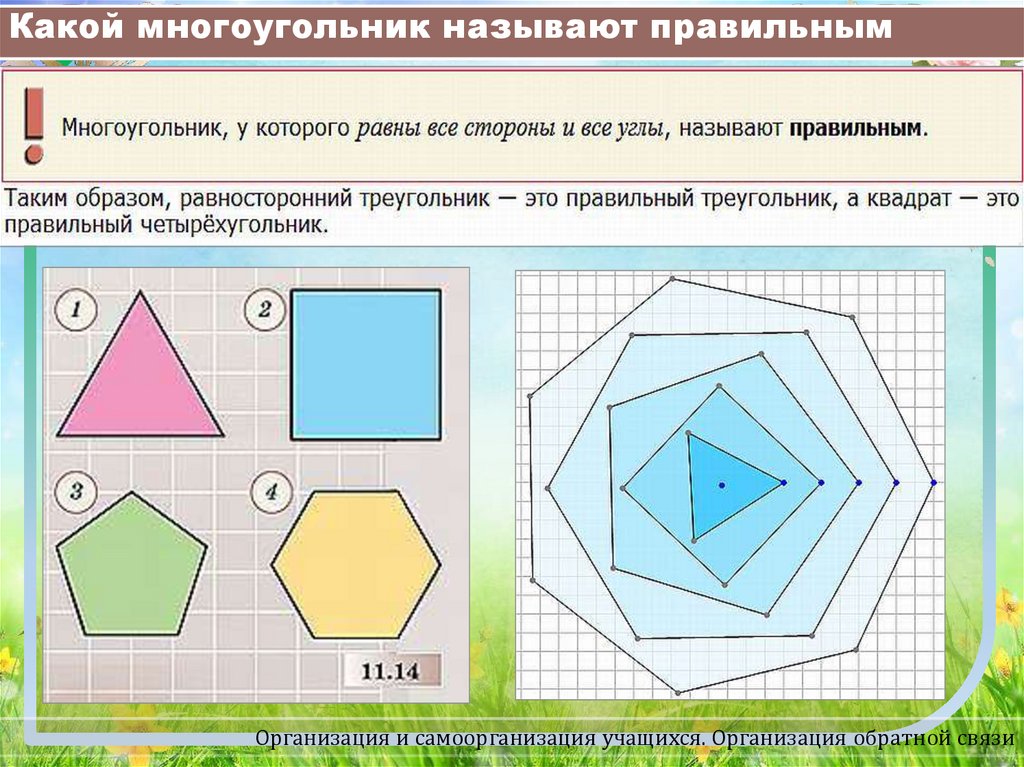
Калькулятор площади неправильного многоугольника по сторонам
Вам понадобится
- — рулетка;
- — электронный дальномер;
- — лист бумаги и карандаш;
- — калькулятор.
Инструкция 1 Если вам нужна общая площадь квартиры или отдельной комнаты, просто прочтите технический паспорт на квартиру или дом, там указан метраж каждого помещения и общий метраж квартиры. 2 Для измерения площади прямоугольной или квадратной комнаты возьмите рулетку или электронный дальномер и измерьте длину стен. При измерении расстояний дальномером обязательно следите за перпендикулярностью направления луча, иначе результаты замеров могут быть искажены. 3 Затем полученную длину (в метрах) комнаты умножьте на ширину (в метрах). Полученное значение и будет площадью пола, она измеряется в квадратных метрах.
Формула площади гаусса
Если требуется посчитать площадь пола более сложной конструкции, например, пятиугольной комнаты или комнаты с круглой аркой, схематично начертите эскиз на листе бумаги. Затем разделите сложную форму на несколько простых, например, на квадрат и треугольник или прямоугольник и полукруг. Измерьте при помощи рулетки или дальномера величину всех сторон получившихся фигур (для круга необходимо узнать диаметр) и занесите результаты на ваш чертеж.
Затем разделите сложную форму на несколько простых, например, на квадрат и треугольник или прямоугольник и полукруг. Измерьте при помощи рулетки или дальномера величину всех сторон получившихся фигур (для круга необходимо узнать диаметр) и занесите результаты на ваш чертеж.
5 Теперь посчитайте площадь каждой фигуры по отдельности. Площадь прямоугольников и квадратов высчитывайте перемножением сторон. Для расчета площади круга диаметр разделите пополам и возведите в квадрат (умножьте его на самого себя), затем умножьте полученное значение на 3,14.
Если вам нужна только половина круга, разделите полученную площадь пополам. Чтобы рассчитать площадь треугольника, найдите Р, для этого сумму всех сторон поделите на 2.
Формула расчета площади неправильного многоугольника
Если точки пронумерованы последовательно в направлении против часовой стрелки, то детерминанты в формуле выше положительны и модуль в ней может быть опущен; если они пронумерованы в направлении по часовой стрелке, детерминанты будут отрицательными.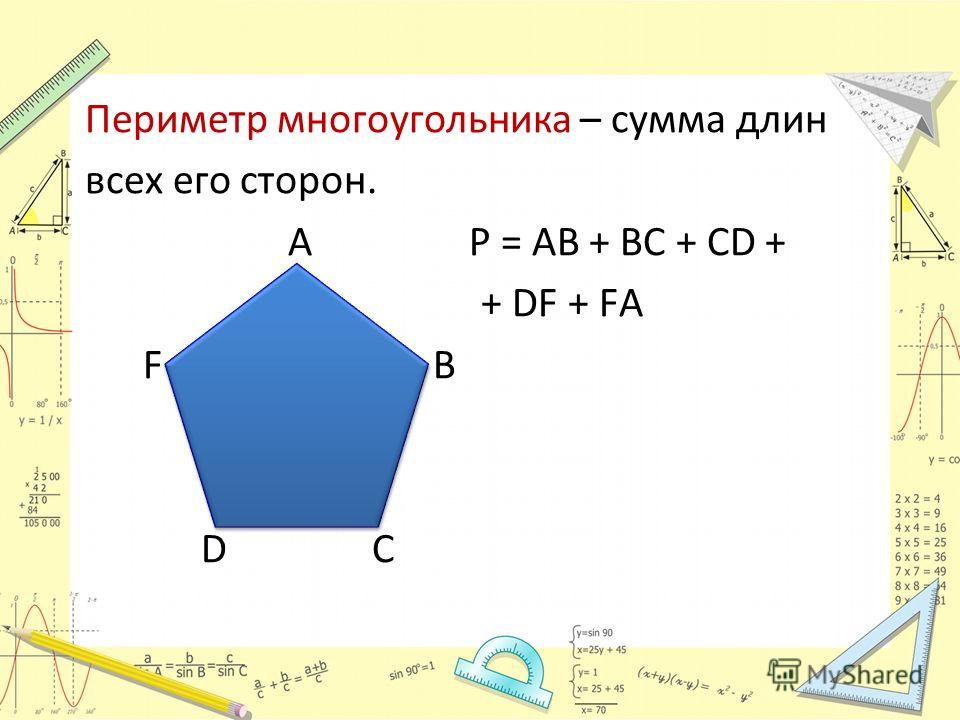 Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина. Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости.
Это происходит потому, что формула может рассматриваться как частный случай теоремы Грина. Для применения формулы необходимо знать координаты вершин многоугольника в декартовой плоскости.
Для примера возьмём треугольник с координатами {(2, 1), (4, 5), (7, 8)}. Возьмём первую х -координату первой вершины и умножим её на y -координату второй вершины, а затем умножим х второй вершины на y третьей. Повторим эту процедуру для всех вершин. Результат может быть определен по следующей формуле: A tri.
Формула расчета площади неправильного четырехугольника
A} _{\text{tri.}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{1}y_{3}|} где xi и yi обозначают соответствующую координату. Эту формулу можно получить, раскрыв скобки в общей формуле для случая n = 3. По этой формуле можно обнаружить, что площадь треугольника равна половине суммы 10 + 32 + 7 − 4 − 35 − 16, что даёт 3. Число переменных в формуле зависит от числа сторон многоугольника. Например, в формуле для площади пятиугольника будут использоваться переменные до x5 и y5: A pent. = 1 2 | x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 5 + x 5 y 1 − x 2 y 1 − x 3 y 2 − x 4 y 3 − x 5 y 4 − x 1 y 5 | {\displaystyle \mathbf {A} _{\text{pent.}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|} A для четырехугольника — переменные до x4 и y4: A quad.
= 1 2 | x 1 y 2 + x 2 y 3 + x 3 y 4 + x 4 y 5 + x 5 y 1 − x 2 y 1 − x 3 y 2 − x 4 y 3 − x 5 y 4 − x 1 y 5 | {\displaystyle \mathbf {A} _{\text{pent.}}={1 \over 2}|x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{4}+x_{4}y_{5}+x_{5}y_{1}-x_{2}y_{1}-x_{3}y_{2}-x_{4}y_{3}-x_{5}y_{4}-x_{1}y_{5}|} A для четырехугольника — переменные до x4 и y4: A quad.
Тема «Площади многоугольников» является неотъемлемой частью школьного курса математики, что вполне естественно. Ведь исторически само возникновение геометрии связано с потребностью сравнения земельных участков той или иной формы. Вместе с тем следует отметить, что образовательные возможности раскрытия этой темы в средней школе используются далеко не полностью.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин и продолжения образования.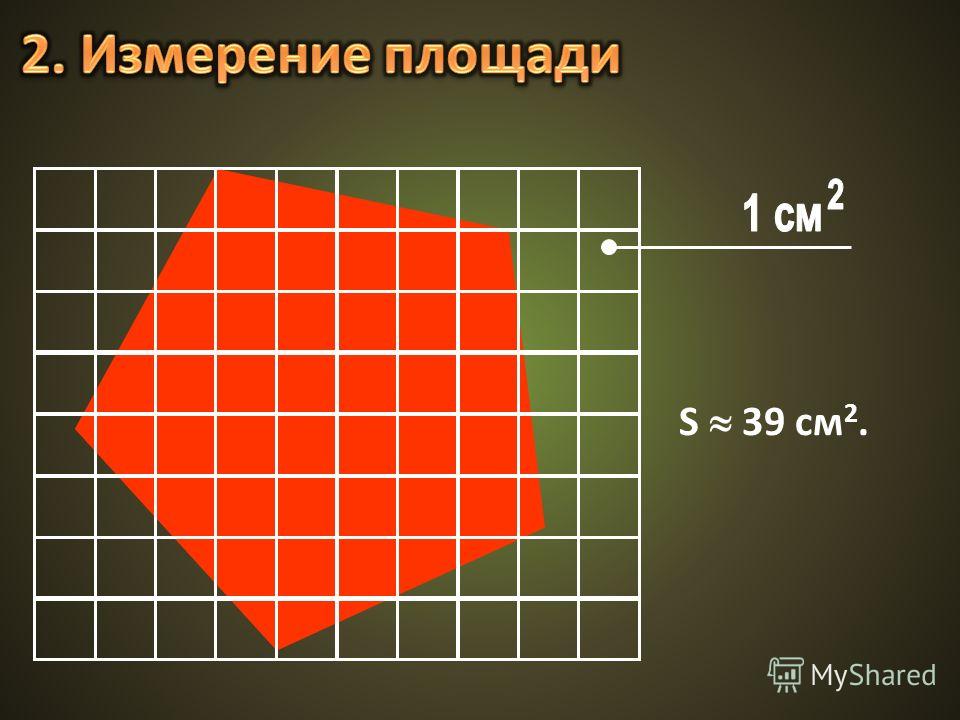
Наряду с решением основной задачи углубленное изучение математики предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии, существенным образом связанные с математикой, подготовку к обучению в вузе.
Квалификационная работа включает содержание курса математики общеобразовательной школы и ряд дополнительных вопросов, непосредственно примыкающих к этому курсу и углубляющих его по основным идейным линиям.
Включение дополнительных вопросов преследует две взаимосвязанные цели. С одной стороны, это создание в совокупности с основными разделами курса базы для удовлетворения интересов и развития способностей учащихся, имеющих склонность к математике, с другой – выполнение содержательных пробелов основного курса, придающее содержанию углубленного изучения необходимую целостность.
Квалификационная работа состоит из введения, двух глав, заключения и цитируемой литературы. В первой главе рассматриваются теоретические основы изучения площадей многоугольников, а во второй главе – непосредственно уже методические особенности изучения площадей.
1.1Вычисление площадей в древности
Зачатки геометрических знаний, связанных с измерением площадей, теряются в глубине тысячелетий.
Еще в 4 – 5 тысяч лет назад вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Квадрат издавна служит эталоном при измерении площадей благодаря многим своим замечательным свойствам: равные стороны, равные и прямые углы, симметричность и общее совершенство формы. Квадраты легко строить, или можно заполнить плоскость без пробелов.
В древнем Китае мерой площади был прямоугольник. Когда каменщики определяли площадь прямоугольной стены дома, они перемножали высоту и ширину стены. Таково принятое в геометрии определение: площадь прямоугольника равна произведению его смежных сторон. Обе эти стороны должны быть выражены в одних и тех же линейных единицах. Их произведение и составит площадь прямоугольника, выраженную в соответствующих квадратных единицах. Скажем, если высота и ширина стены измерены в дециметрах, то произведение обоих измерений будет выражено в квадратных дециметрах. И если площадь каждой облицовочной Плотки составляет квадратный дециметр, то полученное произведение укажет число плиток, нужное для облицовки. Это вытекает из утверждения, положенного в основу измерения площадей: площадь фигуры, составленной из непересекающихся фигур, равна сумме их площадей.
И если площадь каждой облицовочной Плотки составляет квадратный дециметр, то полученное произведение укажет число плиток, нужное для облицовки. Это вытекает из утверждения, положенного в основу измерения площадей: площадь фигуры, составленной из непересекающихся фигур, равна сумме их площадей.
Древние египтяне 4000 лет назад пользовались почти теми же приемами, что и мы, для измерения площади прямоугольника, треугольника и трапеции: основание треугольника делилось пополам, и умножалась на высоту; для трапеции же сумма параллельных сторон делилась пополам и умножалась на высоту и т.п. Для вычисления площади
четырехугольника со сторонами (рис. 1.1) применялась формула (1.1)
т.е. умножались полусуммы противоположных сторон.
Эта формула явно неверна для любого четырехугольника, из нее вытекает, в частности, что площади всех ромбов одинаковы. Между тем, очевидно, что у таких ромбов площади зависят от величины углов при вершинах. Данная формула верна только для прямоугольника. С ее помощью можно вычислить приближенно площадь четырехугольников, у которых углы близки к прямым.
С ее помощью можно вычислить приближенно площадь четырехугольников, у которых углы близки к прямым.
Для определения площади
равнобедренного треугольника (рис. 1.2), в котором , египтяне пользовались приближенной формулой:
(1.2) Рис. 1.2Совершаемая при этом ошибка тем меньше, чем меньше разность между стороной и высотой треугольника, иными словами, чем ближе вершина (и ) к основанию высоты из . Вот почему приближенная формула (1.2) применима лишь для треугольников с сравнительно малым углом при вершине.
Но уже древние греки умели правильно находить площади многоугольников. В своих «Началах» Евклид не употребляет слова «площадь», так как он под самим словом «фигура» понимает часть плоскости, ограниченную той или иной замкнутой линией. Евклид не выражает результат измерения площади числом, а сравнивает площади разных фигур между собой.
Как и другие ученые древности, Евклид занимается вопросами превращения одних фигур в другие, им равновеликие. Площадь составной фигуры не изменится, если ее части расположить по-другому, но без пересечения. Поэтому, например, можно, исходя из формул площади прямоугольника, находить формулы площадей других фигур. Так, треугольник разбивается на такие части, из которых затем можно составить равновеликий ему прямоугольник. Из этого построения следует, что площадь треугольника равна половине произведения его основания на высоту. Прибегая к подобной перекройке, находят, что площадь параллелограмма равна произведению основания на высоту, площадь трапеции – произведению полусуммы оснований на высоту.
Площадь составной фигуры не изменится, если ее части расположить по-другому, но без пересечения. Поэтому, например, можно, исходя из формул площади прямоугольника, находить формулы площадей других фигур. Так, треугольник разбивается на такие части, из которых затем можно составить равновеликий ему прямоугольник. Из этого построения следует, что площадь треугольника равна половине произведения его основания на высоту. Прибегая к подобной перекройке, находят, что площадь параллелограмма равна произведению основания на высоту, площадь трапеции – произведению полусуммы оснований на высоту.
Когда каменщикам приходится облицовывать стену сложной конфигурации, они могут определить площадь стены, подсчитав число пошедших на облицовку плиток. Некоторые плитки, естественно, придется обкалывать, чтобы края облицовки совпали с кромкой стены. Число всех пошедших в работу плиток оценивает площадь стены с избытком, число необломанных плиток – с недостатком. С уменьшением размеров клеток количество отходов уменьшается, и площадь стены, определяемая через число плиток, вычисляется все точнее.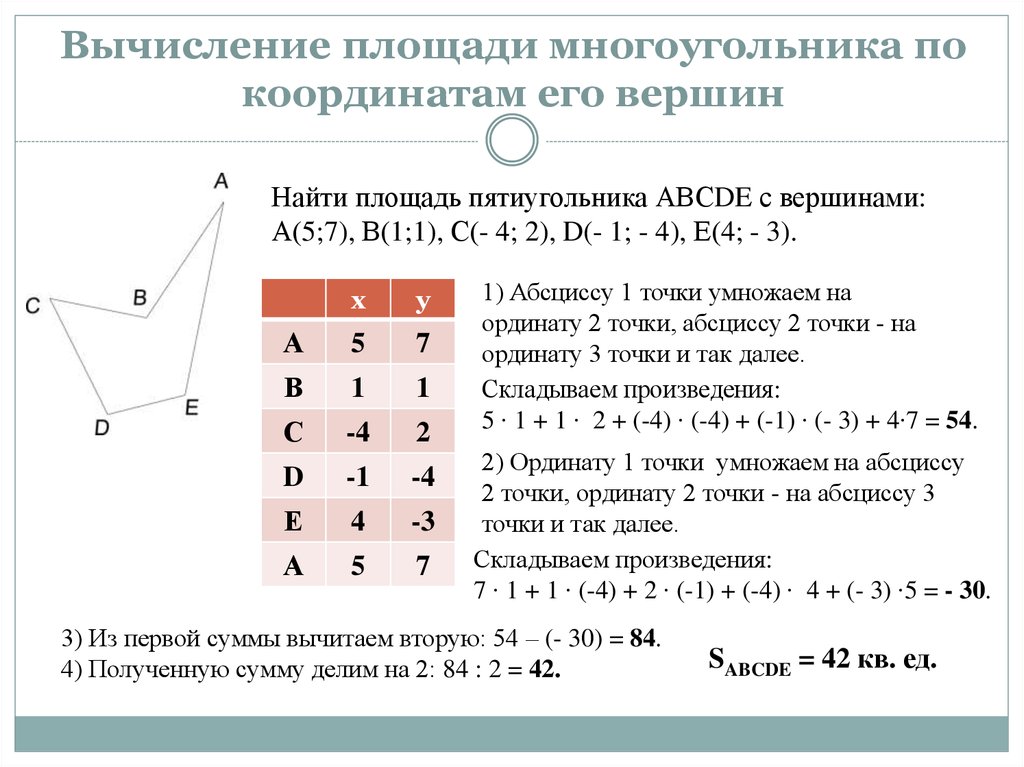
Одним из поздних греческих математиков – энциклопедистов, труды которого имели главным образом прикладной характер, был Герон Александрийский, живший в 1 в. н. э. Будучи выдающимся инженером, он был назван также «Герон Механик». В своем произведении «Диоптрика» Герон описывает разные машины и практические измерительные инструменты.
Одна из книг Герона была названа им «Геометрика» и является своего рода сборником формул и соответствующих задач. Она содержит примеры на вычисление площадей квадратов, прямоугольников и треугольников. О нахождении площади треугольника по его сторонам Герон пишет: « Пусть, например, одна сторона треугольника имеет в длину 13 мерных шнуров, вторая 14 и третья 15. Чтобы найти площадь, поступают вот как. Сложи 13, 14 и 15; получится 42. Половина этого будет 21. Вычти из этого три стороны одну за другой; сперва вычти 13 – останется 8, затем 14 – останется 7 и, наконец, 15 – останется 6. А теперь перемножь их: 21раз по 8 даст 168, возьми это 7 раз – получится 1176, а это еще 6 раз – получится 7056. Отсюда квадратный корень будет 84. Вот сколько мерных шнуров будет в площади треугольника».
Отсюда квадратный корень будет 84. Вот сколько мерных шнуров будет в площади треугольника».
Площадь многоугольников – формула, площадь правильных многоугольников Примеры
Площадь многоугольника определяется как площадь, ограниченная границей многоугольника. Другими словами, мы говорим, что область, занимаемая любым многоугольником, дает его площадь. В этом уроке мы научимся определять площадь многоугольников и детально находить разницу между периметром и площадью многоугольников.
| 1. | Какова площадь многоугольника? |
| 2. | Разница между периметром и площадью полигонов |
| 3. | Формулы площади многоугольника |
| 4. | Площадь полигонов с координатами |
| 5. | Часто задаваемые вопросы о площади полигонов |
Какова площадь многоугольника?
Определение площади многоугольника — это мера площади, заключенной в него. Поскольку многоугольники представляют собой замкнутые плоские формы, то площадь многоугольника — это пространство, которое он занимает в двумерной плоскости. Единица площади любого многоугольника всегда выражается в квадратных единицах. Обратите внимание на следующий рисунок, на котором показана площадь многоугольника на двумерной плоскости.
Поскольку многоугольники представляют собой замкнутые плоские формы, то площадь многоугольника — это пространство, которое он занимает в двумерной плоскости. Единица площади любого многоугольника всегда выражается в квадратных единицах. Обратите внимание на следующий рисунок, на котором показана площадь многоугольника на двумерной плоскости.
Разница между периметром и площадью полигонов
Периметр и площадь многоугольников являются измеримыми величинами, которые зависят от длины сторон многоугольника. Чтобы различать их обоих, необходимо понять основную разницу между периметром и площадью. Обратите внимание на приведенную ниже таблицу, чтобы лучше понять эту разницу.
| Критерии различия | Периметр Полигона | Площадь полигона |
|---|---|---|
| Определение | Определяется как общая длина границы многоугольника, которую можно получить, сложив длины всех его сторон. | Определяется как область или пространство, окруженное любым многоугольником. |
| Формула | Периметр многоугольника = длина стороны 1 + длина стороны 2 + …+ длина стороны N (для N-стороннего многоугольника) | Площадь многоугольника можно найти по разным формулам в зависимости от того, является ли многоугольник правильным или неправильным многоугольником. |
| Блок | Единица измерения периметра многоугольника выражается в метрах, сантиметрах, дюймах, футах и т. д. | Единица площади многоугольников выражается в (метрах) 2 , (сантиметрах) 2 , (дюймах) 2 , (футах) 2 и т. д. |
Сходство между вычислением периметра и площади многоугольника заключается в том, что оба они зависят от длины сторон формы, а не от внутренних или внешних углов многоугольника.
Формулы площади многоугольника
Многоугольник может быть классифицирован как правильный или неправильный многоугольник в зависимости от длины его сторон. Таким образом, эта дифференциация также вносит различие в вычисление площади многоугольников. Площадь некоторых общеизвестных многоугольников определяется как:
Таким образом, эта дифференциация также вносит различие в вычисление площади многоугольников. Площадь некоторых общеизвестных многоугольников определяется как:
- Площадь треугольника = (1/2) × основание × высота
Мы также можем найти площадь треугольника, если известна длина его сторон, используя формулу Герона, которая выглядит следующим образом: Площадь = \(\sqrt{s(s-a)(s-b)(s-c)}\), где s = периметр/ 2 = (a + b + c)/2, a, b и c — длины его сторон. - Площадь прямоугольника = длина × ширина
- Площадь параллелограмма = основание × высота
- Площадь трапеции = (1/2) × (сумма длин ее параллельных сторон или оснований) × высота
- Площадь ромба = (1/2) × (произведение диагоналей)
Чтобы вычислить площадь многоугольника, необходимо сначала узнать, является ли данный многоугольник правильным или неправильным многоугольником.
Площадь правильных многоугольников
Правильный многоугольник — это многоугольник с равными сторонами и равными углами.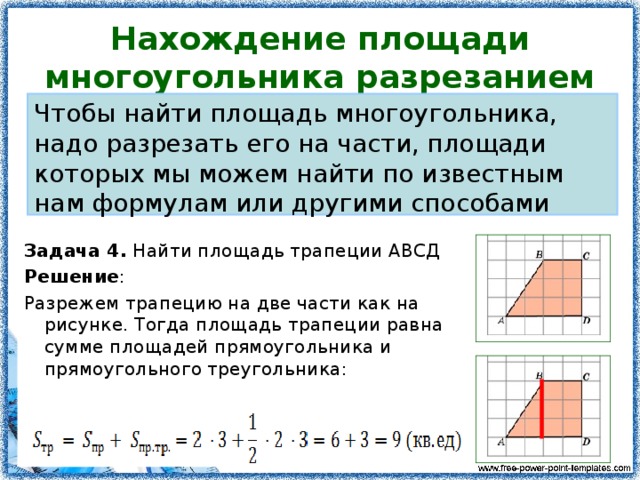 Таким образом, метод расчета площади правильных многоугольников основан на формулах, связанных с каждым многоугольником. Давайте посмотрим на формулы некоторых часто используемых правильных многоугольников:
Таким образом, метод расчета площади правильных многоугольников основан на формулах, связанных с каждым многоугольником. Давайте посмотрим на формулы некоторых часто используемых правильных многоугольников:
| Названия правильных многоугольников | Площадь правильного многоугольника |
|---|---|
| Равносторонний треугольник | Площадь = (√3 ×(длина стороны) 2 )/4 |
| Квадрат | Площадь = (длина) 2 |
| Обычный пятиугольник | Площадь = 5/2 × длина стороны × длина апофемы 92\) |
| Обычный шестигранник | Площадь = [3√3 × (длина стороны) 2 ]/2 |
Для определения площади правильного многоугольника, если известно число его сторон, дается формула:
- Площадь правильного многоугольника = (число сторон × длина одной стороны × апофема)/2 , где длина апофемы задается как \(\dfrac{l}{2\tan(\dfrac{180}{n})}\), где l — длина стороны, а n — количество сторон правильный многоугольник.
 92\)
92\)
⇒ A = 84,3 квадратных дюймаТаким образом, площадь правильного пятиугольника равна 84,3 квадратных дюйма.
Площадь неправильных многоугольников
Неправильный многоугольник представляет собой плоскую замкнутую форму, не имеющую равных сторон и равных углов. Таким образом, чтобы вычислить площадь неправильного многоугольника, мы разобьем неправильный многоугольник на множество правильных многоугольников так, что известны формулы их площадей. Рассмотрим пример, приведенный ниже.
Многоугольник ABCD является неправильным многоугольником. Таким образом, мы можем разделить многоугольник ABCD на два треугольника ABC и ADC. Площадь треугольника можно получить: 92 }\)
- Шаг 2: Зная размеры многоугольников, определите, является ли данный многоугольник правильным многоугольником или нет.
- Шаг 3: Если многоугольник является правильным многоугольником, мы используем формулу площадь правильного многоугольника = (количество сторон × длина одной стороны × апофема)/2, где длина апофемы определяется как (длина одной стороны )/(2 ×(tan(180°/количество сторон))).
 2}\) = 2 единицы 92}\) = 2 единицы
2}\) = 2 единицы 92}\) = 2 единицыТеперь, когда мы знаем, что длина всех сторон данного многоугольника одинакова, это показывает, что это квадрат. Таким образом, площадь многоугольника ABCD определяется как A = (длина) 2 = (2) 2 = 4 квадратных единицы.
Следовательно, площадь многоугольника с координатами (0,0), (0, 2), (2, 2) и (2, 0) равна 4 квадратным единицам.
Важные примечания
- Если известна длина одной стороны, можно найти площадь правильного многоугольника, найдя апофему.
- Апофема падает на середину стороны под прямым углом, разделяя ее на две равные части.
- Равносторонний треугольник — это правильный многоугольник с 3 сторонами, а квадрат — правильный многоугольник с 4 сторонами. Следовательно, они не имеют обычного префикса перед именем формы.
Часто задаваемые вопросы о площади полигонов
Что такое определение площади многоугольника?
Пространство, ограниченное любым многоугольником на двумерной плоскости, определяется как площадь многоугольника.
 Запишем единицу площади многоугольника в квадратных единицах , где единицей измерения могут быть единицы СИ, такие как метры или сантиметры и т. д., или единицы USCS (дюймы или футы и т. д.).
Запишем единицу площади многоугольника в квадратных единицах , где единицей измерения могут быть единицы СИ, такие как метры или сантиметры и т. д., или единицы USCS (дюймы или футы и т. д.).Как найти площадь многоугольника?
Площадь многоугольника можно рассчитать, поняв, является ли данный многоугольник правильным или неправильным многоугольником. Шаги для вычисления площади многоугольников:
- Шаг 1: Определите, является ли данный многоугольник правильным многоугольником или нет.
- Шаг 2: Если это правильный многоугольник или имеет стандартную формулу расчета, используйте ее для определения значения при всех заданных размерах многоугольника, в противном случае площадь многоугольника можно вычислить, разделив его на множество правильные многоугольники, площадь которых можно сложить, чтобы получить площадь требуемого многоугольника.
Какова площадь многоугольника с n сторонами?
Если задано количество сторон многоугольника, площадь многоугольника можно рассчитать по формуле Площадь = [(L 2 n)/4 tan(180/n)]; где L — длина его стороны, а «n» — количество сторон многоугольника.

В чем разница между периметром и площадью многоугольников?
Периметр многоугольника — это общая длина его границы, тогда как площадь многоугольника — это занимаемая им область. Периметр многоугольника получается путем сложения длин всех его сторон, а площадь многоугольника получается с помощью требуемой формулы в зависимости от того, является ли данный многоугольник правильным многоугольником или нет. Единица периметра многоугольника всегда дается в линейных единицах, поскольку она одномерна, в то время как единица площади многоугольника всегда дается в квадратных единицах, поскольку площадь является двумерным понятием. 92 }\)
- Шаг 2: Как только нам известны размеры многоугольников, мы определяем, является ли данный многоугольник правильным многоугольником или нет.
- Шаг 3: Если вывод из шага 2 показывает, что многоугольник является правильным многоугольником, мы используем формулу площадь правильного многоугольника = (количество сторон × длина одной стороны × апофема)/2, где длина апофемы определяется как , Апофема = [(длина одной стороны)/{2 ×(tan(180/количество сторон))}].
 С другой стороны, если многоугольник является неправильным многоугольником, его делят на несколько меньших правильных многоугольников, находя размерность диагоналей по формуле расстояния.
С другой стороны, если многоугольник является неправильным многоугольником, его делят на несколько меньших правильных многоугольников, находя размерность диагоналей по формуле расстояния.
Как найти площадь правильного многоугольника?
Площадь правильного многоугольника можно найти по формуле Площадь = (количество сторон × длина одной стороны × апофема)/2. Соблюдайте следующие шаги для всей процедуры:
- Шаг 1: Найдите количество сторон многоугольника.
- Шаг 2: Если для заданного правильного многоугольника существует стандартная формула, примените ее. Если нет, обратитесь к шагам, приведенным ниже.
- Шаг 3: Проверьте измерение длины одной стороны.
- Шаг 4: Используйте значения, полученные на шагах 1 и 2, для определения значения апофемы по формуле Апофема = [(длина одной стороны)/{2 ×(тангенс(180/количество сторон))}].
- Шаг 5: Теперь найдите площадь правильного многоугольника по формуле Площадь = (количество сторон × длина одной стороны × апофема)/2.

Как найти площадь неправильного многоугольника?
Чтобы вычислить значение площади неправильного многоугольника, мы используем следующие шаги:
- Шаг 1: Разделите заданный многоугольник на меньшие части, образуя различные правильные или известные многоугольники.
- Шаг 2: Найдите площадь каждой секции по отдельности.
- Шаг 3: Добавьте площадь каждой секции, чтобы получить площадь заданного неправильного многоугольника.
Как найти площадь многоугольника с периметром?
Если периметр многоугольника задан, то его площадь можно рассчитать по формуле: Площадь = (Периметр × апофема)/2. В этой формуле также должна быть известна апофема или ее можно вычислить с помощью формулы Апофема = [(длина одной стороны)/{2 ×(tan(180/число сторон))}]. Подставляя значение апофемы и периметра, можно вычислить площадь многоугольника.
Какая формула используется для вычисления площади правильных многоугольников?
Формула для вычисления площади правильного многоугольника: Площадь = (количество сторон × длина одной стороны × апофема)/2, где значение апофемы можно рассчитать по формуле Апофема = [(длина одного сторона)/{2 ×(tan(180/количество сторон))}].
Площадь многоугольника – формулы, примеры
Площадь многоугольника – это общее пространство, заключенное внутри фигуры. Измерение производится в квадратных единицах.
Как известно, многоугольник может быть правильным или неправильным. Стороны правильных многоугольников имеют определенный размер, поэтому их площадь легко вычислить по сравнению с неправильными многоугольниками, стороны которых не имеют фиксированного размера. Давайте изучим основной подход к определению площади обоих типов по отдельности.
Как найти площадь правильного многоугольника
Чтобы определить площадь поверхности правильного многоугольника с n сторон (где каждая сторона представлена как «s»), мы используем формулу, приведенную ниже:
Площадь правильного многоугольникаНайдите площадь правильного многоугольника с периметром 44 см и длиной апофемы 10 см.
Решение:
Как мы знаем,
Площадь (A) = ½ x p x a, здесь p = 44 см и a = 10 см
= ½ x 44 x 10 см
Нахождение площади правильного многоугольника, когда известны СТОРОНА и АПОТЕМ .
Вычислите площадь правильного пятиугольника со стороной 12 см и апофемой 7,5 см.
Решение:
Поскольку многоугольник представляет собой пятиугольник с пятью сторонами, где каждая сторона (s) имеет размер 12 см, его периметр (p) равен (5 x s) = (5 x 12) = 60 см
Теперь , как мы знаем,
Площадь (A) = ½ x p x a, здесь p = 60 см и a = 7,5 см
= ½ x 60 x 7,5 см 2
= 225 см Неправильный многоугольник
Для неправильных многоугольников мы делим многоугольник на два или более правильных многоугольника, находим индивидуальную площадь каждого такого многоугольника, а затем складываем их, чтобы получить площадь общей фигуры.
Площадь неправильного многоугольникаДавайте рассмотрим пример, чтобы лучше понять концепцию.
Найдите площадь неправильного многоугольника ABCDE с данными размерами сторон. (Прием: Разделите многоугольник на два прямоугольника)
Решение:
Чтобы решить данную задачу, разделим данную фигуру на два прямоугольника ABFE и GFDC.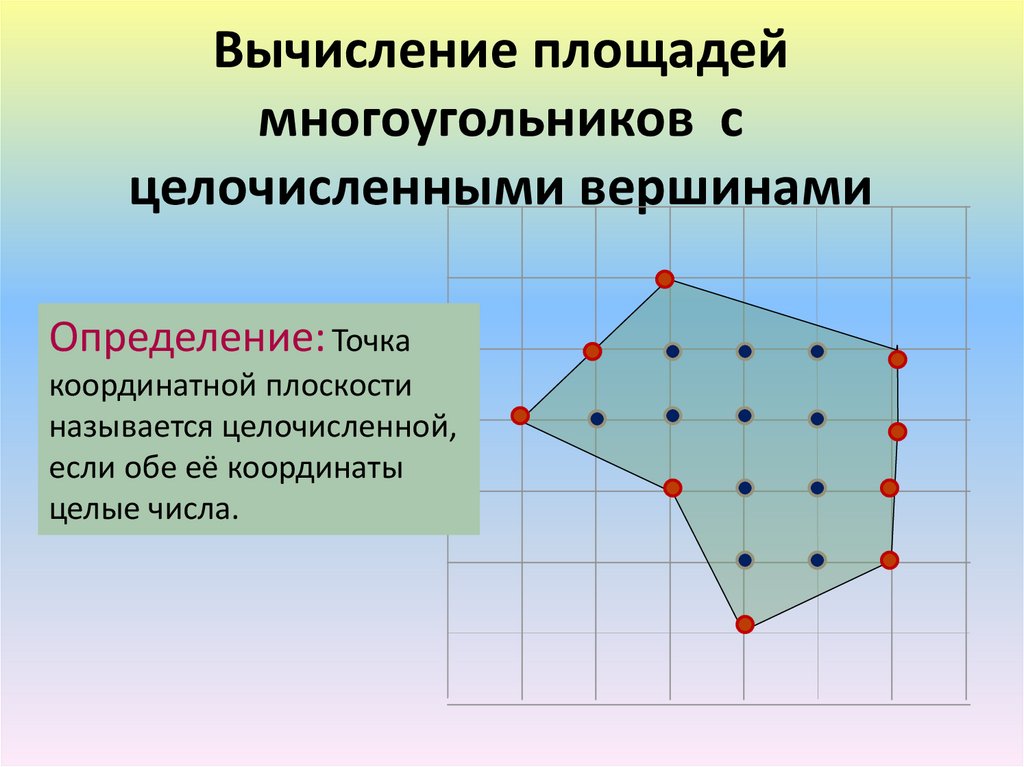


 92\)
92\)  2}\) = 2 единицы 92}\) = 2 единицы
2}\) = 2 единицы 92}\) = 2 единицы Запишем единицу площади многоугольника в квадратных единицах , где единицей измерения могут быть единицы СИ, такие как метры или сантиметры и т. д., или единицы USCS (дюймы или футы и т. д.).
Запишем единицу площади многоугольника в квадратных единицах , где единицей измерения могут быть единицы СИ, такие как метры или сантиметры и т. д., или единицы USCS (дюймы или футы и т. д.).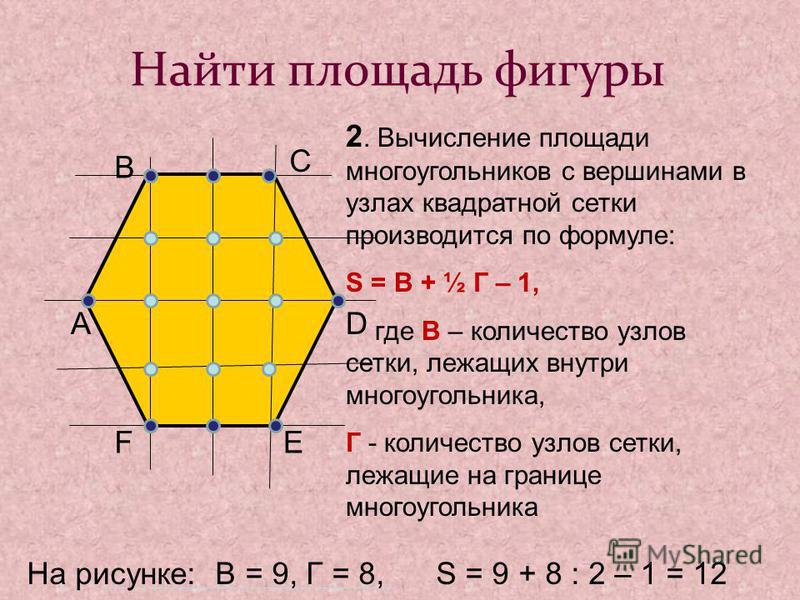
 С другой стороны, если многоугольник является неправильным многоугольником, его делят на несколько меньших правильных многоугольников, находя размерность диагоналей по формуле расстояния.
С другой стороны, если многоугольник является неправильным многоугольником, его делят на несколько меньших правильных многоугольников, находя размерность диагоналей по формуле расстояния.