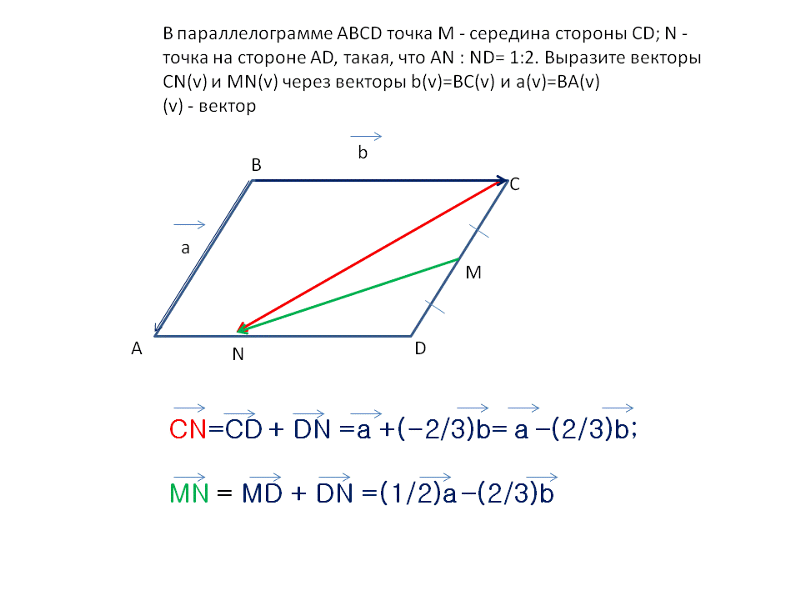
Площадь параллелограмма по координатам векторов. Векторное произведение векторов
Вспомним в начале, что такое векторное произведение.
Замечание 1
Векторным произведением для $\vec{a}$ и $\vec{b}$ является $\vec{c}$, представляющий собой некоторый третий вектор $\vec{c}= ||$, причём этот вектор обладает особенными свойствами:
- Cкаляр полученного вектора — произведение $|\vec{a}|$ и $|\vec{b}|$ на синус угла $\vec{c}= ||= |\vec{a}| \cdot |\vec{b}|\cdot \sin α \left(1\right)$;
- Все $\vec{a}, \vec{b}$ и $\vec{c}$ образуют правую тройку;
- Полученный вектор ортогонален к $\vec{a}$ и $\vec{b}$.
Если для векторов присутствуют некоторые координаты ($\vec{a}=\{x_1; y_1; z_1\}$ и $\vec{b}= \{x_2; y_2; z_2\}$), то их векторное произведение в декартовой системе координат можно определить по формуле:
$ = \{y_1 \cdot z_2 – y_2 \cdot z_1; z_1 \cdot x_2 – z_2 \cdot x_1; x_2 \cdot y_2 – x_2 \cdot y_1\}$
Легче всего запомнить эту формулу записав в форме определителя:
$ = \begin{array} {|ccc|} i & j & k \\ x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ \end{array}$.
Эта формула весьма удобна для использования, но чтобы понимать, как её использовать, для начала следует ознакомиться с темой матриц и их определителей.
Площадь параллелограмма , стороны которого определяются двумя векторами $\vec{a}$ и $vec{b}$ равна скаляру векторного произведения данных двух векторов.
Это соотношение совсем несложно вывести.
Вспомним формулу для нахождения площади обычного параллелограмма, который можно охарактеризовать образующими его отрезками $a$ и $b$:
$S = a \cdot b \cdot \sin α$
При этом длины сторон равны скалярным значениям векторов $\vec{a}$ и $\vec{b}$, что вполне себе подходит нам, то есть, скаляр векторного произведения данных векторов и будет площадью рассматриваемой фигуры.
Пример 1
Даны векторы $\vec{c}$ c координатами $\{5;3; 7\}$ и вектор $\vec{g}$ с координатами $\{3; 7;10 \}$ в декартовой системе координат. Найти, чему равна площадь параллелограмма, образованного $\vec{c}$ и $\vec{g}$.
Данный ход рассуждений справедлив не только для нахождения площади в 3-хмерном пространстве, но и для двухмерного. Познакомьтесь со следующей задачкой на эту тему.
Пример 2
Вычислить площадь параллелограмма, если его образующие отрезки задаются векторами $\vec{m}$ с координатами $\{2; 3\}$ и $\vec{d}$ с координатами $\{-5; 6\}$.
Решение:
Эта задача представляет собой частный пример задачки 1, решённой выше, но при этом оба вектора лежат в одной плоскости, а это значит, что третью координату, $z$, можно принять за нуль.
Подведём итоги по всему вышесказанному, площадь параллелограмма составит:
$S = \begin{array} {||cc||} 2 & 3\\ -5 & 6 \\ \end{array} = \sqrt{12 + 15} =3 \sqrt3$.
Пример 3
Даны векторы $\vec{a} = 3i – j + k; \vec{b}= 5i$. Определите площадь образуемого ими параллелограмма.
$[ \vec{a} \times \vec{b}] = (3i – j + k) \times 5i = 15 – 5 + $
Упростим согласно приведённой таблице для единичных векторов:
Рисунок 1. 2} = 5\sqrt{2}$.
2} = 5\sqrt{2}$.
Предыдущие задачи были о векторах, координаты которых заданы в декартовой системе координат, но рассмотрим также случай, если угол между базисными векторами отличается от $90°$:
Пример 4
Вектор $\vec{d} = 2a + 3b$, $\vec{f}= a – 4b$, длины $\vec{a}$ и $\vec{b}$ равны между собой и равны единице, а угол между $\vec{a}$ и $\vec{b}$ равен 45°.
Решение:
Вычислим векторное произведение $\vec{d} \times \vec{f}$:
$[\vec{d} \times \vec{f} ]= (2a + 3b) \times (a – 4b) = 2 – 8 + 3 – 12 $.
Для векторных произведений согласно их свойствам справедливо следующее: $$ и $$ равны нулю, $ = — $.
Используем это для упрощения:
$[\vec{d} \times \vec{f} ]= -8 + 3 = -8 — 3 =-11$.
Теперь воспользуемся формулой $(1)$ :
$[\vec{d} \times \vec{f} ] = |-11 | = 11 \cdot |a| \cdot |b| \cdot \sin α = 11 \cdot 1 \cdot 1 \cdot \frac12=5,5$.
Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.
Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье . Площадь будет равняться произведению модулей на синус угла между ними:
Рассмотрим пример расчета площади параллелограмма построенного на векторах.
Задача: параллелограмм построен на векторах и . Найдите площадь, если , а угол между ними 30°.
Выразим вектора через их значения:
Возможно, у вас возник вопрос – откуда взялись нули? Стоит вспомнить, что мы работаем с векторами, а для них . также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:
Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.
Расчет длин сторон фигуры, заданной координатами
Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a
(x1;y1;z1), а вектора b
(x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:
Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.
Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же
Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками.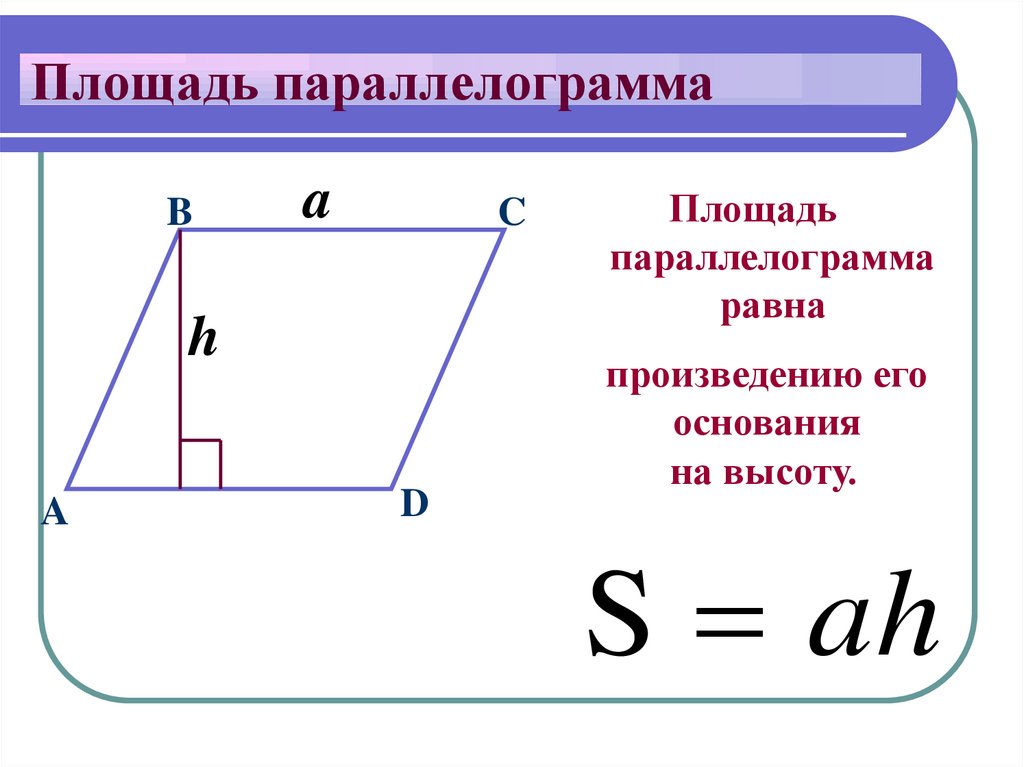
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то и . Обратите внимание, что само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно тоже равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми.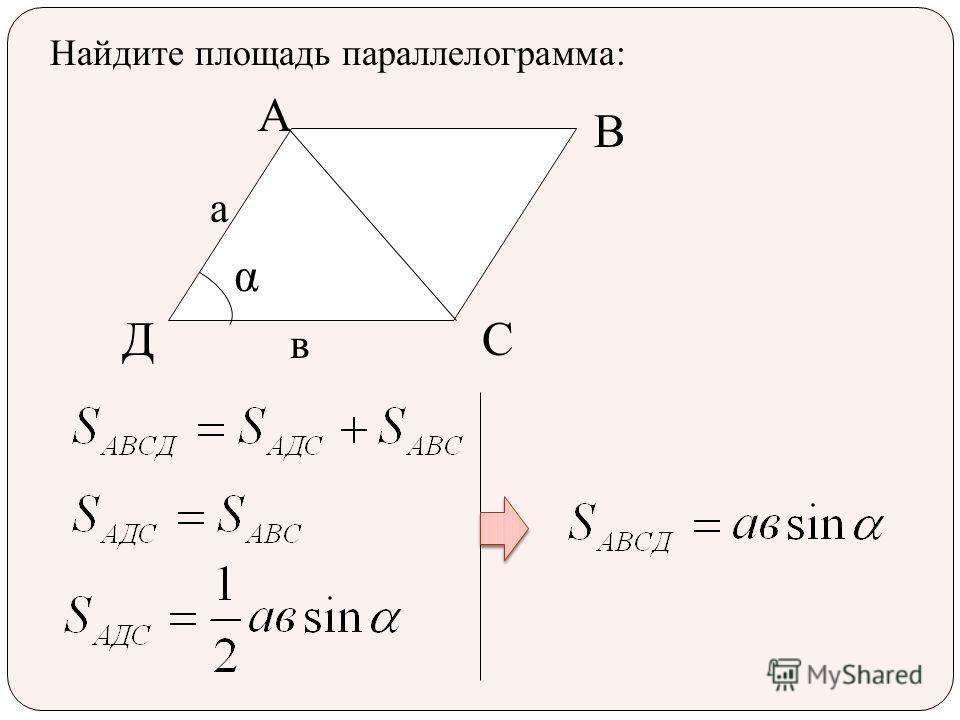 Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.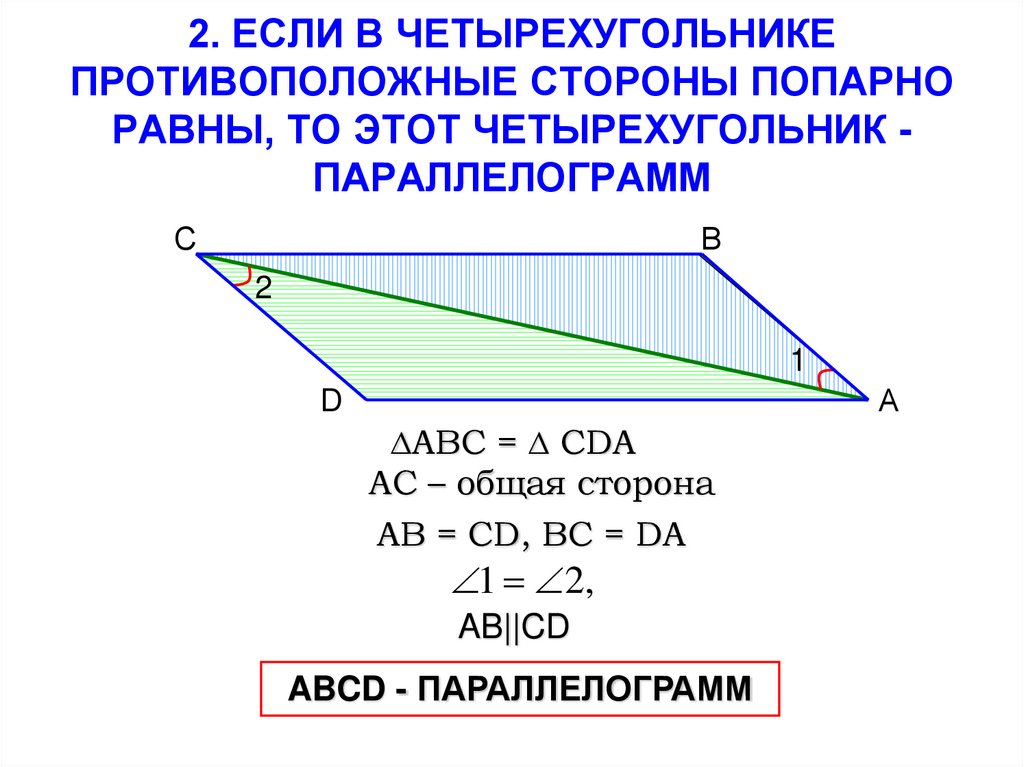
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Решено
В треугольнике АВС точка М – середина стороны АВ, точка N – середина стороны АС, отрезки СМ и BN пересекаются в точке О, ВА = а, ВС = b. Выразите вектор ВО через векторы а и b.
Дана правильная четырёхугольная усечённая пирамида высотой 9 см. В основаниях лежат квадраты со сторонами 4 см и 8 см. Найдите:
A) 1/2AC — BO + BB1 + 2B1O1
Б) [OD + DD1 — O1D1]
В) OO1 *OB1
(вектора)
В основаниях лежат квадраты со сторонами 4 см и 8 см. Найдите:
A) 1/2AC — BO + BB1 + 2B1O1
Б) [OD + DD1 — O1D1]
В) OO1 *OB1
(вектора)
Решено
Даны вершины треугольника М(1,-1,5), N(4,-3,2), P(0,-5,5). Найти внутренний угол при вершине M
Решено
Модуль вектора а равен — 2. Известно, что она образует с осью ОХ — острый угол, осью ОУ-угол 60, а осью ОZ -135. Найдите координату вектора а
Решено
Точка пересечения диагоналей куба — O. Сторона куба равна 3 дм.
Пользуйтесь нашим приложением
Вопрос Видео: Нахождение площади параллелограмма в трех измерениях
Стенограмма видео
𝐴𝐵𝐶𝐷 представляет собой параллелограмм, в котором вектор 𝐴𝐵 имеет отрицательные компоненты один, один, три, а вектор 𝐴𝐷 имеет компоненты три, четыре, один.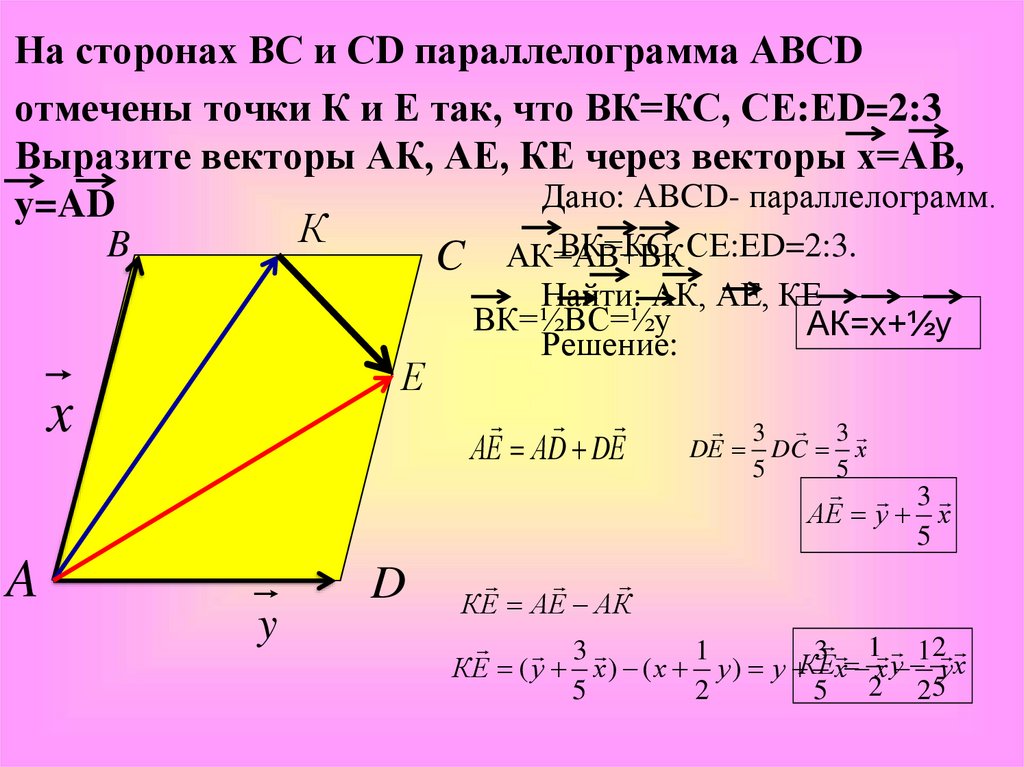 Найдите площадь 𝐴𝐵𝐶𝐷. Дайте ответ с точностью до одного десятичного знака.
Найдите площадь 𝐴𝐵𝐶𝐷. Дайте ответ с точностью до одного десятичного знака.
В вопросе сказано, что 𝐴𝐵𝐶𝐷 — параллелограмм. Итак, давайте нарисуем его. Вот наш параллелограмм. Теперь нам просто нужно пометить его вершины. Как только мы назвали одну из вершин 𝐴, у нас есть только два варианта, куда пойдет 𝐵. Он должен быть рядом с 𝐴. Так что 𝐵 нужно идти либо сюда, либо сюда. И как только мы выбрали, куда идти 𝐴 и 𝐵, у нас нет выбора для 𝐶 и 𝐷. 𝐶 должен быть рядом с 𝐵. А на 𝐷 осталось всего одно место. Итак, начиная с 𝐴, мы можем обойти параллелограмм, сначала посетив 𝐵, затем 𝐶 и, наконец, 𝐷, прежде чем снова окажемся в 𝐴. Другими словами, мы можем посещать вершины в том же порядке, в котором они встречаются в названии параллелограмма 𝐴𝐵𝐶𝐷.
Хорошо, а что еще нам говорят в тексте задачи? Нам даны компоненты вектора 𝐴𝐵. Отметим их на нашей картинке, а также компоненты вектора 𝐴𝐷. И что мы ищем? Мы хотим найти площадь параллелограмма 𝐴𝐵𝐶𝐷.
Чтобы найти эту площадь, мы используем тот факт, что величина векторного произведения двух векторов 𝑢 и 𝑣 является площадью параллелограмма, смежные стороны которого равны 𝑢 и 𝑣. Ищем площадь параллелограмма, смежные стороны которого имеют отрицательные компоненты один, один, три и три, четыре, один. И приведенное выше правило говорит нам, что это величина перекрестного произведения двух векторов. Итак, давайте освободим место и найдем эту величину.
Ищем площадь параллелограмма, смежные стороны которого имеют отрицательные компоненты один, один, три и три, четыре, один. И приведенное выше правило говорит нам, что это величина перекрестного произведения двух векторов. Итак, давайте освободим место и найдем эту величину.
Прежде чем найти величину векторного произведения, конечно, нам нужно найти само векторное произведение. И мы можем записать это перекрестное произведение как определитель матрицы три на три, первая строка которой содержит единичные векторы в 𝑥-, 𝑦- и 𝑧-направлениях 𝑖, 𝑗 и 𝑘. Вторая строка содержит компоненты первого вектора в наших перекрестных произведениях минус один, один и три. И третья строка содержит компоненты второго вектора в нашем перекрестном произведении три, четыре и один.
Можно разложить определитель по первой строке. И оценивая каждое два на два, вот как это означает, что мы получаем отрицательное 11 𝑖 плюс 10 𝑗 минус семь 𝑘, что мы можем записать в компонентах как отрицательное 11, 10, отрицательное семь. Это векторное произведение векторов, площадь которого мы ищем, что является величиной этого векторного произведения. Итак, мы ищем величину вектора с компонентами минус 11, 10 и минус семь.
Это векторное произведение векторов, площадь которого мы ищем, что является величиной этого векторного произведения. Итак, мы ищем величину вектора с компонентами минус 11, 10 и минус семь.
А величина вектора — это просто квадратный корень из суммы квадратов компонентов. Итак, у нас есть квадратный корень из минус 11 в квадрате плюс 10 в квадрате плюс минус семь в квадрате. Мы можем записать это в точности как квадратный корень из 270 или как три умноженный на квадратный корень из 30. Но нас не спрашивают о точном ответе. Нас просят дать правильный ответ до одного знака после запятой. И с точностью до одного десятичного знака квадратный корень из 270 равен 16,4. Итак, наш параллелограмм 𝐴𝐵𝐶𝐷 имеет площадь 16,4 единицы с точностью до одного десятичного знака.
Мы нашли это, вычислив величину векторного произведения векторов вдоль двух смежных сторон параллелограмма. И нам повезло, что нам дали компоненты двух смежных сторон в задаче. Нам не даны, например, компоненты одной из диагоналей ни 𝐴𝐶, ни 𝐵𝐷. И сделать так, чтобы заданные нам векторы шли по двум соседним сторонам. Мы должны были быть осторожны с тем, как мы помечаем вершины нашего параллелограмма.
И сделать так, чтобы заданные нам векторы шли по двум соседним сторонам. Мы должны были быть осторожны с тем, как мы помечаем вершины нашего параллелограмма.
Параллелограмм, который я только что нарисовал, не является правильной диаграммой для параллелограмма 𝐴𝐵𝐶𝐷. Обходя вершины по порядку, мы можем получить 𝐴𝐵𝐷𝐶 или 𝐴𝐶𝐷𝐵, но не 𝐴𝐵𝐶𝐷. Если бы мы использовали эту неверную диаграмму, мы бы получили неверный ответ, поэтому стоило вначале потратить некоторое время на то, чтобы правильно пометить наши вершины.
Как найти площадь параллелограмма с вершинами
••• Jupiterimages/Polka Dot/Getty Images
Обновлено 10 июня 2019 г. быть вычислено с помощью векторного векторного произведения. Площадь параллелограмма равна произведению его основания на высоту. Используя векторные значения, полученные из вершин, произведение основания и высоты параллелограмма равно перекрестному произведению двух его смежных сторон. Вычислите площадь параллелограмма, найдя векторные значения его сторон и оценив векторное произведение.
Найдите векторные значения двух смежных сторон параллелограмма, вычитая значения x и y двух вершин, образующих сторону. Например, чтобы найти длину DC параллелограмма ABCD с вершинами A (0, -1), B (3, 0), C (5, 2) и D (2, 1), из (5) вычтите (2, 1) , 2) чтобы получить (5 — 2, 2 — 1) или (3, 1). Чтобы найти длину AD, вычтите (2, 1) из (0, -1), чтобы получить (-2, -2).
Напишите матрицу из двух строк по три столбца. Заполните первую строку векторными значениями одной стороны параллелограмма (значение x в первом столбце и значение y во втором) и запишите ноль в третьем столбце. Заполните значения второй строки векторными значениями другой стороны и нулем в третьем столбце. В приведенном выше примере напишите матрицу со значениями {{3 1 0}, {-2 -2 0}}.
Найдите значение x перекрестного произведения двух векторов, заблокировав первый столбец матрицы 2 x 3 и вычислив определитель полученной матрицы 2 x 2. Определитель матрицы 2 x 2 {{a b}, {c d}} равен ad — bc. В приведенном выше примере значение x перекрестного произведения является определителем матрицы {{1 0}, {-2 0}}, которая равна 0.
Найдите значение y и значение z перекрестное произведение, блокируя второй и третий столбцы матрицы, соответственно, и вычисляя определитель результирующих матриц 2 x 2. Значение y перекрестного произведения равно определителю матрицы {{3 0}, {-2 0}}, который равен нулю. Z-значение векторного произведения равно определителю матрицы {{3 1}, {-2 -2}}, который равен -4. 92), что равно 4.
Нахождение площади параллелограмма может быть полезно во многих областях науки, включая математику, физику и биологию.
Математика
Математические исследования, пожалуй, наиболее очевидный способ нахождения площади параллелограмма. Знание того, как найти площадь параллелограмма в координатной геометрии, часто является одной из первых вещей, которые вы должны сделать, прежде чем переходить к более сложным формам. Это также может познакомить вас с более сложной графикой и математикой на основе векторов/вершин, которую вы увидите на уроках математики старшего уровня, геометрии, координатной геометрии, исчисления и многого другого.
Физика
Физика и математика идут рука об руку, и это, безусловно, верно для вершин. Знание того, как найти площадь параллелограмма таким образом, может распространяться на поиск других площадей, а также на задачу, которая требует от вас найти площадь треугольника с вершинами в физической задаче о скорости или электромагнитной силе, например. Та же концепция координатной геометрии и вычисления площади может применяться к ряду физических задач.
Связанные статьи
Ссылки
- Математический факультет Калифорнийского университета в Лос-Анджелесе: Найдите площадь параллелограмма с вершинами
- Математические полезные вещи: Площадь параллелограмма
- Штат Бойсе: Координатная геометрия
Об авторе
5 9004 Он написал для веб-сайта «Путеводитель по онлайн-школам», освещая академические и профессиональные темы для молодых людей, ищущих возможности получения высшего образования. Валлулис имеет степень бакалавра психологии колледжа Уитмена.

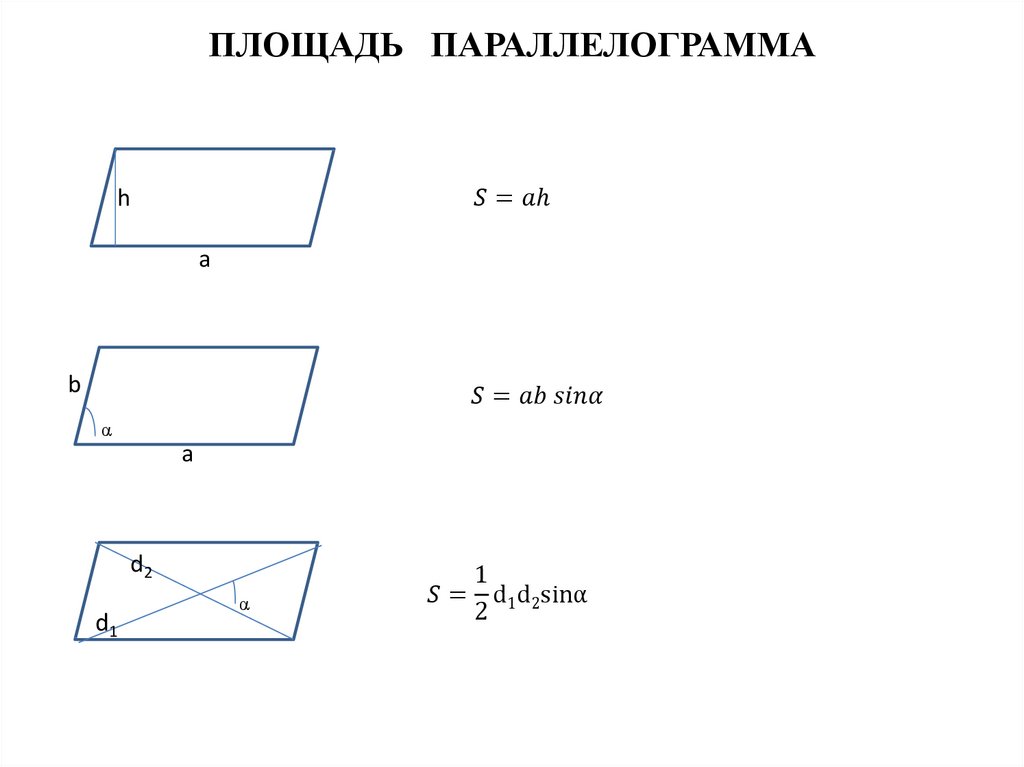 — вопрос №2179254 — Учеба и наука
— вопрос №2179254 — Учеба и наука 10.16
10.16