§ Площадь сферы. Объем шара
Длина окружности. Число Пи Площадь круга Площадь сферы. Объём шара
Многие из нас любят играть в футбол или, по крайней мере, почти каждый из нас слышал про эту знаменитую спортивную игру. Всем известно, что в футбол играют мячом.
Если спросить прохожего, форму какой геометрической фигуры имеет мяч, то часть людей скажут, что форму шара, а часть, что формы сферы. Так кто же из них прав? И в чем разница между сферой и шаром?
Важно!
Шар — это пространственное тело. Внутри шар чем-либо заполнен. Поэтому у шара можно найти объем.
Примеры шара в жизни: арбуз и стальной шарик.
Шар и сфера, подобно кругу и окружности, имеют центр, радиус и диаметр.
Важно!
Сфера — поверхность шара. У сферы можно найти площадь поверхности.
Примеры сферы в жизни: волейбольный мяч и шарик для игры в настольный
теннис.
Как найти площадь сферы
Запомните!
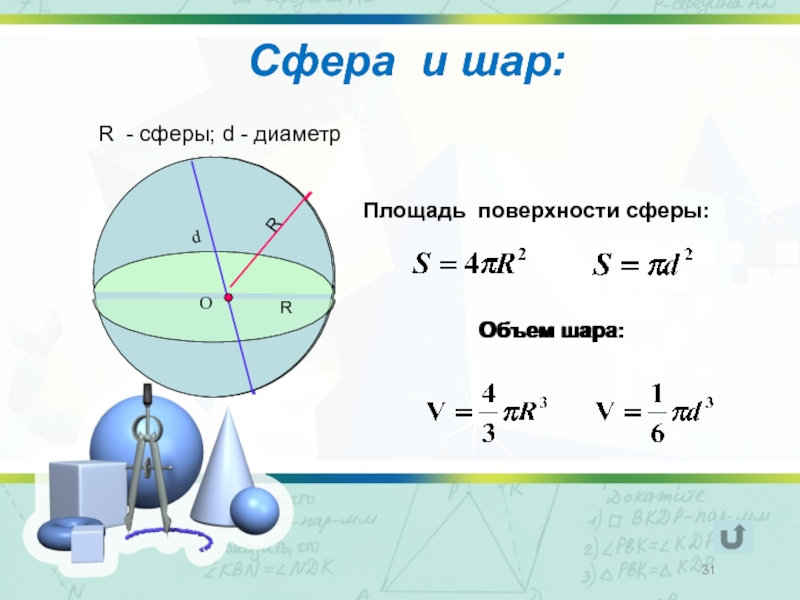
Формула площади сферы: S = 4πR2
Для того, чтобы найти площадь сферы, необходимо вспомнить,
что такое степень числа.
Зная определение степени,
можно записать формулу площади сферы следующим образом.
S = 4π R2 =
4πR · R;
Закрепим полученные знания и решим задачу на площадь сферы.
Зубарева 6 класс. Номер 692(а)
Условие задачи:
- Вычислите площадь сферы, если её радиус равен 1 м. (возьмите π как 3)
Вспомнив, как выделить целую часть и перемножить дроби, воспользуемся формулой площади сферы:
S = 4 · πR2 = 4 · 3
· (1
) 2 = 4 ·
· (
) 2 = 4 ·
·
| 441 |
| 121 |
=
| 4 · 22 · 441 |
| 7 · 121 |
=
=
| 4 · 22 · 63 |
| 121 |
=
| 4 · 2 · 63 |
| 11 |
=
| 504 |
| 11 |
= 45
м2
Как найти объем шара
Запомните!
- Формула объема шара: V = πR3
Зная определение степени,
можно записать формулу объема шара следующим образом.
- V = π R3 = π R · R · R;
Для отработки полученных знаний решим задачу на объем шара.
Зубарева 6 класс. Номер 691(а)
Условие задачи:
- Вычислите радиус шара, если его объем равен 4 м3 (возьмите π как 3)
Выразим из формулы объема шара радиус.
- V = π R3
- π R3 = V
- π R3 =
- R3 =
3V 4 π
Подставим в формулу известные нам значения. Число π возьмем как задано в задании «3
».
R3 = (3 ·
4
) / (4 · 3
)
Чтобы не запутаться, отдельно рассчитаем
числитель дроби.
3 · 4
= 3 ·
| 21 · 4 + 4 |
| 21 |
=
| 3 · 88 |
| 21 |
=
Теперь снова подставим полученное значение в нашу формулу:
- R3 =
/ (4 · 3)
=
/ (4 · )
=
/ (
) = = · (4 · 22 7
) =7 4 · 22
=
=88 · 7 7 · 4 · 22
= = 188 4 · 22 - R3 = 1
- R = 1 м
Важно!
Уважаемые родители!
При окончательном расчете радиуса
не надо заставлять ребенка считать кубический корень.
Учащиеся
6-го класса еще не проходили и не знают определение корней в математике.
В 6 классе при решении такой задачи используйте метод перебора.
Спросите ученика, какое число, если его умножить 3 раза на самого себя даст единицу.
Длина окружности. Число Пи Площадь круга Площадь сферы. Объём шара
Ваши комментарии
Важно!Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи «ВКонтакте».
Оставить комментарий:
| Отправить |
Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия
| Справочник по математике | Геометрия (Стереометрия) | Сферы и шары |
| Шар, сфера и их части |
Площади сферы и ее частей. Объемы шара и его частей |
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
Рис.1
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы (радиусом шара) называют отрезок, соединяющий любую точку сферы с центром сферы.
Длину этого отрезка также часто называют радиусом сферы (радиусом шара).
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Рис.2
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
Высотой шарового слоя называют расстояние между плоскостями расстояние между плоскостями оснований шарового слоя.
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
Рис.3
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.
Соответственно, шаровой сегмент – это шаровой слой, у которого одна из плоскостей оснований касается шара (рис. 4). Высоту такого шарового слоя называют высотой шарового сегмента.
Рис.4
По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис.
5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).
Рис.5
Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
Рис.6
Высотой шарового сектора называют высоту его сферического сегмента.
Замечание. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием. Вершиной конуса является центр сферы.
Площади сферы и ее частей. Объемы шара и его частей
В следующей таблице приведены формулы, позволяющие вычислить объем шара и объемы его частей, а также площадь сферы и площади ее частей.
| Фигура | Рисунок | Формула | Описание |
| Сфера | S = 4πr2, где | Площадь сферы | |
| Шар | где | Объем шара | |
| Сферический пояс | S = 2πrh, где Площадь сферического пояса не зависит от радиусов r1 и r2 ! | Площадь сферического пояса | |
| Шаровой слой | где | Объем шарового слоя | |
| Сферический сегмент | S = 2πrh, где | Площадь сферического сегмента | |
| Шаровой сегмент | где | Объем шарового сегмента | |
| Шаровой сектор | где | Объем шарового сектора |
| Сфера |
Площадь сферы: S = 4πr2, где |
| Шар |
Объем шара: где |
| Сферический пояс |
Площадь сферического пояса: S = 2πrh, где Площадь сферического пояса не зависит от радиусов r1 и r2 ! |
| Шаровой слой |
Объем шарового слоя: где |
| Сферический сегмент |
Площадь сферического сегмента: S = 2πrh, где |
| Шаровой сегмент |
Объем шарового сегмента: где |
| Шаровой сектор |
Объем шарового сектора: где |
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Как найти объем сферы
Все материалы по математике для старших классов
8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
Справка по математике для средней школы » Геометрия » Твердая геометрия » Сферы » Как найти объем сферы
Каков объем сферы с радиусом ?
Возможные ответы:
Правильный ответ:
Чтобы найти объем сферы, вы должны сначала узнать уравнение объема сферы.
В этом уравнении равно радиусу. Мы можем подставить заданный радиус из вопроса в уравнение для .
Теперь мы просто находим .
Объем сферы .
Сообщить об ошибке
Каков объем сферы с радиусом 4? (Округлите до десятых)
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти объем сферы, вы должны сначала узнать уравнение объема сферы.
Уравнение:
Затем подставьте радиус в уравнение, чтобы получить
Затем кубируйте радиус, чтобы получить
Умножьте ответ на и , чтобы получить .
Ответ .
Сообщить об ошибке
Объем сферы определяется как В = (4/3) πr 3 , а площадь поверхности определяется как A = 4 πr 900 08 2 .
Если сфера имеет площадь поверхности 256 π , каков объем?
Возможные ответы:
750 π
683 π
300 π
615 π
Правильный ответ:
683 №
Объяснение:
Зная площадь поверхности, мы можем найти радиус, а затем найти объем.
4 πr 2 = 256 π
4 r 2 = 256
r 2 = 64
r = 8
Теперь решим уравнение объема, заменив r :
V = (4/3) π (8) 3
V 900 08 = (4/3) π * 512
В = (2048/3) π
В = 683 π
Сообщить об ошибке
9 0005
Типичный бейсбольный мяч имеет диаметр .
Найдите объем бейсбольного мяча в кубических сантиметрах.
Возможные ответы:
Недостаточно информации для решения
Правильный ответ:
Объяснение:Чтобы найти объем сферы, используйте формулу
Нам дан диаметр бейсбольного мяча, который необходимо преобразовать в его радиус.
Теперь мы можем найти объем.
Преобразование в сантиметры.
Если вы пришли к , значит, вы не преобразовали диаметр в радиус.
Сообщить об ошибке
Каков объем сферы, радиус которой .
Возможные ответы:
Недостаточно информации для решения
Правильный ответ: 9 0005
Расшифровка:
Чтобы найти объем сферы, используйте формулу
Нам дан радиус сферы, .
Если вы подсчитали, что объем будет тогда вы умножили на , а не на .
Сообщить об ошибке
Определить с точностью до десятой доли кубического сантиметра объем сферы с площадью поверхности 1000 квадратных сантиметров.
Возможные ответы:
Правильный ответ:
Объяснение:
Площадь поверхности сферы по ее радиусу равна
Подставьте и решите:
90 004 Замените в формуле объема сферы:Сообщить об ошибке
Найдите объем следующей сферы.
Возможные ответы:
Правильный ответ:
Объяснение:
Формула объема сферы:
где это радиус сферы.
Подставив наши значения, мы получим:
Сообщить об ошибке
Найдите объем следующей сферы.
Возможные ответы:
Правильный ответ:
Объяснение:
Формула объема сферы:
Где радиус сферы
Подставляя наши значения, получаем:
Сообщить об ошибке
Характеристики официальный баскетбольный мяч НБА заключается в том, что его окружность должна быть 29,5 дюймов. и весить 22 унции. Каков примерный объем баскетбольного мяча? Помните, что объем сферы рассчитывается как V=(4πr 3 )/3
Возможные ответы:
8557,46 куб. дюймов
92,48 куб.дюйма
138,43 куб.дюйма
434,19 куб.дюйма
3468,05 куб.
дюймов
Правильный ответ:
434,19 куб.дюйма
Пояснение:
Чтобы найти ответ, воспользуемся формулой: C=2πr. Нам дано, что C = 29,5. Таким образом, мы можем подключиться, чтобы получить [29,5] = 2πr, а затем умножить 2π, чтобы получить 29,5 = (6,28)r. Наконец, мы делим обе части на 6,28, чтобы получить 4,70 = r. Затем мы подставим в формулу объема V=(4π〖(4.7)〗 3 ) / 3 (Информация о 22 унциях бесполезна)
Сообщить об ошибке
Каков объем сферы диаметром ?
Возможные ответы:
Правильный ответ:
Объяснение:
Формула объема сферы: .
Задача дает нам диаметр, а не радиус. Поскольку диаметр в два раза больше радиуса или , мы можем найти радиус.
.
Теперь подставьте это в наше исходное уравнение.
Сообщить об ошибке
← Назад 1 2 Далее →
Уведомление об авторских правах
Все ресурсы по математике для старших классов
8 диагностических тестов 613 практических тестов Вопрос дня Карточки Learn by Concept
Видео с вопросами: Определение площади поверхности сферы по ее объему
Стенограмма видео
Учитывая, что объем сферы равен 562,5 𝜋 кубических сантиметров, найдите площадь ее поверхности через 𝜋.
Итак, в этом вопросе нам говорят объем сферы. Объем — это количество места, которое занимает объект. Нас просят найти площадь поверхности. Это площадь плоской поверхности вокруг внешней стороны сферы. Чтобы ответить на этот вопрос, мы будем использовать две формулы: объем и площадь поверхности.
Объем сферы равен четырем третям, умноженным на 𝜋, умноженному на 𝑟 в третьей степени.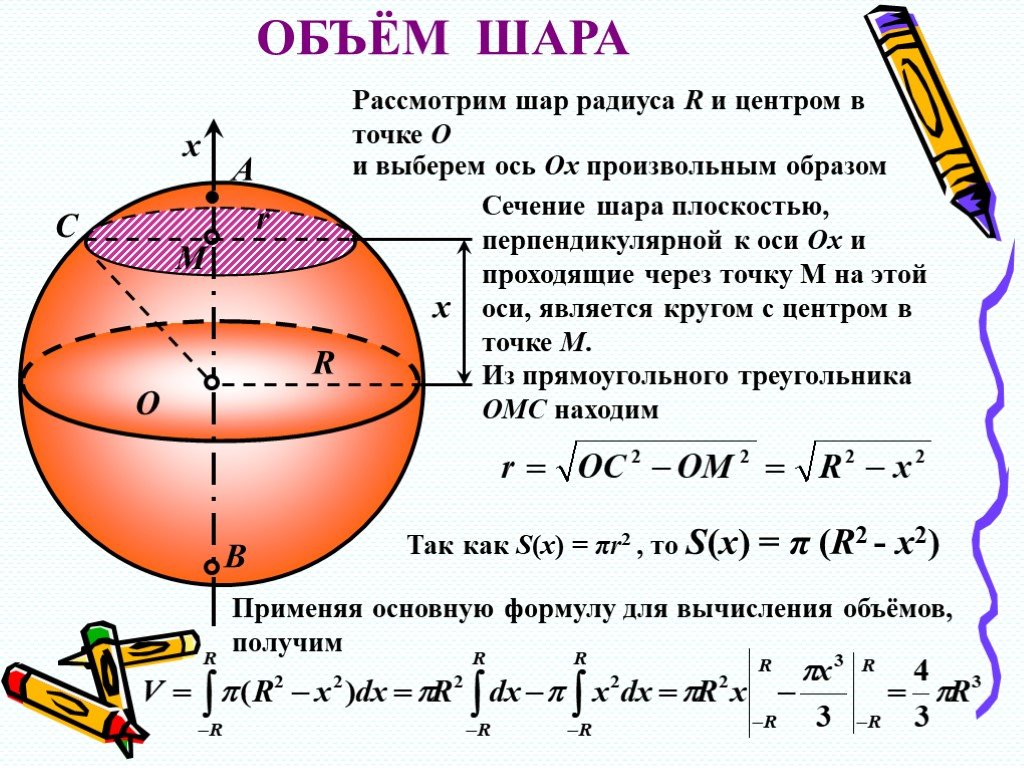
Площадь поверхности сферы равна четырем 𝜋 умноженным на 𝑟 в квадрате. В обоих случаях 𝑟 относится к радиусу сферы. Нарисуем радиус нашей сферы на диаграмме. Нам неизвестно числовое значение радиуса, но мы можем назвать его буквой 𝑟, чтобы обозначить его.
Теперь найдем радиус 𝑟, используя вычисление объема. Мы можем начать с написания формулы объема сферы, которая равна четырем третям, умноженным на 𝜋, умноженному на 𝑟 в третьей степени. И мы можем подставить значение объема 562,5𝜋 в эту формулу, что дает нам 562,5𝜋 равно четырем третям 𝜋𝑟 в третьей степени. Поскольку у нас есть 𝜋 в обеих частях нашего уравнения, мы можем разделить на 𝜋. Что составляет 562,5, равно четырем третям 𝑟 в третьей степени.
Чтобы работать над получением 𝑟 само по себе, мы могли видеть, что в правой части у нас есть четыре трети умноженных на 𝑟 в третьей степени. Чтобы применить обратную операцию, мы должны разделить на четыре трети. А когда мы делим на дробь, мы меняем деление на умножение и меняем местами числитель и знаменатель.
Итак, деление на четыре на три равносильно умножению на три четверти. Итак, три четверти умножить на 562,5 равно 𝑟 в третьей степени. Оценив это с помощью калькулятора, мы получим 421,875, что равно 𝑟 в третьей степени.
Далее, чтобы найти 𝑟 саму по себе, проделываем операцию, обратную нахождению третьей степени. И это для того, чтобы извлечь кубический корень из обеих сторон. Итак, 𝑟 равно кубическому корню из 421,875, что мы можем оценить как 7,5. Это означает, что радиус нашей сферы 𝑟 равен 7,5 сантиметрам. И теперь мы можем использовать значение радиуса, чтобы найти площадь поверхности сферы. И начнем с написания формулы, площадь поверхности сферы равна четырем 𝜋 умножить на 𝑟 в квадрате. Подставив наше значение 7,5 вместо 𝑟, мы получим четыре умножения 𝜋 на 7,5 в квадрате.
Когда мы делаем это вычисление, важно помнить, что возводится в квадрат только 7,5, а не все остальные значения. Таким образом, оценивая 7,5 в квадрате, мы получаем правую часть четырежды 𝜋 умножить на 56,25.