Найти площадь поверхности параллелепипеда онлайн
Пример решили: 27451 раз Сегодня решили: 0 раз
Введите длины сторон параллелепипеда
Сторона a Сторона b Сторона c
Вычисление площади поверхности параллелепипеда
Скачать решение в PDF
Порекомендуйте наш сервис друзьям
Вконтакте
Одноклассники
Google+
Параллелепипед – это призма, основанием которой служит параллелограмм. В параллелепипеде противоположные грани равны и параллельны. Диагонали его пересекаются в одной точке, которая лежит на оси симметрий, и делятся ею пополам.
Виды параллелепипедов:
- Прямой параллелепипед – параллелепипед, боковые рёбра которого перпендикулярны к основаниям.
- Наклонный параллелепипед – параллелепипед, боковые рёбра которого не перпендикулярны к основаниям.

Найти площадь треугольника
Найти площадь поверхности куба
Найти площадь ромба
Найти площадь кругового сектора
Найти площадь поверхности сферы
Попробуйте другие сервисы
Объемы простых тел. Объемы и площади поверхностей правильных тел. Общая информация об объемах и площадях поверхностей правильных тел приведена в таблице.
Пример 1. Бак для воды имеет форму прямоугольного параллелепипеда длиной 1 м, шириной 65 см и высотой 30 см. Определить объем бака в м3, см3, литрах Решение: Объем прямоугольного параллелепипеда равен l*b*h а)Vбака=1*0.65*03=0.195 м3 б) 1 м 315000 мм2=315000/100=3150 см2 1 м3=106 см3, значит, 0.195 м3=0.195*106=195000 см3 в) 1 литр=1000 см3, значит 195000 см3=195 л
Тело, показанное на рис. — это трапецеидальная призма. Так как объем = площадь поперечного сечения * высота, то V=1/2*(10+5)*4*20=30*20=600 cм3 Так как площадь поверхности вычисляется сложением суммы площадей двух трапеций и суммы площадей четырех прямоугольников, то S=(2*30)+3(5*20)+(10*20)=560 см2 Пример 3. Определить объем и общую площадь поверхности правильной пирамиды с квадратным основанием, показанной на рис., если ее высота равна 15 см. Решение: Так как объем пирамиды =1/3(площадь основания)*высота, то V=1/3*(5*5)*15=125 см3 Общая площадь поверхности включает площадь квадратного основания и площади четырех равных треугольников. Площадь треугольника ADE=1/2*основание*(высота грани). Высоту грани АС можно найти по теореме Пифагора из треугольника АВС, где АВ=15 см, ВС=1/2*3=1.5 см, и АС2=AB2+BC2=225+2.25=227.25 AC=15.07 cм Следовательно, площадь треугольника ADE SADE=1/2*3*15.07=22.605 см2 Общая площадь пирамиды S=(3*3)+4*22.605=99.42 cм2. Пример 4. Расчет объема и общей площади поверхности конуса. Определить объем и общую площадь поверхности конуса радиусом 4 см и высотой 10 см. Объем конуса V=1/3πr2h =1/3*π42*10=167.5см3 Общая площадь поверхности равна сумме площади конической поверхности и площади основания, т.е. S=πrl+πr2 Из рисунка видно, что длину образующей l можно найти по теореме Пифагора.l2=102+42=116 см l=10,8 cм Следовательно, общая площадь поверхности равна S=π*4*10.8)+(π*42=185.89 cм2 Пример 5. Расчет объема и общей площади поверхности призмы. На рис. показан деревянный профиль. Найдем: а) его объем в м3 б) общую площадь его поверхности Профиль представляет собой призму, поперечное сечение которой состоит из прямоугольника и полукруга. Поскольку радиус полукруга равен 6 см, диаметр равен 12 см. Тогда размеры прямоугольника 12*11 см Площадь поперечного сечения S.=(11*12)+1/2* π 62=188,52 см2 Поскольку объем деревянной детали равен произведению площади поперечного сечения на длину, то a) V=188,52*200=37704 см3=37704 см3/106= 0,037704 м3 б) Общая площадь включает два торца (площадь каждого 188,52 см S=(2*188,52)+2*(11*200)+(12*200)+1/2*(2π*6*200)=377,04+4400+2400+3768=10945,04 см2=1,094504 м2.
Пример 6. Расчет объема и общей площади поверхности сложного бойлера. Бойлер состоит из цилиндрической секции длиной 9 м и диаметром 5 м, к одному концу которой присоединена полусферическая секция диаметром 5 м, а к другому концу — коническая секция высотой 3 м и диаметром основания 5 м. Вычислить объем бойлера и общую площадь его поверхности.
Vполусферы P =2/3*πr3 =2/3*π*2,53 =10,42 π м3 V цилиндра Q = π r2h=π*2,52*9=56,25 π м3 V конуса R =1/3 π r2=1/3*π*2,52*3=6,25π м 3 Общий объем бойлера V= 10,42 π м3+56,25 π м3+6,25π м 3=72,92π=228,97 м 3 S полусферы P. =2*(πr2)=2*π*2,52=12,5π м2 S бок. Длина образующей конуса l рассчитывается по теореме Пифагора из треугольника ABC; значит l=(32+2,52)1/2=3,9 м. S конуса R. =πrl=π*2,5*3,9=9,75 π м 2 Общая площадь поверхности бойлера S= 12,5π+45π+9,75 π=67,25π=211,2 м 2 | ||||||||||||||||
Дополнительная информация от TehTab.ru: | ||||||||||||||||
Площадь поверхности прямоугольного параллелепипеда
Полная площадь поверхности (TSA) прямоугольного параллелепипеда представляет собой сумму площадей его 6 граней, которая определяется как:
TSA = 2 (lw + wh + hl)
Помните, что площадь поверхности — это общая площадь всех граней трехмерной фигуры.
Площадь боковой поверхности параллелепипеда определяется по формуле:
LSA = 2 (lh + wh) = 2 h (l + w)
Пример 1: Найдите общую площадь параллелепипеда с размерами 8 см по формуле 6 см на 5 см.
TSA = 2 (lw + wh + hl)
TSA = 2 (8*6 + 6*5 + 5*8)
TSA = 2 (48 + 30 + 40)
TSA = 236
Итак, общая площадь поверхности этого прямоугольного параллелепипеда равна 236 см 2 .
Пример 2: Найдите площадь поверхности прямоугольного параллелепипеда с размерами 4,8 см, 3,4 см и 7,2 см.
Площадь лица 1: 4,8 × 7,2 = 34,56 см²
Площадь лица 2: 3,4 × 7,2 = 24,48 см²
Площадь грани 3: 4,8 × 3,4 = 16,32 см²
Сложение площадей этих трех граней дает 75,36 см², поскольку каждая грань дублируется на противоположной стороне, общая площадь поверхности прямоугольного параллелепипеда будет:
TSA = 2 (75,36) = 150,72 см²
Пример 3: Длина, ширина и высота прямоугольного параллелепипеда равны 10 см, 8 см и 7 см соответственно. Найдите площадь боковой поверхности прямоугольного параллелепипеда.
Решение:
Площадь боковой поверхности прямоугольного параллелепипеда определяется как:
LSA = 2h(l+w)
где,
l = длина = 10 см
w = ширина = 8 см
h = высота = 7 см
Подставляем эти значения в формулу получаем:
LSA = 2 ×7(10 + 8)
LSA = 14 × 18
LSA = 252 см 2
Найдите полную площадь поверхности прямоугольного параллелепипеда.
Решение:
Общая площадь поверхности прямоугольного параллелепипеда определяется как:
TSA = 2 (l*b + b*h + h*l)
Учитывая, что:
l = 16 см
b = 14 см
h = 10см
Подставив значения в уравнение получим
ВПС = 2 (16*4 + 14*10 + 10*16)
ВПС = 2(224 + 140 + 160)
ВПС = 2(224 + 140 + 160)
ВПС 2 * 524
TSA = 1048 см 2
Пример 5: Дана коробка с хлопьями, длина которой 20 см, высота 30 см, ширина 8 см. Найдите площадь поверхности коробки.
Решение:
Чтобы найти поверхности коробки, нам нужно найти площадь каждой прямоугольной грани и сложить их все.
Площадь лицевой стороны: 20 х 30 = 600 см2.
Площадь верхней грани: 20 х 8 = 160 см2.
Площадь боковой грани равна: 8 х 30 = 240 см2.
Теперь сложите эти значения вместе, мы получим: 600 + 160 + 240 = 1000 см2.
Таким образом, общая площадь поверхности равна 1000 х 2 = 2000 см2.
Пример 6: Найдите площадь поверхности прямоугольного параллелепипеда, стороны которого равны 3 см х 6 см х 10 см.
Решение:
Площадь поверхности прямоугольного параллелепипеда определяется как:
TSA = 2 (16*4 + 14*10 + 10*16)
TSA = 2(3 x 6 + 6 x 10 + 3 x 10)
TSA = 2(18 + 60 + 30)
TSA = 216 см 2
Калькулятор площади поверхности онлайн
Расчет 1 Справка
Студенты, нуждающиеся в помощи по исчислению 1, получат большую пользу от нашей интерактивной программы.
Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по исчислению 1.
Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы получите много помощи по исчислению 1 в кратчайшие сроки.
Получите помощь сегодня с нашей обширной коллекцией необходимой информации по исчислению 1.
Исчисление — это область математики, которая занимается изучением изменений. Его можно разделить на две категории: дифференциальное исчисление (скорость изменения) и интегральное исчисление (накопление). Вы познакомитесь с обеими категориями в исчислении I, которое основано на понятиях из алгебры и геометрии, охватывая пределы, производные и теоремы выбора. Большинство курсов Calculus 1 также дают базовое введение в дифференциальные уравнения. В то время как некоторые учащиеся изучают исчисление 1 в старшем классе средней школы — обычно в качестве курса повышения квалификации — большинство студентов проходят этот курс на первом курсе колледжа. Почти все колледжи требуют, чтобы студенты завершили исчисление 1, а представленные концепции необходимы для любого студента, желающего продолжить математическую или естественную специальность и карьеру в колледже. Нужен ли вам репетитор по математическому анализу в Атланте, репетитор по математическому анализу в Хьюстоне или в Сан-Франциско, работа один на один с экспертом может быть именно тем, что вам нужно для учебы.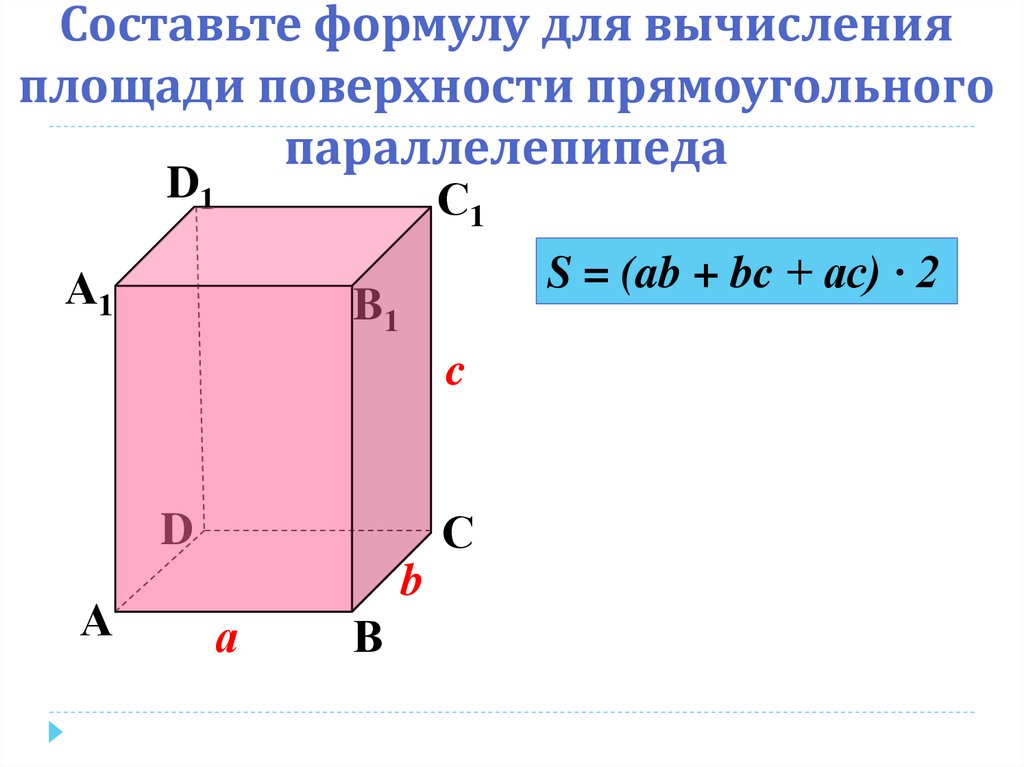
Если вы новичок в исчислении 1 или испытываете трудности с изучением предмета, вы можете найти помощь в обучении с помощью бесплатного учебного пособия Varsity Tutors Learn by Concept Learning Tool. Интерактивная программа Calculus 1 Help на веб-сайте средств обучения состоит из двух основных разделов с многочисленными темами и подтемами. В каждой подтеме есть ряд примеров вопросов, и каждый вопрос содержит проблему и несколько возможных ответов. Вы можете решить каждую задачу и выбрать ответ, который, по вашему мнению, является правильным, прежде чем проверять, правы ли вы. Varsity Tutors также предлагает такие ресурсы, как бесплатные практические тесты по исчислению 1, которые помогут вам в самостоятельном обучении.
Инструмент Learn by Concept делает больше, чем просто говорит вам, правы вы или нет. Каждый образец вопроса содержит подробное объяснение концепций и процесса, используемого для поиска правильного ответа, включая каждый шаг. Например, объяснение не просто скажет вам использовать цепное правило для поиска дифференциальной функции, оно проведет вас через каждый шаг цепного правила, применимого к рассматриваемой проблеме. Учащиеся, давшие правильный ответ, могут перепроверить свою работу, используя эти пояснения. Студенты, давшие неправильный ответ, могут найти, где они сбились с пути и как это исправить. С подтемами, содержащими тысячи примеров вопросов, вы можете получить столько практики исчисления I, сколько вам нужно. В дополнение к справочному разделу по исчислению 1 и обучению по исчислению 1 вы также можете рассмотреть возможность прохождения некоторых наших бесплатных диагностических тестов по исчислению 1.
Учащиеся, давшие правильный ответ, могут перепроверить свою работу, используя эти пояснения. Студенты, давшие неправильный ответ, могут найти, где они сбились с пути и как это исправить. С подтемами, содержащими тысячи примеров вопросов, вы можете получить столько практики исчисления I, сколько вам нужно. В дополнение к справочному разделу по исчислению 1 и обучению по исчислению 1 вы также можете рассмотреть возможность прохождения некоторых наших бесплатных диагностических тестов по исчислению 1.
Учебный материал в инструменте Learn by Concept полезен для любого изучающего исчисление 1 независимо от его будущих целей. Основными модулями в учебном пособии «Learn by Concept» являются «Функции» и «Пространственное исчисление». В этих единицах есть такие темы, как уравнения, графические функции, ставки и регионы. Каждая подтема структурирована как темы «Как», например, «Как найти скорость изменения».
После прохождения бесплатного учебного плана Learn by Concept вы можете использовать дополнительные бесплатные функции на веб-сайте Varsity Tutors Learning Tools, чтобы еще больше подготовиться к Calculus I.


 Прямоугольный параллелепипед, Цилиндр,Пирамида, Конус, Сфера, Параллелепипед.
Прямоугольный параллелепипед, Цилиндр,Пирамида, Конус, Сфера, Параллелепипед. Расчет объема прямоугольного бака.
Расчет объема прямоугольного бака.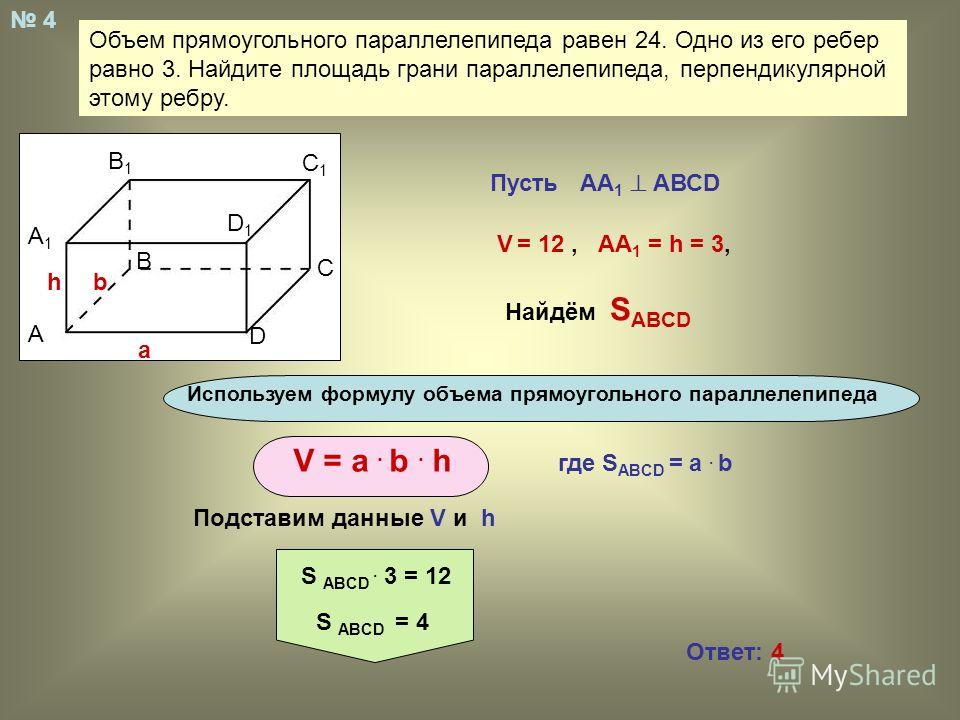 Расчет объема и общей площади поверхности правильной пирамиды.
Расчет объема и общей площади поверхности правильной пирамиды. 
 Следовательно, общая площадь поверхности
Следовательно, общая площадь поверхности поверхности цилиндра Q. =2πrh=2*π*2,5*9=45π м2 (т.к. этот цилиндр представляет собой трубу без оснований)
поверхности цилиндра Q. =2πrh=2*π*2,5*9=45π м2 (т.к. этот цилиндр представляет собой трубу без оснований)