Площадь прямоугольного через высоту треугольника: Как найти площадь треугольника, формула 🔺

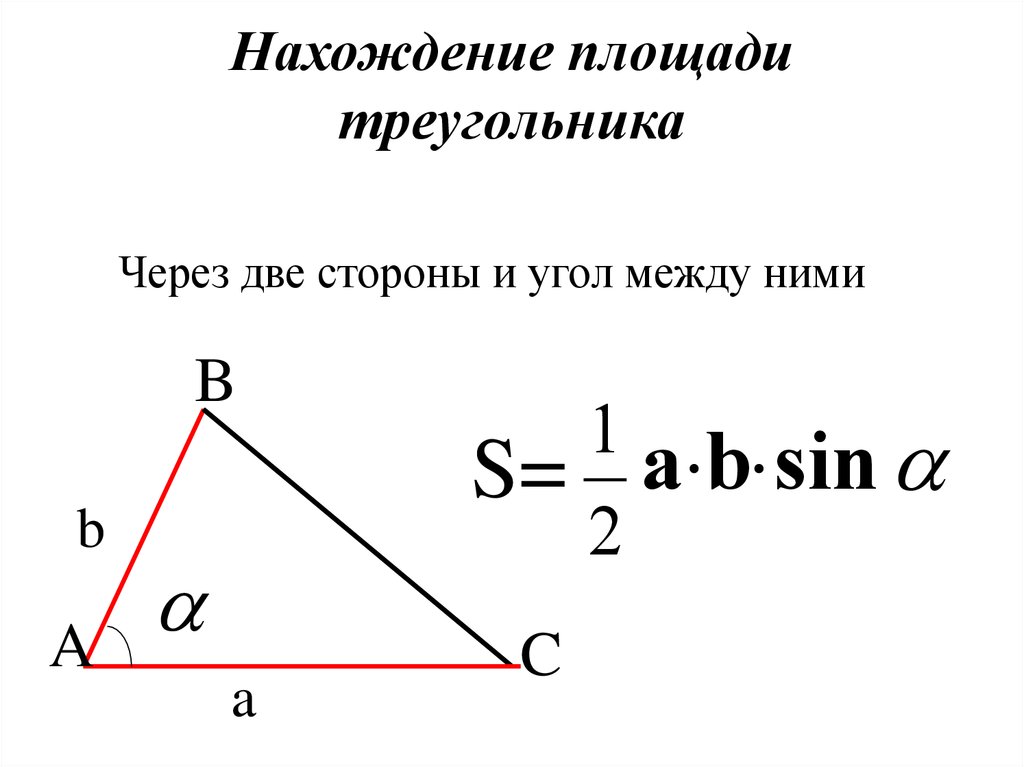
Площадь треугольника равна половине произведения основания на высоту, т.е.     \(S = \frac{1}{2}ah\).

Формула Герона:  \(S = \sqrt {p\,\left( {p — a} \right)\,\left( {p — b} \right)\,\left( {p — c} \right)} \),   где p   —  полупериметр.

Задача 1. Найдите площадь треугольника, если его основание равно 10, а высота, проведенная к основанию, равна 8. Ответ ОТВЕТ: 40.
Задача 2. Найдите высоту треугольника, проведенную к основанию равному 12, если его площадь равна 48. Ответ ОТВЕТ: 8.
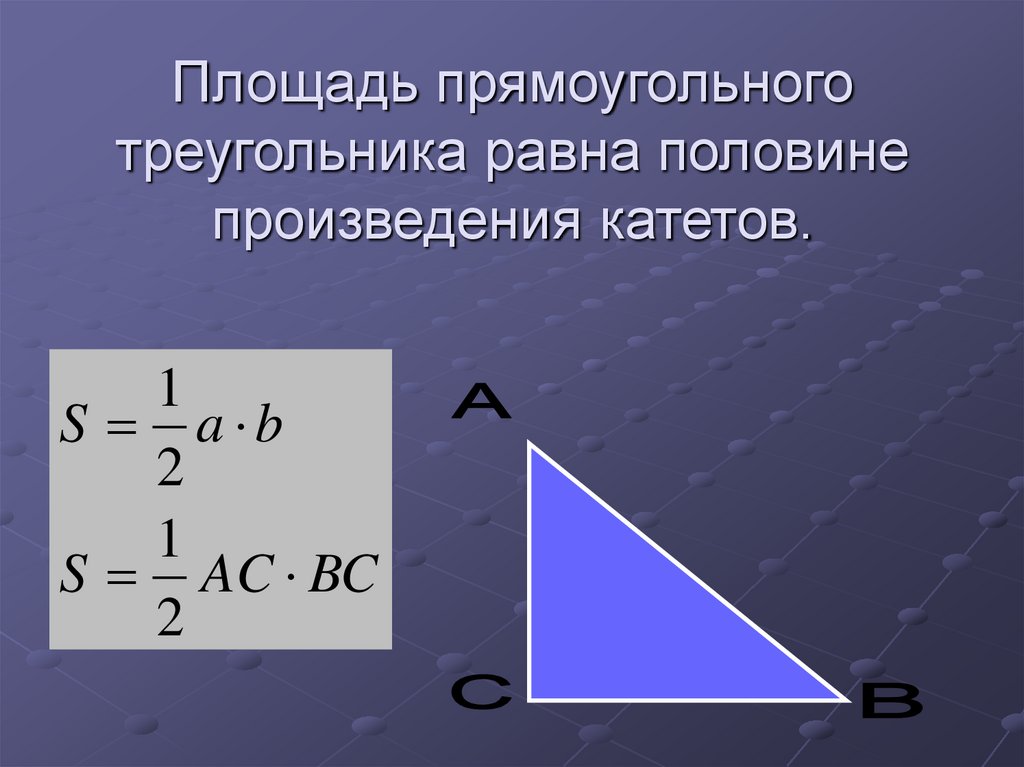
Задача 3. Найдите площадь прямоугольного треугольника, катеты которого равны 7 и 5. Ответ ОТВЕТ: 17,5.
Задача 4. Площадь прямоугольного треугольника равна 28. Один из катетов равен 8. Найдите второй катет. Ответ ОТВЕТ: 7.
Задача 5. По данным на рисунке найдите площадь треугольника ABC. Ответ ОТВЕТ: 80.
Задача 6. По данным на рисунке найдите площадь треугольника ABC. Ответ ОТВЕТ: 168.
Задача 7. По данным на рисунке найдите площадь треугольника ABC. Ответ ОТВЕТ: 196.
Задача 8. По данным на рисунке найдите площадь треугольника ABC. Ответ ОТВЕТ: 64.
Задача 9. По данным на рисунке найдите периметр прямоугольника, если прямоугольник и треугольник равновелики. Ответ ОТВЕТ: 30.
Задача 10. По данным на рисунке найдите высоту x треугольника, если треугольник и прямоугольник равновелики, а стороны прямоугольника 6 и 5. Ответ ОТВЕТ: 7,5.
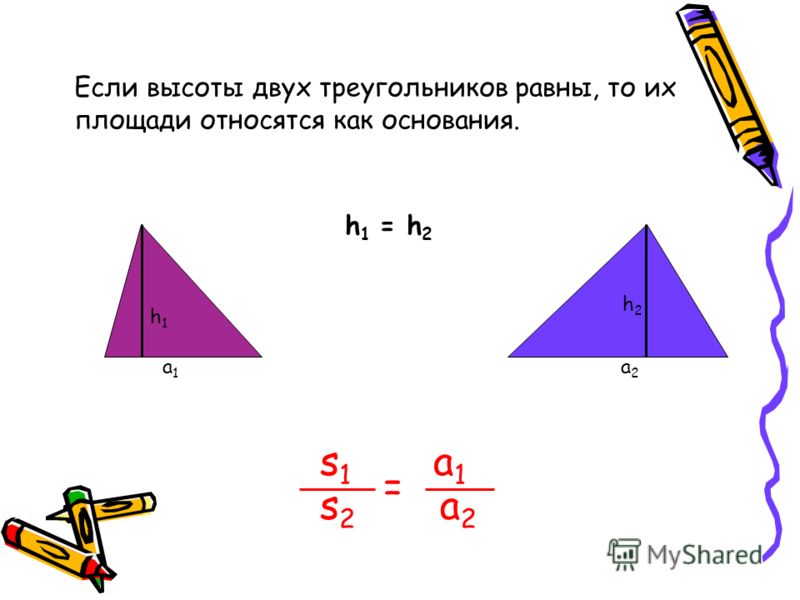
Задача 11. Стороны АВ и ВС треугольника АВС равны соответственно 10 и 15, а высота, проведенная к стороне АВ, равно 6. Найдите высоту, проведенную к стороне ВС. Ответ ОТВЕТ: 4.
Задача 12. Высоты треугольника АВС, проведенные к сторонам АС и ВС равны 8 и 6 соответственно. Сторона АС равна 9. Найдите длину стороны ВС. Ответ ОТВЕТ: 12.
Задача 13.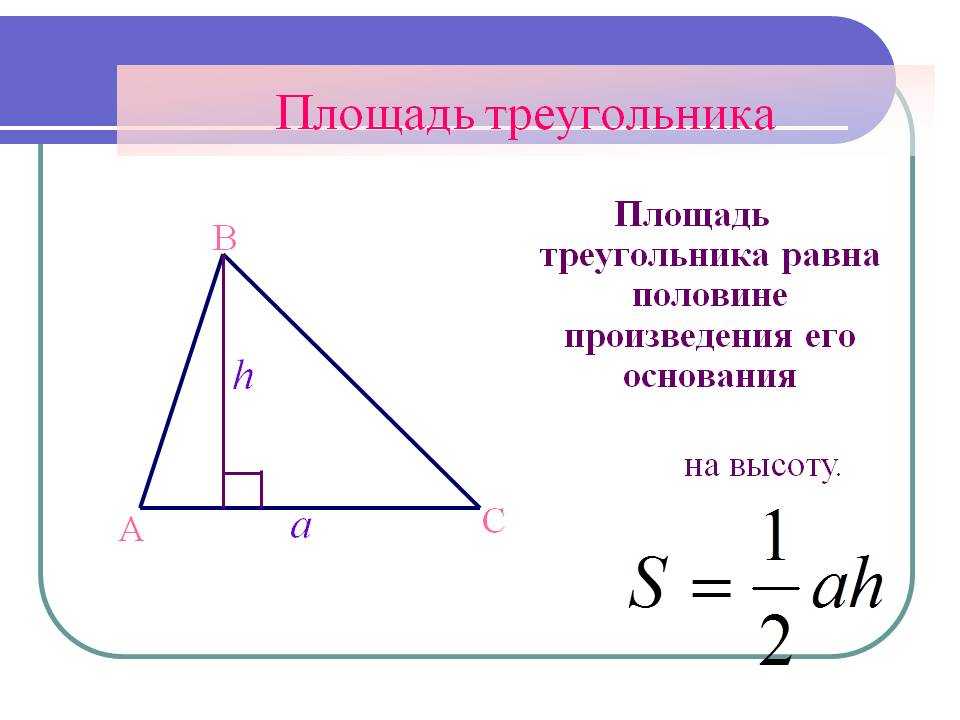 Дан треугольник АВС с медианой ВМ. АК медиана треугольника АВМ. Найдите площадь треугольника АВС, если площадь треугольника АМК равна 8. Ответ ОТВЕТ: 32.
Задача 14. Дан треугольник АВС с медианой ВМ. АК медиана треугольника АВМ. Найдите площадь треугольника АВК, если площадь треугольника АВС равна 40. Ответ ОТВЕТ: 10.
Задача 15. На стороне АС треугольника АВС выбрана точка М так, что АМ : МС = 3 : 1. Найдите площадь треугольника АВС, если площадь треугольника АВМ равна 36. Ответ ОТВЕТ: 48.

Задача 16. На стороне АС треугольника АВС выбрана точка М так, что АМ : МС = 3 : 2. Найдите площадь треугольника МВС, если площадь треугольника АВМ равна 24. Ответ ОТВЕТ: 16.
Задача 17. В треугольнике АВС точки М и К середины сторон АС и ВС соответственно. Найдите площадь треугольника СМК, если площадь треугольника АВС равна 100. Ответ ОТВЕТ: 25.
Задача 18. В треугольнике АВС точки М и К середины сторон АС и ВС соответственно. Найдите площадь треугольника АВС, если известно, что \({S_{\Delta \,ABC}} + {S_{\Delta \,CKM}} = 100.\) Ответ ОТВЕТ: 80.
Задача 19. В треугольнике АВС медианы АК и ВМ пересекаются в точке О. Найдите площадь треугольника АВС, если площадь треугольника АМО равна 4. Ответ ОТВЕТ: 24.
Задача 20. В треугольнике АВС медианы АК и ВМ пересекаются в точке О.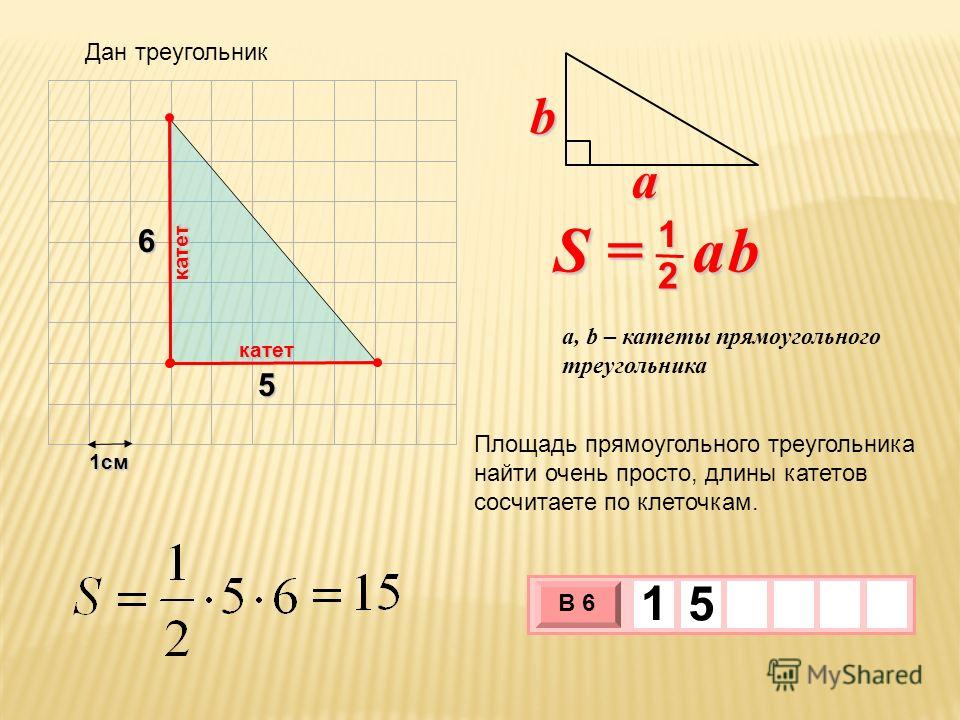 Найдите площадь треугольника АВС, если площадь четырехугольника  СМОК  равна 3. Ответ ОТВЕТ: 9.
Задача 21. По данным на рисунке найдите площадь треугольника АВС, если известно, что CD = 2 BC и площадь треугольника CDE равна 35. Ответ ОТВЕТ: 17,5.
Задача 22. По данным на рисунке найдите площадь треугольника АВС, если известно, что \({S_{\Delta \,DEC}} + {S_{\Delta \,ABC}} = 17.\) Ответ ОТВЕТ: 12.
Задача 23. По данным на рисунке найдите площадь треугольника АВС, если известно, что площадь треугольника AMN равна 6. Ответ ОТВЕТ: 56.
Задача 24. Найдите площадь треугольника со сторонами 13, 14 и 15. Ответ ОТВЕТ: 84.
Задача 25. Найдите площадь треугольника со сторонами 4, 13 и 15. Ответ ОТВЕТ: 24.
Задача 26. Найдите площадь параллелограмма со сторонами 10, 17 и меньшей диагональю 9. Ответ ОТВЕТ: 72.
Задача 27. Найдите площадь параллелограмма со сторонами 13, 15 и меньшей диагональю 4. Ответ ОТВЕТ: 48.
Задача 28. Стороны треугольника 5, 6 и 7. Найдите высоту треугольника, проведенную к большей стороне. Ответ ОТВЕТ: \(\frac{{12\sqrt 6 }}{7}.\)
Задача 29. Стороны треугольника 8, 10 и 12. Найдите высоту треугольника, проведенную к меньшей стороне. Ответ ОТВЕТ: \(\frac{{15\sqrt 7 }}{4}.\)
Задача 30. Внутри параллелограмма ABCD отмечена точка М. Докажите, что сумма площадей треугольников AMD и BMC равна половине площади параллелограмма.
Задача 31. В треугольнике АВС угол С прямой. На сторонах АС, АВ, ВС соответственно отмечены точки М, Р, К так, что четырехугольник СМРК является квадратом, АС = 8, ВС = 12. Найдите длину отрезка МС. Ответ ОТВЕТ: 4,8.
Задача 32. В трапеции ABCD с основаниями AD и ВС диагонали пересекаются в точке О, которая удалена от прямой АВ на 6. Найдите площадь треугольника  DOC, если  АВ = 10. Ответ ОТВЕТ: 30.
Задача 33. Точка Е – середина стороны АВ треугольника АВС, а точки М и H делят сторону ВС на три равные части, ВМ = МН = НС. Найдите площадь треугольника ЕМН, если площадь треугольника АВС равна 15. Ответ ОТВЕТ: 2,5.

Реклама

Поддержать нас

Доказать чему равна площадь треугольника

Площадь треугольника равна половине от произведения его стороны на высоту, проведенную к этой стороне. Сторону, к которой проведена высота, принято в таком случае называть основанием. Таким образом, можно сказать, что площадь треугольника равна половине произведения его основания на высоту.

Если обозначить длину стороны-основания треугольника как a, высоту — как h, то получится формула площади треугольника:

S = ½ ah

Чтобы доказать эту формулу, следует рассмотреть все варианты расположения высоты в треугольнике. Их всего три. Это:

1. Высота совпадает с одной из сторон треугольника. В этом случае мы имеем дело с прямоугольным треугольником, в котором за основание взят один из катетов. Высотой же, проведенной к этому катету, является другой катет.
2. Высота находится внутри треугольника. В этом случае она пересекается с основанием и делит его на два отрезка. При этом данный треугольник делится на два прямоугольных треугольника.
3. Высота проходит за пределами треугольника. В таком случае она пересекается не с самим основанием, а с его продолжением (прямой, на которой лежит основание).

Рассмотрим первый случай. Пусть дан треугольник ABC. В нем к основанию AC длиной a проведена высота h, которая совпала со стороной BC:

Как известно площадь прямоугольника равна произведению его смежных сторон. Если бы у нас был прямоугольник со сторонами, длины которых a и h, то его площадь была бы равна ah. Если в прямоугольнике провести диагональ, то она разбивает его на два равных прямоугольных треугольника (у них соответственно равны все три стороны). Площади этих треугольников также равны между собой и каждая составляет ½ от площади всего прямоугольника. Таким образом доказано, что площадь треугольника в данном случае будет равна ½ah.

Рассмотрим второй случай. Пусть в нем высота BH длиной h пересекает сторону AC длиной a.

В этом случае мы получаем два прямоугольных треугольника: ABH и CBH. Из рассмотренного первого случая мы знаем, что их площади равны соответственно ½ · AH · h и ½ · CH · h.

Площадь же всего треугольника ABC представляет собой сумму этих двух площадей:

S = ½ · AH · h + ½ · CH · h

Вынесем за скобку общие множители:

S = ½ · h · (AH + CH)

Но ведь AH и CH в сумме составляют длину a. Таким образом, приходим к формуле, которую требовалось доказать:

S = ½ · h · a

Теперь рассмотрим третий случай, когда высота находится за пределами треугольника:

Здесь мы тоже можем увидеть два прямоугольных треугольника. Это ∆ABH и ∆CBH. Причем первый включает в себя второй. Искомый же треугольник ABC является дополнением к треугольнику CBH до треугольника ABH. Таким образом мы можем записать, что площадь ∆ABH равна сумме площадей ∆CBH и ∆ABC:

S_∆ABH = S_∆CBH + S_∆ABC

Откуда находим площадь искомого треугольника ABC:

S_∆ABC = S_∆ABH – S_∆CBH

Площадь треугольника ABH равна ½ · AH · h, площадь треугольника CBH равна ½ · CH · h:

S_∆ABC = ½ · AH · h – ½ · CH · h

Выносим общие множители за скобку:

S_∆ABC = ½ · h · (AH – CH)

Но ведь если из отрезка AH вычесть отрезок CH, то получится отрезок AC, длина которого равна a. Следовательно, мы можем записать, что и в этом случае площадь треугольника равна также ½ ah.

Геометрия: Измерения: Площадь четырехугольников

Как мы узнали из SparkNote «Многоугольники», четырехугольники можно разделить на три основные группы:

1. Те, у которых нет пар параллельных сторон.
2. Трапеции — с одной парой параллельных стороны.
3. Параллелограммы — с двумя парами параллельные стороны.

При вычислении площади четырехугольника без параллельных сторон должен разделить четырехугольник на два треугольника и суммировать их площади. Методы вычисления площади треугольника будут обсуждаются на следующем уроке. Когда четырехугольник является параллелограммом или трапецией, однако существуют ярлыки для расчета площади.

Площадь параллелограмма

Чтобы вычислить площадь параллелограмма, мы должны ввести новый термин: площадь высота параллелограмма. Высота параллелограмма равна линия сегмент перпендикулярно одной паре сторон с одной конечная точка на одной из этих сторон параллелограмма, а другая конечная точка на строка, содержащая противоположное стороны параллелограмма. Ниже появляются высоты различных параллелограммов. Рисунок %: Различные параллелограммы и их высоты Как видите, один конец высоты всегда лежит на стороне, а другой конечная точка иногда лежит на противоположной стороне, а иногда нет.

Площадь параллелограмма равна произведению длины его высоты на длина стороны, которая содержит конечную точку высоты. Эта сторона называется основанием параллелограмма. Любая сторона может стать основанием данного параллелограмм: все, что вам нужно сделать, это провести высоту от него до линии, которая содержит противоположную сторону. Распространенный способ описания площади параллелограмм — основание, умноженное на высоту (основание х высота), где высота равна высота.

Формулы площади различных специальных параллелограммов еще проще. Площадь прямоугольника равна произведению длина любых двух смежных сторон. В любом таком В этом случае одна сторона является основанием, а другая — высотой. Площадь квадрат — это длина любой стороны (все четыре равны равные) в квадрате.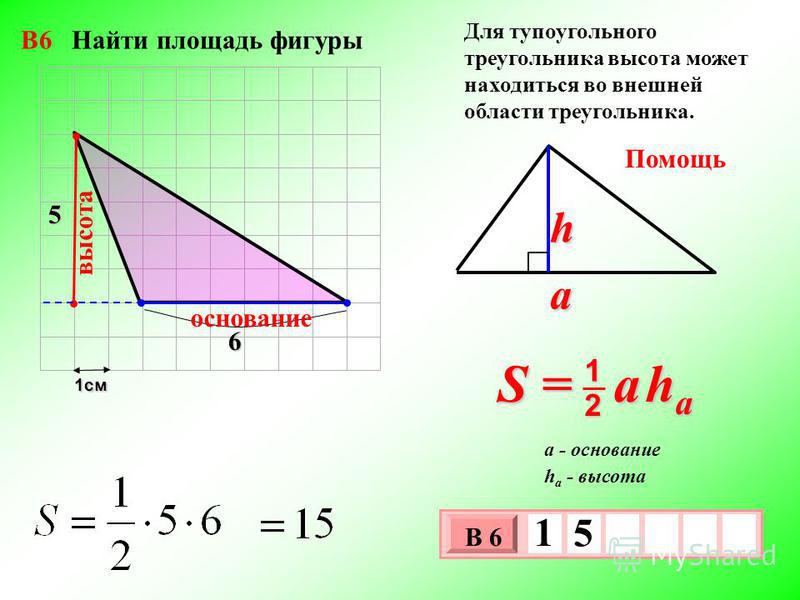 Площадь ромб равен половине произведения его диагонали. Обратите внимание, что эти специальные формулы просто модифицированные версии исходной формулы «база-умножение-высота», данные для площадь параллелограмма.

Площадь трапеции

Формула площади трапеции тоже требует новой лексики. Высота трапеции равна сегмент перпендикулярны основаниям с одним концом на основании трапеции, а другую конечную точку на линии, содержащей другую базу. Здесь различные трапеции изображены с их высотами:

Площадь трапеции равна половине произведения суммы длин ее основания и длину его высоты((1/2(b ₁ + б ₂ )) х А). Половина суммы его оснований есть средняя длина его оснований, равная длина его медианы. Итак, еще один способ найти площадь трапеции — это произведение длин ее высота и медиана.

Геометрия TLP: проблемы-предыстории

Действия и вопросы по области

А.

1. Пример площади прямоугольника (ответьте на эти вопросы, написав или нарисовав на эта страница)

Чему равна площадь каждого прямоугольника? Покажите, как вы вычислили области.

Предложите способ помочь учащемуся понять, как вычислять области. Добавьте что-нибудь к рисунку, чтобы показать эту идею.

Как вы думаете, почему на этом изображении больше одного прямоугольника? страница?

B. Зона параллелограмма

Одним из методов определения площади параллелограмма является рассечение, т. е. разрезание параллелограмм и снова собрать его в виде прямоугольника. Вот картинка того, как это работает.

Обычным способом вычисления площади параллелограмма является формула в терминах ОСНОВАНИЕ и ВЫСОТА . Дайте определение базе и высоту и напишите формулу площади, используя основание и высоту.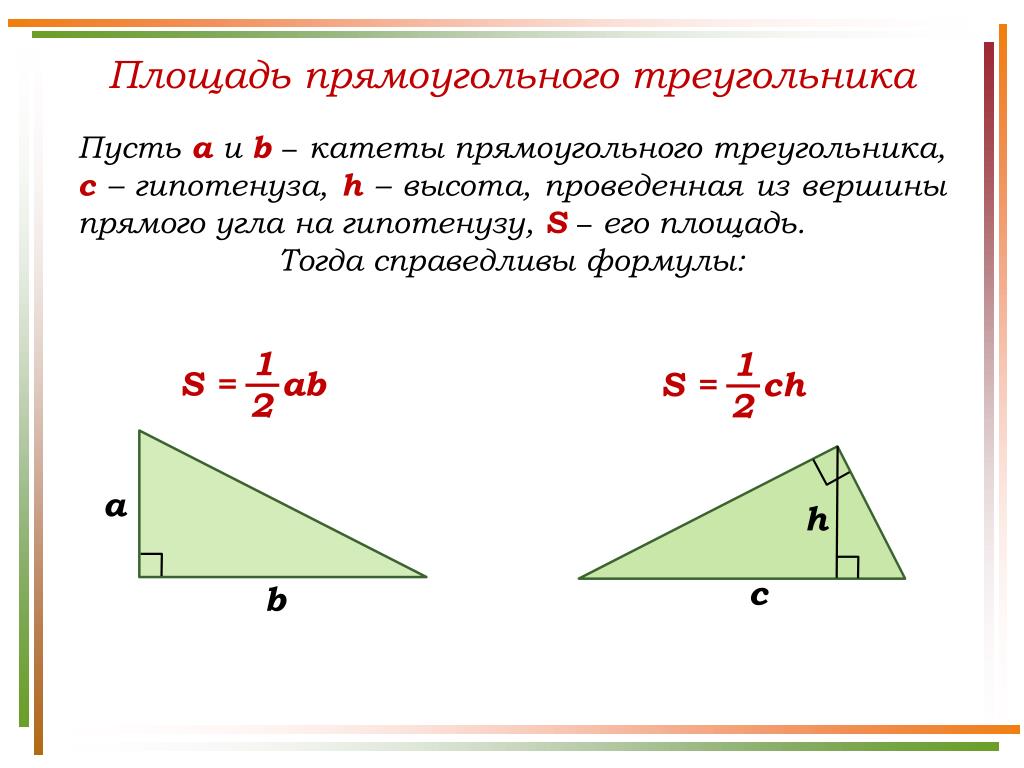

C. Площадь треугольника путем «удвоения треугольника»

Площадь треугольника может быть связана с (известной) площадью параллелограмма следующим битом вырезания и вставки.

Начните с любого треугольника. Сделайте точную вторую копию треугольника.

Переверните один треугольник и соедините с другим, чтобы получился параллелограмм.

Как вы можете убедить дружественного скептика, что это действительно параллелограмм?

Следовательно, площадь треугольника равна половине площади параллелограмма.

И. Как можно вычислить площадь треугольника, если известно основание до н.э. и высота (высота или высота треугольника равна высоте этот параллелограмм)?

5. Разделение треугольников (запишите ответ на этом листе)

Начните с треугольника ABC. Думайте об AB как о базе. Затем переместите C вдоль линии параллельно АВ.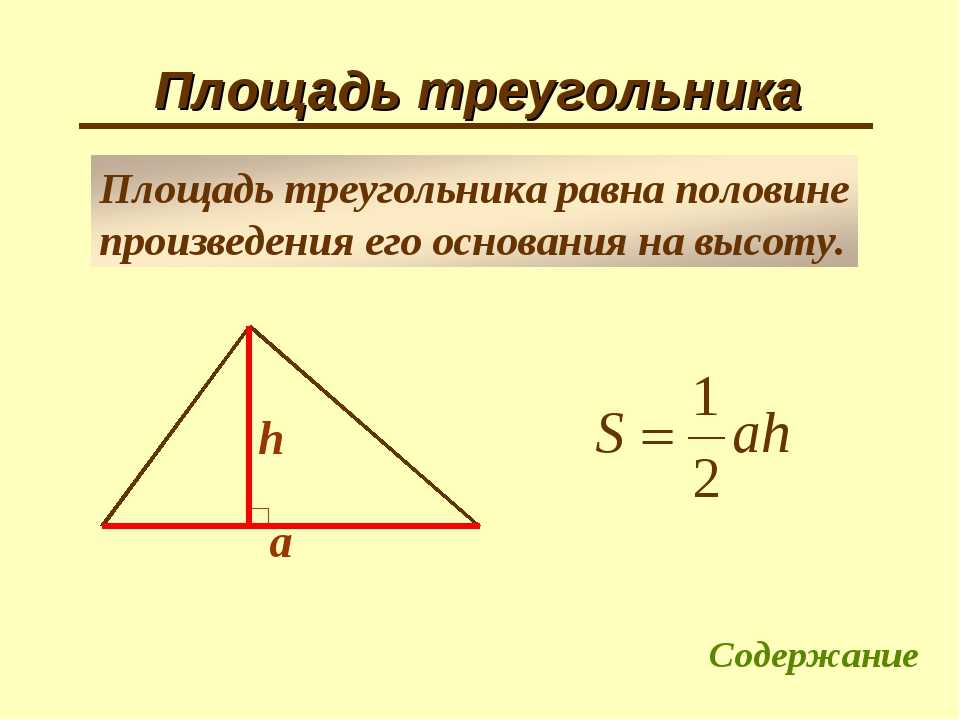 На рисунке получаются такие треугольники, как ABC, ABD, ABE.

Объясните, почему каждый из этих трех треугольников имеет одинаковую площадь.

6. Альтернативное рассечение области

Вырежьте любой треугольник ABC. Отметьте середины D стороны BC и F стороны CA. а затем середина E DF. Сделайте разрезы DF и CE.

Теперь соберите 3 части в виде параллелограмма с основанием АВ.

Как узнать, что ваша фигура является параллелограммом?

8. Сравнение областей

Начните с любого треугольника ABC и расположите 4 точные копии треугольника в следующий рисунок, чтобы сделать больший треугольник. Предположим, что треугольник ABC имеет площадь = T. Вычислите площади многоугольников, перечисленных ниже. (Ответы должны выражаться в T, например, 3T или T/2 и т. д.)

Чему равна площадь треугольника BEC?

Чему равна площадь треугольника ADF?

Чему равна площадь четырехугольника BDEC?

Чему равна площадь треугольника AEF?

Чему равна площадь треугольника ADG? (G — точка на CE с CG/CE = 1/4. )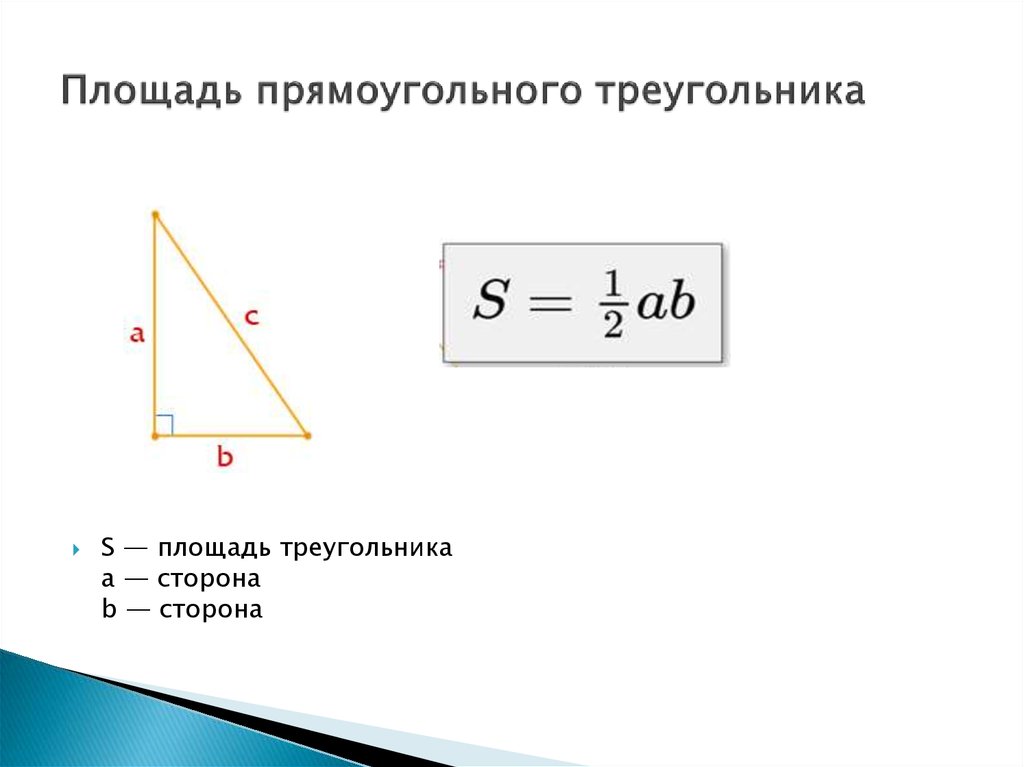

9. Площади прямоугольника

Начните с любого прямоугольника ABCD. Проведите диагонали АС и BD.

Если точка Е является пересечением диагоналей, то какая из треугольники ABE, BCE, CDE, DAE имеют наибольшую площадь?

Какие треугольники имеют наибольший периметр?

Как это изменится, если BC меньше AB?

Как вы можете убедить дружественного скептика, что ваш ответ правильный?

14. Всегда ли можно срезать углы?

Одно из важных следствий среза угла и формулы основания и высоты площади состоит в том, что если два параллелограмма имеют одинаковое основание и одинаковую высоту, у них одинаковая площадь. Но есть ли дыра в наших рассуждениях? Посмотри на это пример.

В этом случае параллелограмм ABEF имеет основание AB, но конструкция точка A’ на основании так, чтобы FA’ была перпендикулярна AB, терпит неудачу, если мы хотим А’ находиться на отрезке АВ.

Как в этом случае измерить высоту от основания АВ? Базовое время высота равна площади в этом случае?

Формула все еще верна?

Если да, то какую причину вы можете указать?

(дополнительное задание) Сможете ли вы разрезать этот параллелограмм и собрать его заново? как прямоугольник с тем же основанием и высотой?

Задачи-вызовы

I. Два квадрата в один

• Нарисуйте два квадрата одинакового размера. Разрежьте квадраты на части и соберите части в один квадрат.
• Если длина стороны исходного квадрата равна 1 единице, какова сторона длина нового одинарного квадрата? Объясните, откуда вы это знаете из-за площади.
• Нарисуйте или приклейте свое решение на странице и сдайте его.

II. Разделение квадратного торта на 5 частей (необязательное задание*)

Эта проблема будет оставлена ​​открытой для вас на некоторое время.

Предположим, вы приготовили лимонный пирог с квадратным основанием и сторонами шириной 8 дюймов.