Упражнение 3. Вычислить площадь треугольника с помощью векторного произведения
Вычислить площадь треугольника с вершинами иИзобразить плоскость треугольника. Как соотносятся (алгебраически и геометрически)площадь треугольника и векторное произведение. Изобразить это соответствие по аналогии с предыдущим упражнением.
Отметим, что векторное произведение векторов и смешанное произведение векторов (которого мы здесь не касались) наряду со скалярным произведением используется не только для вычисления площадей и объёмов, но является одним из основных инструментов для исследования прямых и плоскостей в пространстве (задач на составление уравнений прямых и плоскостей, взаимное расположение прямых и плоскостей и т.д.).
Прямая на плоскости.
Уравнение прямой линии, проходящей через заданную точку перпендикулярно заданному вектору.
(нумерацию рисунков и формул начнем заново)
Пусть
на плоскости (см. рис.1) заданы декартовая
система координат OXY
рис.1) заданы декартовая
система координат OXY
Требуется построить прямую L, проходящую через точку перпендикулярно направлению вектора, и составить ее уравнение
Рассмотрим вектор , где- любая точка прямойL. Точка M принадлежит прямой L тогда и только тогда, когда , см. рис.2.
Рис.1. Рис.2.
Значит, будет выполняться условие равенства нулю скалярного произведения между взаимно перпендикулярными (ортогональными) векторами
(1)
Уравнение (1) – векторное уравнение прямой L, проходящей через заданную точку перпендикулярно вектору .
Вектор называетсянормальным вектором прямой.
Иными
словами нормальный
вектор прямой — это ненулевой вектор, перпендикулярный
прямой.
Записав векторное уравнение (1) в координатной форме получим: если прямая L имеет нормальный вектор и проходит через точку, то её уравнение может быть записано в виде:
. (2)
При построении прямой линии будем использовать функцию plot(x,y), в которой аргумент y будет вычисляться по формуле . Координаты нормального вектораи координаты точки прямойявляются входными параметрами в системуMATLAB.
Построение уравнения прямой, проходящей через заданную точку перпендикулярно данному вектору.
Задача. Построить в тетради и в MATLAB прямую L, проходящую через точку с нормальным вектором. Записать и вывести в заголовок уравнение прямой вида (2).
Обучающий
пример будет состоять из трех частей.
Мы постепенно освоим процедуру создания
графической иллюстрации к задачам
аналитической геометрии.
Часть 1.
Построить штриховую «—» прямую линию красного цвета толщины 2.
Значение абсцисс точек прямой изменяются в диапазоне от – 2 до 6 с шагом 2.
В узловых точках вывести маркеры красного цвета «r» в виде шестиконечных звезд «h».
Вопрос: сколько будет узловых точек у функции plot( )?
В заголовок вывести общее уравнение прямой.
Построить и обозначить оси координат.
Отметить точку .
Решение:
В окне редактора Editor создаем М-файл (скрипт):
% часть 1
% задание исходных данных — коэффициентов уравнения и начальной точки M0(4,2):
A=-1; B=1; x0=4; y0=2;
% формирование диапазона абсцисс
x=-2:2:6; % массив размерности 1х5;
% Вычисление значений ординат
y=(-A/B)*(x-x0)+y0; % также получим массив размерности 1х5;
% Вопрос: сколько будет узловых точек у функции plot( )?
% Ответ:
% Так как для аргументов функции plot были созданы массивы размерности1х5,
%
то узловых точек будет 5.
% построение красной штриховой линии с 5-ю маркерами в виде 6-конечных звезд
plot(x,y,’r—h’, ‘LineWidth’,2)
% построение осей координат
line([-3,0;7,0],[0,-5;0,5],’Color’,’black’)
% обозначение осей и ввод заголовка
xlabel(‘X’),ylabel(‘Y’), title(‘ -3 (x — 4) + 3 (y — 2) = 0’)
% включим отображение координатной сетки и режим добавления графиков
grid on, hold on
% установим одинаковый масштаб
axis equal
% обозначим прямую L и точку M0(4,2)
% пометим прямую L
text(-1.75,-2.5,’L’)
%пометим точку M0(4,2) круговым маркером черного цвета
plot(4,2,’o’,’LineWidth’,2,…
‘MarkerEdgeColor’,’k’,…
‘MarkerSize’,8)
% и выведем обозначение точки M0(4,2) text(4. 2,1,’M_0(4,2)’)
2,1,’M_0(4,2)’)
Получаем график (рис.3) прямой L: , проходящей через точку.
Рис.3.
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
Стр 1 из 8Следующая ⇒ Векторное, смешанное произведения векторов [2], гл.1; [8], гл.2; [10]
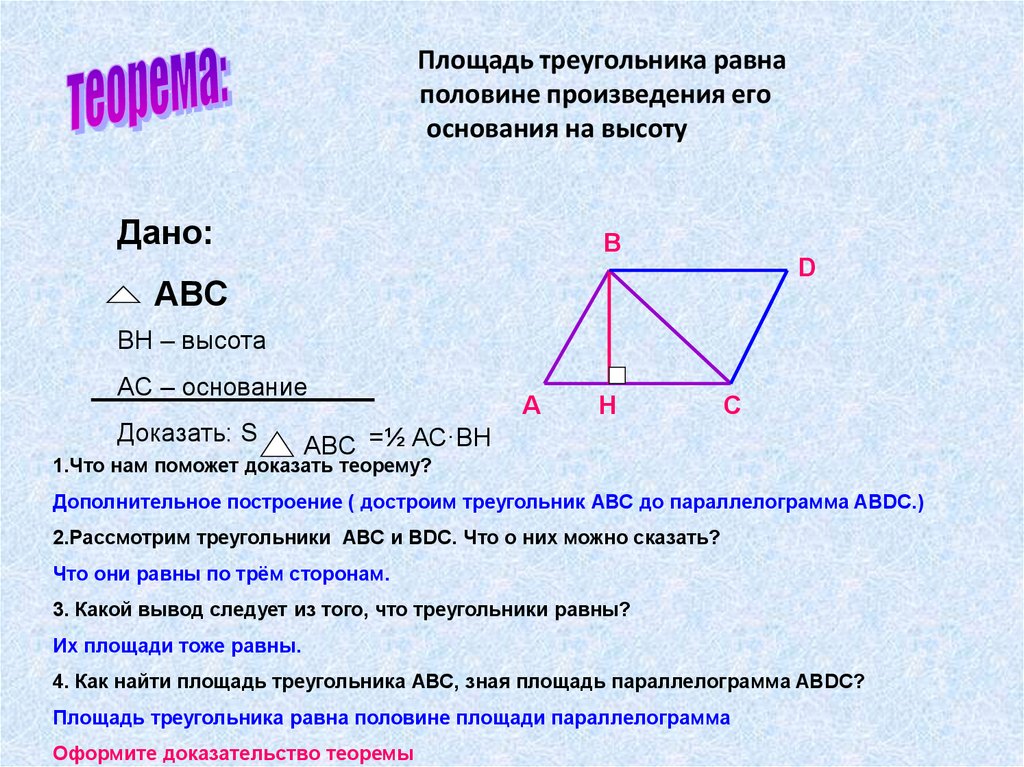
При решении задач на эту тему необходимо знать определения скалярного, векторного и смешанного произведений векторов, уметь вычислять и применять эти произведения. Скалярным произведением векторов и называется число . Зная координаты перемножаемых векторов , можно вычислить скалярное произведение Условием ортогональности (перпендикулярности) векторов а и b является равенство нулю их скалярного произведения Векторным произведением вектора на вектор называется вектор который 1) перпендикулярен векторам и , 2) образует с ними правую тройку , , и 3) длина которого равна площади параллелограмма, построенного на векторах и , как на сторонах, т. Смешанное произведение векторов есть скалярное произведение вектора на векторное произведение и и вычисляется по формуле Абсолютная величина смешанного произведения векторов , , равна объему параллелепипеда, построенного на этих векторах. Если , , -правая тройка векторов, то если левая, то — условие компланарности трех векторов , , . Пример 4. На векторах построен треугольник ABC. Найти площадь треугольника ABC и его высоту, опущенную на сторону ВС, если длины векторов равны соответственно 1 и , а угол, образованный векторами , равен 135°. Решение: 1) Найдем площадь S треугольника ABC. Площадь треугольника, построенного на векторах, равна половине модуля их векторного произведения, то есть Вычислим векторное произведение векторов Для этого применим распределительное свойство векторного произведения: Векторное произведение вектора самого на себя равно нулевому вектору, следовательно при перестановке сомножителей векторное произведение меняет знак на противоположный, значит Отсюда, Находим модуль полученного вектора Следовательно, 2) Найдем сторону ВС треугольника ABC, то есть длину вектора . , откуда Найдем длину полученного вектора по формуле: Под корнем стоит скалярное произведение вектора самого на себя. Найдем его С учетом того, что получаем Таким образом, 3) Найдем высоту h треугольника ABC, опущенную на сторону ВС. По формуле площади треугольника имеем откуда Площадь треугольника S и сторона ВС найдены ранее: S = 26, ВС = 13. Следовательно, Приложение векторной алгебры 12345678Следующая ⇒ Читайте также: Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Сущность недвижимости Решение задач с использованием генеалогического метода История происхождения и развития детской игры |
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Как вычислить площадь треугольника ABC по трем векторам положения $a, b$ и $c$ в 3D?
Спросил
Изменено 3 года, 9 месяцев назад
Просмотрено 104k раз
$\begingroup$
Где $a = (1, 2, 3), b = (2, 1, 3) $ и $c = (3,1,2). $
- треугольников
- векторов
- площадь
$\endgroup$
1
$\begingroup$
Цапля конечно работает, но было бы проще взять половину длины векторного произведения
$(б-а)\раз(с-а)$.
$\endgroup$
$\begingroup$
Решение: Построить векторы $\hat{ab}$, $\hat{ac}$ и взять $\frac{1}{2} |\hat{ab} \times \hat{ac}|$. Берем половину полученного, так как исходное дает площадь параллелограмма, описываемого векторами.
$\endgroup$
$\begingroup$
используйте эту формулу: $$S=\sqrt{p(ps_1)(ps_2)(ps_3)}$$ где $p=\frac{s_1+s_2+s_3}{2}$, а $s_1,s_2,s_3$ — длины трех сторон. Вы можете получить $s_1,s_2,s_3$ из трех позиций.
$\endgroup$
$\begingroup$
Вычислите разницу $a-b$ и $a-c$. затем возьмем их перекрестное произведение $(a-c)\times(a-c)$. Эта норма, деленная на два, и есть площадь треугольника. 92}=\sqrt5$
Вы можете сделать это для всех сторон, и можно найти площадь треугольника, зная длину каждой из его сторон.
$\endgroup$
0
$\begingroup$
Кросс-произведение прекрасно работает как черный ящик, но ему не хватает геометрической интуиции.
Для треугольника ABC построим отрезок, пересекающий C и перпендикулярный стороне AB. Площадь треугольника $0.5\cdot \left \| \overrightarrow{AB} \right \|\cdot \left \| \overrightarrow{CH} \right \|$ $$\слева\| \overrightarrow{CH} \right \|=\left \| \overrightarrow{AC} \право \| \cdot грех(θ)$$ куда $$θ = arccos(\frac{\overrightarrow{AB} \cdot \overrightarrow{AC}}{\left \| \overrightarrow{AB} \right \| \cdot \left \| \overrightarrow{AC} \right \ |})$$
Таким образом: $$Area=0.5\cdot\left\| \overrightarrow{AB} \right \|\cdot \left \| \overrightarrow{AC} \right \|\cdot sin(θ)$$ Это равно: $$0.5\cdot\влево\| \overrightarrow{AB} \times \overrightarrow{AC} \right \|$$
Вот почему
$$0. 5\cdot\влево\| \overrightarrow{AB} \times \overrightarrow{AC} \right \|=0.5\cdot \left \| \overrightarrow{AB} \right \|\cdot \left \| \overrightarrow{AC} \right \|\cdot sin(θ)$$
5\cdot\влево\| \overrightarrow{AB} \times \overrightarrow{AC} \right \|=0.5\cdot \left \| \overrightarrow{AB} \right \|\cdot \left \| \overrightarrow{AC} \right \|\cdot sin(θ)$$
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Площадь с векторным произведением — Задача 2
Давайте используем векторное произведение векторов, чтобы найти площадь треугольника. У меня есть треугольник ABC, который нужно найти по точкам (-3 0), (6 -5) и (-1 6). Теперь любые два вектора, которые они выбирают на этом треугольнике, также будут формировать, они будут определять или определять параллелограмм. И поэтому я могу найти его площадь, используя векторное произведение этих двух векторов. И, конечно же, половина этой площади будет площадью моего треугольника. Итак, что я действительно собираюсь найти, используя векторное произведение, так это площадь всего параллелограмма.
Возьмем эти два вектора AC и AB. И их перекрестное произведение даст мне площадь этого параллелограмма. Знайте, что эти точки являются двумерными точками. Поэтому, когда я придумываю компоненты для векторов AB и AC. Обычно я получаю две компоненты, но вам нужны трехмерные векторы, чтобы получить перекрестные произведения. Так что мне придется добавить третий компонент.
Так что мне придется добавить третий компонент.
Теперь векторы AB будут равны 6 минус -3, 9. –5 минус 0, -5. Но я должен добавить здесь компонент z. Мне нужно сделать эти трехмерные векторы. Вы можете просто представить, что xy. Это все на плоскости xy, поэтому в трехмерном пространстве значение z каждой из этих точек равно 0,9.0005
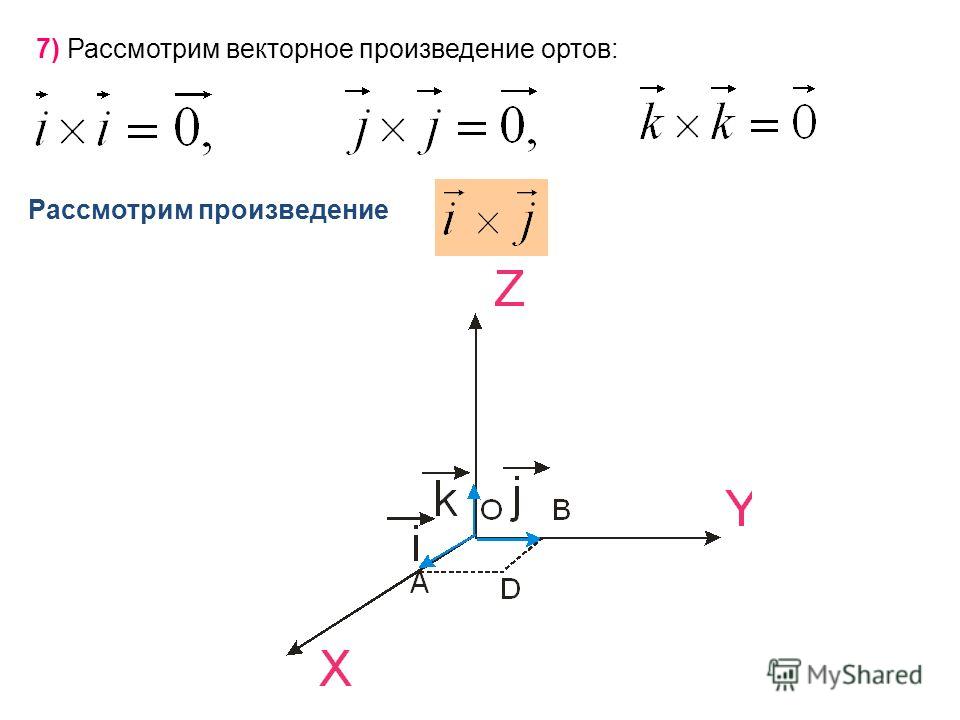
Таким образом, вектор от a до c будет равен -1 минус -3, -1 плюс 3 будет 2, 6 минус 0, 6 и, конечно же, 0. Итак, давайте возьмем векторное произведение этих двух. Теперь помните, перекрестное произведение не дает мне напрямую площадь параллелограмма. Я должен взять величину перекрестного произведения. Перекрестное произведение даст мне вектор, но шаг за шагом. Перекрестное произведение равно ijk, тогда мне нужны компоненты двух векторов. Итак, я хочу <9 -5 0> и <2 6 0>. Теперь, если вы посмотрите на это, когда я расширю верхнюю строку, я умножу этот определитель на i; -5 0, 6 0 это будет 0. И у меня будет минус j раз этот определитель 92 0, этот определитель также будет равен 0.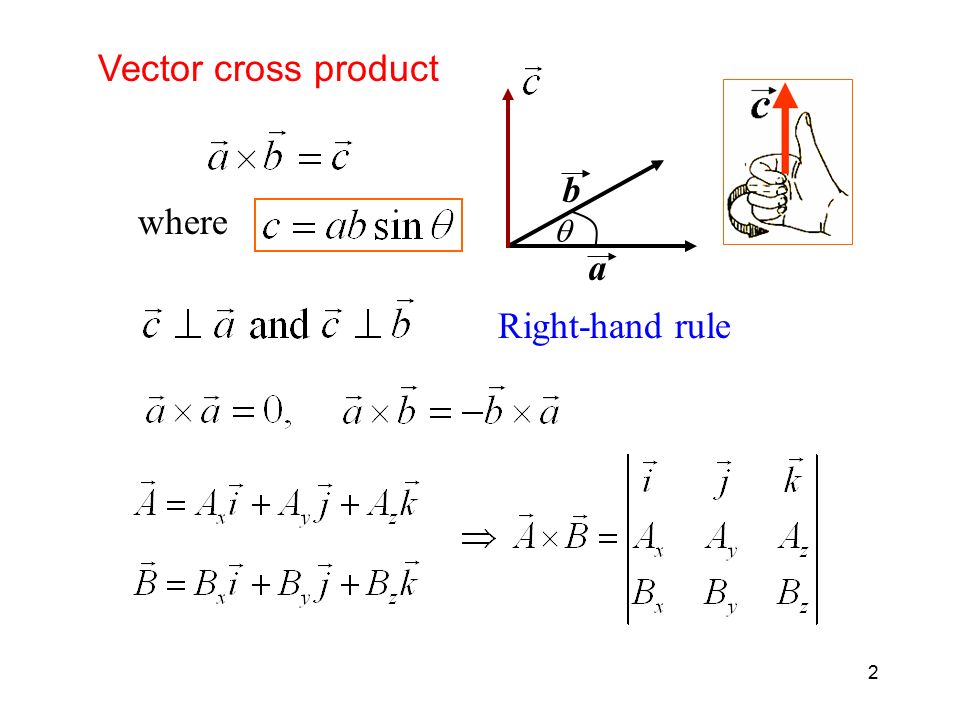

 Все правила по сольфеджио
Все правила по сольфеджио
 е. . Если известны координаты перемножаемых векторов, то векторное произведение вычисляется по формуле:
е. . Если известны координаты перемножаемых векторов, то векторное произведение вычисляется по формуле: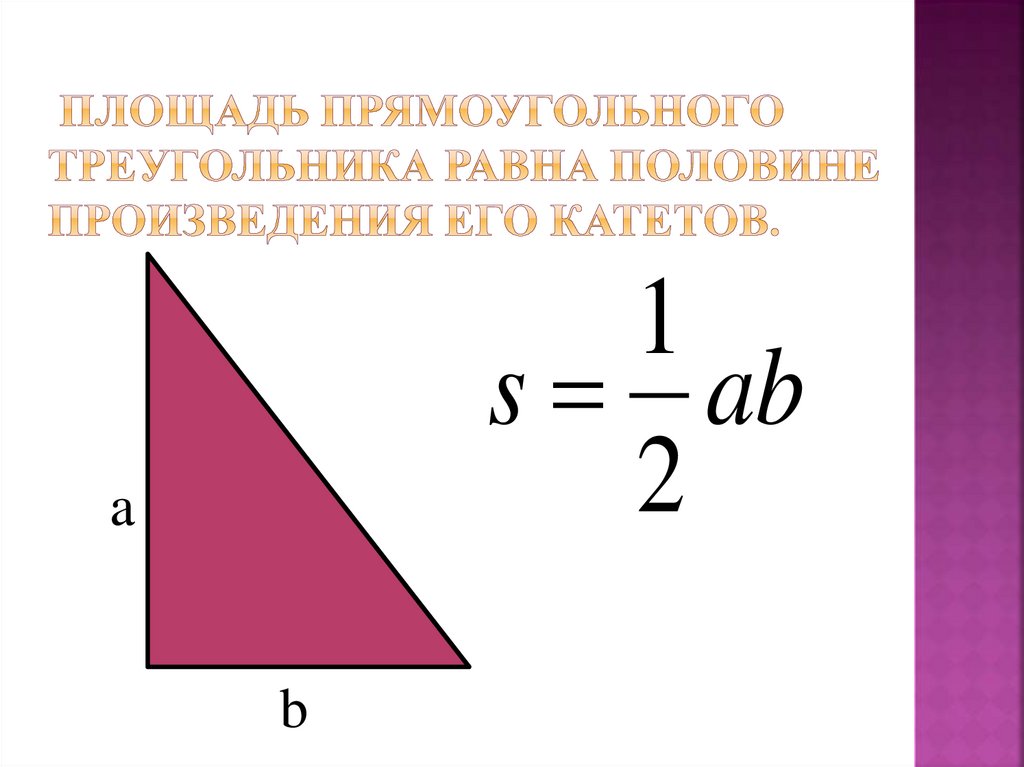
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.007 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.007 с.)