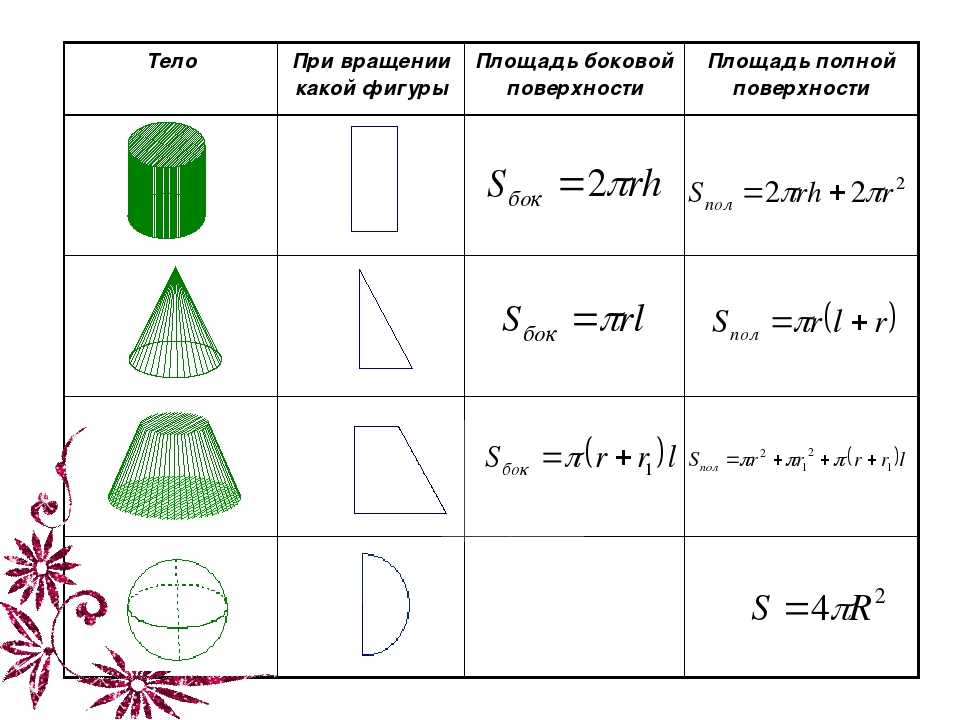
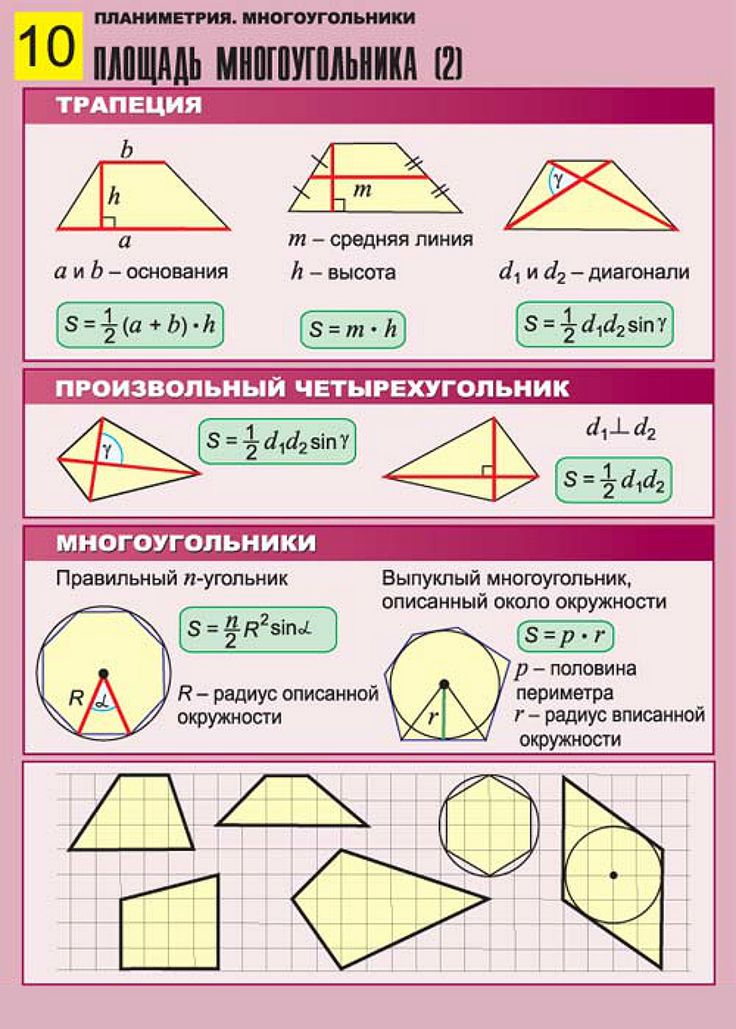
Таблица нахождения всех площадей фигур.
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
- Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Все формулы площади плоских фигур
Площадь равнобедренной трапеции
1. Формула площади равнобедренной
трапеции через стороны и угол
Формула площади равнобедренной
трапеции через стороны и угол
а — нижнее основание
b — верхнее основание
с — равные боковые стороны
α — угол при нижнем основании
Формула площади равнобедренной трапеции через стороны, (S):
Формула площади равнобедренной трапеции через стороны и угол, (S):
2. Формула площади равнобедренной трапеции через радиус вписанной окружности
R- радиус вписанной окружности
D- диаметр вписанной окружности
O- центр вписанной окружности
H- высота трапеции
α, β — углы трапеции
Формула площади равнобедренной трапеции через радиус вписанной окружности, (S):
СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:
3. Формула площади равнобедренной трапеции через диагонали и угол между ними
d- диагональ трапеции
α,β- углы между диагоналями
Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):
4. Формула площади равнобедренной
трапеции через среднюю линию, боковую
сторону и угол при основании
Формула площади равнобедренной
трапеции через среднюю линию, боковую
сторону и угол при основании
c- боковая сторона
m- средняя линия трапеции
α, β — углы при основании
Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании,
(S):
5. Формула площади равнобедренной трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
h — высота трапеции
Формула площади равнобедренной трапеции через основания и высоту, (S):
Площадь треугольника по стороне и двум углам, формула.
a, b, c- стороны треугольника
α, β, γ- противолежащие углы
Площадь треугольника через сторону и два угла (S):
Формула площади правильного многоугольника
a — сторона многоугольника
n — количество сторон
Площадь правильного многоугольника, (S):
Формула (Герона) площади треугольника через полупериметр (S):
Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего
треугольника.
a — сторона треугольника
h – высота
Как вычислить площадь равнобедренного треугольника?
b — основание треугольника
a — равные стороны
h – высота
3. Формула площади трапеции через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
Радиус описанной окружности трапеции по сторонам и диагонали
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание
d — диагональ
h — высота
Формула радиуса описанной окружности трапеции, (R)
найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
a, b — стороны треугольника
Радиус описанной окружности равнобедренного треугольника (R):
Радиус вписанной окружности в шестиугольник
a — сторона шестиугольника
Радиус вписанной окружности в шестиугольник, (r):
Радиус вписанной окружности в ромб
r — радиус вписанной окружности
a — сторона ромба
D, d — диагонали
h — высота ромба
Радиус вписанной окружности в равнобочную трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Радиус вписанной окружности в прямоугольный треугольник
a, b — катеты треугольника
с — гипотенуза
Радиус вписанной окружности в равнобедренный треугольник
a, b — стороны треугольника
Доказать, что площадь вписанного четырёхугольника равна
\/(р — а)(р — b) (р — с) (р — d),
где р — полупериметр и а, b, с и d —
стороны четырёхугольника.
Доказать, что площадь вписанного в круг четырёхугольника равна
1/2 (ab + cb) · sin α , где а, b, с и d — стороны четырёхугольника и α — угол между сторонами а и b.
S = √[ a ƀ c d] sin ½ (α + β). — Читайте подробнее на FB.ru:
Площадь произвольного четырёхугольника (рис. 1.13) можно выразить через его стороны а, b, c и сумму пары противоположных углов:
где р – полупериметр четырёхугольника.
Площадь вписанного в окружность четырёхугольника () (рис. 1.14, а) вычисляется по формуле Брахмагупты
а описанного (рис. 1.14, б) () – по формуле
Если же четырёхугольник вписан и описан одновременно (рис. 1.14, в), то формула становится совсем простой:
Формула Пика
Чтобы оценить площадь многоугольника
на клетчатой бумаге, достаточно
подсчитать, сколько клеток покрывает
этот многоугольник (площадь клетки мы
принимаем за единицу). Точнее, если S –
площадь многоугольника, — число клеток,
которые целиком лежат внутри многоугольника,
и — число клеток, которые имеют с
внутренностью многоугольника хоть одну
общую точку.
Будем рассматривать ниже только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки. Оказывается, что для таких многоугольников можно указать такую формулу:
где — площадь, r – число узлов, которые лежат строго внутри многоугольника.
Эту формулу называют «формула Пика» — по имени математика, открывшего её в 1899 году.
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
Ответ: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
Ответ: .
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Вычисление площадей плоских фигур с помощью определенного интеграла
Тема: “Вычисление площадей плоских фигур с помощью определенного интеграла”.
Образовательные задачи:
- обеспечить повторение, обобщение и систематизацию материала по данной теме;
- создать условия контроля (самоконтроля) знаний и умений.
Развивающие задачи:
- способствовать формированию умений применять приемы сравнения, обобщения, выделения главного;
- продолжить развитие математического кругозора,
мышления и речи, внимания и памяти.

Воспитательные задачи:
- содействовать воспитанию интереса к математике;
- воспитание активности, мобильности, умения общаться.
Тип урока – комбинированный урок с элементами проблемного обучения.
Методика – проблемный, наглядный, самостоятельная работа студентов, самопроверка.
Оборудование – приложение к уроку, таблицы.
План урока
- Организационный момент. Подготовка студентов к работе на занятии.
- Подготовка студентов к активной деятельности (проверка вычислительных навыков и таблиц интегралов по группам).
- Подготовка к изучению нового материала через повторение и актуализацию опорных знаний.
- Работа с новым материалом.
- Первичное осмысление и применение изученного
материала, его закрепление.

- Домашнее задание.
- Применение знаний.
- Подведение итогов.
- Рефлексия.
Ход урока
1. Организационный момент.
Понятие определенного интеграла является одним из основных понятий математики. К концу 17 в. Ньютоном и Лейбницем был создан аппарат дифференциального и интегрального исчисления, который составляет основу математического анализа.
На предыдущих занятиях мы научились “брать” неопределенные интегралы, вычислять определенные интегралы. Но куда важнее применение определенного интеграла. Мы знаем, что с его помощью можно вычислять площади криволинейных трапеций. Сегодня мы ответим на вопрос: “Как это сделать?”
2. Подготовка студентов к активной деятельности.
Но сначала нам необходимо проверить
вычислительные навыки и знание таблицы
интегралов. Перед вами задание, результатом
выполнения которого будет высказывание
французского математика С. Д. Пуассона (Жизнь
украшается двумя вещами: занятием математикой и
ее преподаванием).
Д. Пуассона (Жизнь
украшается двумя вещами: занятием математикой и
ее преподаванием).
Задание выполняется парами (Приложение №1).
3. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний.
Переходим к теме нашего занятия “Вычисления площадей плоских фигур с помощью определенного интеграла”. Кроме умения вычислять определенный интеграл, нам нужно вспомнить свойства площадей. В чем они заключаются?
- Равные фигуры имеют равные площади.
- Если фигура разбита на две части, то её площадь находится как сумма площадей отдельных частей.
Также нам нужно повторить правило интеграла суммы и формулу Ньютона-Лейбница.
4. Работа с новым интегралом
1. Определенный интеграл служит для
вычисления площадей криволинейных трапеций. Но
на практике чаще встречаются фигуры, которые
таковыми не являются и нам необходимо научиться
находить площади именно таких фигур.
Работа по таблице “Основные случаи расположения плоской фигуры и соответствующие формулы площадей” (Приложение №2).
2. Давай проверим себя.
Работа с заданием (Приложение №3) с последующей проверкой (таблица №3).
3. Но умения правильно выбирать формулы для площади недостаточно. На следующей таблице (Приложение №4) в каждом из заданий есть “внешняя” причина, не позволяющая вычислить площадь фигуры. Найдём их.
а) не указаны формулы для графиков функций.
б) нет пределов интегрирования.
в) не указаны названия графиков и нет одного предела.
г) не указана формула одного из графиков.
4. С учетом проделанной работы, сформулируем и запишем алгоритм решения задач на тему урока.
- Построить графики данных линий. Определить искомую фигуру.
- Найти пределы интегрирования.
- Записать площадь искомой фигуры с помощью
определенного интеграла.

- Вычислить полученный интеграл.
5. Первичное осмысление и применение изученного материала, его закрепление.
1. С учетом алгоритма выполним задание №2 из последней таблицы.
Рисунок 1
Решение:
Найдём пределы интегрирования.
Для точки А:
– не удовлетворяет условию задания
Для точки В:
– не удовлетворяет условию задачи.
Ответ: (кв.ед).
2. Но при выполнении этого задания алгоритм применялся не полностью. Для его отработки выполним следующее задание
Задание. Найти площадь фигуры, ограниченной линиями , .
Рисунок 2
Решение:
–
парабола, вершина (m,n).
(0;2) – вершина
-2 |
0 |
2 |
4 |
2 |
4 |
Найдём пределы интегрирования.
Ответ: (кв.ед).
6. Домашнее задание.
Вычислить площадь фигуры, ограниченной линиями (задание разобрать).
7. Применение знаний.
Самостоятельная работа (Приложение №5)
8. Подведение итогов.
- научились составлять формулы для нахождения площадей плоских фигур;
- находить пределы интегрирования;
- вычислять площади фигур.

9. Рефлексия.
Студентам раздаются листочки. Они должны оценить свою работу, выбрав один из предложенных вариантов ответа.
Оценить степень сложности урока.
Вам было на уроке:
- легко;
- обычно;
- трудно.
Оцените степень вашего усвоения материала:
- усвоил полностью, могу применить;
- усвоил полностью, но затрудняюсь в применении;
- усвоил частично;
- не усвоил.
Просмотрев ответы, сделать вывод о подготовленности студентов к практической работе.
Используемая литература:
- Валуцэ И.И., Дилигулин Г.Д. Математика для техникумов.
- Крамер Н.Ш., Путко Б.А., Тришин И.М. Высшая математика для экономистов.
- Данко П.Е., Попов А.Г. Высшая математика, ч.
 1.
1. - Званич Л.И., Рязановский А.Р. М., Новая школа, 1996.
- Газета “Математика”. Издательский дом “Первое сентября”.
Плоские пружины: Расчетные формулы | Tokai Spring Industries, Inc.
1 Формулы расчета плоских пружин по формам
・1-1 Консольные пружины с прямоугольным поперечным сечением
Простейшая плоская пружина представляет собой консольную пружину с прямоугольным поперечным сечением.
Когда фиксированный конец — это А, а свободный конец — это В, а нагрузка Р приложена к точке В, формула расчета выглядит следующим образом.
Здесь I второй момент площади.
Выражается как
, а когда большое, то
Таким образом, расчетная формула для больших
ν представляет собой коэффициент Пуассона, а в случае стали ν ≈ 0,3. Максимальное напряжение находится на фиксированном конце и представлено формулой ниже.
В таблице 2 показано значение модуля продольной упругости (E) основных материалов для плоских пружин.
Таблица 1. Условные обозначения и единицы, используемые в расчетах
| Символ | Значение символа | Блок |
|---|---|---|
| ч | Толщина листа | мм |
| б | Ширина пластины | мм |
| л | Расстояние от точки опоры до точки нагрузки | мм |
| р | Радиус дуги | мм |
| Е | Модуль продольной упругости | Н/мм 2 |
| я | Второй момент площади | мм 4 |
| З | Модуль упругости сечения | мм 3 |
| П | Нагрузка (сила), приложенная к пружине | Н |
| δ | Прогиб в точке нагрузки | мм |
| к | Константа пружины | Н/мм |
| о | Напряжение изгиба | Н/мм 2 |
| v | Коэффициент Пуассона | – |
Таблица 2. Модуль продольной упругости: E (Н/м²)
Модуль продольной упругости: E (Н/м²)
| Материал | E Значение | |
|---|---|---|
| Пружинная сталь Материал | 206×10 3 | |
| Нержавеющая сталь | SUS301 SUS304(соответствует X5CrNi18-9,1.4301,S30400) SUS631(соответствует X7CrNiAl17-7,1.4568,S17700) | 186×10 3 186×10 3 196×10 3 |
| Проволока из фосфористой бронзы | 98×10 3 | |
| Бериллиевая медная проволока | 127×10 3 | |
・1-2 Расчетные формулы для плоских пружин с трапециевидной консолью
Рисунок 2
Как показано на рисунке 2, когда толщина пластины плоской пружины фиксирована, а ширина пластины изменяется линейно, отклонение свободного конца определяется следующей формулой.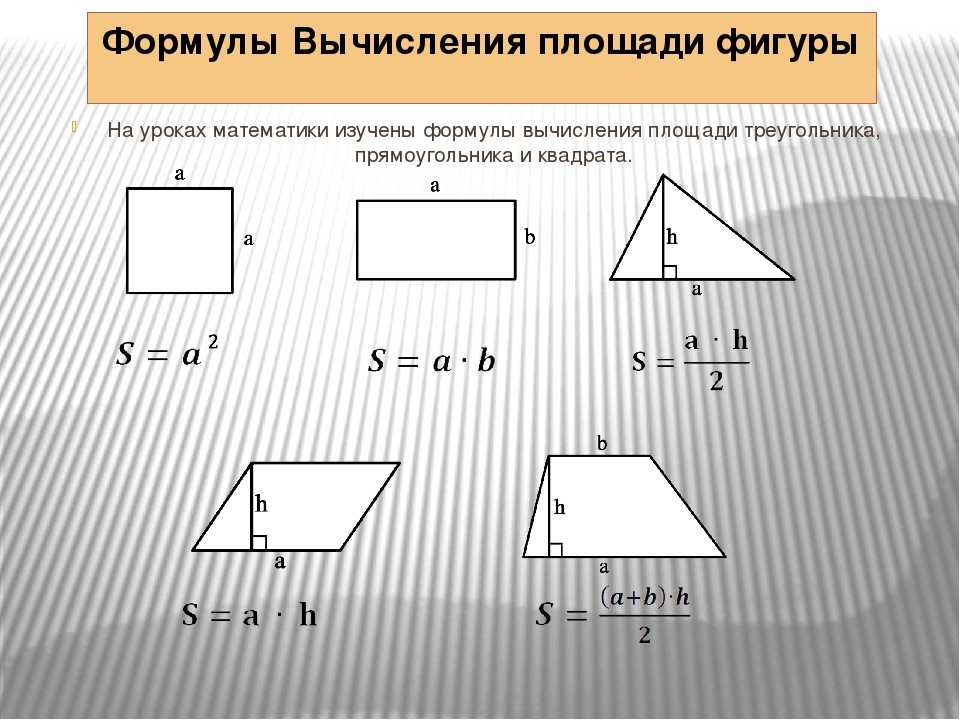
Формула 4
Чтобы рассчитать B по формуле, используйте следующие две формулы в зависимости от толщины листа.
Если пластина толстая, используйте приведенную ниже формулу.
Если пластина тонкая, используйте следующую формулу:
Также значение в формуле можно рассчитать по рисунку 3 по β = b1/b.
Рис. 3
・1-3
Расчетные формулы для плоских пружин с изгибом пластины по ширинеРис. 4 а ширина пластины с изгибом находится в соответствии со следующей формулой.
Формула 5
Здесь 、прогиб и угол отклонения изогнутой части A из-за P, а также прогиб на свободном конце кантилевера длиной l2 и шириной пластины .
・1-4
Расчетные формулы для плоских пружин с круглой консольюРисунок 5
толщина листа представляет собой прямую линию, а центральная линия ширины листа представляет собой дугу, прогиб (δφ) в любом положении φ определяется по следующей формуле.
Формула 6
Здесь C представляет прочность пластины на кручение.
・1-5 Расчетные формулы для плоских пружин с дугообразной консольюРис. 6 толщина — дуга. Результаты расчетов с использованием этой теоремы приведены ниже.
Когда вертикальная нагрузка (P) и горизонтальная нагрузка (W) просто приложены к положению центрального угла дугообразной плоской пружины, показанной на рисунке 6, отклонение в направлении y и отклонение в направлении x направление в центральном угловом положении следующие.
Отклонение из-за P
Когда:
Формула 7
Когда:
Формула 8
Прогиб из-за W:
Когда:
Формула 9
Когда:
Формула 10
Рисунок 7
На рисунке 7 значения δy и δx 、 следующие.
Формула 11
Формула 12
Рисунок 8
На рисунке 8 значения δy и δx следующие.
Формула 13
Формула 14
Максимальное напряжение из-за P всегда возникает на закрепленном конце.
Формула 15
Максимальное напряжение из-за W происходит в точке A на рисунке 8 для и на фиксированном конце для .
Формула 16
・1-6 Формула расчета для кольцевых плоских пружинРисунок 9
Круглая пружина, показанная на рис. 9, вертикально симметрична, поэтому общее отклонение в два раза превышает отклонение формы на рис. 8.
Формула 17
・1-7 Расчетные формулы для плоских пружин с комбинацией полукруга и четверти окружностиРисунок 10
В плоской пружине с комбинацией полукруга и четверти окружности, показанной на рисунке 10, прогиб определяется по следующей формуле.
Формула 18
Максимальное напряжение, возникающее на закрепленном конце, можно рассчитать по следующей формуле:
Формула 19
・1-8 Расчетные формулы для дугообразных плоских пружинРисунок 11
Отклонение свободного конца формы, показанной в левой части рисунка 11, определяется по следующей формуле.
Формула 20
В случае дуги, ограниченной в горизонтальном направлении, как показано в правой части рисунка 11, отклонение можно рассчитать по следующей формуле.
Формула 21
В обоих случаях максимальное напряжение рассчитывается по следующей формуле.
Формула 22
・1-9 Расчетные формулы для плоских пружин с дугообразной и прямой частью ・1-9-1 Расчетная формула для плоской пружины с дуговой и прямой частью (№. 1)Рисунок 12
Как показано на рисунке 12, когда прямолинейная часть (AB) и часть дуги окружности (BD) объединены, один конец (D) зафиксирован, и на него действует вертикальная нагрузка (P) или горизонтальная нагрузка (W). другой конец (А), и будет следующим.
Формула 23
Формула 24
Когда ,
Формула C25
Если действует W, формула будет следующей.
Формула 26
Формула 27
Здесь в формуле представлено
Максимальное напряжение возникает на закрепленном конце при , и в точке С при .
・1-9-2 Расчетные формулы для плоских пружин с дугообразной и прямой частью (№ 2)Рисунок 13
Пружина на рисунке 13 представляет собой комбинацию двух пружин на рисунке 12, а прогиб умножается на прогиб, полученный по формуле 23.
Формула 28
Рисунок 14
Как показано на рисунке 14, прогиб конца А пружины с прямолинейной частью и дугообразной частью определяется по следующей формуле.
Формула 29
Здесь и .
Максимальное напряжение изгиба, возникающее в точке С, можно рассчитать по следующей формуле.
Формула 30
В случае , если максимальное напряжение возникает на закрепленном конце, а при и формула следующая.
Формула 31
・1-9-3 Расчетные формулы для плоских пружин с дугообразной и прямой частью (№ 3)Рисунок 15
В случае формы, показанной на рисунке 15, можно рассчитать прогиб части А, разделив часть АС и часть CD, удвоив прогиб по формуле 25 и вычислив прогиб по каждой формуле перед их объединением.
Формула 32
・1-9-4 Расчетные формулы для плоских пружин с дугообразной и прямой частью (№ 4)Рисунок 16
Как показано на рисунке 16, прямая часть зафиксирована, поэтому, когда нагрузка приложена к концу А дугообразной части, вертикальное отклонение и горизонтальное отклонение конца А соответствуют следующим формула, когда нагрузка P действует как .
Формула 33
Формула 34
Когда действует нагрузка W, формула выглядит следующим образом.
Формула 35
Формула 36
Рисунок 17
Для формы на рисунке 17, когда действует нагрузка (P), формула выглядит следующим образом.
Формула 37
Формула 38
Когда W действует, формула выглядит следующим образом.
Формула 39
Формула 40
Он представлен здесь как .
・1-9-5 Расчетные формулы для плоских пружин с дугообразной и прямой частью (№ 5)Рисунок 18
Для пружины формы, показанной на рисунке 18, которая сочетает в себе дугу с малым радиусом кривизны и прямую линию, отклонение, исключающее радиус дуги, выражается следующей формулой.
Формула 41
Максимальное напряжение возникает в части BC, когда , можно рассчитать по следующей формуле.
Формула 42
Если максимальное напряжение возникает на закрепленном конце, формула выглядит следующим образом.
Формула 43
・1-9-6 Расчетные формулы для плоских пружин со сложной комбинацией дуги и прямой частиФорма плоской пружины часто представляет собой сложную комбинацию дугообразной части и прямой части. Формулы, введенные до сих пор, могут быть использованы для формы тонких листовых рессор. Представленные ниже формы и расчетные формулы можно использовать в качестве практических концепций.
Рисунок 19
Форма на рис. 19 считается комбинацией двух форм на рис. 13, и отклонение можно рассчитать, удвоив значение по формуле 28.
Рисунок 20
В форме на рис. 20 оба конца аналогичны рис. 10, а формулу напряжения можно показать с помощью формулы 19. Прогиб с одной стороны по отношению к оси симметрии является добавленной частью к формуле 18, а прогиб с другой одна сторона определяется формулой ниже.
Прогиб с одной стороны по отношению к оси симметрии является добавленной частью к формуле 18, а прогиб с другой одна сторона определяется формулой ниже.
Формула 44
Формула прогиба:
Формула 45
2.Формулы расчета плоских пружин по характеристикам и применению
・2-1 Формулы расчета плоских пружин с нелинейными характеристикамиФифуре 21
Плоская пружина с нелинейными характеристиками, как показано на рис. 21, достигается за счет использования конструкции с клеевыми частями, в которой фиксированное положение клея изменяется последовательно из-за отклонения.
Формула для плоской пружины с нелинейными характеристиками выглядит следующим образом.
Formula 46
・2-2 Расчетные формулы для плоских пружин, подверженных осевым и боковым нагрузкам
Рисунок 22
Плоские пружины используются в таких приложениях, как оборудование для измерения нагрузки, как показано на рис. 22. Один конец закреплен, а другой конец может двигаться в поперечном направлении, но не может вращаться. В этом случае, предполагая, что осевая нагрузка (P) меньше нагрузки потери устойчивости, отклонение и напряжение из-за поперечной нагрузки (Q) выражаются следующими формулами.
22. Один конец закреплен, а другой конец может двигаться в поперечном направлении, но не может вращаться. В этом случае, предполагая, что осевая нагрузка (P) меньше нагрузки потери устойчивости, отклонение и напряжение из-за поперечной нагрузки (Q) выражаются следующими формулами.
Формула 47
Формула 48
Если P больше, чем нагрузка потери устойчивости, приведенная выше формула умножается на коэффициенты и определяется как . Здесь – критическая нагрузка Эйлера и . Здесь коэффициенты и находятся по следующим формулам.
Formula 49
Formula 50
・2-3 Расчетные формулы для плоских пружин с большим прогибом
・2-3-1 Плоские пружины с прямоугольным поперечным сечением
Рисунок 23
Когда отклонение большое, меняется на . На рис. 24 показан результат расчета с добавлением этого эффекта.
Рисунок 24
Горизонтальная ось рисунка показывает , а вертикальная ось показывает , . представляет изгибную жесткость пластины, и когда она велика, . Как видно из рис. 24, при малых значениях, то есть при малых нагрузках Р, и близких к 1, и при , и . Следовательно, в случае такой степени деформации считается ненужным рассматривать ее как большой прогиб с точки зрения практического применения пружины.
представляет изгибную жесткость пластины, и когда она велика, . Как видно из рис. 24, при малых значениях, то есть при малых нагрузках Р, и близких к 1, и при , и . Следовательно, в случае такой степени деформации считается ненужным рассматривать ее как большой прогиб с точки зрения практического применения пружины.
Рис. . Горизонтальная ось представляет собой, а вертикальная ось показывает скорость уменьшения прогиба или напряжения в качестве параметра. Это просто нужно применить к формуле.
Площади прямоугольников | Новозеландская математика
Цель
В этом разделе учащиеся учатся использовать формулу умножения для нахождения площади прямоугольника. Используя пропорциональные рассуждения, учащиеся исследуют, что происходит с площадью, когда длину и/или высоту прямоугольника удваивают.
Цели достижения
GM3-2: Найдите площади прямоугольников и объемы прямоугольных параллелепипедов, применяя умножение.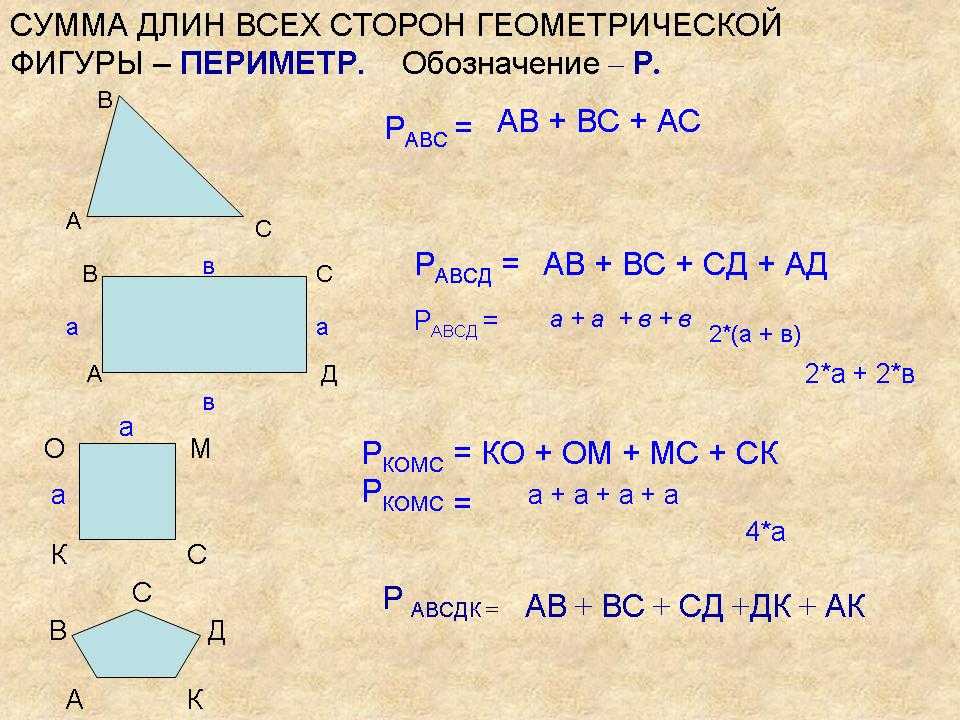
Разработка АО и другие учебные ресурсы
Конкретные результаты обучения
- Используйте умножение для вычисления площади прямоугольника.
- Измерьте длину стороны с помощью линейки.
- Используйте пропорциональные рассуждения, чтобы найти площадь прямоугольника.
Описание математики
Площадь — это количество плоской поверхности, заключенной в фигуру. Обычно используемые стандартные единицы площади: см 2 (квадратные сантиметры), м 2 (квадратные метры) и км 2 (квадратные километры). Квадраты используются для представления этого контекста, потому что они являются примером двумерной фигуры, которая повторяется. Это означает, что форму можно повторять снова и снова, без каких-либо пробелов или наложений.
Прямоугольники — это самые простые фигуры для нахождения площади, потому что структура массива повторяющихся единиц (квадратов) наиболее очевидна. Рассмотрим этот прямоугольник, заполненный квадратными элементами:
Элементы расположены в три ряда по пять квадратов. Общее количество единиц можно найти умножением, 3 х 5 = 15. Точно так же прямоугольник содержит пять столбцов из трех квадратов, поэтому 5 х 3 = 15 также дает общую площадь. Это пример коммутативного свойства — вы можете умножать числа (например, 3 и 5) в любом порядке и получать одинаковый результат (15).
Общее количество единиц можно найти умножением, 3 х 5 = 15. Точно так же прямоугольник содержит пять столбцов из трех квадратов, поэтому 5 х 3 = 15 также дает общую площадь. Это пример коммутативного свойства — вы можете умножать числа (например, 3 и 5) в любом порядке и получать одинаковый результат (15).
Возможности для адаптации и дифференциации
Возможности обучения в этом разделе можно дифференцировать, предоставляя или исключая поддержку учащихся или изменяя требования к заданиям. Рассмотрите возможность использования этих стратегий для поддержки учащихся:
- Управляйте длинами сторон прямоугольников, которые вы используете. Рассмотрите таблицы умножения, с которыми знакомы ваши ученики, и используйте их в качестве базы знаний для построения задач. Например, построение диаграмм прямоугольников, каждый из которых имеет 3 строки, может быть эффективным способом закрепить знания ваших учеников о таблицах умножения на 3, одновременно обучая их понятию площади.

- Используйте прямоугольники с меньшими длинами сторон при представлении концепции массивов и того, как расположение строк и столбцов связано с уравнениями умножения. Как правило, прямоугольники с меньшими длинами сторон делают решения для рисования и счета более доступными. Однако увеличение длины сторон требует более эффективных способов нахождения площади. Таким образом, студенты видят эффективность мультипликативных методов.
- Используйте диаграммы и физические модели (например, квадратные плитки), чтобы помочь учащимся распознавать массивы в границах прямоугольников. Постепенно сокращайте использование диаграмм и физической поддержки, чтобы стимулировать воображение и мышление, опираясь на ранее установленные результаты. Дополнительные идеи см. на страницах 11–13 книги Обучение числам с помощью измерения, геометрии, алгебры и статистики.
- Разрешить доступ к калькуляторам, если вычисления не являются основной целью урока. Например, нахождение всех прямоугольников с площадью 72 см 2 дает возможность применить мультипликативное мышление и систематические рассуждения.
 Эти возможности могут быть упущены, если учащиеся заняты умственными расчетами умножения.
Эти возможности могут быть упущены, если учащиеся заняты умственными расчетами умножения.
Контекст этого раздела можно адаптировать к интересам, культурному происхождению и опыту ваших учащихся. Учащимся может быть предложено найти площадь комнаты в их собственном доме, общественном или школьном саду, их классе, общественной спортивной площадке, скейт-парке или мараэ. Диаграмма с измерениями может быть предоставлена, если это место недоступно во время школьных занятий.
Словарные термины Te reo Māori, такие как mehua (мера), mitarau (сантиметр) и tapawhā rite (квадрат), могут быть введены в этот раздел и использоваться в других математических занятиях.
Требуемые ресурсы Материалы
- Квадраты бумаги или картона 10 см на 10 см, напр. блокноты для заметок
- Большие листы бумаги, напр. мясная бумага
- Разнообразные измерительные приборы, такие как линейки, рулетки, маховые колеса, измерительные линейки (используйте любые подручные средства)
- Газета, переработанный картон, ножницы и скотч
- Бумага с квадратной сеткой 1 см
- Копи-мастер 1
- Копи-мастер 2
Занятие
Занятие 1
На этом занятии учащиеся знакомятся с идеей использования умножения для нахождения площади прямоугольника.
- Покажите учащимся большой прямоугольный лист бумаги размером 30 х 60 см и стопку маленьких квадратов размером 10 х 10 см каждый (как квадраты для заметок). Скажите учащимся, что вы хотите узнать, сколько таких маленьких квадратиков нужно, чтобы покрыть большой бумажный прямоугольник. Вы можете установить такой контекст, как «это школьный сад, а это бетонные плитки, которые мы будем использовать для его покрытия».
Сколько квадратных плиток покроет эту область? - Предложите учащимся кратко обсудить, как они могут оценить ответ, а затем поделитесь своими идеями. Попросите учащихся объяснить два основных процесса:
- Спросите, как будут расположены квадратные блоки. Введите термины, строки (поперек), столбцы (вниз) и массив (структура строк и столбцов), если учащиеся не знакомы с этими словами.
Узнают ли учащиеся структуру массива в расположении квадратных единиц? - Попросите добровольца разместить квадраты рядом друг с другом на прямоугольнике.
 Blu Tac может помочь закрепить блоки на месте.
Blu Tac может помочь закрепить блоки на месте. - Спросите учащихся, как определить общее количество единиц. Подсчет по одному или пропуск подсчета/повторное сложение (6, 12, 18 или 6 + 6 + 6 = 18) являются допустимыми стратегиями, учитывая небольшое количество единиц. Объясните, что площадь прямоугольника равна 18 квадратам.
Можем ли мы считать квадраты еще эффективнее? - Запишите 3 x 6 = 18 и спросите учащихся, где они могут увидеть представления шести и трех в модели (т. е. в количестве строк и столбцов). Спросите, где находится 18 (т. е. это общее количество квадратных единиц).
- Смоделируйте один и тот же процесс с помощью прямоугольников разного размера, например. 20см х 80см, 50см х 40см, 100см х 100см (Квадрат — это особый прямоугольник со всеми сторонами одинаковой длины). Прямоугольники можно вырезать из бумаги, слепить из пластилина, нарисовать на доске или нарисовать мелом на ковре или бетоне.
Ищите учащихся, чтобы:- Распознать структуру массива.

- Используйте умножение как эффективный метод вычисления площади.
- Распознать структуру массива.
- Раздайте учащимся экземпляры Copymaster 1. Попросите их вместе с напарником определить площадь каждого прямоугольника в маленьких квадратах. Пока учащиеся работают, ищите их стратегии расчета. Используют ли они аддитивные или мультипликативные методы?
Признайте, что многое будет зависеть от их знания фактов и стратегий умножения. Меньшие прямоугольники, в которых используются более простые таблицы умножения, могут быть нарисованы и использованы парами учащихся. - Соберите класс и поделитесь решениями. Интересно, что прямоугольник E, квадрат, имеет наибольшую площадь, хотя другие прямоугольники могут выглядеть больше. Чтобы расширить круг учащихся, вы можете начать дискуссию вокруг этого.
Ответы: А (3 х 7 = 21), В (7 х 5 = 35), С (4 х 11 = 44), D (12 х 3 = 36), Е (7 х 7 = 49).), Ж (8 х 6 = 48), Г (11 х 2 = 22).
Что говорят нам ответы об этих прямоугольниках?
Насколько велики маленькие квадраты? Учащиеся могут измерить линейкой, чтобы проверить, являются ли единицы измерения квадратными сантиметрами.
Попросите учащихся включить единицу измерения в свои ответы, например. 21см 2 . Запись обозначений для каждого прямоугольника является хорошей практикой.
Занятия 2 и 3
- Обсудите идею формулы. Вы можете найти забавное видео в Интернете о том, как кто-то использует формулу, чтобы что-то сделать. Рецепт – это своего рода формула. Учащиеся также могут связывать занятия спортом (например, команда следует формуле, чтобы играть хорошо и побеждать), тиканга (правильные способы ведения дел) или автомобильные гонки (например, в гонках Формулы-1 «формула» влечет за собой набор правил). которому должны соответствовать автомобили всех гонщиков).
Что мы подразумеваем под формулой?
Объясняют ли учащиеся, что формула подобна алгоритму или правилу, которому мы можем следовать, чтобы каждый раз получать один и тот же результат?
Запись W x L = A. Это математическая формула, записанная в виде уравнения.
Интересно, что означают буквы W, L и A? - Примените формулу к примерам, над которыми учащиеся работали на предыдущем уроке (Копирайтер 1).

Например, прямоугольник B состоит из семи рядов по пять квадратов.
Строка дает длину прямоугольника. В случае B длина равна 5. (сотрите L в формуле и напишите вместо нее 5)
Количество строк дает ширину прямоугольника. В случае B ширина равна 7. (сотрите W в формуле и на его место напишите 7).
Теперь формула выглядит так: 7 х 5 = А. Интересно, чему равно А? Какое значение площади делает уравнение верным и соответствует формуле? - Попросите учащихся использовать примеры из Copymaster 1. Попрактикуйтесь в группе, начиная с формулы и подставляя значения длины, ширины и площади для каждого прямоугольника. Студентам может быть полезно использовать материалы для моделирования использования формулы.
- Дайте учащимся достойное групповое задание для совместной работы (см. Copymaster 2). Это может быть связано со школьными мероприятиями (например, сделать новый знак для нашего класса, спроектировать школьный сад, спроектировать размер ямы для ханги). Учащимся могут быть даны бумага с сеткой размером 1 см, квадраты со стороной 1 см или работа в тетрадях.
 В Интернете есть несколько программ, которые позволяют учащимся моделировать построение массивов с использованием квадратов размером 1 см. Не забудьте тщательно изучить любую программу, которую вы хотите использовать, чтобы убедиться, что ее использование будет уместным и целеустремленным для ваших студентов.
В Интернете есть несколько программ, которые позволяют учащимся моделировать построение массивов с использованием квадратов размером 1 см. Не забудьте тщательно изучить любую программу, которую вы хотите использовать, чтобы убедиться, что ее использование будет уместным и целеустремленным для ваших студентов. - Предложите учащимся применить формулу Ш x Д = А для построения соответствующих прямоугольников. Например, если они выберут площадь 72 см 2 , им нужно будет учесть все факторы числа 72. Предложите учащимся систематически находить эти факторы. Некоторым учащимся может быть полезна поддержка плаката или списка основных фактов об умножении.
Систематический подход включает в себя начало с 1 в качестве множителя, затем увеличение наименьшего множителя на единицу и проверка 72 на делимость.
1 х 72, 2 х 36 (72 ÷ 2 = 36), 3 х 24 (72 ÷ 3 = 24), 4 х 18 (72 ÷ 4 = 18), 5 х (72 не делится на 5), 6 х 12 (72 ÷ 6 = 12), 7 х (72 не делится на 7), 8 х 9(72 ÷ 8 = 9).
Если процесс продолжится, факторы появятся в обратном порядке, т.е. 9 x 8 = 72. 8 x 9 и 9 x 8 по сути являются одним и тем же прямоугольником, хотя они могут выглядеть по-разному, если учитывать направление этикетки. - Соберите класс, чтобы обсудить решения и посмотреть на схемы возможных надписей в реальном размере. Некоторые опции математически правильны, но неприменимы в качестве опции метки.
Обсудите критерии устранения меток. Например, этикетка шириной менее 5 см может считаться слишком узкой.
Обсудите лучшие варианты, вырежьте их в натуральную величину, затем используйте настоящую банку из-под варенья (или объект, соответствующий контексту обучения), чтобы оценить, насколько хорошо будет работать каждый дизайн этикетки/массива. - В контексте банки с вареньем учащиеся могут написать Карли письмо с изложением того, как они исследовали ее проблему, и дать свои рекомендации. Их математическое мышление можно было бы использовать в качестве основы убедительного письма в других контекстах.

- Еще одно хорошее исследование — замостить большую прямоугольную площадь плиткой площадью 1 м 9 .0089 2 ковровая плитка. Холл или спортзал — идеальное место, хотя классная комната тоже подойдет. Плитки такого размера обычно можно найти в хозяйственных магазинах. Вы легко найдете рекламу в Интернете.
- Предложите учащимся построить квадрат из газет или переработанных коробок. Они могут использовать устройство, чтобы получить представление о масштабе 1 м 2 и оценить площадь помещения, прежде чем приступать к расчетам.
- Попросите учащихся работать в небольших группах, чтобы подсчитать количество плиток, которые потребуются для прямоугольного пространства. Ищите их, чтобы измерить длины сторон прямоугольной области, используя рулетки, маховые колеса или измерительные линейки.
Применяют ли они формулу Ш x Д = А? - Учащиеся могут найти площадь составной фигуры, найдя площадь прямоугольника. Например:
- Можно увидеть, что эта фигура состоит из двух прямоугольников 2 см на 4 см, или прямоугольника 2 см на 6 см и прямоугольника 2 см на 2 см, или прямоугольника 4 см на 6 см без прямоугольника 4 на 2.
 Используйте квадратные элементы размером 1 см (например, блокноты для заметок), чтобы продемонстрировать конструкцию этой составной фигуры. Существуют разные способы решения составных фигур. Однако один из самых простых методов начинается с разбиения составной фигуры на основные формы (например, 2 прямоугольника). Вы можете смоделировать это с помощью блокнотов для заметок или плиток. Затем найдите площадь основных фигур, которые вы построили. Наконец, сложите области основных фигур вместе. Чтобы поддержать развитие этого мышления, вы можете вычислить площадь фигуры, показанной выше, двумя разными способами. Сначала вычислите площадь двух прямоугольников, каждый из которых имеет площадь 4 см х 2 см. Общая площадь каждого прямоугольника 8 см 2 . Таким образом, общая площадь составной формы составляет 16 см 2 . Затем вычислите площадь фигуры как один прямоугольник 2см х 6см (12см 2 ) плюс один 2см х 2см (4см 2 ). Вычисление площади одной и той же формы различными способами позволит улучшить сотрудничество учащихся и позволит учащимся учиться друг у друга.
Используйте квадратные элементы размером 1 см (например, блокноты для заметок), чтобы продемонстрировать конструкцию этой составной фигуры. Существуют разные способы решения составных фигур. Однако один из самых простых методов начинается с разбиения составной фигуры на основные формы (например, 2 прямоугольника). Вы можете смоделировать это с помощью блокнотов для заметок или плиток. Затем найдите площадь основных фигур, которые вы построили. Наконец, сложите области основных фигур вместе. Чтобы поддержать развитие этого мышления, вы можете вычислить площадь фигуры, показанной выше, двумя разными способами. Сначала вычислите площадь двух прямоугольников, каждый из которых имеет площадь 4 см х 2 см. Общая площадь каждого прямоугольника 8 см 2 . Таким образом, общая площадь составной формы составляет 16 см 2 . Затем вычислите площадь фигуры как один прямоугольник 2см х 6см (12см 2 ) плюс один 2см х 2см (4см 2 ). Вычисление площади одной и той же формы различными способами позволит улучшить сотрудничество учащихся и позволит учащимся учиться друг у друга.
Занятие 4
На этом занятии учащиеся изучают использование пропорциональных рассуждений для нахождения площадей прямоугольников.
- Поставьте задачу: семья Сэма покупала новый стол для варекай в местном мараэ. Первый, на который они посмотрели, имел размеры 2 м на 3 м. Сэм сказал, что если они хотят иметь площадь в два раза больше, они должны получить размер 4 м на 6 м. Сэм прав?
- Попросите учащихся нарисовать стол и помочь им решить, прав ли Сэм.
- Вместе с учащимися установите, что удвоение площади означает удвоение только одной стороны прямоугольника. Удвоение обеих сторон прямоугольника увеличивает площадь в четыре раза.
- Используя это пропорциональное рассуждение, учащиеся смогут решать задачи без пересчета длин сторон. Вот несколько примеров проблем:
- По рецепту получилось достаточно глазури, чтобы покрыть верх торта размером 20 на 20 см. Какой размер торта вы можете глазировать, если вы удвоите количество глазури?
- У поздравительной открытки была передняя обложка размером 15 на 10 см.
 Какова площадь картона, использованного для ее изготовления?
Какова площадь картона, использованного для ее изготовления? - В мараэ было два участка, которые нужно было замощением. Каждая площадь имеет размеры 5 м на 8 м. Какова общая площадь асфальтирования?
- Садовник взимал плату со своих клиентов в зависимости от площади их газона. Если счет за стрижку газона размером 6 м на 20 м составляет 20 долларов, то каким должен быть счет за газон размером 20 м на 12 м?
Занятие 5
На занятии учащиеся демонстрируют свою способность самостоятельно применять измерение площади. Подумайте, какие культурно значимые контексты можно включить в это задание, чтобы повысить вовлеченность учащихся.
По следующим ссылкам можно найти подходящие страницы из книг «Разберись»:
- Квадратные навыки
- Adobe Bricks
Учащиеся могут также создать дизайн коврика и указать размеры и площади прямоугольных частей, из которых он состоит. Пример приведен ниже:
Главная Ссылка
Семья и whānau,
На этой неделе в школе мы вычисляли площадь прямоугольника, используя формулу умножения длины на ширину.







 1.
1.
 Эти возможности могут быть упущены, если учащиеся заняты умственными расчетами умножения.
Эти возможности могут быть упущены, если учащиеся заняты умственными расчетами умножения. Blu Tac может помочь закрепить блоки на месте.
Blu Tac может помочь закрепить блоки на месте.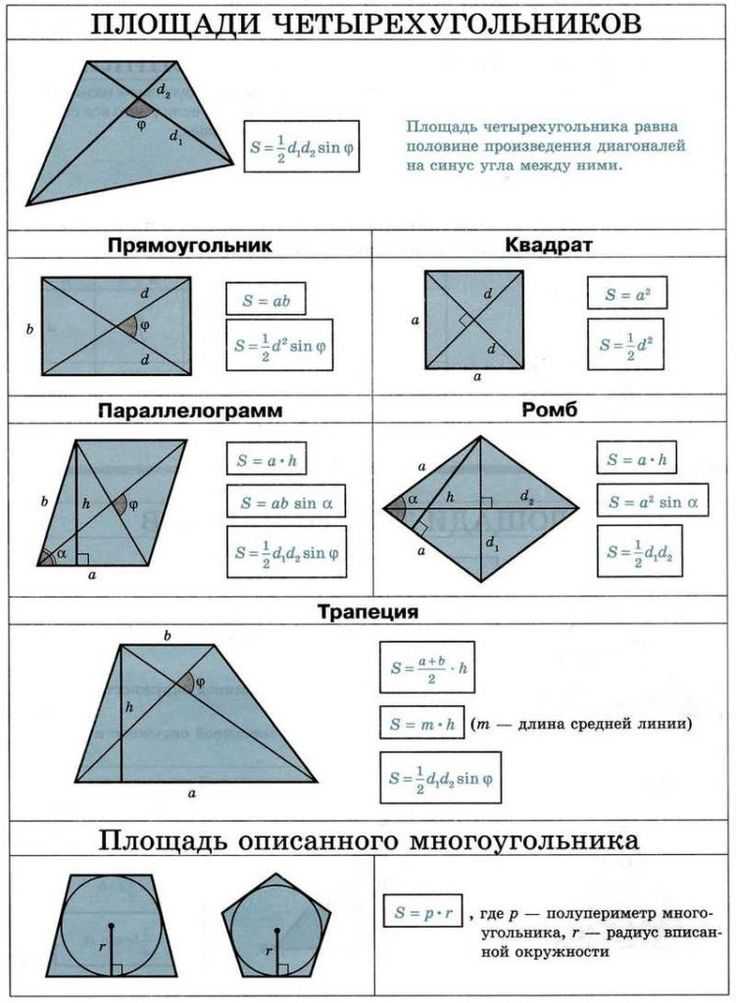


 В Интернете есть несколько программ, которые позволяют учащимся моделировать построение массивов с использованием квадратов размером 1 см. Не забудьте тщательно изучить любую программу, которую вы хотите использовать, чтобы убедиться, что ее использование будет уместным и целеустремленным для ваших студентов.
В Интернете есть несколько программ, которые позволяют учащимся моделировать построение массивов с использованием квадратов размером 1 см. Не забудьте тщательно изучить любую программу, которую вы хотите использовать, чтобы убедиться, что ее использование будет уместным и целеустремленным для ваших студентов.
 Используйте квадратные элементы размером 1 см (например, блокноты для заметок), чтобы продемонстрировать конструкцию этой составной фигуры. Существуют разные способы решения составных фигур. Однако один из самых простых методов начинается с разбиения составной фигуры на основные формы (например, 2 прямоугольника). Вы можете смоделировать это с помощью блокнотов для заметок или плиток. Затем найдите площадь основных фигур, которые вы построили. Наконец, сложите области основных фигур вместе. Чтобы поддержать развитие этого мышления, вы можете вычислить площадь фигуры, показанной выше, двумя разными способами. Сначала вычислите площадь двух прямоугольников, каждый из которых имеет площадь 4 см х 2 см. Общая площадь каждого прямоугольника 8 см 2 . Таким образом, общая площадь составной формы составляет 16 см 2 . Затем вычислите площадь фигуры как один прямоугольник 2см х 6см (12см 2 ) плюс один 2см х 2см (4см 2 ). Вычисление площади одной и той же формы различными способами позволит улучшить сотрудничество учащихся и позволит учащимся учиться друг у друга.
Используйте квадратные элементы размером 1 см (например, блокноты для заметок), чтобы продемонстрировать конструкцию этой составной фигуры. Существуют разные способы решения составных фигур. Однако один из самых простых методов начинается с разбиения составной фигуры на основные формы (например, 2 прямоугольника). Вы можете смоделировать это с помощью блокнотов для заметок или плиток. Затем найдите площадь основных фигур, которые вы построили. Наконец, сложите области основных фигур вместе. Чтобы поддержать развитие этого мышления, вы можете вычислить площадь фигуры, показанной выше, двумя разными способами. Сначала вычислите площадь двух прямоугольников, каждый из которых имеет площадь 4 см х 2 см. Общая площадь каждого прямоугольника 8 см 2 . Таким образом, общая площадь составной формы составляет 16 см 2 . Затем вычислите площадь фигуры как один прямоугольник 2см х 6см (12см 2 ) плюс один 2см х 2см (4см 2 ). Вычисление площади одной и той же формы различными способами позволит улучшить сотрудничество учащихся и позволит учащимся учиться друг у друга.
 Какова площадь картона, использованного для ее изготовления?
Какова площадь картона, использованного для ее изготовления?