Площади всех фигур геометрия: Площадь геометрических фигур — урок. Основной государственный экзамен (9 класс), Математика.

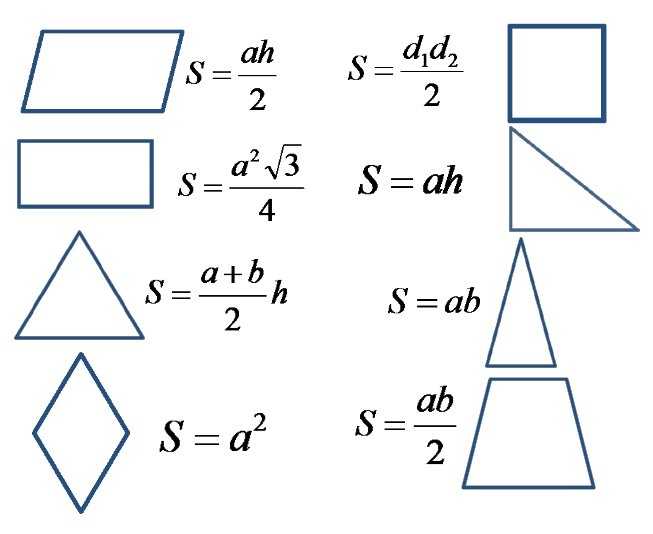
Все площади геометрических фигур, формулы

Существует бесконечное количество плоских фигур самой разной формы, как правильных, так и неправильных. Общее свойство всех фигур – любая из них обладает площадью. Площади фигур – это размеры части плоскости, занимаемой этими фигурами, выраженные в определенных единицах. Величина эта всегда бывает выражена положительным числом. Единицей измерения служит площадь квадрата, чья сторона равняется единице длины (например, одному метру или одному сантиметру). Приблизительное значение площади любой фигуры можно вычислить, умножив количество единичных квадратов, на которые она разбита, на площадь одного квадрата.

 

 

Существует бесконечное количество плоских фигур самой разной формы, как правильных, так и неправильных. Общее свойство всех фигур – любая из них обладает площадью. Площади фигур – это размеры части плоскости, занимаемой этими фигурами, выраженные в определенных единицах. Величина эта всегда бывает выражена положительным числом. Единицей измерения служит площадь квадрата, чья сторона равняется единице длины (например, одному метру или одному сантиметру). Приблизительное значение площади любой фигуры можно вычислить, умножив количество единичных квадратов, на которые она разбита, на площадь одного квадрата.

Другие определения данного понятия выглядят следующим образом:

1. Площади простых фигур – скалярные положительные величины, удовлетворяющие условиям:

– у равных фигур – равные величины площадей;

– если фигура делится на части (простые фигуры), то ее площадь – сумма площадей данных фигур;

– квадрат, имеющий стороной единицу измерения, служит единицей площади.

2. Площади фигур сложной формы (многоугольников) – положительные величины, имеющие свойства:

– у равных многоугольников – одинаковые величины площадей;

– в случае, если многоугольник составляют несколько других многоугольников, его площадь равняется сумме площадей последних. Это правило справедливо для неперекрывающихся многоугольников.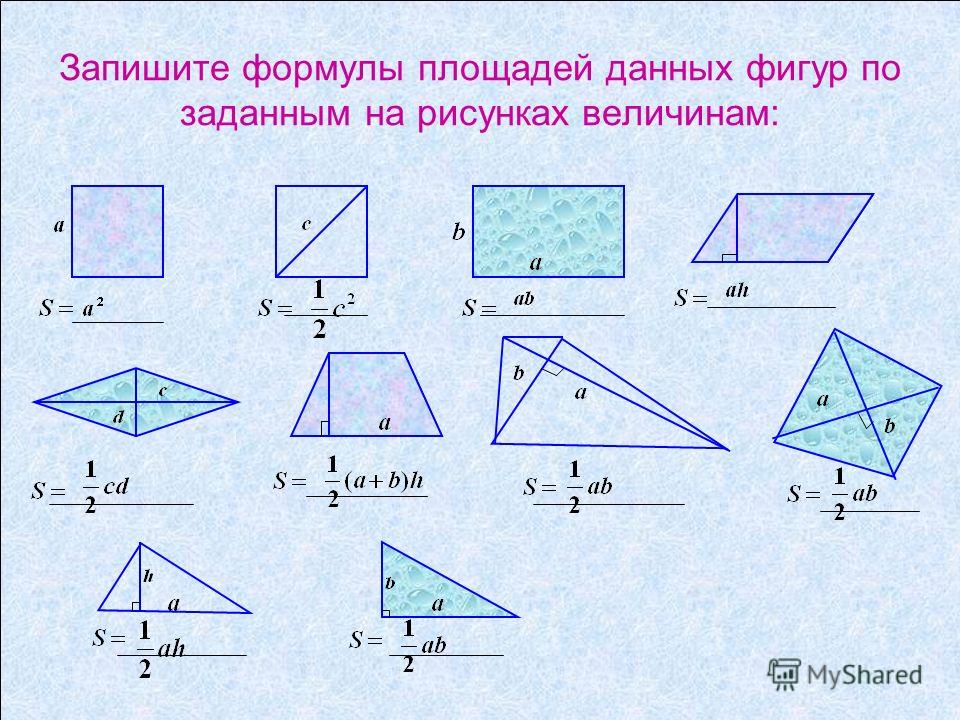

В качестве аксиомы принято утверждение, что площади фигур (многоугольников) – положительные величины.

Определение площади круга дается отдельно как величины, к которой стремится площадь правильного многоугольника, вписанного в окружность данного круга – при том, что число его сторон стремится к бесконечности.

Площади фигур неправильной формы (произвольных фигур) не имеют определения, определяются лишь способы их вычисления.

Вычисление площадей уже в древности было важной практической задачей при определении размеров земельных участков. Правила вычисления площадей за несколько сотен лет до нашей эры были сформулированы греческими учеными и изложены в «Началах» Евклида как теоремы. Интересно, что правила определения площадей простых фигур в них – те же, что и в настоящее время. Площади геометрических фигур, имеющих криволинейный контур, рассчитывались с применением предельного перехода.

Читайте также: отель в Мадриде 2 звезды

Вычисление площадей простых фигур (треугольника, прямоугольника, квадрата), знакомых всем со школьной скамьи, достаточно просто. Необязательно даже запоминать содержащие буквенные обозначения формулы площадей фигур. Достаточно помнить несколько простых правил:

1. Чтобы рассчитать площадь квадрата, нужно длину его стороны умножить саму на себя (или возвести во вторую степень).

2. Площадь прямоугольника вычисляется умножением его длины на ширину. При этом необходимо, чтобы длина и ширина были выражены в одних и тех же единицах измерения.

3. Площадь сложной фигуры вычисляем, разделив ее на несколько простых и сложив полученные площади.

4. Диагональ прямоугольника делит его на два треугольника, чьи площади равны и равняются половине его площади.

5. Площадь треугольника вычисляется как половина произведения его высоты и основания.

6. Площадь круга равняется произведению квадрата радиуса на всем известное число «π».

7. Площадь параллелограмма вычисляем как произведение смежных сторон и синуса лежащего между ними угла.

8. Площадь ромба – ½  результата умножения диагоналей на синус внутреннего угла.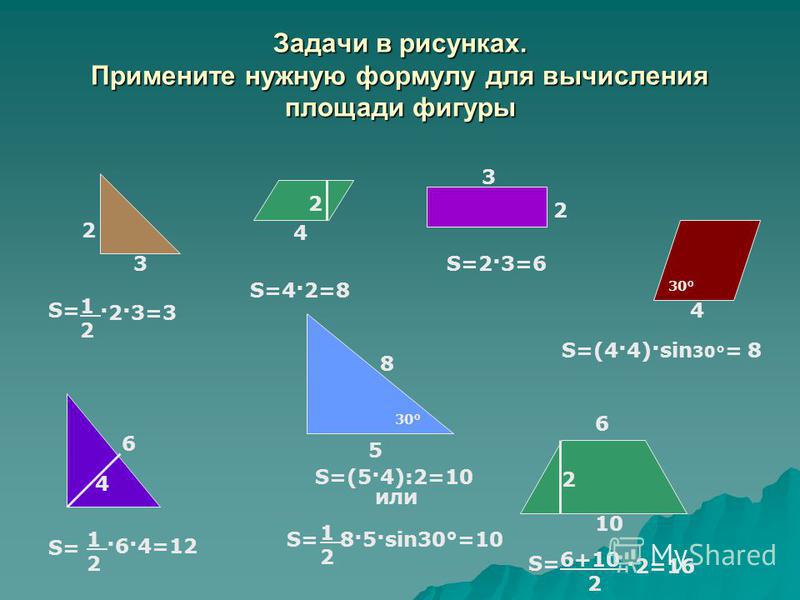

9. Площадь трапеции находим умножением ее высоты на длину средней линии, которая равняется среднему арифметическому оснований. Другой вариант определения площади трапеции – перемножить ее диагонали и синус лежащего между ними угла.

Детям в начальной школе для наглядности часто даются задания: найти площадь нарисованной на бумаге фигуры с помощью палетки или листа прозрачной бумаги, разграфленной на клеточки. Такой лист бумаги накладывается на измеряемую фигуру, считается число полных клеточек (единиц площади), поместившихся в ее контуре, затем число неполных, которое делится пополам.

Как найти площадь геометрических фигур? Как вычислить площадь фигуры

Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины.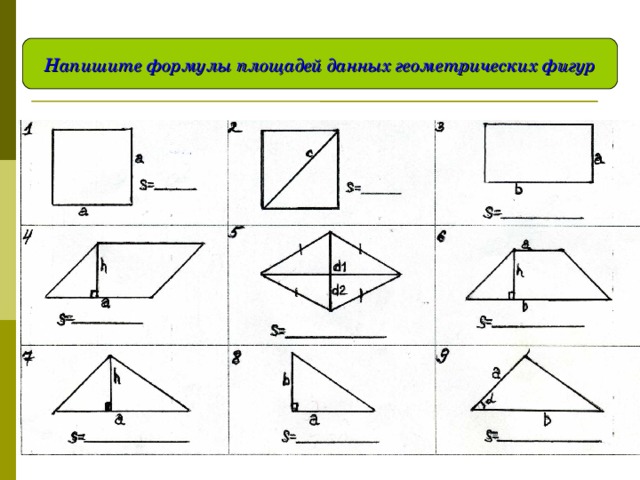 В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.

Геометрия и формулы площадей неразрывно связаны. Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении. Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.

Формулы для нахождения площади любого треугольника представлены несколькими вариантами:

1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:

2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.

На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:

По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.

3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:

Прямоугольник

Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:

Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении.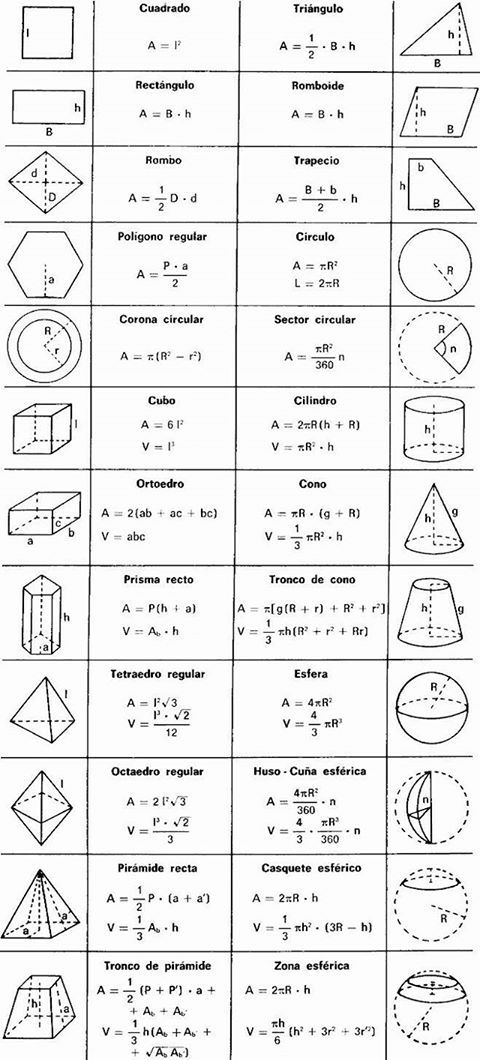

Такая формула площади прямоугольника имеет вид:

Квадрат

Площадь квадрата определяют как вторую степень длины стороны:

Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.

Площадь квадрата можно найти другим способом, например, если использовать диагональ:

Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:

Параллелограмм

Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение. Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.

Формулы площади параллелограмма таковы:

Ромб

Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:

Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:

Трапеция

Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся. Т.к. эту величину содержит выражение для вычисления:

Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.

Цилиндр и параллелепипед

Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра. Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:

Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:

Кольцо

Две окружности с общим центром образуют кольцо. Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы. Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:

Площадь кольца, с использованием длин диаметров, определяют следующим образом:

Многоугольник

Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком. Необходимо сложить количество точек, расположенных внутри ломаной линии с половиной точек, лежащих на ней, и вычесть единицу, т. е. вычисляется это таким образом:

где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.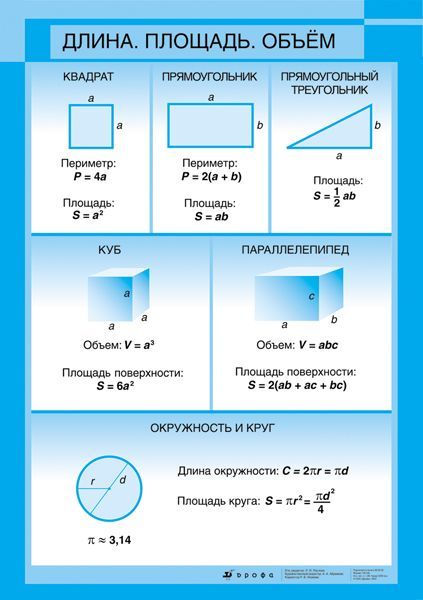

Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.

Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!

Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.

А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.

1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.

Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным .

Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .

Ответ: .

2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.

Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .

Ответ: .

3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .

На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов).

Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.

Все формулы площади плоских фигур

Площадь равнобедренной трапеции

1. Формула площади равнобедренной трапеции через стороны и угол

а — нижнее основание

b — верхнее основание

с — равные боковые стороны

α — угол при нижнем основании

Формула площади равнобедренной трапеции через стороны, (S):

Формула площади равнобедренной трапеции через стороны и угол, (S):

2. Формула площади равнобедренной трапеции через радиус вписанной окружности

R- радиус вписанной окружности

D- диаметр вписанной окружности

O- центр вписанной окружности

H- высота трапеции

α, β — углы трапеции

Формула площади равнобедренной трапеции через радиус вписанной окружности, (S):

СПРАВЕДЛИВО, для вписанной окружности в равнобедренную трапецию:

3. Формула площади равнобедренной трапеции через диагонали и угол между ними

d- диагональ трапеции

α,β- углы между диагоналями

Формула площади равнобедренной трапеции через диагонали и угол между ними, (S):

4.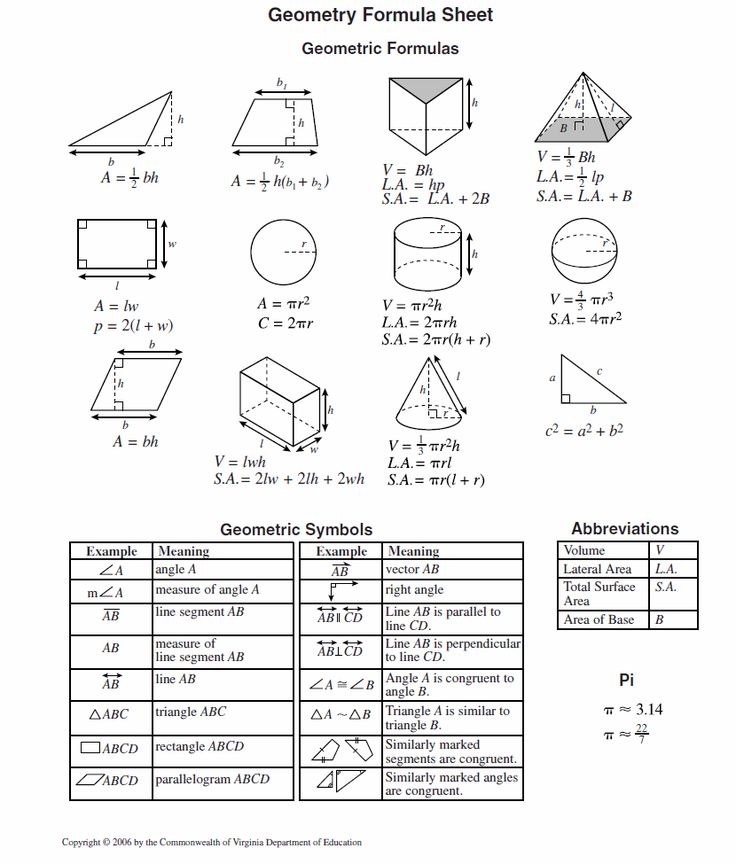 Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании

c- боковая сторона

m- средняя линия трапеции

α, β — углы при основании

Формула площади равнобедренной трапеции через среднюю линию, боковую сторону и угол при основании,

(S):

5. Формула площади равнобедренной трапеции через основания и высоту

a — нижнее основание

b — верхнее основание

h — высота трапеции

Формула площади равнобедренной трапеции через основания и высоту, (S):

Площадь треугольника по стороне и двум углам, формула.

a, b, c- стороны треугольника

α, β, γ- противолежащие углы

Площадь треугольника через сторону и два угла (S):

Формула площади правильного многоугольника

a — сторона многоугольника

n — количество сторон

Площадь правильного многоугольника, (S):

Формула (Герона) площади треугольника через полупериметр (S):

Площадь равностороннего треугольника равна:

Формулы расчета, площади равностороннего треугольника.

a — сторона треугольника

h – высота

Как вычислить площадь равнобедренного треугольника?

b — основание треугольника

a — равные стороны

h – высота

3. Формула площади трапеции через четыре стороны

a — нижнее основание

b — верхнее основание

c , d — боковые стороны

Радиус описанной окружности трапеции по сторонам и диагонали

a — боковые стороны трапеции

c — нижнее основание

b — верхнее основание

d — диагональ

h — высота

Формула радиуса описанной окружности трапеции, (R)

найти радиус описанной окружности равнобедренного треугольника по сторонам

Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.

a, b — стороны треугольника

Радиус описанной окружности равнобедренного треугольника (R):

Радиус вписанной окружности в шестиугольник

a — сторона шестиугольника

Радиус вписанной окружности в шестиугольник, (r):

Радиус вписанной окружности в ромб

r — радиус вписанной окружности

a — сторона ромба

D, d — диагонали

h — высота ромба

Радиус вписанной окружности в равнобочную трапецию

с — нижнее основание

b — верхнее основание

a — боковые стороны

h — высота

Радиус вписанной окружности в прямоугольный треугольник

a, b — катеты треугольника

с — гипотенуза

Радиус вписанной окружности в равнобедренный треугольник

a, b — стороны треугольника

Доказать, что площадь вписанного четырёхугольника равна

\/(р — а)(р — b) (р — с) (р — d),

где р — полупериметр и а, b, с и d — стороны четырёхугольника.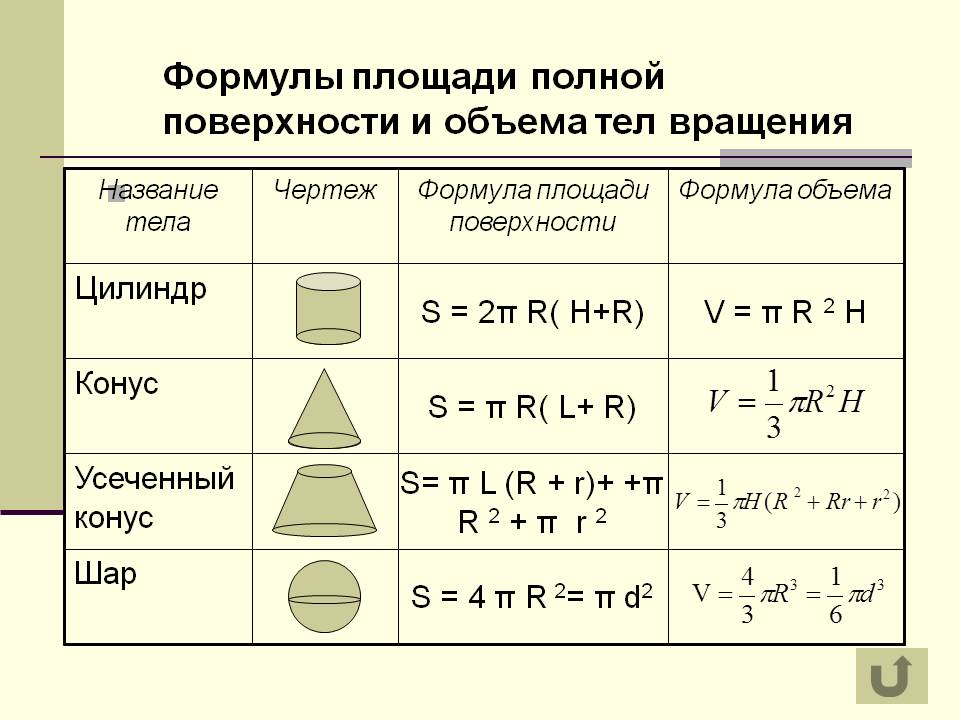

Доказать, что площадь вписанного в круг четырёхугольника равна

1/2 (ab + cb) · sin α , где а, b, с и d — стороны четырёхугольника и α — угол между сторонами а и b.

S = √[ a ƀ c d] sin ½ (α + β). — Читайте подробнее на FB.ru:

Площадь произвольного четырёхугольника (рис. 1.13) можно выразить через его стороны а, b, c и сумму пары противоположных углов:

где р – полупериметр четырёхугольника.

Площадь вписанного в окружность четырёхугольника () (рис. 1.14, а) вычисляется по формуле Брахмагупты

а описанного (рис. 1.14, б) () – по формуле

Если же четырёхугольник вписан и описан одновременно (рис. 1.14, в), то формула становится совсем простой:

Формула Пика

Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S – площадь многоугольника, — число клеток, которые целиком лежат внутри многоугольника, и — число клеток, которые имеют с внутренностью многоугольника хоть одну общую точку.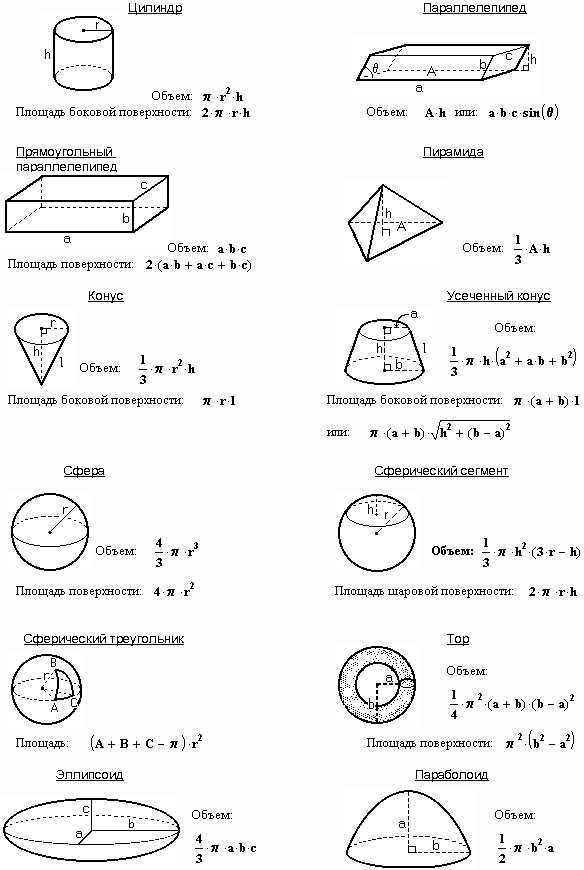

Будем рассматривать ниже только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки. Оказывается, что для таких многоугольников можно указать такую формулу:

где — площадь, r – число узлов, которые лежат строго внутри многоугольника.

Эту формулу называют «формула Пика» — по имени математика, открывшего её в 1899 году.

Что такое площадь?

Площадь – характеристика замкнутой геометрической фигуры (круг, квадрат, треугольник и т.д.), которая показывает ее размер. Площадь измеряется в квадратных сантиметрах, метрах и т.д. Обозначается буквой S (square).

Как найти площадь треугольника?

S = a · h

где a – длина основания, h – высота треугольника, проведенная к основанию.

Причем, основание не обязательно должно находиться снизу. Так тоже сойдет.

Если треугольник тупоугольный , то высота опускается на продолжение основания:

Если треугольник прямоугольный , то основанием и высотой являются его катеты:

2. Другая формула, которая является не менее полезной, но которую почему-то всегда забывают:

S = a · b · sinα

где a и b – две стороны треугольника, sinα – синус угла между этими сторонами.

Главное условие – угол берется между двумя известными сторонами.

3. Формула площади по трем сторонам (формула Герона):

S =

где a , b и с – стороны треугольника, а р – полупериметр. p = (a + b + c )/2.

4. Формула площади треугольника через радиус описанной окружности:

S =

где a , b и с – стороны треугольника, а R – радиус описанной окружности.

5. Формула площади треугольника через радиус вписанной окружности:

S = p · r

где р – полупериметр треугольника, а r – радиус вписанной окружности.

Как найти площадь прямоугольника?

1. Площадь прямоугольника находится довольно-таки просто:

S = a · b

Никаких подвохов.

Как найти площадь квадрата?

1. Так как квадрат является прямоугольником, у которого все стороны равны, то к нему применяется такая же формула:

S = a · a = a 2

2. Также площадь квадрата можно найти через его диагональ:

S = d 2

Как найти площадь параллелограмма?

1. Площадь параллелограмма находится по формуле:

S = a · h

Это связано с тем, что если от него отрезать прямоугольный треугольник справа и приставить его слева, получится прямоугольник:

2. Также площадь параллелограмма можно найти через угол между двумя сторонами:

S = a · b · sinα

Как найти площадь ромба?

Ромб по своей сути является параллелограммом, у которого все стороны равны. Поэтому для него применяются те же формулы площади.

1. Площадь ромба через высоту:

S = a · h

рабочих листов | TPT

by

My Nerdy Teacher by Alina V

100,00 $

19,00 $

⭐⭐⭐ FLASH SALE ⭐⭐⭐Получите Mega Bundle для декодируемых ридеров всего за 1 900 долларов США! Спешите, время истекает! Ваши ученики могут практиковаться в чтении весело и увлекательно, используя эти декодируемые тексты. Наука чтения AlignedLow Требуется подготовка. Просто распечатайте и идите. Эти декодируемые отрывки помогут вашим ученикам практиковать фонетические модели, которым вы их учите. Идеально подходит для центров, домашних заданий, утренней работы и многого другого. Печатные и цифровые (Google Slides™) Идеально подходит для дошкольного детского сада, 1-й класс

Предметы:

Акустика, Чтение, Письмо

Классы:

К — 2-й

Виды:

Занятия, Центры, Печатные формы

CCSS, RF.K.3.K. .K.3c, RF.1.2c, RF.1.2d…

by

My Nerdy Teacher by Alina V

$100.00

$19.00

⭐⭐⭐ ВСЕГО 19 долларов! (СТОИМОСТЬ 100 долл. США) Вы ищете веселые и увлекательные занятия по интервенции при чтении, связанные с наукой о чтении? Получите МЕГА-НАБОР Ultimate Phonics Reading Intervention всего за 19 долл. США! Спешите, время истекает! Ваши студенты станут бегло читать, используя эти забавные действия. Требуется низкая подготовка. Просто распечатайте и приступайте к работе. Эти занятия помогут вашим ученикам практиковать фонетические модели, которые вы преподаете.

CCSS:

RF.K.1, RF.K.1a, RF.K.1b, RF.K.1c, RF.K.1d…

по

Digital Divide and Conquer

Если вы смотрели телевизор или читали журналы, скорее всего, вы видели крошечный дом. Эти маленькие дома повсюду… и теперь мы просим студентов сделать их собственную 3D-версию! «Построить крошечный дом» — это проектное обучение (PBL), в ходе которого ученики передадут проектирование в руки. Учащиеся будут углубляться, чтобы показать, как они понимают, как (и почему) математические понятия, такие как площадь, периметр и геометрия, используются при строительстве дома. Этот проект объединяет несколько элементов, таких как

Предметы:

Математика, Измерение, Специальное образование

Классы:

2-7

Типы:

Занятия, проекты

Также включено в: Пакет проектного обучения! 14 Упражнения PBL

на

Обучаемый учитель

25,00 $

20,00 $

Bundle

All-in-One Reading Passages дают вашим учащимся возможность практиковать фонетику и беглость с этими вопросами и пониманием прочитанного. Лучшая часть? С вашей стороны не требуется никакой подготовки! Теперь включает в себя оригинальный PDF + НОВЫЕ цифровые версии каждого отрывка для чтения по фонетике для дистанционного обучения! Каждый отрывок для чтения дает вашим ученикам возможность практиковать целевой навык фонетики в контексте чтения. Каждый фонический отрывок также развивает беглость речи и понимание. это комплект

Субъекты:

ELA Test Prep, Phonics, чтение

Оценки:

1 -й — 2 -й

Типы:

Английский (Великобритания), книги с управляемым чтением, печатные изделия

на

Обучение с горой

Информационные навыки чтения текста и карточки с заданиями по внимательному чтению для проверки навыков понимания Привлекайте своих читателей интересными отрывками для понимания прочитанного и соответствующими вопросами! Этот ресурс включает в себя 32 карточки с информационными текстовыми заданиями на полстраницы с 4 вопросами на понимание и заданиями на КАЖДОЙ карточке, всего 128 информационных текстовых вопросов! Вовлеките своих учащихся в осмысленную практику внимательного чтения и просмотрите ключевые навыки чтения, связанные с информационным и научно-популярным текстом

Субъекты:

ELA PREP TEST PREP, АНГЛИЙСКОЕ ЯЗЫКИ, информационный текст

Оценки:

3 -е — 5 -е

Типы:

Центры, Занятые карты

CCSS:

RI. 3.1, RI.3.2, RI RI:

RI.3.1, RI.3.2, RI. .3.3, RI.3.4, RI.3.5…

Также включено в: Комплект карточек с заданиями на понимание прочитанного | Цифровые и печатные версии

by

Aimee’s Edventures LLC

10,75 $

5,50 $

У меня разрывалось сердце, когда я смотрел, как мои ученики бродят по комнате, пытаясь не заплакать, когда я сказал: «Пожалуйста, найдите себе партнера». Вот я и создал эти открытки! Теперь их любят тысячи учителей, которые преследуют одну и ту же цель — включить всех учащихся в свой класс. Эти партнерские карточки позволяют быстро и легко организовать дифференцированную работу в малых группах и идеально подходят для детей с любым уровнем способностей. Самое приятное то, что им не нужно угадывать, кто их партнер, это прямо на карте (whi

Тема:

Вернуться в школу, сообщество классных комнат, управление классными комнатами

Оценки:

Не Оценка. Education

Если вы ищете индивидуальную книгу расписаний, наглядные расписания или сначала доску, то в этом ресурсе поддержки позитивного поведения есть все! Обратите внимание: все редактируемые файлы совместимы с Microsoft PowerPoint. Некоторые страницы теперь можно редактировать с помощью Google Slides. В эту загрузку включены: — Варианты флипбука с 6 и 2 вкладками — Более 200 визуальных значков расписания (они не редактируются) — Сначала доска (отдельно от флипбука) — Сначала затем доска (отдельно от флипбука) — доски жетонов (wi

Предметы:

Снова в школу, Специальное образование, Логопедия

Классы:

PreK — 2nd

Типы:

Расписание занятий

настоящие картинки)

на

Lucky Little Learners

Этот набор страниц для рукописного ввода дает вашим учащимся возможность попрактиковаться в письме в увлекательной форме. Они будут развивать выносливость при письме, повторять построение букв и цифр и практиковаться в словах, изучая новые шутки и забавные факты! и почерк, который не является «детским»? Глупые шутки и забавные факты привлекут ваших учеников, пока они

Субъекты:

Сбалансированная грамотность, почерк, написание

. Bundle

Этот комплект содержит ОГРОМНЫЕ 263 математических листа для первого класса! Рабочие листы охватывают сложение и вычитание, числа и разрядность, 2D и 3D фигуры, данные и графики, дроби и разбиение на части и время. Эти веселые рабочие листы отлично подходят для использования в течение всего года, они идеально подходят для занятий в классе, математических станций, быстрых финишеров, домашних заданий и повторения. Этот комплект состоит из следующих пакетов: Рабочие листы для сложения и вычитания для первого классаРабочие листы для первого класса 2D и 3D

Предметы:

Основные операции, математика, числа

Классы:

Типы:

Печатные издания, рабочие тетради, рабочие листы

по

Патрисия Пэт Написание предложения — это трудность для ваших учеников или создание предложения

3 9 Если это так, вам понравится, как эти рабочие листы для построения предложений помогут вам научить писать полные предложения. ✏️ Многочисленные изображения в рабочем листе помогут вашим ученикам ПОНЯТЬ и ЗАПОМНИТЬ правильную структуру предложения. ✏️ Это ресурс без подготовки, который понравится даже неохотным писателям, плюс вы сэкономите много времени с помощью ТРЕХ дифференциаций и строительных лесов, сделанных за вас. ✏️ Эти практические рабочие листы будут

Предметы:

EFL — ESL — ELD, английский язык, специальное образование

Классы:

K — 2nd

Типы:

Центры, Домашнее обучение, Домашнее задание

9.1004 CCSS3: SL.1.6, L.K.1f, L.1.1c, L.1.2b

Также включено в: Центр написания предложений | Полные предложения | Структура предложения | Маленькие группы

на

Simply Kinder

972,00 $

25,00 $

Идеальный набор для детского сада: учебники, игры, раскраска по коду и многое другое для более чем 200 высокочастотных слов! ЛУЧШИЙ ПРОДАВЕЦ на TpT с более чем 7000 отзывов учителей! Оцените эту невероятную стоимость всего, что вам нужно для практики словесного зрения! Ваша практика словесного зрения стала намного лучше благодаря этому огромному файлу печатных форм, занятий, центров и многого другого. Каждое включенное прицельное слово имеет отдельный файл с 67 страницами действий! Идеально подходит для детского сада, первого класса

Предметы:

Английский язык, чтение

Классы:

PreK — 1st

Типы:

Занятия, распечатки, рабочие листы

CCSS, RF.3.K.9002 .K.3c

на

Чтение Запись Средний

В этом увлекательном задании учащиеся делают выводы и выводы, анализируя различные текстовые сообщения. Студенты должны привести доказательства для каждого ответа. Цифровые и печатные варианты: этот продукт теперь включает опцию Google Slides, а также печатный PDF-файл. Этот продукт также включает страницу с двумя пустыми телефонными разговорами. Студентам нравится макет текстового сообщения! Это отличный способ для старших школьников попрактиковаться в выводах и цитировании доказательств в форме для 9.0003

Субъекты:

Чтение

Оценки:

5 -й — 7 -й

Типы:

печатные изготовления, рабочие листы

CCSS:

RL. 5.1, RL.6.1, RL.7.1

Также включены в: rl. Пакет «Анализ» Создание выводов и цитирование доказательств

by

ThatKinderMama

10,00 $

Это четырехнедельный блок иллюстраций, который поможет писателям детского сада/первоклассника стать уверенными в своих навыках рисования и раскрашивания. Учащиеся начальных классов научатся рисовать фигуры и людей с разными выражениями лица, прическами и оттенками кожи. Это иллюстративное исследование настраивает учащихся детского сада на успех до конца года во время писательского семинара. Учащиеся могут обращаться к своей тетради для направленного рисования в течение года, если они забывают, как рисовать объект, который они уже выучили

Предметы:

Искусство и музыка, Снова в школу, Письмо

Классы:

PreK — 1st

Типы:

Уроки, Печатные формы

Также включены в: LEGROWND Writing Units | Мастерская писателей

by

Deanna Jump

Предложите своим ученикам веселые и увлекательные занятия по построению предложений! Этот центр письма для построения предложений — увлекательное занятие, которое учит ваших учеников предложениям и их частям. Учащиеся будут использовать части предложений с цветовой кодировкой для построения и создания предложений. Эти карточки можно использовать снова и снова! Студенты могут использовать различные комбинации для создания тысяч простых предложений. Этот центр печати и письма является ИДЕАЛЬНЫМ дополнением к вашим центрам грамотности.0003

Субъекты:

Сбалансированная грамотность, английский языковой искусство

Оценки:

K — 1st

Типы:

Центры

до

Rachel Lynette

$ 14.98

$ 9.98

3

$ 14.98

$ 9.98

40004. Независимо от того, нужна ли вам печатная или цифровая версия, эти готовые к использованию страницы (и слайды) — эффективный способ помочь вашим учащимся узнать все о написании абзаца. & 20 описательной части)Страницы мозгового штурмаСтраницы организации и планированияСтраницы первых черновиковСтраницы редактирования и редактированияСтраницы финальных черновиковСтраницы публикацииЦИФРОВЫЕ:Google SlidesEasel ActivityВАРИАНТЫ РАЗЛИЧИЯ:Цифровой или печатныйПараграф

Предметы:

Письмо, письменные эссоды, письменное экспозиция

Оценки:

3-е-5-е

Типы:

Независимый рабочий пакет, рабочие листы

CCS:

W. 3.1, W.3.2, W. .3.3, W.3.4, W.3.5…

Также включено в: Написание абзаца недели — Пакет дифференциации для 2–3 классов

by

Mrs Ds Corner

15,00 $

BEST 10,030 900ER 10,030 900ER ON TPT * Функциональная, дифференцированная работа, которая является идеальным дополнением к вашей утренней рутине и расписанию. Эта адаптированная папка поможет вашим ученикам правильно начать свой выходной день, а после освоения может стать набором навыков, которые они успешно и самостоятельно осваивают. Пожалуйста, просмотрите видео-превью, чтобы увидеть некоторые из рабочих страниц, включенных в этот ресурс. Посмотрите видео-превью здесь. Посмотрите его в действии здесь и здесь. Что включено? • 8 редактируемых обложек (добавьте студенческие

Предметы:

Английский язык, математика, специальное образование

Классы:

PreK — 4th

Типы:

Занятия, интерактивные тетради, печатные формы

Испанский )

by

Веснушки первоклассника

Обновление 10/2022: теперь включены фотографии реального рта. Обновление 07/2022: теперь включена цветовая схема Boho. . Этот классный ресурс стоит места на стене! Здесь так много опций, что вы можете повесить то, что нужно вашей конкретной программе или последовательности. Варианты варьируются от базовых навыков фонетики в детском саду до продвинутых навыков, которые можно получить в третьем классе. Они также отлично подходят для классных комнат, где учащиеся нуждаются в поддержке.0003

Предметы:

Акустика, Чтение, Письмо

Классы:

К — 3

Виды:

Доска объявлений Идеи

СССС:

.1К3.РФ. .3.3

by

Lucky Little Learners

34,00 $

23,00 $

Bundle

Phonics Reading Passes, или Phonics Mats, — это идеальный инструмент для обучения студентов навыкам чтения, распечатки и работы с фоном, который поможет учащимся научиться читать текст без предварительной подготовки, распечатать и начать ! Учащиеся практикуют изолированные фонетические навыки, декодирование, беглость речи и понимание в одном ресурсе. *** НОВОЕ ОБНОВЛЕНИЕ *** Этот ресурс обновлен новой версией 2022 года! В новых ковриках для фонетики есть декодируемые отрывки, вопросы на понимание, практика написания слов и страница для разминки для каждого навыка. Обязательно загрузите превью

Предметы:

Акустика, чтение, письмо

Классы:

Типы:

Печатные формы, рабочие листы

CCSS:

RF.2.3, RF.2.3c, RF.2.3b, RF.2.2.2 .2.3d…

по

Мой друг-преподаватель

Этот пакет заполнен листами с заданиями на сложение и вычитание, которые помогут вашим ученикам освоить основные факты. Он включает в себя 36 увлекательных рабочих листов, которые охватывают факты сложения и вычитания до 10. Учащиеся будут практиковаться в сложении/вычитании изображений, использовании числовых линий, поиске недостающих сложений, составлении десяти и многом другом! Он идеально подходит для общеклассных занятий, математических станций, быстрых заданий и повторения. Сэкономьте 30% с комплектом!0003

Предметы:

Базовые операции, математика, текстовые задачи

Классы:

PreK — 1st

Типы:

Центры, печатные формы, рабочие листы

, Фигуры

на

Путь 2 Успех

$14.00

Используйте эти уроки, чтобы развить у детей навыки самоконтроля! Действия сосредоточены на понимании самоконтроля, импульсивного контроля, остановке и обдумывании, чтобы принять решение, ожидании своей очереди, соблюдении правил и указаний, сохранении мотивации, выполнении нашей работы наилучшим образом, управлении эмоциями, использовании стратегий преодоления и практике самоконтроля для укрепления. навыки со временем. Также рассматриваются другие навыки, влияющие на самоконтроль, включая планирование, управление временем и настойчивость. Цифровая версия обновлена ​​до 9.0003

Объекты:

Школьное консультирование, социальное эмоциональное обучение, специальное образование

Оценки:

4 -й — 8 -е

Типы:

Урок, печатные изготовления

на

My Teaching Pal

$ 12. 503

$ 8,00

.

Предложите своим ученикам попрактиковаться во всем, что связано с алфавитом, с помощью этого ОГРОМНОГО комплекта рабочих листов по алфавиту. Студенты будут работать над идентификацией букв, начальными звуками, формированием букв, различением строчных и прописных букв и многим другим. В этот пакет включены 4 различных типа рабочих листов, которые охватывают каждую букву алфавита. Всего включено 104 рабочих листа. Что включено: ♥ Рабочие листы по алфавиту — Работа с буквами ♥ Рабочие листы для начальных звуков — Раскрась по моему звуку ♥ Алфавит M

Предметы:

Английский язык искусства, фонетика, написание

Оценки:

Prek — K

Типы:

, печатные изготовления, рабочие листы

9000 3 9000 3

9000 3

9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3 9000 3

40004

9 интересный способ помочь вашим ученикам развить распознавание чисел! Эти печатные формы для практики с числами — интересный способ помочь вашим маленьким ученикам попрактиковаться в формировании чисел, чувстве чисел и распознавании чисел. Помогите своим учащимся дошкольного, детского сада и первого класса с помощью веселых и увлекательных способов попрактиковаться в развитии чувства числа, определяя, записывая и считая числа до 50. ⭐️СОЕДИНЯЙТЕ И СОХРАНЯЙТЕ⭐️Возьмите эти не требующие предварительной подготовки печатные формы ПЛЮС еще больше заданий на чувство числа с числовыми центрами и числом

Субъекты:

Математика, Числа

Оценки:

Prek — 1 -й

Типы:

Центры, печатные изделия, рабочие листы

также включены в: детские математики. Преподаватель Алины В.

Вы ищете веселые и увлекательные рабочие листы по алфавиту от А до Я для своих учеников? Этот пакет идеально подходит для тех, кто рано заканчивает работу, утренней работы, выполнения домашних заданий и многого другого. Каждый рабочий лист включает 5 различных заданий, которые ваши ученики могут использовать, чтобы узнать все о прописных и строчных буквах. — — — — — — — — — > Проверьте наш БЕСКОНЕЧНЫЙ НАБОР АЛФАВИТА и получите этот ресурс с огромной скидкой!! <- - - - - - - - -ВКЛЮЧЕННЫЕ МЕРОПРИЯТИЯ: • Произнеси по буквам! Напишите буквы в коробках • Раскрасьте! Цвет

Предметы:

Акустика, Изобразительное искусство

Классы:

PreK — K

Виды:

Задания, Печатные формы, Рабочие листы

CCSS,

. К.К.а, РФ. K.1b, RF.K.1c, RF.K.1d…

Также включено в: Рабочий лист «Начало звуков». Вы ищете способ, чтобы ваши ученики были вовлечены и готовы к занятиям, как только они входят в дверь? Мои ежедневные отрывки для понимания прочитанного могут помочь вам сделать это! Эти печатные и цифровые звонари специально разработаны для улучшения навыков чтения учащихся средних школ. Этот ресурс включает в себя короткие и увлекательные отрывки для ежедневного чтения, которые обеспечивают содержательную практику с контекстными подсказками, основной идеей, выводами, определением темы и многим другим! Эти отрывки отлично подходят для: H

Тема:

Английский язык, информационный текст, чтение

Оценки:

6 -й — 8th

Типы:

Рабочие листы

CCSS:

RL.6.1, RL.6.2, RL.6.4, RL. 7.1, RL.7.2…

Список различных типов геометрических фигур с изображениями

Мы сталкиваемся с различными типами объектов и материалов, которые в своей основе определяются определенными геометрическими аспектами, которые делают их по-своему уникальными. Эта статья ScienceStruck предоставит вам подробную информацию о различных видах и названиях геометрических фигур, а также их значения и изображения.

Краткий факт

Область геометрии и связанных с ней исследований форм и фигур, как сообщается, впервые возникла в цивилизации реки Инд и вавилонской цивилизации около 3000 г. до н.э. Некоторые сообщения предполагают, что у египтян была своя версия теоремы Пифагора еще до того, как Пифагор ее сформулировал.

Внешний вид или форма объекта или тела, которые остаются устойчивыми или постоянными при определенных нормальных условиях, называется геометрической формой этого объекта. Проще говоря, геометрические фигуры характеризуются как внешние ориентации рассматриваемых объектов. Поскольку параметры различаются, различаются и типы форм. Если формы двух объектов одинаковы или похожи, говорят, что они конгруэнтны друг другу. Можно сказать, что любое известное тело или материалистическая сущность во всей вселенной присутствует в форме геометрической формы.

В основном существует два типа геометрических фигур: двумерные (2D) и трехмерные (3D). Первый можно рисовать относительно осей X и Y, тогда как последний также включает ось Z. 2D-формы и фигуры в основном состоят из точек и соединительных линий, образующих форму. Они могут быть выпуклыми (обычный вид) или вогнутыми (неправильный вид). Во многих многоугольных 2D-фигурах выпуклые фигуры имеют углы менее 180 градусов, тогда как вогнутые формы имеют по крайней мере один угол больше 180 градусов. Трехмерные фигуры более сложны и состоят в основном из вершин, ребер, граней и т. д.

Следующие разделы помогут вам понять значение основных геометрических фигур вместе с их изображениями. Обратите внимание, что все упомянутые углы являются внутренними.

Различные типы геометрических фигур

Двухмерные (2D) фигуры

Треугольники

Это тип многоугольника, который состоит из трех сторон с тремя вершинами. Сумма углов треугольника равна 180 градусам в любом виде. Более подробную информацию см. в разделе ниже.

Равнобедренный треугольник

Две стороны имеют одинаковую длину, и два угла также равны. Линия симметрии присутствует.

Разносторонний треугольник

Длина всех сторон неодинакова, и все три угла имеют разные значения.

Равносторонний треугольник

Все три стороны и углы равны. Линия симметрии присутствует.

Прямоугольный треугольник

Один из углов равен 90 градусов. Линия симметрии может как присутствовать, так и отсутствовать.

Тупоугольный треугольник

Один из углов больше 90 градусов. Линия симметрии может как присутствовать, так и отсутствовать.

Остроугольный треугольник

Все углы острые (менее 90 градусов). Линия симметрии может как присутствовать, так и отсутствовать.

Четырехугольники

Эти многоугольники состоят из четырех сторон, а сумма углов равна 360 градусов в любом виде. Более подробную информацию см. в разделе ниже.

Прямоугольник

У них есть два набора противоположных сторон, которые равны, и все четыре угла равны 90 градусов. Присутствуют две линии симметрии.

Квадрат

Все четыре угла равны 90 градусов вместе с четырьмя равными сторонами. Этот многоугольник имеет четыре линии симметрии.

Параллелограмм

Они состоят из двух наборов противоположных прямых, равных и параллельных. Противоположные углы также равны относительно любой величины. Линия симметрии может присутствовать.

Ромб

Все четыре стороны равны и параллельны, но равны только противоположные углы. Присутствуют две линии симметрии. Он тесно связан с квадратом и параллелограммом.

Трапеция

Один набор противоположных прямых параллельен, а другой набор непараллелен. Линия симметрии может присутствовать. В Великобритании он называется трапецией.

Трапеция

Все четыре стороны неравны и непараллельны, линия симметрии отсутствует. В Великобритании это называется трапецией.

Воздушный змей

Два набора смежных сторон равны, и два противоположных угла также имеют равные значения. Линия симметрии присутствует.

Неправильный четырехугольник

Имеет четыре неравные стороны и вогнутый вид, т. е. по крайней мере один угол больше 180 градусов.

Многоугольники

Фигуры, состоящие из трех и более сторон, называются многоугольниками. Углы таких геометрических фигур могут быть более 360 градусов. Ниже приведены как правильные, так и неправильные типы многоугольников.

Примечание : Хотя типы треугольников и четырехугольников включены в многоугольники, как они были описаны выше, они не перечислены в следующем разделе.

Пятиугольник

Состоит из пяти равных сторон, а сумма углов равна 540 градусов. Присутствуют пять линий симметрии.

Шестиугольник

Состоит из шести равных сторон, а сумма углов равна 720 градусов. Присутствуют шесть линий симметрии.

Семиугольник

Состоит из семи равных сторон, а сумма углов равна 900 градусов. Присутствуют семь линий симметрии.

Октагон

Состоит из восьми равных сторон, а сумма углов равна 1080 градусов. Присутствуют восемь линий симметрии.

Нонагон

Состоит из девяти равных сторон, а сумма углов равна 1260 градусов. Присутствуют девять линий симметрии.

Десятиугольник

Состоит из десяти равных сторон, а сумма углов равна 1440 градусов. Присутствуют десять линий симметрии.

Додекагон

Состоит из двенадцати равных сторон, а сумма углов равна 1800 градусов. Присутствуют двенадцать линий симметрии.

Неправильный многоугольник

Он может иметь четыре или более четырех неравных сторон, а внешний вид может быть вогнутым, т. е. по крайней мере один угол больше 180 градусов.

Изогнутые фигуры

Фигуры, состоящие из изогнутых линий и связанных точек, называются изогнутыми формами. Основные типы, включенные в эту категорию, описаны ниже:

Окружность

Состоящая только из одной изогнутой линии, эта форма не имеет какой-либо другой точки соединения или вершины.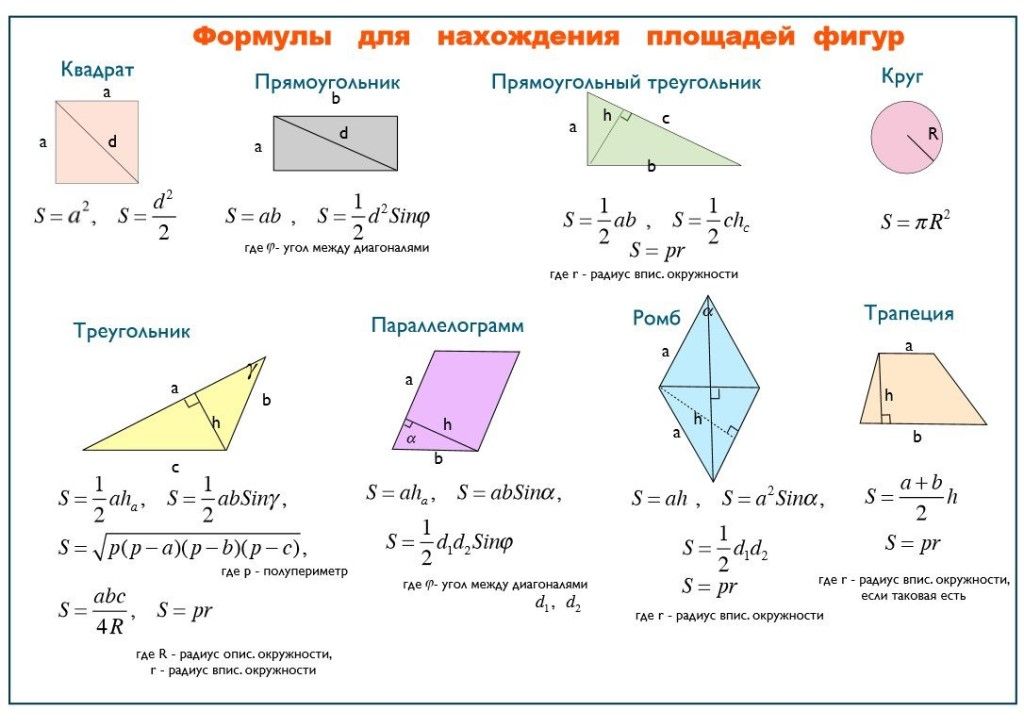 Расстояние от эпицентра до окружности одинаково во всех секторах.

Овал/эллипс

Похож на круг, но расстояние от центра до окружности постоянно меняется. Таким образом, эта форма имеет две оси: большую и малую, а также вытянутую форму.

Линза

Эта фигура похожа на эллипс, но состоит из двух отчетливых изогнутых линий, которые сходятся на противоположных концах. В этом случае на их стыке присутствуют две точки.

Полумесяц

Эта форма характеризуется наличием двух изогнутых линий: одна выпуклая, а другая вогнутая. Они сходятся так же, как и у линзы, образуя своеобразную фигуру.

Арки

Эти фигуры состоят из изогнутой линии, пересекающейся с прямой в двух соседних точках. Первая линия может быть полностью изогнутой или может иметь форму двух параллельных линий, прежде чем соединиться с прямой линией.

Кольцо

Эта фигура характеризуется наличием двух концентрических круглых структур, каждая из которых отличается по размеру.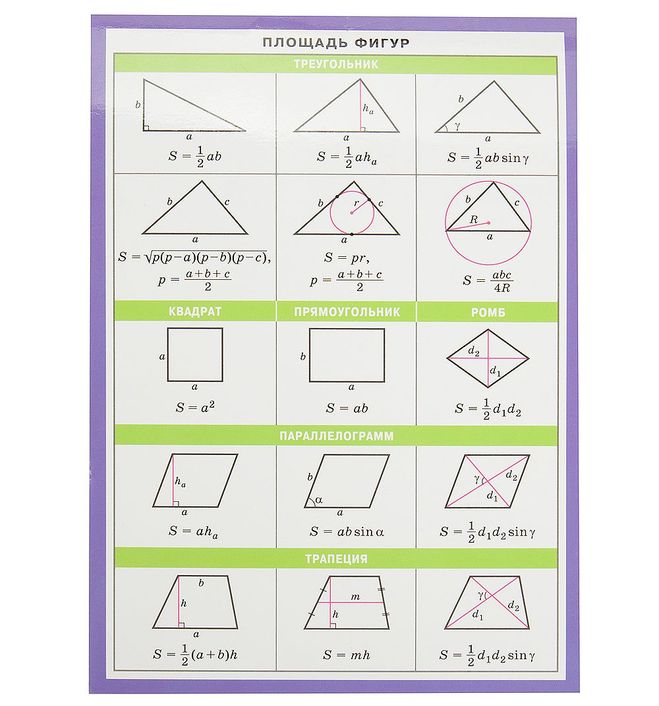 В большинстве случаев внутренняя часть формы не закрыта. Эту фигуру также называют кольцевой структурой.

Сегмент окружности

В основном определяется как часть окружности, которая может состоять из части окружности вместе с хордой. Форма может быть полукругом или может быть фигурой с минимальной частью окружности. Оставшуюся часть также можно назвать сегментом.

Круговой сектор

В основном определяется как треугольная часть, которая отмечена частью окружности окружности и двумя прямыми линиями. Последние встречаются в общей точке, чаще всего в центре круга. Оставшуюся половину круга тоже можно назвать сектором.

Фигуры, описанные выше, являются основными, и помимо них существует множество других фигур в категории 2D-геометрии. Пройдя через эти формы, давайте взглянем на различные виды геометрических фигур, которые относятся к категории 3D.

Трехмерные (3D) фигуры

Куб/гексаэдр

Эта фигура имеет 12 ребер, 8 вершин и 6 граней. Все стороны равны по длине, а грани имеют квадратную форму.

Прямоугольная призма/кубовидная форма

Обладает теми же характеристиками, что и куб, в отношении количества сторон, граней и вершин, за исключением того, что грани имеют прямоугольную форму.

Цилиндр

Эта фигура не имеет вершин, но состоит из двух плоских граней (только в случае замкнутого цилиндра) и одной изогнутой грани. Два ребра также присутствуют.

Сфера

Эта геометрическая фигура не имеет ни ребер, ни вершин, и присутствует только одна изогнутая грань. Это наиболее равномерно изогнутая форма, включенная в категорию 3D.

Треугольная призма

Состоит из шести вершин, девяти ребер и пяти граней. Лица на обоих концах имеют треугольную форму, тогда как все остальные имеют прямоугольную форму.

Конус

Наряду с одной вершиной и одним ребром конусы имеют одну изогнутую грань и одну дополнительную плоскую грань (в закрытых конусах). Угол вершины может варьироваться от острого до тупого.

Шестиугольная призма

Эта фигура, состоящая из двенадцати вершин, восемнадцати ребер и восьми граней, имеет два шестиугольника на противоположных концах. Остальные грани имеют прямоугольную или квадратную форму.

Пятиугольная призма

Эта фигура, состоящая из десяти вершин, пятнадцати ребер и семи граней, имеет два пятиугольника на противоположных концах. Остальные грани имеют прямоугольную или квадратную форму.

Квадратная пирамида

В этой форме основание состоит из квадрата, а остальные грани — треугольники. Всего у него 5 вершин, 8 ребер и 5 граней.

Треугольная пирамида

В этой форме основание и все грани — треугольники. Всего у него 4 вершины, 6 ребер и 4 грани. Базальный треугольник имеет другой размер по сравнению с гранями.

Шестиугольная пирамида

Эта фигура состоит в основном из 7 вершин, 12 ребер и 7 граней. Его основание шестиугольной формы, а грани треугольные.

Параллелепипед

На этой фигуре все грани и основание имеют форму параллелограммов. Размеры граней могут отличаться, а могут быть одинаковыми.

Тетраэдр

Он похож на треугольную пирамиду, за исключением того, что все грани и основание имеют одинаковый размер.

Октаэдр

Эта фигура состоит из восьми треугольников, образующих шесть вершин, восемь граней и двенадцать ребер. Треугольники могут быть как равносторонними, так и равнобедренными.

Додекаэдр

Они состоят из двенадцати пятиугольных граней, двадцати вершин и 30 ребер. Грани представляют собой пятиугольники одинакового размера.

Икосаэдр

Они характеризуются 30 ребрами, 20 гранями и 12 вершинами. Лица состоят из равносторонних треугольников.

Ромбический додекаэдр

Этот тип фигуры состоит из 12 ромбовидных граней, 14 вершин и 24 ребер.

Усеченный конус

Это конусообразная структура, но вместо вершины на одном конце присутствует круг.

Всестороннее знание геометрических форм и фигур очень важно, особенно если есть склонность к этой области математики.