Таблица деления (математика для детей, 2, 3 класс)
На 1
1 ÷ 1 = 1
2 ÷ 1 = 2
3 ÷ 1 = 3
4 ÷ 1 = 4
5 ÷ 1 = 5
6 ÷ 1 = 6
7 ÷ 1 = 7
8 ÷ 1 = 8
9 ÷ 1 = 9
10 ÷ 1 = 10
На 2
2 ÷ 2 = 1
4 ÷ 2 = 2
6 ÷ 2 = 3
8 ÷ 2 = 4
10 ÷ 2 = 5
12 ÷ 2 = 6
14 ÷ 2 = 7
16 ÷ 2 = 8
18 ÷ 2 = 9
20 ÷ 2 = 10
На 3
3 ÷ 3 = 1
6 ÷ 3 = 2
9 ÷ 3 = 3
12 ÷ 3 = 4
15 ÷ 3 = 5
18 ÷ 3 = 6
21 ÷ 3 = 7
24 ÷ 3 = 8
27 ÷ 3 = 9
30 ÷ 3 = 10
На 4
4 ÷ 4 = 1
8 ÷ 4 = 2
12 ÷ 4 = 3
16 ÷ 4 = 4
20 ÷ 4 = 5
24 ÷ 4 = 6
28 ÷ 4 = 7
32 ÷ 4 = 8
36 ÷ 4 = 9
40 ÷ 4 = 10
На 5
5 ÷ 5 = 1
10 ÷ 5 = 2
15 ÷ 5 = 3
20 ÷ 5 = 4
25 ÷ 5 = 5
30 ÷ 5 = 6
35 ÷ 5 = 7
40 ÷ 5 = 8
45 ÷ 5 = 9
50 ÷ 5 = 10
На 6
6 ÷ 6 = 1
12 ÷ 6 = 2
18 ÷ 6 = 3
24 ÷ 6 = 4
30 ÷ 6 = 5
36 ÷ 6 = 6
42 ÷ 6 = 7
48 ÷ 6 = 8
54 ÷ 6 = 9
60 ÷ 6 = 10
На 7
7 ÷ 7 = 1
14 ÷ 7 = 2
21 ÷ 7 = 3
28 ÷ 7 = 4
35 ÷ 7 = 5
42 ÷ 7 = 6
49 ÷ 7 = 7
56 ÷ 7 = 8
63 ÷ 7 = 9
70 ÷ 7 = 10
На 8
8 ÷ 8 = 1
16 ÷ 8 = 2
24 ÷ 8 = 3
32 ÷ 8 = 4
40 ÷ 8 = 5
48 ÷ 8 = 6
56 ÷ 8 = 7
64 ÷ 8 = 8
72 ÷ 8 = 9
80 ÷ 8 = 10
На 9
9 ÷ 9 = 1
18 ÷ 9 = 2
27 ÷ 9 = 3
36 ÷ 9 = 4
45 ÷ 9 = 5
54 ÷ 9 = 6
63 ÷ 9 = 7
72 ÷ 9 = 8
81 ÷ 9 = 9
90 ÷ 9 = 10
На 10
10 ÷ 10 = 1
20 ÷ 10 = 2
30 ÷ 10 = 3
40 ÷ 10 = 4
50 ÷ 10 = 5
60 ÷ 10 = 6
70 ÷ 10 = 7
80 ÷ 10 = 8
90 ÷ 10 = 9
100 ÷ 10 = 10
(на 0 делить нельзя)
Учить таблицу деления — игра
Математическим действием, которое противоположно умножению, называется деление.
Деление обозначается дробной чертой или знаком «:». Число, которое делится, называется «делимым». Делимое всегда находится в числителе дроби – над дробной чертой. Число, на которое делят, называется «делителем». Делитель всегда находится в знаменателе дроби – под дробной чертой. Результат деления называется «частным». Частное всегда положительно, если делятся положительные числа. Если одно из двух чисел, делимое или делитель, отрицательно, результат получается отрицательным – плюс на минус дает минус, минус на плюс дает минус. При делении отрицательного числа на отрицательное получается положительное число – минус на минус дает плюс. Из результатов деления получается таблица деления. Её можно представить правильными или десятичными дробями.
Таблица деления в виде картинки
Чтобы распечатать, скопируйте картинку в любой редактор. Обычно таблицу деления дети проходят на математике в третьем классе.
Открыть в отдельном окне в полном размере
Деление онлайн
/Посмотрите также видео о делении в столбик.
Таблица деления для этого может пригодиться.
Всё для учебы » Математика в школе » Таблица деления (математика для детей, 2, 3 класс)
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/tablica-deleniya
ДЕЛЕНИЕ НА 8: НАЦЕЛО И С ОСТАТКОМ
Примеры.
Открыть в полном размере
‹
›
Благодарен вашему журналу за публикацию моего материала о признаке делимости целых чисел на 7 (см. «Наука и жизнь» № 10, 1997 г.). Рискну предложить еще один новый признак делимости, но уже на 8.
Я перелистал много книг по занимательной математике, но такого признака не нашел нигде.
Общепринятый
признак делимости на 8 выглядит так:
число делится на 8 в том и только в
том случае, если его последние три
цифры образуют число, делящееся на
8.
Этот способ деления основан на том, что все числа, кратные 1000, делятся на 8 без остатка.
Значит, определение признака делимости на 8 любых многозначных целых чисел сводится в итоге к определению признака делимости на 8 трехзначных чисел.
Трехзначные числа и будем рассматривать.
Б. А. Кордемский сводит делимость уже трехзначных чисел к делимости двузначных (образованных цифрами сотен и десятков): «На 8 делится всякое трехзначное число, у которого двузначное число, образованное цифрами сотен и десятков, сложенное с половиной числа единиц, делится на 4».
Он приводит пример с числом 592. Применяя к нему признак делимости, получаем:
59 + 1 = 60,
где 1 — это 2:2, половина числа единиц.
Число 60 делится на 4, значит, число 592 делится на 8 без остатка.
При данном методе
определения остатка от деления
надо учитывать, что трехзначные
числа, оканчивающиеся нечетной
цифрой (1, 3, 5, 7, 9), надо сначала
«округлить» в разряде единиц
до ближайшей большей или меньшей
четной цифры и в конечном
результате опять же учесть эту
единицу, то есть прибавить ее или
отнять.
Второе: в некоторых случаях сумма двузначного числа, образованного цифрами сотен и десятков, и половины единиц будет также трехзначным числом, что опять же не совсем удобно. Это будет происходить с рядом чисел в промежутке от 968 до 999.
Однако всех этих неудобств — прибавления (вычитания) 1 и оперирования трехзначными числами — можно избежать.
Вспомним, что четное число сотен — 2, 4, 6, 8 (200, 400, 600, 800) делится на 8 без остатка. Следовательно, у таких, к примеру, чисел, как 059, 237, 461, 632, 844, определить остаток от деления на 8 можно сразу по двузначному числу, составленному из десятков и единиц, то есть по числам 59, 37, 61, 32, 44. Достаточно в уме разделить эти двузначные числа на 8.
Если цифры сотен в
трехзначных исходных числах
нечетны (1, 3, 5, 7, 9), то опять же делим
на 8 двузначные числа, образованные
десятками и единицами, но в этом
случае прибавляем (или отнимаем) к
двузначным числам цифру 4.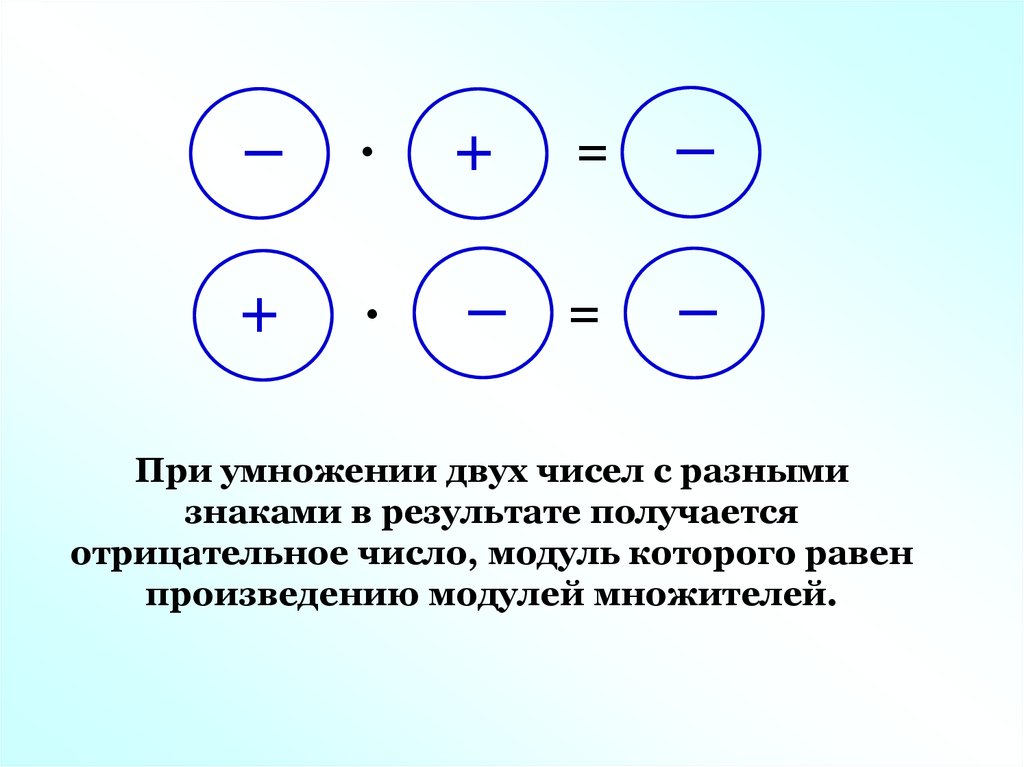
Для примера возьмем числа 165, 371, 587, 716, 923. «Превратим» их в двузначные числа, прибавляя (можно отнимая) 4:
69, 75, 91, 20, 27.
Делить эти двузначные числа на 8 опять же просто. Остатки от делений и будут остатками от деления на 8 исходных трехзначных чисел.
А как поступить, если трехзначное число 997?
Выше говорилось, что цифру 4 можно не только прибавлять, но и отнимать от двузначного числа. Значит, делить на 8 будем уже число 93: 97- 4 = 93.
Так происходит «избавление» от трехзначных чисел.
Обобщая все
вышесказанное, алгоритм
упрощенного признака делимости на 8
целых чисел можно записать так:
отделяем, отсчитывая справа, три
цифры исходного числа; если третья
справа цифра четная (0, 2, 4, 6, 8), то
делим на 8 только число,
образованное двумя крайними
правыми цифрами; остаток от этого
деления и будет остатком от деления
на 8 всего исходного числа; если
третья справа цифра в исходном
числе нечетная (1, 3, 5, 7, 9), делим на 8 число,
образованное двумя крайними
правыми цифрами, плюс (минус) 4;
остаток от деления этой суммы и
даст остаток от деления на 8 всего
исходного целого числа.
Как видно, этот признак делимости совсем прост, и для его освоения понадобятся минимальные усилия и знание элементарной арифметики.
Литература
Кордемский Б. А. Математическая смекалка. М., 1991.
Воробьев Н. Н. Признаки делимости. М., 1980.
Гарднер М. Математические досуги. М., 1995.
Умножение и деление целых чисел
Умножение и деление целых чиселУмножение и деление целых чисел
УМНОЖЕНИЕ
ПРАВИЛО 1: Произведение положительного целого числа на отрицательное число отрицательно.
ПРАВИЛО 2: Произведение двух положительных целых чисел положительно.
ПРАВИЛО 3: Произведение двух отрицательных целых чисел положительно.
Примеров:
Правило 1: 1. (+4) x (-2) = -8 2. (-2) x (+5) = -10
Правило 2: 1. (+6) x (+8) = +48 2. (+6) x (+2) = +12
Правило 3: 1. (-6) x (-8) = +48 2.
(-2) x (-4) = +8
(-2) x (-4) = +8ОТДЕЛ
ПРАВИЛО 1: Частное положительного целого числа и отрицательного целого числа отрицательно.
ПРАВИЛО 2: Частное двух положительных целых чисел положительно.
ПРАВИЛО 3: Частное двух отрицательных целых чисел положительно.
Примеры:
Правило 1: 1. (-8) / (+4) = -2 2. (-12) / (+6) = -2
Правило 2: 1. (+6) / (-3) = -2 2. (+24) / (-6) = -4
Правило 3. 1. (+9) / (+3) = +3 2. (+16) / (+4) = +4
Правило 4: 1. (-6) / (-2) = +3 2. (-42) / (-7) = +6
ОБЗОР ПРАВИЛ УМНОЖЕНИЯ И ДЕЛЕНИЯ
- Если знаки разные, то ответ отрицательный.
- Если знаки одинаковые, ответ положительный .
Проблемы:
- (+3) х (-1) = __________
- (+7) х (+6) = __________
- (-5) х (-5) = ___________
- (-8) х (-6) = ___________
- (-12) х (+5) = _________
- (+16) х (0) = __________
- (-30) х (-3) = __________
- (-18) х (+23) = ________
- (-40) х (-4) = __________
- (-11) х (+4) = _________
- (+3) х (-8) = __________
- (+15) х (0) = __________
- (-7) х (-4) = ___________
- (+9) х (+8) = __________
- (+9) / (+3) = __________
- (+10) /(-5) = __________
- (-12) / (-3) = __________
- (-25) / (+5) = __________
- (-45) / (+15) = _________
- (-18) / (-6) = __________
- (+52) / (13) = __________
- (-30) / (+10) = _________
- (+14) / (-2) = __________
- (+16) / (-4) = __________
- (-42) / (+7) = __________
- (4) / (2) = _____________
- 0 / (-7) = ______________
- 0 / (6) = ______________
Ключ ответа Умножение и деление целых чисел
- 42
- 25
- 48
- 60
- 0
- 90
- 414
- 160
- 44
- 24
- 0
- 28
- 72
- 3
- 2
- 4
- 5
- 3
- 3
- 4
- 3
- 7
- 4
- 6
- 2
- 0
- 0
Умножение и деление положительных и отрицательных чисел
Поиск Правила умножения и деления чисел очень похожи.
Ключ в том, чтобы определить, являются ли знаки данных двух чисел одинаковыми или разными, потому что это определит окончательный знак ответа.
Примеры того, как найти произведение или частное чисел со знаком
Пример 1 : Найдите произведение (3)(6) и частное 12 ÷ 6 .
- Найдите произведение (3)(6):
Поскольку числа 3 и 6 имеют одинаковые знаки (оба положительные), их произведение положительно.
(3)(6) = 18
- Найдите частное 12 ÷ 6:
Поскольку числа 12 и 6 имеют одинаковые знаки (оба положительные), их частное положительно.
12 ÷ 6 = 2
Пример 2 : Найдите произведение (–5)(–3) и частное от – 21 ÷ (–7) .
- Найдите произведение (–5)(–3):
Числа −5 и −3 имеют отрицательные знаки. Наличие одного и того же знака означает, что их произведение также должно быть положительным.
(–5)(–3) = 15
- Найдите частное от – 21 ÷ (–7) :
Числа −5 и −3 оба имеют отрицательные знаки. Частное двух чисел с одинаковым знаком положительно.
– 21 ÷ (–7) = 3
Пример 3 : Умножьте числа (9)(–3) и разделите числа 18 ÷ (–9) .
- Умножение (9)(–3) :
Число 9 имеет положительный знак, а число −3 имеет отрицательный знак. Умножение этих двух чисел с разными знаками должно дать отрицательный ответ.
(9)(–3) = –27
- Разделение 18 ÷ (–9) :
Число 9 положительное, а −3 отрицательное. Деление двух чисел с разными знаками должно дать отрицательный ответ.
18 ÷ (–9) = –2
Пример 4 : Упростите числовое выражение.
Мы можем упростить числитель, перемножив два числа.
Проделайте то же самое со знаменателем.
Числа в числителе имеют разные знаки, поэтому мы ожидаем, что их произведение будет отрицательным. Между тем в знаменателе есть два числа с одинаковым знаком (оба отрицательные), поэтому их произведение должно быть положительным.
Завершим это делением числителя на знаменатель. Не забывайте и о правиле деления. Числитель отрицательный, а знаменатель положительный, при разных знаках ответ должен быть отрицательным.
Пример 5 : Умножьте числа (–1)(–2)(–3)(–4) .
До сих пор мы умножали числа по два. На этот раз у нас возникла ситуация, когда нужно найти произведение трех или более чисел.
Мы можем решить это путем умножения двух чисел за раз, потому что мы знаем, как это сделать.
Но есть быстрый способ определить знак без необходимости умножать их по два за раз.
Обратите внимание, что у нас есть четное количество отрицательных знаков , то есть четыре отрицательных числа.
Если вы столкнулись с чем-то подобным, используйте правило:
Четное количество отрицательных знаков означает, что мы ожидаем, что ответ будет положительным.
(–1)(–2)(–3)(–4) = +24
0185 (–1) (–1) (–1) (–1) (–1) (–1) (–1) (–1) .
Эта задача не предназначена для того, чтобы обмануть вас. Вместо этого подумайте об этом как о еще одной возможности научиться справляться с такими вопросами. Ваш учитель может добавить что-то подобное в ваш тест, чтобы проверить, хорошо ли вы знаете тему.
Не обращая внимания на знаки, все числа равны единицам. Поэтому мы предсказываем, что ответ может быть либо +1 или -1 .
Подсчитав количество отрицательных знаков, мы имеем в общей сложности девять (9), что нечетно!
Помните правило,
Нечетное количество отрицательных знаков означает, что наш окончательный ответ должен быть отрицательным.